Optionspreisbewertung mit stochastischer Volatilität und

Optionspreisbewertung mit stochastischer
Volatilität und Sprungprozessen –
Eine Untersuchung am Deutschen Aktienindex
DIPLOMARBEIT
zur Erlangung des Grades eines Diplom-Ökonomen
der Fakultät Wirtschaftswissenschaften der
Leibniz Universität Hannover
vorgelegt von
Martin Schmelzle
Erstprüfer: Prof. Dr. Daniel Rösch
Hannover, den 13. März 2008
Inhaltsverzeichnis
1
2
Einleitung
1
1.1 Motivation
1
1.2 Gang der Arbeit
3
Optionen und Volatilität
4
2.1 Grundlagen von Optionen
4
2.2 Risikoneutrale Bewertung von Optionen
8
2.3 Die besondere Rolle der Volatilität
3
4
5
6
Analyse des Deutschen Aktienindex und DAX Optionen
14
17
3.1 Ausstattungsmerkmale des DAX, der DAX Option und des DAX Future
17
3.2 Statistische Analyse des DAX
19
3.3 Stochastische Volatilität und DAX Optionen
26
Modell Spezifikationen und ihre charakteristischen Funktionen
35
4.1 Merton Jump Diffusion
37
4.2 Heston Stochastic Volatility
39
4.3 Finite Moment Log Stable
40
4.4 Merton Jump Diffusion – Stochastic Volatility
43
4.5 Finite Moment Log Stable – Stochastic Volatility
44
Simulationsstudie für DAX Optionen
47
5.1 Datenbasis und Aufbereitung
47
5.2 Methodik und Kalibrierung
48
5.3 In-Sample Performance
53
5.4 Out-of-the-Sample Performance
61
5.5 Kritische Würdigung
63
Zusammenfassung und Ausblick
65
Inhaltsverzeichnis
ii
Anhang
66
A
66
B
C
Grundlegende Begriffe und Konzepte der Wahrscheinlichkeitstheorie
A.1 Stochastische Prozesse, Filtrationen und Martingale
66
A.2 Charakteristische Funktionen
68
A.3 α-stabile Verteilungen
70
A.4 Lévy Prozesse
71
Bewertungsperformance der Modelle
73
B.1 Weitere Ergebnisse der Simulationsstudie
74
B.2 Implizite Volatilitätsoberfläche vom 7. Dezember 2007
77
B.3 Merton Jump Diffusion
79
B.4 Heston Stochastic Volatility
80
B.5 Finite Moment Log Stable
81
B.6 Merton Jump Diffusion – Stochastic Volatility
82
B.7 Finite Moment Log Stable – Stochastic Volatility
83
Anmerkungen zur Implementierung der Modelle
84
C.1 Bewertung von Optionen mittels komplexer Fourier Transformation
84
C.2 Excel VBA Programm Code
90
C.3 Verwendete Software und Daten
98
Symbolverzeichnis
iii
Abkürzungsverzeichnis
v
Abbildungsverzeichnis
ix
Tabellenverzeichnis
xi
Literaturverzeichnis
xii
1 Einleitung
1.1 Motivation
Die Volatilität von Wertpapieren ist ein wesentlicher, wenn nicht der wichtigste
Faktor des Risikomanagements, der Portfolio Theorie und der Bewertung von
Derivaten. Die Variabilität von Preisveränderungen spiegelt die Unsicherheit auf den
Finanzmärkten wider und ergibt sich allein durch das Handeln der Marktteilnehmer.
Der
Händler
risikobehafteter
Finanztitel
wird entsprechend
seinen
Markterwartungen die Intention verfolgen, eine optimale Relation zwischen dem
möglichen Ertrag und dem potenziellen Risiko seiner Strategie zu erreichen. Von
zentraler Bedeutung ist hierbei die Quantifizierung des Risikos, denn auf diese wird
er seine Entscheidungen aufbauen. Um Kennzahlen für das Risiko ermitteln zu
können, sind grundlegende Annahmen darüber notwendig, wie sich die Marktpreise
im Zeitablauf entwickeln werden.
Die etablierten Kapitalmarktmodelle basieren weitgehend auf der Hypothese normalverteilter Preisveränderungen. Es zeigte sich jedoch schon früh, dass diese Annahme nur eine unzureichende Annäherung an das tatsächliche Marktgeschehen
erlaubt. Dies wird besonders im Kontext der Optionspreistheorie deutlich, bei der das
Zusammenspiel aus den Theorien der Preisprozesse und Preisbildung von wesentlicher Bedeutung ist. Das Standardmodell zur Bewertung von Optionen, das Modell
von Black/Scholes [1973], basiert auf normalverteilten Renditen und einer Volatilität, die im Zeitverlauf konstant ist. Wie sich zeigen wird, ergeben sich unter Verwendung dieses Modells systematische Abweichungen zwischen den theoretischen Werten und den Marktpreisen, die für Optionen beobachtet werden.
Anschaulich wird diese Diskrepanz, wenn quotierte Marktpreise von Optionen
mit ihren impliziten Volatilitäten ausgedrückt werden. Wie später noch dargelegt
wird, ist die implizite Volatilität diejenige Volatilität, die den theoretischen Preis und
den Marktpreis mit Basispreis und Fälligkeit zum Ausgleich bringt. Dabei wird
ein charakteristisches Muster sichtbar, welches als Smile Effekt in die Literatur einging. Aus diesen Beobachtungen lassen sich Rückschlüsse auf die von den Marktteilnehmern erwartete zukünftige Renditeverteilung ziehen, die mit der Normalverteilungshypothese von Black und Scholes nicht kompatibel ist.
Für den Wertpapierhändler bieten sich nun zwei Möglichkeiten: a) Er kann die
bekannten Unzulänglichkeiten berücksichtigen und weiter mit dem Black–Scholes
Modellrahmen arbeiten oder b) er verabschiedet sich von der idealisierten Black–
Scholes Welt und verwendet alternative Bewertungsmodelle, die in der Lage sind, die
empirischen Fakten zu reproduzieren.
Die vorliegende Arbeit liefert in zweifacher Hinsicht einen Beitrag zu Möglichkeit
b). Zum einen werden alternative Modellkonzeptionen vorgestellt und diskutiert, die
Einleitung
|2
den Anspruch haben, die Realität besser abbilden zu können. Bei Kursverläufen lassen sich immer wieder Kurssprünge beobachten, die durch Einführung von Sprungkomponenten beim Renditeprozess berücksichtigt werden können. Eine weitere
Möglichkeit ist es, die sich ständig im Zeitablauf variierende Volatilität als
eigenständigen stochastischen Prozess zu modellieren. Im Kern sind dies die beiden
elementaren Komponenten bei der Konzeption neuer Modelle. Zum anderen werden
die präsentierten Spezifikationen über 30 Handelstage hinweg einer empirischen
Untersuchung mit liquiden Optionen auf den Deutschen Aktienindex unterzogen. Es
zeigt sich, dass alle untersuchten Modelle wesentlich konsistenter mit den realen
Marktpreisen sind, als das Modell von Black–Scholes.
Mit einem dieser Konzepte hat der Händler in jedem Fall einen realitätsnäheren
Bewertungsrahmen gegenüber dem Standardmodell, mit dem er die zukünftigen
Zahlungsströme seines Portfolios adäquat modellieren kann. Fortschrittliche Berechnungsmethoden erlauben es zudem, die teilweise recht komplexen Renditeprozesse
zeitnah zu evaluieren.
Märkte für Futures, Optionen und andere Derivate sind heutzutage integraler Bestandteil unserer Finanzmärkte. Die weite Verbreitung und ständige Weiterentwicklung von Finanzinstrumenten kann einen erheblichen Beitrag dazu leisten, die
Effizienz einer Volkswirtschaft zu erhöhen. Angesichts des zunehmenden Wachstums
der Derivateindustrie und dem Bedarf an adäquatem Risikomanagement ist es von
höchster Bedeutung, dass verwendete Modelle die am Markt beobachteten Phänomene möglichst gut widerspiegeln. Hieraus wird auch die Relevanz der zu Grunde
liegenden Thematik ersichtlich.
Eine realitätsnahe Modellierung von Preisprozessen ist aber nicht nur für die
Marktteilnehmer von Bedeutung. Fundierte Kenntnisse der Preisdynamik und ihrer
Modellierungsmöglichkeiten sind auch für aufsichtsrechtliche Institutionen und
Zentralbanken wichtig. Es können aus dem Markt Informationen extrahiert werden,
mit denen aktuelle Entwicklungen einer Volkswirtschaft besser verstanden werden
können und die darauf basierenden Schlussfolgerungen können einen Beitrag dazu
leisten, Entscheidungen auf eine breitere Basis zu stellen.
Aufgrund der zunehmenden Bedeutung der Eurex in den letzten Jahren, finden
sich vermehrt Arbeiten mit diesem Schwerpunkt. Im Gegensatz dazu beschäftigen
sich die frühen Arbeiten zur Optionspreisbewertung hauptsächlich mit dem USamerikanischen Markt, doch durch den Erfolg der europäischen Terminbörse Eurex
dürfte sich das Bild nachhaltig verändern. Im Jahr 2007 wurden an der Eurex im
Schnitt 7,5 Mio. Kontrakte pro Tag gehandelt. Hierbei legten die Aktienindexderivate
mit einem Umsatzwachstum von 55 % allein im letzten Jahr besonders deutlich zu
(siehe Eurex [2008a]). Bei diesen gehören die Optionen auf den DAX neben den Optionen auf den DJ EuroSTOXX 50 zu den umsatzstärksten Optionen. Aufgrund der
angedeuteten Bedeutung dieser Optionen für die Finanzmärkte ergibt sich die
Einleitung
|3
Motivation, die Implikationen der betrachteten Modelle an DAX Optionen zu
untersuchen.
1.2 Gang der Arbeit
Die Motivation dieser Arbeit resultiert im Konflikt zwischen der empirischen Anpassungsgüte des Black–Scholes Modells samt ihren Modellannahmen. Um sich diesem
Themenkomplex zu nähern, werden in Kapitel 2 die zu Grunde liegenden Konzepte
der Bewertung von Optionen erläutert. Ferner werden die in diesem Kontext
notwendigen Begrifflichkeiten definiert. Anschließend wird die besondere Bedeutung
der Volatilität und ihrem Einfluss auf die Bewertung von Optionen eingegangen.
Die vielfach in der Literatur beschriebenen Abweichungen realer Daten von den
postulierten stark vereinfachenden Annahmen bei der Modellierung von Preisprozessen werden in Kapitel 3 einer empirischen Untersuchung unterzogen. Es wird zum
einen die Renditezeitreihe des Deutschen Aktienindexes analysiert und zum anderen
die sich aus quotierten Optionspreisen ergebenden impliziten Volatilitäten näher betrachtet.
Alternative Bewertungsmodelle zur Black–Scholes Spezifikation werden in
Kapitel 4 vorgestellt. Die Intentionen dieser Konzepte sind teilweise unterschiedlich
gelagert. Gemeinsam ist ihnen allen der Anspruch die empirischen Fakten
wiederzugeben, um eine realitätsnähere Modellierung von Zahlungsströmen im Kontext der Optionspreisbewertung zu ermöglichen.
Kapitel 5 bildet den zentralen Teil dieser Arbeit. Es erfolgt eine empirische Untersuchung der Modelle auf Basis börsengehandelter Optionen auf den Deutschen Aktienindex. Gegenstand der Untersuchung sind die Settlementpreise von
30 Handelstagen. Die Ermittlung der Modellparameter, die zur Bestimmung von
theoretischen Optionsprämien notwendig sind, basiert auf einem impliziten
Schätzverfahren. Die derart ermittelten Optionspreise werden in einer In-Sample und
Out-of-the-Sample Analyse den quotierten Marktpreisen gegenübergestellt. Mit Hilfe
geeigneter Fehlermaße lässt sich daraufhin die Güte der Bewertungsperformance feststellen. Anschließend werden die Ergebnisse verglichen und eingehend diskutiert.
Die Schlussbetrachtung Kapitel 6 fasst die wesentlichen Erkenntnisse der Arbeit
zusammen. Ferner werden kurz offen gebliebene Fragen skizziert und Richtungen
aufgezeigt, die auf den hier dargelegten Ausführungen aufbauen können.
Der Anhang A enthält eine Darstellung mathematischer Resultate, die für das
Verständnis der Modellkonzeptionen von Bedeutung sind. Der darauf folgende
Anhang B bietet den Rahmen für weitere empirische Ergebnisse. Im Anschluss hieran
werden in Anhang C einige Aspekte bei der praktischen Umsetzung der Modelle in
der Simulationsstudie adressiert. Zum Abschluss erfolgt ein Abdruck des MS Excel
VBA Codes. Hiermit ist es möglich, die in der Arbeit dargestellten Resultate zu reproduzieren.
2 Optionen und Volatilität
In diesem Kapitel erfolgt ein kurzer Überblick über die wesentlichen Eigenschaften
von Optionen und deren Begrifflichkeiten. Weiter wird das klassische
Bewertungsmodell von Black/Scholes [1973] in seinen Grundzügen skizziert. Darauf aufbauend wird gezeigt, dass die Preise von bedingten Ansprüchen (Contingent
Claims) unter bestimmten Voraussetzungen auch als die erwarteten Barwerte
zukünftiger Zahlungen ausgedrückt werden können. Anschließend werden die wichtigsten Determinanten der Optionsbewertung explizit erörtert. Die grundlegenden
Konzepte und Ideen werden im Laufe der Arbeit am Beispiel einer Aktie demonstriert, wobei sich diese Ausführungen prinzipiell auch auf andere Vermögenswerte
übertragen lassen.
2.1 Grundlagen von Optionen
Schon sehr lange werden Optionen für spekulative Zwecke oder als Absicherung gegen unerwünschte zukünftige Entwicklungen verwendet. Bereits die Römer, Griechen
oder auch Phönizier handelten mit Optionen, um ihre Schiffsladungen abzusichern.
Der Grieche Thales erwarb bereits 580 v. Chr. vor einer einträglichen Olivenernte
durch Zahlung einer Prämie eine Option auf das Vorrecht an der Nutzung von
Olivenpressen und kam so zu beachtlichem Reichtum1. Auch im Alten Testament
findet sich ein Eintrag im Buch Genesis Kapitel 29, in dem beschrieben wird, wie
Jakob sich durch sieben Jahre Arbeit das Recht an Labans Tochter Rachel erwirbt2.
Auf Finanzmärkten stellen Optionen Termingeschäfte zwischen zwei Parteien
dar, bei der eine Partei sich das Recht, nicht aber die Pflicht erwirbt, ein bestimmtes
Gut zu kaufen oder zu verkaufen3. Es handelt sich hierbei also um ein bedingtes Geschäft. Im Gegensatz dazu gibt es Termingeschäfte wie bspw. Forwards oder Futures,
bei denen beide Seiten unbedingt zu leisten haben. Das Recht, etwas ohne
Verpflichtung zu kaufen hat einen Wert, für den der Käufer einer Option einen Preis
zu entrichten hat. Der Verkäufer (auch Stillhalter oder Writer) hat im Gegensatz dazu
die Pflicht, bei Ausübung der Option die vorher vereinbarte Leistung in jedem Falle
zu erbringen. Der Preis einer Option leitet sich vom Wert des zu Grunde liegenden
Objektes (Underlying) ab, daher auch die Bezeichnung derivativer Vermögenswerte
oder einfach Derivate (lat. derivare – ableiten). Kaufoptionen (Calls) geben dem Halter einer Option das Recht etwas zu kaufen, während Verkaufsoptionen (Puts) das
1
Einen Überblick zur historischen Entwicklung von Optionen gibt Chance [1995].
Er bekommt aber von Laban die ältere Tochter Lea und erkauft sich durch weitere sieben Jahre Arbeit
die Option auf die jüngere Tochter Rachel…
3
Die Ausführungen in diesem Kapitel orientieren sich im Wesentlichen an Kleinert [2003],
Deutsch [2001], Voit [2005] sowie Taleb [1997].
2
Optionen und Volatilität
|5
Recht verbriefen etwas zu verkaufen. Der hierfür zu entrichtende Preis wird Prämie
genannt. Für gewöhnlich werden Optionen auf Aktien, Anleihen, Rohstoffe, Indizes
und Ähnliches gehandelt. Der Kreativität sind hierbei aber keinesfalls Grenzen gesetzt, so gibt es vielfältigste Geschäfte, die einen Optionscharakter aufweisen und sich
entsprechend mit Hilfe der Optionspreistheorie bewerten lassen. Es gibt Optionen auf
Fußballspieler, auf die Entwicklung von einzelnen Geschäftsbereichen (Realoptionen)
oder die vorzeitige Rückzahlung von Hypothekendarlehen (Vorfälligkeitsentschädigung), um nur einige Beispiele zu nennen.
In einem Optionsvertrag wird ein festes Datum, der Fälligkeitstermin und der bei
Ausübung der Option zu entrichtende Preis, der Basispreis4, eindeutig festgelegt. Zu
unterscheiden sind Europäische Optionen, die nur bei Fälligkeit und Amerikanische
Optionen, die während der gesamten Laufzeit ausgeübt werden können. Weiter gibt
es die Exotischen Optionen, hierunter werden Optionen subsumiert, die zum Teil
sehr komplexe Konstruktionen darstellen. Wesentliche Merkmale sind entweder die
Abhängigkeit vom Kursverlauf (Pfadabhängigkeit) dieser Optionen oder es handelt
sich um Optionen, die auf mehrere Underlyings geschrieben werden, oder beides.
Hierdurch lassen sich vielfältigste Auszahlungsprofile generieren, die den
unterschiedlichen Kundenwünschen oder Marktsituationen gerecht werden5.
150
150
Call long
Put long
100
Call short
50
0
-50
0
50
100
K
150
-100
200
ST (€)
Profit/Verlust (€)
Profit/Verlust (€)
100
Put short
50
0
-50
0
50
100
K
150
200
ST (€)
-100
-150
-150
Aktienkurs S zum Zeitpunkt T
Aktienkurs S zum Zeitpunkt T
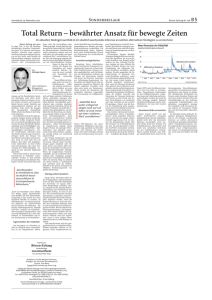
Abbildung 1: Auszahlungsdiagramme (Pay Offs) für europäische Optionen am Laufzeitende mit
Ausübungspreis . Links: Kaufoptionen (Calls). Rechts: Verkaufsoptionen (Puts). Blau dargestellt sind
die jeweiligen Pay Offs für den Inhaber einer Option (long), rot entspricht den Pay Offs für den
Stillhalter (short). Die gestrichelten Linien deuten die Auszahlungen ohne Optionsprämie an. Der
Break-even liegt in diesem Beispiel bei den Calls demnach bei € 110 und bei Puts bei € 95.
Im Folgenden werden einfache Optionen (Plain Vanilla Options) europäischen Typs
näher vorgestellt. Optionen lassen sich durch den Wert am Ende der Laufzeit, also der
Auszahlung an den Investor bei Fälligkeit charakterisieren. Bezeichne den Ausübungspreis und den Preis der Aktie zur Fälligkeit ergibt sich folgendes
4
Auch Ausübungpreis genannt, im Angloamerikanischen Strike Price oder Exercise Price. Die Begriffe
werden im Laufe der Arbeit synonym verwendet.
5
Es handelt sich hierbei um einen stark wachsenden Markt. Eine umfassende Systematisierung der
vielfältigen Ausgestaltungen findet sich bei Zhang [2001].
Optionen und Volatilität
|6
asymmetrisches Auszahlungsprofil (Pay Off) für den Inhaber der Option (long position)
max , 0.
(2.1)
min , 0.
(2.2)
max , 0.
(2.3)
Der Käufer wird sein Optionsrecht nur ausüben, wenn der vorher festgelegte Basispreis geringer als der aktuelle Wert des Underlyings ist ( ). Sobald der Aktienkurs unter dem Ausübungspreis liegen sollte, wird er sie verfallen lassen. Für die
komplementäre Position, also den Stillhalter der Option, stellt sich die Situation diametral dar (short position)
Um den Wert der Option vor Fälligkeit zu bestimmen wird der Pay Off zum Zeitpunkt mit einem stetigen Zinssatz für die Dauer von auf den heutigen Zeitpunkt abgezinst
Notiert eine Aktie genau am Basispreis , wird diese am Geld oder at the money
(ATM) genannt. Entsprechend ist eine Option im Geld oder in the money (ITM),
wenn und aus dem Geld oder out of the money (OTM), falls .
Ein Maß dafür, wie weit eine Option im oder aus dem Geld notiert, ist die
Moneyness. Diese misst für eine Option das Verhältnis vom Spotpreis zum Strike .
In dieser Arbeit wird eine stetige Moneyness mit ln ⁄ verwendet. Eine Option mit 0,1 lässt sich so interpretieren, dass die Option zu 10 % im Geld liegt.
Einflussfaktoren
Bestimmende Faktoren für die Bewertung von Optionen sind der aktuelle Preis der
Aktie , der Ausübungspreis , die Restlaufzeit , die Volatilität der Aktie , der
risikolose Zins und eventuell während der Laufzeit anfallende Dividendenzahlungen.
Am stärksten wird der Wert der Option durch das Underlying beeinflusst. Bei
fixem Strike wird ein Call wertvoller, wenn der Aktienkurs steigt. Genau
entgegengesetzt verhielte es sich, wenn bei festem Aktienkurs der Ausübungspreis
erhöht würde. Die Volatilität ist ein Maß für die Unsicherheit bezüglich der zukünftigen Kursentwicklungen. Wenn die Volatilität hoch ist, steigt die Wahrscheinlichkeit,
dass eine Aktie stark an Wert gewinnt oder verliert. Für den Inhaber eines Calls ist
ein stark steigender Aktienkurs wünschenswert, da somit der Wert seines Investments
zunimmt. Andererseits kann er bei fallenden Kursen maximal seine gezahlte Prämie
Optionen und Volatilität
|7
verlieren. Genau umgekehrt verhält es sich für den Put. Somit ist der Wert der Option
positiv von der Volatilität abhängig.
Weniger intuitiv ist der Einfluss des Zinssatzes auf den Optionswert. Wie im Folgenden noch gezeigt wird, ist es möglich, ein risikoloses Portfolio, bestehend aus Aktien, einem gekauften Put und einem verkauften Call, zu konstruieren. Der Ertrag aus
diesem abgesicherten Portfolio ist nicht mehr stochastisch und entspricht genau dem
Marktzins. Ein steigender Zinssatz geht demzufolge mit einem höheren Wert für den
Call und einem geringeren Wert für den Put einher.
Bei einer Dividendenzahlung verringert sich der Aktienkurs für gewöhnlich um
etwa diesen Betrag, mit der Folge, dass ein Call an Wert verliert und ein Put an Wert
gewinnt. Wenn der Zeitpunkt der Fälligkeit in ferner Zukunft liegt, besteht eine höhere Wahrscheinlichkeit dafür, dass sich die Aktie in die gewünschte Richtung bewegen kann, und somit sinkt mit abnehmender Restlaufzeit auch der Wert der Option.
Put-Call-Parität
Für europäische Optionen gibt es eine feste Beziehung zwischen den Prämien für
Kaufoptionen
und Verkaufsoptionen !. Wenn beide Optionen denselben
Fälligkeitstermin und Basispreis haben, lässt sich der Zusammenhang durch folgende
funktionale Beziehung charakterisieren
! .
(2.4)
Diese Identität ist als Put-Call-Parität bekannt. Die Position ! entspricht dem
Kauf eines Calls und dem Verkauf eines Puts. Die Auszahlung ergibt sich zu
max , 0 max0, , was genau entspricht. Aus der rechten
Seite der Gleichung ist ersichtlich, dass die zu Grunde liegende Aktie erworben
wird und hiervon der Barwert des Basispreises abgezogen wird. lässt sich
auch als Kreditaufnahme interpretieren. Zum Zeitpunkt ist dieses Portfolio genau
wert. Die Auszahlungen beider Seiten sind demnach identisch. Daraus folgt,
dass Finanztitel, welche den gleichen Pay Off zur Folge haben, den gleichen Preis haben müssen. Ansonsten würde sich eine Arbitragegelegenheit bieten und es könnte
ein risikoloser Gewinn erzielt werden, indem das billigere Wertpapier gekauft und
das teurere Wertpapier verkauft wird. Eine Option ist somit im Prinzip mit einem
kreditfinanziertem Aktienkauf vergleichbar.
Bachelier, Vater der modernen Finanzmathematik und Bronzin
Das Handeln und Spekulieren auf Märkten und Wertpapierbörsen ist kein Phänomen
der Neuzeit. Vielmehr handelt es sich hierbei um ein altes gesellschaftliches Phänomen. Moderne Verfahren zur Bewertung von Optionen haben ihren zeitlichen Ursprung zu Beginn des 20. Jahrhunderts. Im Jahre 1900 veröffentlicht Louis Bachelier
Optionen und Volatilität
|8
seine Dissertation Théorie de la Spéculation (Bachelier [1900]), in der erstmals
analytische Bewertungsverfahren angewendet werden. Revolutionär ist hierbei die
Entwicklung einer Theorie für Preisfluktuationen, die Bachelier mit Hilfe einer eindimensionalen Brownschen Bewegung6 modelliert. Bereits fünf Jahre vor Einsteins
physikalischer Deutung der Brownschen Bewegung und 23 Jahre vor Wieners mathematischen Formalisierung dieses Prozesses beschreibt Bachelier Kursbewegungen mit
diesem stochastischen Prozess und legt somit den Grundstein für die moderne
Finanzmathematik, auch wenn seine Erkenntnisse seinerzeit kaum Beachtung fanden.
Einige Jahre später, 1908, veröffentlicht Vincenz Bronzin seine heute wenig bekannte Theorie der Prämiengeschäfte (Bronzin [1908])7. Wenn auch pragmatischer
als die eleganten Ausführungen von Bachelier, enthält seine Arbeit alle später noch zu
erläuternden Elemente der modernen Optionsbewertung. Behandelt werden die
arbitragefreie und risikoneutrale Bewertung, Bedingungen für perfektes Hedging, die
Put-Call-Parität und der Einfluss verschiedener Verteilungsannahmen auf Optionspreise. Aufgezeigt wird die Relation binomial verteilter Aktienkurse mit der Normalverteilung. Ferner wird eine Formel entwickelt, die mit der später entwickelten Formel von Black, Scholes und Merton in vielen Punkten identisch ist. Auch ist ihm die
funktionale Beziehung von der Ableitung des Optionswertes nach dem Ausübungspreis mit der zu Grunde liegenden Zustandspreisdichte bekannt und er verwendet
diese zur analytischen Bestimmung von Optionspreisen.
2.2 Risikoneutrale Bewertung von Optionen
Startpunkt für die Ermittlung von Optionsprämien ist die Festlegung eines
Kursprozesses für das zu Grunde liegende Wertpapier. Die Grundlagen der heute verwendeten Modelle zur Modellierung von Aktienkursen gehen auf die oben erwähnte
Arbeit von Bachelier zurück8. Seine Beobachtung, dass „[…]; past, present and even
discounted future events are reflected in market price, but often show no apparent relation to price changes.” (Bachelier [1900, S. 18]), führte ihn zu der Annahme, dass
die Preiszuwächse stationär und unkorreliert seien. Formalisiert hat er seine
6
Die als Brownsche Bewegung bezeichnete thermisch getriebene Eigenbewegung von Teilchen wird
dem schottischen Botaniker Robert Brown zugeschrieben, der diese im Jahr 1827 wiederentdeckte.
Vgl. hierzu bspw. Wilkens [2000, S. 76] oder Voit [2005, S. 41]. Der römische Dichter und Philosoph Lucretius liefert bereits ca. 60 v. Chr. in Über die Natur der Dinge (lat. De Rerum Natura) eine
Beschreibung über den Einfluss von Atomen auf die Bewegung von kleinen Partikeln, und antizipierte somit die Brownsche Bewegung lange vor der quantitativen Analyse durch Einstein.
7
Zimmermann/Hafner [2005] würdigen die Arbeit von Bronzin [1908] und ordnen seine Erkenntnisse in den zeitlichen sowie inhaltlichen Kontext. Die Ausführungen im Text stützen sich auf diese
Arbeit und die dort enthaltenen Angaben.
8
Die folgenden Darstellungen orientierten sich an Schoutens [2003], Javaheri [2005] sowie
Voit [2005]. Eine Behandlung über die risikoneutrale Bewertung in Buchlänge findet sich bei
Bingham/Kiesel [2004].
Optionen und Volatilität
|9
Überlegungen mit einem eindimensionalen Diffusionsprozess, der später als
Brownsche Bewegung bekannt wurde.
Die Brownsche Bewegung lässt sich mathematisch durch einen Wiener Prozess
spezifizieren. Zuwächse des Wiener Prozesses sind unabhängig und normalverteilt.
Die Brownsche Bewegung stellt somit quasi den dynamischen Gegenpart zur bekannten Normalverteilung dar9. Beide entspringen dem zentralen Grenzwertsatz. Von der
Intuition besagt dieser, dass die Summe von vielen unabhängigen Zufallsvariablen
näherungsweise normalverteilt ist. In einer dynamischen Umgebung, d. h. bei
stochastischen Prozessen, ergibt sich die Brownsche Bewegung in gleicher Weise. Die
folgenden Überlegungen beziehen sich auf den zeitstetigen Fall; bei einer Betrachtung
von Renditen als Folge von Zufallsvariablen zu diskreten Zeitpunkten spricht man
von einem Random Walk.
Die von Bachelier eingeführte Beziehung zwischen Aktienmarkt und dem Konzept der Brownschen Bewegung als Annäherung für Preisfluktuationen wird nun
näher beleuchtet. Bachelier selbst verwendet eine Brownsche Bewegung, bei der die
Preiszuwächse additiv verknüpft sind. Dabei können sich negative Werte ergeben,
weshalb sie für eine Anwendung auf Aktienmärkten nicht gut geeignet ist.
Boness [1964] und Samuelson [1965] greifen diese Idee auf und schlagen vor,
diesen Prozess zur Modellierung von Kursveränderungen (multiplikative
Verknüpfung) zu verwenden. Aus der arithmetischen wird eine geometrische
Brownsche Bewegung womit negative Preise ausgeschlossen werden können.
Bei Gültigkeit der geometrischen Brownschen Bewegung als Beschreibung der
Aktienkursdynamik ergibt sich folgende stochastische Differentialgleichung
d # d $ d% ,
(2.5)
welche sich unter Verwendung von Itô´s Lemma10 lösen lässt
exp &# '
$ d% ),
2
(2.6)
wobei d% einen Wiener Prozess (geometrisch Brownsche Bewegung) bezeichnet, #
ist die erwartete mittlere Kursrendite (Drift) der Aktie je Zeiteinheit d und die
Standardabweichung der Preisveränderungen. Die Standardabweichung als Maß für
die Unsicherheit der zukünftigen Preisentwicklung wird auch vielfach als Volatilität
9
Schoutens [2003, S. 24] spricht in diesem Zusammenhang vom großen Bruder der Normalverteilung. Die Normalverteilung selbst geht auf Carl Friedrich Gauß zurück. Gerüchten folgend leitet er
die normale (Gaußsche) Verteilung von Wahrscheinlichkeiten durch die Schätzung von Ausfallrisiken bei Krediten, die er seinen Nachbarn gewährte, ab. Siehe Voit [2005, S. 6] sowie Anhang A.
10
Die Itô Formel kann als Pendant zur klassischen Kettenregel gesehen werden. Aus diesem Grund
bietet sie sich zur Lösung stochastischer Differentialgleichungen an. Vgl. bspw. Singer [1999, S. 33].
Optionen und Volatilität
| 10
bezeichnet. Im Laufe der Arbeit wird der Begriff der Volatilität aber weiter gefasst
und folgt der Definition von Taleb [1997, S. 88]: “Volatility is best defined as the
amount of variability in the returns of a particular asset.“
Die Zuwächse der geometrischen Brownschen Bewegung wachsen mit der Drift
#, womit sich der Erwartungswert des Kurses zum Zeitpunkt ausgehend von 0
zu * + ergibt. Die hierbei möglichen Kursentwicklungen sind jedoch nicht
beliebig, vielmehr bewegen sie sich innerhalb einer Gesamtmenge von möglichen
Entwicklungen, dem Wahrscheinlichkeitsraum. Diesen Entwicklungspfaden lassen
sich Wahrscheinlichkeiten zuordnen, welche wiederum durch ein Wahrscheinlichkeitsmaß bestimmt werden. Die Kursdynamik wird hier unter einem physikalischen
(oder statistischen) Wahrscheinlichkeitsmaß , definiert, welches die dem Markt zu
Grunde liegende Unsicherheit repräsentiert. Eine formale Darstellung zu diesem
Sachverhalt findet sich in Anhang A.1 und wird für Kapitel 4 noch von wesentlicher
Bedeutung sein.
Dieses Modell kann alternativ auch mit den logarithmierten Aktienkursen ln dargestellt werden. Die obige Darstellung des Renditeprozesses ist zu folgender
äquivalent
1
d ln -# ' . d $ d% .
2
(2.7)
Der beschriebene Prozess lässt sich als Approximation für echte aufeinanderfolgende
Kursbewegungen oder aber als echte, nicht zu beobachtende, Kursdynamik
interpretieren. Die geometrische Brownsche Bewegung und die damit verbundene
Log-Normalverteilung bilden die Basis für das Standardmodell bei der Bewertung
von Optionen.
Das Marktmodell von Black–Scholes und Merton
Investitionen in Optionen sind in aller Regel wesentlich riskanter als Investitionen in
Aktien oder Anleihen. Gründe hierfür sind die begrenzte Laufzeit, die hohe Volatilität (deutlich höher als die des Underlyings) und die Möglichkeit eines Totalverlustes
für den Käufer (long) sowie ein theoretisch unbegrenzter Verlust für den Stillhalter
(short).
Der Verkäufer einer Option steht somit vor folgenden Fragen: a) Welche Prämie
verlange ich für die eingegangene Verpflichtung und b) wie lege ich die erhaltene
Prämie am besten an, um bei Fälligkeit meiner Verpflichtung nachzukommen, falls
der Käufer seine Option ausübt?
Die nobelpreisgewürdigte und überraschende Antwort wird 1973 von Fisher
Black, Myron Scholes und Robert Merton geliefert. Der Stillhalter einer Option benötigt keine Risikoprämie! Das bedeutet nicht, dass diese verschwindet, sondern schon
Optionen und Volatilität
| 11
im Aktienkurs enthalten ist. In der Presseerklärung zum 1997 verliehenen Nobelpreis
wird folgendes Beispiel gegeben11:
Betrachtet wird eine europäische Kaufoption, welche das Recht verbrieft, in drei
Monaten eine Aktie zum Basispreis von $ 100 kaufen zu können. Offenkundig hängt
der Wert der Option vom aktuellen Aktienkurs ab: Je höher der Kurs heute, umso
höher die Wahrscheinlichkeit, dass die Aktie in drei Monaten über $ 100 notiert. In
diesem Falle wird die Option ausgeübt. Bei einer Formel zur Bestimmung von
Optionspreisen sollte demnach der Zusammenhang zwischen Prämie und Aktienkurs
explizit erwähnt werden. Das Ausmaß der Änderung des Optionswerts bei einer
Änderung des Aktienkurses, wird Delta genannt (siehe hierzu auch Abschnitt 2.3).
Angenommen, der Wert der Option steigt um $ 1, wenn die Aktie um $ 2 steigt
und fällt um $ 1 wenn die Aktie um $ 2 fällt. Weiter sei angenommen, dass ein Investor ein Portfolio mit der zu Grunde liegenden Aktie hält und dieses gegen
Kursschwankungen absichern möchte. Dann ist er in der Lage ein risikoloses Portfolio (Hedge-Portfolio) zu konstruieren, indem er doppelt so viele Optionen verkauft,
wie er Aktien besitzt. Für jede kleinste Bewegung, die die Aktie nach oben macht,
entspricht der Gewinn der Aktie dem Verlust der Optionen und vice versa. Da das
Portfolio frei von Risiken ist, muss der Ertrag einer risikolosen Verzinsung entsprechen. Sollte diese Bedingung nicht erfüllt sein, würden Arbitrageure durch entsprechende Geschäfte solange einen sicheren Gewinn (Free Lunch) erwirtschaften können, bis die Möglichkeit von Arbitrage eliminiert ist. Entsprechend der Änderung des
Aktienkurses und bei Näherrücken der Fälligkeit einer Option, ändert sich auch das
Delta der Option. Um weiterhin ein risikoloses Portfolio halten zu können, muss dieses ständig angepasst werden. Es wird hierbei angenommen, dass kontinuierlich und
ohne Transaktionskosten gehandelt werden kann.
Aus der Bedingung, dass das risikolose Portfolio bestehend aus (riskanten)
Optionen und der (riskanten) Aktie zu jeder Zeit einer risikolosen Verzinsung entspricht, ergibt sich eine parabolische partielle Differentialgleichung. Der stochastische
Prozess der Aktienkursdynamik wird durch eine Linearkombination von Option und
Basiswert eliminiert. Die Lösung dieser partiellen Differentialgleichung unter Berücksichtigung der Endbedingung , max , 0, führt zu der berühmten
Formel von Black–Scholes und Merton12.
Der theoretische Wert einer Kaufoption auf eine Aktie zum Zeitpunkt und Strike lautet
11
Die Presseerklärung findet sich auf der Homepage der Royal Swedish Academy of Sciences.
Ausgezeichnet wurden Myron Scholes und Robert Merton. Für Fisher Black kam der Preis zu spät,
er verstarb bereits zwei Jahre vorher. Siehe http://nobelprize.org/nobel_prizes/economics/
laureates/1997/press.html (verifiziert am 29.02.2008).
12
Viele mathematische Details und eine stringente Herleitung finden sich bei Karatzas/Shreve
[1998]. Wie Black [1989] später in einem Artikel über die Entdeckung ihrer Formel anmerkt, war
diese Gleichung in der Physik schon lange als Wärmeleitungsgleichung bekannt.
Optionen und Volatilität
| 12
, Φ01 Φ0' ,
(2.8)
wobei Φ. den Flächeninhalt unter der kumulativen Standardnormalverteilung darstellt und 01 , 0' gegeben sind durch
1
ln 2 3 $ 2 $ ' 3 2
01 und 0' 01 √.
√
(2.9)
Analog ergibt sich die Black–Scholes Formel für Puts, wobei diesmal !, max , 0 als Endbedingung beachtet werden muss. Puts lassen auch auf einfache Weise unter Verwendung der oben beschriebenen Put-Call-Parität ! bewerten. Diese lässt sich im Übrigen auch verteilungsabhängig unter Ausnutzung der Symmetrieeigenschaft für Normalverteilungen Φ8 1 Φ8 herleiten. Der Term Φ01 entspricht dem Delta einer Option, also dem Anteil von Aktien,
die gehalten werden. Bei Φ0' handelt es sich um eine Übergangswahrscheinlichkeit, die angibt wie hoch die Wahrscheinlichkeit ist, dass eine Option ausgeübt wird
respektive im Geld endet. Zusammen mit dem diskontierten Basispreis entspricht
dieser Term den erwarteten Kosten bei Ausübung der Option. Wie oben erwähnt,
basiert das Modell auf der Log-Normalverteilung, hiermit ermittelte Optionspreise
lassen sich demzufolge als transformierte Preisprozesse interpretieren. Mit diesen
Ausführungen werden die eingangs gestellten Fragen beantwortet.
Risikoneutrale Bewertung
Man kann sehen, dass die Drift # der Aktie nicht in der Formel auftaucht und nur die
Volatilität aus dem Aktienkursprozess in die Bewertung mit eingeht. Es erscheint
zunächst erstaunlich, dass die Drift als wesentliche Eigenschaft des Underlyings keinen Einfluss auf das Bewertungsproblem haben soll. In der Realität erwarten Investoren für ihr eingegangenes Risiko eine Kompensation in Höhe der erwarteten Rendite
und diese ist umso höher, je höher das eingegangene Risiko ist. Diese Beobachtung
veranschaulicht, dass die Bewertung von bedingten Ansprüchen in einer Welt stattfindet, in der die Risikoneigung der Marktteilnehmer irrelevant ist.
Die Annahme von Risikoneutralität führt zur zweiten Herangehensweise zur Bewertung zustandsabhängiger Ansprüchen, der risikoneutralen Bewertung. Die
grundlegende Methode wurde von Cox/Ross [1976] entwickelt. Die Formalisierung
dieser Methode und die Diskussion einiger fundamentaler Bewertungsprinzipien
finden sich bei Harrison/Kreps [1979] und Harrison/Pliska [1981].
Die Existenz eines Hedge-Portfolios ermöglicht die Annahme von Risikoneutralität für alle Marktteilnehmer. Das hat zur Folge, dass die erwartete Rendite der Aktie
Optionen und Volatilität
| 13
der risikolosen Verzinsung entsprechen muss. Der faire Optionspreis entspricht
dann dem diskontierten Erwartungswert der Auszahlung zur Fälligkeit.
Der erwartete Wert für einen Call in einer risikoneutralen Welt ist *max , 0. Obigen Überlegungen folgend wird die erwartete Drift # durch eine
risikoneutrale Drift ersetzt. Für den Zeitpunkt folgt daraus
*9 max , 0.
(2.10)
d; # ; d $ ; d% .
(2.11)
Die Wahl der risikoneutralen Drift erfordert die Festlegung auf ein bestimmtes Wahrscheinlichkeitsmaß :, auf das der Erwartungswert *9 . zu bilden ist. Betrachtet
man das obige Aktienkursmodell, so ergibt sich für den diskontierten Aktienkurs
; , welcher die folgende stochastische Differentialgleichung erfüllt
In einer risikoneutralen Welt mit # führt dies zur Beobachtung, dass der abgezinste Kurs ein Martingale ist (d; ;d%). Eine stochastische Variable wird
Martingale genannt, wenn der Erwartungswert dieser Variablen nicht von der Zeit
abhängt. Ein Beispiel für ein Martingale ist ein fairer Münzwurf, bei dem man bei
Kopf € 1 gewinnt und bei Zahl € 1 verliert. Die Erwartung des Spielers für den nächsten Wurf entspricht, gegeben den bisherigen Spielverlauf, einfach dem letzten Wurf.
Das Wahrscheinlichkeitsmaß , ist also nun in Bezug auf zu ändern, da die hierdurch beschriebenen möglichen Umweltzustände nicht mehr von den physikalischen
Wahrscheinlichkeiten der Aktiendrift # abhängen, sondern sich auf die von ergebenden risikoneutralen Wahrscheinlichkeiten beziehen. Ein Wahrscheinlichkeitsmaß mit dieser Eigenschaft wird als äquivalentes Wahrscheinlichkeitsmaß bezeichnet.
Wie Harrison/Kreps [1979] zeigen, ist diese Transformation notwendig, um die
Abwesenheit von Arbitragemöglichkeiten sicherzustellen. Ein zu , äquivalentes
Wahrscheinlichkeitsmaß : heißt äquivalentes Martingalemaß für den Prozess ; ,
wenn ; ein Martingale unter : ist. Bemerkenswert ist, dass sich beim Übergang vom
Maß der realen Welt , zum Martingalemaß : nur die Drift ändert, nicht aber die
Volatilität. Dies folgt aus dem Girsanov Theorem, welches im Prinzip besagt, dass sich
bei einer Transformation zwischen zwei äquivalenten Wahrscheinlichkeitsmaßen nur
die Drift ändert13.
Somit lässt sich die Bewertung von Optionen und anderen bedingten Ansprüchen auf die Bestimmung des erwarteten Pay Offs reduzieren, wobei dieser auf den
jetzigen Aktienkurs bedingt wird und mit der adjustierten, risikolosen Drift abgezinst wird. Man kann also von einer beliebigen Risikoeinstellung der Investoren
13
Für eine Darstellung des äquivalenten Martingalemaßes und weitere wahrscheinlichkeitstheoretische
Grundlagen in diesem Kontext siehe Anhang A.
Optionen und Volatilität
| 14
ausgehen und trotzdem behält das Bewertungsprinzip in einer risikoneutralen Welt
auch in einer riskanten Umgebung seine Gültigkeit. Die Annahme einer risikoneutralen Welt ist somit nicht nur möglich sondern auch praktikabel.
2.3 Die besondere Rolle der Volatilität
Die Volatilität ist zentraler Bestandteil bei der Berechnung von bedingten Ansprüchen wie z. B. Optionen. Warum sie so bedeutend ist, wird in diesem Abschnitt näher
erörtert. Mit dem Kauf oder Verkauf einer Option sind im Wesentlichen drei Risiken
verbunden, die mit der Veränderung des Aktienkurses und der Volatilität zusammenhängen (siehe z. B. Franke et Al [2001, S. 83]).
Um diese Risiken abschätzen zu können, benötigt der Halter Informationen
darüber, wie sich sein Portfolio bei Variation von Einflussfaktoren ändert. Dies lässt
sich mit den Sensitivitätskennzahlen, auch Griechen genannt, die sich aus dem Black–
Scholes Modell ergeben, bewerkstelligen. Unter den Modellannahmen gehen bei
Optionspreisänderungen theoretisch lediglich die verbleibende Laufzeit und die
Variabilität des Aktienkurses mit ein. Die übrigen Faktoren sind annahmegemäß
konstant. Davon abgesehen lassen sich die übrigen Faktoren dennoch als variabel
betrachten und mit partieller Differenzierung ceteris paribus die Auswirkungen von
Änderungen der Einflussfaktoren bestimmen.
Das Delta Δ beschreibt die Reaktion des Optionspreises auf eine marginale
Veränderung des Aktienkurses. Steigt die Aktie um eine Einheit, verändert sich der
Wert der Option um Δ Einheiten. Für Calls ist Δ positiv und für Puts negativ. Das
Delta entspricht der Anzahl von Aktien, die im Duplikationsportfolio zu halten sind,
um eine perfekte Absicherung zu erreichen. Man spricht in diesem Falle auch von der
Hedge-Ratio. Soweit die Theorie; in der Realität ist ein Händler jedoch mit Transaktionskosten, Handelspausen oder verzögerten Orderausführungen konfrontiert (vgl.
bspw. Taleb [1997, Kapitel 4]).
Das Delta-Hedging ist umso genauer, je weniger sensitiv das Delta selbst auf
Kursveränderungen reagiert. Dies wird durch das Gamma Γ gemessen. Mathematisch
entspricht Γ der zweiten partiellen Ableitung nach dem Aktienkurs. Für gekaufte Optionen (long) ist das Gamma positiv, für verkaufte Optionen (short) ist es negativ. Das
Restrisiko einer Δ-neutralen Position lässt sich demnach durch Aufbau einer Γneutralen Position weiter reduzieren.
Ob die Aktie steigt oder fällt ist nunmehr unerheblich; wichtig ist für den Händler, wie heftig die Kursveränderungen ausfallen. Dieses Risiko, oder auch die Chance,
wird durch das Vega14 bestimmt. Damit lässt sich ausdrücken, inwieweit sich der Wert
einer Option bei einer Änderung der Volatilität um eine Einheit verändert. Diese
Kennzahl ist immer positiv.
14
Warum Vega ein Grieche sein soll, konnte nicht ermittelt werden.
Optionen und Volatilität
| 15
Der Einfluss von Zins, (erwarteter) Dividende und Restlaufzeit wurde in
Abschnitt 2.1 schon kurz angedeutet und wird hier nicht weiter erläutert.
Es wird deutlich, dass die Volatilität eine wesentliche Bedeutung bei der Bewertung von Optionen hat. Dies trifft für Calls und Puts gleichermaßen zu und wird
noch einmal anschaulich dargestellt.
300
Drift 5 % p.a.
Volatilität 10 % p.a.
250
Aktienkurs
200
150
100
50
0
0
100
200
Tage
300
400
500
300
400
500
300
Drift 5 % p.a.
Volatilität 40 % p.a.
250
Aktienkurs
200
150
100
50
0
0
100
200
Tage
Abbildung 2: Simulierte Aktienkursverläufe mit identischer Drift und unterschiedlicher Volatilität. Bei beiden Darstellungen liegt die Drift bei 5 % p. a., die Volatilität beträgt oben 10 % p. a. und
unten 40 % p. a.
Eine Option hat bei Fälligkeit nur einen positiven Wert, wenn sie im Geld endet. Man
kann nun mehrere Kursverläufe simulieren; hiervon betrachtet man die Verläufe, die
im Geld enden, gewichtet diese mit der Wahrscheinlichkeit im Geld zu enden und
diskontiert diesen Wert. Als Ergebnis erhält man den Preis der Option zum heutigen
Zeitpunkt.
Zwei Faktoren sind hierbei von entscheidender Bedeutung: Zum einen die Drift
und zum anderen die Volatilität. Wie im vorigen Abschnitt erläutert wird, werden
Optionen und Volatilität
| 16
Optionsprämien ohne die Risikopräferenzen der Investoren bestimmt, da
Veränderungen im Basiswert abgesichert werden können. Die Drift wird durch die
risikoneutrale Drift, den risikolosen Zins, ersetzt. Somit bleibt die Volatilität als Parameter übrig. In einigen Szenarien zeigt die Aktie starke Kursgewinne, bei anderen
zum Teil heftige Kursverluste.
Wie deutlich wird, hängt der Pay Off einer Option bei Fälligkeit von einem asymmetrischen Auszahlungsprofil ab. Für einen Call sind also nur die Szenarien wichtig,
bei denen bei Fälligkeit die Aktienkurse über dem Auszahlungspreis liegen; je weiter
dies der Fall ist, desto besser. Hier kommt die Volatilität zum Tragen: Je höher die
Volatilität, umso höher die Wahrscheinlichkeit tief im Geld zu enden. In Abbildung 2
werden diese Überlegungen graphisch verdeutlicht. Hierzu werden je zehn Zufallspfade für den Aktienkursverlauf simuliert, der Startwert liegt bei € 100 und die Drift
wird auf 5 % p. a. festgesetzt. Variiert wird lediglich die Volatilität, einmal wird ein
sehr niedriges Niveau von 10 % p. a. sowie ein recht hohes Niveau von 40 % p. a. verwendet. Rot gekennzeichnet sind die Zufallspfade, für die ein Call nach 500
Handelstagen im Geld enden würde. Analog gilt die Argumentation für den Put, nur
dass hierbei der Wert des Puts steigt, je tiefer der Aktienkurs unter dem Ausübungspreis liegt.
3 Analyse des Deutschen Aktienindex und DAX Optionen
Die wegweisenden Arbeiten von Black/Scholes [1973] und Merton [1973] bilden
bis heute die Grundlage für die Bewertung von Optionen und haben sich als
Standardmodell etabliert. In zahlreichen Arbeiten wurden jedoch systematische
Abweichungen von den am Markt beobachteten Quotierungen zu den theoretisch
ermittelten Preisen festgestellt. In diesem Kapitel werden sowohl die Renditen des
DAX, als auch die sich aus den Marktpreisen der Optionen ergebenden Volatilitäten
einer statistischen Untersuchung unterzogen. Es wird sich zeigen, dass die
grundlegenden Annahmen des Black–Scholes Modells nicht haltbar sind.
3.1 Ausstattungsmerkmale des DAX, der DAX Option und des DAX
Future
Vor der statistischen Analyse wird zunächst der Untersuchungsgegenstand kurz vorgestellt.
Der Deutsche Aktienindex (ISIN: DE0008469008) bildet das Segment der deutschen Bluechips ab, welche im Prime Standard zugelassen sind. Enthalten sind die 30
größten und umsatzstärksten Unternehmen an der Frankfurter Wertpapierbörse
FWB15. Wie alle anderen Indizes der DAX-Familie ist auch der DAX selbst kapitalgewichtet, d. h. das Gewicht einer im Index enthaltenen Aktie wird nach dem Anteil an
der gesamten Kapitalisierung der im Index enthaltenen Werte bemessen.
Eingeführt wird der DAX am 23. Juni 1988. Die Indexbasis liegt bei
1.000 Punkten per 31. Dezember 1987. Der DAX führt den Index der Börsen-Zeitung
fort, dessen historische Zeitreihe bis 1959 zurückreicht. Als Performanceindex konstruiert, werden Dividendenabschläge ignoriert. Das heißt, in den DAX fließen nicht
nur die festgestellten Kurse mit ein, sondern zusätzlich die jährlichen Ausschüttungen
und Bonizahlungen der Unternehmen. Unterstellt wird hierbei eine Reinvestition der
Bardividende (ohne Abzug der Kapitalertragssteuer). Die Kursfeststellung basiert auf
den Kursen des elektronischen Handelssystems Xetra der Deutsche Börse AG. Der
DAX wird fortlaufend sekündlich berechnet. Der erste Kurs an einem Handelstag
wird veröffentlicht, sobald tagesaktuelle Preise für 20 der in dem Index enthaltenen
Gesellschaften vorliegen. Die insgesamt recht positive Entwicklung hat der DAX wohl
zu einem großen Teil seinem günstigen Starttermin zu verdanken. Wie bereits erwähnt, wurde der DAX zu Beginn des Jahres 1988 eingeführt, direkt nach dem gro-
15
Der Leitfaden zu den Aktienindizes der Deutsche Börse [2008] bietet ausführliche Informationen
zur Berechnung und Zusammensetzung des DAX. Die jeweils aktuelle Version ist auf der Homepage der Deutsche Börse AG zu finden (http://deutsche-boerse.com). Der Vollständigkeit halber sei
angemerkt, dass die Deutsche Börse AG ebenfalls Kursindizes pflegt.
Analyse des Deutschen Aktienindex und DAX Optionen
| 18
ßen Crash von 198716. Die Namensgebung geht im Übrigen auf die Schwaben zurück:
Ursprünglich war als Kürzel DAI vorgesehen. Dieses Kürzel war aber bei der Taufe
vor 20 Jahren vom Autohersteller Daimler belegt. So wurde aus dem I ein X17.
Indexpunkte
3000
300
1966
1971
1975
1980
1984
1988
1993
1997
2002
2006
Abbildung 3: Evolution der täglichen Schlusskurse des DAX vom 30. Dezember 1966 bis zum
24. Januar 2008 in logarithmierter Darstellung. Der maximale Indexstand beträgt 8105,69 Punkte
(16.07.2007) und das Minimum liegt bei 319,93 Punkten (18.01.1969).
Der Handel mit Optionen auf den DAX (ODAX, ISIN: DE0008469495) beginnt im
August 1991 an der 1990 gegründeten Deutschen Terminbörse (DTB). Diese schließt
sich 1998 mit der Schweizer Terminbörse SOFFEX zusammen und es entsteht Europas größte Terminbörse, die Eurex. Bei den Optionen auf den DAX handelt es sich
um Optionen europäischen Typs. Der Kontraktwert beträgt € 5 pro Indexpunkt. Zu
zahlen ist die Optionsprämie am ersten Börsentag, der dem Kauftag folgt. Die Preisermittlung erfolgt in Punkten auf eine Dezimalstelle. Die minimale Preisveränderung
beträgt 0,1 Punkte. Die Erfüllung erfolgt bei Ausübung der Option durch Barausgleich, fällig am ersten Börsentag nach dem Schlussabrechnungstag. Stillhalter von
DAX Optionen haben bei der Eurex, die gleichzeitig als Clearingstelle fungiert, verschiedene Sicherheiten (Margins) zu hinterlegen18.
Die angebotenen Fälligkeitstermine belaufen sich mittlerweile auf bis zu 60 Monate. Bei Einführung einer Optionsserie stehen für jeden Call und Put mindestens
fünf Ausübungspreise für den Handel zur Verfügung. Davon sind zwei Ausübungspreise im Geld, ein Ausübungspreis am Geld und zwei Ausübungspreise aus dem
Geld. Um ständig die Verfügbarkeit von OTM und ITM Optionen zu gewährleisten,
16
Vgl. Die Zeit [2006], http://www.zeit.de/online/2006/24/Querdax (verifiziert am 01.03.2008).
Mittlerweile hat sich das X auch international zu einem beliebten Börsenbuchstaben entwickelt (siehe
Börse Aktuell [2008]).
18
Vgl. hierzu die Clearing Bedingungen der Eurex. Die jeweils aktuelle Version ist auf der Homepage
der Eurex zu finden (www.eurexchange.com).
17
Analyse des Deutschen Aktienindex und DAX Optionen
| 19
werden je nach Entwicklung des DAX für bestehende Optionsserien neue Basispreise
eingeführt.
Wie in Abschnitt 3.3 ausgeführt wird, gehen Futures auf den DAX (FDAX,
ISIN: DE0008469594) ebenfalls mit in die Untersuchung ein. Daher werden diese
ebenfalls kurz beschrieben. Momentan liegt der Kontraktwert bei € 25 je Indexpunkt
des DAX. Die kleinste Preisänderung liegt bei € 12,50. Im Gegensatz zu den Optionen
werden lediglich drei Fälligkeiten angeboten. Dies sind immer die nächsten drei
Quartalsmonate im Zyklus März, Juni, September und Dezember. Läuft ein Kontrakt
aus, folgt unmittelbar darauf ein neuer Kontrakt mit drei Monaten Laufzeit.
3.2 Statistische Analyse des DAX
Bachelier [1900] leistet nicht nur Pionierarbeit auf dem Gebiet von
Diffusionsprozessen zur Modellierung von Preisfluktuationen, sondern legt durch
seine Beobachtungen auch den Grundstein für die deskriptive Theorie von
Finanzzeitreihen. In seinem Marktmodell schlägt er vor, Preisänderungen
> ! !1 (arithmetische Brownsche Bewegung) als Folge von unabhängig und
identisch normalverteilten Zufallsvariablen zu modellieren. Hierbei gibt er jedoch zu
bedenken, dass die Stichprobenvarianz von > nicht konstant ist und dass große
Preisänderungen durch die Normalverteilung nicht erklärt werden können. Auf beide
Aspekte wird im Folgenden näher eingegangen.
Mitte des letzten Jahrhunderts greift Mandelbrot [1963] diesen Komplex
wieder auf und zeigt, dass es signifikante Abweichungen zwischen der
Häufigkeitsverteilung von Kursveränderungen und der Normalverteilung gibt. Auch
sein Student Fama [1963, 1965] zeigt, dass Kursveränderungen ein leptokurtisches
Verhalten aufweisen. Demnach finden sich
bei den empirischen
Häufigkeitsverteilungen verhältnismäßig zu viele kleine und sehr große
Kursbewegungen, als dies von der Normalverteilung zu erwarten wäre. Mandelbrot
bezeichnet den Umstand immer wiederkehrender extremer Preisausschläge mit dem
Begriff Noah Effekt und spielt damit auf die Diskontinuität als Charakterzug des
Marktes an. Die Flut kam und ging – katastrophal, aber nicht von Dauer. Er geht noch
weiter und fordert „that these facts warrant a radically new approach to the problem of
price variation” (Mandelbrot [1963, S. 395]). Er schlägt vor, die logarithmierten
Preisveränderungen > ln ! ln !1 (geometrische Brownsche Bewegung) zu
untersuchen sowie die Normalverteilung durch die Klasse der ?-stabilen Verteilung
zu ersetzen.
Analyse des Deutschen Aktienindex und DAX Optionen
| 20
15%
Tagesrenditen
10%
5%
0%
-5%
-10%
-15%
1966
1971
1975
1980
1984
1988
1993
1997
2002
2006
Abbildung 4: Tägliche Renditen vom 30. Dezember 1966 bis 24. Januar 2008.
Was Mandelbrot mit dem Noah Effekt aussagen möchte, ist in Abbildung 4 zu sehen.
Deutlicher als in Abbildung 3 lässt sich hier erkennen, wie stark einzelne Kursbewegungen an einem einzigen Tag ausfallen können. Weiter wird ersichtlich, dass die Variabilität der Preisveränderungen im Zeitablauf nicht konstant ist (Heteroskedastizität). Die Darstellung zeigt außerdem eine weitere typische Eigenschaft von Preisänderungen
an:
Große
Kursbewegungen
treten
selten
isoliert
auf.
Mandelbrot [1963, S. 418] beschreibt dies folgendermaßen: „[…], large changes
tend to be followed by large changes – of either sign – and small changes tend to be
followed by small changes, […]”. Diese Klumpenbildungen werden vielfach als
Volatility Clustering bezeichnet und beschreiben Phasen, in denen starke Kursausschläge gehäuft auftreten (bedingte Heteroskedastizität). Kursveränderungen müssen
also nicht unbedingt unabhängig voneinander sein.
Eine weitere Beobachtung, wonach Aktienkursrenditen temporär teilweise recht
stark von ihrem Mittelwert abweichen können, hat Mandelbrot zu dem Begriff Joseph
Effekt verleitet, dem zweiten wilden Charakterzug des Marktes, wie er sie nennt.
Joseph, ein hebräischer Sklave, riet dem Pharao, Getreide für schlechte Zeiten
einzulagern. Als es kam, wie Joseph prophezeite, da „tat Joseph alle Kornhäuser auf
und verkaufte den Ägyptern; […] Und alle Welt kam nach Ägypten, um bei Joseph zu
kaufen; denn der Hunger war groß in allen Landen.“ (AT, Genesis, Kapitel 41).
Mandelbrot bezeichnet Joseph denn auch als ersten internationalen Arbitragehändler.
In Anlehnung an die biblischen sieben guten und schlechten Jahre können auch
Preisänderungen eine ausgeprägte Persistenz aufweisen. Unter Persistenz wird eine
Eigenschaft verstanden, bei der ein Prozess seine vergangene Entwicklung nur langsam „vergisst“ und deutet somit eventuell vorhandene langfristige Abhängigkeiten an.
Mandelbrot greift in diesem Zusammenhang auf die Arbeiten von
Harold Edwin Hurst
zurück.
Hurst
untersuchte
die
unregelmäßigen
Überschwemmungen am Nil und sollte sich mit seinen Studien an der Konzeption
Analyse des Deutschen Aktienindex und DAX Optionen
| 21
eines Staudamms beteiligen. Er machte dabei eine Entdeckung, welche nicht nur
unter Hydrologen für Aufsehen sorgte. Hierbei war weniger wichtig warum es zu den
Überschwemmungen kam, als viel mehr wie hoch die nächste Flut ausfallen würde.
Mal stiegen sie kräftig, mal blieben sie niedrig. Hurst [1951] drückt seine Erkenntnis
wie folgt aus:19
„Obwohl viele natürliche Erscheinungen eine fast normale
Häufigkeitsverteilung besitzen, ist das nur der Fall, wenn man die Reihenfolge
des Auftretens ignoriert. Wenn Aufzeichnungen von Naturerscheinungen sich
über lange Zeiträume erstrecken, gibt es von einer Periode zur nächsten
beträchtliche Variationen sowohl der Mittelwerte als auch der Standardabweichungen. Die Tendenz, in Gruppen aufzutreten, macht sowohl den Mittelwert
als auch die Standardabweichung, die aus kurzen Jahresfolgen berechnet
werden, variabler als bei einer Zufallsverteilung.“
Bei Mandelbrot/Hudson [2005] werden die von Mandelbrot entwickelten statistischen Methoden skizziert, mit denen sich die gemachten Beobachtungen des Noah
und Joseph Effektes quantifizieren lassen. Einige konzentrieren sich auf den Tail
Index ? der stabilen Verteilung. Eine Normalverteilung hat einen Tail Index ? von
zwei. Je höher ? ist, desto mehr nähert sich die Verteilung einer Normalverteilung.
Ein niedriges ? bedeutet, dass der betrachtete Markt sehr riskant ist und heftige Kursbewegungen erwarten lässt.
Andere konzentrieren sich auf den Hurst-Koeffizienten @, dieser bezieht sich auf
die geschilderten Abhängigkeiten. Ein höheres @ bedeutet, dass die Daten eine hohe
Persistenz aufweisen, also die Beständigkeit aufweisen, in eine Richtung zu tendieren.
Ein niedrigeres @ hingegen deutet eine häufigere Trendumkehr an. Um diese Effekte
trennen zu können, entwickelte Mandelbrot den Range over Standard Deviation Test,
oder einfach R/S Analyse. Der Test beruht im Wesentlichen darauf, eine bestimmte
Menge an Daten zu untersuchen, sie anschließend durcheinander zu würfeln und sie
erneut zu untersuchen. Wenn Unterschiede zu vorher feststellbar sind, so müssen
diese auf langfristige Abhängigkeiten zurückzuführen sein, welche wiederum auf der
genauen Reihenfolge dieser Daten basieren. Wie bei May [1999, S. 57] dargestellt
wird, ist das Konzept des Hurst Exponenten mittlerweile fester Bestandteil der Werkzeuge von Wertpapierhändlern. Es findet sich z. B. bei den Bloomberg Terminals
unter dem Namen KAOS eine Funktion, die den Hurst Exponenten graphisch darstellt.
Alternative Konzepte finden sich im Bereich der Zeitreihenanalyse bei den
ARCH und GARCH Modellen20. Es handelt sich hierbei um Zeitreihenmodelle, bei
denen die Volatilität variabel modelliert werden kann. Diese können so das Volatility
19
20
Zitiert aus Mandelbrot/Hudson [2005, S. 404], Anmerkungen zu Kapitel 9.
(Generalized) AutoRegressive Conditional Heteroskedasticity.
Analyse des Deutschen Aktienindex und DAX Optionen
| 22
Clustering abbilden und sich im Vergleich zur Normalverteilung leptokurtische Randverteilungen für die stochastischen Prozesse ergeben. Um dies zu ermöglichen wird
die bedingte Varianz zum Zeitpunkt als eine Funktion von zeitverzögerten
quadrierten Renditen spezifiziert. Bei den GARCH Modellen finden zusätzlich die
vergangenen geschätzten Werte für die Varianz Berücksichtigung. Hieraus ist mittlerweile eine große Familie von Modellvarianten entstanden, die verschiedene Aspekte
von Zeitreiheneigenschaften berücksichtigen21.
450
Beobachtungszeitraum
30.12.1966 - 24.01.2008
Beobachtungen 10.705
400
350
Zahl der Tage
300
250
200
Durchschnitt
Median
Maximum
Minimum
Standardabweichung
Skewness
Kurtosis
0,000282
0,000136
0,088725
-0,137099
0,011717
-0,402459
7,792304
Jarque-Bera
27.329,29
150
100
50
0
-8%
-6%
-4%
-2%
0%
2%
4%
6%
8%
Tagesrenditen in Prozent
Abbildung 5: Empirische Dichtefunktion des DAX angepasst an eine Normalverteilung (blau) und
eine A-stabile Verteilung (rot). Für die stabile Verteilung ergibt sich ein Tail Index ? von 1,66. Mit
angegeben sind die deskriptiven Statistiken für die DAX Renditen. Zusätzlich ist der ermittelte Wert
für die Jarque-Bera Teststatistik für die normalisierten Renditen mit angeführt22.
Zum Abschluss dieses Abschnitts wird nun überprüft, inwieweit die Kursveränderungen des DAX einer geometrischen Brownschen Bewegung folgen, wie es das
Modell von Black–Scholes für den Aktienkursprozess zu Grunde legt. Oder anders
ausgedrückt: Folgen die logarithmierten Preisveränderungen einer Normalverteilung?
Als alternative Verteilung wird die von Mandelbrot vorgeschlagene stabile Verteilung
mit in die Untersuchung aufgenommen.
21
Für einen Überblick zu dieser Modellklasse vgl. bspw. Franke et al [2001, Kapitel 12] und die dort
gemachten Angaben.
22
Der Jarque-Bera Test ist ein häufig verwendeter Test auf Normalverteilung. Die Testgröße ist deutlich
größer als der kritische Wert von 9,21 bei einer Irrtumswahrscheinlichkeit von 1%. Für die
Normalisierung der Renditen wird vom Wert der täglichen Änderung der Mittelwert abgezogen
und durch die Standardabweichung geteilt.
Analyse des Deutschen Aktienindex und DAX Optionen
| 23
Die obige Abbildung zeigt eine empirische Dichtefunktion für den DAX. An der Abzisse sind die jeweiligen Tagesrenditen abgetragen und an der Ordinate ist die jeweilige Häufigkeit, also die Anzahl der Tage, angegeben, an denen die Tagesrendite in
dem an der X-Achse spezifizierten Intervall liegt. Technisch gesprochen entspricht
eine Dichtefunktion der ersten Ableitung der Verteilungsfunktion.
Die Normalverteilung wird durch ihre ersten beiden Momente Erwartungswert
und Varianz vollständig bestimmt. Die Schiefe (Skewness) einer Normalverteilung
beträgt Null, da es sich um eine symmetrische Verteilung handelt. Ist die Schiefe einer
Verteilung negativ, so nennt man sie linksschief (=rechtssteil), bei einer positiven
Schiefe rechtsschief (=linkssteil). Die Kurtosis gibt die Wölbung einer Verteilung an;
bei der Normalverteilung hat sie den Wert drei23. In der Abbildung 5 werden die ermittelten Parameter für die DAX Renditen angegeben. Es handelt sich bei der empirischen Dichte um eine linksschiefe Verteilung und eine Kurtosis über drei
(Leptokurtosis) bedeutet, dass im Vergleich zur Normalverteilung mehr Wahrscheinlichkeitsmasse in den Rändern liegt (Fat Tails). Unschwer zu erkennen ist die ungleich bessere Anpassung der stabilen Verteilung an die empirischen Daten24. Sie
kann sowohl die im Zentrum der Verteilung gehäuft auftretenden kleinen
Kursveränderungen abbilden, als auch die seltenen extremen Ereignisse an beiden
Rändern mit berücksichtigen.
Insbesondere die großen Ereignisse sind von wesentlicher Bedeutung für die
Marktteilnehmer, denn an diesen Tagen werden Reichtümer gewonnen oder verloren.
Um die Anpassung an den Rändern deutlicher hervorheben zu können, wird in
Abbildung 6 zum einen der Ausschnitt am Rand der Verteilung vergrößert. Zum
anderen wird ein Semi-Log Plot als ergänzende Darstellung für Abbildung 5 präsentiert. Bei der rechten Abbildung wurde für die Ordinate eine logarithmierte Darstellung gewählt und anstelle des Histogramms eine geglättete Kurve für die empirische
Dichte eingefügt. Die logarithmische Dichte der Normalverteilung zeigt ein quadratisches Abklingen, während die empirische Dichte eher linear abfällt.
23
24
Die Ausführungen zur Normalverteilung wurden Schröder [2002, Kapitel 1] entnommen.
Näheres zu den Eigenschaften ?-stabiler Verteilungen findet sich in Anhang A.3.
Analyse des Deutschen Aktienindex und DAX Optionen
| 24
14
Zahl der Tage
12
10
8
6
4
2
0
-14%
-11%
-8%
Tagesrenditen in Prozent
-5%
Zahl der Tage
1000
100
10
1
-8%
-4%
0%
Tagesrenditen in Prozent
4%
8%
Abbildung 6: Empirische Dichtefunktion des DAX, Teil 2. Oben: Vergrößerter Ausschnitt des linken
Randes aus Abbildung 5. Unten: Semi-log Plot, logarithmische Skalierung der Ordinate. Die gestrichelte Linie spiegelt die geglättete empirische Dichte wider.
Noch deutlicher als oben ist zu sehen, dass die Normalverteilung die
Randwahrscheinlichkeiten der empirischen Daten vollkommen unterschätzt. Wesentlich besser wiederum bildet die stabile Verteilung diese ab. Wie
Höchstötter [2006, S. 12] anmerkt, bieten Quantil Plots, oder auch qq-Plots, eine
weitere einfache Möglichkeit, die Anpassung von Verteilungen an realen Daten zu
überprüfen. Bei einem qq-Plot werden die empirischen Quantile der Beobachtungen
gegen die entsprechenden Quantile einer zu spezifizierenden Verteilung abgetragen.
In diesem Falle sind es die Quantile der Normalverteilung sowie der stabilen Verteilung. Wenn die jeweiligen Paare der beiden Verteilungen nahe beieinander liegen,
laufen sie entlang einer Winkelhalbierenden, die den linearen Zusammenhang der
entsprechenden Quantile widerspiegelt.
Analyse des Deutschen Aktienindex und DAX Optionen
| 25
Empirische Quantile
0,06
0,04
0,02
0,00
-0,02
-0,04
-0,06
-0,04
-0,03
-0,02
-0,01
0,00
0,01
Quantile Normalverteilung
0,02
0,03
0,04
0,08
Empirische Quantile
0,06
0,04
0,02
0,00
-0,02
-0,04
-0,06
-0,08
Empirische Quantile
-0,10
-0,08
-0,04
-0,02
0,00
0,02
Quantile α-stabile Verteilung
-0,01
0,00
0,01
Quantile Normalverteilung
0,04
0,06
0,08
0,03
0,02
0,02
0,01
0,01
0,00
-0,01
-0,01
-0,02
-0,02
-0,03
-0,03
-0,03
Empirische Quantile
-0,06
-0,02
0,02
0,03
0,03
0,02
0,02
0,01
0,01
0,00
-0,01
-0,01
-0,02
-0,02
-0,03
-0,03
-0,03
-0,02
-0,02
-0,01
-0,01
0,00
0,01
Quantile α-stabile Verteilung
0,01
0,02
0,02
0,03
Abbildung 7: Quantil Plot der Tagesrenditen des DAX. Abgetragen werden die Quantile der empirischen Verteilung gegen die Quantile der Normalverteilung (blau) und der stabilen Verteilung (rot). Bei
den beiden oberen qq-Plots werden alle Daten verwendet. Unten werden die inneren 95 % der Daten
verwendet.
Analyse des Deutschen Aktienindex und DAX Optionen
| 26
Insgesamt lässt sich die gute Visualisierung der Daten speziell im Zentrum der Verteilungen erkennen. Haben die Daten allerdings zu schwere Ränder, wie dies beim DAX
der Fall ist, wird die Darstellung durch die extremen Ereignisse verzerrt.
Höchstötter [2006, S. 13] verwendet zusätzlich als Abhilfe nur die inneren 95 %
der Beobachtungen. In beiden Fällen sieht man die deutliche Überlegenheit der
stabilen Verteilung gegenüber der Normalverteilung. Bei der Normalverteilung
werden die Randwahrscheinlichkeiten auch bei Bereinigung von Ausreißern wieder
stark unterschätzt. Etwas anders ist die Situation bei der stabilen Verteilung: Beim
oberen Bild könnte man den Eindruck gewinnen, dass die Wahrscheinlichkeit für
extreme Ereignisse sogar ein wenig überschätzt wird. Dies führte zu Überlegungen,
die Ränder einer stabilen Verteilung ab einem gewissen Punkt abzuschneiden25. Das
untere Bild bietet jedenfalls für das bloße Auge eine nahezu perfekte Anpassung. Es
lässt sich festhalten, dass Mandelbrots Beobachtungen für Baumwollpreise von 1963
auch im Jahr 2008 für den DAX vollkommen zutreffend sind. Allein durch visuelle
Inspektion der Daten kann die Nullhypothese normalverteilter Renditen ganz klar
verworfen werden.
Die beschriebenen Phänomene konnten in zahlreichen Arbeiten für viele
verschiedene Märkte und Vermögenswerte, wie Aktien, Anleihen, Rohstoffe oder
Währungen bestätigt werden. Sie sind heutzutage allgemein als Stilisierte Fakten
(Stylized Facts) anerkannt. Eine tiefergehende Behandlung und andere der hier diskutierten Stylized Facts und einige mehr findet sich bei Cont [2001]. Eine Betrachtung
dieser Fakten für den deutschen Markt findet sich bei Krämer [2004], bei der ebenfalls Fat Tails, Heteroskedastizität, stabile Verteilungen oder auch langfristige Abhängigkeiten thematisiert werden.
3.3 Stochastische Volatilität und DAX Optionen
Wie im vorigen Abschnitt beschrieben, ist das klassische Black–Scholes Marktmodell
nicht in der Lage die statistischen Eigenschaften von Finanzzeitreihen wiederzugeben. Weiter wurde beobachtet, dass die Volatilität sich im Zeitablauf verändert und
die Eigenschaft aufweist, temporär auf unterschiedlichen Niveaus zu verharren. Auf
den letzten Aspekt wird im Folgenden näher eingegangen. Weiter wird das Konzept
der impliziten Bestimmung von Volatilitäten aus Marktquotierungen von Optionen
vorgestellt, wobei sich zeigen wird, dass sich systematische Abweichungen zu den
Modellannahmen ergeben. Einen sehr guten Überblick zu diesem Themenkomplex
bietet die Deutsche Bundesbank [2005].
25
Dies führt zu der Klasse der Truncated Lévy Distributions (TLD). Vgl. bspw. Mantegna/Stanley
[2000]. Im Kontext der Optionstheorie erweitert Matacz [2006] das Black–Scholes Modell und legt
als Aktienkursprozess die TLD zu Grunde.
Analyse des Deutschen Aktienindex und DAX Optionen
| 27
Historische Volatilität
Die Formel von Black–Scholes zur Ermittlung von Optionspreisen besteht aus einer
Funktion von fünf Parametern. Im Falle von Aktien sind dies BC , , , , , wobei
die Volatilität der einzige Parameter ist, der nicht direkt am Markt beobachtet werden kann. Um die Volatilität zu schätzen bieten sich mehrere Verfahren an. Eine recht
einfache Möglichkeit stellt die Schätzung der Volatilität aus historischen Aktienkurszeitreihen dar. Betrachtet werde eine Folge von täglichen Preisen !1 , … , !E mit ihren
entsprechenden Preisveränderungen > ln ! ln !1 und >F als Mittelwert der
Preisveränderungen. Die historische Volatilität, auch realisierte Volatilität genannt,
ergibt sich dann als annualisierte mittlere quadratische Abweichung bzw. Standardabweichung der Renditen
GHIJHIKL M
E1
252
P >Q >F ' .
O 1 QR
(3.1)
Da die Volatilität in der Regel als annualisierte Größe verwendet wird und die Daten
auf täglichen Werten beruhen, wird ein Faktor benötigt um die tägliche Volatilität auf
ein Jahr zu skalieren. Hierbei ist es üblich, nur die Handelstage zu berücksichtigen,
bei denen Preisnotierungen vorliegen. Für gewöhnlich werden hierfür als Annäherung 252 Tage festgesetzt. Denkbar wären natürlich auch wöchentliche oder monatliche Quotierungen. Von Bedeutung ist weiter die Anzahl der Beobachtungen O; hierbei führen zu wenige O zu ungenauen Schätzungen. Da die Volatilität nicht konstant
ist, ist die Verwendung von zu langen Zeiträumen ebenfalls nicht zielführend, da weit
zurückliegende Beobachtungen einen geringen Einfluss auf die heutige Volatilität
haben werden. Üblich sind Zeiträume von bspw. 30, 90 oder 180 Tagen.
Abbildung 8 zeigt den Verlauf der historischen Volatilität des DAX mit einem
gleitenden Fenster über 252 Tage. Wieder wird deutlich, dass die Volatilität nicht
konstant ist und auf unterschiedlichen Niveaus verweilen kann. Des Weiteren lässt
sich die Tendenz erkennen, zu einem Mittelwert zurückzukehren (Mean Reversion).
Die Variabilität des DAX bewegt sich quasi innerhalb einer gewissen Bandbreite. Der
Median von knapp 15 % p. a. könnte einen solchen Mittelwert andeuten. Dies steht im
Widerspruch zu den Kursen selbst, dort gibt es keinen Mittelwert zu dem bspw. der
DAX zurückkehren würde (sehr wohl gibt es aber eine mittlere Kurssteigerung, die
Drift).
Analyse des Deutschen Aktienindex und DAX Optionen
| 28
14%
Min
7,59 % p.a.
Max
46,03 % p.a.
Mittel 17,22 % p.a.
Median 14,87 % p.a.
45%
40%
35%
12%
10%
30%
8%
25%
6%
20%
15%
4%
absolute Tagesrenditen
Historische Volatilität in Prozent p.a.
50%
10%
2%
5%
0%
0%
1966
1971
1975
1980
1984
1988
1993
1997
2002
2006
Abbildung 8: Historische Volatilität und Volatilitätscluster. Linke Skala: Historische Volatilität mit
einem gleitenden Fenster von 252 Tagen. Die Größe des Fensters entspricht somit etwa einem Jahr.
Rechte Skala: Absolute Tagesrenditen des DAX vom 30. Dezember 1966 bis 24. Januar 2008.
In Abbildung 8 werden zusätzlich zur historischen Volatilität nochmals die täglichen
Preisveränderungen (diesmal in absoluten Werten) aufgegriffen. Augenfällig ist hierbei der analoge Verlauf der historischen Volatilität mit den (absoluten) Renditen.
Dort wo starke Kursbewegungen gehäuft auftreten, ist auch allgemein das Volatilitätsniveau recht hoch.
Kalibrierung an Marktpreise
Außer der Volatilität sind alle Inputfaktoren bekannt. Der fehlende Modellparameter
lässt sich auch ermitteln, indem die Abstände der theoretischen Preise von den
Marktpreisen durch Variierung von minimiert werden. Dies geschieht über eine
Anpassung mit der Methode der kleinsten Quadrate über alle Restlaufzeiten und
Basispreise. Eine Diskussion dieser Vorgehensweise sowie der resultierenden Fehlermaße findet in Kapitel 5 statt. Die Volatilität für das Modell von Black–Scholes,
welche die Marktpreise am besten wiedergibt, ermittelt sich zu 21,60 %.
Tabelle 1: Anpassungsgüte der Black–Scholes Kalibrierung an Marktdaten vom 7. Dezember 2007.
Modell
Black–Scholes
MAE
MARE
€ 44,05
80 %
Analyse des Deutschen Aktienindex und DAX Optionen
| 29
1.600
1.400
Optionspreis
1.200
1.000
800
600
400
200
0
7200
7400
7600
7800
8000
Basispreis K
8200
8400
8600
8800
Abbildung 9: Reale und Black–Scholes Preise für den 7. Dezember 2007. Die Kreise repräsentieren
die Marktpreise und die Pluszeichen die Modellpreise.
Implizite Volatilitäten von DAX Optionen
Im Gegensatz zu der historischen Volatilität, welche definitionsgemäß auf vergangenen Daten beruht, handelt es sich bei dem Konzept der impliziten Volatilität um die
Erwartungen der Marktteilnehmer, die sie in Bezug auf die zukünftige Volatilität bilden. Die Akteure werden sich demnach ihren Erwartungen entsprechend auf dem
Markt positionieren. Mit der Volatilität als Parameter des Optionspreismodells lässt
sich nun aus den Quotierungen für Puts und Calls und mit Kenntnis der anderen
beobachtbaren Variablen implizit die Volatilität ermitteln. Der Theorie von Black–
Scholes folgend, ergibt die implizite Bestimmung von Volatilitäten für alle Fälligkeitstermine und Strikes immer den gleichen Wert, da die Volatilität annahmegemäß
konstant ist. Es zeigen sich aber für unterschiedliche Fälligkeiten und Ausübungspreise Charakteristika, die nicht modellkonform sind. Um diesen Sachverhalt zu
veranschaulichen, bietet es sich an, die Volatilität als zeitabhängige Funktion von und zu definieren , . Zeitabhängig deshalb, weil sie immer nur die
Markterwartung an dem betrachteten Tag widerspiegelt. Im Prinzip muss man von
Black–Scholes impliziten Volatilitäten sprechen, da die Volatilität nur im Zusammenhang mit diesem Modell Sinn ergibt. Formal stellt sich die Situation folgendermaßen
dar
, BC S , , , , , , T.
Analyse des Deutschen Aktienindex und DAX Optionen
| 30
Smile Effekt der impliziten Volatilität
26%
Dez 07
24%
Feb 08
Implizite Volatilität
22%
Jun 08
20%
18%
16%
14%
12%
10%
-0,1
-0,08
-0,06
-0,04
-0,02
0
0,02
moneyness ln(K/S)
0,04
0,06
0,08
0,1
Abbildung 10: Smile und Smirk Effekt. Implizite Volatilitäten der ODAX Optionen vom 7. Dezember
2007 für drei verschiedene Restlaufzeiten.
Der Begriff Volatility Smile ist inzwischen ein Oberbegriff für die Beobachtungen, die
gemacht werden, wenn die impliziten Volatilitäten für je eine Restlaufzeit gegen die
Ausübungspreise abgetragen werden. Bei der Dezember ´07 Option lässt sich die
Intuition gut nachvollziehen. Im Bereich von Indexoptionen zeigt sich jedoch, dass
der Verlauf eher schief ist. So spricht man in diesem Zusammenhang auch von der
Volatilitätsschiefe (Volatility Smirk).
Beachtenswert ist die Beobachtung, wonach Optionen mit niedrigen Basispreisen
wesentlich höhere Volatilitäten implizieren als die Optionen mit höheren Strikes. Anders ausgedrückt sind OTM Puts wesentlich teurer als die korrespondierenden OTM
Calls. Zahlreiche Untersuchungen können bestätigen, dass dieses Muster prinzipiell
weltweit auf allen Leitindizes anzutreffen ist (siehe z. B. Foresi/Wu [2005]). Es zeigt
sich bei Untersuchungen für den amerikanischen Markt, dass die impliziten
Volatilitäten bis zu dem großen Krach von 1987 in der Tat einen relativ flachen Verlauf haben. Erst danach bildet sich das bis heute bestehende Muster heraus. Einige
Forscher glauben daher, dass die Märkte gelernt hätten eine Crashwahrscheinlichkeit
einzupreisen,
welche
für
den
Smile
mitverantwortlich
ist
(siehe
Javaheri [2005, S. 7]).
Rubinstein [1994] prägte hierfür den Begriff Crash-O-Phobia, womit auch einer
der Gründe für diesen Verlauf angedeutet wird. Die Nachfrage nach OTM Puts stieg
sprunghaft an, um sich gegen marktweite Abwärtsbewegungen absichern zu können
und dies bei geringem Angebot. Hinzu kommt, dass die Strategie, OTM Puts auf den
Index zu verkaufen und diese Position mit dem oben skizzierten Delta-Hedge mit
dem Index abzusichern, bei Kurssprüngen zusammenbricht. Demnach wird man
hierfür als Entschädigung einen höheren Preis verlangen. Auch ist nachvollziehbar,
dass es wahrscheinlicher erscheint, dass ein ganzer Markt aus verschiedensten Grün-
Analyse des Deutschen Aktienindex und DAX Optionen
| 31
den eher heftig abrutscht, als dass er nach oben springt. Bei einzelnen Aktien stellt
sich die Situation anders dar, hier reicht z. B. eine gute Nachricht, um den Wert nach
oben schießen zu lassen.
Ein weiterer Erklärungsansatz bezieht sich auf den Verschuldungsgrad von
Unternehmen (Leverage Effect). Demnach sinkt bei fallenden Aktienkursen das
Eigenkapital in Relation zum Fremdkapital. Ergo steigt der Verschuldungsgrad. Dies
geht im Allgemeinen mit erhöhter Unsicherheit einher, so dass sich das
Verschuldungsrisiko zusätzlich auf die Schwankungen der Renditen auswirken kann.
Zum Teil lässt sich so die oftmals feststellbare negative Korrelation zwischen Volatilität und Aktienkursen erklären (vgl. bspw. Wallmeier [2003, S. 56]). Da es aber den
Leverage Effekt auch schon vor 1987 gegeben hat, ist der Wirkungszusammenhang in
Bezug auf den Smile bzw. Smirk Effekt nicht vollständig geklärt.
Fristenstruktur der impliziten Volatilität
Ein anderes Phänomen lässt sich erkennen, wenn die impliziten Volatilitäten eines
Basispreises, für gewöhnlich der at the money Strike, über die Fälligkeiten abgetragen
wird. In Abbildung 11 werden zwei Handelstage gegenübergestellt. Am 07.12.2007
herrscht ein recht niedriges Volatilitätsniveau, die Marktteilnehmer werden dann in
Zukunft von einem höheren Niveau ausgehen. Entgegengesetzt verhält es sich am
24.01.2008, hier hat es an den vorangegangenen Tagen am Markt heftige
Kursbewegungen gegeben, so dass das Niveau recht hoch liegt. Die Investoren
antizipieren wieder ein niedrigeres Niveau für die Zukunft. Es handelt sich hierbei
um den eingangs beschriebenen Mean Reversion Effekt. Zwischen dem roten und
blauen Graphen könnte man sich einen imaginären Mittelwert der Volatilität denken.
Ähnlich der Fristenstruktur bei Zinsen wird diese Struktur auch Forwardkurve genannt.
Analyse des Deutschen Aktienindex und DAX Optionen
| 32
40%
ATM 07.12.2007
Implizite Volatilität
35%
ATM 24.01.2008
30%
25%
20%
15%
10%
Dez 07
Mrz 08
Jun 08
Sep 08
Jan 09
Apr 09
Jul 09
Nov 09
Fälligkeit
Abbildung 11: Fristenstruktur der impliziten Volatilität. Abgebildet sind die at the money Volatilitäten von zwei Handelstagen die sich bei verschiedenen Fälligkeiten ergeben.
Einige weitere mögliche Einflussfaktoren auf den Smile seien noch kurz erwähnt.
Börsengehandelte Optionen unterliegen wie andere Wertpapiere auch dem Gesetz
von Angebot und Nachfrage. Weiter können Transaktionskosten und
Liquiditätseffekte eine stetige Anpassung von Hedge-Portfolios soweit erschweren,
dass der Arbitragemechanismus, auf dem das Modell von Black–Scholes basiert,
empfindlich beeinflusst wird (vgl. bspw. Wallmeier [2003, S. 62]).
Einfluss von Steuern und Dividenden
Die Put-Call-Parität verlangt, dass die impliziten Volatilitäten von Calls nicht
systematisch von den impliziten Volatilitäten von Puts abweichen dürfen. Es lassen
sich jedoch an vielen Handelstagen Abweichungen wie bei dem linken Punktediagramm in Abbildung 12 feststellen.
Diese lassen sich auf ein verzerrtes Indexniveau zurückführen, welche durch
Dividendenzahlungen verursacht werden. Hafner/Wallmeier [2000] argumentieren, dass die individuelle Besteuerung der Investoren sich von den zu Grunde gelegten Annahmen bei der Berechnung des Indexstandes unterscheiden kann. Wenn dies
der Fall ist, kann die Nettodividende für den Investor höher oder auch niedriger sein,
als die für die Indexberechnung verwendete. Die Differenzdividende, wie diese
Diskrepanz auch genannt wird, hat dann den gleichen Effekt wie eine
Dividendenzahlung auf eine ungeschützte Option, d. h. die Optionspreise fallen auseinander und damit auch die impliziten Volatilitäten.
Analyse des Deutschen Aktienindex und DAX Optionen
22%
| 33
22%
Calls
Puts
20%
Implizite Volatilität
Implizite Volatilität
Calls
Puts
18%
16%
14%
12%
10%
20%
18%
16%
14%
12%
10%
-0,10
-0,05
0,00
0,05
moneyness ln(K/S)
0,10
-0,10
-0,05
0,00
0,05
moneyness ln(K/S)
0,10
Abbildung 12: Implizite Volatilitäten vom 21.12.2007 für die ODAX Januar 08 Optionen. Bei der
linken Abbildung wird der Xetra Schlusskurs (17:30 Uhr) in Höhe von 8002,67 Punkten verwendet.
Rechts wird der implizite Indexstand aus dem März 08 Future (17:30 Uhr) ermittelt und ergibt
7997,88 Indexpunkte.
Sei ΔUVW, der Wert der Differenzdividende zum Zeitpunkt , die zwischen und anfällt. Um die genannten Probleme zu bewältigen schlagen die Autoren eine
dividendenadjustierte Future Formel vor
sowie eine Put-Call Parität
X Y Y ZUVW,Y ,
! ZUVW,[ [ [ [ [ ,
(3.2)
(3.3)
zu verwenden, wobei die Subskripte X und \ für Future respektive Option stehen.
Durch Kombination der beiden Gleichungen erhält man
ZUVW,Y ,[ ZUVW,Y Y Y ZUVW,[ [ [ ,
(3.4)
; X Y Y $ ZUVW,Y ,[ .
(3.5)
was der gesuchten Differenzdividende entspricht.
Ein adjustiertes Indexniveau ergibt sich zu
Dies ist genau das Indexniveau, welches bei Eingabe in die Black–Scholes Formel
identische implizite Volatilitäten für Calls und Puts ergibt. Das ist nicht nur für die
Bestimmung von impliziten Volatilitäten von Bedeutung. Sollte die Put-Call-Parität
tatsächlich verletzt sein, ergibt sich eine profitable Arbitragestrategie, wie sie in Abschnitt 2.1 beschrieben wird.
Die Ausführungen bei Hafner/Wallmeier [2000] beziehen sich auf das
Körperschaftsteuer-Anrechnungsverfahren, welches bis zum Jahre 2001 in Kraft war.
Danach wurde es durch das Halbeinkünfteverfahren ersetzt. Dies ändert
offensichtlich nichts grundlegend an der Situation.
22%
22%
20%
20%
| 34
Implizite Volatilität
Implizite Volatilität
Analyse des Deutschen Aktienindex und DAX Optionen
18%
18%
16%
16%
14%
14%
12%
12%
10%
10%
-0,10
-0,05
0,00
0,05
moneyness ln (K/S)
0,10
-0,10
-0,05
0,00
0,05
moneyness ln (K/S)
0,10
Abbildung 13: Implizite Volatilitäten für quotierte Jan 08 Optionen vom 21.12.2007. Verwendung
von Letzter Kurs und Bid sowie Ask Kursen von Put und Call Optionen. Daten wie oben.
Zusätzlich veranschaulicht Abbildung 13 die impliziten Volatilitäten zu Quotierungen
der Januar 08 Optionen zu Handelsschluss um 17:30 Uhr. Auch hier sind deutliche
Diskrepanzen erkennbar (links), die durch einen adjustierten Indexstand gemildert
werden können (rechts). Zu beachten ist hierbei, dass die Daten nicht zeitlich
synchronisiert sind.
4 Modell Spezifikationen und ihre charakteristischen
Funktionen
Das Marktmodell von Black–Scholes und die von ihnen entwickelte Formel zur
Bewertung von Optionen erfreuen sich großer Beliebtheit, erlauben sie doch bei
geringem Aufwand eine präferenzfreie Bestimmung von Optionsprämien. Dessen
ungeachtet finden die Annahmen konstanter Volatilität und normalverteilter Renditen in der Realität keine Bestätigung. In den letzten Jahrzehnten wurde eine ganze
Reihe von Modellen entwickelt, die diese empirischen Beobachtungen berücksichtigen.
Bereits Merton [1973] schlägt vor, die Volatilität als deterministische Funktion
der Zeit zu modellieren. Dies erlaubt es die unterschiedlichen Volatilitätsniveaus für
unterschiedliche Laufzeiten zu modellieren, nicht aber den Smile Effekt zu erklären.
Dupire [1994], Derman/Kani [1994] und Rubinstein [1994] erweitern dieses Konzept und erlauben zusätzlich eine zustandsabhängige Volatilität, womit auch der
Smile berücksichtigt werden kann. Diese Local Volatility Modelle erlauben eine perfekte Anpassung an die Marktdaten, können den Smile jedoch nicht erklären, sondern nur beschreiben. Eine andere Möglichkeit ist es, die Volatilität selbst als
stochastischen Prozess zu modellieren. Hull/White [1987], Stein/Stein [1991] und
Heston [1993] liefern hierbei die grundlegenden Arbeiten für die Stochastic
Volatility Modelle. Es handelt sich hierbei um Zwei-Faktoren-Modelle, bei denen die
Faktoren je für die Aktienkursdynamik und die sich ändernde Volatilität
verantwortlich sind.
Die Beobachtung, dass Aktienkurse sich nicht kontinuierlich entwickeln sondern
in immer wiederkehrenden Abständen Sprünge aufweisen, führt Merton [1976]
dazu den Diffusionsprozess mit einem Poissonprozess zu erweitern. Durch diese
Sprungkomponente wird es möglich, die Diskontinuität der Märkte zu berücksichtigen. Merton entwickelt diese Erweiterung bemerkenswerterweise lange vor den alternativen Modellen mit stochastischer Volatilität.
Um eine noch bessere Anpassung an die Marktpreise zu erreichen kombinieren
Bates [1996] und Bakshi et Al [1997] die letzten beiden Ansätze, womit beide
wesentlichen Kritikpunkte am Black–Scholes Modell adressiert werden.
In eine ganz andere Richtung gehen die Entwicklungen, die ausschließlich auf
Sprungprozessen basieren, auch Lévy Prozesse genannt. Sie bilden eine neue Familie
von Modellen, die zur Bewertung von Derivaten verwendet werden (siehe bspw.
Carr/Wu [2004]). Bei den Lévy Prozessen sind die Brownsche Bewegung und Poissonprozesse als Spezialfälle enthalten. Nach aktuellem Stand der Forschung sind dies
die Modelle, die am ehesten die empirischen Fakten bei Aktienkursen wiedergeben
können. Wie bei der gewöhnlichen Brownschen Bewegung erlauben diese Modelle
aber keine variable Volatilität, keine Berücksichtigung des Leverage Effekts und auch
Modell Spezifikationen und ihre charakteristischen Funktionen
| 36
nicht das Volatility Clustering. Doch lassen sich diese Phänomene problemlos
bewältigen, wenn wie bei Bates [1996] und Bakshi et Al [1997] die Volatilität durch
einen eigenen Prozess beschrieben wird.
Ein weiterer wichtiger Aspekt ist, dass alle hier betrachteten Modelle zu einem
Markt führen, der nicht mehr vollständig ist. Damit ist eine Bewertung alleine auf
Arbitrageüberlegungen nicht mehr möglich, d. h. es gibt kein risikoloses HedgePortfolio mehr, sobald die Volatilität nicht mehr als konstant angenommen wird oder
Sprünge beim Kursverlauf auftreten. So ist man darauf angewiesen, den Markt durch
zusätzliche Wertpapiere zu vervollständigen oder aber es werden bestimmte Annahmen bezüglich eines neuen Wahrscheinlichkeitsmaßes getroffen (vgl. hierzu z. B.
Rathgeber [2007]). Formal bedeutet dies, dass es viele äquivalente Martingalemaße
: ] , gibt, unter denen der diskontierte Preisprozess ein Martingale ist (vgl.
Harrison/Pliska [1981]). Das hat zur Folge, dass es theoretisch eine ganze Bandbreite von resultierenden Optionspreisen gibt. Bei Cont/Tankov [2004, Kapitel 10]
werden eine ganze Reihe von Möglichkeiten diskutiert, wie sich Derivate unter diesen
Umständen bewerten und hedgen lassen. Aus Sicht eines Optionshändlers wird die
Situation bei Taleb [1997] geschildert. Wie Cartea [2005] darlegt, ist das Hedgen
von Finanztiteln ebenso wichtig wie die Bewertung von derivativen Wertpapieren
selbst. Hierzu schlägt er eine Erweiterung des klassischen Delta-Gamma-Hedgen (vgl.
Abschnitt 2.3) vor, bei der die Eigenheiten der Modelle, wie sie hier präsentiert werden, berücksichtigt werden können. Dies ist aber nicht Thema dieser Arbeit und es
sei auf die oben genannte Literatur verwiesen.
Bei der Simulationsstudie in Kapitel 5 werden die theoretischen Preise mit den
Marktpreisen von Optionen verglichen. Wie in Abschnitt 2.2 beschrieben, werden die
Preise für bedingte Ansprüche unter einem risikoneutralen Wahrscheinlichkeitsmaß
: bestimmt. Somit beziehen sich die folgenden Ausführungen ausschließlich auf :.
Unter diesen Umständen ist es für die vorliegende Studie auch nicht relevant, ob der
Markt vollständig ist oder ob es viele verschiedene äquivalente Wahrscheinlichkeitsmaße gibt. Das gesuchte risikoneutrale Wahrscheinlichkeitsmaß : wird einfach
implizit aus den quotierten Optionspreisen ermittelt. Im anschließenden Kapitel 5
erfolgt eine genaue Darlegung dieser Vorgehensweise.
Hiermit ist eine Richtung der zeitgenössischen Optionspreisbewertung skizziert.
Es folgt eine Einführung der Modelle, welche im nächsten Kapitel empirisch untersucht werden. Bei allen diesen Konzeptionen handelt es sich um unterschiedlich rigorose Erweiterungen des Black–Scholes Modells, die dieses jeweils als Spezialfall
enthalten. Bei der Präsentation der Spezifikationen wird der Fokus auf die ökonomische Intuition und eine klare Darstellung der Modelle gerichtet. Die für diese Modelle
notwendigen mathematischen Details der zu Grunde liegenden Prozesse und für das
Konzept von charakteristischen Funktionen samt ihrem Nutzen für die Bewertung von
Optionen werden im Anhang näher erörtert.
Modell Spezifikationen und ihre charakteristischen Funktionen
| 37
4.1 Merton Jump Diffusion
Mit dem Jump Diffusion Modell (MJD) legt Merton [1976] den Grundstein für Modelle, die dem kontinuierlichen Black–Scholes Diffusionsprozess eine Sprungkomponente hinzufügen.
Es ist einer der ersten Versuche, im Bereich von Aktienderivaten den schiefen
Verlauf des Smile sowie die Überschusskurtosis, d. h. den leptokurtischen Verlauf der
empirischen Wahrscheinlichkeitsdichtefunktion zu bewältigen. Hiermit zeigen sich
Sprungdiffusionen grundsätzlich in der Lage den Smile Effekt bzw. Skew Effekt
abzubilden.
Bei dem Konzept der Jump Diffusion handelt es sich um ein exponentielles Lévy
Modell der Form
^_ ,
(4.1)
d
d $ d% $ da .
(4.2)
womit der Aktienkursprozess einem Lévy Prozess ` folgt. Spezifiziert wird dieser
Lévy Prozess mit einer Brownschen Bewegung und einem zusammengesetztem Poissonprozess. Damit erweitert sich die Aktienkursdynamik des Black–Scholes
Marktmodells um einen diskontinuierlichen Sprungpart a
Die Sprünge a folgen einem zusammengesetzten Poissonprozess der Intensität b mit
logarithmisch normalverteilten Sprunghöhen. Diese Sprunghöhen sind unabhängig
und identisch normalverteilte Zufallsvariablen mit Mittelwert c und Varianz d. Des
Weiteren sind der Poissonprozess und die Sprunghöhe unabhängig vom Wiener Prozess % und gibt die Volatilität des Diffusionsprozesses an.
Die Preise der Aktie sind als Exponential des Lévy Prozesses ` modelliert.
Daraus folgt, dass die logarithmierten Preisveränderungen e log ⁄ einem
Lévy Prozess folgen.
Die Wahrscheinlichkeitsdichte dieses Lévy Prozess lässt sich unter einem risikoneutralen Maß : mit Hilfe folgender charakteristischen Funktion fIg h darstellen
1
o o
fIg h exp iih# k h' ' $ bS lmnm p /' 1Tr,
2
fsHtt h · fvmwx h.
(4.3)
Modell Spezifikationen und ihre charakteristischen Funktionen
| 38
Hierbei stellt # k ' bS nyp /' 1T einen Konvexitätskorrekturfaktor dar.
'
Diese Korrektur betrifft die risikoneutrale Drift und stellt sicher, dass der diskontierte
Preisprozess ein Martingale ist. Ermittelt wird er durch fIg i 1 mit i √1. Da
der Poissonprozess und die Sprunghöhe unabhängig von der Brownschen Bewegung
sind, können die jeweiligen charakteristischen Funktionen fsHtt h und fvmwx h
einfach miteinander multipliziert werden.
1
o
7
25%
6
Implizite Volatilität
30%
5
PDF (s)
20%
15%
4
3
10%
2
5%
1
0%
0
50 60 70 80 90 100 110 120 130 140 150
Basispreis K
-40%
-20%
0%
s=ln(ST/S0)
20%
40%
Abbildung 14: Implizite Volatilitäten und zugehörige Zustandspreisdichte MJD. Zu Grunde liegende Daten: 100, 0,05, 0,5, b 1, c 0,05, d 0,1 und 0,07. Rot: Jump
Diffusion, blau: Black–Scholes.
Bei der Interpretation der Volatilität gilt es zu beachten, dass diese nicht der üblichen Form des Modells von Black–Scholes entspricht
VolatilitätBC e BC √,
(4.4)
Volatilität{|JQ e }{|JQ ' $ bd' $ bc ' ,
(4.5)
sondern die Standardabweichung in Periode im Merton Modell als
gegeben ist. Wenn nun BC {|JQ gesetzt würde, wären die Merton Preise für
Optionen aufgrund der zusätzlichen Unsicherheitsfaktoren immer größer (oder mindestens gleich) als die von Black–Scholes.
In Abbildung 14 wird illustriert, wie sich mit den drei zusätzlichen Risikoquellen
ein Verlauf von impliziten Volatilitäten und damit einhergehend eine Dichtefunktion
beschreiben lässt, mit der sich die beobachtete negative Schiefe und eine spitzgipflige
Verteilung mit dicken Rändern insbesondere bei kurzen Restlaufzeiten reproduzieren
lässt. Zum Vergleich sind die Verteilung und die Volatilität mittels Black–Scholes
ebenfalls dargestellt. Damit wird der Vorteil der Sprungdiffusionen deutlich insbesondere in kurzer Sicht starke Abwärtsbewegungen modellieren zu können. Für eine
tiefergehende Behandlung wird auf Matsuda [2004] verwiesen. Hier wird dieses
Modell sehr umfassend und mit vielen Beispielen behandelt.
Modell Spezifikationen und ihre charakteristischen Funktionen
| 39
4.2 Heston Stochastic Volatility
Mit seinem populären Stochastic Volatility Modell adressiert Heston [1993] die Beobachtung, wonach die Volatilität selbst variabel ist. Hierzu ersetzt Heston bei dem
Black–Scholes Modell die konstante Volatilität aus Gleichung (2.7) durch einen eigenständigen stochastischen Prozess ~ . Unter dem Martingalemaß : resultiert folgende Aktienkursdynamik
d
d $ }~ d%C ,
(4.6)
d~  € ~ d $  }~ d%‚ .
(4.7)
fG|IJQ h exp , h $ U, h~ ,
(4.8)
Mit ~ wird die zeitveränderliche, instantane Varianz beschrieben, auch lokale oder
Momentanvarianz genannt. Die Dynamik von ~ folgt hierbei einer zum Mittelwert
zurückkehrenden Quadratwurzeldiffusion. Im Bereich der Finanzmathematik wurde
dieser Prozess ursprünglich von Cox et Al [1985a, b] zur Modellierung von
kurzfristigen Zinssätzen verwendet, weshalb dieser Prozess auch unter dem Synonym
CIR Prozess geläufig ist (vgl. auch Cont/Tankov [2004, S. 474]). Ursprünglich
eingeführt wurde er jedoch von Feller [1951]. Der Ausdruck }~ garantiert eine
nichtnegative Volatilität. Wenn der Prozess Null würde, reduzierte sich (4.7) zu €0,
der stochastische Teil verschwände und die Volatilität würde sofort wieder positiv.
Wenn zusätzlich die Feller Bedingung 2€ ' erfüllt ist, kann ~ nicht negativ
werden. Der deterministische Teil von (4.7) ist asymptotisch stabil, wenn  0 und
ein Gleichgewicht ist erreicht, wenn ~ € ist.
Die beiden Brownschen Bewegungen %C und %‚ korrelieren über ƒd *d%C d%‚ . Der Parameter  gibt die Geschwindigkeit der Mean-Reversion an, €
ist der langfristige Mittelwert des Varianzprozesses und  beschreibt die Volatilität
der Varianz (auch bekannt als vol of vol). Insgesamt besitzt dieses Modell vier freie
Parameter und mit ~ eigentlich eine latente Zustandsvariable, die aber nicht direkt
am Markt beobachtet werden kann und somit für gewöhnlich ebenfalls als freier
Parameter betrachtet wird.
Die charakteristische Funktion für die Rendite e lautet
wobei
€
1 † ‡
, h ' „ ƒ hi 0 2 log …
ˆ‰,
1†

1 ‡
~ '
ˆ‰,
U, h ' „ ƒ hi 0 …
1 † ‡

Modell Spezifikationen und ihre charakteristischen Funktionen
mit
| 40
0 Šƒ hi' $ ' ih $ h' ,
†
 ƒ hi 0 .
 ƒ hi $ 0 5
25%
4
Implizite Volatilität
30%
3
PDF (s)
20%
15%
2
10%
5%
1
0%
0
50 60 70 80 90 100 110 120 130 140 150
Basispreis K
-40%
-20%
0%
s=ln(ST/S0)
20%
40%
Abbildung 15: Implizite Volatilitäten und zugehörige Zustandspreisdichte Heston. Zu Grunde
liegende Daten: 100, 0,05, 0,5,  2, € 0,01, ƒ 0,5,  0,1 und ~ 0,02.
Rot: Heston, blau: Black–Scholes.
Es lässt sich erkennen, dass auch die Berücksichtigung von stochastischer Volatilität
einen Smile gut abbilden kann. Die bei Aktien und Aktienindizes typischerweise
schief
verlaufenden
asymmetrischen
Smiles
können
durch
den
Korrelationskoeffizienten ƒ berücksichtigt werden. So erhält man im Vergleich zur
Normalverteilung mehr Wahrscheinlichkeitsmasse am linken Rand. Das Modell von
Heston [1993] zeigt sich in der Lage, eine Vielzahl von verschiedenen Smiles
abzubilden. Durch die Stetigkeit beider Prozesse bedingt kann es jedoch nur sehr
eingeschränkt den recht steilen Skew kurz vor Fälligkeit modellieren. Viele Details
und Hinweise zur Implementierung finden sich bei Mikhailov/Nögel [2003] sowie
Muck/Rudolf [2006].
4.3 Finite Moment Log Stable
Die stilisierten Fakten in Abschnitt 2.3 sind vielfach dokumentiert und als solche
anerkannt. Eine weitere Beobachtung findet in der neueren Literatur bisher relativ
wenig Beachtung. Bei einer Untersuchung von S & P 500 Indexoptionen beschreiben
Carr/Wu [2003] ein Phänomen, bei dem sich der Volatility Smirk im Zeitablauf
nicht abflacht. Dies steht im Gegensatz zu vielen Bewertungsmodellen sowie den
Implikationen des Zentralen Grenzwertsatzes, wonach sich eine Renditeverteilung im
Zeitablauf immer mehr der Normalverteilung annähert (siehe z. B. Cont [2001]).
Modell Spezifikationen und ihre charakteristischen Funktionen
| 41
30%
Dez 07
Jan 08
Implizite Volatilität
25%
Feb 08
Jun 08
Dez 08
20%
Jun 09
15%
10%
-2,00
-1,50
-1,00
-0,50
0,00
moneyness d
0,50
1,00
1,50
2,00
Abbildung 16: Laufzeitmuster von impliziten Volatilitäten. Die Linien beschreiben die impliziten
Volatilitäten für ODAX Optionen vom 7. Dezember 2007 gemessen an einem Standard Moneyness
Maß 0 ln⁄⁄ k √26.
Die impliziten Volatilitäten in Abbildung 10 werden gegen die Moneyness mit
ln ⁄ abgetragen, wie es in vielen Arbeiten in diesem Kontext üblich ist
(gängig sind ebenfalls ⁄X oder einfach ). Eine andere Möglichkeit die Verbindung zwischen dem Verlauf des Volatility Smirk und der risikoneutralen Wahrscheinlichkeitsdichte darzustellen, ergibt sich unter Verwendung eines standardisierten Maßes für Moneyness
0
ln ⁄
√
.
(4.9)
Wie Carr/Wu [2003] beschreiben, ist diese Definition von Moneyness ein Industriestandard geworden (siehe auch Foresi/Wu [2005]). Hierbei bezeichnen und den
Basispreis und den Preis der Aktie. ist ein Maß für die Volatilität und die Restlaufzeit der Option. Die Skalierung mit √ ist wichtig, um die Moneyness über verschiedene Laufzeiten vergleichbar zu machen. Die Verwendung einer Standardabweichung
im Nenner erlaubt es, verschiedene Wertpapiere mit unterschiedlichen Volatilitätsniveaus vergleichbar zu machen. Weiterhin kann man so die Moneyness 0 als die Anzahl von Standardabweichungen interpretieren, die der log Strike vom log Spot in
einer Black–Scholes Welt entfernt ist.
26
Als Annäherung für die Volatilität wird bei dieser Darstellung der Tageswert des VDAX in Höhe
von 15,35 % verwendet. Der VDAX ist ein von der Deutschen Börse AG täglich veröffentlichter Index, der die implizite Volatilität des DAX wiedergibt (siehe Deutsche Börse [2007]). Die Moneyness 0 entspricht zudem dem Mittel von – 01 und – 0' , welche in der Black–Scholes Formel für
Puts auftauchen.
Modell Spezifikationen und ihre charakteristischen Funktionen
| 42
In Abbildung 16 wird derselbe Tag wie in Abbildung 10 dargestellt, nur ergibt
sich hier ein gänzlich anderes Bild. Deutlich erkennbar ist, dass die impliziten
Volatilitäten mit längeren Fälligkeiten keineswegs abflachen. Es zeigt sich, dass die
Steigung sogar leicht zunimmt. Das Laufzeitmuster spiegelt damit die Erkenntnis
wider, dass die auf die Fälligkeiten bedingten risikoneutralen Wahrscheinlichkeitsverteilungen ein persistentes Verhalten aufweisen. Dies lässt zwei Schlussfolgerungen zu:
1) Die Marktteilnehmer sehen das Risiko eines Crash nicht nur kurzfristig, sondern
auch auf lange Sicht und 2) Händler, die Put Optionen gegen eben diese Crashs verkaufen, stufen das Risiko einer unvollständigen Absicherung (Delta-Hedging) ihrer
Positionen ebenfalls auf lange Sicht als bedeutend ein (vgl. auch Abschnitt 3.3).
Diese Beobachtung stellt alle Bewertungsmodelle in Frage, bei denen der zentrale
Grenzwertsatz zur Modellierung von Preisveränderungen zum Tragen kommt. Anders ausgedrückt sind dies die Modelle mit endlichen Momenten (z. B. Schiefe oder
Kurtosis) und stationären Zuwächsen. In dieser Arbeit betrifft das alle Modelle außer
dem FMLS–SV. Die Sprungmodelle können nur kurzfristig den Smirk erklären. Modelle mit einem persistenten stochastischen Volatilitätsprozess können durch Aufgabe
von stationären Zuwächsen eine gewisse Fristenstruktur abbilden, obwohl auch hier
ab einem gewissen Zeitpunkt der zentrale Grenzwertsatz greift.
Carr/Wu [2003] finden eine Möglichkeit Preisveränderungen mit Hilfe der
?-stabilen Verteilung zu modellieren und zur Bewertung von Optionen einzusetzen.
Bei der stabilen Verteilung existieren nur die Renditemomente, die größer als ? sind
(für eine Charakterisierung von stabilen Verteilungen siehe Anhang A.3). Somit gilt
der zentrale Grenzwertsatz nicht mehr. Weiter zeigen sie, dass unter diesen Voraussetzungen eine Lösung existiert, unter der der abgezinste Preisprozess ein Martingale ist.
Bei der Aktienkursdynamik handelt es sich um einen puren Sprungprozess mit
unendlicher Aktivität
d
,
d $ d` .
(4.10)
` bezeichnet einen ?-stabilen Prozess mit Mittelwert 0, Dispersion 0 ‘ , Tail
Index ? ’ “0,2“ und Skewness Index ” ’ 1,1.
Dem Modell liegt eine ?-stabile Verteilung zu Grunde, wodurch bei ? 2 die
Varianz unendlich ist. Mit ” 1 werden aber endliche Preismomente ermöglicht
(daher auch der Begriff Finite Moment Log Stable, FMLS). Diese sind notwendig für
die Existenz eines Martingalemaßes und somit endliche Optionspreise finden zu können.
Für ” 1 (maximum negative skewness) nimmt das rechte Ende der Verteilung
exponentiell ab, während das linke Ende dick bleibt und einem Potenzgesetz folgt.
Ein Prozess dieser Form wird auch one-sided ?-stable process genannt (siehe
Kyprianou/Loeffen [2005, S. 6]. Für ” 1 wäre das rechte Ende zu dick und
,
1
Modell Spezifikationen und ihre charakteristischen Funktionen
| 43
erwartete Rendite sowie Optionspreise wären unendlich. Durch diese Spezifikation
wird dieses Modell von alternativen ?-stabilen Optionspreismodellen abgegrenzt (vgl.
z. B. Cartea/Howison [2007]).
Je mehr sich ? von 2 entfernt, desto dicker werden die Enden der Renditeverteilung (Fat Tails) und desto spitzgipfliger wird die Mitte der Verteilung (Leptokurtosis).
gibt die Weite der Verteilung an und entspricht somit quasi der Volatilität. Bei
? 2 ergibt sich die Normalverteilung und das Black–Scholes-Modell als Spezialfall.
Die charakteristische Funktion unter : ist gegeben durch
f•{^C h exp –ih#k ih sec
mit einem Konvexitätskorrekturfaktor #k  sec
™
'
.
(4.11)
4
Implizite Volatilität
50%
—?
˜,
2
40%
3
PDF (s)
30%
20%
2
1
10%
0%
0
50 60 70 80 90 100 110 120 130 140 150
Basispreis K
-40%
-20%
0%
s=ln(ST/S0)
20%
40%
Abbildung 17: Implizite Volatilitäten und zugehörige Zustandspreisdichte FMLS. Zu Grunde liegende Daten: 100, 0,05, 0,5, ? 1,8, 0,11. Rot: FMLS, blau: Black–Scholes.
Gut erkennbar ist der dünne rechte Rand der Verteilung und die wesentlich größere
Wahrscheinlichkeit für Kursstürze im Vergleich zur entsprechenden Black–Scholes
Wahrscheinlichkeit. Bemerkenswert ist bei diesem Modell, dass es lediglich einen
Parameter mehr als das Modell von Black–Scholes hat. Insbesondere
Aktienindexoptionen lassen sich hiermit realitätsnah bewerten.
4.4 Merton Jump Diffusion – Stochastic Volatility
Wie oben angerissen wird, ist der kurzfristige Smile nicht allein durch eine
veränderliche Volatilität akkurat beschrieben. Durch Kombination von stochastischer
Volatilität mit dem Ansatz von Merton [1976] lässt sich ein sehr flexibler
Bewertungsrahmen schaffen, durch den die beiden wesentlichen Kritikpunkte am
Black–Scholes Modell gemildert werden können. Dieses Vorgehen wird erstmals von
Bates [1996] beschrieben, weshalb es auch Bates Modell genannt wird.
Genau genommen ergibt sich diese Spezifikation durch die Verbindung des stetigen Heston Modells mit dem Sprungpart des Merton Jump Diffusion Prozesses. Als
Preisdynamik ergibt sich unter :
Modell Spezifikationen und ihre charakteristischen Funktionen
| 44
d
d $ ~ d%C $ da ,
(4.12)
d~  € ~ d $  }~ d%‚ .
(4.13)
Die beiden Prozesse korrelieren wieder über ƒd *d%C d%‚ miteinander. Die
charakteristische Funktion für e bestimmt sich aus dem Produkt der jeweiligen charakteristischen Funktionen
f{vsC‚ h exp , h $ U, h~ × exp›bihS nyp
o /'
1T $ bS lmnm
fG|IJQ h · fvmwx h.
o p o /'
1Tœ,
(4.14)
Die Bedeutung der sieben Parameter sowie der instantanen Varianz, sowie , h
und U , h entsprechen obigen Definitionen. Um ein Martingale zu sein, ist auch bei
diesem Modell eine Konvexitätskorrektur notwendig. Sie ist in (4.14) enthalten und
tritt somit nicht explizit in Erscheinung.
5
25%
4
Implizite Volatilität
30%
3
PDF (s)
20%
15%
10%
2
1
5%
0%
0
50 60 70 80 90 100 110 120 130 140 150
Basispreis K
-40%
-20%
0%
s=ln(ST/S0)
20%
40%
Abbildung 18: Implizite Volatilitäten und zugehörige Zustandspreisdichte MJD–SV. Zu Grunde
liegende Daten: 100, 0,05, 0,5,  2, € 0,01, ƒ 0,  0,1, b 1,21, c 0,05, d 0,06 und ~ 0,01. Rot: MJD–SV, blau: Black–Scholes.
Diese Konzeption des Merton Jump Diffusion – Stochastic Volatility (MJD–SV) vereint die Vorteile der beiden Spezifikationen und beseitigt die skizzierten Nachteile.
Ein anderes Problem entspringt der Tatsache, dass dieses Modell aufgrund der vielen
Parameter nur schwierig zu handhaben ist. Mehr hierzu in Kapitel 5.
4.5 Finite Moment Log Stable – Stochastic Volatility
Carr/Wu [2003] skizieren im Anschluss ihrer empirischen Überprüfung eine
Möglichkeit, ihr FMLS Modell mit der Konzeption einer stochastischen Volatilität zu
verknüpfen (FMLS–SV). Mit ? 2 ist die Varianz unendlich, mit gibt es jedoch
Modell Spezifikationen und ihre charakteristischen Funktionen
| 45
einen Skalenparameter, der die Weite der Verteilung angibt. Es ist auf diese Weise
möglich, anstelle der nicht existenten Volatilität, die Weite der Verteilung stochastisch
zu modellieren. Dazu schlagen sie vor, durch eine aus dem Heston Modell bekannte
Quadratwurzeldiffusion zeitveränderlich zu gestalten. Dies erfolgt bei
Carr/Wu [2003] unter dem Modellierungsrahmen einer zeitverschobenen Brownschen Bewegung27. Hier wird eine alternative Herangehensweise vorgeschlagen und direkt mittels eines Quadratwurzelprozesses stochastisch modelliert. Es ergibt sich
hierbei als Spezialfall der Konzeption von Carr und Wu28.
Den Ausführungen von Carr/Wu [2003] folgend wird der Dispersionsparameter

des FMLS Renditeprozesses durch eine zeitveränderliche instantane Varianz ~
ersetzt
1‘
d
d $ ~  d`,1
,
(4.15)
d~  € ~ d $  }~ d%‚ .
(4.16)
Der Prozess der Aktienkursdynamik `,1
korreliert mit der Volatilitätsdiffusion über
,1
ƒd *›d` d%‚ œ miteinander. Unter der Kenntnis, dass die charakteristische
Funktion voneinander unabhängiger Zufallsvariablen durch Multiplikation der involvierten charakteristischen Funktionen ermittelt werden kann, ergibt sich folgende
Darstellung
f•{^CC‚ h exp , h $ U, h~  exp –ih  sec
™
'
ih sec
fG|IJQ h · f•{^C h.
™
'
˜,
(4.17)
Die Definitionen der fünf Parameter sowie der instantanen Varianz sind wie oben
gegeben.
27
Bei einer zeitverschobenen Modellierung von Zufallsprozessen (stochastic time change) wird die
Kalenderzeit durch die Handelszeit ersetzt. Wenn viele Informationen auf dem Markt eintreffen,
wird diese Handelszeit entsprechend schnell vergehen und mit einer erhöhten Volatilität einhergehen. Aus der instantanen Varianz ~ wird eine instantane Handelsaktivität. Diese Möglichkeit der
Verwendung einer „stochastischen Uhr“ führt zu einer ganzen Reihe von Modellen, wie z. B. Varianz Gamma, Normal Inverse Gaussian und viele andere, die ebenfalls erfolgreich zur Modellierung von Wertpapieren inklusive Optionen eingesetzt werden. Für einen umfassenden
Grundlagenartikel siehe Carr/Wu [2004].
28
Diese Schlussfolgerung beruht auf der Tatsache, dass das Modell von Heston als Brownsche Bewegung betrachtet werden kann, bei der die Handelsaktivität als Quadratwurzelprozess spezifiziert
wird (siehe Carr/Wu [2004, S. 118]).
Modell Spezifikationen und ihre charakteristischen Funktionen
| 46
4
40%
3
PDF (s)
Implizite Volatilität
50%
30%
20%
2
1
10%
0
0%
50 60 70 80 90 100 110 120 130 140 150
Basispreis K
-40%
-20%
0%
s=ln(ST/S0)
20%
40%
Abbildung 19: Implizite Volatilitäten und zugehörige Zustandspreisdichte FMLS–SV. Zu Grunde
liegende Daten: 100, 0,05, 0,5,  1, € 0,03, ƒ 1,  0,1, ? 1,8 und
~ 0,01. Rot: FMLS–SV, blau: Black–Scholes.
Der Verlauf des Volatility Smirk in Abbildung 19 entspricht aufgrund der ähnlichen
Spezifikation dem einfachen FMLS Modell. Nur ist der Skalenparameter in diesem
Fall nicht mehr zeit-homogen sondern in der Lage auch eine Fristenstruktur zu
reproduzieren.
5 Simulationsstudie für DAX Optionen
Die Analyse der Bewertungsperformance von alternativen Optionspreismodellen
basiert in dieser Studie auf liquiden DAX Optionen. Die Prognosequalität der
verschiedenen Spezifikationen wird einmal In-Sample (ex post) sowie Out-of-theSample (ex ante) überprüft. Bei der In-Sample Analyse werden die Variablen der Modelle aus den Marktdaten des Tages geschätzt und die Güte der Anpassung durch
den Vergleich der theoretischen Werte mit den realen Marktpreisen bestimmt. Die
Out-of-the-Sample Performance wird durch Verwendung der ermittelten
Modellparameter vom Vortag 1 auf den heutigen Tag ermittelt. Durch die
ex ante Analyse wird die Erklärungskraft der Modelle für den folgenden Handelstag
überprüft. Die Qualität der Bewertungsperformance wird einmal relativ als durchschnittliche prozentuale Abweichung und auch als durchschnittliche absolute Abweichung in € dargestellt. Vor der Präsentation der Ergebnisse werden die Inputfaktoren
und ihre Aufbereitung für die empirische Überprüfung dargelegt.
5.1 Datenbasis und Aufbereitung
Die Datenbasis für die vorliegende Studie umfasst alle Settlementdaten der DAX
Optionen im Untersuchungszeitraum vom 7. Dezember 2007 bis zum 24. Januar
2008. Dies entspricht 30 Handelstagen. Die börsentäglich von der Eurex ermittelten
Settlementpreise bilden die Basis für die Abrechnung der Kontrakte und spiegeln das
Marktgeschehen an dem betrachteten Tag wider (siehe Eurex [2008b]). Ein Vorteil
bei Verwendung dieser Preise ist die Zeitgleichheit der Daten, hiermit lassen sich etwaige Verzerrungen durch unterschiedliche Beobachtungszeitpunkte vermeiden.
Als Annäherung für den risikolosen Zins werden die jeweiligen Tageswerte des
EURIBOR verwendet (für 1 Woche und 1, 3, 6, 9 sowie 12 Monaten Laufzeit). Für die
längeren Laufzeiten dienen die Tageswerte der REX 2 Jahre, sowie REX 3 Jahre als
sicherer Zins. Um sicherzustellen, dass die Zinssätze exakt der Restlaufzeit der Optionen gleichen, werden die entsprechenden Zinssätze linear interpoliert. Den
Ausführungen in Abschnitt 3.3 folgend, werden die benötigten Kassa-Indexstände für
den DAX implizit aus den zeitgleichen Futures auf den DAX (FDAX) für jeden Tag
und jede Restlaufzeit ermittelt29.
Bei Inspektion der Querschnittsdaten von DAX Optionen zeigt sich, dass die
Handelsaktivität insbesondere bei kürzeren Restlaufzeiten sehr hoch ist. Bei längeren
Laufzeiten von über zwei Jahren finden nur noch sporadisch Umsätze statt. Aus die29
Ein ähnliches Verfahren verwendet die Deutsche Börse AG bei der Berechnung des VDAX. Auch
hier werden als sichere Zinssätze für längere Laufzeiten die Renditen aus den REX Kursindizes verwendet. Die Verwendung von implizit ermittelten Spotpreisen scheint gängige Praxis für Untersuchungen in Bezug auf Terminmärkte zu sein (vgl. z. B. Jackwerth/Rubinstein [2001]).
Simulationsstudie für DAX Optionen
| 48
sen Gründen finden nur Optionen bis Fälligkeit Dezember 2009 Berücksichtigung.
Weiter werden Optionen mit einer Restlaufzeit von unter sechs Tagen aus dem Datensatz entfernt. Damit wird vermieden, dass ungewöhnliche Preisschwankungen aufgrund von Positionsschließungen kurz vor Fälligkeit die Ergebnisse zu sehr
beeinflussen (vgl. z. B. Schmitt et Al [1997]). Zusätzlich werden die Optionen
gefiltert, die sehr weit aus dem Geld sind (|| ln⁄ 0.1), da diese nicht liquide gehandelt werden. Ausgeschlossen werden zusätzlich Optionen mit einem Preis
von unter € 0,50 (entspricht € 5 Kontraktwert*minimale Preisveränderung von
0,1 Indexpunkten).
5.2 Methodik und Kalibrierung
Wenn die Parameter der Modelle bekannt sind, lassen sich damit die Kursdynamik
modellieren und Optionsprämien bestimmen. In diesem Kapitel verhält es sich entgegengesetzt. Bei bekannten Marktdaten werden die latenten Variablen der vorgestellten
Modelle gesucht, welche die beobachteten Preise am besten wiedergeben können. In
Bezug auf eine arbitragefreie Bewertung von Optionen sollte das gesuchte Preismaß
: mit den quotierten Optionspreisen möglichst gut übereinstimmen. Eine ad hoc
Wahl eines solchen Martingalemaßes ist hierbei nicht zielführend. Es handelt sich
vielmehr um ein inverses Problem, bei dem die gesuchten Parameter so gewählt werden, dass die sich daraus ergebenden Werte die Marktpreise reproduzieren können.
Im Prinzip kann man dieses Vorgehen als Erweiterung der impliziten Bestimmung
von Black–Scholes Volatilitäten auf einen Fall mit mehreren Variablen betrachten.
Dieses Vorgehen wird als Kalibrierung bezeichnet.
Interessanterweise wird vielfach auf die Wichtigkeit von gut kalibrierten Modellen hingewiesen, zur eigentlichen Verfahrensweise um ökonomisch plausible Parameter zu erhalten, gibt es jedoch relativ wenig Literatur. Dabei ist eine robuste Kalibrierung ähnlich wichtig wie die Bewertung von Optionen selbst, wie
Lindström et Al [2006] betonen. Umfassende Darstellungen in diesem Kontext
finden sich auch bei Cont/Tankov [2004, Kapitel 13] und Galluccio/Le Cam
[2005]. Die folgenden Ausführungen beziehen sich im Wesentlichen auf diese
Arbeiten.
Bei der Kalibrierung handelt es sich um ein sehr rechenintensives Verfahren, bei
dem viele Optionspreise auf einmal bestimmt werden müssen. Da für die hier behandelten Modelle in der Regel keine geschlossenen Lösungen existieren, oder diese sehr
aufwändig sind, ist ein Algorithmus wünschenswert, welcher eine schnelle Bestimmung von Optionspreisen ermöglicht. Aufgrund der Spezifikationen der Modelle
lassen sich jedoch die charakteristischen Funktionen der log Renditen explizit
bestimmen. Durch eine inverse Fouriertransformation dieser charakteristischen
Funktionen erhält man die jeweiligen Randwahrscheinlichkeiten der Preisprozesse.
Simulationsstudie für DAX Optionen
| 49
Wie in Abschnitt 2.2 erörtert wird, lassen sich Optionspreise als transformierte
Preisprozesse auffassen. Dieser Logik folgend und unter Beachtung der Endbedingung aus Gleichung (2.1) bzw. (2.2) reduziert sich das Bewertungsproblem auf die
Lösung eines eindimensionalen Integrals. Eine explizite Darstellung dieser
Vorgehensweise und der Evaluierung des Integrals erfolgt in Anhang C.1.
Die Standardmethode zur Ermittlung der gesuchten Werte ist die Methode der
kleinsten Quadrate. Hierbei wird der Vektor von Parametern der jeweiligen Modelle Θ gesucht, welcher die Summe der quadrierten Fehler (sum of squared errors)
zwischen theoretischem und realem Preis minimiert
E
eeΘ min P ¢H £\H{¤¥ \H{J‡|¦¦ Θ£ $ !§¨©ª Θ, Θ1 .
¡
'
HR1
(5.1)
Diese Beziehung wird auch als objektive Funktion oder Verlustfunktion bezeichnet.
\H{¤¥ steht für den Marktpreis der Option \ und \H{J‡|¦¦ entspricht dem Modellpreis in Abhängigkeit der jeweiligen Modellparameter Θ. !§¨©ªΘ, Θ1 ist ein
Strafterm, der der Kalibrierung zusätzliche Stabilität verleihen kann und ¢H können
Gewichtungsfaktoren sein, die den einzelnen Beobachtungen ein vorher definiertes
Gewicht geben.
Einen bedeutenden Aspekt bei der Wahl geeigneter Gewichtungsfaktoren stellt
der hohe Zeitwert von Optionen bei langen Restlaufzeiten dar. Diese würden so gegenüber Optionen kürzerer Laufzeiten zu stark gewichtet. Detlefsen/Härdle [2006]
wählen Gewichtungsfaktoren, bei denen alle Laufzeiten den gleichen Einfluss auf die
objektive Funktion haben. Hierbei bekommt jede Laufzeit ein Gewicht ¢H 1⁄§ ,
wobei § die Anzahl der Laufzeiten bis zur betrachteten Laufzeit angibt. Um diese
Werte in einen passenden zeitlichen Kontext zu bringen, wird die individuelle
Restlaufzeit mit berücksichtigt. Es ergibt sich
Q
P
HR1
H ¢H
,
∑QHR1 ¢H
(5.2)
welches sich zu eins addiert. Huang/Wu [2004] betonen ebenfalls die Bedeutung
geeigneter Gewichtungsfaktoren zur Ermittlung robuster Ergebnisse und wählen ein
ähnliches Verfahren, um die verschiedenen Fälligkeiten vergleichbar zu gestalten.
!§¨©ªΘ, Θ1 |Θ Θ1 |' .
(5.3)
Eine Möglichkeit das Kalibrierungsproblem zu regularisieren bietet eine Darstellung
wie in (5.3). Die zu ermittelnden Werte werden hierbei über eine quadratische Abweichung an die Werte des Vortages bedingt. Die Verwendung eines Strafterms dieser
Simulationsstudie für DAX Optionen
| 50
Art ist einfach implementierbar und hat den Vorteil, dass sich die Modellparameter
im Zeitablauf konstanter verhalten. Die Verwendung der ermittelten Parameter des
Vortages Θ¬1 ist nicht problematisch, da die Modellparameter definitionsgemäß
konstant und niveauunabhängig sind. Andererseits ist die Verwendung bei der am
Markt nicht beobachtbaren instantanen Varianz ~ bzw. des Vortages nicht mit den
Modellannahmen vereinbar. Dies entspräche der Ermittlung eines Optionspreises
heute mit dem zu Grunde liegenden Aktienkurs von gestern (siehe z. B.
Nagel [2001, S. 151]) Die Varianz wird unter Verwendung der Regularisierung
weiterhin als freier Parameter betrachtet.
Wie Carr/Wu [2003] ausführen ist es ein Industriestandard ausschließlich OTM
Optionen für die Kalibrierung zu verwenden. \ entspricht demnach einem Call wenn
und einem Put, wenn . Begründet wird dieses Vorgehen dadurch, dass
OTM Optionen wesentlich liquider und modellsensitiver sind, als ihre ITM Äquivalente.
Die Methode der gewichteten kleinsten Quadrate wird einmal mit dem Strafterm
(penalised weighted least squares, PWLS) und einmal ohne (weighted least squares,
WLS) zur Ermittlung der latenten Parameter verwendet. Diese ist äquivalent zur Methode der maximum likelihood estimation (MLE), hierbei werden die Parameter solange variiert, bis die Wahrscheinlichkeit, dass die gesuchten Werte den echten Werten entsprechen, am höchsten ist (vgl. bspw. Carr/Wu [2003]).
Die sich ergebenden Implikationen durch die beiden unterschiedlichen Verfahren
zur impliziten Bestimmung des risikoneutralen Maßes : werden im Folgenden
diskutiert.
Um die risikoneutrale Dynamik der Modelle zu ermitteln, werden diese simultan
über alle Strikes und Laufzeiten kalibriert. Dies entspricht der bei
Bakshi et Al [1997] gewählten Vorgehensweise. Alternativ ließen sich die Modelle
auch je für eine Restlaufzeit anpassen, wie dies z. B. bei Bates [1996] gemacht wird.
Bei dieser Herangehensweise wird zu bedenken gegeben, dass nur die Modelle von
Heston, MJD–SV und FMLS–SV in der Lage sind eine Fristenstruktur abzubilden.
Bei MJD und FMLS sind die Volatilitätsparameter zeit-homogen, d. h. sie können
keine zeitliche Abhängigkeitsstruktur modellieren. Bei der Interpretation der
Ergebnisse werden diese Implikationen entsprechend berücksichtigt.
Je nach Anzahl und Interdependenzen der Parameter konvergiert die Kalibrierung über die Minimierung der objektiven Funktion (5.1) nicht immer zu einem
globalen Minimum. Es handelt sich in der Regel um ein nicht-konvexes
Optimierungsproblem mit nicht-linearen Abhängigkeiten. Es ist möglich eine exakt
gleiche Anpassungsgüte mit unterschiedlichen Kombinationen von Parametern zu
erhalten. Das bedeutet, dass man zum einen auf einen robusten
Optimierungsalgorithmus angewiesen ist und zum anderen auch die ermittelten
Werte immer kritisch zu hinterfragen hat, ob sie auch ökonomisch plausibel sind. In
dieser Untersuchung findet der BFGS Algorithmus Verwendung. Die Parameter der
Simulationsstudie für DAX Optionen
| 51
Modelle unterliegen diversen Beschränkungen, was ihren Wertebereich angeht, so
darf bspw. die Volatilität nicht negativ werden, der Korrelationskoeffizient muss zwischen -1 und 1 liegen etc. Um dies zu berücksichtigen werden diese Nebenbedingungen derart transformiert, dass der Optimierungsalgorithmus im gesamten Wertebereich der reellen Zahlen suchen kann (zum BFGS Algorithmus und der Variablentransformation siehe Anhang C.1).
Da 30 Tage an Querschnittsdaten zur Verfügung stehen, wird eine Zeitreihe mit
kalibrierten Variablen resultieren. Das ermöglicht einerseits zu beobachten, wie stabil
die Parameter im Zeitablauf sind und andererseits, wie sich die Regularisierung durch
einen Strafterm auf die Stabilität auswirken kann. Robuste Parameter sind für einen
Risikomanager oder Optionshändler von immenser Bedeutung, da er hiermit seine
Hedge-Ratios bestimmen wird. Auch illiquide Optionen, Over the Counter (OTC)
Optionen und auch Exotische Optionen werden mithilfe von Parametern bewertet,
die auf liquiden Plain Vanillas basieren. Die jeweiligen Eigenheiten der verschiedenen
Spezifikationen werden kurz skizziert.
Merton Jump Diffusion
Dem einfachen Diffusionsprozess aus (2.5) werden drei weitere Parameter hinzugefügt. Dieser zusammengesetzte Poissonprozess erklärt den Smirk von kurzlebigen
Optionen recht gut. Alle Parameter lassen sich reibungslos ermitteln und sind ökonomisch vertretbar. Eine Eigenschaft des Merton Modell ist die zunehmende Fristenstruktur. Das lässt sich darauf zurückführen, dass Sprünge allgemein das
Volatilitätsniveau anheben (siehe auch Sepp [2003]). Im Hinblick auf die länger
laufenden Optionen zeigt sich somit, dass das Modell nicht in der Lage ist eine inverse Fristenstruktur abzubilden.
Heston
Bei dem Modell von Heston mit fünf Parametern ergeben sich bei der Kalibrierung
keine nennenswerten Probleme. Alle Parameter sind ökonomisch nachvollziehbar.
Wenn man nur den kurzfristigen Smile abbilden möchte, ergeben sich unrealistisch
hohe Werte für die Mean Reversion . Diese mangelnde Variabilität lässt sich auf die
stetige Konzeption des Modells zurückführen. Für die längerfristigen Laufzeiten ergeben sich sehr gute Übereinstimmungen mit den Marktpreisen. Wie es für Aktienindizes üblich ist, kann die Beobachtung einer ausgeprägten negativen Korrelation ƒ auch
hier bestätigt werden.
Finite Moment Log Stable
Durch die ganzheitliche Konzeption mit nur zwei Parametern verläuft die Kalibrierung reibungslos. Der Smirk wird modellbedingt gut abgebildet. Defizite ergeben sich
in der Zeitdimension. Dies resultiert aus der Eigenschaft von Lévy Prozessen, dass die
Simulationsstudie für DAX Optionen
| 52
Parameter und somit auch der Volatilitätsfaktor zeit-homogen sind. Das FMLS Modell zeichnet sich als sehr ganzheitliche Konzeption aus, da nur ein zusätzlicher Parameter im Gegensatz zum Black–Scholes Modell hinzukommt.
Merton Jump Diffusion – Stochastic Volatility
Wie oben skizziert wird kann sowohl eine stochastische Volatilität, als auch die Integration von Sprüngen einen Smile erzeugen. Bei dem MJD–SV Modell sind diese beiden Aspekte kombiniert, d. h. die beiden Effekte überlagern sich. Mit der Kenntnis,
dass der kurzfristige Smirk auf Sprünge zurückzuführen ist und der langfristige Smile
auf die Effekte der stochastischen Volatilität, lässt sich das multidimensionale
Optimierungsproblem mit acht Parametern in Teilaufgaben zerlegen. Aus der
Spezifikation des Modells ist ersichtlich, dass der zusammengesetzte Poissonprozess
vom Volatilitätsprozess unabhängig ist. Damit besteht die Möglichkeit die Parameter
der Volatilitätsdiffusion zu fixieren und die Sprungintensität an die kurzlaufenden
Optionen anzupassen. Im nächsten Schritt werden diese wiederum fixiert und die
verbleibenden Parameter an die verbleibenden Laufzeiten kalibriert. Wie
Galluccio/Le Cam [2005] darlegen, bewegen sich optimale Werte der Mean Reversion bei MJD–SV Modellen stets im Bereich von [0,4; 0,7]. Bei dieser Studie erweist
sich  0,5 als guter Startwert. Dieser Parameter wird zu Beginn des beschriebenen
Prozederes auf diesen Wert fixiert und erst später an die Fristenstruktur angepasst.
Dadurch erklärt sich auch, dass die Mean Reversion im gesamten Untersuchungszeitraum nahe 0,5 liegt. Allgemein geht dieses Vorgehen meist mit einer minimal verringerten Anpassungsgüte einher, jedoch sinkt die Wahrscheinlichkeit in einem lokalen
Minimum zu enden, führt zu realistischen Parametern und ist zudem praktikabel.
Finite Moment Log Stable – Stochastic Volatility
Die Motivation diese Spezifikation zu untersuchen, folgt aus der Idee dem zeit-homogenen Volatilitätsparameter des FMLS Modells mehr Flexibilität zu erlauben. Für die
in Abschnitt 4.5 entwickelte Spezifikation gibt es nach meinem Kenntnisstand keine
vergleichbaren Arbeiten für den deutschen Markt.
Dieses Modell lässt sich von der Komplexität zwischen dem Heston und MJD–SV
Modell einordnen. Es zeigt sich, dass bei dieser Spezifikation der Mean Reversion
Parameter an einigen Tagen ungewöhnliche Werte anzeigt. Folgt man der
Argumentation von Weron/Wystup [2005, S. 172] lässt sich der Einfluss der Mean
Reversion durch eine höhere Volatilität der Varianz  kompensieren, so dass man 
fixieren kann und nur die restlichen Parameter kalibriert. Dieses Vorgehen erweist
sich als recht robust. Im Falle der Regularisierung ist dieses Vorgehen nicht notwendig, durch die Bedingung an den Vortag kann sich dieser Parameter nicht weit vom
Vortageswert entfernen. Die Aufgabe von stationären Zuwächsen erlaubt die Anpassung an verschiedene Volatilitätsniveaus in der Zeitdimension. Daraus ergibt sich
Simulationsstudie für DAX Optionen
| 53
eine deutlich bessere Anpassung an die Marktdaten in Bezug auf die verschiedenen
Strikes und Fälligkeiten.
Allgemein zeigt sich, dass bei der Volatilitätsdiffusion drei Parameter von Bedeutung
sind. Das langfristige Mittel der Volatilität € beeinflusst das ATM Niveau,  die
Konvexität des Smile und der Korrelationskoeffizient ƒ den Skew. Bei
Weron/Wystup [2005] wird eine detailierte Darstellung der einzelnen Parameter
geboten.
Bei den Sprungdiffusionen besteht ein direkter Zusammenhang zwischen der
Volatilität des Diffusionsprozesses und der Sprungintensität. Insbesondere zum Ende
des Untersuchungszeitraums erhöht sich die Sprungintensität vom 18. Januar auf den
21. Januar 2008 drastisch von 0,4 Sprüngen im Jahr auf über 2 und gleichzeitig reduziert sich die Volatilität von knapp 14 % auf 5 %, an einem Tag! Bei keinem anderen
Modell sind die Auswirkungen des Crash so deutlich wie beim MJD Modell.
Messung der Bewertungsperformance
Um die Anpassungsgüte der theoretisch ermittelten Preise gegenüber den Marktpreisen beurteilen zu können, bieten sich verschiedene Fehlermaße an (vgl. z. B.
Daal/Yu [2006] oder Schoutens [2003, S. 7]). Gängig in diesem Zusammenhang
sind
Mean Average Error (MAE)
­®¯ 1
P |¨° ±0©Θ|,
O
JxHJQI
(5.4)
Mean Average Relative Error (MARE)
­®²¯ 1
¨° ±0©Θ
³.
P ³
O
¨°
JxHJQI
(5.5)
Mit diesen Bewertungsfehlern wird die Qualität der Anpassung gemessen. MAE zeigt
an, wie hoch die durchschnittliche Fehlbewertung in € zum Marktpreis pro Prämie
ist. MARE bezieht hierbei die Höhe der Optionsprämien mit ein und gibt die durchschnittliche prozentuale Abweichung pro Prämie an.
5.3 In-Sample Performance
Wenn ein Modell an einen Querschnittsdatensatz von Optionen angepasst wird, sollte
man davon ausgehen, dass die Anpassung an diesem Tag sehr gut sein wird. Diese
Annahme in diesem Abschnitt überprüft. Hierbei werden die Modellparameter ein-
Simulationsstudie für DAX Optionen
| 54
mal mit und einmal ohne Strafterm ermittelt. Nur bei dem MJD–SV wird aufgrund
des mehrstufigen Kalibrierungsprozesses auf die Regularisierung verzichtet. In dem
Untersuchungszeitraum gab es marktweite Kursbewegungen, die so heftig waren, dass
der DAX von einem Tag auf den anderen so viele Punkte verloren hat, wie seit dem
11. September 2001 nicht mehr. Bei der Präsentation der Ergebnisse werden aus diesem Grund die Medianwerte mit angegeben, durch den Crash wird die einfache
Mittelwertbildung zum Teil empfindlich verzerrt. Auch sollten die ermittelten Werte
im Kontext der Anzahl von Freiheitsgraden der jeweiligen Modelle betrachtet werden. Ein Modell mit vielen Parametern wird eher in der Lage sein, die Marktgegebenheiten wesentlich besser abzubilden, als es ein Modell mit wenigen Parametern vermag.
In Tabelle 2 werden die Ergebnisse der In-Sample Analyse zusammengefasst. Zusätzlich sind in Abbildung 22 die hierbei ermittelten Werte im Zeitablauf illustriert.
Insgesamt zeigt sich, dass sich in den ersten 25 Tagen des Untersuchungszeitraums
keine nennenswerten Variationen der Parameter ergeben. Diese Situation ändert sich
abrupt vom 18.01.2008 auf den 21.01.2008. Hier zeigen sich bei allen Modellen zum
Teil starke Änderungen bei den ermittelten Werten.
Am deutlichsten wird dies beim MJD Modell, die Sprungintensität b springt von
0,4 pro Jahr auf über 2. Während bei den anderen Modellen die Volatilität zunimmt,
wird sie bei MJD durch die Sprungkomponente scheinbar überkompensiert. Zusätzlich mit dem Volatilitätsniveau steigen bei den SV Modellen die Werte für die Mean
Reversion  und  in ähnlichem Maße. Dies sind die beiden Werte, die am stärksten
schwanken. Abgelesen werden kann dies an der mit angegeben Standardabweichung
der Variablen.
Bei dem FMLS–SV stellt sich die Situation etwas anders dar. An dem zeithomogenen Modell FMLS erkennt man, dass die Parameter für die Volatilität relativ stabil
verlaufen. In Erweiterung als zeit-inhomogenes Modell erklärt sich somit für das
FMLS–SV, dass die Volatilität der Varianz  nicht so stark wie bei den
diffusionsbasierten Modellen variieren muss, um die neuen Marktumstände abzubilden. Beim FMLS–SV zeigt jedoch  eine höhere Variabilität an. Eine interessante
Beobachtung ist die absolut feste negative Korrelation von -1 für den gesamten
Zeitraum.
Das MJD–SV zeigt im Vergleich zu den anderen Modellen überall eine geringere
Schwankungsanfälligkeit. Vermutlich lässt sich dies auf hohe Zahl der Freiheitsgrade
und die oben beschriebenen Interdependenzen der Sprung- mit den
Diffusionsvariablen zurückführen. So können sich gegenläufige Effekte teilweise kompensieren. Eine weitere Auffälligkeit zeigt sich bei den Bewertungsfehlern im
Zeitverlauf. Die Sprungmodelle MJD und FMLS verlaufen bis zu dem Crash genau
entgegengesetzt den Bewertungsfehlern der Diffusionsmodelle. Irgendwie dazwischen
ist der Pfad für das FMLS–SV einzuordnen. Augenfällig ist zudem die inverse
Beziehung der absoluten € Abstände zu den Marktpreisen mit den relativen.
Simulationsstudie für DAX Optionen
| 55
Tabelle 2: In-Sample geschätzte Parameter, ohne Regularisierung (WLS). In der jeweils ersten Zeile
sind die Mittelwerte aus den 30 untersuchten Handelstagen angegeben. Darunter wird zusätzlich der
Median mit angegeben. In Klammern sind die Standardabweichungen der Parameter eingetragen. Bei
der instantanen Varianz ϑ0 handelt es eigentlich um eine Zustandsvariable und keinen Modellparameter, der Vollständigkeit halber werden die Werte mit angegeben.
Parameter
Tail Index
α
Volatilität
σ
Sprung
Parameter
λ
ω
η
Stochastische
Volatilität
κ
θ
σϑ
ρ
Instantane
Varianz
ϑ0
MJD
Heston
FMLS
MJD–SV
FMLS–SV
–
–
–
0,1186
0,1351
(0,0431)
0,4859
0,2447
(0,6204)
-0,3390
-0,3619
(0,0772)
0,1903
0,2044
(0,0544)
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
1,9555
1,5865
(0,7789)
0,0658
0,0658
(0,0028)
1,5721
1,5506
(0,0774)
0,1254
0,1209
(0,0162)
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
0,3670
0,3607
(0,1319)
-0,1132
-0,0669
(0,0821)
0,1847
0,1700
(0,0601)
0,5003
0,5004
(0,0010)
0,0685
0,0769
(0,0175)
1,4063
1,4149
(0,0486)
–
–
–
–
–
–
–
–
–
–
–
–
3,6739
3,5362
(1,0247)
0,0037
0,0029
(0,0041)
–
–
–
–
–
–
0,6975
0,5749
(0,3324)
-0,7733
-0,7893
(0,0823)
–
–
–
–
–
–
0,3720
0,4035
(0,1058)
-0,8416
-0,8509
(0,0916)
0,0974
0,1013
(0,0129)
-1,0000
-1,0000
(0,0000)
–
–
–
0,0507
0,0407
(0,0322)
–
–
–
0,0259
0,0262
(0,0045)
0,0230
0,0137
(0,0253)
Simulationsstudie für DAX Optionen
| 56
0,30
2,50
MJD
0,20
2,00
0,10
0,00
1,50
sigma
eta
-0,10
1,00
-0,20
-0,30
0,50
omega
lambda
-0,40
-0,50
0,00
0
5
10
15
20
25
30
5,00
0,20
0,18
0,16
0,14
0,12
0,10
0,08
0,06
0,04
0,02
0,00
4,00
3,00
2,00
1,00
0,00
-1,00
0
5
10
15
20
25
Heston
kappa
rho
sigmaV
theta
v0
30
1,90
0,18
1,80
0,17
1,70
0,16
1,60
FMLS
0,15
1,50
1,40
1,30
0,14
alpha
0,13
sigma
1,20
0,12
1,10
0,11
1,00
0,10
0
5
10
15
20
25
30
Abbildung 20: Geschätzte Parameter im Zeitablauf, ohne Regularisierung (WLS). Angegeben sind
die 30 Handelstage vom 7. Dezember 2007 bis zum 24. Januar 2008. Jeweils an der rechten Skala
abgetragen sind: MJD λ, Heston θ, ϑ0, FMLS σ, MJD–SV λ, σϑ, FMLS–SV θ, ϑ0 und σϑ.
Simulationsstudie für DAX Optionen
| 57
0,60
7,00
MJD-SV
0,40
6,00
kappa
0,20
5,00
theta
rho
0,00
4,00
v0
-0,20
3,00
-0,40
omega
2,00
-0,60
eta
-0,80
1,00
sigmaV
-1,00
0,00
lambda
0
5
10
15
20
25
30
7,00
0,14
6,00
0,12
5,00
0,10
FMLS-SV
kappa
rho
4,00
0,08
alpha
3,00
0,06
2,00
theta
0,04
1,00
0,00
0,02
-1,00
0,00
0
5
10
15
20
25
sigmaV
v0
30
Abbildung 20: Geschätzte Parameter im Zeitablauf, ohne Regularisierung (WLS), Fortsetzung.
Während die absoluten Abstände bis zum Crash im Allgemeinen recht gering sind,
zeichnen die prozentualen Differenzen ein diametrales Bild. Zu Beginn sind sie relativ
hoch, fallen abrupt ab steigen wieder langsam bis zum Crash, wo sie auf niedrigeres
Niveau abfallen. Die Mittel- und Medianwerte der Anpassungsgüten sind in Tabelle 4
aufgelistet. Insgesamt ist die Anpassung gemessen in € beim MJD–SV am besten,
dicht gefolgt vom Heston Modell. Auch das FMLS–SV Modell schneidet recht gut ab.
Anders stellt sich die Lage bei den relativen Abständen dar. Hier ist das Modell von
Heston deutlich überlegen.
Dieselbe Prozedur wurde für die Modelle (außer MJD–SV) mit einem Strafterm
wie in Gleichung (5.3) wiederholt (PWLS). Es wird hierbei geprüft, in wieweit ein
solches Vorgehen sich auf die Stabilität der Variablen auswirkt. Die Ergebnisse werden in Tabelle 3 präsentiert. Im Großen und Ganzen ähneln sich die Resultate mit
dem WLS Verfahren. Der Einfluss auf die beiden Lévy Modelle FMLS und MJD ist
verschwindend gering und wird daher nicht weiter thematisiert. Bei den beiden
regularisierten SV Modellen werden einige Punkte angesprochen. Die Variabilität von
 wird deutlich reduziert, bei FMLS–SV gar um die Hälfte. Das Niveau dieser
Variablen im Untersuchungszeitraum ist hierbei bei dem Heston Modell leicht
erhöht, während es bei dem FMLS–SV etwas niedriger liegt. Grafisch lässt sich das
gut in Abbildung 21 erkennen. Insbesondere  verläuft wesentlich ruhiger.
Simulationsstudie für DAX Optionen
| 58
Tabelle 3: In-Sample geschätzte Parameter, mit Regularisierung (PWLS). Aufbau wie in Tabelle 2.
Parameter
Tail Index
α
Volatilität
σ
Sprung
Parameter
λ
ω
η
Stochastische
Volatilität
κ
θ
σϑ
ρ
Instantane
Varianz
ϑ0
MJD
Heston
FMLS
FMLS–SV
–
–
–
0,1211
0,1351
(0,0388)
0,4326
0,2487
(0,4756)
-0,3419
-0,3598
(0,0674)
0,1850
0,2041
(0,0634)
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
2,0753
1,9397
(0,5028)
0,0653
0,0643
(0,0043)
1,5799
1,5510
(0,0831)
0,1269
0,1211
(0,0175)
–
–
–
–
–
–
–
–
–
–
–
–
–
–
–
1,3956
1,3940
(0,0475)
–
–
–
–
–
–
–
–
–
–
–
–
2,8225
2,6430
(0,5514)
0,0040
0,0031
(0,0041)
–
–
–
–
–
–
0,7510
0,7244
(0,2209)
-0,7370
-0,7517
(0,0839)
–
–
–
–
–
–
0,0951
0,0982
(0,0122)
-1,0000
-1,0000
(0,0000)
–
–
–
0,0493
0,0425
(0,0243)
–
–
–
0,0208
0,0137
(0,0201)
Die Auswirkung indes auf die Bewertungsperformance ist bei beiden Modellen unterschiedlich. Bei dem Modell von Heston steigen absoluter und relativer Fehler. Dies
erscheint auch logisch, da durch den Strafterm die ermittelten Parameter in der Nähe
und nicht bei ihrem Minimum (in Bezug auf die Kalibrierung) liegen. Für das FMLS–
SV zeigt sich das Gegenteil für die € Abstände. Ein Vergleich der Ergebnisse zwischen
Simulationsstudie für DAX Optionen
| 59
regularisierten Werten (PWLS) und nicht restringierter Kalibrierung (WLS) zeigt
somit ein uneinheitliches Bild.
0,30
2,50
MJD
0,20
2,00
0,10
0,00
1,50
sigma
eta
-0,10
-0,20
-0,30
1,00
omega
0,50
lambda
-0,40
-0,50
0,00
0
5
10
15
20
25
30
4,00
3,50
3,00
2,50
2,00
1,50
1,00
0,50
0,00
-0,50
-1,00
0,20
0,18
0,16
0,14
0,12
0,10
0,08
0,06
0,04
0,02
0,00
0
5
10
15
20
25
Heston
kappa
rho
sigmaV
theta
v0
30
1,90
0,18
1,80
1,70
1,60
0,17
FMLS
0,16
0,15
1,50
1,40
1,30
1,20
0,14
alpha
0,13
sigma
0,12
0,11
1,10
1,00
0,10
0
5
10
15
20
25
30
5,00
0,12
4,00
0,10
kappa
3,00
0,08
rho
2,00
0,06
alpha
1,00
0,04
theta
0,00
0,02
-1,00
0,00
FMLS-SV
sigmaV
v0
0
5
10
15
20
25
30
Abbildung 21: Geschätzte Parameter im Zeitablauf, mit Regularisierung (PWLS). Angegeben sind
die 30 Handelstage vom 7. Dezember 2007 bis zum 24. Januar 2008. Jeweils an der rechten Skala
abgetragen sind: MJD λ, Heston θ, ϑ0, FMLS σ, FMLS–SV θ, ϑ0 und σϑ.
Simulationsstudie für DAX Optionen
| 60
Tabelle 4: In-Sample Anpassungsgüte, ohne Regularisierung (WLS). In Klammern sind die
Standardabweichungen (Std Abw) angegeben. Zusätzlich ist die Parameteranzahl der Modelle aufgeführt.
Fehlermaß
Anzahl Parameter
MJD
Heston
FMLS
MJD–SV
FMLS–SV
4
5
2
8
6
MAE
in €
Mittelwert
Median
Std Abw
Min
Max
13,38
10,53
(9,76)
5,30
44,67
3,84
3,69
(1,04)
2,18
6,07
13,45
9,72
(11,11)
5,44
48,85
3,60
3,08
(2,22)
1,65
12,21
5,11
4,08
(3,09)
3,30
16,05
MARE
in %
Mittelwert
Median
Std Abw
Min
Max
16,38 %
15,24 %
(0,07)
5,82 %
33,46 %
5,08 %
4,52 %
(0,02)
1,86 %
10,18 %
19,46 %
19,16 %
(0,08)
9,26 %
40,68 %
10,12 %
7,55 %
(0,08)
1,15 %
27,45 %
11,83 %
9,40 %
(0,08)
3,51 %
33,96 %
Tabelle 5: In-Sample Anpassungsgüte, mit Regularisierung (PWLS). In Klammern sind die
Standardabweichungen (Std Abw) angegeben.
Fehlermaß
MAE
in €
MARE
in %
MJD
Heston
FMLS
FMLS–SV
Mittelwert
Median
Std Abw
13,60
10,65
(9,74)
4,09
3,92
(1,71)
13,70
9,87
(11,23)
4,90
4,05
(2,32)
Min
Max
5,30
44,63
2,29
9,36
5,44
48,85
3,44
12,36
Mittelwert
Median
Std Abw
16,07 %
14,80 %
(0,07)
5,47 %
5,14 %
(0,02)
19,17 %
18,94 %
(0,08)
11,44 %
8,82 %
(0,08)
Min
Max
5,82 %
33,47 %
2,07 %
10,72 %
9,26 %
40,68 %
3,45 %
33,96 %
Simulationsstudie für DAX Optionen
| 61
18,00
60,00
MAE
Mittlerer absoluter Fehler in €
16,00
50,00
14,00
12,00
40,00
10,00
30,00
8,00
Heston
MJD-SV
FMLS-SV
6,00
20,00
MJD
FMLS
4,00
10,00
2,00
0,00
0,00
0
5
10
15
20
25
30
45%
MARE
Mittlerer prozentualer Fehler
40%
35%
30%
MJD
25%
Heston
20%
FMLS
15%
MJD-SV
10%
FMLS-SV
5%
0%
0
5
10
15
20
25
30
Abbildung 22: Bewertungsfehler im Zeitablauf, ohne Regularisierung (WLS). Angegeben sind die
30 Handelstage vom 7. Dezember 2007 bis zum 24. Januar 2008. Oben: Mittlere absolute Preisabweichung in € (MAE). An der rechten Skala abgetragen sind die Modelle: MJD und FMLS. Unten: Mittlere
prozentuale Abweichung (MARE).
5.4 Out-of-the-Sample Performance
Die verschiedenen Anpassungstests über die Zeit geben eine Vorstellung über die
statistischen Eigenschaften der Modelle und ihre Fähigkeit, die beobachteten Preise
an dem betrachteten Tag abzubilden. Es zeigt sich, dass die direkte (WLS), als auch
regularisierte Anpassung (PWLS) die Marktpreise in akzeptabler Weise wiedergeben
können. Um die erklärende Kraft der Modelle für folgende Optionsprämien zu überprüfen, wird ein einmal ermittelter Parametersatz Θ von Tag 1 für den kommenden Tag verwendet. Die regularisierten Datensätze werden nur für das Modell von
Heston sowie FMLS–SV verwendet. Wie sich bei der In-Sample Analyse zeigt, ändern
sich die ermittelten Werte für die zeit-homogenen Modelle nur geringfügig. Somit
Simulationsstudie für DAX Optionen
| 62
lässt sich kein nennenswerter Einfluss bei der ex ante Analyse erwarten und für das
MJD–SV Modell wurde keine PWLS Schätzung vorgenommen. Dies könnte interessante Implikationen für die Out-of-the-Sample Analyse haben. Da die PWLS Werte
stabiler über die Zeit sind, könnte man vermuten, dass die Out-of-the-Sample Anpassungsgüte in diesem Falle besser ist. Dies könnte bedeuten, dass die besseren Ergebnisse der WLS Ermittlung bei der In-Sample Analyse auf einem Overfitting beruhen.
Damit sind zum Teil auf verrauschten Daten beruhende Messfehler gemeint.
Bei der Out-of-the-Sample Analyse werden die Preise mit den als konstant angenommenen Modellparametern des Vortages Θ1 und dem heutigen Wert für den
latenten Prozess der instantanen Varianz des betrachteten Tages ~ ermittelt. Um die
globale Anpassung der ermittelten Werte zu bestimmen, werden die oben dargelegten
Fehlermaße auch für die ex ante Analyse verwendet.
Tabelle 6: Out-of-the-Sample Anpassungsgüte, ohne Regularisierung (WLS).
Fehlermaß
MJD
Heston
FMLS
MJD–SV
FMLS–SV
MAE
in €
Mittelwert
Median
Std Abw
Min
Max
14,34
10,51
(11,34)
5,26
47,63
4,62
3,92
(2,28)
2,51
11,69
14,18
9,88
(11,74)
5,27
52,17
4,30
3,39
(3,03)
1,94
13,26
5,69
4,33
(3,26)
3,35
16,93
MARE
in %
Mittelwert
Median
Std Abw
Min
Max
15,95 %
14,60 %
(0,08)
5,88 %
34,26 %
5,41 %
4,98 %
(0,02)
2,36 %
10,58 %
19,53 %
19,72 %
(0,08)
9,58 %
40,04 %
11,56 %
9,62 %
(0,09)
1,18 %
33,65 %
11,85 %
8,56 %
(0,09)
2,83 %
34,15 %
Die resultierenden Zeitreihen für die Out-of-the-Sample Analyse ähneln den InSample Verläufen. Sie unterscheiden sich nur im Niveau. Für weitere grafische
Darstellungen wird auf den Anhang B.1 verwiesen. Bei Verwendung der freien
Modellparameter des Vortages zeigt sich, dass der durchschnittliche Bewertungsfehler
etwa um € 1 erhöht ist. In der Reihenfolge der besten Anpassungen kommt das FMLS
nun vor dem Modell von Merton. Bei der prozentualen Abweichung bleibt es bei dem
alten Bild. Aber das FMLS–SV ist nun gleichauf mit dem MJD–SV Modell. Es zeigte
sich im vorigen Abschnitt, dass die Regularisierung für die FMLS und MJD
Konzeptionen keinen großen Einfluss auf das Bewertungsproblem haben. Für die
Out-of-the-Sample Analyse werden demnach das Heston Modell und das FMLS–SV
Modell untersucht.
Simulationsstudie für DAX Optionen
| 63
Tabelle 7: Out-of-the-Sample Anpassungsgüte, mit Regularisierung (PWLS).
Fehlermaß
Heston
MAE
Mittelwert
in €
FMLS–SV
4,88
5,90
Median
Std Abw
Min
Max
4,25
(2,65)
2,29
11,98
4,33
(3,66)
3,36
17,50
MARE
Mittelwert
5,80 %
11,75 %
in %
Median
Std Abw
Min
Max
6,26 %
(0,02)
2,30 %
10,67 %
9,62 %
(0,09)
3,15 %
33,91 %
Es lassen sich keine Verbesserungen bei der Standardabweichung der Bewertungsabstände feststellen, die ein solches Vorgehen rechtfertigen würden. Interessant bleibt
das Verfahren aber aus dem Grund, dass das Kalibrierungsverfahren selber zusätzliche Stabilität erhält.
5.5 Kritische Würdigung
Die Resultate zeigen ein überraschendes Bild. Das Modell mit stochastischer Volatilität in Kombination mit Sprüngen ist mit drei zusätzlichen Parametern nur geringfügig besser als das Modell von Heston mit fünf. Der zusätzliche Aufwand ein so
umfangreiches Modell zu kalibrieren scheint für den untersuchten Zeitraum nicht
angemessen zu sein.
Die in Abschnitt 4.5 entwickelte Spezifikation erwies sich im Umgang als recht
robust und liefert gute Anpassungen. Die teilweise ungewöhnlichen Variationen der
Mean Reversion und eine negative Korrelation von -1, weisen daraufhin, diese
Konzeption näher zu untersuchen. Die Intention dieses Modells ist wie die vom
FMLS Modell von Grund auf ganzheitlich angelegt.
Durch die Möglichkeit unabhängige Prozesse über die Multiplikation ihrer
charakteristischen Funktionen zu kombinieren, kann dies als Basis für weitere
Spezifikationen dienen. Ein Vergleich der stochastischen Volatilitätsmodelle mit den
Sprungmodellen MJD und FMLS ist weder fair noch angebracht, da sich diese Konzepte Grund legend unterscheiden.
Die einfachen Lévy Prozesse sind definitionsgemäß nicht in der Lage die Volatilität im Zeitablauf zu modellieren. Bei Kalibrierungen an einzelne Laufzeiten können
Simulationsstudie für DAX Optionen
| 64
sie ihre Stärken ausspielen. Bei dem MJD insbesondere bei den kurzlaufenden Optionen. Damit wird auch die Schwäche des Heston Modells und allgemein der
Diffusionsmodelle deutlich. Sie können den kurzfristigen Smile kaum mildern. Es
gibt daher Überlegungen, die Parameter von Optionspreismodellen mit
zeitabhängigen Parametern zu modellieren. Für diese Richtung siehe z. B.
Mikhailov/Nögel [2003] oder Elices [2007].
Beachtung verdient das FMLS Modell. Mit nur einem zusätzlichen Parameter ist
es während dieses Untersuchungszeitraums mit dem Modell von Merton mit vier
Variablen gleichauf. Bei ähnlichen Ergebnissen ist immer die einfachere Variante zu
bevorzugen.
Allgemein zeigt sich, dass zeit-homogene Modelle wie die Lévy Prozesse nicht
flexibel genug sind um die Fristenstruktur von impliziten Volatilitäten an der Eurex
abzubilden. Modelle mit zeitveränderlichen Volatilitätsfaktoren schneiden ungleich
besser ab. Weron/Wystup [2005, S. 172] spekulieren, dass insbesondere das Modell
von Heston [1993] so gut abschneidet, weil es womöglich auf breiter Ebene in der
Praxis Anwendung findet.
Alle hier behandelten Modelle sind parametrische Modelle. Sie basieren auf vereinfachenden Annahmen bezüglich einer Preisdynamik. In der Realität wird das Marktgeschehen jedoch durch ein Interagieren von Individuen bestimmt, die nicht unbedingt
rational handeln. Ein spezifizierter stochastischer Prozess kann also nur eine
Annäherung für einen echten Preisprozess sein (vgl. Lindström et Al [2006]).
Auch ist die Notwendigkeit diese Modelle ständig zu kalibrieren, um sie in Übereinstimmung mit dem Markt zu bringen, ein Indiz für das sich ständig wandelnde
Umfeld. Es lässt sich festhalten, dass die Verwendung von Modellen, wie sie hier präsentiert werden, wesentlich näher an der Realität sind, als mit dem Standardmodell
von Black–Scholes.
6 Zusammenfassung und Ausblick
Mit ihrem Modell zur Bewertung von Optionen haben Black/Scholes [1973] und
Merton [1973] einen wichtigen Beitrag für die Bewertung von Optionen geliefert.
Zusammen mit dem Beginn des Derivatehandels an der Terminbörse in Chicago hat
dies zu einem regelrechten Boom geführt, der bis heute anhält. Ihre revolutionäre
Erkenntnis des Hedge-Portfolio führt zu dem Prinzip der risikoneutralen Bewertung
von Optionen und jedem anderen zustandsabhängigen Wertpapier.
Vielfach wird in der Literatur bestätigt, dass die für dieses Modell zu Grunde liegenden Annahmen sich als realitätsfremd erweisen. Alternative Konzepte werden
entwickelt, die sich mit den realen Daten bedeutend besser in Einklang bringen lassen. Dabei werden verschiedene Herangehensweisen gewählt. Zwei davon wurden in
dieser Arbeit berücksichtigt. Zum einen die diskontinuierlichen Pfade der Kursentwicklungen sowie die Beobachtung, dass die Volatilität im Zeitverlauf selbst variabel
ist.
Die zum Teil komplexen Preisprozesse konnten mit Hilfe der nützlichen Eigenschaften der Fourier Transformation und charakteristischen Funktionen in Optionswerte übersetzt werden. Diese wurden mit den Preisen von Optionen auf den DAX
über eine Dauer von 30 Handelstagen verglichen. Es zeigt sich, dass mit allen diesen
Varianten die qualitativen Daten der Realität bei der Bewertung von Optionen
berücksichtigt werden können.
Der Nutzen von charakteristischen Funktionen bei der Bewertung von Derivaten
lässt sich Grunde auf viele Bereiche in einem kapitalmarktheoretischen Kontext
anwenden. Eine natürliche Erweiterung der Sprungmodelle ist die Modellierung von
pfadabhängigen Wertpapieren wie z. B. Barrier Optionen. Auch können die Konzepte
bei der Modellierung von Ausfallwahrscheinlichkeiten verwendet werden. Eine Inversion der charakteristischen Funktion über die Fourier Transformation ist in diesem
Falle nicht mehr möglich. Es existieren jedoch Alternativen hierzu, mit denen eine
numerische Inversion der charakteristischen Funktion zur Berechnung von Randverteilungen möglich ist. So gibt es weiterhin einen analytischen Bewertungsrahmen.
Eine abschließende Beurteilung zu der Eignung der Modelle zur Bewertung von
Optionen kann im Prinzip nicht gegeben werden. Sie wurden lediglich kalibriert und
nicht getestet. Dass die Gesetze der Wahrscheinlichkeit im Kontext der behandelten
Thematik aber von wesentlicher Bedeutung sind, ist unbestritten. Diese Arbeit wird
in diesem Sinne mit einem Zitat von Bachelier [1900, S. 87] abgeschlossen:
„[…], I have compared the results of observation with those of theory, it was not to
verify formulas established by mathematical methods, but only to show that the market,
unwittingly, obeys a law which governs it, the law of probability.”
Anhang
A Grundlegende Begriffe und Konzepte der Wahrscheinlichkeitstheorie
Dieses Kapitel gibt einen kompakten Überblick über die wesentlichen Konzepte der
Maß- und Wahrscheinlichkeitstheorie, die zum Verständnis der Arbeit von Bedeutung sind. Sehr gute Darstellungen der folgenden Prinzipien finden sich bei
Schoutens [2003], Bauer [2002], Sandmann [1999], Cont/Tankov [2004] sowie
Irle [2003]. Für weitere Resultate und Darstellungen sei auf diese Quellen verwiesen.
A.1 Stochastische Prozesse, Filtrationen und Martingale
Um die Preisverläufe von Wertpapieren in stetiger Zeit formal abbilden zu können,
wird eine Darstellung benötigt, die es erlaubt Aktienkursverläufe als stochastische
Prozesse zu modellieren. Die Wahrscheinlichkeitstheorie bietet einen solchen
Modellierungsrahmen, der eine abstrakte und allgemeine Behandlung von stochastischen Abhängigkeiten ermöglicht.
Wahrscheinlichkeitsraum und Filtration
Angenommen wird ein endlicher Planungshorizont . Zur Definition von stochastischen Prozessen wird ein Wahrscheinlichkeitsraum benötigt (Ω, µ, ,. Die möglichen
Ergebnisse eines Zufallsexperimentes werden in einer nichtleeren Menge Ω
zusammengefasst, die Zustandsraum genannt wird. Alle möglichen Ergebnisse ω ’ Ω
eines Zufallsexperimentes heißen Elementarereignisse. Hinzu kommt ein System µ
von Ereignissen oder Teilmengen, eine -Algebra, , ordnet jedem Ereignis eine Eintrittswahrscheinlichkeit zu. Weiter gebe es eine Filtration · auf diesen
Wahrscheinlichkeitsraum. Eine Filtration ist eine nichtabnehmende Familie
· µ , 0 ¸ ¸ von Unter--Algebren von µ
µI ¹ µ ¹ µ ¹ µ für 0 ¸ e ¸ ¸ ,
(A.1)
wobei µ die Information zum Zeitpunkt t repräsentiert, und die Filtration
· µ , 0 ¸ ¸ ist der Informationsfluss über die Zeit.
Dies zusammen ergibt einen gefilterten Wahrscheinlichkeitsraum (Ω, µ, ,, ·.
Eine Filtration gibt also den Informationsverlauf auf einem Finanzmarkt an. Hierbei
geht keine Information verloren. Die Menge an Information bleibt gleich oder wächst.
Grundlegende Begriffe und Konzepte der Wahrscheinlichkeitstheorie
| 67
Stochastische Prozesse
Ein stochastischer Prozess, º »º , 0 ¸ ¸ ¼, ist eine Familie von Zufallsvariablen,
die auf einem Wahrscheinlichkeitsraum (Ω, µ, , definiert sind. Man sagt º ist auf
die Filtration · adaptiert, wenn º für jedes µ -messbar ist, º ist also zum Zeitpunkt bekannt. Durch die µ -Messbarkeit kann bestimmt werden, welchen Wert die
Zufallsvariable annimmt, wenn der Informationsstand bis beobachtet werden kann.
Die Evolution eines Aktienkurses entspricht so einem Pfad von Zufallsvariablen.
Bei der Modellierung von Aktienkursen wird oft unterstellt, dass die vergangenen
Kurse keinen Rückschluss auf künftige Kursentwicklungen zulassen. Der bis zum
Zeitpunkt bekannte Informationsverlauf ist dann irrelevant. Der beste Schätzer für
den Kurs morgen ist einfach der Kurs von heute. Oder wie Sandmann [1999, S. 241]
ausdrückt: „Ist die Gegenwart bekannt, so ist die Zukunft unabhängig von der Vergangenheit.“ Einen solchen Prozess nennt man Markoff Prozess. Voraussagen sind unsicher und werden in Wahrscheinlichkeiten ausgedrückt. Ein Markoff Prozess impliziert demnach, dass die Wahrscheinlichkeitsverteilung einer Aktie in der Zukunft
nicht davon abhängt, wo der Kurs gestern war. Wenn eine Aktie » , 0 ¸ ¸ ¼
einem solchen Markoff Prozess folgt und · µ , 0 ¸ ¸ den Informationsverlauf von angibt, ergibt sich für folgende funktionale Beziehung
*½ |µ *½ | .
(A.2)
Die Brownsche Bewegung ist ein Beispiel für solch einen Markoff Prozess.
Ein stochastischer Prozess º »º , ¾ 0 ¼ ist ein Martingale in Relation zu ,, ·,
wenn i) º an · adaptiert ist, ii) *|º | ∞ für alle ¾ 0 und iii) *º |µI ºI fast
sicher (,-f.s.) ist für 0 ¸ e ¸ .
Ein Martingale ist im Durchschnitt konstant, es handelt sich somit um ein
faires Spiel. Dies wird aus iii) ersichtlich, die beste Vorhersage für einen zukünftigen
Wert º bei Bekanntsein von µI , ist einfach der Wert von ºI . Oder speziell, der
Erwartungswert eines Martingale º zum Zeitpunkt gleicht seinem Anfangswert º
Martingale
*º |µ º .
(A.3)
Es handelt sich also um Prozesse, bei denen die zukünftigen Änderungen so schwanken, dass sich im Mittel stets Null ergibt. Es gibt keine positiven oder negativen
Trends.
Grundlegende Begriffe und Konzepte der Wahrscheinlichkeitstheorie
| 68
Äquivalentes Martingalemaß
Man sagt ein Wahrscheinlichkeitsmaß :, definiert auf (Ω, µ , ist ein äquivalentes
Martingalemaß, wenn
ˆ
ˆ
: äquivalent zu , ist, d. h. ein Ereignis, welches nicht unter , passiert, kann
auch nicht unter : passieren und vice versa (sie haben dieselben Nullmengen)
der abgezinste Aktienkursprozess ; »; , t ¾ 0¼ ein Martingale
unter : ist.
Die Existenz eines äquivalentes Martingalemaßes ist mit Abwesenheit von Arbitrage
verbunden, während ein eindeutiges äquivalentes Martingalemaß nur durch einen
vollständigen Märkt bestimmt werden kann.
In stetiger Zeit impliziert die Existenz eines äquivalentes Martingalemaßes
Arbitragefreiheit, wobei der umgekehrte Fall nicht unbedingt zutreffen muss. Die
Annahme von Arbitragefreiheit allein ist zu schwach, um ein äquivalentes
Martingalemaß abzuleiten. Diese Bedingung lässt sich verschärfen, wenn es nicht
möglich ist, eine Annäherung an eine Arbitragemöglichkeit zu erreichen. In diesem
Falle kann man daraus folgern, dass es ein äquivalentes Martingalemaß gibt.
Unter : entspricht die erwartete Rendite der Aktie genau dem Ertrag einer
risikolosen Verzinsung
*9 |µ .
(A.4)
A.2 Charakteristische Funktionen
Die Verteilung einer Zufallsvariablen X kann in drei äquivalenten Darstellungen
repräsentiert werden. Eine Möglichkeit ist die Wahrscheinlichkeitsdichtefunktion
(PDF), wie sie z. B. in Abbildung 5 dargestellt ist. Um Wahrscheinlichkeiten ausrechnen zu können, muss die Dichtefunktion ½Á über ein bestimmtes Intervall integriert
werden. Die kumulative Verteilung (2. Möglichkeit) einer Zufallsvariablen (CDF) XÁ
gibt die Wahrscheinlichkeit an, dass ein bestimmter Wert 8 nicht überschritten wird
Ã
XÁ 8 !»º ¸ 8 ¼  ½Á hdh.
Ä
(A.5)
Die Dichtefunktion entspricht somit der Ableitung der kumulativen Verteilung. Eine
dritte Möglichkeit ist, mit Hilfe einer charakteristischen Funktion eine Verteilung zu
beschreiben. Die charakteristische Funktion f einer Verteilung bzw. einer Zufallsvariablen º lässt sich als Erwartungswert ausdrücken
Grundlegende Begriffe und Konzepte der Wahrscheinlichkeitstheorie
fÁ h *›
HmÁ œ
yÄ
Â
Ä
lmà dXÁ ,
| 69
(A.6)
mit i √1 als imaginärer Einheit. Die charakteristische Funktion kann also Werte
aus dem komplexen Wertebereich annehmen. Es lässt sich zeigen, dass die
charakteristische Funktion die Fourier Transformierte einer Dichtefunktion ist
fÁ µ ½Á .
(A.7)
½Á µ 1 fÁ .
(A.8)
fÁyÇ h fÁ hfÇ h.
(A.9)
Im Umkehrschluss erhält man die Dichtefunktion einer Zufallsvariablen durch eine
inverse Fouriertransformation
Einige Eigenschaften von charakteristischen Funktionen sind f0 1 und
|f0| ¸ 1, für alle h ’ Å. Die charakteristische Funktion für eine Verteilungsfunktion existiert immer und ist stetig. Am Wichtigsten dürfte folgende Eigenschaft sein:
Durch f wird eine Verteilungsfunktion X eindeutig bestimmt.
Die charakteristische Funktion einer Summe von unabhängigen Zufallsvariablen
ist gleich dem Produkt ihrer charakteristischen Funktionen. Wenn z. B. º und Æ
unabhängige Zufallsvariablen sind und fÁ und fÇ ihre charakteristischen Funktionen, dann ist die charakteristische Funktion von º $ Æ gegeben durch
Mit anderen Worten: Die Verteilungsfunktion der Summe von º und Æ entspricht der
Konvolution bzw. Faltung der jeweiligen Verteilungsfunktionen.
Beispiele von charakteristischen Funktionen
Die charakteristische Funktion einer Normalverteilung Φ#, ' X8 1
√2— '
exp …
ist gegeben durch
fh exp …Ê#h º # '
ˆ,
2 '
(A.10)
' h'
ˆ.
2
(A.11)
Grundlegende Begriffe und Konzepte der Wahrscheinlichkeitstheorie
| 70
Für eine Poissonverteilung
Ë bÃ
,
8!
(A.12)
fh exp›bS là 1Tœ.
(A.13)
ist folgende Darstellung äquivalent
Man beachte, dass Gleichung (4.3) des Merton Jump Diffusion Modells genau der
Multiplikation der beiden obigen Gleichungen entspricht, nur dass die Drift adjustiert
wird, um die Eigenschaft eines Martingale sicherzustellen.
A.3 α-stabile Verteilungen
?-stabile Verteilungen bilden eine weite Klasse von Verteilungsfunktionen. Sie geht
auf Paul Lévy zurück, der sich zu Beginn des 20. Jahrhunderts mit unabhängigen und
identisch verteilten Zufallsvariablen beschäftigte. Für einen Tail Index ? von 2 ergibt
sich die Normalverteilung, für eine stabile Verteilung mit ? 2 wird die Varianz der
Verteilung unendlich und für ? 1 hat diese keinen Erwartungswert. Bis auf wenige
Ausnahmen existiert für die stabilen Verteilungen keine geschlossene Lösung. Dies
dürfte mit ein Grund dafür sein, dass sie im Bereich der Finanzwissenschaften bisher
nicht sehr verbreitet ist. Dennoch zeichnet sie sich durch Eigenschaften aus, mit denen sich beobachtbare Phänomene an Finanzmärkten gut beschreiben lassen. Auch
wenn das Phänomen der unendlichen Varianz und die damit verbundenen
Implikationen kontrovers diskutiert werden, nimmt die Literatur im
finanzwirtschaftlichen Kontext stetig zu. Durch leistungsfähige Rechner ist auch die
numerische Bestimmung der Wahrscheinlichkeitsdichtefunktion kein wirkliches
Problem mehr. Ein sehr umfassendes Werk zu vielfältigen Anwendungsbereichen
dieser Verteilungsklasse stellt die Arbeit von Rachev/Mittnik [1999] dar. Zu den
folgenden Ausführungen vgl. auch Schmid/Trede [2006, S. 56].
Gekennzeichnet wird die stabile Verteilung durch vier Parameter, wodurch eine
große Flexibilität gewährleistet wird. Der Tail Index ?, auch charakteristischer Exponent genannt, beeinflusst die Kurtosis einer Verteilung, d. h. wie viel Wahrscheinlichkeitsmasse im Zentrum bzw. an den Rändern einer Verteilung liegt. Für ? 2 ergibt
sich die Normalverteilung, für ? 1 die Cauchy Verteilung. Für diese beiden
Spezialfälle sind die Dichten und Verteilungsfunktionen bekannt. Im Kontext der
Finanzmarktstatistik wird in der Regel 1 ? ¸ 2 festgelegt, da es allgemein anerkannt ist, dass für Renditen ein Erwartungswert existiert.
Ein weiterer Parameter #̂ , gibt die Lage der Verteilung an und ist ein
Skalenparameter, der die Weite der Verteilung repräsentiert. Ferner kann eine stabile
Grundlegende Begriffe und Konzepte der Wahrscheinlichkeitstheorie
| 71
Verteilung asymmetrisch gestaltet werden, dies geschieht mit einem Schiefeparameter
”.
Für ? 2 ergeben sich dickere Enden einer Verteilung als bei der Normalverteilung. Des weiteren ist diese Verteilungsklasse in Bezug auf die Addition von unabhängig stabil verteilten Summanden abgeschlossen. Diese sind wiederum stabil verteilt
mit gleichem ?, nur evtl. mit anderem Lage- oder Skalenparameter.
Diese Eigenschaft lässt sich insbesondere bei der Skalierung von
Finanzmarktzeitreihen ausnutzen. Tagesrenditen sind dann z. B. mit gleichem ? verteilt, wie Wochenrenditen oder Monatsrenditen. Aufgrund dieser Eigenschaften und
Flexibilität der stabilen Verteilung schlägt Mandelbrot [1963] vor, diese als
Preisprozess für Finanztitel zu verwenden.
Eine Wahrscheinlichkeitsfunktion für die stabile Verteilung ergibt sich durch eine
inverse Fourier Transformation folgender charakteristischer Funktion
—?
exp 2|h| –1 i”signh tan 2 3 $ i#̂ h˜3 , α Ò 1
2
“
f h Î
2
exp - |h| i1 $ i” signh ln|h|r $ i#̂ h. , ? 1
—
(A.14)
wobei signh eine Vorzeichenfunktion darstellt.
A.4 Lévy Prozesse
Die im Verlauf der Arbeit immer wieder erwähnten Prozesse: Wiener Prozess,
(zusammengesetzter) Poissonprozess und auch die stabile Verteilung stellen allesamt
Beispiele von Lévy Prozessen dar.
Zuerst wird angenommen, dass fh die charakteristische Funktion einer Verteilung sei. Wenn, für jedes positive und ganzzahlige §, f h auch die §-te Potenz einer
charakteristischen Funktion ist, handelt es sich um eine unendlich teilbare Verteilung.
Durch folgende Eigenschaften wird ein Lévy Prozess º definiert:
Der Startwert von º ist 0, fast sicher. Die Zuwächse sich unabhängig und statio-
när, d. h. ein Zuwachs über e, e $ mit e, ¾ 0, also ºyI ºI , hat SfhT als ihre
charakteristische Funktion.
Die Pfade von Lévy Prozessen sind rechtsseitig stetig. Für die linke Seite existieren Grenzwerte. Das bedeutet, dass die Zufallspfade eines Lévy Prozess Sprünge
enthalten können.
Die Eigenschaft der unendlichen Teilbarkeit macht Lévy Prozesse insbesondere
im Kontext der Modellierung von Preisprozessen interessant. Die Summe von
stationären und unabhängigen Zufallsvariablen entspricht wiederum der Verteilung,
aus der sie stammen. Die Verteilung eines Lévy Prozess ist also komplett durch eine
eindimensionale Verteilung determiniert. Dies lässt sich folgendermaßen darstellen
Grundlegende Begriffe und Konzepte der Wahrscheinlichkeitstheorie
*› lmÁ_ œ S*› HmÁ_ œT .
| 72
(A.15)
Die Verteilung eines Lévy Prozess ist demnach unabhängig vom Zeitpunkt . Aufgrund der Darstellung durch charakteristische Funktionen, ist über die Fourier Transformation immer auch die Dichtefunktion bekannt. Mit dieser sehr kurzen Darstellung wird der potenzielle Nutzen für die Modellierung von Preisdynamiken skizziert.
Bei Schoutens [2003] werden weitere Resultate und insbesondere die Anwendung
von Lévy Prozessen für die Bewertung von Optionen ausführlich diskutiert.
B Bewertungsperformance der Modelle
An dieser Stelle werden weitere Illustrationen in Bezug auf die Prognosequalität der
untersuchten Modelle dargestellt. Beispielhaft wird zudem die Volatilitätsoberfläche
vom 7. Dezember 2007 präsentiert. Diese wird mit den Volatilitätsoberflächen verglichen, die aus den kalibrierten Modellen an diesem Tag resultieren. Ferner werden die
Differenzen zwischen den realen mit den theoretischen impliziten Volatilitäten für
alle Strike/Laufzeitkombinationen mit Hilfe von 3 D–Balkendiagrammen veranschaulicht.
Zudem wird unten die Übereinstimmung von Marktpreisen mit den
korrespondierenden theoretischen MJD Preisen demonstriert. Die Darstellungen für
die anderen Modelle unterscheiden sich nur geringfügig und werden nicht extra
aufgeführt. Im Vergleich zu Abbildung 9 stimmen die theoretischen Preise sehr gut
mit den Marktquotierungen überein.
1.600
1.400
Optionspreis
1.200
1.000
800
600
400
200
0
7200
7400
7600
7800
8000
Basispreis K
8200
8400
8600
8800
Abbildung 23: Reale und MJD Preise für den 7. Dezember 2007. Die Kreise repräsentieren die
Marktpreise und die Pluszeichen die Modellpreise.
Bewertungsperformance der Modelle
| 74
B.1 Weitere Ergebnisse der Simulationsstudie
In diesem Abschnitt werden die In-Sample Schätzergebnisse mit Regularisierung
(PWLS) sowie sämtliche Darstellungen für die Out-of-the-Sample Analyse über den
Untersuchungszeitraum vom 7. Dezember 2007 bis zum 24. Januar 2008 illustriert.
Dies entspricht 30 Handelstagen.
14,00
60
MAE
Mittlerer absoluter Fehler in €
12,00
50
10,00
40
Heston
8,00
30
6,00
FMLS SV
MJD
20
4,00
2,00
10
0,00
0
0
5
10
15
20
25
FMLS
30
45%
MARE
Mittlerer prozentualer Fehler
40%
35%
30%
MJD
25%
Heston
20%
FMLS
15%
FMLS-SV
10%
5%
0%
0
5
10
15
20
25
30
Abbildung 24: In-Sample Bewertungsfehler im Zeitablauf, mit Regularisierung (PWLS). Oben:
Mittlere absolute Preisabweichung in € (MAE). An der rechten Skala abgetragen sind die Modelle:
MJD und FMLS. Unten: Mittlere prozentuale Abweichung (MARE).
Bewertungsperformance der Modelle
| 75
18,00
60
MAE
Mittlerer absoluter Fehler in €
16,00
50
14,00
12,00
40
10,00
30
8,00
Heston
MJD-SV
FMLS-SV
6,00
20
MJD
FMLS
4,00
10
2,00
0,00
0
0
5
10
15
20
25
30
45%
MARE
Mittlerer prozentualer Fehler
40%
35%
30%
MJD
25%
Heston
20%
FMLS
15%
MJD-SV
10%
FMLS-SV
5%
0%
0
5
10
15
20
25
30
Abbildung 25: Out-of-the-Sample Bewertungsfehler im Zeitablauf, ohne Regularisierung (WLS).
Oben: Mittlere absolute Preisabweichung in € (MAE). An der rechten Skala abgetragen sind die Modelle: MJD und FMLS. Unten: Mittlere prozentuale Abweichung (MARE).
Bewertungsperformance der Modelle
| 76
20,00
MAE
Mittlerer absoluter Fehler in €
18,00
16,00
14,00
12,00
10,00
Heston
8,00
FMLS-SV
6,00
4,00
2,00
0,00
0
5
10
15
20
25
30
40%
MARE
Mittlerer prozentualer Fehler
35%
30%
25%
20%
Heston
15%
FMLS-SV
10%
5%
0%
0
5
10
15
20
25
30
Abbildung 26: Out-of-the-Sample Bewertungsfehler im Zeitablauf, mit Regularisierung (PWLS).
Oben: Mittlere absolute Preisabweichung in € (MAE). An der rechten Skala abgetragen sind die Modelle: MJD und FMLS. Unten: Mittlere prozentuale Abweichung (MARE).
Bewertungsperformance der Modelle
| 77
B.2 Implizite Volatilitätsoberfläche vom 7. Dezember 2007
In Tabelle 8 wird die implizite Volatilitätsmatrix vom 7. Dezember 2007 für die
ODAX Optionen dargestellt. Mit aufgelistet sind benötigten Inputfaktoren für die
Bestimmung von den impliziten Volatilitäten. Aus Gründen der Übersichtlichkeit
wird auf die kürzeste Laufzeit von 14 Tagen und längste Laufzeit von 742 Tagen verzichtet. ∆ Div gibt die in Abschnitt 3.3 beschriebene Differenzdividende an. Adj. Spot
steht für die implizit ermittelten Kassa-Indexstände je Laufzeit.
Abbildung 27 zeigt die impliziten Volatilitäten als Kombination in der Strike mit
der Laufzeitdimension an. An diesem Tag herrscht ein relativ niedriges Volatilitätsniveau. Aus der steigenden Volatilität in der Zeitdimension lässt sich folgern, dass die
Marktteilnehmer in Zukunft ein höheres Niveau antizipieren.
Tabelle 8: Implizite Volatilitätsmatrix für DAX Optionen vom 7. Dezember 2007.
Zins 0,0488
0,0488
0,0488
0,0483
0,0479
0,0472
0,0419
0,1151
0,1918
0,2877
0,5397
0,7863
1,0356
1,5342
42
70
105
197
287
378
560
-4,18
-7,06
-8,02
-16,70
-28,36
-36,95
-4,27
7988,36
7985,48
7984,52
7975,84
7964,18
7955,59
7988,27
Jan 08
Feb 08
Mrz 08
Jun 08
Sep 08
Dez 08
Jun 09
7200
0,2189
0,2286
0,2324
0,2330
0,2370
0,2396
0,2397
7300
0,2112
0,2217
0,2262
0,2284
0,2329
0,2363
0,2369
7400
0,2037
0,2148
0,2201
0,2237
0,2288
0,2330
0,2342
7500
0,1957
0,2075
0,2138
0,2190
0,2247
0,2294
0,2315
7600
0,1876
0,2002
0,2074
0,2142
0,2206
0,2261
0,2288
7700
0,1790
0,1928
0,2012
0,2093
0,2166
0,2226
0,2261
7800
0,1702
0,1853
0,1949
0,2046
0,2125
0,2191
0,2235
7900
0,1615
0,1777
0,1884
0,1997
0,2085
0,2156
0,2207
8000
0,1532
0,1705
0,1820
0,1948
0,2045
0,2121
0,2181
8100
0,1457
0,1633
0,1755
0,1899
0,2007
0,2086
0,2155
8200
0,1389
0,1564
0,1692
0,1851
0,1968
0,2051
0,2130
8300
0,1335
0,1502
0,1633
0,1803
0,1929
0,2016
0,2104
8400
0,1292
0,1448
0,1578
0,1757
0,1892
0,1983
0,2079
8500
0,1263
0,1403
0,1531
0,1715
0,1856
0,1951
0,2053
8600
0,1243
0,1367
0,1488
0,1676
0,1822
0,1919
0,2029
8700
0,1234
0,1336
0,1452
0,1641
0,1790
0,1889
0,2003
8800
0,1232
0,1312
0,1422
0,1608
0,1757
0,1858
0,1979
Restlaufzeit Tage
∆ Div
Adj. Spot
Fälligkeit
Strike
Bewertungsperformance der Modelle
| 78
24%
Implizite Volatilität
22%
22%-24%
20%
20%-22%
18%
18%-20%
16%
16%-18%
14%
Jun 09
12%
Sep 08
10%-12%
8800
Jan 08
8700
8500
8300
8400
8200
8100
7900
12%-14%
Fälligkeit
8600
Strike
8000
7700
7800
7500
7600
Mrz 08
7400
7200
7300
10%
14%-16%
Abbildung 27: Implizite Volatilitätsoberfläche von DAX Optionen für den 7. Dezember 2007.
Bewertungsperformance der Modelle
| 79
B.3 Merton Jump Diffusion
28%
26%-28%
Implizite Volatilität
26%
24%
24%-26%
22%
22%-24%
20%
20%-22%
18%
18%-20%
16%
Jun 09
14%
12%
14%-16%
Sep 08
12%-14%
Fälligkeit
10%-12%
8800
8600
8700
8500
8300
8400
8100
Strike
8200
7900
8000
7800
7600
7700
7400
Mrz 08
7500
7200
7300
10%
Jan 08
16%-18%
Abbildung 28: Implizite Volatilitätsoberfläche Merton Jump Diffusion. DAX Optionen vom
7. Dezember 2007.
1,0%
Diffrerenz in der Volatilität
Jan 08
0,0%
Feb 08
-1,0%
Mrz 08
-2,0%
Jun 08
-3,0%
Sep 08
Jun 09
-4,0%
Dez 08
Sep 08
-5,0%
Jun 09
Mrz 08
Jan 08
-6,0%
Strike
Abbildung 29: Differenz in der Volatilität von Markt und Modell, MJD.
Fälligkeit
Bewertungsperformance der Modelle
| 80
B.4 Heston Stochastic Volatility
Implizite Volatilität
26%
24%
24%-26%
22%
22%-24%
20%
20%-22%
18%
18%-20%
16%
16%-18%
14%
Jun 09
12%
Sep 08
8800
8700
Jan 08
8600
8400
8500
8200
Fälligkeit
8300
8000
8100
7900
7700
7800
7500
7600
7300
Strike
12%-14%
10%-12%
Mrz 08
7400
7200
10%
14%-16%
Abbildung 30: Implizite Volatilitätsoberfläche Heston. DAX Optionen vom 7. Dezember 2007.
Dez 07
Differenz in der Volatilität
1,0%
Jan 08
0,5%
Feb 08
0,0%
Mrz 08
-0,5%
Jun 08
-1,0%
Dez 08
Jun 08
Feb 08
Fälligkeit
Dez 07
-1,5%
-2,0%
-2,5%
Strike
Abbildung 31: Differenz in der Volatilität von Markt und Modell, Heston.
Sep 08
Dez 08
Jun 09
Bewertungsperformance der Modelle
| 81
B.5 Finite Moment Log Stable
28%
26%-28%
Implizite Volatilität
26%
24%
24%-26%
22%
22%-24%
20%
20%-22%
18%
18%-20%
16%
Jun 09
14%
12%
Sep 08
Fälligkeit
8800
8600
Jan 08
8700
8500
8400
8200
8300
8000
10%-12%
8100
7800
7900
7600
7700
7400
14%-16%
12%-14%
Mrz 08
7500
7200
7300
10%
16%-18%
Strike
Abbildung 32: Implizite Volatilitätsoberfläche FMLS. DAX Optionen vom 7. Dezember 2007.
Dez 07
Differenz in der Volatilität
2,0%
Jan 08
1,0%
0,0%
-1,0%
-2,0%
-3,0%
-4,0%
-5,0%
-6,0%
-7,0%
Feb 08
Mrz 08
Jun 08
Dez 08
Jun 08
Feb 08
Fälligkeit
Dez 07
Strike
Abbildung 33: Differenz in der Volatilität von Markt und Modell, FMLS.
Sep 08
Dez 08
Jun 09
Bewertungsperformance der Modelle
| 82
B.6 Merton Jump Diffusion – Stochastic Volatility
Implizite Volatilität
26%
24%
24%-26%
22%
22%-24%
20%
20%-22%
18%
18%-20%
16%
Jun 09
14%
12%
Sep 08
16%-18%
14%-16%
12%-14%
10%-12%
8800
8600
Jan 08
8700
8500
8300
8400
8100
Strike
8200
7900
8000
7700
Fälligkeit
7800
7600
7400
Mrz 08
7500
7200
7300
10%
Abbildung 34: Implizite Volatilitätsoberfläche MJD–SV. DAX Optionen vom 7. Dezember 2007.
Dez 07
Differenz in der Volatilität
1,0%
Jan 08
Feb 08
0,0%
Mrz 08
-1,0%
Jun 08
-2,0%
Dez 08
Jun 08
Feb 08
Fälligkeit
Dez 07
-3,0%
-4,0%
Strike
Abbildung 35: Differenz in der Volatilität von Markt und Modell, MJD–SV.
Sep 08
Dez 08
Jun 09
Bewertungsperformance der Modelle
| 83
B.7 Finite Moment Log Stable – Stochastic Volatility
28%
26%-28%
24%
24%-26%
22%
22%-24%
20%
20%-22%
18%
18%-20%
16%
Jun 09
14%
12%
10%
8700
14%-16%
Fälligkeit
10%-12%
8800
8600
8500
8300
8400
8100
8200
7900
8000
7800
7600
7700
7400
Strike
Jan 08
16%-18%
12%-14%
Mrz 08
7500
7200
Sep 08
7300
Implizite Volatilität
26%
Differenz in der Volatilität
Abbildung 36: Implizite Volatilitätsoberfläche FMLS–SV. DAX Optionen vom 7. Dezember 2007.
1,0%
Dez 07
0,0%
Jan 08
-1,0%
Feb 08
-2,0%
Mrz 08
-3,0%
Jun 08
Dez 08
Jun 08
Feb 08
Dez 07
-4,0%
-5,0%
-6,0%
Fälligkeit
Sep 08
Dez 08
Jun 09
Strike
Abbildung 37: Differenz in der Volatilität von Markt und Modell, FMLS–SV.
C Anmerkungen zur Implementierung der Modelle
C.1 Bewertung von Optionen mittels komplexer Fourier
Transformation
Die Modelle sind in ihrer Struktur derart gestaltet, dass die charakteristischen
Funktionen der Preisprozesse explizit bestimmt werden können und sich anschließend mittels Fourierinversion Optionspreise ermitteln lassen.
Genau genommen handelt sich bei den hier behandelten Konzeptionen um Modelle, die in ihrer Struktur affin gestaltet sind.
Affine Prozesse
In der modernen Finanzanalyse erweisen sich affine Prozesse als ein sehr nützliches
Werkzeug. In Erscheinung treten sie bei der Bewertung von Optionen, der Modellierung von Zinssätzen sowie Kreditderivaten und zunehmend auch im Bereich der
Portfolio Allocation. Die geometrisch Brownsche Bewegung ist das einfachste Beispiel einer affinen Struktur.
Ein Prozess ln ist affin, wenn die charakteristische Funktion von ln ,
9 lm ÔÕ CÖ
œ sich in einer exponentiellen affinen Form exp ¨, , h $
* ›
×, , hln darstellen lässt. ¨ und × sind hierbei komplexe Funktionen von h.
Für das Beispiel von Black–Scholes ergibt sich
* › lm ÔÕ CÖ œ expi ' ⁄2 h ' ⁄2h' $ ih ln .
(C.1)
*9 › lm ÔÕ CÖ œ exp¨ , h $ × , h ' $ ih ln ,
(C.2)
9
Auf diese Weise bieten affine Strukturen Flexibilität und gleichzeitig eine gute Handhabbarkeit. Sie erlauben, dass Renditen seriell korreliert sein können, verschiedene
Wertpapiere können miteinander korrelieren und auch Sprünge können berücksichtigt werden, was insbesondere zur Modellierung von Aktienkursen (Fat Tails) von
Bedeutung ist. Durch die affine Struktur einer charakteristischen Funktion können
oftmals die Koeffizienten ¨ und × in geschlossener Lösung evaluiert werden. Mit einer inversen Fouriertransformation können auf diese Weise direkt die risikoneutralen
Verteilungen und damit Optionpreise ermittelt werden.
Bei dem Modell von Heston sind bspw. zwei Brownsche Bewegungen miteinander korreliert. Die charakteristische Funktion von ln hat hierbei die folgende exponentielle affine Form
Anmerkungen zur Implementierung der Modelle
| 85
wobei ¨ und × in geschlossener Form bekannt sind. Im Fall von Heston entspricht die
obige Darstellung genau der von Gleichung (4.8), wobei ¨ , h und × U, h
entspricht (siehe zu diesen Ausführungen Černý [2004, S. 170]).
Im Folgenden wird skizziert, wie sich mit Hilfe der komplexen Fourier Inversion direkt Optionspreise ermitteln lassen.
Ökonomische Bedeutung charakteristischer Funktionen
Im Prinzip lassen sich Modelle, wie sie hier betrachtet werden, mit einer Formel á la
Black–Scholes berechnen
, , Π1 Π' ,
(C.3)
Π1 bezeichnet das Delta einer Option und Π' gibt die Wahrscheinlichkeit an im Geld
zu enden. Vorausgesetzt die charakteristische Funktion f ist bekannt, ergeben sich
die beiden Π als inverse Fourier Transformationen
Ä
1 1
lm¥ fh i
ˆ dh,
Π1 $  Re …
2 —
ih
Ä
1 1
lm¥ fh
Â
…
ˆ dh,
Π' $
Re
2 —
ih
(C.4)
(C.5)
mit i √1 und ° ln 2Ù 3 $ .
C
Diese Darstellung wird von Bakshi/Madan [2000] ausführlich dargelegt und die
Autoren liefern zusätzlich eine ökonomische Interpretation von charakteristischen
Funktionen. Sie argumentieren, dass durch die charakteristischen Funktionen implizit Zustandsräume vervollständigt werden (Spanning). Dies ist im Zusammenhang
der Vollständigkeit von Märkten und Arrow-Debreu Wertpapieren von Bedeutung.
Arrow-Debreu Wertpapiere versprechen in einem bestimmten Zustand in der Zukunft eine Zahlung von eins, in allen anderen von null. Die Gesamtheit dieser
zustandsabhängigen Zahlungen ergibt eine Zustandspreisdichte, auf einem
vollständigen Markt ist diese mit einer risikoneutralen Dichtefunktion äquivalent
(siehe Wallmeier [2003, S. 66]). Bei gegebenen Preisen aller möglichen ArrowDebreu Wertpapiere lässt sich jedes andere Wertpapier, welches eine vom Kurs des
Underlyings abhängige Zahlung liefert, eindeutig und arbitragefrei bewerten. Diese
Erkenntnis geht auf die Arbeit von Breeden/Litzenberger [1978] zurück. Eine
Anmerkungen zur Implementierung der Modelle
| 86
Diskussion zu Zustandspreisen und Martingalemaßen im Rahmen des Black–Scholes
Modells findet bei Sandmann [1999] statt.
Bakshi/Madan [2000] können zeigen, dass die Vervollständigung von Wertpapiermärkten durch Optionen mit einer Vervollständigung über charakteristische
Funktionen austauschbar ist.
fÔÕ CÖ h *9 › lmÔÕ CÖ œ
*9 coshln $ i sinhln (C.6)
Man kann sich nun zwei bedingte Ansprüche von ln mit den Auszahlungen
coshln und sinhln vorstellen. Bei dieser Sichtweise ist fÔÕ CÖ h ein
Wertpapier, welches aus zwei trigonometrischen Funktionen besteht, während der
Aktienkurs der Exponent von ln ist. Für die Äquivalenz des Spanning durch
Optionen und charakteristische Funktionen gelten die beiden folgenden Bedingungen
Ä
coshln 1 Â h' cos hln max0, ln ln dln Ä
sinhln ln  h' cos hln max0, ln ln dln (C.7)
(C.8)
Diese beiden Ausdrücke zeigen, dass die trigonometrischen Funktionen als
Auszahlungen von Optionen dargestellt werden können. Diese Ausführung wird bei
Zhu [2000, S. 10] ausführlich dargelegt.
Verwendete Formel zur Bestimmung von Optionspreisen
So intuitiv die obige Darstellung erscheint, verlangt sie, dass zwei komplexwertige
Integrale gelöst werden. Lewis [2001] hat eine alternative Darstellung gefunden, bei
der lediglich ein Integral zu lösen ist. Lewis transformiert hierbei den Pay Off einer
Option, um zu folgendem Preisfunktional zu gelangen
Ä
1
i
dh
, , √ /' Â Re i lm¥ f -h .r
.
—
2 h' $ 1
4
(C.9)
Dies ist die zu Grunde liegende Bewertungsformel für die Simulationsstudie. Put Optionen lassen sich durch Anwendung der Put-Call Parität berechnen. Im Vergleich zu
(C.4) gibt es einen quadratischen Term im Nenner, mit der Folge, dass das Integral
wesentlich schneller konvergiert. Abbildung 38 zeigt den beispielhaft den Verlauf des
Integranden bei dem FMLS–SV Modell.
Anmerkungen zur Implementierung der Modelle
| 87
4,0
FMLS-SV Integrand
3,5
Integral (u)
3,0
2,5
2,0
1,5
1,0
0,5
0,0
0
1
1
2
2
3
u
3
4
4
5
5
Abbildung 38: Integrand des FMLS–SV Modells bei der numerischen Integration. Zu Grunde
liegen dieselben Daten wie bei Abbildung 19.
Numerische Evaluierung der Integrale
Die gesuchten Werte für die Integrale lassen sich nur numerisch annähern, eine Möglichkeit hierfür besteht in der Verwendung einer Gaußschen Quadratur. In diesem
Falle liegt der Integrationsbereich bei 0, ∞, für diesen Bereich bietet sich die GaußLaguerre Quadratur an. Dieses Vorgehen ermöglicht eine recht genaue Annäherung
unter Vermeidung unnötig vieler Berechnungen
Ä
E
 ½ 8 08 Ý P cH ½ 8H ,
HR1
(C.10)
wobei cH und 8H die Gauß-Laguerre Gewichte und Stützstellen über 0, ∞ darstellen.
Von Vorteil ist, dass die Stützstellen und Gewichte unabhängig von der zu
integrierenden Funktion gewählt werden können. So können im Vorfeld berechnete
cH und 8H im Bewertungsalgorithmus verwendet werden, was eine effiziente Berechnung ermöglicht. Bei der Simulationsstudie in Kapitel 5 wird eine 32 Punkte GaussLaguerre Quadratur verwendet. Hiermit resultieren Ergebnisse, die auf zwei Nachkommastellen gerundet das gleiche Ergebnis zeigen, wie die folgende genauere Variante das Integral zu berechnen.
Im nächsten Abschnitt, bei der Darstellung des VBA Codes wird eine GaussLegendre Quadratur verwendet, hiermit lassen sich sehr genaue Optionswerte ermitteln. Dabei wird der Integrationsbereich von 0, ∞ auf ein endliches Intervall
transformiert und in einzelne Subintervalle aufgeteilt. Diese werden daraufhin mit
einer 10 Punkt Gauss-Legendre Quadratur evaluiert. Für einen Vergleich und die
Anmerkungen zur Implementierung der Modelle
| 88
bevorzugten Anwendungsgebiete der verschiedenen Gauss Quadraturen siehe
Judd [1998, Kapitel 7].
Effiziente Berechnung von vielen Optionspreisen
Wie Bates [1996] ausführt, werden bei der Bewertung von Optionen einer Restlaufzeit dieselben Werte der charakteristischen Funktion benötigt. Diese Werte sind
unabhängig von Basispreis und Spotpreis. So lässt sich die Rechenzeit deutlich verringern, wenn die charakteristische Funktion für eine bestimmte Parameterkonstellation
vorberechnet wird und zur Berechnung von Optionen für verschiedene Basispreise
und einer Restlaufzeit dann auf die zwischengespeicherten Werte zugegriffen wird.
Bei der Gaußschen Quadratur wird zunächst nur der Term fh i⁄2 aus (C.9)
für alle Stützstellen berechnet. Danach erfolgt die Multiplikation dieses Vektors mit
den dazugehörigen Gewichtungsfaktoren. Erst danach erfolgt die Multiplikation mit
lm¥ für die gewünschten Strike/Spot Kombinationen.
Auf diese Weise lassen sich auf einen Schlag alle Preise für eine Laufzeit ermitteln. Diese Methode wird bei Kilin [2007] detailliert dargelegt. Er führt aus, dass
diese Vorgehensweise unter Verwendung fortschrittlicher Integrationsverfahren wie
der Gaußschen Quadratur bei gleicher Genauigkeit sogar schneller als die Fast
Fourier Transformationen (FFT) Verfahren sind. Für eine Verwendung der FFT in
Bezug auf das Modell von Heston, Merton und MJD–SV siehe z. B.
Borak et Al [2005].
Transformation von Parametern
Um die Kalibrierung von Modellparametern ohne Nebenbedingungen durchführen
zu können, ist eine Variablentransformation notwendig. Dies ermöglicht dem Optimierungsalgorithmus im gesamten Wertebereich der reellen Zahlen zu suchen.
Nebenbedingung
80
1 8 1
8 ’ ¨, ×
Parameter Transformation
8 fÞ, ∞ Þ ∞
Rücktransformation
8 Þ ' oder 8 ß
ß 1
8 ß
$1
× ß $ ¨
8 ß
$1
Þ ln 8
Þ ln 21Ã3
Ãy1
Þ ln 2àà 3
ä
Gegeben die Transformationsfunktion 8 fÞ, wird die objektive Funktion ½8
zu XÞ ½fÞ. Somit ist das Optimierungsproblem mit Nebenbedingungen von
½ in Bezug auf 8 äquivalent zu einem Optimierungsproblem ohne Nebenbedingungen von X in Bezug auf Þ (siehe auch Li/Pearson [2007]).
Anmerkungen zur Implementierung der Modelle
| 89
Alternative Darstellung der charakteristischen Funktion bei dem Heston Modell
Wie Albrecher et Al [2006] oder auch Lord/Kahl [2006] ausführen, kann es bei
der ursprünglichen Darstellung der charakteristischen Funktion bei Heston [1993]
zu numerischen Schwierigkeiten kommen. Dies hängt damit zusammen, dass bei der
numerischen Annäherung für die Wahrscheinlichkeitsverteilung ein komplexwertiger
Logarithmus evaluiert werden muss. Ein solcher Logarithmus hat je nach verwendetem Ast unterschiedliche Werte. Falls nicht auf den richtigen Wert geachtet wird,
kann das dazu führen, dass der Integrand nicht stetig verläuft. Wenn die bei
Albrecher et Al [2006] dargestellte äquivalente Form der charakteristischen Funktion verwendet wird, ergeben sich hierbei keine Probleme.
Anmerkungen zur Implementierung der Modelle
| 90
C.2 Excel VBA Programm Code
In diesem Abschnitt wird der entwickelte VBA Programmcode zur Bestimmung von
arbitragefreien Optionspreisen mittels komplexer Fourier Inversion offengelegt. Der
Code für das FMLS Modell wird komplett abgedruckt. Die anderen Modelle unterscheiden sich lediglich bei der Spezifikation der charakteristischen Funktion Function
Integ(phi#, l#, tau#, … ). Die Evaluierung des Integrals erfolgt mit einer GaussLegendre Quadratur, wobei 200 Subintervalle mit vorberechneten 10 Punkte GaussLegendre Stützstellen und Gewichten berechnet werden. Bei dieser Funktion (hier
FMLS) ist für die anderen Modelle der Name der Funktion zu ändern (z. B. Function
Heston(S#, K#, r#, tau#, kappa#, theta#, rho#, sigmaV#, V#, PutCall As String) und
bei dem Integral entsprechend die Parameter anzupassen (bei Heston integral =
integral + w(i) * Integ(phi, l, tau, kappa, theta, rho, sigmaV, V). Analog gilt dies
für die anderen Modelle.
Finite Moment Log Stable
Option Explicit
Option Base 1
' declare every used variable separately
' index starts at 1 in array
Private Const thePI# = 3.14159265358979
' Carr/Wu [2003] "The Finite Moment Log Stable Process and Option Pricing"
' for alpha=2 you get the celebrated Black-Scholes model as special case
' # means As Double and & means As Long
Function Integ(phi#, l#, tau#, alpha#, sigma#) As Double
Dim i As Complex, im As Complex, imi As Complex, AA As Complex, KaFu As Complex
Dim mu#, secc#, BB#
' for ease of calculations
i = Cplx(0, 1)
im = CRSub(phi, Cplx(0, 0.5))
imi = CMult(i, im)
secc = Sec((thePI * alpha) / 2)
' Convexity Correction for riskless drift
' needed for the discounted stock price process to be a martingale
mu = sigma ^ alpha * Sec((thePI * alpha) / 2)
' Characteristic Function
KaFu = CExp(CSub(CMultR(imi, mu * tau), CMultR(CPower(CMultR(imi, sigma), alpha), tau
* secc)))
' part of complex integral in Lewis formula
AA = CExp(CMultR(i, phi * l))
BB = 1 / (phi * phi + 0.25)
' real part for integration
Integ = CReal(CMultR(CMult(AA, KaFu), BB))
End Function
Function FMLS(S#, K#, tau#, r#, alpha#, sigma#, PutCall As String) As Double
' 10 point Gauss - Legendre c.f.
http://www.efunda.com/math/num_integration/findgausslegendre.cfm
Dim u(10) As Double
Dim w(10) As Double
Dim i&, j&, cutoff&, intvl&
Anmerkungen zur Implementierung der Modelle
| 91
Dim integral#, CallPrice#, l#, phi#
l = Log(S / K) + r * tau
u(1) = -0.973906528517
u(2) = -0.865063366689
u(3) = -0.679409568299
u(4) = -0.433395394129
u(5) = -0.148874338982
u(6) = 0.148874338982
u(7) = 0.433395394129
u(8) = 0.679409568299
u(9) = 0.865063366689
u(10) = 0.973906528517
w(1) = 0.0666713443087
w(2) = 0.149451349151
w(3) = 0.219086362516
w(4) = 0.26926671931
w(5) = 0.295524224715
w(6) = 0.295524224715
w(7) = 0.26926671931
w(8) = 0.219086362516
w(9) = 0.149451349151
w(10) = 0.0666713443087
If alpha <= 1 Or alpha > 2 Or sigma <= 0 Then
MsgBox "Entered value is outside of admissible domain!"
Exit Function
End If
' a cutoff value about 200 gives very accurate results, less should be all right ...
cutoff = 200
intvl = 2
' length of each interval, a value of 2 is just fine ...
' evaluates every subinterval with a 10 point Gauss-Legendre Quadrature
integral = 0
For j = 1 To cutoff / intvl
For i = 1 To 10
phi = intvl * u(i) / 2 + intvl * (2 * j - 1) / 2
integral = integral + w(i) * Integ(phi, l, tau, alpha, sigma)
Next i
integral = intvl / 2 * integral
Next j
CallPrice = S - Sqr(S * K) / thePI * Exp(-r * tau / 2) * integral
Select Case PutCall
' Put Value via Put-Call-Parity
Case "Call"
FMLS = CallPrice
Case "Put"
FMLS = CallPrice + K * Exp(-r * tau) – S
End Select
End Function
Private Function Sec(z#) As Double
' secant function needed for log stable model, it´s not implemented in excel
' cf Abramowitz/Stegun [1972] Handbook of Mathematical Functions, p 72
Sec = 1 / Cos(z)
End Function
Heston
' Heston [1993] "A Closed-form Solution for Options with Stochastic Volatility with
Application to Bond and Currency Options"
' modified characteristic function from Albrecher et al [2006] "The Little Heston
Trap"
Function Integ(phi#, l#, tau#, kappa#, theta#, rho#, sigmaV#, V#) As Double
Anmerkungen zur Implementierung der Modelle
Dim i As
Complex,
Complex,
Dim BB#,
| 92
Complex, im As Complex, imi As Complex, im2 As Complex, d As Complex, g As
dd_1 As Complex, dd_2 As Complex, AA As Complex, DD As Complex, cc_1 As
cc_2 As Complex, cc_3 As Complex, CC As Complex, KaFu As Complex
sigma2#
' for ease of calculations
sigma2 = sigmaV * sigmaV
i = Cplx(0, 1)
im = CRSub(phi, Cplx(0, 0.5))
imi = CMult(i, im)
im2 = CMult(im, im)
' Excel does not like things like sigmaV^2
d = CSqrt(CAdd(CPower(CSubR(CMultR(imi, rho * sigmaV), kappa), 2), CAdd(CMultR(imi,
sigma2), CMultR(im2, sigma2))))
g = CDiv(CSub(CRSub(kappa, CMultR(imi, rho * sigmaV)), d), CAdd(CRSub(kappa,
CMultR(imi, rho * sigmaV)), d))
cc_1
cc_2
cc_3
CC =
= CMultR(CSub(CRSub(kappa, CMultR(imi, rho * sigmaV)), d), tau)
= CMultR(CLn(CDiv(CRSub(1, CMult(g, CExp(CMultR(d, -tau)))), CRSub(1, g))), 2)
= CMultR(CSub(cc_1, cc_2), theta * kappa)
CDivR(cc_3, sigma2)
dd_1 = CMult(CRSub(1, CExp(CMultR(d, -tau))), CSub(CRSub(kappa, CMultR(imi, rho *
sigmaV)), d))
dd_2 = CMultR(CRSub(1, CMult(g, CExp(CMultR(d, -tau)))), sigma2)
DD = CDiv(dd_1, dd_2)
' Characteristic Function
KaFu = CExp(CAdd(CC, CMultR(DD, V)))
' part of complex integral in Lewis formula
AA = CExp(CMultR(i, phi * l))
BB = 1 / (phi * phi + 0.25)
' real part for integration
Integ = CReal(CMultR(CMult(AA, KaFu), BB))
End Function
Merton Jump Diffusion
' Merton [1976] "Option pricing when the underlying stock returns are discontinuous"
' Merton´s Jump Diffusion Model
Function Integ(phi#, l#, tau#, lambda#, sigma#, omega#, eta#) As Double
Dim i As Complex, im As Complex, imi As Complex, im2 As Complex, AA As Complex, EE As
Complex, KaFu As Complex
Dim BB#, eta2#, sigma2#, mu#
' for ease of calculations
eta2 = eta * eta
sigma2 = sigma * sigma
i = Cplx(0, 1)
im = CRSub(phi, Cplx(0, 0.5))
imi = CMult(i, im)
im2 = CMult(im, im)
' Convexity Correction for riskless drift
mu = -lambda * (Exp(omega + eta2 / 2) - 1) - 0.5 * sigma2
EE = CSubR(CExp(CSub(CMultR(imi, omega), CMultR(im2, 0.5 * eta2))), 1)
KaFu = CExp(CAdd(CSub(CMultR(imi, mu * tau), CMultR(im2, 0.5 * sigma2 * tau)),
CMultR(EE, lambda * tau)))
' part of complex integral in Lewis formula
AA = CExp(CMultR(i, phi * l))
BB = 1 / (phi * phi + 0.25)
Anmerkungen zur Implementierung der Modelle
| 93
' real part for integration
Integ = CReal(CMultR(CMult(AA, KaFu), BB))
End Function
Merton Jump Diffusion – Stochastic Volatility
' Merton Jump Diffusion with Stochastic Volatility
' First implemented by Bates [1996] "Jumps and Stochastic Volatility: Exchange Rate
Processes Implicit in Deutsche Mark Options"
Function Integ(phi#, l#, tau#, kappa#, theta#, rho#, sigma#, V#, lambda#, omega#,
eta#) As Double
Dim i As
Complex,
Complex,
Complex,
Dim BB#,
Complex, im As Complex, imi As Complex, im2 As Complex, d As Complex, g As
dd_1 As Complex, dd_2 As Complex, AA As Complex, DD As Complex, EE As
cc_1 As Complex, cc_2 As Complex, cc_3 As Complex, CC As Complex, CarFunc As
CarFuHeston As Complex, CarFuMerton As Complex
mu#, sigma2#, eta2#
' for ease of calculations
sigma2 = sigma * sigma
eta2 = eta * eta
i = Cplx(0, 1)
im = CRSub(phi, Cplx(0, 0.5))
imi = CMult(i, im)
im2 = CMult(im, im)
'Heston Characteristic Function
d = CSqrt(CAdd(CPower(CSubR(CMultR(imi, rho * sigma), kappa), 2), CAdd(CMultR(imi,
sigma2), CMultR(im2, sigma2))))
g = CDiv(CSub(CRSub(kappa, CMultR(imi, rho * sigma)), d), CAdd(CRSub(kappa,
CMultR(imi, rho * sigma)), d))
cc_1
cc_2
cc_3
CC =
= CMultR(CSub(CRSub(kappa, CMultR(imi, rho * sigma)), d), tau)
= CMultR(CLn(CDiv(CRSub(1, CMult(g, CExp(CMultR(d, -tau)))), CRSub(1, g))), 2)
= CMultR(CSub(cc_1, cc_2), theta * kappa)
CDivR(cc_3, sigma2)
dd_1 = CMult(CRSub(1, CExp(CMultR(d, -tau))), CSub(CRSub(kappa, CMultR(imi, rho *
sigma)), d))
dd_2 = CMultR(CRSub(1, CMult(g, CExp(CMultR(d, -tau)))), sigma2)
DD = CDiv(dd_1, dd_2)
' Merton Characteristic Function
' Convexity Correction for riskless drift
mu = -lambda * (Exp(omega + eta2 / 2) - 1)
EE = CSubR(CExp(CSub(CMultR(imi, omega), CMultR(im2, 0.5 * eta2))), 1)
CarFuHeston = CExp(CAdd(CC, CMultR(DD, V)))
CarFuMerton = CExp(CAdd(CMultR(imi, mu * tau), CMultR(EE, lambda * tau)))
CarFunc = CMult(CarFuHeston, CarFuMerton)
' part of complex integral in Lewis formula
AA = CExp(CMultR(i, phi * l))
BB = 1 / (phi * phi + 0.25)
' real part for integration
Integ = CReal(CMultR(CMult(AA, CarFunc), BB))
End Function
Finite Moment Log Stable – Stochastic Volatility
' Combines Log Stable Option Pricing with Stochastic Volatility
Function Integ(phi#, l#, tau#, kappa#, theta#, rho#, sigma#, V#, alpha#) As Double
Anmerkungen zur Implementierung der Modelle
Dim i As
Complex,
Complex,
Complex,
Dim BB#,
| 94
Complex, im As Complex, imi As Complex, im2 As Complex, d As Complex, g As
dd_1 As Complex, dd_2 As Complex, AA As Complex, DD As Complex, EE As
cc_1 As Complex, cc_2 As Complex, cc_3 As Complex, CC As Complex, CarFunc As
CarFuHeston As Complex, CarFuFMLS As Complex
secc#, mu#, sigma2#
' for ease of calculations
sigma2 = sigma * sigma
secc = Sec((thePI * alpha) / 2)
i = Cplx(0, 1)
im = CRSub(phi, Cplx(0, 0.5))
imi = CMult(i, im)
im2 = CMult(im, im)
' Characteristic Function Heston
d = CSqrt(CAdd(CPower(CSubR(CMultR(imi, rho * sigma), kappa), 2), CAdd(CMultR(imi,
sigma2), CMultR(im2, sigma2))))
g = CDiv(CSub(CRSub(kappa, CMultR(imi, rho * sigma)), d), CAdd(CRSub(kappa,
CMultR(imi, rho * sigma)), d))
cc_1
cc_2
cc_3
CC =
= CMultR(CSub(CRSub(kappa, CMultR(imi, rho * sigma)), d), tau)
= CMultR(CLn(CDiv(CRSub(1, CMult(g, CExp(CMultR(d, -tau)))), CRSub(1, g))), 2)
= CMultR(CSub(cc_1, cc_2), theta * kappa)
CDivR(cc_3, sigma2)
dd_1 = CMult(CRSub(1, CExp(CMultR(d, -tau))), CSub(CRSub(kappa, CMultR(imi, rho *
sigma)), d))
dd_2 = CMultR(CRSub(1, CMult(g, CExp(CMultR(d, -tau)))), sigma2)
DD = CDiv(dd_1, dd_2)
' Characteristic Function FMLS
mu = sigma ^ alpha * Sec((thePI * alpha) / 2)
CarFuHeston = CExp(CAdd(CC, CMultR(DD, V)))
CarFuFMLS = CExp(CSub(CMultR(imi, mu * tau), CMultR(CPower(CMultR(imi, sigma),
alpha), tau * secc)))
CarFunc = CMult(CarFuHeston, CarFuFMLS)
' part of complex integral in Lewis formula
AA = CExp(CMultR(i, phi * l))
BB = 1 / (phi * phi + 0.25)
' real part for integration
Integ = CReal(CMultR(CMult(AA, CarFunc), BB))
End Function
Komplexe Zahlen in VBA
Im Folgenden werden Funktionen für komplexe Operationen in Excel aufgelistet.
Diese können alternativ zu den Standard Excel Funktionen für komplexe Zahlen verwendet werden. Diese Implementierung rechnet hierbei ausschließlich mit numerischen Werten, während Excel jede komplexe Zahl immer erst in einen String (Textdatei in der Form: x$ªi) umwandelt. Bei http://www.alglib.net finden sich komplexe
Funktionen als VBA Funktionen. Diese werden mit weiteren benötigten komplexen
Funktionen erweitert. Der Performancegewinn bei Verwendung dieser Funktionen
liegt im Vergleich zu den Excel Funktionen im Schnitt bei etwa Faktor 10 (gemessen
mit GetTickCount Lib "kernel32").
Anmerkungen zur Implementierung der Modelle
| 95
Option Explicit
Type Complex
X As Double
y As Double
End Type
' definition of new variable type: complex number
Public Function Cplx(ByVal real#, ByVal imag#) As Complex
Cplx.X = real
Cplx.y = imag
End Function
Public Function CReal(ByRef z As Complex)
CReal = z.X
End Function
' define complex number
' returns real part of complex number
Public Function CAdd(ByRef Z1 As Complex, ByRef Z2 As Complex) As Complex
Dim Result As Complex
' addition
Result.X = Z1.X + Z2.X
Result.y = Z1.y + Z2.y
CAdd = Result
End Function
Public Function CAddR(ByRef Z1 As Complex, ByVal r#) As Complex
Dim Result As Complex
' addition of complex number with real number
Result.X = Z1.X + r
Result.y = Z1.y
CAddR = Result
End Function
Public Function CSub(ByRef Z1 As Complex, ByRef Z2 As Complex) As Complex
Dim Result As Complex
' substraction
Result.X = Z1.X - Z2.X
Result.y = Z1.y - Z2.y
CSub = Result
End Function
Public Function CSubR(ByRef Z1 As Complex, ByVal r#) As Complex
Dim Result As Complex
' substraction of complex number with real number
Result.X = Z1.X - r
Result.y = Z1.y
CSubR = Result
End Function
Public Function CRSub(ByVal r#, ByRef Z1 As Complex) As Complex
Dim Result As Complex
' substraction of real number with complex number
Result.X = r - Z1.X
Result.y = -Z1.y
CRSub = Result
End Function
Public Function CMult(ByRef Z1 As Complex, ByRef Z2 As Complex) As Complex
Dim Result As Complex
' multiplication
Result.X = Z1.X * Z2.X - Z1.y * Z2.y
Result.y = Z1.X * Z2.y + Z1.y * Z2.X
CMult = Result
End Function
Anmerkungen zur Implementierung der Modelle
| 96
Public Function CMultR(ByRef Z1 As Complex, ByVal r#) As Complex
Dim Result As Complex
' multiplication of complex number with real number
Result.X = Z1.X * r
Result.y = Z1.y * r
CMultR = Result
End Function
Public Function CExp(ByRef z As Complex) As Complex
Dim Result As Complex
' exponentiation
Result.X = Exp(z.X) * Cos(z.y)
Result.y = Exp(z.X) * Sin(z.y)
CExp = Result
End Function
Public Function CPower(ByRef z As Complex, ByVal X#) As Complex
Dim Result As Complex, r#, y#
' takes the n-th power of complex number
r = Sqr(z.X * z.X + z.y * z.y)
y = Atn(z.y / z.X)
Result.X = r ^ X * Cos(X * y)
Result.y = r ^ X * Sin(X * y)
CPower = Result
End Function
Public Function CSqrt(ByRef z As Complex) As Complex
Dim Result As Complex, r#, y#
' square root
r = Sqr(z.X * z.X + z.y * z.y)
y = Atn(z.y / z.X)
Result.X = Sqr(r) * Cos(y / 2)
Result.y = Sqr(r) * Sin(y / 2)
CSqrt = Result
End Function
Public Function CLn(ByRef z As Complex) As Complex
Dim Result As Complex, r#, y#
' logarithm
r = Sqr(z.X * z.X + z.y * z.y)
y = Atn(z.y / z.X)
Result.X = Log(r)
Result.y = y
CLn = Result
End Function
Public Function CDiv(ByRef Z1 As Complex, ByRef Z2 As Complex) As Complex
Dim Result As Complex
' division
Dim a#, b#, C#, d#, E#, F#
a = Z1.X
b = Z1.y
C = Z2.X
d = Z2.y
If Abs(d) < Abs(C) Then
E = d / C
F = C + d * E
Result.X = (a + b * E) / F
Result.y = (b - a * E) / F
Else
E = C / d
F = d + C * E
Result.X = (b + a * E) / F
Result.y = (-a + b * E) / F
End If
CDiv = Result
End Function
Anmerkungen zur Implementierung der Modelle
| 97
Public Function CDivR(ByRef Z1 As Complex, ByVal r#) As Complex
Dim Result As Complex
' division by real number
Result.X = Z1.X / r
Result.y = Z1.y / r
CDivR = Result
End Function
Public Function CRDiv(ByVal r#, ByRef Z2 As Complex) As Complex
Dim Result As Complex
' division of real number by complex number
Dim a#, b#, C#, d#, E#, F#
a = r
C = Z2.X
d = Z2.y
If Abs(d) < Abs(C)
E = d / C
F = C + d * E
Result.X = a /
Result.y = -(a
Else
E = C / d
F = d + C * E
Result.X = a *
Result.y = -(a
End If
CRDiv = Result
End Function
Then
F
* E / F)
E / F
/ F)
Anmerkungen zur Implementierung der Modelle
| 98
C.3 Verwendete Software und Daten
Die Anpassung der log Renditen des DAX an eine stabile Verteilung (Abbildung 5)
erfolgte mit dem Tool stable.exe von John Nolan. Auch die Daten für die Quantil
Plots wurden hiermit generiert (Abbildung 7). Das Programm und viele weiterführende Informationen zu stabilen Verteilungen sind erhältlich unter
http://academic2.american.edu/~jpnolan/stable/stable.html.
Der bei der Kalibrierung verwendete BFGS Optimierungsalgorithmus ist in dem
Freeware Tool PopTools implementiert. Dieser kann als Alternative zum mitgelieferten Solver benutzt werden und erweist sich als sehr robust und leicht zu bedienen.
Neben einer Vielzahl von anderen Funktionen lassen sich hiermit auch qualitativ
hochwertige Zufallszahlen generieren (Abbildung 2), verwendet wird hierbei der
Mersenne Twister Algorithmus.
Erhältlich unter http://www.cse.csiro.au/poptools/.
Eine Alternative hierzu bietet das Tool Optimiz, ebenfalls Freeware. Hierbei erfolgt
die Optimierung On-Site, d. h. man kann auf dem Bildschirm verfolgen, was während
der Optimierung passiert. Wurde für die Studie nicht benutzt, erwies sich aber im
Vorfeld als sehr nützlich.
Erhältlich unter http://digilander.libero.it/foxes/Optimiz_tool.zip.
Alle anderen Berechnungen und Statistiken wurden mit MS Excel 2007 durchgeführt
bzw. erstellt und die Ergebnisse grafisch dargestellt.
Die Zeitreihe des DAX vom 30.12.1966 bis 23.02.2007 wurde am 12.02.2008 von
http://www.wiwi.uni-muenster.de/05/download//Vorlesungen/Statistik_I/
Wittmann/Z2-Aufg_7.xls runtergeladen. Die fehlenden Daten bis zum Ende des
Untersuchungszeitraumes (24.01.2008) wurden mit Daten von Yahoo.com ergänzt.
Tagesaktuelle Daten für DAX Optionen sind mit je 15 Min. Verzögerung kostenlos
erhältlich unter http://boerse.de/ oder direkt bei http://www.eurexchange.com/.
Settlementpreise für den jeweiligen Tag stehen erst deutlich nach Handelsschluss um
17:30 Uhr zur Verfügung.
Alle weiteren benötigten tagesaktuellen Werte für die Berechnung von Optionspreisen wurden von comdirect.de/informer/tools/chartanalyzer aufgenommen. Für die
implizite Bestimmung der Indexstände des DAX kann hierfür auch auf die Intraday
Daten des FDAX zurückgegriffen werden.
Anmerkungen zur Implementierung der Modelle
| 99
Die weiteren Daten umfassen die EURIBOR 1 Woche, 1, 3, 6, 9, 12 Monate Zinssätze
sowie die REX 2 und 3 Jahre Rentenindizes. Auch VDAX Stände sind hier erhältlich.
Dieser Service steht nach kostenfreier Anmeldung zur Verfügung.
Bis zu 32 vorberechnete Stützstellen und Gewichte für verschiedene Gauss
Quadraturen sind erhältlich unter http://www.efunda.com/math/num_integration
/num_integration.cfm.
Werden mehr benötigt, so gibt es unter http://www.alglib.net/ VisualBasic
Prozeduren, um beliebig viele Stützpunkte zu ermitteln.
Ganz allgemein erwies sich das Wilmott Forum als unbegrenzte Quelle der
Inspiration und war stets erste Anlaufstelle bei Problemen aller Art, die
finanzmathematische Fragestellungen und praktische Umsetzungsmöglichkeiten
betreffen. http://wilmott.com/.
Symbolverzeichnis
0
i
>
h
BC
, X
a
`
!
;
%
*9 . ,
:
·
?
”
d
€
~
b
#
#k
—
Moneyness ln⁄⁄ k √
Euler’sche Zahl 2,71828 …
imaginäre Einheit √1
Moneyness ln/
(logarithmierte) Preisveränderung
stetiger risikoloser Zinssatz
Kalenderzeit
Integrationsvariable
Callpreis
Black–Scholes Callpreis
Callpreis in Abhängigkeit von und zum Zeitpunkt Future
poissonverteilte Sprünge
Ausübungspreis, Basispreis, Strike
Lévy Prozess
Putpreis
Aktienkurs zum Zeitpunkt diskontierter Aktienkurs zum Zeitpunkt Fälligkeit; Laufzeit einer Option
Brownsche Bewegung, Wiener Prozess
Erwartungswertoperator unter :
physikalisches (statistisches) Wahrscheinlichkeitsmaß
risikoneutrales Wahrscheinlichkeitsmaß, Martingalemaß
Filtration
Tail Index der stabilen Verteilung
Schiefeparameter der stabilen Verteilung
Varianz der Sprungintensität
langfristiger Mittelwert des Volatilitätsprozesses ~
instantane Varianz, auch Momentanvarianz oder lokale Varianz
Sprungintensität
mittlere erwartete Aktienkursrendite, Drift
Konvexitätskorrekturfaktor
Kreiszahl 3,14159 …
Symbolverzeichnis
ƒ

, f h c
cH
Γ
Δ
Θ

Π. Φ. Ω
µ
µ
Re
sec()
ΔUVW
Korrelationskoeffizient
Variabilität der Preisprozesse; Volatilität bzw. Skalenparameter
Volatilität der stochastischen Varianz
zeitveränderliche Volatilität in Abhängigkeit von und verbleibende Restlaufzeit einer Option
charakteristische Funktion einer Wahrscheinlichkeitsverteilung
Mittelwert der Sprungintensität
Gewichtungsfaktor für Option Ê
Gamma einer Option
Delta einer Option
Parametervektor der Modellvariablen
Anpassungsgeschwindigkeit der stochastischen Varianz
numerisch ermittelte Verteilungsfunktion
kumulative Standardnormalverteilung
Zustandsraum möglicher Ereignisse
Fouriertransformierte
Information zum Zeitpunkt Realteil einer komplexen Zahl
Sekantenfunktion, trigonometrische Funktion für Kreisberechnungen
Differenzdividende
iv
Abkürzungsverzeichnis
(G)ARCH
ATM
BFGS
DAI
DAX®
DJ
DTB
Eurex®
EURIBOR®
FDAX®
FMLS
FMLS–SV
FWB®
ISIN
ITM
MAE
MARE
MJD
MJD–SV
MLE
MSE
ODAX®
OTC
OTM
PWLS
R/S
REX®
RMSE
S & P 500
SOFFEX
sse
SV
TLD
WLS
Xetra®
(Generalized) AutoRegressive Conditional Heteroskedasticity
at the money
Broydon-Fletcher-Goldfarb-Shanno
Börsenkürzel für die Daimler AG
Deutscher Aktienindex
Dow Jones
Deutsche Terminbörse
European Exchange
Euro Interbank Offered Rate
Futures auf den DAX
Finite Moment Log Stable
Finite Moment Log Stable – Stochastic Volatility
Frankfurter Wertpapierbörse
International Securities Identification Number
in the money
mean average error
mean average relative error
Merton Jump Diffusion
Merton Jump Diffusion – Stochastic Volatility
maximum likelihood estimation
mean squared error
Optionen auf den DAX
Over the Counter
out of the money
penalised weighted least squares
Range over Standard Deviation
Deutscher Rentenindex
root mean squared error
STANDARD & POOR’S 500 Aktienindex
Swiss Options and Financial Futures Exchange
sum of squared errors
Stochastic Volatility
Truncated Lévy Distributions
weighted least squares
vollelektronisches Handelssystem (Electronic Trading)
Abkürzungsverzeichnis
vi
DAX®, ODAX®, FDAX®, VDAX®, REX®, FWB®, Eurex® und Xetra® sind eingetragene
Handelsmarken der Deutsche Börse AG. EURIBOR® ist eine eingetragene Handelsmarke der Fédération Bancaire Européenne. Dow Jones EuroSTOXX 50® ist eine
Dienstleistungsmarke der STOXX Ltd. und/oder der Dow Jones & Company, Inc. Auf
die Verwendung des ® Logos im Laufe der Arbeit wird verzichtet.
Abbildungsverzeichnis
Abbildung 1: Auszahlungsdiagramme für europäische Optionen.
5
Abbildung 2: Simulierte Aktienkursverläufe mit identischer Drift und
unterschiedlicher Volatilität.
15
Abbildung 3: Evolution der täglichen Schlusskurse des DAX.
18
Abbildung 4: Tägliche Renditen vom 30. Dezember 1966 bis 24. Januar 2008.
20
Abbildung 5: Empirische Dichtefunktion des DAX angepasst an eine
Normalverteilung und eine ?-stabile Verteilung.
22
Abbildung 6: Empirische Dichtefunktion des DAX, Teil 2.
24
Abbildung 7: Quantil Plot der Tagesrenditen des DAX.
25
Abbildung 8: Historische Volatilität und Volatilitätscluster.
28
Abbildung 9: Reale und Black–Scholes Preise für den 7. Dezember 2007.
29
Abbildung 10: Smile und Smirk Effekt.
30
Abbildung 11: Fristenstruktur der impliziten Volatilität.
32
Abbildung 12: Implizite Volatilitäten vom 21.12.2007 für die
ODAX Januar 08 Optionen.
33
Abbildung 13: Implizite Volatilitäten für quotierte Jan 08 Optionen
vom 21.12.2007.
Abbildung 14: Implizite Volatilitäten und zugehörige Zustandspreisdichte MJD.
34
38
Abbildung 15: Implizite Volatilitäten und zugehörige Zustandspreisdichte Heston. 40
Abbildung 16: Laufzeitmuster von impliziten Volatilitäten.
41
Abbildung 17: Implizite Volatilitäten und zugehörige Zustandspreisdichte FMLS. 43
Abbildung 18: Implizite Volatilitäten und zugehörige Zustandspreisdichte MJD–SV.44
Abbildung 19: Implizite Volatilitäten und zugehörige Zustandspreisdichte FMLS–SV.46
Abbildung 20: Geschätzte Parameter im Zeitablauf, ohne Regularisierung (WLS). 56
Abbildung 21: Geschätzte Parameter im Zeitablauf, mit Regularisierung (PWLS). 59
Abbildungsverzeichnis
x
Abbildung 22: Bewertungsfehler im Zeitablauf, ohne Regularisierung (WLS).
61
Abbildung 23: Reale und MJD Preise für den 7. Dezember 2007.
73
Abbildung 24: In-Sample Bewertungsfehler im Zeitablauf, mit
Regularisierung (PWLS).
74
Abbildung 25: Out-of-the-Sample Bewertungsfehler im Zeitablauf, ohne
Regularisierung (WLS).
75
Abbildung 26: Out-of-the-Sample Bewertungsfehler im Zeitablauf, mit
Regularisierung (PWLS).
76
Abbildung 27: Implizite Volatilitätsoberfläche von DAX Optionen für den
7. Dezember 2007.
78
Abbildung 28: Implizite Volatilitätsoberfläche Merton Jump Diffusion.
79
Abbildung 29: Differenz in der Volatilität von Markt und Modell, MJD.
79
Abbildung 30: Implizite Volatilitätsoberfläche Heston.
80
Abbildung 31: Differenz in der Volatilität von Markt und Modell, Heston.
80
Abbildung 32: Implizite Volatilitätsoberfläche FMLS.
81
Abbildung 33: Differenz in der Volatilität von Markt und Modell, FMLS.
81
Abbildung 34: Implizite Volatilitätsoberfläche MJD–SV.
82
Abbildung 35: Differenz in der Volatilität von Markt und Modell, MJD–SV.
82
Abbildung 36: Implizite Volatilitätsoberfläche FMLS–SV.
83
Abbildung 37: Differenz in der Volatilität von Markt und Modell, FMLS–SV.
83
Abbildung 38: Integrand des FMLS–SV Modells bei der numerischen Integration. 87
Tabellenverzeichnis
Tabelle 1: Anpassungsgüte der Black–Scholes Kalibrierung.
28
Tabelle 2: In-Sample geschätzte Parameter, ohne Regularisierung (WLS).
55
Tabelle 3: In-Sample geschätzte Parameter, mit Regularisierung (PWLS).
58
Tabelle 4: In-Sample Anpassungsgüte, ohne Regularisierung (WLS).
60
Tabelle 5: In-Sample Anpassungsgüte, mit Regularisierung (PWLS).
60
Tabelle 6: Out-of-the-Sample Anpassungsgüte, ohne Regularisierung (WLS).
62
Tabelle 7: Out-of-the-Sample Anpassungsgüte, mit Regularisierung (PWLS).
63
Tabelle 8: Implizite Volatilitätsmatrix für DAX Optionen.
77
Literaturverzeichnis
Albrecher, H., P. Mayer, W. Schoutens und J. Tistaert [2006]: The Little Heston
Trap, Working Paper, Linz and Graz University of Technology, K.U. Leuven,
ING Financial Markets.
Bachelier, L. [1900]: Théorie de la Spéculation, Dissertation, Sorbonne, Annales
Scientifiques de l’Ecole Normale Supérieure, Paris, Sér. 3, 17, S. 21–88.
Englische Übersetzung in: The Random Charakter of Stock Market Prices (Hrsg.
P. Cootner), MIT Press (1964), Cambridge, S. 18–87.
Bakshi, G. und D. Madan [2000]: Spanning and derivative-security valuation,
Journal of Financial Economics 55, S. 205–238.
Bakshi, G., C. Cao und Z. Chen [1997]: Empirical Performance of Alternative
Option Pricing Models, Journal of Finance 52, S. 2003–2049.
Bates, S. [1996]: Jumps and Stochastic Volatility: Exchange Rate Processes Implicit in
Deutsche Mark Options, Review of Financial Studies 9, S. 69–107.
Bauer, H. [2002]: Wahrscheinlichkeitstheorie, Fünfte Auflage, Walter de Gruyter,
Berlin.
Bingham, N. und R. Kiesel [2004]: Risk-Neutral Valuation: Pricing and Hedging of
Financial Derivatives (Springer Finance), Springer, Berlin.
Black, F. und M. Scholes [1973]: The Pricing of Options and Corporate Liabilities,
Journal of Political Economy 81, S. 637–654.
Black, F. [1989]: How we came up with the option formula, Journal of Portfolio
Management, Winter, S. 4–8.
Boness, A. [1964]: Elements of a Theory of Stock-Option Value, Journal of Political
Economy 72, S. 163–175.
Borak, S., K. Detlefsen und W. Härdle [2005]: FFT Based Option Pricing,
Discussion Paper, Sonderforschungsbereich (SFB) 649, Humboldt Universität
Berlin.
Literaturverzeichnis
xiii
Börse Aktuell [2008]: Stuttgarter Aktienbrief, Februar 2008, Homepage:
www.boerse-aktuell.com.
Breeden, D. und R. Litzenberger [1978]: Prices of state-contingent claims implicit
in option prices, Journal of Business 51, S. 621–651.
Bronzin, V. [1908]: Theorie der Prämiengeschäfte, Franz Deuticke, Wien.
Carr, P. und L. Wu [2003]: The Finite Moment Log Stable Process and Option
Pricing, Journal of Finance 58, S. 753–777.
Carr, P. und L. Wu [2004]: Time-changed Lévy processes and option pricing, Journal
of Financial Economics 71, S. 113–141.
Cartea, A. [2005]: Dynamic Hedging of Financial Instruments When the
Underlying Follows a Non-Gaussian Process, Working Paper, University of
London.
Cartea, A. und S. Howison [2007]: Option Pricing With Lévy-Stable Processes
Generated by Lévy-Stable Integrated Variance, Working Paper, University of
London, University of Oxford.
Černý, A. [2004]: Mathematical Techniques in Finance, Tools for Incomplete Markets,
Princeton University Press, Princeton.
Chance, D. [1995]: A Chronology of Derivatives, Derivatives Quarterly, Winter,
S. 53–60.
Cont, R. [2001]: Empirical properties of asset returns: stylized facts and statistical
issues, Quantitative Finance 1, S. 223–236.
Cont, R. und P. Tankov [2003]: Financial Modelling with Jump Processes (Financial
Mathematics Series), Chapman & Hall/CRC, New York.
Cox, J. und S. Ross [1976]: The valuation of options for alternative stochastic
processes, Journal of Financial Economics 3, S. 145–166.
Cox, J., J. Ingersoll und S. Ross [1985a]: An Intertemporal General Equilibrium
Model of Asset Prices, Econometrica 53, S. 363–384.
Cox, J., J. Ingersoll und S. Ross [1985b]: A Theory of the Term Structure of Interest
Rates, Econometrica 53, S. 385–407.
Literaturverzeichnis
xiv
Daal, E. und J. Yu [2006]: An Examination on the Roles of Diffusions and Stochastic
Volatility in the Exponential Lévy Jumps Models, Working Paper, University of
New Orleans.
Derman, E. und I. Kani [1994]: Riding on a Smile, RISK 2, S. 32–39.
Detlefsen, K. und W. Härdle [2006]: Calibration Risk for Exotic Options,
Discussion Paper, Sonderforschungsbereich (SFB) 649, Humboldt Universität
Berlin.
Deutsch, H. [2001]: Derivate und interne Modelle: Modernes Risikomanagement,
Zweite Auflage, Schäffer-Poeschel, Stuttgart.
Deutsche Börse [2007]: Leitfaden zu den Volatilitätsindizes der Deutschen Börse,
Version 2.4, Januar 2007.
Deutsche Börse [2008]: Leitfaden zu den Aktienindizes der Deutschen Börse,
Version 6.5, Februar 2008, http://deutsche-boerse.com/dbag/dispatch/de/kir/
gdb_navigation/listing/10_Market_Structure/31_auswahlindizes/10_DAX
(verifiziert am 01.03.2008).
Deutsche Bundesbank [2005]: Zur Rolle von Volatilitätsmustern an den
Finanzmärkten, Monatsbericht September, S. 61–75.
Dupire, B. [1994]: Pricing with a Smile, RISK 7, S. 18–20.
Einstein, A. [1905]: Die von der molekularkinetischen Theorie der Wärme
geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen,
Annalen der Physik 17, S. 549–560.
Elices, A. [2007]: Models with time-dependent parameters using transform methods:
application to Heston’s model, Working Paper, arXiv:0708.2020v1.
Eurex [2008a]: Eurex Xpand, Januar 2008.
Eurex [2008b]: Clearing-Bedingungen der Eurex Clearing AG, Version vom
11.02.2008, http://www.eurexchange.com/documents/regulations/
clearing_conditions_de.html (verifiziert am 01.03.2008).
Fama, E. [1963]: Mandelbrot and the Stable Paretian Hypothesis, Journal of
Business 36, S. 420–429.
Literaturverzeichnis
xv
Fama, E. [1965]: The Behavior of Stock-Market Prices, Journal of Business 38,
S. 34–105.
Feller, W. [1951]: Two Singular Diffusion Problems, Annals of Mathematics 54,
S. 173–182.
Foresi, S. und L. Wu [2005]: Crash-O-Phobia: A Domestic Fear or a Worldwide
Concern, Journal of Derivatives, Winter, S. 1–14.
Franke, J., W. Härdle und C. Hafner [2001]: Einführung in die Statistik der
Finanzmärkte, Springer, Berlin.
Galluccio, S. und Y. Le Cam [2005]: Implied Calibration of Stochastic Volatility
Jump Diffusion Models, Working Paper, BNP Paribas und University of Evry.
Hafner, R. und M. Wallmeier [2000]: The Dynamics of DAX Implied Volatilities,
Working Paper, University of Augsburg.
Harrison, J. und D. Kreps [1979]: Martingales and arbitrage in multiperiod
securities markets, Journal of Economic Theory 20, S. 381–408.
Harrison, M. und S. Pliska [1981]: Martingales and stochastic integrals in the
theory of continuous trading, Stochastic Processes Applications 11, S. 215–260.
Heston, S. [1993]: A Closed-form Solution for Options with Stochastic Volatility
with Application to Bond and Currency Options, Review of Financial Studies 6,
S. 327–343.
Höchstötter, M. [2006]: The Pareto Stable Distribution as a Hypothesis for Returns
of Stocks Listed in the DAX, Verlag Dr. Kovač, Kalsruhe.
Huang, J. und L. Wu [2004]: Specification Analysis of Option Pricing Models Based
on Time-Changed Lévy Processes, Journal of Finance 59, S. 1405–1440.
Hull, J. und A. White [1987]: The Pricing of Options on Assets with Stochastic
Volatilities, Journal of Finance 42, S. 281–300.
Hurst, H. [1951]: Long-term storage capacity of reservoirs, Transactions of the
American Society of Civil Engineers 116, S. 770–808.
Irle, A. [2003]: Finanzmathematik: die Bewertung von Derivaten, Zweite Auflage,
Teubner, Stuttgart.
Literaturverzeichnis
xvi
Jackwerth, J. und M. Rubinstein [2001]: Recovering Stochastic Processes from
Option Prices, Working Paper, University of Konstanz, Haas School of Business.
Javaheri, A. [2005]: Inside Volatility Arbitrage: The Secrets of Skewness, John Wiley &
Sons, Chichester.
Judd, K. [1998]: Numerical Methods in Finance, MIT Press, Cambridge.
Karatzas, I. und S. Shreve [1998]: Methods of Mathematical Finance, Springer,
Berlin.
Kilin, F. [2007]: Accelerating the Calibration of Stochastic Volatility Models, Working
Paper, Frankfurt School of Finance & Management.
Kleinert, H. [2003]: Path Integrals in Quantum Mechanics, Statistics, Polymer
Physics, and Financial Markets, World Scientific Publishing Company, Singapur.
Krämer, W. [2004]: Statistische Besonderheiten von Finanzmarktdaten,
Sonderforschungsbereich (SFB) 475, Universität Dortmund.
Kyprianou, A. und R. Loeffen [2005]: Lévy Processes in Finance Distinguished by
their Coarse and Fine Path Properties, S. 1–28, in: Exotic Option Pricing and
Advanced Lévy Models (Hrsg. A. Kyprianou, W. Schoutens und P. Wilmott),
John Wiley & Sons, Chichester.
Lewis, A. [2001]: A Simple Option Formula for General Jump-Diffusion and other
Exponential Levy Processes, nicht veröffentlicht, erhältlich unter
http://optioncity.net/pubs/ExpLevy.pdf (verifiziert am 01.03.2008).
Li, M. und N. Pearson [2007]: A “Horse Race” Among Competing Option Pricing
Models using S&P 500 Index Options, Working Paper, Georgia Institute of
Technology, University of Illinois.
Lindström, E., Brodén, M., Holst, J., Ströjby, J. und M. Wiktorsson [2006]:
Sequential Calibration of Options, Technical report, Lund University.
Lord, R. und C. Kahl [2006]: Why the rotation count algorithm works, Discussion
Paper TI 2006-065/2, Tinbergen Institute.
Mandelbrot, B. und R. Hudson [2005]: Fraktale und Finanzen. Märkte zwischen
Risiko, Rendite und Ruin, Piper, München.
Literaturverzeichnis
xvii
Mandelbrot, B. [1963]: The Variation of Certain Speculative Prices, Journal of
Business 36, S. 394–419.
Mantegna, R. und H. Stanley [2000]: An Introduction to Econophysics: Correlations
and Complexity in Finance, Cambridge University Press, Cambridge.
Matacz, A. [2006]: Financial Modeling and Option Theory with the Truncated Levy
Process, Working Paper, University of Sydney.
Matsuda, K. [2004]: Introduction to Merton Jump Diffusion Model, Working Paper,
City University of New York.
May, C. [1999]: Nonlinear Pricing – Theory and Applications (Wiley Trading Series),
John Wiley & Sons, Chichester.
Merton, R. [1973]: Theory of rational option pricing, Bell Journal of Economics and
Management Science 4, S. 141–183.
Merton, R. [1976]: Option pricing when the underlying stock returns are
discontinuous, Journal of Financial Economics 3, S. 125–144.
Mikhailov, S. und U. Nögel [2003]: Heston’s Stochastic Volatility Model –
Implementation, Calibration and some Extensions, Wilmott Magazine, July.
Muck, M. und M. Rudolf [2006]: Optionsbewertung mit stochastischer Volatilität –
Implementation des Heston Modells, Wirtschaftswissenschaftliches Studium 6,
S. 325–330.
Nagel, H. [2001]: Optionsbewertung bei stochastischer Volatilität, Deutscher
Universitäts Verlag, Gabler, Wiesbaden.
Rachev, S. und S. Mittnik [2000]: Stable Paretian Models in Finance (Financial
Economics and Quantitative Analysis Series), John Wiley & Sons, Chichester.
Rathgeber, A. [2007]: Optionsbewertung unter Lévy-Prozessen, Eine Analyse für
den deutschen Aktienindex, Kredit und Kapital 3, S. 451–484.
Rubinstein, M. [1994]: Implied Binomial Trees, Journal of Finance 3, S. 771–818.
Samuelson, P. [1965]: Rational theory of warrant pricing, Industrial Management
Review 6, S. 13–32.
Literaturverzeichnis
xviii
Sandmann, K. [1999]: Einführung in die Stochastik der Finanzmärkte, Springer,
Berlin.
Schmid, F. und M. Trede [2006]: Finanzmarktstatistik: mit 35 Tabellen, Springer,
Berlin.
Schmitt, C., J. Kähler und E. Hehn [1997]: Die Profitabilität von
Volatilitätsstrategien auf Optionsmärkten: Ein Modellvergleich für DAXOptionen, Die Bank 12, S. 743–747.
Schoutens, W. [2003]: Lévy Processes in Finance: Pricing Financial Derivatives (Wiley
Series in Probability and Statistics), John Wiley & Sons, Chichester.
Schröder, M. [2002]: Statistische Eigenschaften von Finanzmarkt-Zeitreihen, S. 1–32,
in: Finanzmarkt-Ökonometrie, Basistechniken, Fortgeschrittene Verfahren,
Prognosemodelle, (Hrsg. M. Schröder), Schäffer-Poeschel, Stuttgart.
Sepp, A. [2003]: Pricing European-Style Options under Jump Diffusion Processes
with Stochastic Volatility: Applications of Fourier Transform, Working Paper,
University of Tartu.
Singer, H. [1999]: Finanzmarktökonometrie. Zeitstetige Systeme und ihre Anwendung
in Ökonometrie und empirischer Kapitalmarktforschung
(Wirtschaftswissenschaftliche Beiträge Bd. 171), Physica-Verlag, Heidelberg.
Stein, E. und J. Stein [1991]: Stock Price Distributions with Stochastic Volatility: An
Analytic Approach, Review of Financial Studies 4, S. 727–752.
Taleb, N. [1997]: Dynamic Hedging: Managing Vanilla and Exotic Options, John
Wiley & Sons, Chichester.
Voit, J. [2005]: The statistical mechanics of financial markets, Dritte Auflage, Springer,
Berlin.
Wallmeier, M. [2003]: Der Informationsgehalt von Optionspreisen
(Betriebswirtschaftliche Studien), Physika-Verlag, Heidelberg.
Weron, R. und U. Wystup [2005]: Heston’s Model and the Smile, S. 161–182, in:
Statistical Tools for Finance and Insurance (Hrsg. P. Cízek, W. Härdle und
R. Weron), Springer, Berlin.
Wiener, N. [1923]: Differential–Space, Journal of Math and Physics 2, S. 131–174.
Literaturverzeichnis
xix
Wilkens, S. [2000]: Zur Eignung numerischer Verfahren für die Optionsbewertung –
Mit einer ausführlichen Einführung in Derivatehandel und –bewertung, VVW,
Karlsruhe.
Zhang, P. [2001]: Exotic Options: A Guide to the Second Generation Options, Zweite
Auflage, World Scientific Publishing Company, Singapur.
Zhu, J. [2000]: Modular Pricing of Options, An Application of Fourier Analysis,
Springer, Berlin.
Zimmermann, H. und W. Hafner [2005]: Vincenz Bronzin’s Option Pricing Theory:
Contents, Contribution, and Background, WWZ-Research Report 2005/04,
University of Basel.
Erklärung
Hiermit versichere ich, dass ich die vorliegende Arbeit selbständig verfasst und keine
anderen als die angegebenen Quellen und Hilfsmittel benutzt habe, dass alle Stellen
der Arbeit, die wörtlich oder sinngemäß aus anderen Quellen übernommen wurden,
als solche kenntlich gemacht worden sind, und dass die Arbeit in gleicher oder
ähnlicher Form noch keiner anderen Prüfungsbehörde vorgelegt wurde.
Hannover, den 13. März 2008