Anregungen zur Umsetzung

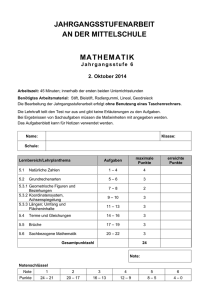
Neuer Lehrplan im Fach Informationstechnologie
– Anregungen zur Umsetzung –
G1: Modellierung und Codierung von Algorithmen (14)
Aufbauend auf den bisher gesammelten Erfahrungen zu objektorientierten Systemen beschäftigen sich die Schüler mit Zustandsänderungen von Objekten. Sie erkennen, dass sich die hierfür
verwendeten Methoden mithilfe algorithmischer Grundstrukturen beschreiben lassen. Diese
Strukturen werden von ihnen mit einem geeigneten Werkzeug codiert.
 Abläufe verbalisieren
 Die Grundstrukturen Sequenz, Auswahl und Wiederholung bei der Modellierung geeigneter
Probleme verwenden
 Algorithmen mit einem Programmierwerkzeug implementieren
I.
Didaktische Erläuterungen
Das Wissen über die Modellierung von Algorithmen wird aufgebaut. Zunächst analysieren die
Schüler die Aufgabenstellung und erarbeiten mögliche Lösungswege. Sie verbalisieren Lösungsabläufe und halten diese in kurzer schriftlicher Form fest. Daraus entwickeln sie Algorithmen unter geeigneter Verwendung der drei Grundstrukturen. Die Schüler gelangen von sequentiellen Lösungsmustern durch den überlegten Einsatz von Auswahl- und Wiederholungsstrukturen zu optimierten Kontrollstrukturen (z. B. Programmablaufpläne).
Nach ihren Entwürfen implementieren die Schüler ihren Lösungsalgorithmus mit einem schülergeeigneten Programmierwerkzeug. Dabei kann es sich auch um schon bekannte Standardwerkzeuge handeln.
II. Fertigkeiten und Kompetenzen
Die Schüler vertiefen ihre Kenntnisse über die objektorientierte Analyse. Dabei erkennen sie,
dass es sinnvoll ist, bei der Erarbeitung von Problemlösungen Aktivitäten und Abläufe zu verbalisieren und kleinschrittig festzuhalten. Hieraus ergibt sich dann bei der Entwicklung von Algorithmen die Verwendung der drei Grundstrukturen. Durch den Einsatz selbst entwickelter Algorithmen vertiefen die Schüler ihre Fähigkeit, Problemstellungen zu lösen.
© 2011 – Staatsinstitut für Schulqualität und Bildungsforschung – Abteilung Realschule
Neuer Lehrplan im Fach Informationstechnologie
– Anregungen zur Umsetzung –
III. Aufgabenbeispiele
III.a
Pythagoräischen Tripel
Ein Pythagoräischen Tripel setzt sich aus den drei natürlichen Zahlen a, b und c zusammen und
erfüllen den Satz des Pythagoras, der heißt: a2  b2  c 2 . In der Geometrie zeigt dieser Satz
den Zusammenhang zwischen den beiden Katheten und der Hypotenuse in einem rechtwinkligen Dreieck.
Das Tripel (3 | 4 | 5) erfüllt diese Bedingung: 32  42  52 , da 32  42  25 und 52  25
Alle ganzzahligen Vielfachen dieses Tripels erfüllen dann auch diese Bedingung, z. B.:
(3  3 | 3  4 | 3  5)  (9 | 12 | 15) erfüllt diese Bedingung, da 92  122  225 und 152  225
Auch Tripel wie (5 | 12 | 13) , (223 | 24864 | 24865) , usw. erfüllen diese Bedingung.
Man kann solche Pythagoräischen Tripel aus zwei natürlichen Zahlen m und n (es gilt: n > m)
durch folgende Algorithmen erzeugen:
a  n2  m2
c  n2  m2
b  2nm
Hiermit lassen sich z. B. folgende Pythagoräische Tripel erzeugen:
m
n
a
b
c
a2  b2
c2
1
2
3
4
5
25
25
1
3
8
6
10
100
100
1
4
15
8
17
289
289
1
5
24
10
26
676
676
2
6
32
24
40
1600
1600
2
7
45
28
53
2809
2809
2
8
60
32
68
4624
4624
2
9
77
36
85
7225
7225
2
10
96
40
104
10816
10816
5
10
75
100
125
15625
15625
7
10
51
140
149
22201
22201
9
10
19
180
181
32761
32761
…
…
…
…
…
…
…
© 2011 – Staatsinstitut für Schulqualität und Bildungsforschung – Abteilung Realschule
Neuer Lehrplan im Fach Informationstechnologie
– Anregungen zur Umsetzung –
Die Berechnung der Pythagoräischen Tripel soll mit einem Programm durchgeführt werden. Der
Algorithmus lässt sich so beschreiben:






Es werden die beiden Zahlen m und n eingelesen, dabei wir überprüft, ob die Zahl n größer
als die Zahl m ist.
Die phythagoräische Zahl a wird berechnet, indem das Quadrat von der Zahl m vom Quadrat der Zahl n subtrahiert wird.
Die phythagoräische Zahl b wird berechnet, indem das Produkt aus 2 und den Zahlen m
und n gebildet wird.
Die phythagoräische Zahl c wird berechnet, indem das Quadrat von der Zahl m zum Quadrat der Zahl n addiert wird.
Zur Kontrolle wird zum einen die Summe aus den Quadraten der beiden pythagoräischen
Zahlen a und b berechnet und zum anderen das Quadrat der pythagoräischen Zahl c.
Die beiden Ergebnisse werden verglichen.
© 2011 – Staatsinstitut für Schulqualität und Bildungsforschung – Abteilung Realschule
Neuer Lehrplan im Fach Informationstechnologie
– Anregungen zur Umsetzung –
lesen(m)
lesen(n)
Aussage1:=m < n
[Aussage=falsch]
[Aussage=wahr]
a:=n*n - m*m
b:=2*n*m
c:=n*n + m*m
ausgeben (a)
ausgeben (b)
ausgeben (c)
Kontrolle1:=a*a+b*b
Kontrolle2:=c*c
ausgeben(Kontrolle1)
ausgeben(Kontrolle2)
Aussage2:=Kontrolle1=Kontrolle2
[Aussage=falsch]
[Aussage=wahr]
© 2011 – Staatsinstitut für Schulqualität und Bildungsforschung – Abteilung Realschule
Neuer Lehrplan im Fach Informationstechnologie
– Anregungen zur Umsetzung –
Die für das Programm benötigten Operationen sind in der nachfolgenden Tabelle angegeben.
Zelle
Operation
Wirkung
C9
=WENN(D7<=D5;
"n muss größer als m sein";"")
Es wird überprüft, ob die Zahl m
kleiner als die Zahl n ist.
D11
=POTENZ(D7;2)-POTENZ(D5;2)
Es wird die Zahl a berechnet.
D13
=2*D5*D7
Es wird die Zahl b berechnet.
D15
=POTENZ(D7;2)+POTENZ(D5;2)
Es wird die Zahl c berechnet.
DE18
=POTENZ(D11;2)+POTENZ(D13;2)
Es wird die Summe aus den Quadraten der beiden Zahlen a und b
berechnet
DE20
=POTENZ(D15;2))
Es wird das Quadrat der Zahl c berechnet.
B22
=WENN(D18<>D20;
"Fehler bei der Eingabe";
"Die Zahlen a, b und c bilden
ein pythagoräisches Tripel")
Es wird überprüft, ob die drei Zahlen a, b und c ein pythagoräisches
Tripel bilden.
Das Programm kann verbessert werden, dass bei keiner Eingabe der Zahlen m oder n auch in
den Zellen D11, D13, D15, DE18 und DE20 keine Werte bzw. Fehlermeldungen angezeigt werden.
© 2011 – Staatsinstitut für Schulqualität und Bildungsforschung – Abteilung Realschule
Neuer Lehrplan im Fach Informationstechnologie
– Anregungen zur Umsetzung –
Zelle
Operation
C9
=WENN(ODER(D5="";D7="");"";
WENN(D7<=D5;"n muss größer als m sein";""))
D11
=WENN(ODER(D5="";D7="";D5>=D7);"";POTENZ(D7;2)-POTENZ(D5;2))
D13
=WENN(ODER(D5="";D7="";D5>=D7);"";2*D5*D7)
D15
=WENN(ODER(D5="";D7="";D5>=D7);"";POTENZ(D7;2)+POTENZ(D5;2))
DE18
=WENN(ODER(D5="";D7="";D5>=D7);"";POTENZ(D11;2)+POTENZ(D13;2))
DE20
=WENN(ODER(D5="";D7="";D5>=D7);"";POTENZ(D15;2))
B22
=WENN(ODER(D5="";D7="";D5>=D7;D18<>D20);
"Fehler bei der Eingabe";
"Die Zahlen a, b und c bilden ein pythagoräisches Tripel")
© 2011 – Staatsinstitut für Schulqualität und Bildungsforschung – Abteilung Realschule
Neuer Lehrplan im Fach Informationstechnologie
– Anregungen zur Umsetzung –
III.b
Fibonaccizahlen
Leonardo Fibonacci hat 1202 mit seiner Folge von Zahlen recht gut das Wachstum von Kaninchenpopulationen beschrieben.
Die Zahlenreihe entsteht dadurch, dass jede neue Zahl, die Summe aus den beiden vorherigen
Zahlen ist.
1 1  2
1 2  3
23  5
35 8
5  8  13
8  13  21
13  21  34
21 34  55
34  55  89
55  89  144
89  144  233
...  ...  ...
Ausnahme ist, dass die ersten beiden Fibonacci-Zahlen jeweils 1 sind.
Fibonacci-Zahlen
1
1
2
3
5
8
13 21 34 55 89 …
Zähler
1
2
3
4
5
6
7
8
9
10 11
© 2011 – Staatsinstitut für Schulqualität und Bildungsforschung – Abteilung Realschule
n
Neuer Lehrplan im Fach Informationstechnologie
– Anregungen zur Umsetzung –
berechneFibonacci(n)
Antwort1 := 1
Zähler := 1
[n = 1]
Antwort := Antwort1
ausgeben(Zähler, Antwort)
[n > 1]
Antwort2 := 1
Zähler := 2
[n = 2]
Antwort := Antwort2
[n > 2]
Antwort := Antwort1 + Antwort2
Zähler := Zähler + 1
[n = Zähler]
[n > Zähler]
Antwort1 := Antwort2
Antwort2 := Antwort
© 2011 – Staatsinstitut für Schulqualität und Bildungsforschung – Abteilung Realschule
Neuer Lehrplan im Fach Informationstechnologie
– Anregungen zur Umsetzung –
Die für das Programm benötigten Operationen sind in der nachfolgenden Tabelle angegeben.
Zelle
Operation
Wirkung
=WENN($G$4>=1;1;"")
Wenn der Zähler n den Wert 1 oder
größer hat, wird in die Zelle der
Wert 1 geschrieben.
C7
=WENN($G$4>=C6+1;C6+1;"")
Wenn der Zähler n den Wert 2 oder
größer hat, wird in die Zelle der
Wert 2 geschrieben.
C8
=WENN($G$4>=C7+1;C7+1;"")
Wenn der Zähler n den Wert 3 oder
größer hat, wird in die Zelle der
Wert 3 geschrieben.
…
…
H30
=WENN($G$4>=H29+1;H29+1;"")
Wenn der Zähler n den Wert 50 hat,
wird in die Zelle der Wert 50 geschrieben.
D6
=WENN(C6<>"";". Fibonacci Zahl";"")
Wenn in der Zelle C6 ein Wert steht,
dann wird in diese Zelle . Fibonacci
Zahl geschrieben.
…
…
I30
=WENN(H30<>"";". Fibonacci Zahl";"")
Wenn in der Zelle H30 ein Wert
steht, dann wird in diese Zelle . Fibonacci Zahl geschrieben.
E6
=WENN($G$4>=C6;1;"")
Wenn der Zähler gleich oder größer
als 1 ist, dann wird hier als 1. Fibonacci-Zahl die 1 geschrieben.
E7
=WENN($G$4>=C7;1;"")
Wenn der Zähler gleich oder größer
als 2 ist, dann wird hier als 2. Fibonacci-Zahl die 1 geschrieben.
E8
=WENN($G$4>=C8;SUMME(E6:E7);"")
…
…
J30
=WENN($G$4>=H30;SUMME(J28:J29);"")
C6
Wenn der Zähler gleich oder größer
als 3 ist, dann wird hier als 3. Fibonacci-Zahl die 2 geschrieben.
…
Wenn der Zähler gleich 50 ist, dann
wird hier als 50. Fibonacci-Zahl die
12586269025 geschrieben.
© 2011 – Staatsinstitut für Schulqualität und Bildungsforschung – Abteilung Realschule
Neuer Lehrplan im Fach Informationstechnologie
– Anregungen zur Umsetzung –
© 2011 – Staatsinstitut für Schulqualität und Bildungsforschung – Abteilung Realschule