Konus, Anzug und Neigung

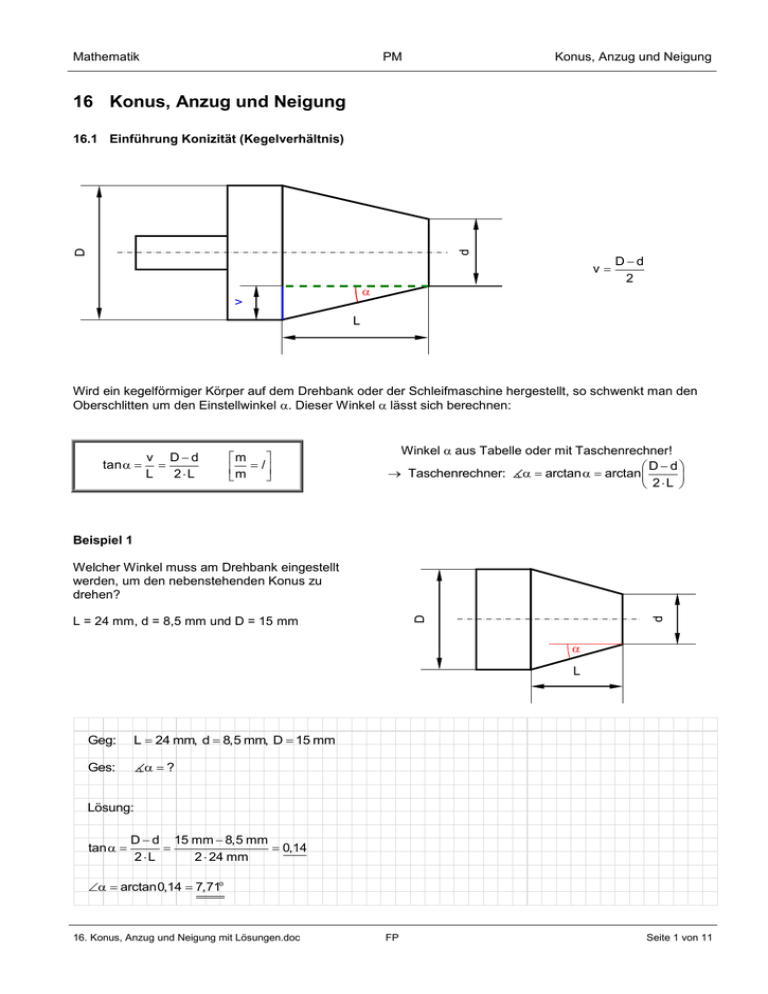
Mathematik
PM
Konus, Anzug und Neigung
16 Konus, Anzug und Neigung
d
D
16.1 Einführung Konizität (Kegelverhältnis)
v
v

Dd
2
L
Wird ein kegelförmiger Körper auf dem Drehbank oder der Schleifmaschine hergestellt, so schwenkt man den
Oberschlitten um den Einstellwinkel . Dieser Winkel  lässt sich berechnen:
tan  
v Dd

L
2L
m

m  /


Winkel  aus Tabelle oder mit Taschenrechner!
D d
 Taschenrechner:   arctan   arctan 

 2L 
Beispiel 1
L = 24 mm, d = 8,5 mm und D = 15 mm
d
D
Welcher Winkel muss am Drehbank eingestellt
werden, um den nebenstehenden Konus zu
drehen?

L
Geg:
L  24 mm, d  8,5 mm, D  15 mm
?
Ges:
Lösung:
tan  
D  d 15 mm  8,5 mm

 0,14
2L
2  24 mm
  arctan0,14  7,71o
16. Konus, Anzug und Neigung mit Lösungen.doc
FP
Seite 1 von 11
Mathematik
PM
Konus, Anzug und Neigung
Beispiel 2
Gegeben sind die Masse nach Skizze.
Bestimmen Sie den grossen Durchmesser.
D
50º
L = 40
Geg:
L  40 mm, 2  50o
Ges:
D?
Lösung:
0
tan  
Dd
2 L
mit d  0 und   25o

einsetzen:
D  tan   2  L  tan25o  2  50 mm  37,30 mm
16. Konus, Anzug und Neigung mit Lösungen.doc
FP
Seite 2 von 11
Mathematik
PM
Konus, Anzug und Neigung
16.2 Konizität als Verhältnis und in %
Nach VSM kann man die Konen auch als Verhältnis oder in % vermassen:
d
D
15%
L
Die Konizität als Verhältnis berechnet sich nach:
1 Dd

x
L
m

m  /


zur Erinnerung:
tan  
Dd
1

2L
2 x
Die Konizität als Verhältnis gibt die Länge an, wenn (D - d) = 1 ist.
Die Konizität in Prozenten berechnet sich nach:
x%
Dd
1
 100   100
L
x
m

m  /


Wird die Formel entsprechend umgeformt, wird ersichtlich, dass die Konizität in Prozenten den Durchmesserunterschied angibt, bei einer Länge von 100.
umgeformt:
x % Dd

100
L
16. Konus, Anzug und Neigung mit Lösungen.doc
FP
Seite 3 von 11
Mathematik
PM
Konus, Anzug und Neigung
 92
Gegeben sind die Masse nach Skizze.
Berechnen Sie die Konizität in % und als
Verhältnis.
 60
Beispiel 1
135
Geg:
D  92 mm, d  60 mm, L  135 mm
Ges:
a) x%  ? und b)
Konizität in %
1
?
x
Konizität als Verhältnis
Lösung:
a) x% 
b)
Dd
92 mm  60 mm
 100 
 100  23.70 %
L
135 mm
1 Dd

x
L

x
L
135 mm

 4,22
D  d 92 mm  60 mm

1
1

x 4,22
Merke:
Wenn man die beiden Formeln oben genau anschaut, wird ersichtlich, dass x (aus der Verhältnisgleichung)
multipliziert mit x% (aus der Prozentgleichung) immer 100 ergibt!
Beweis: x  x% 
L Dd

 100  100
Dd L
16. Konus, Anzug und Neigung mit Lösungen.doc
FP
Seite 4 von 11
Mathematik
PM
Konus, Anzug und Neigung
Beispiel 2
Gegeben sind die Masse nach Skizze.
Berechnen Sie:
1:20
d
D
a) Konizität in Prozenten = ?
b) D – d = ?
c)  = ?

82.5
Geg:
1
1

, L  82,5 mm
x 20
Ges:
a) x%  ?, b) D  d  ?, c)
?
Lösung:
b)
1 Dd

x
L
a)
x% 
c)
tan  
 Dd 
L 82,5 mm

 4,13 mm
x
20
Dd
1
1
 100   100 
 100  5%
L
x
20
Dd
1
1
1



 0,025
2L
x  2 20  2 40
16. Konus, Anzug und Neigung mit Lösungen.doc

FP
  arctan0,025  1,43o
Seite 5 von 11
Mathematik
PM
Konus, Anzug und Neigung
Beispiel 3
Gegeben sind die Masse nach Skizze.
Berechnen Sie:
1:20
30
33.5
a)  = ?
b) Konizität in Prozenten = ?
c) q = ?

q
60
L
Geg:
1
1

, L  q  60 mm, d  30 mm, D  33,5 mm
x 20
Ges:
a)
  ?, b) x%  ?, c) q  ?
Lösung:
a)
1 Dd
1


x
L
20
tan  
1
Dd
2L
in  2 :
Dd
 100
L
1 in  3  :
b) x% 
c)
1
 2
tan  
1
1
1


 0,025
x  2 20  2 40

  arctan0,025  1,43o
3 
x% 
1
1
 100 
 100  5%
x
20
1 Dd
Dd


 q  60 mm  D  d  x 
x
L
q  60 mm
q  D  d  x  60 mm   33,5 mm  30 mm  20  60 mm  10 mm
16. Konus, Anzug und Neigung mit Lösungen.doc
FP
Seite 6 von 11
Mathematik
PM
Konus, Anzug und Neigung
16.3 Übungen
 78
Berechnen Sie den Einstellwinkel an der
Schleifmaschine.
 48
1.

Gegeben sind der Winkel  = 0,384 rad
und die Masse nach Skizze. Bestimmen
Sie den Durchmesser d.
d
2.
 62
82

58
Gegeben sind die Masse nach Skizze.
Bestimmen Sie:
57
a) den Winkel 
b) den Konus in %
c) das Mass z
1:17
29
3.

12
Gegeben sind der Winkel  = 3,6 (Neugrad) und die Masse nach Skizze. Bestimmen Sie die Länge L.
8
 10
g
 15
4.
z

L
16. Konus, Anzug und Neigung mit Lösungen.doc
FP
Seite 7 von 11
Mathematik
PM
Konus, Anzug und Neigung
16.4 Einführung Neigung
Der Keil hat die Aufgabe, zwei Körper durch gegeneinanderpressen in eine feste Verbindung zu bringen. Seine
Kraftänderung beruht auf der Wirkung der schiefen Ebene.
h
H

L
Die Neigung als Verhältnis berechnet sich nach:
1 Hh

x
L
m

m  /


(entspricht dem tan β)
Die Neigung als Verhältnis gibt die Länge an, wenn (H – h) = 1 ist.
Die Neigung in Prozenten berechnet sich nach:
Neigung % 
Hh
1
 100   100
L
x
m

m  /


Wird die Formel entsprechend umgewandelt, wird ersichtlich, dass die Neigung in Prozenten den Höhenunterschied angibt, bei einer Länge von 100.
umgeformt:
Neigung %
Hh

100
L
12 % Steigung bedeutet z. B., dass die Strasse auf eine Länge von 100 m um 12 m ansteigt.
Der Winkel  berechnet sich:
tan  
Hh 1

L
x
m

m  /


16. Konus, Anzug und Neigung mit Lösungen.doc
Winkel  aus Tabelle oder mit Taschenrechner
FP
Seite 8 von 11
Mathematik
PM
Konus, Anzug und Neigung
Beispiel 1
%
Gegeben sind die Masse nach Skizze.
Bestimmen Sie:

12.5
15
a) den Anzug in %
b) die Neigung als Verhältnis
c) den Neigungswinkel
160
Geg:
H  15 mm, h  12,5 mm, L  160 mm
Ges:
N%  ?,
Anzug in %
1
? ,
x
?
Neigung
als Verhältnis
Lösung:
a) N% 
b)
Hh
15 mm  12,5 mm
 100 
 100  1,56%
L
160 mm
1 Hh

x
L
c) tan  

x
L
160 mm

 64
H  h 15 mm  12,5 mm
Hh 1
1
 
 0,0156
L
x 64
16. Konus, Anzug und Neigung mit Lösungen.doc

Kontrolle: N%  x  100
  arctan0, 0156  0,90o
FP
Seite 9 von 11
Mathematik
PM
Konus, Anzug und Neigung
Beispiel 2
75
Gegeben sind die Masse nach Skizze.
Bestimmen Sie:
a) die Höhen h und q
b) den Weg von Keil B, wenn Keil A 22 mm
einfährt
c) den Winkel 
B
q
1:10
42

h
A
120
Geg:
H  42 mm, L A  120 mm, LB  75 mm, sA  22 mm,
Ges:
a) h  ? und q  ?, b) sB  ?, c)
1 1

x 10
?
Lösung:
a)
b)
1 Hh

x
LA

LA
 Hh
x
1 q0

x
LB

q
1 sB  0

x
sA

anschaulich:
 h  H
LA
120 mm
 42 mm 
 30 mm
x
10
LB 75

 7,5 mm
x 10
sB 
sA 22

 2,2 mm
x 10
auf 75 mm : 7,5 mm
auf 22 mm : 2,2 mm
c) tan  
Hh 1 1
 
 0,10
LA
x 10
   5,71o
16. Konus, Anzug und Neigung mit Lösungen.doc
FP
Seite 10 von 11
Mathematik
PM
Konus, Anzug und Neigung
16.5 Übungen
1.
Eine Standseilbahn überwindet eine Höhe von 920 m. Die Schienenlänge beträgt 1’420 m. Berechnen
Sie die durchschnittliche Steigung in %.
2.
Wie gross ist der Neigungswinkel, wenn die Steigung 300 % beträgt?
3.
Der Keil A wird 5,8 mm eingetrieben.
a) Welchen Weg s macht der Keil B?
b) Wie gross ist der Neigungswinkel ?
c) Wie gross ist h?
B
1:8
11

h
A
42
Berechnen Sie die Höhe H des
skizzierten Keils!
24%
H
1:45
20
4.
68
5.
Berechnen Sie D!
85
D
 62
1:5
8º
38
16. Konus, Anzug und Neigung mit Lösungen.doc
FP
Seite 11 von 11