Das Minimum-Spanning

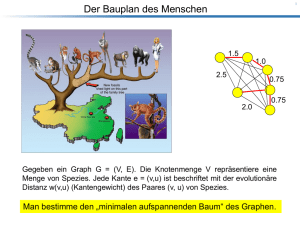
Das Minimum-Spanning-Tree Problem MST
Die Problemstellung
Das folgende Beispiel zeigt eine spezielle, aber auch typische Aufgabenstellung mit deren Lösung wir uns
beschäftigen wollen:
Gegeben seien n Punkte in der Ebene zusammen mit den paarweisen Abständen. Wähle von den n2 Kanten
zwischen den Punkten n − 1 Kanten so aus, dass sie einen Baum bilden und dass außerdem die Gesamtlänge
der ausgewählten Kanten möglichst klein ist!
Etwas allgemeiner: Sei G = (V, E) ein ungerichteter zusammenhängender Graph und w eine Gewichtsfunktion, die jeder Kante eine reelle Zahl zuordnet, dies könnte zum Beispiel deren Länge sein.
Wir wissen, dass G mindestens einen aufspannenden Baum hat. Sei T = (V, E ′ ) ein solcher aufspannender
Baum. Wir definieren das Gewicht von T als
w(T ) =
∑ w(e).
e∈E ′
Aufgabe: Finde unter allen aufspannenden Bäumen einen mit minimalem Gesamtgewicht! Einen solchen
Baum nennt man einen minimal aufspannenden Baum oder minimum spanning tree (MST).
Offensichtlich hat jeder gewichtete zusammenhängende Graph einen MST, aber im Allgemeinen muss dieser
nicht eindeutig sein.
Wir werden zuerst einen generischen MST–Algorithmus kennenlernen und danach zwei konkrete Umsetzungen.
Der generische MST–Algorithmus
Definition: Ein Schnitt von G = (V, E) ist eine Zerlegung seiner Knotenmenge in zwei nichtleere Teilmengen
(S,V \ S).
Eine Kantenmenge A respektiert einen Schnitt (S,V \S), falls keine Kante aus A einen Knoten aus S mit einem
aus V \ S verbindet.
Eine Kantenmenge A heißt sicher, wenn es einen MST T von G gibt, so dass A in der Kantenmenge von T
enthalten ist.
Satz (Grundlage des generischen MST–Algorithmus):
Sei G = (V, E) ein gewichteter, ungerichteter, zusammenhängender Graph und sei A eine sichere Menge von
Kanten, die einen Schnitt (S,V \ S) respektiert. Wir betrachten eine leichteste Kante e = {u, v}, mit u ∈ S,
v ∈ V \ S. Dann ist A ∪ {e} sicher.
Beweis: Sei T ein MST, der A enthält. Wir nehmen an, dass e = {u, v} nicht zu T gehört, ansonsten ist nichts
zu beweisen.
Wenn wir die Kante e zu T hinzunehmen, entsteht genau ein Kreis C. Wir betrachten in C alle Kanten {x, y}
mit x ∈ S, y ∈ V \ S. Außer {u, v} muss es wenigstens noch eine weitere solche Kante geben. Sei dies e′ =
{u′ , v′ }.
Streichen wir e′ aus T ∪ {e}, so entsteht ein anderer aufspannender Baum T ′ . Da nach Annahme w(e) ≤ w(e′ )
und T ein MST ist, folgt sofort, dass auch T ′ ist MST ist und mithin ist A ∪ {e} sicher.
1
Die folgende Abbildung illustriert den Beweis des Satzes:
Schnitt
sichere Kanten
v’
u’
v
u
S
V\S
Der MST T und die Kante uv definieren Kreis!
Der Satz kann algorithmisch zur Berechnung eines MST eingesetzt werden. Man startet mit der leeren Menge
/ sucht sich einen Schnitt, der von A respektiert wird (dies sind am Anfang alle Schnitte), nimmt die
A = 0,
leichteste Kante über den Schnitt hinzu und interiert so lange, bis (V,A) ein aufspannender Baum ist.
Die beiden MST–Algorithmen von Prim und Kruskal sind konkrete Umsetzungen davon und unterscheiden
sich darin, welche Schnitte man in den einzelnen Schritten betrachtet.
Der MST–Algorithmus von Prim
Der Algorithmus von Prim ist konzeptionell sehr einfach. Wir lassen den MST–Baum von einem beliebigen
Startknoten r aus ‘wachsen’. Die Frage ist, um welche Kante die Teillösung in einem Schritt erweitert wird.
Dazu betrachtet man jeweils den Schnitt, der den bisherige Teilbaum vom Rest trennt.
Zur Realisierung dieser Idee verwenden wir eine sogenannte Prioritätswarteschlange zur Verwaltung aller
noch nicht erreichten Knoten w. Jedes Objekt in einer Prioritätswarteschlange Q besitzt einen Schlüssel der bestimmt, welches Objekt den Kopf der Warteschlange bildet. Der Kopf kann mit der Funktion Extract-Min(Q)
aus Q entfernt werden. In unserem Fall gibt der Schlüssel eines Knoten w an, was im Moment das Gewicht
einer leichtesten Kante ist, mittels derer w von einem der bereits in den Teilbaum aufgenommenen Knoten
aus erreichbar ist. Es kommt also nicht darauf an, wann ein Knoten in Q aufgenommen wurde sondern der
Knoten mit dem kleinsten Schlüssel bildet den Kopf von Q.
Effiziente Implementierungen von Prioritätswarteschlangen werden wir später kennenlernen, merken aber
an dieser Stelle schon an, dass man bei dieser Anwendung auch in der Lage sein muss, die Schlüssel der
gespeicherten Knoten gegebenenfalls zu verändern (Updates). Wie schon bei BFS und DFS verwenden wir
π–Zeiger, um den aktuell gefundenen Teil–MST mit Wurzel r sowie die bisher bekannten leichtesten Kanten
zu jedem Knoten in Q darzustellen.
Die Laufzeit des Algorithmus hängt von der konkreten Realisierung des abstrakten Datentyps Prioritätswarteschlange ab, sowie von der Umsetzung der update–Operationen. Benutzt man für die Implementierung der Prioritätswarteschlange einen binären Heap , so ist die Komplexität O(|V | log |V | + |E| log |V |) =
O(|E| log |V |).
2
MST-Prim (G,w,r)
for all u ∈ V(G)
insert u in Q
π[u] = NIL
key[u] = ∞
key[r] = 0
while (Q not empty)
u = Extract-Min(Q)
for all v ∈ Adj[u]
if ( v ∈ Q and w(u,v) < key[v]) then
π[v] = u
key[v] = w(u,v)
Die folgende Abbildung illustriert den Schnitt des Graphen, der in einem Schritt des Algorithmus zur Auswahl
der nächsten Kante verwendet wird:
Schnitt
restliche Graphkanten
Π (w)
w
r
bekannte leichteste
Kanten zu Knoten in Q
Kanten im Teil−MST
Der MST–Algorithmus von Kruskal
/ und nimmt schrittweise Kanten in den
Auch dieser Algorithmus startet mit dem kantenlosen Graphen (V, 0)
MST auf. Im Gegensatz zum Algorithmus von Prim wächst dieser MST nicht nur an einer sondern möglicherweise an vielen Komponenten. In jedem Schritt wird von allen Kanten, die keinen Kreis schließen (d.h. die
zwei Knoten aus aktuell verschiedenen Komponenten verbinden), die leichteste in den MST aufgenommen.
Dazu werden die Kanten zuerst nach aufsteigenden Gewichten sortiert. Danach wird in dieser Reihenfolge, mit der leichtesten Kante beginnend, getestet, ob diese Kante einen Kreis im bisher konstruierten Wald
schließt (falls ja wird die Kante verworfen). Falls nein wird die sichere Menge um diese Kante erweitert.
Anders gesagt, wir testen, ob es für die akuelle Kante einen Schnitt gibt, der von der bisherigen Løßung
respektiert wird und für den sie eine leichteste überbrückende Kante ist.
Das Interessanteste an der Umsetzung dieser Idee ist die verwendete Datenstruktur, eine sogenannte UnionFind–Struktur zur Verwaltung von Partitionen einer endlichen Menge, hier der Knotenmenge V .
Die von der Datenstruktur unterstützten Operationen sind:
3
• makeSet(v): Aus dem Element v ∈ V wird eine Menge gemacht.
• union(u,v): Die beiden Mengen, zu denen u bzw. v gehören, werden vereinigt.
• findSet(v): Bestimme die Menge, zu der v gehört.
Dazu stelle man sich vor, dass jede Menge einen Repräsentanten hat, auf den alle Elemente der Menge zeigen.
Bei der union–Operation müssen also die Zeiger der Knoten einer Teilmenge auf den Repräsentanten der
zweiten Teilmenge umgeleitet werden. Eine einfache Realisierung besteht darin, bei union zweier Mengen,
die Zeiger der kleineren Menge auf den Repräsentanten der größeren umzuleiten.
Man überlegt sich wie folgt, dass die Gesamtzahl der Zeigerumleitungen höchstens |V | log |V | sein kann: Betrachten wir einen konkreten Knoten v ∈ V . Nach dem ersten Umhängen seines Zeigers landet er in einer
Menge, die mindestens doppelt so groß ist, also mindestens zwei Knoten hat. Wenn er das nächste Mal angefasst wird, landet er in einer Menge mit ≥ 4 Knoten usw. Insgesamt kann er also nur log2 |V | umgelenkt
werden, danach ist ganz V erreicht. Das gilt für jeden Knoten, also insgesamt höchstens |V | log |V — Zeiger
werden während des gesamten Algorithmus umgehangen. (Dies ist ein Beispiel einer sogenannten amortisierten Analyse.)
Hier ist der Pseudocode für Kruskals Algorithmus.
MST-Kruskal(G,w)
A = 0/
for all v ∈ V(G)
makeSet(v)
Sort E(V) by increasing weight w
for all e= {u,v} ∈ E(V) (sorted)
if ( find-Set(u) 6= find-Set(v)) then
A = A ∪{e}
union(u,v)
return A
Mit der oben erwähnten Union–Find–Implementierung erreicht der Algorithmus eine Laufzeit von
O(|E| log |E| + |V | log |V |).
Das Beispiel auf der nächsten Seite zeigt einen Graphen G mit einem MST (es gibt in diesem Fall mehrere)
und zwei Phasen aus dem Ablauf der Algorithmen von Prim und Kruskal.
Zum Schluss wenden wir uns der folgenden Frage zu: Wie findet man einen zweitleichtesten aufspannenden
Baum?
Diesen gibt es offenbar immer dann, wenn der zusammenhängende Ausgangsgraph kein Baum ist. Zunächst
konstruiert man einen MST T = (V, E ′ ). Wir betrachten nacheinander alle Kanten e ∈ E \E ′ . Dann hat T ∪ {e}
genau einen Kreis. Aus diesem Kreis streichen wir die schwerste von e verschiedene Kante de . Dies liefert
einen aufspannenden Baum Te mit dem Gewicht w(T )+w(e)−w(de ). Die Kante e∗ ∈ E \E ′ mit w(e∗ )−w(de∗ )
minimal ergibt den gesuchten zweitleichtesten aufspannenden Baum. Man beachte, dass e∗ nicht unbedingt
die leichteste Kante in E \ E ′ sein muss.
4
8
b
d
2
4
11
a
7
c
7
8
h
4
i
14
6
e
10
g
1
9
f
2
Die dicken Kanten bilden einen MST mit Gewicht 37
(die Kante bc könnte auch durch ah ersetzt werden)
8
b
7
d
2
4
11
a
7
c
7
8
h
4
i
14
6
e
10
f
g
1
9
2
4
6
Prim−Algorithmus: Zustand , nachdem a,b,c,i in dieser
Reihenfolge aus Prioritätswarteschlange entfernt wurden.
An den verbleibenden Knoten ist der aktuelle Schlüssel
vermerkt.
7
8
b
11
7
8
d
2
4
a
7
c
h
4
i
14
6
1
9
e
10
g
2
f
Kruskal−Algorithmus: Nach der Aufnahme der ersten
5 Kanten werden in den nächsten beiden Schritten die
Kanten ig und ih verworfen, da sie jeweils Kreise schließen.
5