Sternentwicklung - Baader Planetarium
Werbung

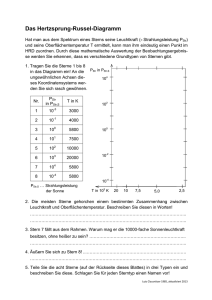
Sternentwicklung Von der Geburt bis zum Tod eines Sterns Verfasst von: Justus Neußer Und Steffen Prior Carl-Fuhlrott-Gymnasium Jahrgangsstufe Q1 Wuppertal Schuljahr 2014/15 Projektarbeit im Rahmen des Projektkurses Astronomie Abgabedatum: 27.05.2015 Kursleiter: Bernd Koch 1 Inhaltsverzeichnis 1. Einleitung…………………………………………………………………………………………………………………………….03 1.1 Einleitung………………………………………………………………………………………………………………………03 1.2 Themenwahl…………………………………………………………………………………………………………………03 2. Theoretische Grundlagen……………………………………………………………………………………………………04 2.1 Atomphysik…………………………………………………………………………………………………………………..04 2.2 Hertzsprung-Russell-Diagramm…………………………………………………………………………………...06 2.3 Spektroskopie……………………………………………………………………………………………………………….08 3. Aufbau…………………………………………………………………………………………………………………………………09 3.1 Deep-Sky Fotografie……………………………………………………………………………………………………..09 3.2 Sternbild Fotografie………………………………………………………………………………………………………13 3.3 Ablauf eines Beobachtungsabends……………………………………………………………………………….14 4. Sternentstehung…………………………………………………………………………………………………………………16 4.1 Experiment M42……………………………………………………………………………………………………………16 4.2 Theorie zur Sternentstehung………………………………………………………………………………………..20 5. Hauptreihenstern………………………………………………………………………………………………………………..23 6. Roter Riese…………………………………………………………………………………………………………………………..25 6.1 Experiment und Anwendung der Spektroskopie…………………………………………………………..26 6.2 Berechnung der Oberflächentemperatur……………………………………………………………………..34 6.3 Theorie zum Stadium Roter Riese………………………………………………………………………………….35 7. Weißer Zwerg und planetarischer Nebel…………………..………………………………………………………..37 7.1 Experiment M57 und Anwendung des Stacking-Verfahrens…………………………………………37 7.2 Theorie zum Stadium Weißer Zwerg und planetarischer Nebel…………………………………….41 8. Supernova…………………………………………………………..……………………………………………………………….44 8.1 Kernkollaps-Supernova…………………………………………………………………………………………………44 8.2 Thermonukleare Supernova…………………………………………………………………………………………46 9. Schwarzes Loch…………………………………………………………..………………………………………………………47 10. Fazit…………………………………………………………..……………………………………………………………………....49 11. Danksagung…………………………………………………………..……………………………………………………………49 12. Abschlusserklärung…………………………………………………………..………………………………………………..50 2 1. Einleitung 1.1 Einleitung Als wir erfahren haben, dass für uns Schüler die beinahe einmalige Möglichkeit besteht eine astronomische Arbeit zu verfassen, stand für uns bereits fest diesen Kurs zu belegen. Nach längerer Überlegungszeit haben wir uns schließlich doch für ein Thema entscheiden können. In unserer Arbeit wollen wir die einzelnen Lebensstadien, die ein Stern durchläuft genauer darstellen und kennenlernen. Das Ziel ist somit ein genaues Verständnis des Lebenszyklus beim Leser zu erzeugen, ohne das spezielle Kenntnisse in der Astronomie oder der Physik vorausgesetzt werden. Angefangen mit der Geburt wollen wir das Heranwachsen und das Sterben eines Sterns betrachten. Vor allem wollen wir, dass der Leser am Ende der Arbeit eine genaue Kenntnis über den Verlauf eines Sternlebens hat. 1.2 Themenwahl Bei unserem ersten Besuchen der Sternwarte sind uns bereits die faszinierenden Bilder von diversen planetarischen Nebeln, wie dem Ringnebel oder dem Orionnebel, aufgefallen. Daraufhin haben wir uns selbst die Frage gestellt: Wie kommt es zu diesen unglaublichen Gebilden? Ohne erwähnenswerte eigenen Kenntnisse über unser letztendlich gewähltes Thema wollten wir unsere Arbeit auf dem gleichen Stand wie unsere Leser beginnen mit dem Gedanken, wenn wir die komplexen Abläufe nachvollziehen können, dann sollte es auch möglich sein es den Lesern zu erläutern. Außerdem stellt der Projektkurs eine einmalige Möglichkeit dar eine wissenschaftliche Arbeit im Bereich der Astronomie während unserer Schullaufbahn zu verfassen. 3 2. Theoretische Grundlagen 2.1 Atomphysik Um die Entwicklung eines Sterns nachvollziehen zu können, sind einige Vorkenntnisse, die die Bereiche der Atomphysik, das Hertzsprung-Russel-Diagramm und die Spektroskopie umfassen, notwendig. Beginnen wir mit den atomphysikalischen Grundlagen. Diese sind wichtig, um den Aufbau eines Sterns erklären zu können, sowie die Entstehung der Leuchtkraft und Temperatur. Niels Bohr ergänzte 1913 mit dem nach ihm benannten Modell das Rutherford´sche Atommodell um wesentliche Aspekte. Die zur damaligen Zeit revolutionären Annahmen waren weitgehend ungeklärte Theorien, wurden daher Bohr´sche Postulate genannt. Das erste Postulat besagt, dass sich die Elektronen eines Atoms auf Kreisbahnen, auch Schalen genannt, um den Atomkern bewegen, jedoch sind nur bestimmte Kreisbahnen möglich. Das zweite Postulat besagt, dass bei einem Schalenwechsel auf eine höhere, weiter vom Kern entfernte Schale, Energie zugeführt werden muss oder abgegeben wird, wenn das Elektron auf eine niedrigere fällt. 1 Abbildung 1 - Darstellung des Bohr´schen Atommodells mit eingezeichnetem Schalenwechsel und Emission 1 http://de.wikipedia.org/wiki/Bohrsches_Atommodell#mediaviewer/File:Bohr-atom-PAR.svg (20.11.14) 4 Abbildung 1 stellt eine Skizze des Bohr´schen Atommodells dar. Zu erkennen sind der positiv geladene Atomkern im Zentrum, die Elektronen, welche sich auf den hier grau gezeichneten Kreisbahnen bewegen und die Schalenwechsel der Elektronen. Bei der Absorption trifft Energie, beispielweise in Form eines Photons aus dem Sonnenlicht, auf ein Elektron des Moleküls. Durch die Aufnahme der Energie hat das Elektron die Möglichkeit auf eine höhere Ebene aufzusteigen. Dieser Effekt ist zu vergleichen mit einem Billardspiel, bei dem durch das Anstoßen einer Kugel (Photon) durch den Spieler (Sonne) eine weitere Kugel (Elektron) in Bewegung gesetzt wird und, so zu sagen, von der bisherigen Hülle weggeschossen wird. Auf dieser höheren Ebene hat das Elektron ein gewisses Energiepotential. Ebenfalls aus Abbildung 1 zu entnehmen ist dieser Vorgang, genannt Emission. Das Elektron ist auf einer der höheren Schalen, durch einen Fall auf eine untere Ebene muss somit, wie das zweite Postulat besagt, Energie abgegeben werden. 2 Abbildung 2 - Darstellung der möglichen Schalenwechsel mit Erkennbarkeit der unterschiedlich großen Fallhöhen der Elektronen In Abbildung 2 sind die verschiedenen Serien der elektronischen Übergänge für das H-Atom dargestellt. Die Lyman-Serie zum Beispiel hat, wie zu erkennen, den größten Abstand zur untersten Ebene, dadurch wird auch am meisten Energie abgegeben. Diese Energie ist so stark, dass es nur Übergänge im UV-Bereich, also für den Menschen nicht sichtbar, sind. Bei der Balmer-Serie hingegen sind einige Übergänge im sichtbaren Bereich. Die Übergänge in der Paschen-Serie sind im 2 http://commons.wikimedia.org/wiki/File:Wasserstoff-Termschema.svg (20.11.14) 5 Infrarotbereich. Als letztes Beispiel entsteht durch die Brackett-Serie Wärmestrahlung. Die Ebene n = 1 ist der Grundzustand, höhere Ebenen erhalten zunehmende Ziffernwerte. Doch obwohl theoretisch unendlich viele Schalen möglich sind, sind nur bestimmte Bahnen bzw. Abstände erlaubt, diese werden auch stationäre Bahnen genannt. Elektronen können ebenfalls durch Bewegung, wie beispielweise das Zusammenstoßen zweier Moleküle aufeinander auf eine höhere Ebene gehoben werden. In diesem Fall ist die zugeführte Energie nicht die eines Photons, sondern die Bewegungsenergie, die die Moleküle mit sich führen. Durch diese Erkenntnisse kann man über die messbare Energie des Lichtes auf die Temperatur und Bestandteile des Sterns rückschließen. Diese Zusammenhänge sind für die Spektroskopie von besonderer Bedeutung. 2.2 Das Hertzsprung-Russell-Diagramm Die nächste wichtige Grundlage ist das Hertzsprung-Russel-Diagramm. Man verwendet das Diagramm zum Einordnen und Bestimmen der Sterntypen. Es wurde im Jahr 1910 von den Astronomen Ejnar Hertzsprung und Henry Norris Russel entwickelt. 3 Abbildung 3 - Hertzsprung-Russell-Diagramm mit eingezeichneten Sternen und Beschriftung der Sternkategorien 3 http://www.andromedagalaxie.de/html/sterne_hrd.htm (06.05.2015) 6 Erläuterung des Diagramms: Auf der waagerechten X-Achse ist die Oberflächentemperatur, die in Kelvin gemessen (0 Kelvin gibt den absoluten Nullpunkt bei -273,15°C an)wird. Auf der vertikalen Y-Achse ist die Leuchtkraft des Sterns verzeichnet, wobei der Wert 0 die Helligkeit der Sonne angibt. Die Einteilung auf der X-Achse ist in die Spektralklassen O, B, A, F, G, K, M, L und T gegliedert. In Spektralklasse O sind die heißesten Sterne zu finden, auf der anderen Seite des Spektrums unter Klasse T die kühlsten Sterne. Der Wert 1 auf der in der Abbildung rechten Y-Achse ist die Helligkeit unserer Sonne. Sterne, die oberhalb der Sonne eingetragen werden besitzen eine höhere Leuchtkraft als die Sonne. Sterne die darunter zu finden sind, besitzen eine geringere Leuchtkraft als die Sonne. Die Leuchtkraft stellt die absolute Helligkeit eines Himmelsobjektes dar, sie wird gemessen in Magnituden. Anhand dieses Verzeichnisses sind alle Sterne in Kategorien klassifiziert, die in Abbildung 3 beschriftet sind. Der größte Anteil der Sterne ist auf der Hauptreihe zu finden. Die Reihe beginnt in der rechten unteren Ecke bei den roten Zwergen. In der Mitte sind die sonnenähnlichen gelben Sterne und in der linken oberen Ecke bei bläulich weißen Sternen mit hoher Leuchtkraft. Alle auf dieser Reihe angesiedelten Sterne nennt man Hauptreihensterne. Ein Stern verbringt die meiste Zeit seines da Seins auf der Hauptreihe, das ist auch der Grund, weshalb diese am dichtesten besiedelt ist. Sobald bestimmte Ereignisse zum Ende des Lebens des Sterns stattfinden, auf die wir an späterer Stelle eingehen werden, dann kann ein Hauptreihenstern in eine der anderen Gruppen übergehen. Eine dieser Gruppen sind die roten Riesen. Sie sind im Diagramm auf der rechten Seite oberhalb der Hauptreihe zu finden. Die Eigenschaften eines roten Riesens sind, bei einer Oberflächentemperatur, vergleichbar mit der eines Hauptreihensterns, eine deutlich höhere Leuchtkraft. Die letzte vorerst als Voraussetzung notwendige Gruppe ist die der weißen Zwerge. Sie liegen unterhalb der Hauptreihe und haben demnach eine geringere Leuchtkraft bei vergleichbarer Oberflächentemperatur. 7 2.3 Spektroskopie Doch um herauszufinden wo sich ein Stern im HRD befindet, nutzt man das Verfahren der Spektroskopie. Dies ist eine Methode, bei der das Licht, welches der Stern ausstrahlt, nach einem Attribut, wie zum Beispiel nach der chemischen Zusammensetzung oder der Temperatur zerlegt wird. Wir nutzen für diese Zerlegung einen Spaltspektrographen, der das Licht, mithilfe eines Gitters, welches das Licht zerstreut, in sein Spektrum zerlegt. Die Teleskop-Optik bündelt das Licht des zu spektroskopierenden Objekts auf den Spektrographen Spalt. Das aus dem Spalt austretende Licht geht durch eine Linse, um dann als paralleles Lichtbündel auf ein Gitter zu treffen. Dieses Gitter ist das dispergierende Element, welches das Licht in seine spektralen Bestandteile zerlegt. Eine zweite Linse nach dem Gitter leitet das in die vorhandenen Spektralfarben aufgespaltene Licht zur visuellen Beobachtung oder zur Fotografie weiter. Aus diesem Spektrum können wir nun die Oberflächentemperatur, die chemische Zusammensetzung und die Geschwindigkeit des Sterns angeben. Die 3 29000∗10 Å𝐾 Temperatur lässt sich bestimmen, indem man die maximale max = Wellenlänge herausfindet und diese dann in das Wien´schen 𝑇 Verschiebungsgesetzes einsetzt, welche den Zusammenhang der Wien´sches Verschiebungsgesetz Temperatur des Körpers und der Wellenlänge bei der am meisten Energie abgestrahlt wird, beschreibt. Lambda max. ist die Wellenlänge bei der die höchste Absorption für eine gegebene Substanz stattfindet. λ Die chemische Zusammensetzung kann man ebenfalls aus dem Spektrum ablesen. Ein Stern strahlt immer ein kontinuierliches Spektrum ab. Diese Strahlung muss aber auf dem Weg zu uns durch die Sternenatmosphäre, welche aus verschiedenen Elementen besteht. Beim Durchdringen absorbiert diese Atmosphäre bestimmte Wellenlängen des Lichts. Im kontinuierlichen Spektrum, das wir auf der Erde empfangen, fehlen diese Wellenlängen und wir sehen an diesen Stellen schwarze Linien im Spektrum. An der Intensität dieser Linien kann man die Häufigkeit eines bestimmten Elements sehen. Die verschiedenen Anteile von Elementen sagen uns, in welchem Entwicklungszustand der Stern ist, wie alt er ist und welche Masse er wahrscheinlich hat. 4 Abbildung 4 – Foto des Dados-Spaltspektrographen 4 http://de.wikipedia.org/wiki/Spektroskopie#Spektroskopiearten (19.04.15) und http://de.wikipedia.org/wiki/Spektrograf (19.04.15) sowie Michael Winkhaus; Tageskurs Spektroskopie; 29.11.14 8 3. Versuchsaufbau 3.1 Deep-Sky Fotografie Abbildung 5 – Seitenansicht des Versuchsaufbaus Deep-Sky Abbildung 6 – Frontalansicht des Versuchsaufbaus Deep-Sky 1. Teleskop: Celestron 1100 EHD 2. Teleskop: Pentax 75 SDHF 3. Netzteil 4. Steuerelement 5. Laptop 9 Eckdaten zu den verwendeten Geräten: Nummer aus Abbildung 5: Celestron 1100 EHD Öffnung 280mm Brennweite 2800mm Öffnungsverhältnis f/10 Maximal sinnvolle Vergrößerung 661x Grenzgröße 14m7 Auflösung 0,41“ Abschattung durch den Fangspiegel 95,25mm (34%) Tubuslänge 609mm Gewicht 12,7 kg 5 Nummer aus Abbildung 5: Pentax 75 SDHF Optischer Aufbau 3 Linsen / 3 Gruppen Freie Öffnung 75mm Brennweite 500mm Öffnungsverhältnis 1 : 6,7 Grenzgröße visuell 11,5m Auflösungsvermögen 1,55“ Lichtsammelvermögen 115 x Tubusdurchmesser 75mm Länge über alles 530 (480)mm Gewicht 2,2kg 6 5 http://www.teleskop-express.de/shop/product_info.php/info/p3260_Aktion--Celestron-Edge-HD-1100---2802800mm-Flatfield-Cassegrain-Tubus.html (28.03.15) 10 Canon EOS 450D Sensor CMOS-Sensor APS-C 22,5 x 15,0 mm (Cropfaktor 1,6) 12,4 Megapixel (physikalisch) und 12,2 Megapixel (effektiv) Pixelpitch 5,3 µm Fotoauflösung 4.272 x2.848 Pixel(3:2) 3.088 x2.056 Pixel(3:2) 2.256 x1.509 Pixel(3:2) Bildformate JPG, RAW Farbtiefe 24 Bit bei JPG-Format, 42 Bit bei RAW-Format Abmessungen B x H x T 129 x 98 x 62 mm Gewicht 510 g (betriebsbereit) 7 Abbildung 7 – Frontalansicht der modifizierten Canon EOS 450D 6 http://www.baader-planetarium.de/pentax/pentax.htm#75 (28.03.15) 7 http://www.digitalkamera.de/Kamera/Canon/EOS_450D.aspx (28.03.15) 11 Filter Abbildung 7.1 – H-alpha Filter zur Reduktion der Auswirkung der Lichtverschmutzung auf den Aufnahmen Wir nutzen zur Deep-Sky Fotografie des Orionnebels den H-Alpha Narrowband 7nm CCD-Filter von Baader Planetarium. Unser Modell ist planoptisch poliert, was bedeutet, dass es ohne Schärfe zu verlieren weit vom Brennpunkt der Kamera eingesetzt werden kann. Zusätzlich ist der Filter in ein Einschraubgewinde mit einem Durchmesser von 2“ (48mm) gefasst.8 8 http://www.baader-planetarium.de/sektion/s43d/s43d.htm#h_passfilter_7nm (12.05.15) 12 3.2 Sternbild Fotografie 1. Teleskop: Pentax 75 SDHF 2. Kamera: Modifizierte Canon EOS 450D Aufgesetzt auf einen Kugelkopf 3. Teleskop 4. Steuerelement 5. Netzteil Abbildung 8 – Ansicht des Sternbildaufbaus 13 3.3 Ablauf eines Beobachtungsabends Um unser Experiment durchführen zu können müssen wir erst auf die Sternwarte des Carl-FuhlrottGymnasiums, um dort das Teleskop und unser Equipment aufzubauen. Ein Beobachtungsabend läuft folgendermaßen ab: Wenn wir sehen, dass der Himmel weitestgehend klar sein wird, fangen wir schon nachmittags im Hellen mit dem Aufbau an. Wir schrauben die Teleskope auf die, dafür vorgesehenen, Stationen. Anschließend verkabeln wir den Aufbau und schließen Netzteil, Laptop und die Kamera an. Abbildung 9 – Frontalansicht unseres Experiments, zu sehen sind Laptop und Teleskop Abbildung 10 – Rückansicht unseres Experiments, zu sehen sind Steuereinheit, Teleskop mit Kamera und Netzteil Wenn nun alles fertig aufgebaut ist beginnt das Warten auf die Dunkelheit. Diese Zeit können wir dazu nutzen uns noch einmal zu stärken und die Wetterlage zu beobachten. Ist es dann dunkel geht der eigentliche Beobachtungsabend los. Zuerst fahren wir den Laptop hoch, wenn dies noch nicht geschehen ist. Dann öffnen wir das Kamera Programm EOS Utility und wählen den Modus Kamera-Einstellungen/Fernaufnahme. Hier können wir nun alles für unsere Aufnahmen einstellen: Die ISO Zahl, die Belichtungszeit, sowie den Speicherort für die Bilder. Dazu öffnen wir das Remote Live View-Fenster, indem wir sehen können, was die Kamera grade im Fokus hat, dargestellt in den Abbildungen auf der folgenden Seite. 14 Abbildung 12 – Remote Live View Fenster EOS Utility Abbildung 11 – Einstellungsfenster EOS Utility Der nächste Schritt ist das Ausrichten des Teleskops in Richtung des Objekts, das wir fotografieren möchten. Dazu nehmen wir die Steuerungseinheit, in welchem wir eine große Auswahl an Objekten haben. Möchten wir zum Beispiel den Ringnebel aufnehmen, wählen wir Messier → M57 aus. Das Teleskop richtet sich dann automatisch in seine Richtung aus. Leider kann die Steuerungseinheit das Objekt in den seltensten Fällen genau erfassen, weswegen der nächste Schritt die Feinjustierung ist. Hier benutzen wir das Remote Live View-Fenster um zu sehen, ob das Objekt im Bild ist. Ist das nicht der Fall korrigieren wir die Ausrichtung Stück für Stück mit der Steuereinheit. Damit ist die Einrichtung komplett fertiggestellt und das Fotografieren kann startet. Wir wählen eine beliebige Belichtungszeit und machen ein Foto. Jetzt werten wir aus, ob das Foto zu hell ist und wir die Zeit verringern oder ob es zu dunkel ist und wir sie erhöhen müssen. Wir machen nun von jeder Belichtungszeit, welche einigermaßen gut ist ca. 10-20 Fotos, um diese später zu „stacken“ (Erklärung folgt) und auszuwerten. Dieser Prozess kann sehr lange dauern und ebenfalls sehr anstrengend sein, da es bei besonders dunklen Objekten bis zu einer Minute pro Foto dauern kann. Wir müssen die ganze Zeit ruhig neben der Kamera sitzen oder stehen, da durch das stampfen auf dem Boden das Bild verwackeln kann und damit die gesamte Aufnahme unbrauchbar ist. Da man die besten Bilder im Winter bekommt, muss man also manchmal bis zu einer oder zwei Stunden in Kälte und Wind sitzen bis man ein Objekt fertig fotografiert hat. Doch nun wollen wir uns dem eigentlichen Thema widmen. 15 4. Sternentstehung 4.1 Experiment M42 Wie zu Beginn eines jeden Lebens steht auch bei einem Stern die Geburt. Doch nicht überall kann ein Stern entstehen. Es gibt bestimmte Regionen, die als Sternentstehungsregionen bezeichnet werden, in denen die Geburt möglich ist. Es sind Gaswolken, die zum größten Teil aus Wasserstoff bestehen und von früheren Sterngenerationen zeugen. Dieser Kreislauf wird sich an späterer Stelle mit dem Ende eines Sterns schließen. Das erste Objekt, das wir in unserer Arbeit behandeln wollen, ist der Orionnebel, eine der aktivsten Sternentstehungsregionen. In Abbildung 13 sieht man den Orionnebel rot markiert im Sternbild Orion. Abbildung 13 - Sternbild Orion [Aufbau: Sternbild; Aufnahmedatum: 11.03.15; Uhrzeit: 20:03 ; Belichtungszeit 74s; ISOFilmempfindlichkeit: 800] 16 In der folgenden Tabelle sind einige Eckdaten über den Orionnebel zusammengefasst: Sternbild Orion Position Rektaszension: 5h 35.3m Deklination: -5° 23,5´ Scheinbare Helligkeit 4,0 mag Entfernung zur Erde 1350 (+/- 23) Lichtjahre Durchmesser 30 Lichtjahre Entdeckung Im Jahre 1610 von Nicolas Claude Fabri de Peiresc Katalogbezeichnung M 42 9 Der Grund für seine deutliche Erkennbarkeit ist, dass er im Gegensatz zu Reflexionsnebeln von sich aus leuchtet, also Photonen abgibt und nicht nur angestrahlt wird. Man nennt ihn daher auch Emissionsnebel. Bei der Durchführung unseres Experiments, der Aufnahme des Orionnebels, kooperieren wir mit einer anderen Gruppe unseres Kurses, die sich das Thema „Fotografie galaktischer Nebel“ zur Aufgabe gemacht hat. Die Bearbeitung der Aufnahmen mit dem Stacking-Verfahren werden wir in unserer Arbeit an späterer Stelle ausführlicher erläutern, jedoch ist eine sehr detaillierte Beschreibung in der Arbeit „Deep-Sky-Fotografie galaktischer Nebel im Sternbild Orion“ von Tobias Stamp und Christian Zahn vorhanden. Doch nun zur Durchführung unseres Experiments. Wir arbeiten bei der Aufnahme mit Deep-Sky Aufbau. Das Ziel war es vor allem eine, in allen Bereichen des Nebels, präzise Aufnahme des Objektes zu erhalten. Damit das Zentrum des Nebels bei einer langen Belichtungszeit von 30 Sekunden in dem fertigen Bild nicht überbelichtet ist, nutzen wir verschieden lange Belichtungszeiten, um alle Bereiche mit einer passenden Schärfe abzubilden. Das Ziel mit den verschieden langen Belichtungszeiten und dem anschließenden Stacking ist in der folgenden Abbildung dargestellt. 9 http://de.wikipedia.org/wiki/Orionnebel (05.04.15) 17 Abbildung 14 - Darstellung der Belichtungszeiten mit den zugehörigen Bereichen des Orionnebels, innen kurze Belichtungszeit, außen lange Belichtungszeit Das innere Viereck wird mit einer Belichtungszeit von einer Sekunde dargestellt, je größer die Vierecke bzw. die Bereiche werden, desto höher wird die benötigte Belichtungszeit. Nach diesem Prinzip sind unsere Aufnahmen entstanden und die Verarbeitung abgelaufen. Besonders wenn man die Bilder mit Belichtungszeiten von 30 und 1 Sekunde vergleicht, sieht man den wesentlichen Unterschied zwischen dem einerseits gut erkennbaren Zentrum (Abbildung 15) und andererseits dem überbelichteten und nicht erkennbaren Zentrum (Abbildung 16). 18 Abbildung 16 – Aufnahme des Orionnebels bei 30 Sekunde Belichtungszeit Abbildung 15 – Aufnahme des Orionnebels bei einer Sekunden Belichtungszeit (bereits etwas aufgehellt) Der Vorteil des Bildes mit einer Belichtungszeit von 30 Sekunden ist, dass man auch die Ausläufer des Nebels erkennen kann. Jedoch kann man hier das Zentrum nicht erkennen. Da dieses vollkommen überbelichtet ist. Die Sterne im Zentrum sind bei einer Belichtungszeit von nur einer Sekunde hingegen gut zu sehen. Insgesamt haben wir 87 Aufnahmen unterteilt in Belichtungszeiten von 1,2,4,8, 15, und 30 Sekunden. Pro Belichtungszeit entspricht das zwischen 11 und 27 Aufnahmen. Das ergibt eine Gesamtbelichtungszeit von 1100 Sekunden. Mit all diesen Bildern können wir nun das Stacking beginnen. Da wir das Stacking erst an späterer Stelle unserer Arbeit genauer erklären, verweisen wir erneut auf die Arbeit „Deep-Sky-Fotografie galaktischer Nebel im Sternbild Orion“ und kommen direkt zu dem Ergebnis unseres Experiments in Abbildung 17. 19 Abbildung 17 - Ergebnis des Experiments Orionnebel [ Aufbau: Experiment Deep-Sky; Aufnahmedatum: 11.02.15; Uhrzeit: 19:03-19:56;Gesamtbelichtungszeit: 1100s; ISO-Empfindlichkeit: 400] 4.2 Theorie zur Sternentstehung Der Orionnebel ist eine der aktivsten Sternentstehungsregionen. Doch nun stellt sich die Frage: Wie entsteht aus einer Gaswolke ein Stern? 20 In den Gaswolken könne räumliche Inhomogenitäten entstehen. Das bedeutet, dass in bestimmten Bereichen mehr Moleküle im gleichen Raum sind, wie an anderen Stellen, das heißt, dass eine höhere Dichte vorhanden ist. Auslöser für solche Inhomogenitäten können beispielweise die Stoßfronten eines explodierten Sterns, einer Supernova, sein. Durch das Kollabieren einer solchen Gaswolke können Sterne entstehen. Kollabieren wird eine Gaswolke jedoch erst dann, wenn ihre eigene Gravitation größer ist als der Strahlungsdruck, der von innen nach außen wirkt. Wie seine Bezeichnung schon erahnen lässt, wird dieser hervorgerufen, durch die Ausstrahlung von Licht und der damit verbundenen Energie bei Reaktionen im Zentrum. Das Jeans-Kriterium beschreibt, welche Gaswolken, durch kollabieren als Sternentstehungsregion in Frage kommen können: 10 Entscheidende Faktoren für diese Eigenschaft sind Masse(M), Temperatur(T) und die Dichte(p) der Gaswolke. Durch die enorme Größe der Gaswolken und einer typischen Masse von 1-10 Sonnenmassen eines Sterns entstehen in den Sternentstehungsregionen häufig mehrere Sterne. Diese dicht beieinander liegenden Sterne werden dann als Sternhaufen bezeichnet. Wenn in der Wolke ein Bereich mit hoher Dichte auftritt und somit das Jeans-Kriterium erfüllt, dann bezeichnet man diesen als Globule. Die Globule entwickelt eine eigene Gravitation, wodurch fortlaufend Materie aus dem Umfeld angezogen wird und in Richtung des Zentrums der Globule fällt. Durch den Sturz der Materie wird Energie freigesetzt, die sich in Wärme umwandelt und den weiter verdichtenden Bereich aufheizt. Außerdem wird die Globule durch die steigende Dichte undurchsichtiger, daher kann man diese Protosterne optisch wahrnehmen. Im hell leuchtenden Zentrum des Orionnebels sind einige dieser Zonen erkennbar (Abbildung 15 und 17). Der Protostern hat zu diesem frühen Stadium seines Lebens nur ca. 1% seiner späteren Masse erreicht. Im HRD ist der Protostern mit einer geringen Temperatur und hoher Leuchtkraft in der rechten oberen Ecke zu finden. Anschließend an die Entstehung des Protosterns nimmt dieser fortlaufend Materie auf. Während dieses Vorgangs steigt die Effektiv-Temperatur nicht weiter an. Da der Stern aufgrund der eigenen Gravitation weiter kontrahiert, nimmt die Größe seiner Oberfläche ab. Dadurch kann weniger Licht nach außen abgestrahlt werden und seine Helligkeit sinkt. Dieser Entwicklungsweg verläuft im HRD entlang der Hayashi-Linie und wird als „Hayashi track“ bezeichnet. Die Hayashi-Linie verläuft näherungsweise von der rechten oberen Ecke des HRD in Richtung des unteren Endes der Hauptreihe. Rechts unterhalb dieser Linie ist der „verbotene Bereich“ in dem kein Gleichgewicht zwischen Strahlungsdruck und Gravitation herrscht, dementsprechend entsteht hier kein stabiler Stern. Es ist zunächst ein Verlauf, bei dem die Temperatur relativ konstant bleibt, aber die Helligkeit abnimmt, zu sehen in Abbildung 18 auf der folgenden Seite. 10 https://lp.uni-goettingen.de/get/text/7165 (10.4.15) 21 11 Abbildung 18 – Darstellung des Hayashi track und Henyey track im HRD mit den wesentlichen Eigenschaften, Erläuterung im folgenden Text Auf dem Hayashi track hat der Stern einen Zustand erreicht, der laut Abbildung als „ vollkonvektiv“ und „konvektionsdominiert“ bezeichnet wird. Vollkonvektiv bedeutet, dass die heißeren Schichten im inneren des Sterns die Energie nicht durch Strahlung nach außen abgeben, sondern, ähnlich wie in unserer Atmosphäre, sich die Schichten von innen nach außen bewegen, dort abkühlen und wieder ins Zentrum zurück sinken. Konvektionsdominiert bedeutet, dass die Konvektion gegenüber dem Strahlungstransport dominiert, aber nicht ausschließlich stattfindet. Sterne, deren Masse kleiner als die halbe Sonnenmasse ist, kontrahieren bis die Wasserstofffusion im Kern einsetzen kann. Der Hayashi track geht dann unmittelbar in die Hauptreihe über. Sterne hingegen, deren Masse größer als die halbe Sonnenmasse ist, gehen anschließend in den Henyey track über. Wie ebenfalls aus Abbildung 18 entnommen werden kann, ist dieser Pfad fast waagerecht im HRD. Die Temperatur des Sterns ist also zunehmend, bei gleicher Leuchtkraft. Ein Stern geht dann auf den Henyey track über, wenn durch die gestiegene Temperatur die Opazität, also die Transparenz, sinkt und der Strahlungstransport gegenüber der zuvor stattfindenden Konvektion dominiert. Beim Strahlungstransport wird die Wärmeenergie durch Strahlung von Schicht nach Schicht in Richtung der Sternoberfläche befördert. Die schweren Elemente verweilen somit im Zentrum und geben die Energie über die äußeren Schichten, bestehend aus leichteren Elementen, nach außen ab. Mit dem Übergang des Protosterns in die Hauptreihe und dem Beginn der Wasserstoffverbrennung ist die Geburt des Sterns vollbracht. Der Strahlungsdruck, der bei der Verbrennung entsteht und nach außen wirkt, und die Gravitation befinden sich auf der Hauptreihe nun in einem Gleichgewicht, sodass der Stern dieses Stadium für einen längeren Zeitraum aufrecht erhalten kann, bis der Wasserstoffvorrat im Inneren aufgebraucht ist.12 11 12 https://lp.uni-goettingen.de/get/text/7165 (10.4.15) https://lp.uni-goettingen.de/get/text/7165 (10.4.15) 22 5. Hauptreihenstern Die Hauptreihe im HRD (siehe Abbildung 19) ist eine leicht erkennbare Linie die besonders dicht von Sternen bevölkert wird. Hier verbringt der Stern mit 10^6 bis 10^11 Jahren die längste Zeit seines Lebens. 13 Abbildung 19 – HRD mit Beschriftung der Sternkategorien Die Sterne, welche gerade erst auf die Hauptreihe gewandert sind werden auch ZAMS-Sterne (Zeroage main Sequence) oder Alter-Null-Hauptreihensterne genannt, da sie gerade erst entstanden sind und ihre Fusionsreaktion gezündet haben. Das besondere bei Hauptreihensternen ist, dass man mit der „Masse-Leuchtkraft-Beziehung“ die Masse aus der Leuchtkraft ermitteln kann. Die Masse dieser Sterne misst man in Sonnenmassen, wobei eine Näherung der Beziehung Leuchtkraft~Masse^3,5 lautet. Daraus folgt, dass die Masse eines Sterns nach oben links auf der Hauptreihe zunimmt. Dies 13 http://www.andromedagalaxie.de/html/sterne_hrd.htm (12.04.15) 23 ist aber nicht linear gültig, da zum Beispiel ein Stern mit zweifacher Sonnenmasse 11-mal so stark leuchtet wobei ein Stern mit vierfacher Sonnenmasse 128-mal so stark leuchtet.14 Abbildung 20 – HRD mit Annäherung der Masse für die Sterne in der Hauptreihe Der Hauptreihenstern wird generell nun dadurch definiert, dass er Wasserstoff zu Helium verbrennt. Der Strahlungsdruck, der dabei entsteht wirkt der Gravitation entgegen, wodurch der Stern stabil bleibt. Dies funktioniert solange, wie Wasserstoff im Kern vorhanden ist. Je höher die Masse des Sterns, desto länger lebt der Stern. An diesem Prozess kann man außerdem erkennen, warum die Position im HRD von der Masse abhängig ist. Ist der Stern groß, so sind auch der Druck und damit die Temperatur höher, wodurch die Kernfusion heftiger abläuft und fortlaufend mehr Energie liefert. So hat der Stern sowohl eine höhere Oberflächentemperatur als auch eine höhere Leuchtkraft.15 14 https://lp.uni-goettingen.de/get/text/7168 und http://www.wissenschaftonline.de/astrowissen/lexdt_h03.html#LettB (12.04.15) 15 http://www.andromedagalaxie.de/html/sterne_hrd.htm (12.04.15) 24 6. Roter Riese Nach dem Stadium des Hauptreihensterns folgt die Entwicklung zum Roten Riesen. Wir werden anhand des Sterns Aldebaran beispielhaft anwenden, wie man mit Hilfe der Spektroskopie die Oberflächentemperatur des Sterns herausfinden kann. Diese Größe wird benötigt um den Stern im Hertzsprung-Russell-Diagramm auf der X-Achse einzuordnen. Doch zunächst zum Stern selbst. Aldebaran, auch bekannt als α Tauri, liegt im Sternbild Stier, er ist der rot umkreiste Stern in Abbildung 21. Abbildung 21 - Sternbild Stier [Aufbau: Sternbild; Aufnahmedatum: 11.03.15; Uhrzeit: 20:23; Belichtungszeit 45s; ISOFilmempfindlichkeit: 800] Zusätzlich zu der Lage im Sternbild sind in der folgenden Tabelle einige Informationen über Aldebaran zusammengefasst: Sternbild Stier Position Rektaszension: 04h 35m 55,24s Deklination: +16° 30′ 33,5″ Scheinbare Helligkeit 0,87 mag Entfernung (66,6 ± 1,0) Lichtjahre 25 Radius (45.2 ± 4,1) x Sonnenradius Masse 2.5 Erdmassen Katalogbezeichnung α Tauri 16 6.1 Experiment und Anwendung der Spektroskopie Das Anfertigen und Auswerten eines Spektrums ist eine allgegenwärtige analytische Methode in der Astronomie. Wir werden diese Methode, an Hand des Sterns Aldebaran, beispielhaft anwenden. Für die Bearbeitung des Spektrums verwenden wir das Programm VisualSpec. Mit dem Ergebnis können wir die Klassifizierung des Sternes nachvollziehen und belegen. Zunächst muss das Spektrum, das wir mit dem zuvor beschriebenen Aufbau aufgenommen haben, in dem Programm geöffnet werden. Als erstes muss mit Options →Preferences der Quellenpfad angegeben werden. Danach kann das Bild geöffnet werden, mit dem Befehl Open Image. Das Bild muss horizontal ausgelegt werden, dazu kann als Hilfsmittel Angles, zu Deutsch Winkel, genutzt werden. Abbildung 22 - Schwarz/Weiß Spektrum in Visual Spec 16 http://de.wikipedia.org/wiki/Aldebaran (05.04.15) 26 Anschließend subtrahieren wir mit Extraction→Sky background subtraction den Himmelshintergrund und erstellen aus dem Einfluss minimierten Spektrum mit dem Befehl Extraction profil brut. Das Programm scannt dann die Helligkeit der Balken in X-Richtung. Das Ergebnis dieses Vorgangs ist der in Abbildung 22 zu sehende Graph. Je heller die Pixel sind, desto höher ist an der gleichen Stelle auch der vom Programm erstellte Graph. Dieser Graph ist das Spektralprofil des Sterns Aldebaran. Abbildung 22 – Spektralprofil unseres Spektrums Jedoch ist nun zu beachten, dass die x-Achse in Pixeln statt in Wellenlängeneinheiten kalibriert ist. Um von Pixeln zu den für uns relevanten Wellenlängeneinheiten zu wechseln, müssen einige Bezugspunkte festgelegt werden. Für die Orientierung verwenden wir den „Spektralatlas für Astroamateure“ von Richard Walker der Version 1.2 von Oktober 2010. Aldebaran selbst ist in dem Atlas zu finden, er ist ein Stern der Klasse K5 III. Im Programm verwenden wir den Befehl Calibration Multiple Lines, mit dem wir mehrere bekannte Stellen am Graph markieren können und ihnen ihre eigentliche Wellenlänge zuordnen, welche wir dem Spektralatlas entnommen haben (zu sehen in Abbildung 23). 27 Abbildung 23 - Werte für die Kalibrierung, Kombination aus Stelle am Graphen und zugehöriger Lambda Wert Abbildung 24 - Wellenlängenkalibriertes Spektralprofil Mit den in Abbildung 23 angegebenen Werten erhalten wir die in Abbildung 24 zu sehende Kurve. Die Differenzwerte von Lambda, in 23 als d_lambda bezeichnet, sollten möglichst gering sein, in unserer Kurve lag die maximale Abweichung bei gerundet 2 Lambdas. Werte zwischen Null und Eins wären ideal. Die daraus resultierende Dispersions- Kurve sollte einen möglichst gleichmäßigen Anstieg haben. Durch verschiedene Funktionsgrade lässt sich die Kurve anpassen. Die Kurve, die wir erhalten haben, ist jedoch durch unterschiedliche natürliche Einflüsse manipuliert. Durch Atmosphäre oder Lichtverschmutzung entsteht somit ein Pseudokontinuum. 28 Das bedeutet, dass das Licht des Sterns tatsächlich stärker im infraroten Bereich wäre, somit hätte der Stern eine andere Temperatur als unser Spektrum ergeben wird. Um jedoch ein genaueres Ergebnis zu erhalten, müssen wir diesen Effekt ausgleichen. Dieser Ausgleich nennt sich Instrumentenfunktion. Im folgenden Abschnitt gehen wir genauer auf die Berechnung dieser Funktion und der Oberflächentemperatur des Sterns ein. Dazu benötigen wir ein „Profispektrum“, welches uns Visualspec bietet. Mit dem Befehl Assistant→Instrumenal response kann man eine vollständig kalibrierte Aldebaran Spektralkurve aufrufen. Über Pickles und unsere Sternklasse K5iii, in Rot markiert, wird die Kurve in das Koordinatensystem eingefügt, siehe Abbildung 25 in lila Farbe. Abbildung 25 - Aldebaran Spektrum (eigenes Spektrum in Blau & Referenzspektrum in lila) Mit der folgenden Formel lässt sich das Verhältnis zwischen dem eigenen Rohspektrum, dem Profibzw. flußkalibrierten Spektrum und der Instrumentenfunktion beschreiben. = Instrumentenfunktion 17 17 Ernst Pollmann: „Reduktion, Bearbeitung und Auswertung von Sternspektren“, Herbstkurs Sternspektroskopie Carl-Fuhlrott-Gymnasium 29 Das bedeutet nun für uns, dass wir unser Spektrum durch das flußkalibrierte Spektrum dividieren müssen. Mit dem Befehl Division and extraction, in Bild 25 rot markiert zu sehen, erzeugt das Programm die Instrumentenfunktion. Abbildung 26 – Angepasste Instrumentenfunktion in lila Die blaue Kurve, die wir als Ergebnis erhalten, muss noch geglättet werden, da die exakten Werte nicht derart ausschlaggebend sind. Mit dem Befehl Operations→Spline filter… öffnet sich das in Abbildung 26 auf der linken Seite zu sehende Fenster. Durch das Verändern des Koeffizienten lässt sich die Kurve glätten. Das Resultat dieses Schrittes, die Instrumentenfunktion, ist die in lila abgebildete Kurve. Da diese anschließend noch verwendet wird, müssen wir diese speichern. Um das kalibrierte Aldebaran-Spektrum zu erhalten, lässt sich die oben bereits angeführte Formel wie folgt umstellen: = Kalibriertes Spektrum 18 18 Ernst Pollmann: „Reduktion, Bearbeitung und Auswertung von Sternspektren“, Herbstkurs Sternspektroskopie Carl-Fuhlrott-Gymnasium 30 Da wir sowohl unser eigenes Spektrum als auch die Instrumentenfunktion vorliegen haben, können wir nun im nächsten Schritt das fertige Spektrum von Aldebaran erstellen. Dazu rufen wir Rohspektrum und Instrumentenfunktion auf, wie in Abbildung 27 zu sehen ist. Abbildung 27 - Rohspektrum und Instrumentenfunktion Mit dem Befehl Operations→divide profile by profile lässt sich das Spektrum durch die Instrumentenfunktion dividieren. Das Ergebnis ist das in Abbildung 28 als grün abgebildete Spektrum. Abbildung 28- Ergebnis der Division in grün 31 Im darauf folgenden Schritt schneidet man die überflüssigen Ränder des Spektrums mit dem Scheren-Tool ab. Abbildung 29 - Fertig wellenlängenkalibriertes Aldebaran-Spektrum Zur Veranschaulichung kann man parallel unter den Graphen das Farbspektrum einfügen. Dies funktioniert mit den Befehlen Tool→Synthesis→Colorer. Hierbei muss darauf geachtet werden, dass die Banden den richtigen Tiefpunkten des Graphen zugewiesen werden, wie in Abbildung 30 zu sehen ist. Zur Orientierung dienen vor allem markante Stellen wie die Sauerstoffbanden, sowohl mit einem extremen Tiefpunkt im Graphen als auch einer dicken dunklen Bande Im Farbspektrum. 32 Abbildung 30 - Graph und Farbspektrum passend zugeordnet, finales Resultat des Experiments Aldebaran Das Ergebnis unseres Experiments kann nun für die Berechnung der Oberflächentemperatur verwendet werden. Dieses Verfahren der Spektroskopie findet in der Astronomie häufig statt. Es ist beispielweise bei den Sternen notwendig, um diese zu klassifizieren, aber auch um genauere Erkenntnisse über die Bestandteile des Sterns zu erfahren. Das Ergebnis in Abbildung 30 werden wir im folgenden Schritt für die Berechnung der Oberflächentemperatur nutzen. Die Kombination aus dem Graph und dem Farbspektrum dient als Verdeutlichung der Erkenntnisse, die wir aus dem Graphen entnehmen können. 33 6.2 Berechnung der Oberflächentemperatur von Aldebaran Mit dem fertigen Spektrum kann man nun die Temperatur auf der Oberfläche des Sterns berechnen. Die Theorie der Planck´schen Strahlungskurve und dem Wien´schen Verschiebungsgesetz sind für die Berechnung notwendig. Darauf gehen wir im folgenden Teil genauer ein. Die Planck´sche Strahlungsformel besagt, dass mit zunehmender Temperatur des Sterns auch die für uns messbare Strahlungsleistung wächst, also die Temperatur und Strahlungsleistung in einem bestimmten Verhältnis zueinander stehen. Dementsprechend können wir im Umkehrschluss über das Wellenlängenmaximum auf die Temperatur rückschließen. Denn wenn der Stern bei hoher Temperatur eine verhältnismäßig hohe Strahlungsleistung erbringt, dann muss das Strahlungsmaximum uns auf dem gleichen Weg umgekehrt auch zur Temperatur führen. Mit dem Wien´schen Verschiebungsgesetz kann man nun die Temperatur der strahlenden Fläche berechnen. Es lautet: λmax = 29000∗103 Å 19 → λmax: Wellenlänge der maximalen Intensität, die wir aus unserem Spektrum abgelesen haben. Der Wert beträgt 7742 Å → 3 Å : Wien´sche Verschiebunskonstante → T: Absolute Temperatur der strahlenden Fläche Stellen wir diese Formel nun nach T um und setzen die Werte ein, dann ergibt sich die folgende Formel: T= 29000∗103 Å∗ 42 Å = 3746 K Vergleicht man unseren Wert mit dem Literaturwert von 4100 Kelvin20, stellt man eine Abweichung von 354 Kelvin fest. Diese Abweichung ist zu erklären durch Einflüsse während unserer Aufnahme wie beispielweise Wind, Auswirkungen und Einflüsse der Atmosphäre, sowie Lichtverschmutzung. Dennoch ist die Abweichung von lediglich 8,6% ein sehr genaues Ergebnis, das wir dazu verwenden können den Stern zu klassifizieren. Mit der nun bekannten Oberflächentemperatur ist einer der zwei notwendigen Schritte getan, um den Stern an der korrekten Stelle im Hertzsprung-Russell-Diagramm zu lokalisieren. Auf der X-Achse des Diagramms ist Aldebaran nun, laut unserem Ergebnis, in der Spektralklasse K aufzufinden. In der 19 20 Bernd Koch „Einführung in die Sternspektroskopie mit dem DADOS-Spaltspektrografen“ http://www.andromedagalaxie.de/html/sterneb_aldebaran.htm (02.04.15) 34 genaueren Unterteilung von 0-9 ist Aldebaran als K5 gekennzeichnet. Der Wert 0 nähert sich der nächst höheren Klasse M an und der Wert 9 ist näher an der niedrigeren Klasse G. Unser Ergebnis stimmt trotz der Abweichung mit der vorherigen Klassifizierung zufriedenstellend überein. 6.3 Theorie zum Roten Riesen Wir wollen das Ergebnis unseres Experimentes nutzen, um die Sternklasse bzw. das Sternstadium Roter Riese genauer in Augenschein zu nehmen. Bereits die optische Wahrnehmung dieses Sterns am Himmel ist rötlich. Diese Färbung kommt zustande durch die geringe Oberflächentemperatur. Bei der vergleichsweise geringen Temperatur strahlt der Stern, nicht ausschließlich aber hauptsächlich, die energiearme Lichtfarbe Rot aus. Dieses Licht wird bei dem Prozess der Schalenverbrennung abgegeben.21 In dem Stadium sind die Fusionsprozesse so weit fortgeschritten, dass das WasserstoffSchalenbrennen einsetzt. 22 Abbildung 31 – Darstellung des Wasserstoff-Schalenbrennens mit der expandierenden Hülle und dem komprimierenden Kern In Abbildung 31 ist veranschaulicht, wie der Prozess die Erscheinung des Sterns beeinflusst. Durch die Verbrennung wird der Kern immer weiter komprimiert, während sich gleichzeitig die Hülle, in der nun ebenfalls die Wasserstoffverbrennung stattfindet, ausdehnt. Für diesen Prozess ist keine übermäßige Hitze notwendig, daher nimmt die Effektivtemperatur des Sterns ab. Verwunderlich scheint nun jedoch, dass sich bei sinkender Temperatur die Leuchtkraft erhöht. Diese Entwicklung hängt mit der Expansion des Sterns zusammen. Die vergrößerte Oberfläche kann im 21 22 http://www.spektrum.de/lexikon/astronomie/roter-riese/415 (02.04.15) https://lp.uni-goettingen.de/get/text/7168 (02.04.15) 35 Vergleich zu einer kleineren Oberfläche mehr Licht abgeben, daher erhöht sich die abgegebene Lichtmenge. Solange das notwendige Fusionsmaterial vorhanden ist und die Parametergrenzen, wie die Temperatur, erreicht werden, kann der Stern das Stadium des Roten Riesen beibehalten. Der Stern setzt sich dann nach und nach aus verschiedenen Schichten zusammen. Im Zentrum ist das schwerste Material, wenn die Voraussetzungen den Fortschritt bis zu diesem Element erlauben, ist das finale Material Eisen. Nach außen werden die Elemente leichter. Über Silizium, Sauerstoff, Kohlenstoff, Helium bis Wasserstoff setzen sich die Schichten zusammen.23 In der folgenden Abbildung ist der Aufbau dargestellt: 24 Abbildung 32 - Schichtenaufbau verschieden schwerer Elemente im Roten Riesen, die schwersten im inneren, nach außen immer leichtere Elemente Auch ein wahrnehmbares Pulsieren des Sterns ist möglich. Die Wasserstoffverbrennung kann vorrübergehend zum Erliegen kommen, wodurch weniger Licht abgegeben wird. Der Prozess kann jedoch erneut entzündet werden, wodurch die abgegebene Lichtmenge wieder zunimmt. Diese Schwankungen können als auf und ab wahrgenommen werden. In diesem Zeitraum befindet sich der Stern im Hertzsprung-Russell-Diagramm (HRD) auf dem Asymptotischen Riesenast, gekennzeichnet durch niedrige Temperatur und Helligkeit in etwa von der Sonnenhelligkeit, im HRD der Wert 0 auf der Y-Achse. Der Ast befindet sich auf der rechten Seite des HRD in etwa im mittleren Bereich. Der Rote Riese ist das letzte Stadium vor dem Ende, dem Tod eines Sterns. Können keine weiteren Fusionsprozesse entzündet werden, ergeben sich die folgenden Sternendstadien. 23 24 https://lp.uni-goettingen.de/get/text/7168 (02.04.15) https://lp.uni-goettingen.de/get/text/7168 (02.04.15) 36 7. Weißer Zwerg und planetarischer Nebel Der Ringnebel (M57) stellt gleich zwei Teile der möglichen Endstadien eines Sterns dar. Er besteht aus einem Weißen Zwergstern und einem planetarischen Nebel, der sich um ihn herum ausbreitet. In der folgenden Tabelle sind einige Daten zu diesem Objekt zusammengefasst. Sternbild Leier Position Rektaszension: 18h 53m 35,079s Deklination: +33° 01′ 45,03″ Helligkeit (visuell) +8,8 mag Entfernung 2300 Lichtjahre Durchmesser 0,9 Lichtjahre Entdeckung 1779 von Antoine Darquier Katalogbezeichnung M 57 25 Mit dem Deep-Sky Aufbau haben wir ein weiteres Objekt aufgenommen. Der ehemals Rote Riese hat seine äußeren Gashüllen bereits vor ca. 20.000 Jahren abgestoßen. Anhand dieses Beispiels werden wir nun erklären, wie der gesamte Verlauf eines unserer Experimente vorgeht und wie wir von einigen Aufnahmen zu einem zufriedenstellendem Bild des Objekts gelangen. Die Aufnahmen machen wir mit dem C11 Teleskop und einer Belichtungszeit von 30 Sekunden. Insgesamt haben wir am Ende 22 nutzbare Bilder, die wir zur Verarbeitung verwenden können. Für das sogenannte „Stacking“ verwenden wir das Programm „Maxim DL Pro 5“. 25 http://de.wikipedia.org/wiki/Ringnebel (10.05.15) 37 Abbildung 33 – Öffnen der Aufnahmen in Maxim DL Pro 5 Wie in Abbildung 33 zu erkennen, ist der erste Schritt die Auswahl der Bilder, die wir zum Stacken verwenden wollen. Da jedoch einige Aufnahmen auf Grund von Einflüssen, wie beispielweise durch den Wind verwackelt, unbrauchbar geworden sind, mussten wir diese einzeln betrachten und aussortieren. Nachdem dieser Vorgang abgeschlossen ist und das Programm eine vollständige Liste der Bilder erstellt hat, folgt der nächste Schritt mit dessen Hilfe wir die Verschiebung des Objekts auf den verschiedenen Bildern ausgleichen werden. Um dem Programm die Möglichkeit zu geben die Verschiebungen zu ermitteln, müssen wir zwei Bezugspunkte, dazu eignen sich markante Sterne in der Umgebung des Objekts, wählen. Wie man diese Auswahl tätigt ist in der Abbildungen 34 dargestellt. Abbildung 34 –Auswahl der brauchbaren Bilder und Auswahl der Bezugspunkte (zwei markante Sterne) Das Programm geht im Anschluss daran in zwei Durchläufen alle Bilder durch. Im ersten Durchlauf muss der Nutzer manuell den ersten Stern auf jedem der Bilder markieren. Im Zweiten wird der andere Stern markiert. Durch die Differenz aus dem Abstand und der Größe der Sterne kann das 38 Programm die Bilder angleichen, die Unterschiede reduzieren und so ist es im Anschluss möglich aus allen unterschiedlichen Bildern ein Resultat zu erzeugen, in dem alle Bilder übereinander gelegt sind. Sie sind nun „gestackt“. Dieses Resultat ist jedoch noch nicht zufriedenstellend. Der Grund dafür ist, dass das Histogramm nicht im richtigen Bereich ist. In Abbildung 35, im rechten kleineren Fenster, ist zu erkennen, dass der Definitionsbereich des Histogramms deutlich zu weit ausgelegt ist. Abbildung 35 –Gestacktes Bild, jedoch ungünstiger Definitionsbereich des Histogramms Um die rötliche Verfärbung auf dem aktuellen Bild zu eliminieren, müssen wir den Bereich anpassen. Indem wir den Minimalwert und den Maximalwert durch einige Versuche angleichen, erreichen wir ein deutlich verbessertes Ergebnis, wie in Abbildung 36 zu sehen ist. Das Ergebnis, dass wir durch verschieben des Histogramms erreicht haben, hat eine deutlich bessere Qualität als zuvor. Der Nebel ist nun erstmals auf dem gestackten Bild in einer annehmbaren Form zu erkennen. 39 Abbildung 36 – Erstmals gut erkennbar: Der Ringnebel, durch Anpassung des Histogramms im rechten oberen Fenster Der letzte Schritt zum fertigen Bild ist die Bearbeitung des Bildes mit „Photoshop“. Mit Hilfe dieses Programms schneiden wir die Ränder weg und könnten eine Beschriftung in das Bild einfügen. Das fertige Ergebnis ist in Abbildung 37 zu sehen. Abbildung 37 - Ergebnis aus dem Experiment Ringnebel 40 Der Ringnebel ist ein Beispiel für den Fortverlauf eines Roten Riesen. Man kann dieses Stadium in zwei Teile differenzieren: einerseits den weißen Zwergstern im Zentrum und den planetarischen Nebel um den Stern herum. Betrachten wir zunächst genauer den Nebel und seine Entstehung. Auf unserer Aufnahme sind bereits die Struktur und die Ausdehnung des Nebels von dem Zentralstern aus zu erkennen. Abbildung 38 - Ergebnis aus dem Experiment Ringnebel mit markiertem Ausschnitt für die spätere Verwendung Besonders auf dem Ausschnitt aus dem Bild ist in verschiedenen Schichten mit blauer Verfärbung außen und roter Färbung darunter die Ausbreitung des Nebels von der Sternoberfläche erkennbar. 7.2 Theorie zum Stadium Weißer Zwerg und planetarischer Nebel Ein Roter Riese dessen Masse geringer ist als die 8-fache Sonnenmasse, bewegt sich am Ende seiner Entwicklung auf den asymptotischen Riesenast im HRD. Der Kern besteht zu diesem Zeitpunkt aus Kohlenstoff und Wasserstoff, was Ergebnis der Helium-Fusion ist. Die Temperatur reicht nicht aus, um die Elemente im Kern weiter zu verbrennen. In den äußeren Schichten läuft die Verbrennung des Heliums und Wasserstoffs weiter. Bereits bei der Betrachtung des Roten Riesen haben wir festgestellt, dass der Stern pulsiert. Das liegt daran, dass die Fusionsrate enorm temperaturabhängig ist. Mit hoher Temperatur steigt die Fusionsrate und damit erneut die Temperatur. Durch diesen Effekt erhöht sich mit der Fusionsrate auch der ausgeübte Strahlungsdruck. Er ist demnach höher als die Gravitationskraft, die nach innen wirkt. Folge daraus ist, dass der Stern expandiert. Mit der nun vergrößerten Oberfläche, sinkt die Temperatur, die Fusionsrate und damit auch der Strahlungsdruck. 41 Durch den gesunkenen Strahlungsdruck kontrahiert die Hülle, da die Gravitationskraft wieder stärker ist. Während die Hülle in Richtung des Kerns fällt, wird ein Teil der Hülle nach außen abgegeben. Dieses Pulsieren wiederholt sich und es werden große Teile der Hülle nach außen abgestoßen. Da immer die äußeren Schichten abgestoßen werden, bestehen die abgegebenen Schichten aus den leichtesten Elementen der äußeren Schichten wie Wasserstoff und zu geringerem Teil Helium, teilweise können auch schwerere Elemente auftreten.26 Die Geschwindigkeit mit der sich der Nebel ausbreitet wird auf 19 km/s 27 geschätzt. Zudem beträgt die Ausdehnung dieses Nebels ca. ein Lichtjahr. Die Größe des Nebels wird durch diese Ausdehnung beschränkt. Durch die Ausbreitung verdünnt sich der Nebel immer weiter bis er letztendlich nicht mehr wahrgenommen werden kann. Dadurch, dass mit dem Abstoßen der oberen Hüllen immer heißere Schichten des Sterns freigelegt werden, treten nach dem Abstoßen einiger Schichten Photonen aus. Diese Photonen haben ausreichend Energie, um die abgegebenen Schichten zu ionisieren, wodurch der planetarische Nebel sichtbar wird. 28 Beim Ionisieren trifft ein Elektron auf ein Atom oder Molekül, dieses schlägt ein weiteres Elektron aus dem getroffenen Atom, sodass es positiv geladen zurück bleibt. Im Bezug auf das Beispiel Ringnebel gibt der Zwergstern im Inneren beim Verbrennungsprozess Elektronen nach außen ab, diese treffen auf Moleküle des Nebels, ionisieren diese und der Nebel kann von uns als leuchtende Erscheinung wahrgenommen werden. Abbildung 39 - Ausschnitt aus dem Ergebnis des Experiments Ringnebel Im Ausschnitt des Ergebnisses erkennt man, dass exakt im Zentrum des Ringnebels ein Stern ist. Dieser Stern ist ein ehemaliger Roter Riese, von dem aus der Nebel abgestoßen wird. Er selbst hat auch ein neues Entwicklungsstadium erreicht, genannt Weißer Zwerg. 26 https://lp.uni-goettingen.de/get/text/7180 (03.04.15) http://www.planetarium-berlin.de/PotW/04_09/PotW.html (04.04.15) 28 https://lp.uni-goettingen.de/get/text/7180 (04.04.15) 27 42 Während die äußeren Schalen des Roten Riesen expandieren, komprimiert sich der Kern des Sterns immer weiter. Im Stern finden keine Fusionsprozesse mehr statt, daher wirkt der Gravitation kein Strahlungsdruck mehr entgegen. Da die Gravitation jedoch fortlaufend wirkt, wird die Masse immer weiter komprimiert und der Stern kann eine enorm hohe Dichte von bis zu 1000kg/ 3 .29 Diese Entwicklung findet jedoch nur für Sterne statt, deren Masse unter 1,44 Sonnenmassen liegt. Der Weiße Zwerg hat im Gegensatz zum Roten Riesen eine hohe Oberflächentemperatur, jedoch ist seine Oberfläche vergleichsweise klein, daher auch seine Bezeichnung als Zwerg. Die Kombination aus hoher Oberflächentemperatur und geringer Helligkeit führt dazu, dass die Weißen Zwerge in der unteren linken Ecke des HRD eingeordnet werden. Wenn der Weiße Zwerg fortlaufend auskühlt, da keine Kernreaktionen mehr stattfinden, endet dieser als Schwarzer Zwerg.30 Zuletzt betrachten wir die räumliche Ausbreitung des Ringnebels: 31 Abbildung 40 - Räumliche Darstellung des Ringnebel, fotografiert mit dem Hubbelteleskop In Abbildung 40 kann man erkennen, dass der blaue Bereich die Form eines Rotationsellipsoids hat, vergleichbar und allgemein besser bekannt als Form eines American Footballs. In einem ca. 90° Winkel zu diesem steht eine schwimmringförmige, deutlich voluminösere Gaswolke. Aus unserem Blickwinkel sieht man den Nebel, im Bezug auf das Bild, von der oberen linken Ecke. Daher nehmen wir die blaue Ellipse auf unseren Aufnahmen wie eine Scheibe war, ebenso den voluminöseren gelb-orangen Ring. Da das Bild aus einer anderen Perspektive aufgenommen wurde sehen wir den tatsächlichen Aufbau des Nebels. 29 https://lp.uni-goettingen.de/get/text/7180 (04.04.15) Metzler Physik; 3. Auflage; Herausgeber: Joachim Grehn und Joachim Krause; Erscheinungsjahr: 1998; Verlag: Schrödel; Seite: 560 31 ESA/Hubble and NASA, M. Kornmesser 30 43 8. Supernovae Wenn sich das Leben eines Sterns mit hoher Masse dem Ende neigt, geschieht dies in einer Supernova Explosion, bei der er für kurze Zeit seine Leuchtkraft um das millionenfache steigert. Man unterscheidet hier zwischen der Kernkollaps und der Thermonuklearen Supernova. Die freigesetzte Energie bei einer durchschnittlichen Supernova liegt bei 10^46 Joule und die Supernova leuchtet nach ihrer Explosion noch einige Wochen mit einer extrem hohen Helligkeit, welche sich mit der von einer Milliarde Sonnen vergleichen lässt, bevor sie anfängt abzuklingen. Supernovae kommen nur sehr selten vor, weshalb wir in unserer Galaxie nur sieben Stück kennen. Supernova Explosionen sind vor allen Dingen wichtig für die Häufigkeit der chemischen Elemente. Bei einem weißen Zwerg bleibt der C-O-Kern erhalten, aber dafür werden alle zuvor fusionierten Elemente weg gestoßen. Dabei können dank des hohen Drucks und der hohen Temperatur Kettenreaktionen ablaufen, die sonst nicht möglich wären. Somit können radioaktive Elemente wie Uran entstehen, indem sich Eisenkerne in Goldkerne und dann in Bleikerne umwandeln. Dieses verwandelt sich dann durch Neutroneneinfang zu schwereren Radioaktiven Elementen. Diese entstandenen Gase, die sowohl durch Fusion als auch durch Neutroneneinfang entstehen, stehen nun zur Verfügung um neue Sterne zu bilden. Dementsprechend können aus den Überresten eines toten Sterns neue Sterne entstehen. 8.1 Kernkollaps-Supernova Eine Kernkollaps-Supernova entsteht, wenn bei einem Roten oder Blauen Riesen mit achtfacher Sonnenmasse die letzte Fusionsstufe eintritt, bei der Silizium zu Eisen verbrennt. Hier sammelt sich nun solange Eisen im Kern, bis er ca. 1,44 Sonnenmassen überschreitet und somit innerhalb von wenigen Millisekunden kollabieren kann. Dieser wird dann zum Neutronenstern, dessen Kern eine sehr hohe Dichte hat und die Neutronen im Kern stoppen schließlich den Kollaps. Da dieser Kollaps sehr schnell stattfindet wird eine riesige Energiemenge freigesetzt und die äußeren Schalen des Sterns fallen in Richtung des Zentrums. Beim plötzlichen Ende dieses Kollapses prallen die nach innen fallenden Elemente vom Kern ab und werden mit einer riesigen Kraft in den Raum gesprengt. Dies ist dann die besagte Kernkollaps-Supernova. 44 Abbildung 41 – Simulation des Anfangs einer SternkollapsSupernova Abbildung 42 – Simulation der Explosion des Sterns, anschließend an Zustand in vorheriger Abbildung Das einzige was nun noch vom Stern übrig ist, ist der Neutronenstern mit einem Durchmesser von ca. 10 km und einer außerordentlich hohen Dichte von einigen Millionen Tonnen pro Kubikzentimeter. Nun breitet sich die abgestoßene Hülle sehr schnell vom Neutronenstern aus. Abbildung 43 – Darstellung des sich ausbreitenden Gases nach der Explosion Abbildung 44 – Darstellung des Fortlaufs der Ausbreitung des Gases mit erkennbaren Neutronenstern im Zentrum 32 Die obere Massegrenze eines Neutronensterns liegt bei 2 Sonnenmassen, alle kollabierenden Sterne darüber werden zu einem Schwarzen Loch. Die Kernkollaps-Supernova hat eine absolute Helligkeit von -17 bis -18 Mag, was bedeutet, dass wir eine Supernova in ca. 32 Lichtjahren Entfernung heller sehen würden als den Vollmond. Die Stoßfronten solcher Explosionen können, wie bei der Sternentstehung bereits erwähnt, räumlichen Inhomogenitäten in planetarischen Nebeln hervorrufen, wodurch neue Sterne entstehen können. 32 (Abbildung 41-44) http://www.andromedagalaxie.de/html/sterne_supernova.htm (25.05.15) 45 8.2 Thermonukleare Supernova Abbildung 45 – Weißer Zwerg mit Akkretionsscheibe im Doppelsternsystem mit einem Roten Riesen Eine thermonukleare Supernova entsteht bei einem Doppelsternsystem, dass aus einem Weißen Zwerg und aus einem Roten Riesen. Nach heutigen Erkenntnissen ist dies die einzige Möglichkeit. Hierbei dehnt sich der Rote Riese soweit aus, dass seine Materie auf den Weißen Zwerg fließt. Der Wasserstoff fließt vom Roten Riesen erst auf eine rotierende Gasscheibe, eine Akkretionsscheibe, und dann langsam auf die Oberfläche des Weißen Zwergs. Hier wird die Materie nun weiter erhitzt und eine Kernfusion tritt ein, wobei Wasserstoff zu Helium und Helium zu Kohlenstoff fusioniert. Wenn die Masse des Weißen Zwerges durch die Fusionsrückstände zunimmt und auf über 1,44 Sonnenmassen zunimmt, kollabiert dieser. Anders als bei der Kernkollaps-Supernova besteht der Kern aus fusionsfähigen Elementen, was zur Folge hat, dass extreme Temperaturen und Druck auftreten. Durch die darauf folgende Fusion des Kohlenstoffs im Weißen Zwerg kommt es zu einer riesigen Explosion in der der Stern zur Supernova wird, wobei der gesamte Stern zerstört wird. Durch die Zerstörung des Weißen Zwergs verschwindet des Massenschwerpunktes im Doppelsternsystem und dadurch wird der Begleitstern weggeschleudert. Diese Supernova ist heller als die KernkollapsSupernova. Ihre Helligkeit liegt bei -19 Mag.33 33 http://www.andromedagalaxie.de/html/sterne_supernova.html (12.04.15) und Metzler Physik; 3. Auflage; Herausgeber: Joachim Grehn und Joachim Krause; Erscheinungsjahr: 1998; Verlag: Schrödel; Seite: 562 46 9. Schwarzes Loch Bei Supernova-Überresten, deren Masse höher als die zweifache Sonnenmasse ist, findet die Entwicklung zu einem Schwarzen Loch statt. Dem weiterhin wirkenden Gravitationspotential kann weder Strahlungsdruck noch eine andere kompensierende Kraft entgegenwirken. Das Objekt verdichtet sich somit noch über den Neutronenstern hinaus. Auch ein Neutronenstern kann sich über sein Endstadium hinaus noch zu einem Schwarzen Loch entwickeln. Dazu ist es jedoch notwendig, dass er von außerhalb Materie aufnimmt, somit seine Masse erhöht und schließlich die Massegrenze überschreitet, um durch die Gravitation zu einem Schwarzen Loch zu kollabieren. Materie oder auch Licht, das sich in der Nähe des Schwarzen Lochs befindet, wird von der extrem hohen Gravitation angezogen und aufgenommen. 34 Abbildung 46 - Skizzenhafte Darstellung von Lichtstrahlen, die in unterschiedlichen Distanzen auf ein Schwarzes Loch treffen Wie in Abbildung 46 zu erkennen ist, wird ein Schwarzes Loch häufig als eine kegelförmige Vertiefung in einem Netz dargestellt. Objekte, die eine hohe Masse und damit auch eine hohe Gravitation verursachen, haben eine tiefere Einbuchtung. Vergleichbar ist diese Darstellung mit einem gespannten Tuch oder Netz auf das man ein Objekt legt. Ein schwereres Objekt zieht dieses Tuch an seinem Auflage Punkt weiter hinunter als ein leichtes. 34 http://astrokramkiste.de/schwarzes-loch (18.04.15) 47 In der Abbildung erkennt man, dass fünf Lichtstrahlen, gekennzeichnet mit den Buchstaben A-E, an dem Schwarzen Loch vorbeiführen. Während bei Lichtstrahl A und B die Richtung des Lichtes durch die enorme Gravitationskraft wesentlich abgelenkt wird, wird Lichtstrahl C um das Schwarze Loch herum geführt, sodass seine Ausgangsrichtung um 180° abgelenkt wurde. Wenn jedoch das Licht nah genug am Objekt vorbei führt, kann es dazu führen, dass es wie bei Lichtstrahl E zu sehen, in das Schwarze Loch hineingezogen wird. Das Objekt verschluckt demnach nicht nur Materie in seiner direkten Umgebung, sondern ebenso unter den passenden Voraussetzungen auch Licht, daher stammt auch die Bezeichnung. Das Objekt gibt kein eigenes Licht mehr von sich und die Eigenschaft des Aufnehmens und Ablenkens des Lichtes aus der Umgebung führen zu der Bezeichnung. Über das Stadium des Schwarzen Lochs ist kein weiteres Stadium bekannt, daher endet mit diesem Zustand auch der Lebenszyklus eines Sterns. 48 10. Fazit der Arbeit Abschließend können wir sagen, dass wir selbst im Verlauf unserer Arbeit viel über das Thema gelernt haben und hoffen, dass der Leser selbige Erkenntnisse erlangen konnte. Insgesamt sind wir sehr zufrieden mit unserer Arbeit. Die Durchführung der Experimente ist überwiegend einwandfrei verlaufen und hat zu beeindruckenden Ergebnissen geführt, wie beispielweise das Bild des Orionnebels oder die Oberflächentemperatur des Roten Riesen Aldebaran. Leider konnten wir nicht mehr die genaue Verfahrensweise zur Bestimmung der absoluten Helligkeit der Sterne durchführen bzw. in unsere Arbeit implementieren. 11. Danksagung Zuletzt wollen wir uns bei allen bedanken, die uns bei unserer Arbeit unterstützt haben. Allen voran wollen wir uns bei unserem Kursleiter Bernd Koch bedanken, der uns sowohl den Umgang mit den Geräten und Programmen, als auch inhaltliche Aspekte unserer Arbeit beigebracht hat. Natürlich wollen wir uns auch für die Möglichkeit, die uns am Carl-Fuhlrott-Gymnasium geboten wird, bedanken. Denn ohne diese Voraussetzung wäre es nicht annähernd möglich gewesen eine Arbeit dieses Umfangs zu verfassen. Zuletzt möchten wir uns für die Zusammenarbeit mit Christian Zahn und Tobias Stamp während des Experiments Orionnebel bedanken. 49 12. Abschlusserklärung Hiermit versichern wir, dass wir diese Arbeit selbstständig angefertigt, keine anderen als die von uns angegebenen Quellen und Hilfsmittel benutzt und die Stellen der Projektarbeit, die im Wortlaut oder dem Inhalt aus anderen Werken entnommen wurden, in jedem einzelnen Fall mit genauer Quellenangabe kenntlich gemacht haben. Die verwendeten Informationen aus dem Internet sind als PDF auf einer CD am Ende der Facharbeit beigefügt. Wir sind damit einverstanden, dass die von uns verfasste Projektarbeit der schulinternen Öffentlichkeit in der Bibliothek der Schule zugänglich gemacht wird. Ort, Datum Unterschrift Für eventuelle Rückfragen zu unserer Arbeit stehen wir ihnen gerne unter den E-Mail Adressen [email protected] und [email protected] zur Verfügung. 50