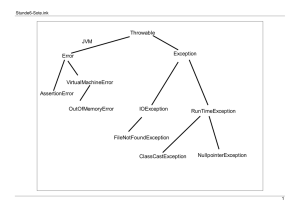
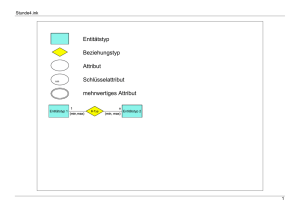
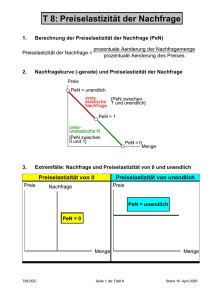
DataMining

Steffen Thomas 96I
DATA MINING
Allgemein:
• Suche in riesigen Datenbanken
• Finden interessanter Trends oder Muster
• diese können auch unerwartet sein
• soll zukünftige Entscheidungen
vereinfachen
Inhalt:
1 Grundlagen des Data Mining
2 Finden von zusammengehörigen Daten
3 Generierung von Regeln
4 Regeln in Form von Bäumen
5 Clustering
6 Ähnlichkeitssuche über Sequenzen
7 Weitere DataMining-Aufgaben
8 Darwin
1 Grundlagen des Data Mining
• verwandt mit der Erforschenden Daten-Analyse und der KI
• Ideen dieser Gebiete auf Data Mining anwendbar
• wichtigster Unterschied: Größe der Datenmengen
• neues Kriterium:
- Algorithmen müssen skalierbar sein
- d.h. linearer Anstieg der Rechenzeit
Grundlagen
• in der Realität enthalten Daten Rauschen und Lücken
• herkömmliche Methode wie SQL-,OLAP-Queries reichen
nicht aus
• der KDD-Prozess (Knowledge Discovery Process)
data selection: identifizieren des Zieldatensatzes
data cleaning: Beseitigung unnötiger Information
Vereinheitlichung von Feldwerten
Erzeugen neuer Felder
data mining: Extrahieren der vorhandenen Muster (patterns)
evaluation: visuelle Ausgabe der Ergebnisse
2 Zusammengehörige Daten
•
Ausgangspunkt: Probleme wie Warenkorb-Analyse
•
Warenkorb ist Sammlung von Artikeln eines einzelnen
Einkaufs
•
Ziel: finde Artikel, welche zusammen gekauft werden
dadurch bessere Platzierung und Werbung möglich
Zusammengehörige Daten
2.1 Frequent Itemsets
• itemset: Satz unterschiedlicher Artikel
• support: Anteil eines itemsets (%)
– BSP:
itemset {pen,ink} mit support von 75%
{milk,juice}
25%
d.h. Milch und Saft werden nicht sehr häufig zusammen gekauft
• frequent itemsets: alle itemsets mit support über einer
bestimmten Schranke (minsup)
• relativ wenig, besonders bei steigender Datenmenge
Frequent Itemsets
Zusammengehörige Daten
Algorithmus:
• beruht auf einer Eigenschaft von frequent itemsets
• a priori Eigenschaft: jede Unterteilung eines frequent
itemsets ist ebenfalls ein frequent itemset
foreach Artikel
// Level 1
prüfe ob dieser frequent itemset ist // Artikel >minsup vorhanden
k=1
repeat
foreach frequent itemset Ik mit k Artikeln
// Level k+1
generiere alle itemsets Ik+1 mit k+1 Artikeln
scanne alle Transaktionen einmal und prüfe ob
die generierten k+1 itemsets frequent sind
k = k+1
until keine neuen frequent itemsets gefunden werden
Frequent Itemsets
Ein Beispiel:
Zusammengehörige Daten
minsup = 70%
erste Iteration(Level 1):
gefunden werden {pen},{ink},{milk}
zweite Iteration(Level 2):
neue Kandidaten sind
{pen,ink},{pen,milk},{pen,juice},{ink,milk},{ink,juice},{milk,juice}
nach dem Scannen bleiben folgende frequent itemsets übrig
{pen,ink},{pen,milk}
dritte Iteration(Level 3):
Kandidaten sind {pen,ink,milk},{pen,ink,juice},{pen,milk,juice}
keiner der Kandidaten ist frequent, sie werden verworfen
• Verbesserung der Laufzeit durch Anwendung der a priori Eigenschaft
Zusammengehörige Daten
2.2 Iceberg Queries
• wenig Resultate, auch bei goßen Datenbasen
• Anfrage in SQL (Bsp.):
SELECT
P.custid,P.item,SUM (P.qty)
FROM
Purchase P
GROUP BY P.custid,P.item
HAVING
SUM (P.qty) > 5
• iceberg queries nutzen die selbe bottom-up Strategie wie frequent
itemsets
• ebenfalls Performance-Gewinn durch a priori Eigenschaft
3 Generierung von Regeln
• wichtige Muster in Datenbasen sind Regeln
• effektive Beschreibung der Daten
• es existieren vielfältige Formen von Regeln
• ebensoviele Algorithmen
Generierung von Regeln
3.1 Association Rules
• haben die Form
LHS => RHS
; LHS,RHS sind itemsets
BSP:
{pen} => {ink}
• sprachlich: “Wenn bei einem Einkauf ein Füller gekauft wird, so ist es
wahrscheinlich, dass auch gleichzeitig Tinte gekauft wird.”
• support: ist der support für ein itemset LHS RHS
im BSP: support {pen,ink} = 75%
• confidence(Vertrauen): verdeutlicht die Stärke einer Regel
ergibt sich aus sup(LHS) / sup(LHS RHS)
im BSP: 75% der Transaktionen die {pen} enthalten
enthalten auch {ink}
Generierung von Regeln
3.2 Ein Algorithmus zum Finden
von Association Rules
• Gegeben: minsup, minconf
• Ausgangspunkt sind frequent itemsets > minsup
–
–
–
–
X ist frequent itemset mit support sX
X wird in LHS und RHS zerlegt
confidence von LHS => RHS ist sX/sLHS
alle Regeln mit confidence > minconf werden
akzeptiert
• der Aufwand zur Generierung von Regeln ist relativ gering
Generierung von Regeln
3.3 Association Rules und ISA
Hierarchien
• itemsets können oft auch in Hierarchien auftreten
• dadurch können Beziehungen von Artikeln auf unterschiedlichem
Level erkannt werden
Stationary
Pen
• BSP:
Ink
Beverage
Juice
Milk
support von {ink,juice} = 50%
jetzt juice = beverage
support von {ink,beverage} = 75%
• der support eines Artikels kann nur steigen, wenn dieser Artikel durch
einen Vorgänger in der Hierarchie ersetzt wird
Generierung von Regeln
3.4 Allgemeine Association Rules
• Association Rules meist im Zusammenhang mit Warenkorb-Analyse
• kann aber allgemeiner aufgefasst werden
• bei Sortierung nach anderen Merkmalen können Regeln gefunden
werden, die anders interpretiert werden müssen
Bsp:
Sortierung nach custid
Regel: {pen} => {milk}
support = confidence = 100%
bedeutet:”Wenn ein Käufer einen Füller kauft, so kauft er
wahrscheinlich auch Milch.”
• ebenso Sortierung nach Datum usw. möglich
Allgemeine Association Rules
Generierung von Regeln
• Sortierung nach Datum wird auch als kalendrische Warenkorb-Analyse
bezeichnet
• ein Kalender ist dabei Gruppierung von Daten:
z.B.: jeder Sonntag im Jahr 1999
jeder Erste des Monats
• durch Spezifizierung von interessanten Kalendern, können Regeln
entdeckt werden, die in der gesamten Datenbasis nicht auffallen
würden u.ä.
BSP:
Regel: pen => juice
allgemein: support = 50%
Kalender = jeder Erste des Monats
jetzt: support = confidence = 100%
• durch die Wahl verschiedener Gruppierungsmöglichkeiten, kann man
viel komplexere Regeln identifizieren
Generierung von Regeln
3.5 Sequentielle Muster
• Sequenz ist eine Gruppe von Tupeln, die nach bestimmten Merkmalen
geordnet ist
• macht, genau wie association rules, Aussagen über diese Tupel
Bsp.: Sortierung nach custid und item: Sequenz von Einkäufen eines
Kunden (custid = 201 {pen,ink,milk,juice},{pen,ink,juice})
• Teilsequenz ist ebenfalls Sequenz; eine Sequenz {a1,..,am} ist in
Sequenz S enthalten, wenn S eine Teilsequenz
{b1,..,bm} hat
BSP: Sequenz {pen},{ink,milk},{pen,juice} ist enthalten in
{pen,ink},{shirt},{juice,ink,milk},{juice,pen,milk}
• Algorithmen zur Berechnung von Sequenzen sind ähnlich denen zum
Finden von frequent itemsets
Generierung von Regeln
3.6 Association Rules und
Vorhersagen
• association rules werden häufig zur Vorhersage benutzt
• diese müssen aber durch weitere Analysen und Grundlagenwissen
gesichert sein
BSP:
Annahme: Tinte wird durch Füller, Füller mit Bleistiften verkauft
Regel {pen} => {ink}, hat confidence(Vertrauen) von 100%
(in der gegebenen Datenbasis),d.h.:
um mehr Tinte zu verkaufen, könnte man Füller billiger anbieten
aber
{pencil} => {ink}, hat ebenfalls confidence von 100%, d.h.:
billigere Bleistifte, verkaufen mehr Tinte
wäre ein falscher Schluß
Association Rules und Vorhersagen
Generierung von Regeln
• in Wirklichkeit, nicht so triviale Entscheidungen
• kausale Verbindung zwischen LHS und RHS notwendig
• gefundene Regeln sollten als Ausgangspunkt für weitere
Analysen dienen
• Expertenwissen ist nützlich
• gefundene Regeln als alleiniger Entscheidungsgrund sind
zu unsicher
Generierung von Regeln
3.7 Bayesische Netze
• sind Graphen, die kausale Beziehungen zwischen Variablen oder
Ereignissen darstellen können
• jede Kombination von kausalen Verbindungen ist ein Model der realen
Welt
BSP:
kaufe Füller
kaufe Tinte
Bedarf an
Schreibinstrumenten
kaufe Bleistifte
• Zahl der Modelle ist exponential zu Zahl der Variablen
• nur einige wichtige Verbindungen sollten ausgewertet werden
Generierung von Regeln
3.8 Classification und Regression
Rules
• Bsp:
VersicherungsInfo(Alter: integer, Autotyp: string, Risiko: boolean)
es werden Regeln gesucht, die das Versicherungsrisiko bestimmen
z.B.:
“Wenn das Alter zwischen 16 und 25 ist und das Auto ein Sportwagen
oder Truck, so ist ein Risiko gegeben.”
• gesuchtes Attribut heißt: dependent(abhängiges) Attribut Risiko
• bestimmende Attribute: predictor Attribute Alter, Autotyp
Classification und Regression
Generierung von Regeln
• Allgemeine Form:
P1(X1) ^ P2(X2)... ^ Pk(Xk) => Y
X1..Xk: predictor Attribute
P1..Pk: Prädikate
Y: dependent Attribut
• Form der Prädikate abhängig vom Typ der predictor Attribute:
– numerisch:
Pi hat die Form li R Xi R hi
– kategorisiert:
Pi hat die Form Xi i {v1,..,vj}
• die Regel heißt:
– classification rule, wenn dependent Attribut kategorisiert ist
– regression rule, wenn dependent Attribut numerisch ist
Bsp:
(16 R Alter R
25) ^ (Auto i {Sport,Truck}) => Risiko = true
Classification und Regression
Generierung von Regeln
• support:
– für eine Bedingung C ist % von Tupeln, die C wahr machen
– für Regel C1 => C2 ist support für Bedingung C1 ^ C2
• confidence:
– angenommen alle Tupeln die C1 wahrmachen
– für Regel C1 => C2, % der Tupeln, die auch C2 wahr machen
• das effiziente Finden solcher Regeln ist nichttriviales Problem
• diese Regeln werden auf vielfältigste Weise eingesetzt
4 Regeln in Form von Bäumen
• repräsentieren classification und regression rules
• der Baum ist dabei die Ausgabe der Datamining-Anfrage
• Bezeichnungen:
– Entscheidungsbäume, repräsentieren classification rules
– regression-Bäume, repräsentieren regression rules
Bsp:
Alter
Entscheidungsbaum
<= 25
>25
Auto
NEIN
Kombi
Sport, Truck
NEIN
JA
“Wenn jemand 25 oder jünger ist und einen Kombi fährt, so hat er ein
niedriges Risiko.”
Baumartige Regeln
4.1 Entscheidunsbäume
•
•
•
•
•
stellt einen Datensatz von einer Wurzel bis zu einem Blatt dar
jeder interne Knoten ist mit einem predictor Attribut bezeichnet
heißt auch splitting Attribut, d.h. teilt die Daten in Zweige auf
ausgehende Kanten werden mit Prädikaten bezeichnet
Information über splitting Attribut und Prädikat heißt splitting
criterion (Kriterium)
• jedes Blatt ist mit dem Wert des dependent Attributs bezeichnet
• eine classification Regel ergibt sich wie folgt:
der Weg von Wurzel zum Blatt über verschiedene Prädikate = LHS
der Wert des Blattes = RHS
Entscheidunsbäume
Baumartige Regeln
• Entscheidungsbäume werden in 2 Phasen konstruiert:
– growth(Wachstums) Phase:
• ein übergroßer Baum, mit sämtlichen Daten wird erzeugt
• die Regeln dieses Baumes sind überspezialisiert
– pruning(Stutzungs) Phase :
• die finale Größe wird bestimmt
• die Regeln sind allgemeiner
Berechnung eines gestutzten Baums:
• split selection Methode:
– hat als Input die Datenbasis oder einen Teil von ihr
– erzeugt daraus ein split Kriterium
Entscheidunsbäume
Baumartige Regeln
• Schema zur Erzeugung eines gestutzten Baums:
– Input: Knoten n, Partition D, split selection Methode S
– Output: Entscheidungsbaum für D, mit Wurzel in n
– BuildTree(Knoten n, Datenpartition D, split selection methode S)
• wende S auf D an, um ein splitting Kriterium zu finden
• if(gutes Kriterium gefunden)
– Erzeuge zwei Knoten n1, n2 aus n
– Teile D in D1, D2
– BuildTree(n1, D1, S)
– BuildTree(n2, D2, S)
• endif
Baumartige Regeln
4.2 Ein Algorithmus für
Entscheidungsbäume
• obiges Schema sofort anwendbar, wenn Daten in Hauptspeicher passen
• andernfalls versagt Algorithmus
• Lösung:
– die split selection Methode untersucht jeweils einzelne Attribute
– benötigt nicht unbedingt die ganze Datenbasis
– zusammengefasste(aggregierte) Daten sind ausreichend
– wird als AVC set bezeichnet (Attribut-Value,Classlabel)
Entscheidunsbäume
Baumartige Regeln
• Die split selection Methode benötigt AVC set für jedes predictor
Attribut
Bsp:
AVC set für Knoten Alter
SELECT
R.Alter,R.Risiko, COUNT (*)
FROM
VersicherungsInfo R
GROUP BY R.Alter, R.Risiko
AVC set für Knoten Auto
SELECT
FROM
WHERE
GROUP BY
• AVC group
R.Auto,R.Risiko, COUNT (*)
VersicherungsInfo R
R.Alter <= 25
R.Auto, R.Risiko
Satz aller AVCs aller Attribute am Knoten n
5 Clustering
• Ziel: Aufteilung der Daten in Gruppen, die Aussagen über Ähnlichkeit
machen
• Daten einer Gruppe sind ähnlich, unterschiedlicher Gruppen unähnlich
• dies wird durch Abstandsfunktion gemessen
• die Ausgabe eines Clustering-Algorithmus besteht aus zusammengefassten Repräsentationen für jeden Cluster
• Cluster werden zusammengefasst durch Center C und Radius R einer
Sammlung von Daten r1..rn
Bsp:
KundenInfo(Alter: int, Gehalt: real)
Clustering
Gehalt
60k
30k
20
40
60
Alter
• 2 Arten von Clustering-Algorithmen:
– partielles: unterteilt die Daten in k Gruppen (benutzerdefiniert)
– hierarchisches: generiert Sequenz von Teildaten,
verschmilzt in jeder Iteration 2 dieser Teile, bis
eine Partition übrig bleibt
Clustering
5.1 Ein Clustering Algorithmus
• der BIRCH Algorithmus
• Annahmen:
– Zahl der Datensätze ist sehr gross
– möglichst nur ein Scan der Datenbasis
– Hauptspeicher ist limitiert
• 2 Kontrollparameter:
– Größe des Hauptspeichers, resultiert in k Speicherblöcken
– e anfängliche Schranke für Radius der Cluster
• wenn e klein ist, werden viele kleine Cluster berechnet, sonst wenige,
relativ grosse
• ein Cluster heißt kompakt, wenn Radius < e
BIRCH Algorithmus
Clustering
• der Algorithmus behält immer <= k Cluster-Zusammenfassungen
(Ci,Ri) im Speicher
• er behandelt immer kompakte Cluster
• es werden sequentiell Einträge gelesen und wie folgt bearbeitet:
1. Berechne den Abstand des Eintrags r und jedes existierenden C
i ist der Index des Clusters mit kleinstem Abstand (r, Ci)
2. Berechne den neuen Radius Ri’, des i-ten Clusters
wenn Ri’ <= e, weise r dem i-ten Cluster zu (neues Ci, Ri = Ri’)
sonst, erzeuge neuen Cluster mit r
• Problem: weitere Cluster passen nicht in Hauptspeicher
• Lösung: erhöhe e, es werden Cluster verschmolzen
6 Ähnlichkeitssuche über
Sequenzen
• Viele Informationen in Datenbasen bestehen aus Sequenzen
• Annahme: der Benutzer gibt Query-Sequenz an, will ähnliche
Sequenzen erhalten
• ist eine Art unscharfe Suche
• Daten-Sequenz X ist eine Reihe von Zahlen X = {x1,..,xk}
• k ist Länge der Sequenz
• Teilsequenz Z = {z1,..,zj} erhält man aus X durch Löschen von Zahlen
an Anfang und Ende
Ähnlichkeitssuche
• Abstand zweier Sequenzen = Euklidische Norm ||X-Y|| =
• benutzerdefinierte Schranke e
• Ziel: Finden aller Sequenzen im e -Abstand
• Ähnlichkeits-Anfragen können in zwei Arten unterteilt werden:
Komplett-Sequenz Matching:
Query-Sequenz und Sequenzen der Datenbasis sind gleich lang
Ziel: alle Sequenzen im e -Abstand
Teilsequenz Matching:
Query-Sequenz ist kürzer als Sequenzen der Datenbasis
Ziel: Finde alle Teilsequenzen im e -Abstand
Ähnlichkeitssuche
6.1 Suche ähnlicher Sequenzen
• Annahme: Komplett-Sequenz Matching
• Suche ist ein mehrdimensionales Indizierungs-Problem
• Daten- und Query-Sequenzen sind Punkte im k-dimensionalen Raum
• Anlegen eines Hyper-Rechtecks mit Seitenlänge 2* e und QuerySequenz als Zentrum
• alle Sequenzen im Rechteck werden ausgegeben
• durch Benutzung der Indizes deutliche Reduzierung von Rechenzeit
und Zahl der betrachteten Daten
7 Weitere DataMining-Aufgaben
• bisher nur Suche nach Mustern
• weitere wichtige Aufgaben:
Datensatz und Feature Auswahl:
Suche des ‘richtigen’ Datensatzes und dazugehöriger Attribute
Sampling:
Samples reduzieren den Aufwand in übergrossen Datenbanken
Nachteil: wichtige Informationen können übersehen werden
Berechnung der Samples noch rückständig (Forschungsgebiet)
Visualisierung:
verbessert Verständniss über komplexe Datensätze
hilft interessante Muster zu erkennen
8 Darwin
• Daten Mining Tool in Oracle-Umgebung
• parallele, skalierbare Client/ServerArchitektur
• beliebig grosse Datenmengen
• einfachste Point-and-Click Bedienung
• visuelle Ausgabe der Ergebnisse
Darwin
Client:
Windows 95/NT/98
Server:
Windows NT(ab 4.0)
SUN Solaris
HP-UX
Darwin
• Verwendete Algorithmen:
–
–
–
–
–
Neuronale Netze mit Spezialfällen
Entscheidungsbäume(classification, regression)
speicherbasiertes Beweisen
Bayesisches Lernen (ab 4.0)
erweitertes Clustering