Woher kommen Laengen und Massen Dortmund DPG 2006

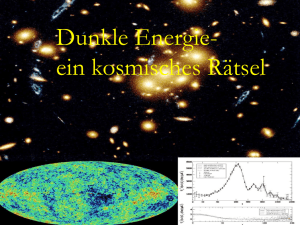
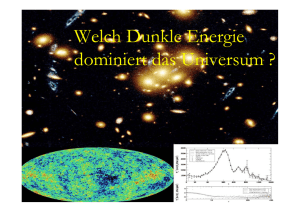
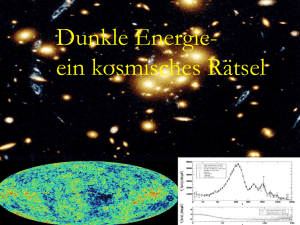
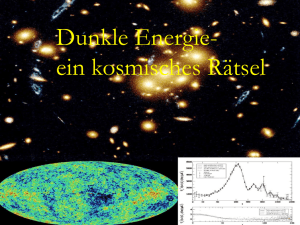
Woher kommen
Längen und Massen ?
C. Wetterich
Woher kommen
Längen und Massen ?
Dilatations - Symmetrie und
Dunkle Energie
Ωm + X = 1
?
Ωm : 25%
Ωh : 75%
Dunkle Energie
Messung , Beobachtung :
nur dimensionslose Größen !

Aber : mElektron = 511 keV : gemessen!

Was ist eV?
1 eV = Grundzustands-Energie des
Wasserstoffatoms/13.6


Messung: Verhältnis der Grundzustands-Energie des
Wasserstoffs zu Elektronenmasse.
Einheiten

Man könnte die Elektron – Masse als
Masseneinheit wählen

1 Gramm = 1.1 x 10 27 mElektron

proportional zu Avogadro’s Zahl
QED
me = 1 : einziger dimensionsloser Parameter e
dann auch Proton- Masse etc.
Standard – Modell der
elektroschwachen Wechselwirkung :
Higgs - Mechanismus


Die Massen aller fundamentalen Fermionen und
Eichbosonen sind proportional zum VakuumErwartungswert eines Skalarfelds φ ( Higgs Skalar )
Für Elektron , Quarks , W- und Z- Bosonen gilt
mElektron = hElektron
*
φ
etc.
Skalar - Feld φ(x,y,z,t)
ähnlich elektrischem Feld , aber keine Richtung :
daher Erwartungswert möglich,
ohne Isotropie zu verletzen
Spontane Symmetrie - Brechung
SYM
<φ>=0
SSB
<φ>=φ ≠ 0
0
Higgs – Potenzial in SM
Massen und Kopplungskonstanten
werden bestimmt durch die
Eigenschaften des Vakuums !
ähnlich Maxwell – Gleichungen in Materie
LHC
Hatten Kopplungskonstanten im
frühen Universum
andere Werte ?
Ja !
Restoration der Symmetrie
bei hohen Temperaturen
im frühen Universum
Niedrige T
SSB
<φ>=φ0 ≠ 0
Hohe T
SYM
<φ>=0
hohe T :
weniger Ordung
mehr Symmetrie
Beispiel:
Magnete
Im heissen Plasma
des frühen Universums :
Keine unterschiedlichen Massen
für Elektron und Myon !
Zusammenfassung
Der Wert von Massenverhältnissen und
Kopplungskonstanten hängt vom Zustand ab !
Nicht ein für alle mal gegeben !
Das Rätsel
der winzigen Zahlen
8
Vereinheitlichung und Dimensionen




Vereinheitlichung fixiert dimensionsbehaftete
Parameter
Spezielle Relativitätstheorie : c ( = 1 )
Quantenmechanik :
h ( = 2π )
Vereinheitlichung mit Gravitation
( Quantengravitation)
fundamentale Massenskala
( Planck Masse , string tension , …)
Gravitationseinheiten
 Newton’s
Konstante
GN=1/(8πM²)
 Reduzierte
Planck Masse
M=2.44×1018GeV

M=1 :
GeV = 4.1×10 -19
Gravitationseinheiten
( reduzierte Planck – Masse = 1 )







mProton = 3.9 x 10 -19
mElektron = 2.1 x 10 -22
Gramm = 2.3 x 10 5
Meter = 1.2 x 10 34
Sekunde = 3.7 x 10 42
Alter des Universums ( 13.7 x 10 9 yr ) = 1.6 x 10 60
Energiedichte des Universums : ρ = 10 -120
Kleine Parameter –
grosse Rätsel
Laufende Kopplung : QCD
Effektive Eichkopplung
hängt von Impulsskala μ ab
QCD : Dimensionale Transmutation






Ohne Quark – Massen : nur dimensionslose Kopplung !
Charakteristisches μ , bei dem Kopplung groß wird
Massenskala ΛQCD
Proton - Masse ~ ΛQCD
Für gegebene Kopplung αs (μ=M) = α0 :
MProton = b exp( - c / α0 ) M , c ≈ 0.9
Kleines α0 , winziges MProton !
Trick der Natur
Quanten - Fluktuationen erzeugen
Massen-Skalen durch
laufende dimensionslose Kopplungen
Dilatations - Anomalie
Hypothese:
Quantengravitation Theorie ohne explizite
Massenskala ?
12
Fundamentale Massenskala
 Fester
“Parameter” oder
dynamische Skala ?
 Dynamische Skala
Feld
Kosmon und
Fundamentale Massen - Skalen

Annahme : Alle Parameter mit Dimension Masse sind
proportional zu Skalar - Feld χ
(GUTs, Superstrings,…)
M ~ χ , mproton~ χ , ΛQCD~ χ , MW~ χ

χ kann sich mit der Zeit ändern

mproton/M : ( fast ) konstant - Beobachtung !
Nur Verhältnisse von Massenskalen sind beobachtbar !

Trick für Theorie
ohne fundamentale Massenskala:
Ersetze alle Massen durch
dimensionslose Konstante mal χ
Dilatations – symmetrische
Gravitationstheorie

Lagrange Dichte:

Dilatations - Symmetrie für

Konforme Symmetrie für δ=0
Dilatations - Symmetrie
Reskalieren der Längenskalen
x → c -1 x
Sieht die Physik noch genauso aus ?
Skalen – invariant = Dilatations – symmetrisch
Wichtig für kritische Phänomene in statistischer Physik
Wenn eine feste Massen – oder Längen - Skala eine Rolle spielt :
Keine Dilatations – Symmetrie !
Dilatations - Symmetrie
Reskalieren der Längenskalen
x → c -1 x
begleitet von Reskalieren des Skalar - Felds
χ → cχ
Verschiedene Längeneinheiten entsprechen
verschiedenen Werten des Kosmon – Felds χ !
Dilatations – symmetrische
Gravitationstheorie

Lagrange Dichte:

Dilatations - Symmetrie für
Woher kommen die beobachteten
Massen – Skalen ?
Spontane Symmetriebrechung :
χ ≠ 0
Verletzt das Reskalieren der Massen und Längenskalen
χ → cχ
Goldstone Boson = Dilaton
masseloses Teilchen !
Dilatations Anomalie
Quanten - Fluktuationen führen zu
Dilatations - Anomalie
 Laufende Kopplungen : Hypothese



Renormierungs-Skala μ : (Impuls-Skala )
λ~(χ/μ) -A
Dilatations Anomalie

V~χ4-A , Mplanck(χ )~ χ

V/Mp4 ~ χ-A :
fällt für wachsendes χ !!
Grundlage für Kosmologie
Graviton + Kosmon
Kosmologie
Kosmologie : χ wächst mit der Zeit !
( Grund: Kopplung von χ zum gravitationellen
Krümmungs - Skalar )
Für wachsendes χ : Das Verhältnis V/M4
tendiert zu Null !
Effektive kosmologische Konstante
verschwindet asymptotisch für große t !
Weyl Reskalierung
Weyl Reskalierung : gμν→ (M/χ)2 gμν ,
φ/M = ln (χ 4/V(χ))
Exponentielles Potenzial : V = M4 exp(-φ/M)
Keine zusätzliche Konstante !
Ohne Dilatations – Anomalie :
V= const.
Masseloses Goldstone Boson = Dilaton
Dilatations – Anomalie :
V (φ )
Winzige zeitabhängige Masse : Kosmon
Kosmologie mit
Dunkler Energie
22
Homogenes und isotropes
Universum

φ(x,t)=φ(t)
Homogenes Kosmonfeld
Homogener Beitrag zur Energiedichte

Dynamische Dunkle Energie !


Kosmologische Gleichungen
( k(φ) = 1 )
Kosmische Attraktorlösung
Lösung unabhängig von
Anfangsbedingungen
typisch V~t -2
φ ~ ln ( t )
Ωh ~ V/ρm ~ const.
Details hängen von V(φ)
ab
Frühe Kosmologie
Vorhersage (1987):
homogenene Dunkle Energie
beeinflusst heutige Kosmologie
zeitlich veränderlich und
von der gleichen Größenordnung wie
Dunkle Materie
Ursprüngliche Modelle stimmen nicht mit
heutigen Beobachtungen überein
…. Modifizierungen
Realistische Modelle der Dunklen Energie:
Quintessenz wird heute wichtig
w=p/ρ
Woraus besteht unser Universum ?
Quintessenz !
Feuer , Luft,
Wasser,
Erde !
Ωtot= 1
Foto des
Urknalls
WMAP 2006
Polarisation
Dunkle Materie

Ωm = 0.25
“Materie” insgesamt

Die meiste Materie ist dunkel !

Bisher nur durch Gravitation spürbar

Alles was klumpt!
Gravitationspotential
Ωm= 0.25
Gravitationslinse,HST
Dunkle Energie
Ωm + X = 1
Ωm : 25%
Ωh : 75% Dunkle Energie
h : homogen , oft auch ΩΛ statt Ωh
Dunkle Energie :
homogen verteilt
Vorhersagen für Kosmologie mit Dunkler Energie
Die Expansion des Universums
beschleunigt sich heute !
Fluktuations-Spektrum
Baryon - Peak
Galaxien –
Korrelations –
Funktion
Strukturbildung :
Ein primordiales
Fluktuations-Spektrum
SDSS
Dunkle Energie :
Konsistentes Bild der Kosmologie
Zusammensetzung des Universums
Ωb = 0.045
sichtbar
klumpt
Ωdm= 0.2
unsichtbar
klumpt
Ωh = 0.75
unsichtbar
homogen
Ist Dunkle Energie
statisch oder dynamisch ?
32
Kosmologische Massenskalen

Energie - Dichte
ρ ~ ( 2.4×10 -3 eV )- 4
Reduzierte Planck Masse
M=2.44×1018GeV
 Newton’s Konstante
GN=(8πM²)

Nur Verhältnisse von Massenskalen sind beobachtbar !
homogene dunkle Energie:
ρh/M4 = 6.5 10ˉ¹²¹
Materie:
ρm/M4= 3.5 10ˉ¹²¹
Alter des Universums in Gravitationseinheiten : 1.6 10 60
Zeitentwicklung
tˉ²

ρm/M4 ~ aˉ³ ~

ρr/M4 ~ aˉ4 ~ t -2
Materie dominiertes Universum
tˉ3/2 Strahlungsdominiertes Universum
Strahlungsdominiertes Universum
Grosses Alter
kleine Grössen
Gleiche Erklärung für dunkle Energie ?
Kosm. Konst. | Quintessenz
statisch
| dynamisch
Quintessenz
Dynamische dunkle Energie ,
vermittelt durch Skalarfeld
(Kosmon)
C.Wetterich,Nucl.Phys.B302(1988)668
B.Ratra,P.J.E.Peebles,ApJ.Lett.325(1988)L17,
24.9.87
20.10.87
Frühe Dunkle Energie
mit
A.Hebecker,M.Doran,M.Lilley,J.Schwindt,
C.Müller,G.Schäfer,E.Thommes,
R.Caldwell
Zeitabhängigkeit der dunklen Energie
w=p/ρ
Kosmologische Konstante : Ωh ~ t² ~ (1+z)-3
M.Doran,…
Dunkle Energie
im frühen Universum :
unter 5 %
Early Dark Energy
A few percent in the
early Universe
Not possible for a
cosmological
constant
1σ and 2σ limits
Doran,Karwan,..
Eine neue
“fundamentale”
Wechselwirkung ?
45
Kosmon
 Skalarfeld
ändert seinen Wert auch in der
heutigen kosmologischen Entwicklung
 Potenzielle und kinetische Energie des
Kosmons tragen zur Energiedichte des
Universums bei
 Zeitabhängige dunkle Energie :
ρh(t) fällt mit der Zeit !
Kosmon
 Winzige
 mc
Masse
~H
 Neue
langreichweitige Wechselwirkung
“Fundamentale” Wechselwirkungen
Starke,elektromagnetische,schwache
Wechselwirkung
Auf
astronomischen
Skalen:
Graviton
+
Gravitation
Kosmodynamik
Kosmon
Quintessenz
und
Zeitabhängigkeit
fundamentaler
Konstanten
C.Wetterich , Nucl.Phys.B302,645(1988)
Sind fundamentale “Konstanten”
zeitabhängig ?
Feinstrukturkonstante α (elektrische Ladung)
Verhältnis Neutron-Masse zu Proton-Masse
Verhältnis Nukleon-Masse zu Planck-Masse
Quintessenz und
Zeitabhängigkeit der
“fundamentalen Konstanten”

Feinstrukturkonstante hängt vom Wert des
Kosmon Felds ab: α(φ)
ähnlich Higgsfeld in schwacher Wechselwirkung

Zeitentwicklung von φ
Zeitentwicklung von α
Jordan
Primordiale
Häufigkeiten der
leichten Elemente
aus der
Nukleosynthese
A.Coc ‘05
typische mögliche Werte der
Variation der Feinstrukturkonstanten:
Δα/α ( z=1010 ) = -1.0 10-3 GUT 1
Δα/α ( z=1010 ) = -2.7 10-4 GUT 2
Zeitvariation der Kopplungskonstanten
ist winzig –
wäre aber von grosser Bedeutung !
Mögliches Signal für Quintessenz
Zusammenfassung
o
Ωh = 0.7
o
Q/Λ : dynamische und statische
dunkle Energie unterscheidbar
o
Q : zeitlich veränderliche
“fundamentale Kopplungen” ,
Verletzung des Äquivalenzprinzips sind möglich
Noch viele offene Fragen ????
Die Antwort der Künstlerin …
Laura Pesce
Die Antwort der Künstlerin …
Laura Pesce
Und was war die Frage ?
Ende
Kosmodynamik
Kosmon vermittelt neue langreichweitige
Wechselwirkung
Reichweite : Grösse des Universums – Horizont
Stärke : schwächer als Gravitation
Photon
Elektrodynamik
Graviton
Gravitation
Kosmon
Kosmodynamik
Kleine Korrekturen zum Gravitationsgesetz
“Fünfte Kraft”

vermittelt durch skalares Feld
R.Peccei,J.Sola,C.Wetterich,Phys.Lett.B195,183(1987)


Kopplungsstärke schwächer als Gravitation
( nicht-renormierbare Wechselwirkung ~ M-2 )
Abhängigkeit von der Zusammensetzung
scheinbareVerletzung des Äquivalenzprinzips
Verletzung des Äquivalenzprinzips
Verschiedene Kopplung
des Kosmons an
Proton und Neutron
Differentielle
Beschleunigung
Verletzung des
Äquivalenzprinzips
p,n
Erde
Kosmon
p,n
Verknüpfung zwischen Zeitabhängigkeit von α
und Verletzung des Äquivalenzprinzips
differentielle Beschleunigung η
typisch : η = 10-14
MICROSCOPE – Satteliten-Mission
Differentielle Beschleunigung η
Für vereinheitlichte Theorien ( GUT ) :
Q : Zeitabhängigkeit anderer Parameter
Zunehmende Wichtigkeit der
Dunklen Energie
Vorhersage:
Die Expansion
des Universums
beschleunigt sich heute !
wh < -1/3
Kritische Dichte
 ρc
=3 H² M²
Kritische Energiedichte des
Universums
( M : reduzierte Planck-Masse , M-2=8 π G ;
H : Hubble Parameter
)
 Ωb=ρb/ρc
Anteil der Baryonen an der (kritischen)
Energiedichte