PPT

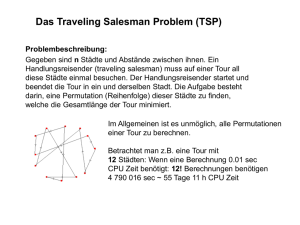
Ein kurzer Ausflug in die Welt
„harter“ Probleme... [der 2. Teil zur
ersten Vorlesung in GIN1B]
Prof. Dr. Wolfram Conen
21. Juni 2005
Vorlesung zu GIN2
Alan Turing – Mini-Rückblick auf die
erste GIN1b-Vorlesung




23. Juni 1912, London
1936: On computable
numbers ... (es gibt keine
„definite“ Methode, die für
jede mathematischlogische Aussage
entscheiden kann, ob sie
beweisbar ist oder nicht.)
1939-40: Entwicklung der
Bombe (zur Entschlüsselung
der deutschen EnigmaCodes)
7. Juni 1954: Selbstmord
Von der Intuition zur Exaktheit

Hilbert suchte nach einem Verfahren, das für jede mathematischlogische Aussage einen Beweis oder eine Widerlegung liefert:
„Das Entscheidungsproblem ist gelöst, wenn man ein Verfahren kennt, das
bei einem vorgelegten logischen Ausdruck durch endlich viele
Operationen die Entscheidung über die Allgemeingültigkeit bzw.
Erfüllbarkeit erlaubt. (...) Das Entscheidungsproblem muss als das
Hauptproblem der mathematischen Logik bezeichnet werden“,
Hilbert, Ackermann, Grundzüge der theoretischen Logik, 1928



Um zu zeigen, dass es so ein Verfahren gibt, könnte man einfach
eines angeben.
Turing wollte zeigen, das es ein solches Verfahren nicht geben
kann!
Er mußte etwas finden, dass Hilberts Intuition eines Verfahrens
entsprach, diese präzisierte und wesentliche Eigenschaften aller
anderen „möglichen“ Verfahren beinhaltete und so als „Prototyp“
dienen konnte:

Wenn der Prototyp die gewünschte Antwort nicht geben kann, dann kann es
auch kein anderes Verfahren!
Die Turing-Maschine:
Ein Modell der Berechenbarkeit
...
0
0
Zustand: z1
„Programm“
0
0
0
0
1
...
Falls Zustand == z1 und
Zeichen unter Schreib/Lesekopf == 0,
dann schreibe 1,
gehe in den Zustand z1 und
bewege dich ein Feld nach rechts.
Kurz: (z1,0)  (1,z1,R)
(z1,1)  (0,z1,R)
(z1,_)  (_,ende,L)
Was macht dieses Programm?
Die Turing-Maschine:
Eine Berechnung
...
1
0
0
Zustand: z1
„Programm“
0
0
0
1
(z1,0)  (1,z1,R)
(z1,1)  (0,z1,R)
(z1,_)  (_,ende,L)
...
Die Turing-Maschine:
Eine Berechnung
...
1
1
1
1
(z1,0)  (1,z1,R)
(z1,1)  (0,z1,R)
(z1,_)  (_,ende,L)
1
1 1
Zustand: z1
„Programm“
...
Die Turing-Maschine:
Eine Berechnung
...
1
1
1
1
1
(z1,0)  (1,z1,R)
(z1,1)  (0,z1,R)
(z1,_)  (_,ende,L)
1
0
0
Zustand: z1
„Programm“
...
Die Turing-Maschine:
Eine Berechnung
...
1
1
1
1
(z1,0)  (1,z1,R)
(z1,1)  (0,z1,R)
(z1,_)  (_,ende,L)
1
1 0
...
Zustand: ende
„Programm“
Die Berechnung hält an!
Noch wichtig: Programm, Eingabe und Zeichensatz sind endlich.
Universelle TM (1)

Turing führt eine Turing-Maschine UTM ein, die
andere Turingmaschinen simulieren kann

Bisher:


Jetzt:



Eingabestring x ! Turingmaschine TM ! Ausgabestring y;
kurz: TM(x) = y
Kodieren des Anweisungen der Turingmaschine als String z
Eingabestring zx ! Turingmaschine UTM simuliert TM und
wendet die Simulation auf x an ! Ausgabe y;
kurz also: UTM(zx) = y bzw. UTM(TM,x) = y
Die UTM von Turing kann alle Turingmaschinen
simulieren...sie ist in einem bestimmten Sinn
universell
Universelle TM (2)
Eine „binäre“ UTM von Stephen V. Gunhouse mit 176 Zuständen
B0.UTM=10000001011101000000010101101000000100101101000010101101000001000101101010011101000001010101110100001110100001001
0101110100100110100001010010110101000110100010001010110101010011101001010101001011101000001110100000000011101000000101011
0100000100101101001000110100010101001011010010001000110100101010001110101000011101001010010010111010010001001011010100010
1001110100100000011101010100101110100100101001110101010101011101000000111010010101010101110100001001101000110100010100001
1010000010111010100101000101110100010101011101001000011010101001010010110101001011010010010101101010001010110100101001011
1010101000010011101001010101011101000101010011101010000101101010010001101010001010110100010000101110101001011010010010011
0101001010101101001001000101110101010001011101010101000110101010010101101001000101101010101001011001110100010010111010010
0000111010001000101110100100011010000010101101001001001001110100001001011010010011010000101010110101001001011101001101000
0000111010001001010110100100010101110100010100101110101001000101110100100001011101001010001010111010100100010111010010010
0101110100101000101110100100100011101001010000111010001000110100101001001110100100010011101000011101001010011101010010011
1010010100111010010101011101000000111010100010001011101010001010010111010100000101110100100000111010100001010110100010011
0101000100101110101001001110101001010111010010101001010111010100010010101110101010100010111010100100101011101000010101101
0101000101011001110101010101010010110100010101101010100001011101010100100101101010000001110100010000011101000100011101000
0111010101010010101110101000001001110100101000001110100001110101010010111010010000010111010000000011010010011010000101010
1011010100000010110100001010101101000100110100001000011010001010110100000100110101001110100000010101011101001011010000100
0101101000011101010100101010111010010011010101010101010110100100110100010010101101001001010111010101011101010001101010100
0101010110101000010010110101010010111010000000111010001010010101101001000010011101000101000101101000000011101000101001011
1010010001101000101010101011010010001101001000101010110100010000110101010101000111010101010100100111010010000100111010000
0010011010000010001101001000110100001001011010001010111010100100100111010100000111010111010101010101010101101001001010101
0110101000010011010001010011101010101000011101010101010000111010000100101110101000101110101000011101001010010101011101010
0001110100101010001011101010000111010100010010111010001000101110101010101110101010011101001010101010101110101010011101010
0001010101110100000000110100000001011010100001000110101000000011010001001000110100010010010110101010011101010100001011101
0000001110101001000010111010100000011101010010010101011101000110101000101010101110100011010100100010101110100000011101010
1000001011101000110101001001001011101000110101010101011101000101001110101001110100110101001010010101110100110101001010100
1011101001101010010101010101110100110100101010101110100101000111010010011010001001011010101000100101110101010010011010100
1010011010100011010101001000101101010001101010100100101011010000101110101001010101011010010000110101010010101010110100100
0011010101010000101101001000011010000000001110100001011101010101001001011101000010111010101010010101011101000010111010010
0100010111010100000101011101001010000101110110111001110101000010110011101010101010101101000010111010101010001010111010000
0101011010101101000100101010110100100101001011010100111010000010010101110100001010110101001010010110101001110100000101001
0111010101000101110100001
Was kann die Turing-Maschine?
„Alles Machbare!“
Genauer formuliert dies die Church-Turing-These:
„Genau das, was wir intuitiv für „effektiv berechenbar“ halten, kann
durch die Turing-Maschine tatsächlich berechnet werden.“
Wir nennen ab jetzt etwas berechenbar, wenn es eine Turingmaschine gibt
(geben kann), die mit dem richtigen Ergebnis anhält!
Es wurden noch viele andere Modelle der Berechenbarkeit „erfunden“
(generelle rekursive Funktionen, -Definierbarkeit, Kombinatorische
Systeme, Termersetzungssysteme, Registermaschinen, ...),


aber alle (zumindest alle physikalisch realisierbaren) erwiesen sich als
„äquivalent“, sie können die gleichen Probleme lösen!
Zeigen kann man dies, in dem man ein Modell durch ein anderes simuliert
(und vice versa).
Merke: Modelle der Berechenbarkeit präzisieren den Begriff Algorithmus /
Lösungsverfahren (F1)
Noch ein Beispiel...fleissige Bieber


Bieber bauen Dämme aus Baumstämmen...
Als Turingmaschine sieht das z.B. so aus:
_/1,R
1/1,R
z1
z2
z3
1/1,R
_/1,L
_/1,L
1/1,L
_
Satz:
halt
_
1
_
1
_
1
_
1
_
1
_
1
_
_
_
_
Die Rado-Funktion kann nicht durch eine Turing-Maschine berechnet werden
Luftholen... [Ende des Rückblicks]

Wahre Titanen des Geistes (auch, wenn manche von Ihnen
ein unglückliches Ende gefunden haben...) legten die
Grundlagen.

Wir wissen jetzt: es gibt Probleme, die sich nicht lösen
lassen, obwohl sie „mathematisch genau“ beschrieben sind!

Modelle der Berechenbarkeit erlauben eine Analyse der
Berechenbarkeit/Lösbarkeit eines Problems! (F2)

Aber: wie schwer kann es werden, ein konkretes Problem
tatsächlich zu lösen?
Komplexität


Gegeben: ein berechenbares
Problem P und ein bestimmtes
Modell der Berechenbarkeit (z.B.
Turing-Maschinen oder RAMs)
Zentrale Frage: Erfordert die
Lösung des Problems einen Zeit
oder Speicheraufwand, der
polynomial oder
(möglicherweise) exponentiell
zur Größe der Eingabe ist?
Zur Größenordnung:
Annahme: Jede Operation benötigt eine
Mikrosekunde
Eingabegröße
n = 10 =100 =1000 =1000000
Zeitaufwand als Funktion von n:
n
10us 0.1ms 1ms 1s
n2 0.1ms 10ms 1s
2W
n5 0.1s 3h
30J 3*1016J
2n
1ms 3*1016 J 3*10288J groß
• 3*1016 J ist übrigens mehr als eine
Millionen mal die geschätzte
bisherige Dauer des Universums...
TSP - Traveling Salesman Problem

Gegeben ist eine Menge von „Städten“, so dass jede von jeder
direkt erreichbar ist (z.B. per Hubschrauber ;-)

Mit den Reisen sind Kosten verbunden (wir nehmen mal an, dass
die Dreiecksungleichung erfüllt ist, d.h. kein „Umweg“ ist kürzer, als
die direkte Verbindung)

Gesucht ist eine Rundtour durch alle Städte, die minimale Kosten
über alle möglichen Rundtouren hat (jede Stadt wird nur einmal
besucht)

Das ist das „metrische“ TSP
TSP
TSP
TSP




Wir können das TSP als
Graphproblem auffassen
n Knoten (die Städte), n*n-1
ungerichtete Kanten (die
Wege)
Der Graph ist also
vollständig (er kann natürlich
auch unvollständig sein...)
Wenn Hin- und Rückfahrt
zwischen je zwei Städten
gleich teuer sind, dann ist es
ein symmetrisches TSP

Naiver Lösungsalgo:


Suche zufällig einen
Startpunkt aus
Generiere nach und nach alle
möglichen Rundtouren



Vergleiche die Länge jeder
Rundtour mit der Länge der
bisher besten
Merke dir ggfs. die neue
„beste“ Tour
Aufwand?


n-1*...*2*1 = (n-1)!
im symmetrischen Fall (n-1)!/2
TSP

Für ein symmetrisches TSP gibt es also eine Menge
Lösungskandidaten:




n = 5:
n = 10:
n = 20:
12 Touren
181.440 Touren
60.822.550.204.416.000 Touren
(~ 61 Billiarden Touren)
Das heißt: Die Anzahl von Lösungskandidaten explodiert
exponentiell mit steigendem n
TSP

Das geht natürlich besser!

Aber wenn wir wirklich das Optimum haben wollen, dann erfordert
jedes exakte Lösungsverfahren im worst case exponentiellen
Aufwand
 es sei denn, NP = P (was das ist, sehen wir gleich)

Man kann metrische TSPs aber zu polynomialen Kosten
approximieren (wie gut?)
Approximationen metrischer TSPs

Jetzt kommt unser alter MST zu Ehren:

Gegeben: 8 Knoten, vollständiger, ungerichteter Graph
v
MST
„Doppelter“ MST: jede
Rundtour mit
Kante wird verdoppelt und die
„Abkürzungen“
Kanten eines jeden Paares werden
in gegensätzliche Richtungen orientiert
Approximationen metrischer TSPs

Algo APP_TSP




Bestimme einen MST T
Wähle zufällig einen Knoten
v und laufe komplett um den
Baum (=verdopple alle
Kanten und mache eine
Eulertour)
Vermerke dabei die Besuche
der Knoten in einer Liste L
Entferne alle bis auf das
jeweils erste Vorkommen der
Knoten, zurück bleibt der
Kreis C (oder kürze bei der
Tour gleich ab)
[C ist ein Preorder-Traversal
von T]

Kosten für Prim:
O(m + n log n) = O(n2) für
kompletten Graph
O(1) (Auswahl)
O(n) (n-1 Kanten * 2)

O(n) Speicher

O(n)

Dominiert von MST-Kosten,
insgesamt O(n2)


Approximationen metrischer TSPs

Satz: C ist eine 2-Approximation der kürzesten Tour (Beweis gleich)

Aber: was ist eine 2-Approximation?

Gegeben ist ein Optimierungsproblem OPT mit der optimalen
Lösung C*

Gegeben ist außerdem ein Approximationsalgorithmus, der eine
Näherungslösung zu OPT bestimmt, seine Lösung hat den Wert C
Approximationen metrischer TSPs

C* = optimale Lösung, C = approximative Lösung

Approximationsfaktor für eine bestimmte Instanz bei einem
Minimierungsproblem: C/C*

Approximationsfaktor des Algorithmus:
p = sup C/C*
Hier wird das Supremum (also die Schranke nach oben) über alle
Instanzen bestimmt (also eine Schranke für die schlechteste
Approximation, die der Algo liefert)

p ist hier immer größer als 1 (klar, C kann ja nicht besser als C*
sein)
Approximationen metrischer TSPs

Relativer Fehler  des Approximationsalgorithmus:
 = sup |C-C*|/C*

Für Minimierungsprobleme äquivalent zu
C · (1 + ) C*, d.h. p · (1 + )

Approximationsschema:
 Eingabe: eine Probleminstanz I und ein  > 0

Ausgabe: eine (1+)-Approximation des Optimums (für
Minimierungsprobleme)

D.h. einem Approximationschema können sie sagen, welche
Qualität es liefern soll! (sie geben also den maximal erlaubten
relativen Fehler  vor)
Approximationen metrischer TSPs

2-Approximation:  = 1,



d.h der relative Fehler ist schlechtestenfalls 1, der
Approximationsfaktor also nicht schlechter als (1+)=2,
d.h. C ist höchsten doppelt so teuer, wie C*
Zurück zum Satz, dass APP_TSP eine 2-Approximation
liefert (zur Erinnerung: T ist unser MST, C unser Kreis)




Wenn man aus der optimalen Tour eine Kante entfernt, hat
meinen einen Spannbaum, d.h. C* ¸ Cost(T)
In L wird jede Kante aus T zweimal aufgenommen, also
Cost(L) = 2*Cost(T)
C entsteht aus L durch Hinzufügen von Abkürzungen. Weil die
Dreiecksungleichung gilt, kann C nicht länger als L sein, also
C · Cost(L)
Insgesamt also: Cost(T) · C* · C · Cost(L) = 2*Cost(T)
Approximationen metrischer TSPs

Christofides hat 1976 einen verbesserten polynomiales 3/2Approximations-algorithmus gefunden (mittels MST und minimum
weight matching)

Engebretsen hat 1999 gezeigt, dass kein Approximationsfaktor
5381/5380 -  für  > 0 möglich ist

Spannend wird es, wenn man gute polynomiale
Approximationsschemata (AS) findet:
 PTAS sind AS, deren Laufzeit polynomial zu n bei gegebenem  ist
(PT = polynomial time)
 FPTAS sind AS, deren Laufzeit polynomial zu n und 1/ (FPT = fully
polynomial time)
 O(n1/), O(n/): Beides PTAS, nur das zweite FPTAS
Approximationen metrischer TSPs





Mit einem solchen Schema können sie in der Praxis wie folgt arbeiten:
Sie haben 2 Wochen Zeit, bis sie ein möglichst gute Lösung brauchen:
 sie bestimmen mit der Abschätzung  und lassen das PTAS loslaufen,
 nach ungefähr 2 Wochen wird es in der entsprechenden Güte antworten –

dann brauchen sie aber natürlich eine Abschätzung, in der auch die
Konstanten enthalten sind und sie müssen wissen, wie lang elementare
Operation (im Mittel) wirklich brauchen.
Sie können also den Trade-Off zwischen Aufwand und Güte bewusst steuern
– was will man mehr!
 (wenn dann die zur Verfügung stehende Zeit auch noch für „gute“
Lösungen reicht, dann haben sie wirklich Glück ;-)
Für euklidische TSP (=metrisch und in der Ebene, also ohne Berg-auf, Bergab) hat Arora 1996 ein gutes PTAS gefunden (und ist damit berühmt
geworden)!
Uneingeschränktes TSP ist in der Klasse der schwierigsten
Optimierungsprobleme (NPO-complete), d.h. es gibt keine 2n^-Approximation
für kleine  (Orponen, Mannila, 1987)
Wie schwer ist TSP „wirklich“?

TSP lässt sich mit einer nicht-deterministischen Turingmaschine, die
den richtigen Abarbeitungsweg „raten“ kann, in polynomialer Zeit
lösen
 Man sagt: TSP ist in der Komplexitätsklasse NP

Es ist aber keine deterministische Turingmaschine bekannt, die alle
TSPs in polynomialer Laufzeit lösen könnte
 Sonst wäre TSP in der Komplexitätsklasse P. Zu Problemen in P
(z.B. Kürzeste-Wege-mit-nicht-negativen-Kanten) sagt man auch:
Problem dieser Problemklasse sind effizient lösbar!

Offene Frage: Ist P=NP?
TSP und Komplexität




TSP gehört zu den „schwersten“ Problemen in NP: wenn man
dieses polynomiell lösen könnte, dann ginge das auch mit allen
anderen Problemen aus NP!
 TSP ist deshalb ein NP-vollständiges Problem
Als erstes NP-vollständiges Problem wurde 1971 von Cook das
SAT-Problem identifiziert: Erfüllbarkeit von aussagenlogischen
Formeln! (kennen sie aus GIN1b) – alle anderen Probleme in NP
lassen sich auf dieses Problem „reduzieren“.
Es gibt noch viele andere NP-harte Problem: Matching-Probleme
(„Stabile Heirat“), Graph-Färbe-Probleme, div.
Scheduling/Planungsprobleme (Stundenplan! ;-), ganzzahlige
Programmierung, usw. – einen Überblick finden sie auch im Web:
Es gibt auch noch sogenannte NP-harte-Probleme, diese sind
„mindestens so schwer, wie Probleme aus NP“ und ihre Lösung
würde zur Lösung aller Probleme aus NP führen (alle NP-Probleme
lassen sich auf sie reduzieren), aber es ist nicht sicher, ob sie
wirklich in NP liegen (oder aber in EXP, also sicher exponentiellen
Aufwand erfordern, auch im nichteterministischen Fall!)
Mögliche Auswege für den
Informatiker (1)

Nicht alle Probleminstanzen sind schwer!
Vielleicht gehören „unsere“ Probleminstanzen dazu?
 manchmal kann man das generell sagen (wenn das
Problem nicht „stark NP-schwer“ ist), manchmal helfen
Experimente!

manchmal findet man auch „langsam wachsende“
exponentielle Algorithmen
Mögliche Auswege für den
Informatiker (2)

Alternativ kann man vielleicht approximieren!

Man sucht nach polynomialen Algorithmen, die eine
bestimmte Güte der Lösung garantieren können (etwa immer
mindestens halb so gut wie das Optimum)

Manche Probleme lassen sich nicht sinnvoll approximieren,
auch das kann man formal untersuchen!
Mögliche Auswege für den
Informatiker (3)

Oder man wendet eine Heuristik an, die versucht mit
Daumenregeln oder beispielsweise in Anlehnung an natürliche
Prozesse „schnell“ „gute“ Lösungen zu finden

Das kann natürlich grandios schief gehen!
Auch hier kann man einiges analysieren!
Bei allem hilft die Theorie zu Komplexität und Approximierbarkeit,
die aus den Modellen zur Berechenbarkeit hervorgegangen ist:




Die Analysen von Komplexität und Approximierbarkeit stecken den
Rahmen für die erreichbare Lösungsqualität ab! (F3)
Sie weisen den Weg zu verwandten Problemen und bereits
bekannten exakten, approximativen oder heuristischen
Problemlösungen! (F4)
Rückblick: Bedeutung für den
Informatiker
Zentrale Aufgaben: Problemanalyse und Problemlösung.
(F1) Wie lassen sich mein Problem und eine ev.
Lösung präzise beschreiben?

Präzision ist eine wesentlich Voraussetzung für Analyse und
Lösung von Problemen (Übergang zur Logik)

Modelle der Berechenbarkeit präzisieren den Begriff
Algorithmus/Lösungsvorschrift
(F2) Ist das Problem überhaupt lösbar?

Modelle der Berechenbarkeit erlauben eine Analyse der
Berechenbarkeit/Lösbarkeit eines Problems!
Rückblick: Bedeutung für die
Anwendungsentwicklung (2)
(F3) Wenn ja, kann ich es auch mit vertretbarem
Aufwand lösen?


Die Komplexitätstheorie hilft uns, die Schwere des Problems
einzuschätzen!
Die Analysen von Komplexität und Approximierbarkeit stecken den
Rahmen für die erreichbare Lösungsqualität ab!
(F4) Wie kann ich das Problem lösen?
 Die Komplexitätstheorie hilft auch, verwandte Probleme zu
identifizieren!
 Die Analysen von Komplexität und Approximierbarkeit weisen den
Weg zu verwandten Problemen und bereits bekannten exakten,
approximativen oder heuristischen Problemlösungen! (Übergang
zur Algorithmik)
Rückblick: Bedeutung für die
Anwendungsentwicklung


Zentrale Aufgaben: Problemanalyse und Problemlösung
Was genau ist mein Problem? Ist das Problem überhaupt lösbar?




Historische Bedeutung: Entwicklung von Formalismen zur Beschreibung von
Problemen und Lösungseigenschaften.
Entwicklung der Modelle der Berechenbarkeit zur Präzisierung des
Algorithmusbegriffe und zur Untersuchung der Lösbarkeit von Problemen
Speziell die Turingmachine hat die Entwicklung von „mechanischen“
Computern und Programmiersprachen beeinflußt und Intuitives mit Formalem
verbunden!
Wenn ja, kann ich es auch mit vertretbarem Aufwand lösen?



Turingmachine diente als Grundlage zur Entwicklung der Komplexitätstheorie –
wie lange braucht eine deterministische bzw. eine nicht-deterministische
Turingmachine für diese Problem?
Komplexität und Approximierbarkeit sind wesentliche Problemeigenschaften –
nach welchem Typ von Algorithmus soll ich suchen (exakte Lösung,
approximative Lösung, heuristische Lösung)
Die moderne Algorithmik ist eng mit der Forschung zu Komplexität und
Approximierbarkeit verbunden - ganz wichtig für den Anwendungsentwickler:
Problemlösen durch Nachschlagen!