K12 I - 1. Klausur - Hans-Carossa

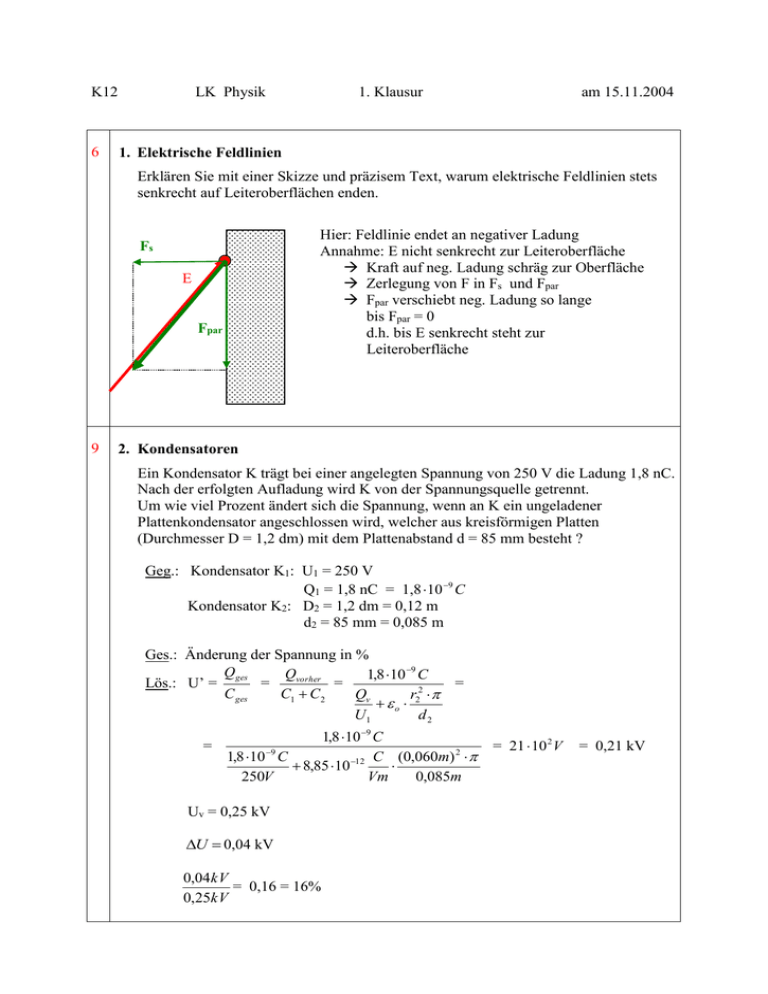
K12
6
LK Physik
1. Klausur
am 15.11.2004
1. Elektrische Feldlinien
Erklären Sie mit einer Skizze und präzisem Text, warum elektrische Feldlinien stets
senkrecht auf Leiteroberflächen enden.
Hier: Feldlinie endet an negativer Ladung
Annahme: E nicht senkrecht zur Leiteroberfläche
 Kraft auf neg. Ladung schräg zur Oberfläche
 Zerlegung von F in Fs und Fpar
 Fpar verschiebt neg. Ladung so lange
bis Fpar = 0
d.h. bis E senkrecht steht zur
Leiteroberfläche
Fs
E
Fpar
9
2. Kondensatoren
Ein Kondensator K trägt bei einer angelegten Spannung von 250 V die Ladung 1,8 nC.
Nach der erfolgten Aufladung wird K von der Spannungsquelle getrennt.
Um wie viel Prozent ändert sich die Spannung, wenn an K ein ungeladener
Plattenkondensator angeschlossen wird, welcher aus kreisförmigen Platten
(Durchmesser D = 1,2 dm) mit dem Plattenabstand d = 85 mm besteht ?
Geg.: Kondensator K1: U1 = 250 V
Q1 = 1,8 nC = 1,8 10 9 C
Kondensator K2: D2 = 1,2 dm = 0,12 m
d2 = 85 mm = 0,085 m
Ges.: Änderung der Spannung in %
Qges
Qvorher
1,8 10 9 C
Lös.: U’ =
=
=
=
C ges
C1  C 2
Qv
r22  
 o 
U1
d2
=
1,8 10 9 C
1,8 10 9 C
(0,060m) 2  
12 C
 8,85 10

250V
Vm
0,085m
Uv = 0,25 kV
U  0,04 kV
0,04kV
= 0,16 = 16%
0,25kV
= 21  10 2 V
= 0,21 kV
2
3. Pendelchen im radialsymmetrischen Feld
Eine isoliert aufgestellte Metallkugel M mit dem
Radius r = 5,0 cm trägt die negative
Radius r = 5,0 cm trägt die negative Ladung Q.
Ladung Q.
Der Betrag der Feldstärke des von Q im Abstand
Der Betrag des von Q im Abstand r
r erzeugten elektrischen Feldes ist gegeben
erzeugten elektrischen Feldes ist gegeben
Q
1
durch:
E(r) = Q  1 2 .
durch: E(r) = 4 o  r2 .
4 o r
Es gelte:   = 0

M
K
r
In der Nähe von M befindet sich eine an einem 1,0 m langen Faden isoliert
aufgehängte Kugel K mit der Masse m = 0,50 g und der negativen
M Ladung
9
q = - 5,0  10 C . In der Gleichgewichtslage befinden sich die beiden Kugelmittelpunkte auf gleicher Höhe.
K
Bei r = 12 cm liegt ein Auslenkwinkel von  = 10 o vor.
Geg.: M:
r = 5,0 cm
Q
Q
1
 = 0
 2
E(r) =
;
4 o r
K:
l = 1,0 m
m = 0,50 g = 0,50 10 3 kg
q = - 5,0  10 9 C .
Bei r = 12 cm gilt:  = 10 o
3
s
a) Führen Sie einen anschaulich plausiblen Grund dafür an, dass die elektrische
Feldstärke E(r) in einem Feldpunkt eines radial symmetrischen Feldes indirekt
proportional zum Quadrat (!) des Abstandes r des Feldpunktes zur
felderzeugenden Ladung ist.
Begr.: Die Feldlinien durchsetzen Kugelschalen
Mit größerem r nimmt die Oberfläche der durchsetzten Kugelschale
mit r2 zu, denn OKugel = 4  r2
Die Dichte der Feldlinien nimmt also mit r2 ab.
Da man die Dichte der Feldlinien als Maß für die Feldstärke auffassen
kann, ist es plausibel, dass mit zunehmendem r die Feldstärke mit r2
abnimmt.
3
6
b) Berechnen Sie den Betrag der elektrischen Feldstärke, die von der Ladung Q
V
am Ort des Mittelpunkts von K erzeugt wird. (ZWERG: 1,7  10 5 )
m
Fel
qE
=
FG
mg
tan  =
Lös.:
 E
mg
 tan 
q
=
0,50 10 3 kg  9,81
=
5,0 10 9 C
= 1,7 10 5
3
N
kg
 tan(10 o )
N
C
c) Berechnen Sie die Zahl der Überschusselektronen auf M.
E(r) =
Q
4 o

1
r2
E(r)  4o r 2 = 1,7 10 5
 Q=
N
C
 4  8,85 10 12
 (0,12m) 2
C
Vm
= 2,7 10 7 C
Q = N e 
N=
Q
2,7 10 7 C
=
= 1,7 1012
e
1,60 10 19 C
Oder : Q = 2,7 10 7 C = 2,7 10 7  6,25 1018 e = 1,7 1012 e
Also 1,7 1012 Überschusselektronen
4
d) Berechnen Sie die mechanische Höhenenergie von K bezüglich der Ruhelage von
K im unausgelenkten Zustand.
ccos 10o =
x
l
hh = 2,0 cm
x
l
;  x = l  cos10 o = 1,0m  cos 10 o = 0,984 m
bzw.
N
 0,02 m = 9,8 10 5 J
kg
N
kg  9,81  0,016 m = 7,8 10 5 J
kg
E = mgh = 0,50 10 3 kg  9,81
bzw. = 0,50 10 3
h
1,6 cm
4
4. Zylindersymmetrisches Feld
ro
Ein l = 3,0 m langer Leiter mit kreisförmigem
Querschnitt (Radius ro = 2,5 mm) ist mit einer Ladung
von Q = + 6,0  10 9 C aufgeladen.
r
Der Betrag des von Q im Abstand r erzeugten
elektrischen Feldes ist gegeben durch:
Q
1
 .
E(r) =
2 o l r
Die Vektoren der elektrischen Feldstärke liegen in
Ebenen senkrecht zum Leiter.
l
Betrachtet werden sollen Raumpunkte in einer Ebene
senkrecht zum Leiter. Im Nullpunkt des
Koordinatensystems durchstößt der Leiter die Ebene.
y
x
Festgelegt seien: Der Nullpunkt der potentielle Energie
einer positiven Probeladung befinde sich auf der
Oberfläche des Drahtes. Potential  (ro ) = 0 .
8
a) Berechnen Sie, welche („äußere“) Arbeit verrichtet werden muss, um eine
Probeladung q = + 5,0 nC von A( 0 / - 12,0 cm ) nach B ( 5,0 cm / 0 ) zu überführen.
Sei C ( 12,0 cm / 0 )
Wäußere, AB = Wäußere, AC + Wäußere, CB = Wäußere, CB =
B
=
F
äußere
B
B
 dr
=
C
 F (r )  cos dr =  F (r )
C
5, 0 cm
 F (r )
= 
12, 0 cm
C
5, 0 cm
dr = 
 q  E (r )
dr =
12, 0 cm
5, 0 cm

= 
q
12, 0 cm
Q
1
 dr
2    o  l r
5, 0 cm
=


12, 0 cm
5, 0 cm
Q
1
q
 
dr
2     o  l 12, 0cm r
=
-
=
- q
dr
=
- q
q
Q
1
 dr
2     o  l r
5, 0 cm
Q
 ln( r ) 12,0cm
2    o  l
Q
 [ln(5,0cm) – ln(12,0cm)] =
2    o  l
=
5
=
4
=
6,0  10 9 C
 5,0 
- 5,0  10 C 
=
 ln
C
12,0 
2    8,85  10 12
 3,0m 
Vm
7
- 1,798  10 CV  (0,87) = 1,6  10 7 CV = 1,6  10 7 J
9
b) Begründen Sie ohne explizite Berechnung: Für alle Punkte P, deren Abstand r vom
Mittelpunkt des Drahtes größer als ro ist, gilt hier:  (r ) < 0 .
 (ro ) = 0 und r > ro 
E pot,rr
Wäußere,r r
 (r ) =  r -  o =  rr =
=
< 0 , denn:
q
q
Begr.: z.B.:
Es ist
o
0
o
Q > 0 , denkt man sich q > 0 , so ist
Wäußere ,r r < 0 ,
Q > 0 , denkt man sich q < 0 , so ist
Wäußere ,r r > 0
Oder:
o
o
„Das Potential wird in Richtung der Feldlinien immer kleiner.“
Oder:
„Wenn der Nullpunkt des Potentials im Unendlichen liegt wird das Potential immer
größer, je mehr man sich der positiven felderzeugenden Ladung annähert.
Wenn aber bei einer positiven felderzeugenden Ladung das Nullpotential auf der
Ladung selbst gelegt wird, dann muss konsequenterweise das Potential sinken, je
weiter man sich von dieser Ladung entfernt: D.h. Das Potential in der Umgebung
dieser Ladung muss dann negativ sein. Bei einer positiven felderzeugenden Ladung
ist das Potential immer positiv, wenn der Nullpunkt des Potentials im Unendlichen
liegt.
Oder:
Da  rro =
11
E pot,rro
ist und sich eine positive Probeladung q vom positiven Draht
q
abstößt verliert q potentielle Energie wenn sie sich vom Draht entfernt.
Nach Festlegung ist das Potential auf dem draht Null, also muss es für jedes r > ro
negativ sein.
c) Leiten Sie die Funktion  (r ) für alle Punkte P her, deren Abstand vom Mittelpunkt
des Leiters r (wobei r > ro) beträgt und berechnen Sie das elektrische Potential im
Punkt P ( 4,0 cm / 3,0 cm ) .
 (r ) =  r =  r -  r =  rr =
o
E pot,rro
o
q
= ...
oder:
Po
 (r ) =  r =  r -  r =  rr
o
o
=
 E (r )dr
P
ro
=   E (r )  (1) dr
r
6
ro
ro
r
o
1
1
Q
Q
 dr =
  dr =
=  E ( r ) dr = 
 ln( r) rro =
2o l r
2 o l r r
2 o l
r
r
r
r
Q
Q
 ln( o ) = 
=
 ln( )
r
2o l
2 o l
ro
Q
P ( 4,0 cm / 3,0 cm )  r = 5,0 cm
r
Q
 (r ) = 
 ln( ) = 
2o l
ro
6,0 10 9 C
50mm
 ln(
)=
2
,
5
mm
12 C
2  8,85 10
3,0m
Vm
= 107,8 V = 0,11 kV
= - 36 V  3,0
6
d) Der knoff-hoff-Professor schlägt vor, genauso wie bei einem radialsymmetrischen
Feld den Nullpunkt des Potentials „ins Unendliche“, „auf den unendlich fernen
Punkt“ zu verlegen.
Was halten Sie von diesem Vorschlag ? Geben Sie Ihre Stellungnahme dazu ab und
begründen Sie diese mit einer mathematisch-physikalischen Argumentation.
 (r )
= 
Q
 ln(
r
)
2o l
ro
Würde man den Nullpunkt des Potentials ins Unendliche legen, dann wäre ro =  ,
dann stünde  unter dem ln.  Man bekäme ein mathematisches Problem.