12 Binärbäume

12
Binärbäume
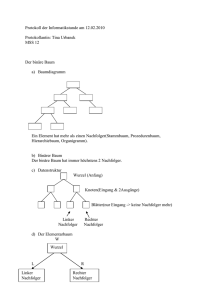
12.1 Grundlagen - Denitionen
Denition:
Ein
Baum
ist eine Menge, die durch eine sog. Nachfolgerrelation
strukturiert ist.
In einem Baum gilt:
1
(I)
∃
Knoten
w
ohne VATER(w ), das ist die Wurzel
1
(II)
∀ Knoten k 6= w ∃ Knotenfolge k0 , k1 , . . . , kt mit k0 = k , kt = w
ki =VATER(ki−1 ) für i = 1, 2, ..., t (Ast zwischen k und w, Länge t)
und
Ein Binärbaum ist ein spezieller Baum, in dem jeder Knoten maximal zwei
Söhne besitzt.
12.2 Nötige Funktionen
Ausgehend von einem Pointer
k auf einen beliebigen Knoten sind folgende FunkB implementiert werden kann:
tionen nötig, damit ein Binärbaum
•
LINKS(k): zeigt auf den linken Sohn des
•
RECHTS(k): zeigt auf den rechten Sohn des
•
VATER(k): zeigt auf den Vaterknoten des
•
WERT(k): liefert den Wert des Knotens
•
WURZEL(B): zeigt auf die Wurzel des Baumes
k -ten
k
Knotens
k -ten
k -ten
Knotens
Knotens
zurück
Anmerkung: Falls keine Sohnknoten oder Vaterknoten existieren wird nil zurückgeliefert.
1
12.3 Reihenfolge der Knoten
Die Knoten können in verschiedener Art und Weise eingefügt bzw. ausgelesen
werden.
12.3.1 Symmetrische Reihenfolge (SR)
Die Knoten werden in folgender Reihenfolge ausgelesen: Linker Teilbaum rekursiv in SR, Wurzel, rechter Teilbaum rekursiv in SR. Arithmetische Ausdrücke
werden als
SR(k)
1: IF
2:
3:
4:
Inx -Notation ausgelesen.
k6=nil THEN
SR(LINKS(k))
SCHREIBE k
SR (RECHTS(k))
12.3.2 Haupreihenfolge (HR)
Analog die Auslesefolge: Wurzel, linker Teilbaum rekursiv in HR und rechter
Teilbaum rekursiv in HR.
12.3.3 Nebenreihenfolge (NR)
Analog die Auslesefolge: linker Teilbaum rekursiv in NR, rechter Teilbaum rekursiv in NR und die Wurzel. Arithmetische Ausdrücke werden als
Postx -
Notation ausgelesen.
12.4 Sortierte Binärbäume
Im weiteren Abschnitt wird die SR verwendet. Der Binärbaum ist eine sehr
mächtige Datenstruktur, mit der viele Funktionen eektiv implementiert werden
SUCHEN, EINFÜGEN, LÖSCHEN, MINIMUM, MAXIMUM, VORGÄNGER, NACHFOLGER.
können:
Alle Funktionen können in
O(Höhe
des Baumes) implementiert werden.
Vorteil: Es kann das Wörterbuchproblem dynamisch gelöst werden
Nachteil: Laufzeiten bis
Θ(n)
12.4.1 Suchen in Binärbäumen
Suche den Wert
CHE
w
im Binärbaum
B.
Der rekursive Algorithmus wird mit
(b,Wurzel) gestartet.
2
SU-
SUCHE(w,k)
1: IF k=nil OR w=WERT(k)THEN
2:
RETURN k
3: ELSE
4:
IF w<WERT(k) THEN
5:
SUCHE(w,LINKS(k))
6:
ELSE
7:
SUCHE(w,RECHTS(k))
12.4.2 Finden des Maximus in einen Binärbaum
Liefert den gröÿten Wert des Binärbaumes zurück. Der Algorithmus wird mit
Baum_Maximum(Wurzel(B))
aufgerufen.
BAUM_MAXIMUM(k)
1: WHILE RECHTS(k)6=nil
2:
k=RECHTS(k)
3: RETURN WERT(k)
12.4.3 Finden des Minimums in einen Binärbaum
Liefert den kleinsten Wert des Binärbaumes zurück. Der Algorithmus wird mit
Baum_Minimum(Wurzel(B))
aufgerufen.
BAUM_MINIMUM(k)
1: WHILE LINKS(k)6=nil
2:
k←LINKS(k)
3: RETURN WERT(k)
12.4.4 Finden des Vorgängers eines Knotens
Es wird der nächstkleinere Wert zum
WERT(k)
VORGÄNGER(k)
1: IF LINKS(k)6=nil
2:
RETURN BAUM_MAXIMUM(LINKS(k))
3: y←VATER(k)
4: WHILE y6=nil AND k=LINKS(y)
5:
k←y
6:
y←VATER(y)
7: RETURN(WERT(y))
3
gefunden.
12.4.5 Finden des Nachfolger eines Knotens
Es wird der nächsthöhere Wert zum
WERT(k)
gefunden.
NACHFOLGER(k)
1: IF RECHTS(k)6=nil
2:
RETURN BAUM_MINIMUM(RECHTS(k))
3: y=VATER(k)
4: WHILE y6=nil AND k=RECHTS(y)
5:
k=y
6:
y=VATER(y)
7: RETURN(WERT(y))
12.4.6 Einfügen in den Binärbaum
In den Binärbaum
B
wird der Wert
w
eingefügt.
EINFÜGEN(B,w)
1: y←nil
2: x←WURZEL(B)
3: WHILE x6=nil
4:
DO y ← x
5:
IF w<WERT(x) THEN
6:
x←LINKS(x)
7:
ELSE x←RECHTS(x)
8: VATER[w]←y
9: IF y=nil
10:
THEN WURZEL(B)←w
11: ELSE IF w<WERT(y)
12:
THEN LINKS(y)←w
13: ELSE RECHTS(y)←w
12.4.7 Löschen eines Werts
Der Knoten
k
soll gelöscht werden. Dabei müssen drei Fälle unterschieden wer-
den, da die Sortierung in SR erhalten bleiben muss:
1.
k
ist ein Blatt: einfach entfernen
2.
k
hat nur einen Sohn: Den Sohn von
k
3.
k
hat zwei Söhne: Finde den Knoten
k0
4
an den Vater von
k
anhängen
mit dem nächst gröÿten Wert
LÖSCHEN(k)
1: IF LINKS(k)=nil OR RECHTS(k)=nil
2:
THEN y←k
3:
ELSE y ← NACHFOLGER(k)
4: IF LINKS(y)6=nil
5:
THEN x←LINKS(y)
6:
ELSE x←RECHTS(y)
7: IF x6=nil
8:
THEN VATER(x)←VATER(y)
9: IF VATER(y)=nil
10:
THEN WURZEL(B)←x
11:
ELSE IF y = LINKS(VATER(y))
12:
THEN LINKS(VATER(y))←x
13:
ELSE RIGHT(VATER(y))←x
14: IF y6=k
15:
THEN WERT(k)←WERT(y)
16:
IF ('andere Felder vorhanden, mitkopieren')
17: RETURN y
5