Vorlesung 2 - Physik (Uni Würzburg)

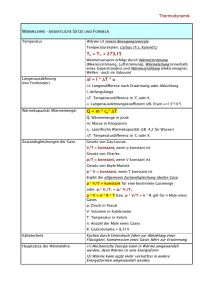
Einführung in die Physik I
Wärmelehre/Thermodynamik
Wintersemester 2007
Vladimir Dyakonov
#2 am 10.01.2007
Raum E143, Tel. 888-5875, eMail: [email protected]
10.2 Temperaturmessung
Wärmeausdehnung fester und flüssiger Stoffe*:
Ausdehnung von Festkörpern/Flüssigkeiten:
Wärmeausdehnung fester und flüssiger Stoffe bei T = 20 oC
Feste Stoffe α / 10-6 K-1
Flüssige Stoffe
Aluminium
23.8
Wasser
2.07 · 10-4
Eisen
12
Benzin
0.95 · 10-3
Kupfer
16.8
Benzol
1.06 · 10-3
Natrium
71
Quecksilber
1.8 · 10-4
Hartgummi
75-100
Glyzerin
5·
γ / K-1
10-4
Benzintank in der Sonne
1
10.2 Temperaturmessung
Versuch: Wärmeausdehnung eines Festkörpers:
10.2 Temperaturmessung
Versuch: Bimetallstreifen
2
10.2 Temperaturmessung
Wärmeausdehnung fester und flüssiger Stoffe:
•
Bimetallstreifen*: Metalle mit verschiedenen Längenausdehnungskoeffizienten, die
fest miteinander verbunden sind. Mit steigender Temperatur krümmt sich dieser
Bimetallstreifen in Richtung des Metalls mit dem kleineren Ausdehnungskoeffizienten.
Abkühlung
αZN > αFe
Zn
Fe
zum Relais
Erwärmung
•
Thermostat:
Biegung bei einer bestimmten Temperatur öffnet
oder schließt einen elektrischen Stromkreis
* „bi“ kommt vom Lateinischen „bis“ für doppelt
10.2 Temperaturmessung
Versuch: Thermoelement
3
10.2 Temperaturmessung
Thermoelement:
Austrittsarbeit WA=
(typ.: wenige eV)
Energie, die Elektronen zum Verlassen eines
Metalls benötigten (Materialspezifisch !)
Oberfläche
Metallionen
+
Elektronen
- Je größer die kinetische Energie der Elektronen,
desto mehr Elektronen können aus dem Metall austreten
- Kinetische Energie steigt mit der Temperatur !
(Glühemission!)
10.2 Temperaturmessung
Thermoelement:
• An einer Kontaktstelle werden zwei Metalle mit unterschiedlicher
Austrittsarbeit in Kontakt gebracht:
Elektronen aus dem Metall mit der geringeren Austrittsarbeit gehen in das
Metall mit der höheren Austrittsarbeit über. Dadurch gibt es im
Metall mit der höheren Austrittsarbeit einen Elektronenüberschuss und damit
einen Potentialunterschied zwischen den beiden Metallen
• Bei der Berührung unterschiedlicher Metalle (mit unterschiedlichen
Austrittsarbeiten WA der Elektronen) entsteht eine elektrische
Spannungsdifferenz: „Kontaktspannung“ = temperaturabhängig !
UKontakt ~ T
+
+
+
Me I
Me II
+
-
UKontakt = E ·T
E -Thermokraft
WA1 < WA2
Typ. Paarungen z.B. Kupfer-Konstantan
E = 0.06 mV/K
4
10.2 Temperaturmessung
Gasthermometer (Eichthermometer):
Beobachtung:
(1) Bei konstanten Druck p steigt das Volumen V idealer Gase
linear mit der Temperatur T (Gay-Lussac-Gesetz)
V (T ) = V0 (1 + γ V T )
(2)
Bei konstantem Gasvolumen V0 steigt der Gasdruck p
linear mit der Temperatur T (Charles-Gesetz)
p (T ) = p0 (1 + γ pT )
(3)
Diese Beobachtung gilt für alle (verdünnten) Gase (weit oberhalb des Siedepunktes)
(ideale Gase, z.B. He)
γV = γ p = γ =
1 o −1
C
273.16
γ = Volumenausdehnungskoeffizient
10.2 Temperaturmessung
Gasthermometer mit konstantem Volumen:
- Gas in Glaskolben
- V wird mittels Hg-U-Rohr konstant gehalten
Skala
gasgefüllter
Kolben
- Gasdruck p = ρ g ∆h (+Atmosphärendruck)
•
Die Temperatur wird beim Gasthermometer
durch eine Druckmessung bestimmt:
T ( p) =
1
T
h
p
p
= 273.16 °C
γ p0
p0
⋅
p0 = Tripelpunkt des Wassers, 610.6Pa
Gasthermometer mit konst. V liefert Zugang zur universellen
Temperaturskala
5
10.2 Phasendiagramm - Wasser
In der Thermodynamik ist der Tripelpunkt (auch Dreiphasenpunkt) der Punkt,
beschrieben durch Druck und Temperatur, an dem drei Phasen eines Systems mit genau
einer Komponente im Gleichgewicht sind.
Der Tripelpunkt des Wassers nach dem international akzeptierten Bestwert von Guildner,
Johnson & Jones 1976 liegt bei 611,657 ± 0,010 Pa und 273,16 K (0,01 °C).
10.2 Temperaturskalen
• Die Temperatureinheit Kelvin wurde 1954 auf
Beschluss der 10. Generalkonferenz für Maß und
Gewicht durch:
1 K:= Ttr /273,16
definiert (Ttr die Temperatur des Trippelpunkts
von Wasser)
• Die Festlegung von Einheit ist Menschenwerk und
nicht die Folge der Naturgesetzen
• Allerdings: Im täglichen Leben benutzt man eine
Temperatur mit willkürlich festgesetztem
Nullpunkt, die Celsius-Temperatur:
T:= T- T0= T-273,15 K,
T0 – Temperatur des Eispunkts
6
10.2 Phasendiagramm - Wasser
Temperatur des
Eispunkts
In der Thermodynamik ist der Tripelpunkt (auch Dreiphasenpunkt) der Punkt,
beschrieben durch Druck und Temperatur, an dem drei Phasen eines Systems mit genau
einer Komponente im Gleichgewicht sind.
Der Tripelpunkt des Wassers nach dem international akzeptierten Bestwert von Guildner,
Johnson & Jones 1976 liegt bei 611,657 ± 0,010 Pa und 273,16 K (0,01 °C).
10.2 Kelvin-Skala
• Amtliche Übersetzung: „Das Kelvin, die Einheit
der thermodynamischen Temperatur, ist der
273,16te Teil der thermodynamischen Temperatur
des Tripelpunktes des Wassers.“
• Die Kelvin-Skala ist per Definition seit 1968 nicht
mehr in Grad unterteilt. Es heißt deshalb nicht
mehr „19 Grad Kelvin“ (oder „19 °K“) sondern
einfach nur „19 Kelvin“ (19 K).
• Es wurde nach William Thomson, dem späteren
Lord Kelvin (1824-1907) benannt, der mit 24
Jahren die thermodynamische Temperaturskala
einführte.
7
10.2 Temperatur-Skalen
Kelvinskala: TC=TK-273.15º
10.2 Temperaturmessung
Gasthermometer/Temperaturskala des idealen Gases:
•
Bei der Extrapolation des Druckes zu niedrigen Temperaturen ergibt sich für
alle (idealen) Gase:
p
He
p = 0 bei T = -273.15 ºC
-273
Temperatur/ºCelsius
-300
-100
100
300
•
Dieser Wert (stoffunabhängig!) wird als „Nullpunkt“ der
thermodynamischen Temperaturskala definiert
•
Kelvinskala: 0 Kelvin (0K): -273.15 ºC
Umrechnung: T ( K ) = (T ( o C ) + 273)( K )
T = 0 stellt den prinzipiell nie erreichbaren unteren Grenzwert der
Kelvinskala dar; d.h. es gilt immer T > 0 K
Die thermodynamische Temperatur eines Körpers (oder Systems) steht
im Zusammenhang mit seinem Energiegehalt: keine Energie, dann hat er
die Temperatur 0 K
•
•
8
10.3 Gase
Eigenschaft von Gasen:
• feste/flüssige Stoffe ändern unter Einwirkung äußerer Kräfte kaum
ihr Eigenvolumen
• ↔ Gase nutzen jedes Raumangebot (d.h. expandieren beliebig)
• ↔ Unter Einwirkung eines äußeren Druckes lassen sie sich bis zu
einer gewissen Grenze auch beliebig komprimieren
• Gasdichte bei Atmosphärendruck um ca. 103 kleiner als die der
festen/flüssigen Phase: ca. 6 ·1023 Atome (Moleküle)/22 Liter
- Mittlere Abstand der Teilchen ist ca. 10-mal größer
- Mittlere Ekin ist größer als die Epot ihrer Wechselwirkung
10.3 Ideales Gas
Modellvorstellung des idealen Gases:
(i)
Gasteilchen sind „punktförmig“ (kein Eigenvolumen)
(ii) Gasteilchen üben keine gegenseitige Wechselwirkungskräfte aufeinander aus
(iii) Es gibt nur elastische Stöße untereinander, bzw. mit
der Wand
Modell hinreichend gut erfüllt für viele Gasarten bei hohen
Temperaturen und niedrigem Druck !
9
10.3 Einschub: Stoffmenge
Eine Substanz hat die Stoffmenge 1 mol, wenn die Zahl der darin enthaltenen
Teilchen gleich der Zahl der Kohlenstoffatome in 12 g reinem 12C ist.
- Die Zahl der Teilchen pro Mol heißt:
Avogadrozahl NA = 6.023 ·1023 mol-1
(Loschmidt-Konstante)
- Liegen ν mol einer Substanz vor, dann ist die Teilchenzahl N:
N = ν · NA
-Physikalische Größen, die auf Stoffmengen bezogen werden, heißen molare Größen:
Molare Masse M (Masse einer Substanz pro Mol)
Beispiele: Masse von 1 mol Wasserstoff (atomar): 1.0078 g
Masse von 1 mol H2O: 2 ⋅1,0078g + 16g =18.015 g
Masse von 1 mol CO2: 12g +2· 16g = 44 g
(natürliche Isotopenverhältnisse beachten)
Nebenbemerkung: Molvolumen eines Gases = Volumen, das ein Mol dieses Gases enthält
10.3 Ideales Gas
Versuch: Boyle - Mariottsches Gesetz:
10
10.3 Ideales Gas
Experimentelle Bestimmung der Zustandsgleichung (ideales Gas):
(i) Serie von Experimenten bei konstanter Temperatur T
(ii) Gas der molaren Masse M
(iii) Variation des Druckes p
F = p· A
p·V = konstant
Durch Einfüllen verschiedener Gasmengen X
desselben Gases in die Apparatur findet man:
Reibungsfreier
Kolben
p·V = X·konstant
V
Durch Variation der Gasart findet man:
p·V = ν ·C
p
ν = Stoffmenge in Mol
C = (temperaturabhängige) Konstante
T
Wärmereservoir
10.3 Ideales Gas
Experimentelle Bestimmung der Zustandsgleichung (ideales Gas):
(i) Untersuchung der Temperaturabhängigkeit des Produkts p·V
(ii) Feste Menge Helium-Gas ist in einem konstanten Volumen
eingeschlossen
F = p· A
(iii) Variation der Temperatur T
„Fixer“
Kolben
V
p
Resultat zeigt, dass das Produkt p·V eine
lineare Funktion von T ist
T
Wärmereservoir
11
10.3 Ideales Gas
Zustandsgleichung des idealen Gases:
Beschreibt den Zusammenhang zwischen den Zustandsgrößen:
( p ⋅V )
Druck p
Volumen V
Temperatur T
T
= konstant = C
- Gültig für alle Gase genügend kleiner Dichte
- C ist proportional zu „Gasmenge“, oder Stoffmenge ν, siehe vorhergehenden Einschub
10.3 Ideales Gas
Zustandsgleichung
p ⋅V = N ⋅ k ⋅ T
p ⋅V = ν · N A ⋅ k B ⋅ T = v · R ⋅ T
N = Teilchenzahl
ν = Stoffmenge
R = NA ·kB = Gaskonstante = 8.314 J mol-1 K-1
Gilt für ideale Gase
(ohne Wechselwirkungskräfte, ohne Eigenvolumen)
12
10.3 Ideales Gas
Folgerung aus der Zustandsgleichung
In vielen Experimenten kann eine der Zustandsgrößen jeweils konstant gehalten werden:
1. Gesetz von Boyle-Mariotte:
p ∝ V −1 (T = konstant)
T = konstant
(Isotherme)
ν- konstant
p1 · V1 = p2 · V2 = p · V = konst.
p
T3 > T2 > T1
T2
T1
V
10.3 Ideales Gas
Folgerung aus der Zustandsgleichung
In vielen Experimenten kann eine der Zustandsgrößen jeweils konstant gehalten werden:
2. (2tes) Gesetz von Gay-Lussac:
V, ν = konstant
(Isochore)
p ∝ T (V = konstant)
(führt zur Festlegung der Kelvinskala !!!)
p
p1 p 2
=
T1 T2
T
13
10.3 Ideales Gas
Folgerung aus der Zustandsgleichung
In vielen Experimenten kann eine der Zustandsgrößen jeweils konstant gehalten werden:
3. Gesetz von Charles:
p, ν = konstant
(Isobare)
V ∝ T ( p = konstant)
V
V1 V2
=
T1 T2
T
10.3 Ideales Gas
Folgerung aus der Zustandsgleichung
In vielen Experimenten kann eine der Zustandsgrößen jeweils konstant gehalten werden:
4. Gesetz der Gleichförmigkeit (bzw. Homogenität):
p, Τ = konstant
V ∝v
V
V1
ν1
=
V2
ν2
ν
14
10.3 Ideales Gas
4. Gesetz von Avogadro:
p, Τ = konstant
• Gleiche Volumina Gas von gleichem Druck und gleicher Temperatur enthalten gleich viele
Moleküle unabhängig von ihrer chemischen Beschaffenheit
• d.h. ein bestimmtes Normalvolumen V0 enthält daher eine bestimmte Einheitsstoffmenge
mit einer bestimmten Anzahl von Teilchen.
Häufig verwendete „Normbedingungen“:
Normdruck:
pn = 1013.25 hPa
Normtemperatur: Tn = 273.15K
1 mol eines idealen Gases hat das molare Volumen:
Vmol = 22.4 l/mol
15