Baum

Gliederung
5. Compiler
1.
2.
3.
4.
Struktur eines Compilers
Syntaxanalyse durch rekursiven Abstieg
Ausnahmebehandlung
Arrays und Strings
6. Sortieren und Suchen
1.
2.
3.
4.
5.
Grundlegende Datenstrukturen
Bäume
B-Bäume und Tries
Sortieren in Vektoren
Streuspeicherung
7. Graphen
1. Darstellung und Topologisches Sortieren
2. Kürzeste Wege
3. Fluß- und Zuordnungsprobleme
Bäume
• Bäume gehören zu den fundamentalen Datenstrukturen der
Informatik
• Bäume können als zweidimensionale Verallgemeinerung von
Listen aufgefasst werden
• In Bäumen können zusätzlich zu Daten auch relevante
Beziehungen der Daten untereinander (z.B. Ordnungsoder hierarchische Beziehungen) gespeichert werden
• Aufgrund ihrer Struktur eignen sich Bäume besonders gut
dazu, gesuchte Daten rasch wieder aufzufinden.
2
Beispiele von Bäumen
• Beispiele von Bäume
– Stammbäume
– Systematik in der Biologie
– Dateibäume
3
Bäume: Grundbegriffe (1)
• Ein Baum ist eine Menge von Knoten (dargestellt als Punkte,
Kreise, Rechtecken, ...), die miteinander durch Kanten
(dargestellt als Pfeile) verbunden sind
• Führt von Knoten A zu Knoten B eine Kante, sagt man:
A ist Vater von B bzw. Vorgänger von B
B ist Sohn von A bzw. Vorgänger von A
• Ein Pfad von A nach B ist eine Folge von Knoten und Pfeilen,
die von A nach B führen: A → X1→ X2→ X3→ X4......B
• Die Länge eines Pfades wird als Anzahl der Knoten in diesem
Pfad definiert
• Gibt es ein Pfad von A nach B, so heißt A ein Vorfahre von B
und B ein Nachkomme von A
4
Bäume: Grundbegriffe (2)
• Bäume müssen folgende Axiome erfüllen
– Es gibt genau einen Knoten ohne Vater: die Wurzel
– Jeder anderer Knoten hat genau einen Vater
• Daraus folgt:
– Es gibt keinen zyklischen Pfad
– Von der Wurzel aus gibt es zu jedem Knoten genau einen Pfad
– Die Nachkommen eines beliebigen Knotens K zusammen mit allen
Kanten bilden einen Baum mit K als Wurzel, den Unterbaum mit
Wurzel K
5
Bäume: Grundbegriffe (3)
• Die Länge des Pfades von der Wurzel zu einem Knoten wird
die Tiefe eines Knoten benannt
• Die Tiefe eines Baumes ist das Maximum der Tiefe seiner
Knoten
• Der Grad eines Knotens K g(K) ist gleich der Anzahl der
Nachfolger von K
– Ein Knoten ohne Nachfolger (g(K) =0) wird Blatt genannt, sonst wird
er innerer Knoten genannt
• Der Grad g(B) eines Baumes ist gleich dem maximalen
Grad seiner Knoten
6
Bäume: Grundbegriffe (4)
Rekursive Definition:
Ein Baum ist leer oder er besteht aus einer Wurzel W und
einer leeren oder nichtleeren Liste B1, B2, ..., Bn von Bäumen.
Von W zur Wurzel Wi von Bi führt jeweils eine Kante
W
W1
W2
...........
Wn
7
Bäume: Beispiel
• Baum der Tiefe 4
• (W, A, E, K ) ist ein Pfad der Länge 4
W
Kante
A
Wurzel
I
Innerer Knoten
E
K
Ein Blatt der Tiefe 4
8
Binärbäume
• Definition: Ein Binärbaum ist ein Baum vom Grad ≤ 2, d.h. er ist
entweder leer oder er besteht
– aus einem Knoten (Wurzel) und
– zwei mit der Wurzel verbundenen Binärbäumen, dem linken und rechten
Teilbaum.
• Ein Binärbaum der Tiefe T hat höchstens 2T-1 viele Knoten (Beweis über
Induktion)
Linker Teilbaum
Rechter Teilbaum
9
Binärbäume: anwendbare Operationen
•
•
•
•
empty : Baum → boolean liefert true, falls Baum leer ist
left : Baum → Baum liefert linken Teilbaum
right : Baum → Baum liefert rechten Teilbaum
value : Baum → Objekt liefert die Wurzel des Baumes
10
Binärbäume: Implementierung (1)
• Jeder Knoten ist wiederum die Wurzel eines Teilbaumes
• Der Wurzelknoten muss verwaltet werden, alle andere
Knoten sind durch verfolgen der Verweise erreichbar
Inhalt
public class TreeNode {
Object inhalt;
TreeNode left = null,
TreeNode right = null;
}
Links
Rechts
Inhalt
Links
Inhalt
Links
Rechts
Rechts
Inhalt
Links
Rechts
11
Binärbäume: Implementierung (2)
public class TreeNode {
Object elem;
TreeNode left = null, right = null;
public TreeNode (Object e) { elem = e; }
public TreeNode getLeft () { return left; }
public TreeNode getRight () { return right; }
public Object getElement () { return elem; }
public void setLeft (TreeNode n) { left = n; }
public void setRight (TreeNode n) { right = n; }
public boolean isLeaf () {
return left == null && right == null;
}
}
public Class BinaryTree{
protected TreeNode root =null
public BinaryTree(){}
public BinaryTree(TreeNode n){ root = n;}
..............
}
12
Darstellung arithmetischer Ausdrücken mit Binärbäumen
• Die inneren Knoten enthalten
die Operatoren, die Blätter
enthalten die (einfachen)
Operanden
• Einstellige Operatoren werden
als Knoten mit nur einem
Nachfolger repräsentiert
• In der Baumdarstellung sind
Klammern und Präzedenzregeln
überflüssig
-
12
9
*
!
3
-
7
12 - ( 3 * (7 - 5 ) ! - 9 )
5
13
Traversierung von Bäumen (1)
• Einen Baum zu durchlaufen bedeutet, alle seine Knoten in
einer bestimmten Reihenfolge zu besuchen. Dabei können
auf die Daten im jeweiligen Knoten spezielle Operationen
angewandt werden.
• Für das Durchlaufen (traversal) von Bäumen können
verschiedene Reihenfolgen festgelegt werden, in denen die
einzelnen Knoten zu besuchen sind:
–
–
–
–
Inorder
Preorder
Postorder
Levelorder
14
• Inorder
Traversierung von Bäumen (2)
– Besuche rekursiv den linken Teilbaum
– Besuche die Wurzel
– Besuche rekursiv den rechten Teilbau
D->B->E->A->F->C->G
A
• Preorder
– Besuche die Wurzel
– Besuche rekursiv den linken Teilbaum
– Besuche rekursiv den rechten Teilbaum
A->B->D->E->C->F->G
• Postorder
C
B
D
E
F
G
– Besuche rekursiv linken Teilbaum
– Besuche rekursiv den rechten Teilbaum
– Besuche die Wurzel
D->E->B->F->G->C->A
Merke: Postorder liefert eine Postfix-Notation für arithmetische Ausdrücke!
• Levelorder: Besuche die Knoten schichtenweise
– Zuerst die Wurzel
– Dann die Nachfolger
– Dann die Nächste Ebene
A->B ->C->D->E ->F->G
15
Suchbäume
• Ein Suchbaum ist ein Baum, auf dessen Daten (meistens
mittels eines Schlüssels) eine Ordnungsrelation definiert ist
• Ein binärer Suchbaum ist ein Binärbaum mit folgenden
Eigenschaften:
– Alle Knoten k haben einen Schlüsselwert s(k)
– Ist w ein innerer Knoten und sind TL und TR der linke bzw. rechte
Nachfolger von w, so gilt:
s(kL) ≤ s(w) < s(kR) für alle Knoten kL von TL und kR von TR
16
Binäre Suchbäume
w
Alle Elemente
im linken
Teilbaum sind ≤ w
•
•
Alle Elemente
im rechten
Teilbaum sind > w
Auf den Schlüsseln der Elemente muss eine totale Ordnung definiert sein
Sortierungseingenschaft: Die Daten in einem binären Suchbaum sind in
17
Inorder-Reihenfolge immer korrekt sortiert!
Suchen in binären Suchbäumen
• Suche nach Element x:
– Vergleichen mit der Wurzel, falls x=w: Element gefunden
– Falls x ≤ w , suche im linken Teilbaum weiter
– Falls x > w suche im rechten Teilbaum
• Suchalgorithmus: Pseudo-Code
BinTreeSearch(k,x)
– Eingabe: Wurzel k des zu durchsuchenden Teilbaumes
– Ausgaben: Element mit dem gesuchten Wert bzw. null, wenn x nicht
gefunden wurde
if k=null then return null;
Else if x =k.key then return k;
Else if x< k.key then return BinTreeSearch(k.left,x)
Else return BinTreeSearch(k.right,x)
18
Minimale und maximales Element
• Minimales Element: die kleineren Elemente sind immer die
linken Nachfolger eines Knotens: Das minimale Element
muss sich ganz links im Baum befinden
• Maximales Element: die größeren Elemente sind immer die
rechten Nachfolger eines Knotens: Das maximale Element
muss sich ganz rechts im Baum befinden
Minimum
while k.left != null do
k:= k.left
od
return k
Maximum
While k.right != null do
k:= k.right
od
Return k
19
Implementierung: Elemente von Suchbäumen
• Die Elemente von binären Suchbäumen müssen untereinander
vergleichbar sein.
• Die Vergleichbarkeit wird durch die Implementierung der JavaSchnittstelle Comparable erreicht: Für die abstrakte Methode
• public abs t r a c t int compareTo ( Objec t o )
muss eine konkrete Implementierung bereitgestellt werden: liefert einen
negativen Wert, Null oder einen positiven Wert zurück, je nachdem, ob
das aktuelle Objekt kleiner als o, gleich o oder größer ist.
• Beispiel:
class TreeElem implements Comparable {
String inhalt;
Elem (String x) { inhalt = x; }
public int compareTo (Object o) {
Elem e = (Elem) o;
return inhalt.compareTo(e.inhalt);
}
Verwendung der in
String definierte
compareTo-Methode
20
Einfügen in binären Suchbäumen
• Korrekte Einfügeposition
– Knoten, dessen Schlüsselwert größer
als der des einzufügenden Knoten ist
und noch keinen linken Nachfolger
hat
– Knoten, dessen Schlüsselwert kleiner
als der des einzufügenden Knoten
und noch keinen rechten Nachfolger
hat
6
9
3
5
1
7
10
• Mögliche Fälle
– Baum ist leer: Der einzufügende
Knoten ist wird die Wurzel des
Baumes
– Baum enthält bereits Knoten: Knoten
identifizieren, der Elternknoten des
neuen Elementes werden soll
4
Einfügen von 4
21
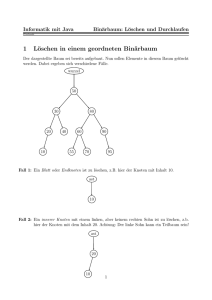
Löschen aus binären Suchbäumen (1)
• Beim Entfernen eines inneren Knotens muss einer der
Teilbäume hochgezogen und u.U. umgeordnet werden!
• Mögliche Fälle
– Der zu entfernende Knoten k ist ein Blatt: Der Knoten kann einfach
abgetrennt werden (Dies ist der einfachste Fall)
– Der zu entfernende Knoten k besitzt einen Kindknoten: Verweis vom
Elternknoten von k muss auf den Kindknoten von k umgelenkt
werden
– Der zu entfernende Knoten ist ein innerer Knoten mit zwei
Kindknoten
• Der Knoten mit dem nachfolgenden Schlüsselwert muss aus seiner
bisherigen Position entfernt werden und an die Stelle von k kopiert
werden
• Merke: Der Knoten mit dem kleinsten Element des rechten Teilbaumes
von k ist der Nachfolger (Schlüsselwert) von k und besitzt keinen linken
Teilbaum
22
Löschen aus binären Suchbäumen (2)
6
6
9
3
5
1
7
Element 5 löschen
3
9
10
1
4
7
10
4
23
Löschen aus binären Suchbäumen (3)
6
6
9
3
5
1
left
4
7
Element 3 löschen
4
10
1
9
5
7
10
right
24
Löschen aus binären Suchbäumen (4)
6
7
9
4
1
5
7
Element 6 löschen
9
4
10
1
5
10
25
Komplexität der Operationen in binären Suchbäumen
• Der Aufwand der Operationen hängt ausschließlich von der
Tiefe des Baumes ab, d.h. O(t) für ein Baum der Tiefe t
• Problem: Bestimmte Einfügereihenfolgen können zu
entarteten Bäumen führen
Eingabe: 1,3,5,6,7,9,10
1
Eingabe: 6,3,9,1,5,7,10
3
5
6
6
9
3
7
9
1
5
7
10
10
26