Document

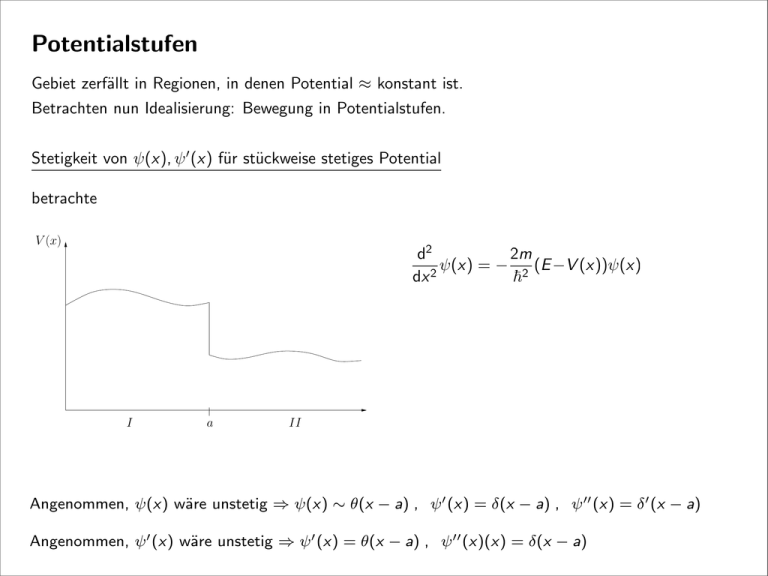
Potentialstufen
Gebiet zerfällt in Regionen, in denen Potential ≈ konstant ist.
Betrachten nun Idealisierung: Bewegung in Potentialstufen.
Stetigkeit von ψ(x), ψ ! (x) für stückweise stetiges Potential
betrachte
V (x)
d2
2m
ψ(x) = − 2 (E −V (x))ψ(x)
dx 2
!
I
a
II
Angenommen, ψ(x) wäre unstetig ⇒ ψ(x) ∼ θ(x − a) , ψ ! (x) = δ(x − a) , ψ !! (x) = δ ! (x − a)
Angenommen, ψ ! (x) wäre unstetig ⇒ ψ ! (x) = θ(x − a) , ψ !! (x)(x) = δ(x − a)
⇒ Widerspruch mit der rechten Seite der Schrödingergleichung
⇒ ψ(x), ψ ! (x) müssen stetig sein
⇒ ψI (a) = ψII (a), ψI! (a) = ψII! (a)
3.2 Potentialstufen
!
gilt nicht mehr, wenn V die Form einer
aufweist.
1; xδ-Distribution
>0
V (x) = V0 Θ(x); Θ(x) =
0; x < 0
59
(3.45)
Beispiel:
PotentialstufeV0 ≥ 0. Betrachten wir dazu die Schrödinger-Gleichung
mit der Konstanten
gesondert in den Gebieten I!(x < 0) und II (x > 0):
1 x ≥0
2
2
V (x) =
V0 Θ(x)2mE
, Θ(x) = d ψ
2m(E
− V0 )
d ψ
0
x
<
0
=− 2 ψ;
=−
ψ.
(3.46a,b)
2
2
2
dx
!
dx
!
Abb. 3.5a. Potentialstufe
Abb. 3.5b. Potentialstufe, E > V0
d2
2mE
d2
2m(E − V0 )
I:
ψ(x)
=
−
ψ(x)
II:
ψ(x)
=
−
ψ(x)
2
2
2
2
!
dx Stetigkeitsforderungen
!
! uns Relationen zwischen den
Die
fürdxψ und ψ werden
freien Konstanten der Lösungen in den Gebieten I und II liefern. Wir unterscheidendie
dieFälle
Fälle
E<
<VV00getrennt.
, da sie unterschiedlichen physikalischen
Betrachte
fürEE >
> VV00 und
und E
Situationen entsprechen.
Teilchenenergien oberhalb der Potentialstufe E > V0
!
2
d
2mE
2
ψ(x) = −k ψ(x) mit k =
I:
2
dx
!2
d2
2m(E − V0 )
2
II:
ψ(x)
=
−q
ψ(x)
mit
q
=
sqrt
dx 2
!2
Fundamentallösungen:
e iKx , e −iKx , K =
"
k
q
x ≥0
x <0
Wir machen den folgenden Ansatz:
ψI (x) = e ikx + Re −ikx ,
einfallende
Welle
ψII (x) = Te iqx ,
reflektierte
Welle
ψ(x) = Θ(−x)ψI (x) + Θ(x)ψII (x)
durchgehende
Welle
Stetigkeit von ψ(x) bei x = 0:
1+R =T
Stetigkeit von ψ ! (x) bei x = 0:
ik(1 − R) = iqT
k −q
=⇒ R =
,
k +q
2k
T =
k +q
4. Nach (3.49) ist R > 0, d. h. reflektierte und einfallende Welle sind in
Phase. Wenn andererseits die Potentialstufe nach rechts
hin abfallend ist,
!
Bemerkungen:
d. h. V0 < 0, dann ist in (3.48) und (3.49) q = 2m(E + |V0 |)/! und
folglich R < 0; die reflektierte Welle erleidet einen 2Phasensprung“ um π.
i) Teilchen wird mit Wahrscheinlichkeit r = |R|” reflektiert.
Wir stellen noch den Real- und Imaginärteil von ψ(x) und die Wahrklassisch
keine Reflektion, Teilchen wird nur langsamer
scheinlichkeitsdichte |ψ(x)|2 in Abb. 3.6 dar. Für die Einfallsenergie wählen
wir E = 4V0 /3; dann ist das Verhältnis der Wellenzahlen q/k = 1/2.
ii) E → ∞ =⇒ q → k : R → 0 , T → 1
E = 4/3V0 , q/k = 1/2
Abb. 3.6. Der Realteil und der Imaginärteil von ψ(x) und die Wahrscheinlichkeits-
Teilchenenergie unterhalb der Potentialstufe E < V0
d2 ψ
2
I:
=
−k
ψ,
2
dx
k=
√
2mE /!
d2 ψ
2m(E − V0 )
2
II:
=
−
ψ
=
κ
ψ,
2
2
dx
!
ψI = e ikx + Re −ikx
1 + R = T,
ψII = Te −κx
ik(1 − R) = −κT
i2k = ikT − κT
k − iκ
R=
,
k + iκ
⇒
!
κ = 2m(V0 − E )/!
i2k
2k
T =
=
ik − κ
k + iκ
2k
T =
k + iκ
Bemerkungen:
i) |R|2 = 1
V0
Eindringtiefe ∼ κ−1
ii) V0 → ∞ :
⇒
κ → ∞, T = 0, R = −1
ψI = e ikx − e −ikx
⇒ ψI (0) = 0
⇒ allgemeine Randbedingung an unendlich hoher Schwelle:
ψSchwelle = 0
Tunneleffekt
Potentialbarriere V (x) = V0 θ(a − |x|)
V0
Betrachte nur E < V0

ikx
−ikx

Ae
+
Be

ψ(x) = Ce −κx + De +κx

 ikx
Fe + Ge −ikx
k=
√
2mE
, κ=
!
%
−a
x < −a
−a < x < a
x >a
2m(V0 − E )
!
Stetigkeit für ψ, ψ " bei x = a, x = −a
x = −a :
Ae −ika + Be ika = Ce κa + De −κa
& −ika
'
& κa
'
ika
−κa
ik Ae
− Be
= −κ Ce − De
0
a
In Matrixschreibweise:
! −ika
e
e −ika
" ! " ! κa
e
A
e
= iκ κa
ika
B
−e
k e
"! "
e
C
−κa
D
− iκ
e
k
−κa
ika
! "
! ika
1 e
A
⇒
=
B
2 e −ika
ika
e
−e −ika
! "
! "
C
A
= M(a)
⇒
B
D
%
1
M(a) =
2 %
x =a:
! "
! "
F
C
= M(−a)
G
D
κa
e
iκ κa
k e
"! "
e
C
−κa
D
− iκ
e
k
−κa
mit
&
1+
iκ
k
1−
&
iκ
k
"!
e
κa+ika
e κa−ika
%
%
1−
1+
iκ
k
&
&
iκ
k
e
−κa+ika
e −κa−ika


Zusammenhang zwischen
!
A
B
"
!
"
A
B
−1
!
1−
ik
κ
= M(a)M(−a)
und
F
G
!
"
F
G
:
"
Mit
M(−a)−1
folgt


A
B

1
=
%
2
 %
=
 %
1+
ik
κ
cosh(2κa) +
i"
2
κ k
"= − ,
k
κ
− iη2
&
&
e
e
κa+ika
−κa−ika
&
%
sinh(2κa) e
sinh(2κa)
κ k
η= +
k
κ
%
1+
1−
ik
κ
ik
κ
&
&
e
κa−ika
e −κa−ika
iη
2
2ika
%


sinh(2κa)
cosh(2κa) −
i"
2
&
sinh(2κa) e −2ika


F
G


Betrachte von links einlaufendes Teilchen, also G = 0
!
⇒
"
i"
A = F cosh(2κa) + sinh(2κa) e 2ika
2
!
"
iη
B=F −
sinh(2κa)
2
Transmissionsamplitude
F
e −2ika
# i! $
S(E ) := =
A
cosh(2κa) + 2 sinh(2κa)
Durchlässigkeitskoeffizient
2
|S(E )| =
1+
!2
(4
1
2
sinh (2κa))
= Wahrscheinlichkeit für das Durchdringen der Potentialschwelle
betrachte hohe und breite Barriere: κa ! 1
1 2κa
=⇒ sinh(2κa) ≈ e
!1
2
−4κa
2
1
4e
16(κk)
−4κa
⇒ |S(E )|2 =
≈
=
e
"2 1 4κa
"2
(κ2 + k 2 )2
1 + (1 + 4 ) 4 e
1+ 4
! "
16E (V0 − E )
a#
=
exp −4 2m(V0 − E )
2
!
V0
$
%
&'
"
a
16E (V0 − E )
= exp −4 2m(V0 − E ) + log
!
V02
! "
#
a
⇒ |S(E )|2 ≈ exp −4 2m(V0 − E )
!
Klassisches Teilchen würde reflektiert
QM: endliche Durchgangswahrscheinlichkeit
Tunneleffekt
Beispiel: α-Zerfall, Josephson-Effekt, Kernfusion
Potentialbergegenauer begründet
mitKontinuierliche
der WKB-Methode
Diskretisieren: dx ←→ Stufenbreite 2a
$
"
"seine
# Zerlegung in Stufen
otentialberg und
(b)
N
!
2
|S(E )| =
i=1
exp −
2m(V (xi ) − E )
2dx
!
"
#
= exp −2
N→∞:
Der α-Zerfall
&
b
$
2m(V (x) − E ) den in
2 Kern hat näherungsweise
s in einem
|S(E )| = exp −2
dx
!
a
f. Dabei ist die Reichweite der Kernkräfte
hl eines α-Teilchens Z2 = 2, und die Kernla-
N
%
i=1
$
#
2m(V (xi ) − E )
dx
!
Potentialtopf
Abb. 3.1
gebundene Zustände im Potentialtopf
V (x) = −V0 θ(a − |x|)
Wie in den vorausgegangenen Abschnitten b
Gleichung
für Gebiete
verschiedener Potenti
Modell für kurzreichweitige Kräfte (Kernphysik, abgeschirmte
Störstellen
in Festkörpern)
gien der Bindungszustände im Intervall
Bindungszustände: −V0 ≤ E ≤ 0
!!
2
ψ =κ ψ,
ψ !! = −q 2 ψ ,
!
2m(−E )
κ=
! !
2m(E + V0 )
q=
!
|x| > a: Fundamentallösungen e +κx ,e −κx
Normierung: Wähle nach außen abfallende Lösung
|x| < a: cos qx, sin qx
−V0 ≤ E ≤ 0
liegen,für
haben
wira
|x| >
ψ =κ ψ
!!
und
2
!
mit κ = 2m(−E)/!
für
für |x| < a
ψ = −q ψ
!!
2
mit
!
q = 2m(E + V0 )/!
Um die Normierbarkeit der Wellenfunktion z
aus den beiden Fundamentallösungen e±κx
die exponentiell abfällt. Innerhalb des Topfes
cos qx, sin qx – und eventuell auch Linearkom
mentallösungen. Wegen der Spiegelungssymm
Spiegelungssymmetrie des Potentials ⇒ gerade oder ungerade
ψ(x) =
ψ(x) =
!
!
A cos qx
e ∓κx
|x| < a
x<
>±a
A sin qx
±e ∓κx
|x| < a
x<
>±a
gerade Symmetrie
A cos qa = e −κa ,
⇒ (nach Division)
mit ζ =
√
2mV0 a/!
Aq sin qa = κe −κa
2
2
κ
|ζ − (qa) |
tan (qa) = =
q
qa
1
2
(dimensionsloser Parameter)
Aus −V0 ≤ E ≤ 0 folgt:
0 < qa =
"
2m(E + V0 )a/! ≤ ζ
(q!)2
(qa)2
= −VLösung.
E = Gleichung:
−V0 + graphische
0 1−
transzendente
2m
ζ2
(3.86)
.
Physik steckt in ζ: ζ vorgegeben.
Abb. 3.13. Graphische Lösung der transzendenten Gleichung (3.84! );
(—) tg z, (– · –) (ζ 2 − z 2 )1/2 /z für verschiedene Werte von ζ(ζ1 < ζ2 < ζ3 )
Schnittpunkte ⇒ z = qa
!
"
Man liest aus Abb. 3.13 folgende charakteristische
2 Eigenschaften der Eigenq!
(qa)
⇒ E = −V0 +
= −V0 1 − 2
werte ab:
2m
ζ
Eigenschaften:
# 2
$1
2 2
bei z = ζ ⇒ Anzahl der Schnittpunkte ng = [ζ/!]
i) ζ − z
([α] nächst größere natürliche Zahl zu α)
ii) Es gibt mindestens einen geraden gebundenen Zustand.
3.4.2 Ungerade Symmetrie
ungerade
Symmetrie
Die Stetigkeitsbedingungen
lauten nun:
−κa
A
sin
qa
=
e
Stetigkeitbedingungen,
Aq cos qa = −κe−κa
(3.88)
und nach Division
−κa
2
− (qa)
κ A(ζ
sin(qa)
=2 )e1/2
.
− ctg qa = ≡
q
qa
,
Aq cos(qa) = −κe −κa
1
2
κ
(ζ 2 − (qa)2 )
⇒ −ctg(qa) = =
Die graphische Lösung von (3.89)
q ist in Abb.
qa 3.14 illustriert.
(3.89)
Abb. 3.14. Graphische Lösung der transzendenten Gleichung (3.89);
(—) − ctg z, (– · – ·) (ζ 2 − z 2 )1/2 /z
π
π
ζ ∈ ] (2nu − 1), (2nu + 1)[ ⇒ nk Lösungen
2
2
Wenn ζ im Intervall
π2
⇒πes gibt ungerade Lösungen,
wenn 2mV0 a /! >
π
! "# $
4
(2nu − 1) < ζ < (2nu + 1)
2
2
2
ζ2
2
(3.90)
liegt, hat (3.89) genau nu Lösungen. Insbesondere ersehen wir daraus, daß es
Zustand
Grundzustand
1. angeregter Zustand
2. angeregter Zustand
..
.
qa
[0, π2 ]
[ π2 , π]
[π, 32 π]
..
.
Symmetrie
gerade
ungerade
gerade
..
.
unendlich tiefer Potentialtopf: V0 → ∞
!
1
k+
2
ψq = Θ(a − |x|) cos(qx)
qa =
ψq = Θ(a − |x|) sin(qx)
qa = kπ
Symmetrie
Parität (Spiegelung)
Pf (x) = f (−x)
gerade Funktion
ungerade Funktion
Pfg = fg , EW 1
Pfu = −fu , EW −1
betrachte spiegelsymmetrische Potentiale: PV = V
kinetische Energie: Ableitung zweiter Ordnung =⇒
⇒
⇒
PHf (x) = Hf (−x) = HPf (x)
[H, P] = 0
Knotenzahl
0
1
2
..
.
für symmetrische Potentiale
"
π
k = 0, 1, ...
k = 0, 1, ...
zeitunabhängige Schrödingergleichung:
Hψ (x) = E ψ (x)
und
Hψ (−x) = E ψ (−x)
⇒ mit ψ (x) ist auch ψ (−x) Eigenfunktion zum Eigenwert E .
⇒ Summe und Differenz sind EF zum EW E .
ψg (x) = ψ (x) + ψ (−x)
Pψg = ψg
ψu (x) = ψ (x) − ψ (−x)
Pψu = −ψu
⇒ kann Basissystem wählen, das nur aus geraden
und ungeraden stationären Zuständen besteht
V symmetrisch:
Wenn EW nicht entartet ist ⇒ Eigenfunktion gerade oder ungerade!