B - Michael Gamer

Algorithmen und
Datenstrukturen
Binäre Bäume
Zum Speichern und Suchen von Daten werden häufig
Baumstrukturen verwendet
•
Abspeichern von n Datenobjekten in einer Baumstruktur
•
Ablegen von Daten ist in O(log(n)) möglich
•
Auffinden von Daten ist ebenfalls in O(log(n)) möglich
•
Nachteil:
•
die entstehende Struktur ist von der Reihenfolge der
Eingangsdaten abhängig
•
ggf. ist eine Reorgansisation der Baumstruktur notwendig
Bäume (1/2)
•
Wir betrachten hier speziell Wurzelbäume, d.h.
zykelfreie Graphen mit einem ausgezeichneten
Knoten, der Wurzel.
w
k
k
b
k
b
w:
Wurzel
k: Knoten
b: Blatt
k
b
b
Bäume (2/2)
•
Wir werden hier binäre Bäume betrachten. D.h.
•
•
Jeder Knoten hat höchstens zwei Nachfolger
Die Tiefe eines Baumes ist der längste vorhandene
Weg von der Wurzel zu einem Blatt
•
Jeder binäre Baum der Tiefe n hat höchstens (2n
-1) Knoten
Fibonacci Bäume
•
Ein Baum heißt Fibonacci Baum, genau dann, wenn
•
Der linke Ast (Sohn) der Wurzel ist ein Fibonacci
Baum der Höhe h-1
•
Der rechte Ast (Sohn) der Wurzel ist eine Fibonacci
Baum der Höhe h-2
•
Der leere Baum ist ein Fibonacci Baum der Höhe 0
•
Ein Baum, der aus nur einem Knoten (der Wurzel)
besteht ist ein Fibonacci Baum der Höhe 1
5
Beispiel (1/2)
•
Einfügen ganzer Zahlen in eine Baumstruktur mit
folgender Regel
•
kleinere Werte im linken Teilbaum abspeichern
•
größere Werte im rechten Teilbaum abspeichern
•
Eingegeben werden die Zahlenfolgen
•
8,4,9,2,3,6,7,1,5
•
1,2,3,4,5,6,7,8,9
6
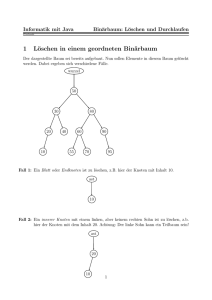
Beispiel (2/2)
1
8
2
4
9
4
2
1
3
6
3
5
7
9
Suchbäume
Wie das Beispiel zeigt können Suchbäume zu Listen „entarten“
•
Lösungsansätze:
•
Strukturanforderung an Suchbäume
•
Bei Verletzung dieser Anforderungen ist eine Reorganisation
des Baums notwendig
•
Die Anforderung, daß in jedem Knoten der linke und rechte
Teilbaum gleich tief sind ist zu streng, da zu hoher
Reorganisationsaufwand, bzw. nicht erfüllbar
•
Daher die Forderung: Tiefendifferenz höchstens 1
AVL Bäume
Ein binärer Suchbaum heißt AVL Baum, wenn für jeden
Knoten v im Baum gilt, daß die Differenz der Höhe des
rechten Teilbaums und der des linken Teilbaums
höchstens 1 beträgt.
Es wird also gefordert, daß
balance(v) = heigth(v.left) - heigth(v.right)∈{-1, 0, 1}
gilt.
Derartige Bedingungen nennt man auch Strukturinvariante
AVL : Adelson-Velski und Landis, die Namen der „Erfinder dieser Struktur“
Beispiel
AVL Bäume der Höhe 1 und 2 mit maximaler
Blattanzahl
w
w
k
b
k
b
b
b
b
b
Anzahl der Blätter in AVL Bäumen
•
Sei Fi die i-te Fibonacci Zahl, d.h es ist
•
Fi+2 = Fi + Fi+1
mit F0 = 0 und F1 = 1
•
So hat ein AVL Baum mit Höhe h mindestens Fh+2
Blätter. Es ist
Beispiele AVL Bäume
8
8
4
2
9
3
6
AVL Baum
4
2
9
3
AVL Baum
8
8
4
4
2
AVL Baum
3
3
kein AVL Baum
Beispiel mit Restrukturierung (1/2)
Einfügeoperation
kein AVL Baum
8
„2“ einfügen
8
4
4
4
2
8
2
AVL Baum
Reorganisation
AVL Baum
Beispiel mit Restrukturierung (1/2)
Löschoperation
kein AVL Baum
AVL Baum
2
3
8
8
3
AVL Baum
3
9
4
„9“ löschen
2
2
4
4
8
Reorganisation
Rotationen
•
Zur Restrukturierung von Bäumen, die der
Höhenbedingung nicht mehr genügen werden
sogenannte Rotationen durchgeführt.
•
Zielsetzung: Herstellung der Strukturbedingung
•
Aufwand zur Restrukturierung sollte möglichst
gering sein
Rotationen
•
x
y
A
h-1
•
B
C
h-1
h
Datenelemente in
A haben einen
kleineren
Schlüsselwert als
x
Alle
Datenelemente in
B haben einen
kleineren
Schlüsselwert als
y
Alle
Datenelemente in
C haben einen
größeren
Schlüsselwert als
y
Rotationen
x
y
y
x
A
C
h-1
B
A
B
h-1
h-1
C
h-1
h
h
Warum Rotation? Was rotiert?
t = Zx
Zeiger rotieren!
x
ZA
y
Zy
Zx
ZC
y
ZB
x
ZC
A
h-1
ZA
ZB
B
C
C
A
B
h-1
h-1
h-1
h
h
Strukturverletzung innerer Teilbäume
x
y
z
x
z
A
y
A
C
B1
B2
B1
B2
C
Beispiel: Löschen in Bäumen
5
5
3
8
2
4
7
10
6
1
8
2
9
3
1
9
11
5
2
2
7
3
10
6
11
5
1
7
6
1
10
9
11
10
3
7
11
9
Aufwand der Reorganisation
•
Beim Einfügen kann eine Rotation (um einen oder zwei Knoten)
erforderlich sein.
•
Beim Löschen kann jeder Knoten entlang des Suchpfades
erforderlich sein
•
Empirische Ergebnisse. Notwendigkeit der Rotation
•
bei jedem zweiten Einfügen
•
bei jedem fünften Löschen
•
Löschen und Einfügen ist bei AVL-Bäumen im Mittel
gleichaufwendig
Traversieren von Bäumen
Es gibt unterschiedliche Verfahren, die Knoten eines Baumes (als
Weg im Graphen) zu besuchen. Bei binären Bäumen unterscheidet
man
•
Preorder
•
•
Inorder
•
•
Wurzel, linker Teilbaum, rechter Teilbaum
linker Teilbaum, Wurzel, rechter Teilbaum
Postorder
•
linker Teilbaum, rechter Teilbaum, Wurzel
Beispiel Inorder
Vorgehensweise
Traversiere linken Teilbaum (in Inorder)
Wurzel
Traversiere rechten Teilbaum (in Inorder)
Bei der Inorder-Traversierung werden die Inhalte in sortierter Reihenfolge ausgegeben, falls es
sich um einen binären Suchbaum handelt
5
2
1
10
3
7
11
9
Traversierung in Inorder:
1, 2, 3, 5, 7, 9, 10, 11
Beispiel Preorder
Vorgehensweise
Wurzel
Traversiere linken Teilbaum (in Preorder)
Traversiere rechten Teilbaum (in Preorder)
5
2
1
10
3
7
11
9
Traversierung in Preorder:
5, 2, 1, 3, 10, 7, 9, 11
Beispiel Postorder
Vorgehensweise
Traversiere linken Teilbaum (in Postorder)
Traversiere rechten Teilbaum (in Postorder)
Wurzel
5
2
1
Traversierung in Postorder:
1, 3, 2, 9, 7, 11, 10, 5
10
3
7
11
9
UPN: Umgekehrte Polnische Notation
•
Bei einigen Taschenrechnern (insb. hp) werden
arithmetische Ausdrücke in Postorder eingegeben.
•
Dieses Verfahren heißt umgekehrte, polnische
Notation. Vorteile:
•
Es werden keine Klammern benötigt
•
man braucht weniger Tastendrücke als mit
„herkömmlichen“ Taschenrechnern
Beispiel
Der arithmetischer Ausdruck: 3*(7-2) + 4 hat den
Ableitungsbaum:
+
*
4
-
3
7
2
Durchlauf in Postorder:
3, 7, 2, - * 4 +
Arithmetische Ausdrücke in Postorder
•
Gegeben 3*x-1
•
Eingabe in UPN: 3 x * 1 -
•
Gegeben: 3*(4+x*(2-x)))
•
Eingabe in UPN: 2 x - x * 4 + 3 *
•
Es besteht ein Zusammenhang mit dem
Durchlaufen eines Ableitungsbaums für
arithmetische Ausdrücke bei geeigneter Grammatik
Levelorder
•
Traversierungsreihenfolge
•
Besuch der Knoten eines Baumes
„schichtenweise“
•
Besuche zuerst die Wurzel
•
danach die Wurzel des linken Teilbaums und die
Wurzel des rechten Teilbaums
•
u.s.w
Beispiel Levelorder
Traversierung in Levelorder:
5
Wurzel
Wurzel linker Teilbaum
2
1
10
3
7
11
9
Wurzel rechter Teilbaum
usw.
Traversierung in Levelorder:
5, 2, 10, 1, 3, 7, 11, 9