Formelsammlung zur beschreibende Statistik. - klaus

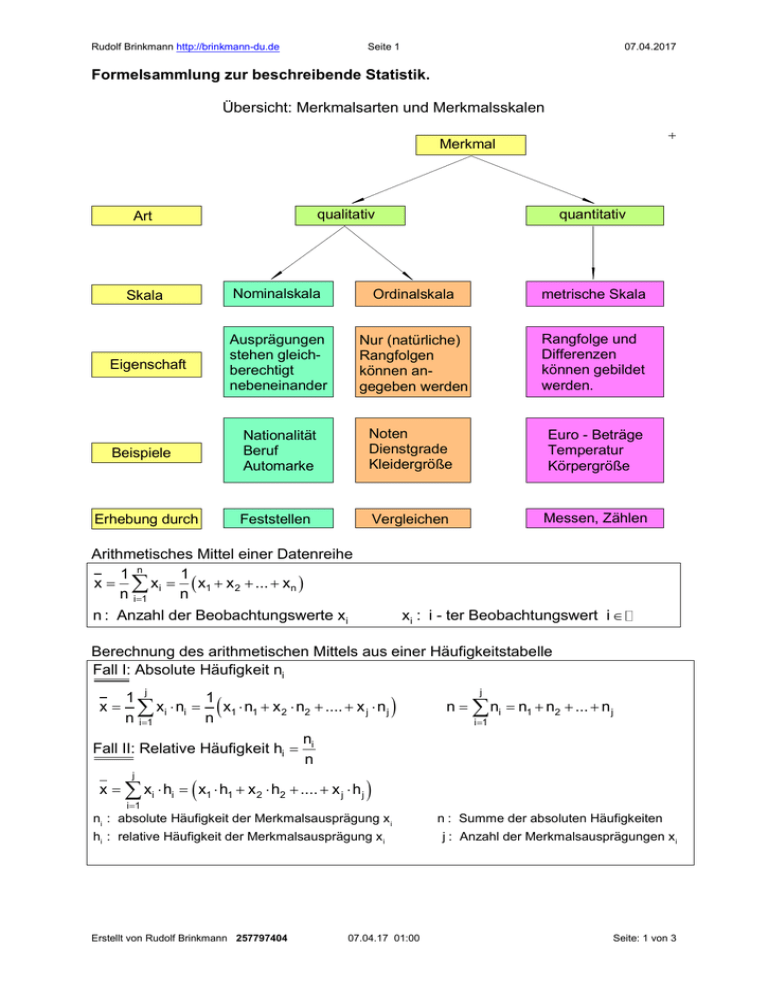
Rudolf Brinkmann http://brinkmann-du.de
Seite 1
07.04.2017
Formelsammlung zur beschreibende Statistik.
Übersicht: Merkmalsarten und Merkmalsskalen
Merkmal
qualitativ
Art
quantitativ
Skala
Nominalskala
Ordinalskala
metrische Skala
Eigenschaft
Ausprägungen
stehen gleichberechtigt
nebeneinander
Nur (natürliche)
Rangfolgen
können angegeben werden
Rangfolge und
Differenzen
können gebildet
werden.
Nationalität
Beruf
Automarke
Noten
Dienstgrade
Kleidergröße
Euro - Beträge
Temperatur
Körpergröße
Feststellen
Vergleichen
Messen, Zählen
Beispiele
Erhebung durch
Arithmetisches Mittel einer Datenreihe
1 n
1
x   xi   x1  x 2  ...  xn 
n i1
n
xi : i - ter Beobachtungswert i 
n : Anzahl der Beobachtungswerte xi
Berechnung des arithmetischen Mittels aus einer Häufigkeitstabelle
Fall I: Absolute Häufigkeit ni
x
1 j
1
xi  ni  x1  n1  x 2  n2  ....  x j  n j

n i 1
n

Fall II: Relative Häufigkeit hi 
j


ni : absolute Häufigkeit der Merkmalsausprägung x i
hi : relative Häufigkeit der Merkmalsausprägung x i
Erstellt von Rudolf Brinkmann 257797404
i 1
ni
n
x   xi  hi  x1  h1  x 2  h2  ....  x j  h j
i 1

j
n   ni  n1  n2  ...  n j
07.04.17 01:00
n : Summe der absoluten Häufigkeiten
j : Anzahl der Merkmalsausprägungen x i
Seite: 1 von 3
Rudolf Brinkmann http://brinkmann-du.de
Seite 2
07.04.2017
Berechnung des arithmetischen Mittels bei klassierten Daten
Fall I: Absolute Häufigkeit ni
x
1 k
1
mi  ni   m1  n1  m2  n2  ...  mk  nk 

n i 1
n
Fall II: Relative Häufigkeit hi 
k
n   ni  n1  n2  ...  nk
i 1
ni
n
k
x   mi  hi  m1  h1  m2  h2  ...  mk  hk
i 1
ni : absolute Häufigkeit der i - ten Klasse
n : Summe der absoluten Häufigkeiten
hi : relative Häufigkeit der i - ten Klasse
k:
Anzahl der Klassen
mi : Klassenmitte der i -ten Klasse
Allgemeine Rechenvorschrift zur Berechnung des Medians
Ist n ist die Anzahl der Beobachtungswerte xi , dann gilt:
n ungerade  xMed  x n 1
 xMed 
n gerade
2

1
 x n  x n 
1
2 2
2 
Die Spannweite
Spannweite = größter Beobachtungswert - kleinster Beobachtungswert
R  xmax  xmin
Quartilsabstand
Der mittlere 50% - Bereich aller Beobachtungswerte heißt Quartilsabstand.
QA  Q3  Q1
Berechnung:
Varianz einer Datenreihe

1 n
s2   x i  x
n i1

2
x

1
x
  x
2
2
x

2

 ...  xn  x

2
n
n: Anzahl der Beobachtungswerte, xi : i - ter Beobachtungswert, x : Mittelwert
Standardabweichung:
Erstellt von Rudolf Brinkmann 257797404
s  s2  Varianz
07.04.17 01:00
Seite: 2 von 3
Rudolf Brinkmann http://brinkmann-du.de
Seite 3
07.04.2017
Berechnung der Varianz aus einer Häufigkeitstabelle
Fall I: Absolute Häufigkeit ni
j
n   ni  n1  n2  ...  n j
i 1

1 j
s2   x i  x
n i 1

2
x
n 
1
x

2
i
j

s   xi  x
i 1

2

2

 n2  ...  x j  x

2
 nj
n
ni
n
Fall II: Relative Häufigkeit hi 
2

 n1  x 2  x

 hi  x1  x

2

 h1  x 2  x


2
 h2  ...  x j  x

2
 hj
Standardabweichung: s  s2
ni : absolute Häufigkeit der Merkmalsausprägung x i
n : Summe der absoluten Häufigkeiten
hi : relative Häufigkeit der Merkmalsausprägung x i
j : Anzahl der Merkmalsausprägungen x i
Berechnung der Varianz aus einer klassierten Häufigkeitstabelle
Fall I: Absolute Häufigkeit ni
k
n   ni  n1  n2  ...  nk
i 1

1 k
s   mi  x
n i1
2

2
m  x 
n 
1
k

i 1

2

 n1  m2  x
i
Fall II: Relative Häufigkeit hi 
s2   mi  x
2

 hi  m1  x

2

2

 n2  ...  mk  x

2
 nk
n
ni
n

 h1  m2  x

2

 h2  ...  mk  x

2
 hk
Standardabweichung: s  s2
ni : absolute Häufigkeit der i - ten Klasse
n : Summe der absoluten Häufigkeiten
hi : relative Häufigkeit der i - ten Klasse
k:
Anzahl der Klassen
mi : Klassenmitte der i -ten Klasse
Erstellt von Rudolf Brinkmann 257797404
07.04.17 01:00
Seite: 3 von 3