Lineare Gleichungen (2)

Bausteine zur Wiederholung und Vertiefung
Mathematik 8
Inhalt
Termumformungen
Faktorisieren
Binomische Formeln
Lineare Gleichungen 1
Lineare Gleichungen 2
Lineare Ungleichungen
Extremwertbestimmung
Bruchterme 1
Bruchterme 2
Geradengleichungen
Vierte Parallelogrammecke
Seitenlängen und Winkelmaße im Dreieck
Geometrische Ortslinien
Vierecke
Bemerkung
mit Aufgaben und Lösungen
Seiten
2
mit Aufgaben und Lösungen
2
mit Aufgaben und Lösungen
2
mit Aufgaben und Lösungen
2
mit Aufgaben und Lösungen
1
mit Aufgaben und Lösungen
1
mit Aufgaben und Lösungen
2
mit Aufgaben und Lösungen
1
Mit Übungen
1
mit Aufgaben und Lösungen
2
mit Aufgaben und Lösungen
3
1
1
mit Aufgaben
1
Bausteine zur Wiederholung und Vertiefung: Faktorisieren
Arten
Eine Summe kann in ein Produkt
umgewandelt (faktorisiert) werden
durch:
I.
Ausklammern
Beispiele
Summe
Übungen
Produkt
Faktorisieren
3x + 9y – 12
=
3 (x + 3y – 4)
2x3 – 4x2 + 6x
=
2x (x2 – 2x + 3)
3 (x + 5) – 6x (x + 5)
=
(x + 5) ( 3 – 6x)
x2 + 4x + 4 = x2 + 2. 2 . x + 22
=
(x + 2)2
9x2 - 30 xy + 25y2
=
(3x - 5y)2
81a2 – 64b2
=
(9a + 8b) (9a – 8b)
(x + 3)2 – 25
=
(x + 3 + 5) (x + 3 – 5) =
=
(x + 8) (x – 2)
Zur Wiederholung:
Jeder Summand muß durch den
ausgeklammerten Term dividiert
werden .
II. Binomische Formeln
Zur Wiederholung:
(a + b )2 = a2 + 2ab + b2
(a - b )2 = a2 - 2ab - b2
(a – b) (a + b) = a2 – b2
III. Linearfaktorenzerlegung
Zur Wiederholung:
Manche quadratischen Terme
lassen sich nach der
quadratischen Ergänzung in
Faktoren zerlegen
x2 – 4x – 12 =
x2 – 4x +22 – 22 – 12 =
(x – 2)2 – 16
=
(x – 2 +4) ( x – 2 – 4) =
=
(x + 2) (x – 6)
1.
2.
3.
4.
5.
6.
12a + 16b + 24c =
3x2 – 6xy =
9x4 + 6x3 – 3x2 =
144a2b2 – 12ab =
10x (x + y) + 12y (x + y) =
4 (2a – 1) – 8a (2a – 1) =
1.
2.
3.
4.
5.
x2 + 8 x + 16 =
r2 – 6r + 9 =
4y2 + 4y + 1 =
144 – 100a2 =
1 – 0,25x2 =
1.
2.
3.
4.
(x – 2)2 – 16 =
(x + 4)2 – 25 =
(y – 12)2 – 16 =
(2x + 4)2 – 25 =
5.
6.
7.
8.
9.
10.
x2 + 8x + 12 =
x2 – 12x + 27 =
y2 – 9y + 14 =
x2 + 4x – 5 =
a2 – 8a + 7 =
x2 – 5x + 6 =
Lösungen zu I.
Lösungen zu II.
Lösungen zu III.
1. 4 (3a + 4b + 6c)
1. (x + 4)2
1. (x – 2 + 4) (x – 2 – 4) = (x + 2) (x – 6)
2. 3x (x – 2y)
2. (r – 3)2
2. (x + 4 + 5) (x + 4 – 5) = (x + 9) (x – 1)
3. 3x2 (3x2 + 2x – 1)
3. (2y + 1)2
3. (y – 12 + 4) (y – 12 – 4) = (y – 8) (y – 16)
4. 12ab (12ab – 1)
4. (12 – 10a) (12 + 10a)
4. (2x + 4 + 5) (2x + 4 – 5) = (2x + 9) (2x – 1)
5. (x + y) (10x + 12y)
5. (1 – 0,5x) (1 + 0,5x)
6. (2a – 1) (4 – 8a)
5. x2 + 8x + 42 – 42 + 12 = (x + 4)2 – 4 =
= (x + 4 + 2) (x + 4 –2) = (x + 6) (x + 2)
6. x2 – 12x + 62 – 62 + 27 = (x – 6)2 – 9 =
= (x – 6 + 3) (x – 6 – 3) = (x – 3) (x – 9)
7. y2 – 9y + 4,52 – 4,52 + 14 = (y – 4,5)2 – 6,25 =
= (y – 4,5 + 2,5) (y – 4,5 – 2,5) =
= (y – 2) (y – 7)
8. x2 + 4x + 22 – 22 – 5 = (x + 2)2 – 9 =
= (x + 2 + 3) (x + 2 – 3) = (x + 5) (x – 1)
9. a2 – 8a + 42 – 42 + 7 = (a – 4)2 – 9 =
= (a – 4 + 3) (a – 4 – 3) = (a – 1) (a – 7)
10. x2 – 5x + 2,52 – 2,52 + 6 = (x – 2,5)2 – 0,25 =
= (x – 2,5 + 0,5) (x – 2,5 – 0,5) =
= (x – 2) (x – 3)
Bausteine zur Wiederholung oder Vertiefung: Beziehungen zwischen Seiten und Winkeln im Dreieck
Formeln
c>a  >
c > b  > 
Satz
Im Dreieck liegt der größten Seite der
größte Winkel gegenüber
Veranschaulichung
Je größer ein Winkel in einer Ecke wird, um so größer wird die
gegenüberliegende Seite:
a>b  >
a+b>c
b+c>a
Zwei Dreiecksseiten zusammen sind
immer größer als die dritte Seite
c+a>b
Die Strecke ist die kürzeste Verbindung zwischen zwei Punkten:
C
b
a
A
B
c
Der Winkel * ist Nebenwinkel zu  und Außenwinkel im Dreieck:
C

* =  + 
* =  + 
* =  + 
Jeder Außenwinkel im Dreieck ist gleich
der Summe der nichtanliegenden
Innenwinkel

A
*

B
Bausteine zur Wiederholung und Vertiefung: Binomische Formeln
Formeln
I. (a + b )2 = a2 + 2ab + b2
Beispiele
(3 + x)2 = 32 + 2 . 3 . x + x2 = 9 + 6x + x2
doppeltes Produkt
(5x + 3y)2 = (5x)2 + 2 . 5x . 3y + (3y)2 = 25x2 + 30xy + 9y2
Übungen
1.
2.
3.
4.
(12a + b)2 =
(0,5xy + 2)2=
(2x2 + 5)2 =
(1,5 + 10x2)2
2
5
3
2 2
3 2
3 .2
2 2
9 2
4 2 5. ( a + b )2 =
.
( a + b ) = ( a) + 2
a
b + ( b) =
a + ab + b
3
5
4
3
4
4
3
3
16
9
6. (1 + 0,5b)2 =
7. (3,6x + 2,4y) (3,6x - 2,4y) =
Finde selbst weitere Beispiele!
II. (a - b
)2
=
a2
- 2ab +
b2
(3 - x)2 = 32 - 2 . 3 . x + x2 = 9 - 6x + x2
doppeltes Produkt
(5x - 3y)2 = (5x)2 - 2 . 5x . 3y + (3y)2 = 25x2 - 30xy + 9y2
3
2
3
3
2
2
9 2
4
( a - b )2 = ( a)2 - 2 . a . b + ( b)2 =
a - ab + b2
4
3
4
4
3
3
16
9
Achtung: Die II. Binomische Formel unterscheidet sich von der I. Binomischen Formel nur durch das
Minuszeichen beim doppelten Produkt (fett gedruckt!)
III. (a – b) (a + b) = a2 – b2
(3 - x) ( 3 + x) = 32 – x2 = 9 – x2
(5x + 3y) (5x – 3y) = (5x)2 – (3y)2 = 25x2 – 9y2
(
3
2
3
2
3
2
9 2 4 2
a b ) ( a + b ) = ( a)2 - ( b)2 =
a b
4
3
4
3
4
3
16
9
1.
2.
3.
4.
(100 – ab)2 =
(14x2 – 1)2 =
(1,2 – 0,5y3)2 =
(6s – 12t)2 =
5. (
3
4
a – b)2 =
4
9
6. (2,5xy – y)2 =
7. (
3
a – 4)2 =
2
Finde selbst weitere Beispiele!
1.
2.
3.
4.
5.
6.
7.
(3x – 4y) (3x + 4y) =
(22 – 3a) (22 + 3a) =
(0,5x + 1) (0,5x – 1) =
(2ab2 – 3) (2ab2 + 3) =
(a + 3b) (3b – a) =
( 0,2 – x2) (0,2 +x2) =
196 . 204 = (200 – 4) (200 + 4) =
Finde selbst weitere Beispiele!
Lösungen zu I.
1.
2.
3.
4.
144a2 + 24ab + b2
0,25x2y2 + 2xy + 4
4x4 + 20xy + 25
2,25 + 30x2 + 100x4
5.
4 2
1
25 2
a + 1 ab +
b
25
3
9
6. 1 + b + 0,25b2
7. 12,96x2 - 5,76y2
Lösungen zu II.
1.
2.
3.
4.
10000 – 200ab + a2b2
196x4 – 28x2 + 1
1,44 – 1,2y3 + 0,25y6
36s2 – 144st + 144t2
5.
9 2 2
16 2
a - ab +
b
16
3
81
6. 6,25x2y2 – 5xy2 + y2
7. 2,25a2 – 12a + 16
Lösungen zu III.
1.
2.
3.
4.
5.
6.
7.
9x2 – 16y2
484 – 9a2
0,25x2 – 1
4a2b4 – 9
9b2 – a2
0,04 – x4
40000 – 16 = 39984
Baustein zur Wiederholung oder Vertiefung: Geometrische Ortslinien
Definition
Allgemein
Linien, deren Punkte eine gemeinsame
(geometrische) Eigenschaft besitzen, heißen
Ortslinien.
Die Kreislinie k
Die Kreislinie ist die Ortslinie für alle Punkte P,
die von einem festen Punkt M (Mittelpunkt)
gleiche Entfernung (Radius) haben.
Die Mittelsenkrechte m
Die Mittelsenkrechte ist die Ortslinie für alle
Punkte P, die von zwei festen Punkten A und B
die gleiche Entfernung haben.
Kurzschreibweise
Veranschaulichung
P
k(M;r)
M
k = {P/ PM = r}
m[AB]
p
m[AB] = {P/ AP = PB }
B
A
m
Die Winkelhalbierende w
Die Winkelhalbierende ist die Ortslinie für alle
Punkte P, die von den Winkelschenkeln g und h
gleichen Abstand d (Distanz) haben.
r
M
w()
w( ) = {P/ d( P ; g ) = d( P ; h )
P
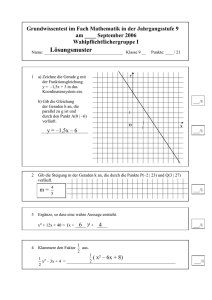
Bausteine zur Wiederholung oder Vertiefung: Lineare Gleichungen (2)
Baustein
III.Modell
Beispiel
III.
1.)
3 x
= 3 . 9
9
Übungen
G=Q
3 – x = 27
Merke:
2.
Grundmodell
Tauchen in einer Gleichung
Brüche oder Bruchterme auf,
kann man durch Multiplizieren
der Gleichung mit dem
Hauptnenner zu einer Gleichung
ohne Brüche oder Bruchterme
(Grundmodell) gelangen.
Achtung: Bruchterm!
Der Nenner darf nicht 0 werden!
Man braucht eine
Definitionsmenge D, das ist die
Grundmenge o h n e die Zahlen,
die den Nenner 0 werden
lassen!
Seitentauschen ist
erlaubt!
III. 1.) 1.
– x = 24
x = - 24
L = {- 24}
3.
Probe: Einsetzen
3  (24)
=3
9
27
= 3 (w)
9
2.)
5
= 2 . (x + 3)
x3
4.
5.
G=Q
D = Q \ {-3}
5 = 2x + 6
2.) 1.
2.
Grundmodell
2x + 6 = 5
2x
=-1
x = - 0,5
3.
L = { - 0,5}
4.
Probe: Einsetzen
5
=2
 0,5  3
5
=2
2,5
2 = 2 (w)
5.
6.
3 x
=3
5
24  2 x
=x
4
10  5 x
=-x
4
x  12
=2+x
9
2(3  x)
=-3
9
3
=3
9 x
3  2x
=1
4  2x
5
=2
x3
3
6
=
x4 5
3
2
=
12  x 12
2
3
=0
3x  4 7
L = { 12 }
L={4}
L = {-
10
}
9
L = { - 0,75 }
L = { 16,5 }
D = Q \ {- 9}
L={-8}
D = Q \ {2}
L = { 0,25 }
D = Q \ {-3}
L = { - 0,5 }
D = Q \ {4}
L = { 6,5 }
D = Q \ {12}
D = Q \ {-
4
}
3
L = {-6}
L={
2
}
9
Bausteine zur Wiederholung oder Vertiefung: Lineare Gleichungen (1)
Baustein
I. Grundmodell
I. 3x + 7
Beispiel
=x+4
Übungen
G=Q
I.
Merke:
„Alle Variablen nach links,
Alle Zahlen nach rechts“
3x – x + 7 = 4 – 7
2x = -3 :2
x = -1,5
5. 7y +
L={-3}
6.
7.
8.
9.
10.
Probe: Einsetzen
3 ( - 1,5 ) + 7 = - 1,5 + 4
- 4,5 + 7 = 2,5
2,5 = 2,5 ( w )
II.
II. Modell
Merke:
Das II. Modell kann durch
Ausmultiplizieren, Anwenden
der Binomischen Formeln und
Zusammenfassen auf das
Grundmodell zurückgeführt
werden
II. 5x (5x + 6) = (5x – 6)2 + 54 G = Q
25x2 + 30x = 25x2 - 60x + 36 + 54
30x =
- 60x + 90
Grundmodell
30x + 60x = 90
90x = 90:90
x = 1
1. 3x – 5 = 2x + 4
2. –4x + 8 = -5x + 2
3. 0,5y –1,5 = 3 - 2y
4. 3a – 9 = a – 6
L={1}
Probe: Einsetzen
5 (5 . 1 + 6) = (5 . 1 – 6)2 + 54
5 . 11
=
(-1)2 + 54
55
=
1
+ 54
55
=
55 (w)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
3 2
=
+ 6,5y
2 3
–1 – x = - 2x – 1
4x + 6 = - 6x + 6
–2,5y = 15 y + 35
22b – 33 = 11b + 121
10,5x + 1 = 10 x – 3
3 (x – 2) + 5 (7 – x) + 7x = 4 (x + 8)
5 (2x + 4) – 3 (x – 1) – 3 = 2 (x + 5)
(x + 4)2 = (x + 7)2 – 17x
(3- x)2 = 9 – 5x + x2
(3 – x) (6x + 2) = (3x + 1) (4 – 2x) – 4
(4x + 1)2 – 12x = (2x – 3)2 + 12x2
3 (x – 1) (x + 3) – 15 = 6x2 – 3 (x – 2)2
0,5x + 3,7 – 0,2 (x + 1,8) = 7,6 – 0,3 (x – 4)
4 (x + 5) (x – 5) = (2x – 10)2
(x + 2)2 – (x – 2)2 = 3 (4x + 10)
L= {9}
L= {-6}
L = { 1,8 }
L = { 1,5 }
L={-
5
}
3
L={0}
L={0}
L={-2}
L = { 14 }
L={-8}
L={3}
L={-2}
L={3}
L={0}
L={-1}
L={1}
L={-2}
L = { 9,1 }
L={5}
L = { - 7,5 }
III.Modell
IV.
1.)
Merke:
3 x
= 3 . 9
9
G=Q
Grundmodell
Tauchen in einer Gleichung
Brüche oder Bruchterme auf,
kann man durch Multipli-zieren
der Gleichung mit dem
Hauptnenner zu einer Gleichung
ohne Brüche oder Bruchterme
(Grundmodell) gelangen.
3 – x = 27
– x = 24
x = - 24
L = {- 24}
Probe: Einsetzen
3  (24)
=3
9
27
=3
9
3 = 3 (w)
Achtung: Bruchterm!
Der Nenner darf nicht 0 werden!
Man braucht eine
Definitionsmenge D, das ist die
Grundmenge o h n e die Zahlen,
die den Nenner 0 werden
lassen!
2.)
5
= 2 . (x + 3)
x3
G=Q
D = Q \ {-3}
3 x
=3
5
24  2 x
6.
=x
4
10  5 x
7.
=-x
4
x  12
8.
=2+x
9
2(3  x)
9.
=-3
9
( x  2)( x  2)
10.
=7
3
III. 1.) 1.
3.) 1.
2.
5 = 2x + 6
Grundmodell
7.
Seitentauschen ist erlaubt!
2x + 6 = 5
2x
=-1
x = - 0,5
Probe: Einsetzen
5
=2
 0,5  3
5
=2
2,5
2 = 2 (w)
8.
L = { - 0,5}
9.
10.
11.
3
=3
9 x
3 x
=4
2x
3  2x
=1
4  2x
5
=2
x3
3
6
=
x4 5
3
2
=
12  x 12
2
3
=0
3x  4 7
L = { 12 }
L={4}
L = {-
10
}
9
L = { - 0,75 }
L = { 16,5 }
Ungewönlich!
L = { - 5; + 5 }
D = Q \ {- 9}
L={-8}
D = Q \ {2}
L={
D = Q \ {2}
L = { 0,25 }
D = Q \ {-3}
L = { - 0,5 }
D = Q \ {4}
L = { 6,5 }
D = Q \ {12}
D = Q \ {-
4
}
3
5
}
3
L = {-6}
L={
2
}
9
Bausteine zur Wiederholung oder Vertiefung: Lineare Ungleichungen
Baustein
I. Grundmodell
I. 3x + 7
Beispiel
< x+4
Übungen
G=Q
II.
Merke:
„Alle Variablen nach links,
alle Zahlen nach rechts“
3x – x + 7 < 4 – 7
2x < -3 :2
x < -1,5
1. 3x – 5 < 2x + 4
2. –4x + 8 > -5x + 2
11. 0,5y –1,5 < 3 - 2y
12. 3a – 9 > a – 6
13. 7y +
L = {x/ x<-1,5}
14.
15.
16.
17.
Probe: Einsetzen e i n e r Lösungszahl
3 2
<
+ 6,5y
2 3
–1 – x  - 2x – 1
4x + 6 < - 6x + 6
22b – 33 > 11b + 121
10,5x + 1  10 x – 3
L = {x/x<9 }
L = {x/x>- 6 }
L = {y/y< 1,8}
L = {a/a> 1,5 }
L = {y/y< -
5
}
3
L = {x/x 0 }
L = {x/x< 0 }
L = {b/b> 14 }
L = {x/x - 8 }
3 ( - 2 ) + 7 <- 2 + 4
-6
+7< 2
1 < 2 (w)
III.
II. Grundmodell
II.
3x + 7
< 5x + 4
G=Q
Merke:
„Alle Variablen nach links,
alle Zahlen nach rechts“
und
Inversionsgesetz:
Bei Multiplikation bzw. Division
einer Ungleichung mit bzw.
durch eine n e g a t i v e Zahl
wird das < - bzw. > - Zeichen
u m g e k e h r t.
3x – 5x
< 4–7
-2x
< -3 :(-2)
x
> 1,5
Inversionsgesetz:
1. 5x –9 > 10x – 4
2. 8x +1 < 12x – 3
3. –2x < - x + 9
4. 3(y + 6) > 4y – 8
5. 4x + 6 < 6x + 6
6. 7y +
L = {x/ x> 1,5}
3
< 8y
2
7. 3 (x – 2) + 5 (7 – x) + 7x > 4 (x + 8) + 2x
8. (x + 2)2 – (x – 2)2 < 3 (4x + 10)
9. 3 (x – 1) (x + 3) – 15 > 6x2 – 3 (x – 2)2
Probe: Einsetzen e i n e r Lösungszahl
3.2+ 7
13
<5.2+4
< 14 (w)
Bausteine zur Wiederholung und Vertiefung: M8 - Extremwertbestimmung
L = {x/ x< -1}
L = {x/ x> 1}
L = {x/x > - 9}
L = {y/ y< 26}
L = {x/x> 0 }
L = {y/y> 1,5}
L = {x/ x<- 3 }
L = {x/x> - 7,5 }
L = {x/x< - 2 }
Erklärung / Schema
Besitzt ein quadratischer Term diese Form, dann kannst du direkt seinen
Extremwert ablesen: T(x) = a(x + b)² + c
oder: T(x) = c + a(x + b)²
Aus dieser Darstellung lassen sich drei Informationen ablesen:
Art (Maximum oder Minimum): Vorzeichen von a (+ => Min; - => Max.)
Extremwert: Ist die Zahl c
Belegung, für die der Extremwert angenommen wird: Gegenzahl von b
1. Bsp.: T(x) = +7(x +4)² 13
Antwort:
Tmin = 13 für x = 4
2. Bsp.: T(x) = 5 –2(x –3)²
Antwort:
Aufgaben
Weitere Aufgaben
Aufgabe 1
Aufgabe 4
T1(x) = 2(x –1)² +3 ;
T5(x) = (x +0)² +5
T2(x) = (x +5)² 4 ;
T6(x) = x² +1
T3(x) = 2(x –8)² ;
T7(x) = x²
T2(x) = (2x +3)(x 2)
Tmax = +5 für x = +3
Bsp.: T(x) = 2x² +12x -28
Ausklammern (Faktor vor dem Quadrat)
= 2 [ x² 6x +14 ]
Quadratisch ergänzen
= 2 [ x² 2·3·x +3² 9 +14 ]
Aufgabe 2
= 2 [ (x 3)² +5 ]
Aufgabe 5
T1(x) = 3x² +27x 0,75 ;
T5(x) = 5x² +50x 125
T2(x) = x² 10x +9 ;
T6(x) = 1,5x² +6x +15
T3(x) = 2x² 12x +18 ;
Binomische Formel
T7(x) =
T4(x) = 0,5x² x +4 ;
1
x² +2x
3
Ausmultiplizieren (eckige Klammer)
= 2(x 3)² 10
Antwort
Tmax = 10 für x = +3
Bsp.:
T1(x) = x(4 +x)
T3(x) = (x 1)² +4x 7
T4(x) = (x +1,5)² +2 ;
Jeder quadratische Term kann mit der quadratischen Ergänzung in die
gewünschte Form umgewandelt werden (höchstens vier Schritte)
Einfacher wird die Umformung,
wenn der Faktor a vor dem Quadrat
die Zahl +1 ist.
(dann entfallen Ausklammern und
Ausmultiplizieren)
Zunächst vereinfachen:
T(x) = x² +8x +15
= x² +2·4·x +4² 16 +15
= (x +4)² 1
Tmin = 1 für x = 4
Aufgabe 3
T1(x) = x2 16x +71 ;
T3(x) = x2  7x
T2(x) = x2 + 10x + 25 ;
T4(x) = x2 +x +1
Ein Rechteck mit dem
Umfang u = 24 cm
besitzt die Länge
l = AB = x cm.
Berechne seine Breite
b = BC in Abhängigkeit
von der Variablen x.
Berechne den extremen
Flächeninhalt Amax und
die zugehörige
Belegung von x.
Aufgabe 1
Lösungen
Aufgabe 4
Tmax = 3 für x = 1
Tmax = 5 für x = 0
Tmin = -4 für x = -5
Tmin = 1 für x = 0
Tmin = 0 für x = 8
Tmax = 0 für x = 0
Tmax = 2 für x = -1,5
Zwischenergebnis: T1(x) = x² +4x
Tmin = -4 für x = -2
Zwischenergebnis: T2(x) = 2x² -x -6
Tmin = -6,125 für x = 0,25
Zwischenergebnis: T3(x) = x² +2x -6
Tmin = -7 für x = -1
Aufgabe 2
Tmin = 61,5 für x = 4,5
Tmax = 0 für x = 5
Tmax = 34 für x = -5
Tmax = 21 für x = 2
Tmin = 0 für x = 3
Tmin = -3 für x = -3
Aufgabe 5
u = 2l +2b
...
( setze für l allgemein x cm ein )
( stelle nach b um )
b = (12 -x) cm
Tmin = 3,5 für x = 1
Aufgabe 3
Tmin = 7 für x = 8
Tmin = -12,25 für x = 3,5
Tmin = 0 für x = -5
Tmin = 0,75 für x = -0,5
A(x) = l · b
...
...
( setze ein: l=xcm , b=(12-x)cm )
( vereinfachen )
( quadratische Ergänzung )
Amax = 36 cm2 für x = 6
Bausteine zur Wiederholung und Vertiefung: Vierecke
Aufgabenstellung
Haus der Vierecke
Schreibe die Namen neben die Vierecke.
Überlege und sieh nach (Heft, Buch,
Formelsammlung): Wann nennt man ein Viereck
Rechteck, Quadrat, Parallelogramm, Raute,
Drachenviereck, (gleichschenkliges) Trapez ?
Zeichne in jedem Viereck die Diagonalen.
Kennzeichne auch alle rechte Winkel.
Zeichne (blau) Symmetrie- achsen und -punkte.
Zeichne Pfeile ein, die bedeuten sollen
"Jede/s ..... ist auch ein/e ....."
(z.B. Jedes Quadrat ist auch ein Rechteck =>
Pfeil vom Quadrat zum Rechteck)
Kennzeichne in jedem Viereck die Seiten, die
gleich lang sind (gleiche Bezeichnungen: a, b, ...)
Kennzeichne in jedem Viereck die Winkel, die
gleich groß sind (gleiche Bezeichnungen:   ...)
Welche Vierecke besitzen einen Umkreis?
(setze hinter den jeweiligen Namen ein U)
Welche Vierecke besitzen einen Inkreis?
(setze hinter den jeweiligen Namen ein I)
Überlege und sieh nach (Heft, Buch, FS): Wie erhält man den Mittelpunkt und den Radius vom
Umkreis: Mu: Schnitt der
r u:
Inkreis: Mi: Schnitt der
ri :
Bausteine zur Wiederholung und Vertiefung: Bruchterme (1)
Rechenschritte
Definitionsmenge D:
Enthält der Nenner
Variablen, dürfen nur solche
Zahlen eingesetzt werden,
für die der Nenner nicht Null
wird.
Alle diese Zahlen zusammen
bilden die Definitionsmenge.
Beispiel
1.
T1 (x) =
7
3 x
G=Q
Nenner untersuchen (wann wird dieser Null?)
3-x
= 0 +x

3
= x
Übung
T2(x) =
x 1
x ( x  4)
G=Q
Nenner untersuchen:
x(x + 4) = 0

x=0  x+4 =0

x=0 
x =-4
Daraus folgern wir: D = Q \ {- 4; 0 }
3.
T3(x) =
14x
6x  2x ²
G=Q
Nenner untersuchen:
6x - 2x² = 0
 2x ( 3 - x) = 0

x=0  3-x=0

x=0 
3 = x
Daraus folgern wir: D = Q \ {0 ; 3}
Lösungen:
G=Q
1.
2
x3
D = Q \ { -3}
2.
1 x
x2
D=Q\{2}
3.
x 1
x ²  3x
D=Q\{0;3}
4.
5x
4x ²  3x
D = Q \ { 0; - 1,25}
5.
5x
4x ²  12x  9
D = Q \ { - 1,5}
Daraus folgern wir Definitionsmenge D = Q \ { 3 }
Zahlen, für die der Nenner
Null wird, werden aus der
2.
Grundmenge
herausgenommen!
mit
Bausteine zur Wiederholung und Vertiefung: Bruchterme (2)
Rechenschritte
Beispiel
Erweitern und Kürzen
1.
Beim Erweitern wird Zähler
und Nenner mit derselben
Zahl multipliziert.
T1 (x)
=
7
3 x
Übung
 erweitert mit 2:
1.
2x
gekürzt mit x!
x
2.
1
erweitert mit 3y!
4y
3.
x
4
Zähler und Nenner mit 2 multiplizieren:
7*2
(3  x ) * 2
=
2.
T2(x)
=
3.
T3(x)
Beim Kürzen wird Zähler und
Nenner durch dieselbe Zahl
dividiert.
T4(x)
(für x  3)
14
 erweitert mit x:
6  2x
14x
=
(für x  0; 3)
6x  2x ²
=
=
4.
14
6  2x
2( x  1)
 gekürzt mit 2:
2x ( x  4)
x 1
x ( x  4)
x 1
 gekürzt mit x-1:
x ( x  1)
1
=
(für x  0; 1)
x
=
erweitern mit x+1!
M 8I / 9II - Bausteine zur Wiederholung und Vertiefung: Aufstellen einer Geradengleichung
Arten
Wenn du die Koordinaten von zwei
Geradenpunkten kennst, kannst du
die Gleichung g: y = mx + t dieser
Geraden berechnen!
Beispiel
Geg.: g = PQ mit P ( 4 | 3 ) und Q ( 2 |  6 )
1. A ( 1 | 2 )
; B(5|6)
2. C ( 2 | 8 )
; D ( 1 | 1 )
3. E ( 4 | 1 )
; F(2|3)
3  (6)
9
3

   1,5
42 6
2
4. G ( 5 | 0 )
; H ( 4 | 3,6 )
5. K ( 6 | 4 )
; L ( 2 | 4 )
63 9
3

   1,5
2  (4)
6
2
6. M ( 3 | 2 )
; N(6|8)
7. O ( 1 | 6 )
; P ( 2 | 1,5 )
8. Q ( 1,5 | 3 )
; R(5|3)
9. S ( 1 | 7,5 )
; T ( 1,5 | 5 )
I. Möglichkeit:
a) Berechne zuerst die Steigung m
mit der Formel
m
y 2  y1
x 2  x1
(siehe Formelsammlung)
Setze die Koordinaten der Geradenpunkte in die Formel ein!
Du kannst entweder mit P oder mit Q beginnen!
m
oder
m
y P  yQ
x P  xQ
yQ  y P
xQ  x P


Übungen
Gegeben sind jeweils 2 Punkte einer Geraden.
Berechne die zugehörige Funktionsgleichung!
G=QxQ
Setze m und einen Geradenpunkt ein in y = m x + t !
b) Berechne nun den
y-Achsenabschnitt t
P ( 4 | 3 ) einsetzen in
y = 1,5 x + t
3 = 1,5  ( 4 ) + t
3=6+t
t = 3
Du kannst t genauso durch Einsetzen von Q berechnen!
Ergebnis:
g : y = 1,5 x – 3
10. U ( 13 | 2,5 ) ; V ( 26 | 17 )
II. Möglichkeit:
a) Berechne die Steigung m
eines Vektors auf g
 vx 
v  PQ   
vy 
m
Geg.: g = PQ mit P ( 4 | 3 ) und Q ( 2 |  6 )
 2  ( 4)   6 
   
PQ  
  6  3    9
y = 2,5x – 3,5
9
3
   1,5
6
2
y = 0,5x + 4
m
vy
y = m ( x – xP ) + yP
b) Setze nun m und die
Koordinaten eines
Geradenpunktes in die PunktSteigungs-Form ein
y=3
y = x + 5
b) weiter wie bei I. b)
a) Berechne die Steigung m
mithilfe der Punkt-SteigungsForm
y = 0,4x – 2
y = 2x – 4
vx
III. Möglichkeit:
Schreibe die Aufgabennummer vor das zugehörige
Ergebnis!
y = 5x  2,5
Berechne m durch Einsetzen der beiden Geradenpunkte in die
Punkt-Steigungsform (oder mit dem Verfahren I.a) bzw. II.a))!
Du kannst sowohl mit P als auch mit Q beginnen!
P ( 4 | 3 ) eingesetzt :
y = m [ x – ( 4 ) ] + 3
y=m(x+4)+3
Q ( 2 | 6 ) eingesetzt:
6=m(2+4)+3
6=6m+3
9=6m
m =  1,5
m =  1,5 eingesetzt in y = m ( x + 4 ) + 3
y = 1,5 ( x + 4 ) + 3
Punkt-Steigungs-Form
y = 1,5 x – 6 + 3
y = 1,5 x – 3
Normalform
y = 3x + 2
y = 4
y=
2
x+4
3
Bausteine zur Wiederholung und Vertiefung : Einfache Termumformungen
Arten
Beispiele
Übungen
Ordne richtig ein:
2 + x; 11x2 + 1; 3x; x2; x2 + 4; a2 + 4; 4a2; a2; 8a;
Grundwissen:
Summenterme
T1(x) = 3 + x
T2(y) = 8 + y
Produktterme
T1(x) = 3x
T2(a) = 4a2
Lineare Terme
T1(x) = 3x
T2(a) = 4a
Quadratische Terme
T1(x) = 3 + x2
T2(y) = 9 + 2y2
Gleichartige Terme
T1(x) = 3x
T2(x) = 7x
Addition und Subtraktion
3x + 7x = 10x
4y2 + 9y2 = 13y2
8x2 + 6x – 3x2+ 2x = 5x2 + 8x
1.
2.
3.
4.
5.
6.
9a + 3a + 16a =
–2x –3x –5x =
2x2 + 3x2 – 8x2 =
–0,5xy + 1,5 xy – xy =
6a + 6a2 +2a – 6a2 =
–11 +15x3 – 4 – 5x3 + 7 =
Multiplikation und Division
x2 . x3 = x2+3 =x5
3x . 7x = 21 x2
4xy . 3x = 12x2y
Beachte die Potenzgesetze!
x6 : x4 = x6-4 =x2
6x5 : 2x2 = 3x3
12x3 : 3x2 = 4x
7.
8.
9.
10.
11.
12.
13.
x2 . x3 . x 3 =
3x4 . x =
-10 x2 . (-3) x2 =
5ab : 5 =
20x3 : 2x
–12ab2 : 3a =
8x : 2x =
Achtung!!!!!!
3x + 5x = 8x
Aber: 3x . 5x = 15x2
2x + 5x2 = 2x + 5x2 (nicht gleichartig!)
Aber: 2x. 5x2 = 10x3
6a + 3b = 6a + 3b (nicht gleichartig!)
Aber: 6a . 3b = 18ab
14.
15.
16.
17.
18.
5a 2 +3a2 =
13a + 10a3 =
–3x – 4x =
6b + 3 =
4ab – 5ba =
Es können nur gleichartige
Terme addiert (subtrahiert)
werden. Die Koeffizienten
(Beizahlen) werden addiert!
5a2 . 3a2 =
13a. 10a3 =
-3x . (-4x) =
6b . 3 =
4ab : 5ba =
Ergebnisse
Summenterme
: 2 + x; 11x2 + 1; x2 + 4; a2 + 4
Produktterme
: 3x; 8a
Lineare Terme
. 2 + x ; 3x; 8a
Quadratische Terme
: 11x2 + 1; x2; x2 + 4; a2 + 4; 4a2; a2
Gleichartige Terme
: 4a2; a2
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
28a
–10x
–3x2
0
8a
10x3 – 8
x8
3x5
30x4
1ab = ab
10x2
–4b2
4
8a2
13a + 10a3
–7x
6b + 3
–1ab = -ab
15a4
130a4
12x2
18b
0,8b
Baustein zur Wiederholung und Vertiefung: Berechnung der vierten Parallelogrammecke
Aufgabenstellung
Beispiel
5
Berechnung der
vierten
Parallelogrammecke
4
C
Aufgaben:
3
D
Das Viereck ABCD ist ein Parallelogramm.
2
B
1. Gegeben sind die Punkte
A(2/-1), B(5/1) und D(-2/2)
Bestimme durch Rechnung die
Koordinaten des Punktes C so, dass das
Viereck ABCD ein Parallelogramm ist.
Übungen
Bestimme durch Rechnung die Koordinaten
des fehlenden Punktes.
1
-3
-2
-1
O
1
-1
2
3
4
5
6
1.
A(-3/-1), B(2/-3) und D(-1/3)
2.
B(2/-1), C(5/4) und D(-2/2)
3.
A(-2/-3), B(5/1) und C(3/4)
4.
A(0/1), B(5/-3) und D(3/3)
5.
B(1/-2), C(5/1) und D(2/4)
A
1.Möglichkeit:

Pfeilkette

1.Möglichkeit:

Pfeilkette
OC = OA  AB  BC
wegen ABCD Parallelogramm gilt:
  2
OA =  
1 
5  2  3 
 =  
AB = 
1  ( 1)   2 
BC = AD
  2  2    4
 =  
AD = 
 2  ( 1)   3 
Spitze minus Fuß !!
  2
3
  4
OC =          OC =
1 
2
3 
1 
 
4
C(1/4)
2.Möglichkeit:
2.Möglichkeit:
C(x/y)
Ist das Viereck ABCD ein Parallelogramm dann gilt:

AB = DC
oder

AD = BC
 AB
=
DC
oder
 3   x  ( 2) 
  = 

2  y  2 
 -4 = x –
 3= y-1
y=4
d.h.
AD = BC
  4   x  5
  = 

 3   y  1
 3= x+2
 2= y–2
x=1

x=1
C(1/4)
y=4
5
C
4
3
Aufgaben:
2
D
2. Gegeben sind die Punkte
A(1/-2), D(-2/1) und M(2/1)
-3
-2
-1
AC = 2 AM
3
4
5
Bestimme durch Rechnung die Koordinaten
der fehlenden Punkte.
6
-2A
1.Möglichkeit:
C(xC/yC)
AM = MC
und
DM = MB
 2  ( 2)   x  2 

 = 

1  1
  y 1
 1 = xC – 2  xC = 3
 4 = x B – 2  xB = 6
 3 = yC – 1  yC = 4
 0 = yB – 1  yB = 1
C(3/4)
B(6/1)
2.Möglichkeit:
C(xC/yC)
AC = 2 AM






1.
A(-2/-3), D(-1/2) und M(3/0)
2.
A(1/-4), B(5/-1) und M(2/1)
3.
B(4/-2), C(3/3) und M(0/1)
B(xB/yB)
2 1   x  2

 = 

1  ( 2)   y  1 
d. h.
2.Möglichkeit:
2
B
-1
1.Möglichkeit:
AM = MC
M
1
M ist der Schnittpunkt der
Diagonalen eines Parallelogramms
ABCD.
Bestimme durch Rechnung die
Koordinaten der Punkte B und
C.
Das Viereck ABCD ist ein Parallelogramm.
1
B(xB/yB)
und
DB = 2 DM





