I Grundkompetenzen im gemeinsamen Kern Zahlen und Maße
Werbung
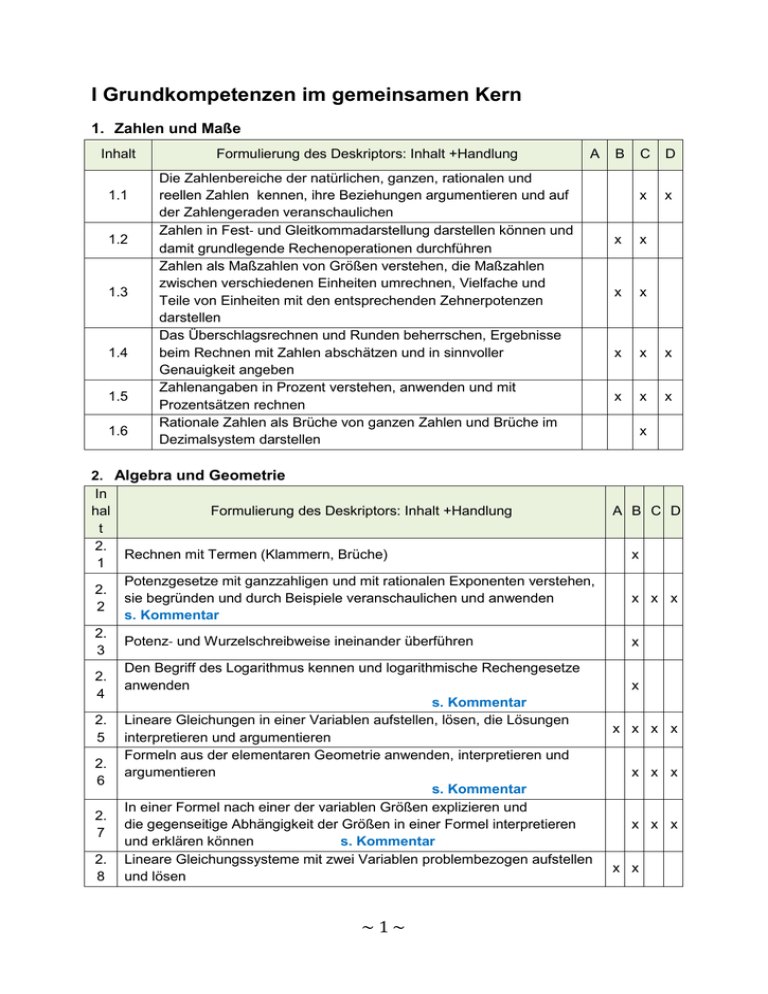
I Grundkompetenzen im gemeinsamen Kern 1. Zahlen und Maße Inhalt 1.1 1.2 1.3 1.4 1.5 1.6 Formulierung des Deskriptors: Inhalt +Handlung A Die Zahlenbereiche der natürlichen, ganzen, rationalen und reellen Zahlen kennen, ihre Beziehungen argumentieren und auf der Zahlengeraden veranschaulichen Zahlen in Fest‐ und Gleitkommadarstellung darstellen können und damit grundlegende Rechenoperationen durchführen Zahlen als Maßzahlen von Größen verstehen, die Maßzahlen zwischen verschiedenen Einheiten umrechnen, Vielfache und Teile von Einheiten mit den entsprechenden Zehnerpotenzen darstellen Das Überschlagsrechnen und Runden beherrschen, Ergebnisse beim Rechnen mit Zahlen abschätzen und in sinnvoller Genauigkeit angeben Zahlenangaben in Prozent verstehen, anwenden und mit Prozentsätzen rechnen Rationale Zahlen als Brüche von ganzen Zahlen und Brüche im Dezimalsystem darstellen 2. Algebra und Geometrie In hal Formulierung des Deskriptors: Inhalt +Handlung t 2. Rechnen mit Termen (Klammern, Brüche) 1 Potenzgesetze mit ganzzahligen und mit rationalen Exponenten verstehen, 2. sie begründen und durch Beispiele veranschaulichen und anwenden 2 s. Kommentar 2. Potenz‐ und Wurzelschreibweise ineinander überführen 3 Den Begriff des Logarithmus kennen und logarithmische Rechengesetze 2. anwenden 4 s. Kommentar 2. Lineare Gleichungen in einer Variablen aufstellen, lösen, die Lösungen 5 interpretieren und argumentieren Formeln aus der elementaren Geometrie anwenden, interpretieren und 2. argumentieren 6 s. Kommentar In einer Formel nach einer der variablen Größen explizieren und 2. die gegenseitige Abhängigkeit der Größen in einer Formel interpretieren 7 und erklären können s. Kommentar 2. Lineare Gleichungssysteme mit zwei Variablen problembezogen aufstellen 8 und lösen ~1~ B C D x x x x x x x x x x x x x A B C D x x x x x x x x x x x x x x x x x x 2. 9 2. 10 2. 11 2. 12 2. 13 2. 14 Die verschiedenen möglichen Lösungsfälle von linearen Gleichungssystemen mit zwei Variablen argumentieren und grafisch veranschaulichen Probleme aus verschiedenen Anwendungsbereichen in lineare Gleichungssysteme mit mehreren Variablen übersetzen, mit Hilfe von Technologieeinsatz lösen und das Ergebnis in Bezug auf die Problemstellung interpretieren und argumentieren Quadratische Gleichungen in einer Variablen aufstellen, lösen und die verschiedenen möglichen Lösungsfälle interpretieren und argumentieren Exponentialgleichungen vom Typ a kx = b nach der Variablen x auflösen Komplexere Exponentialgleichungen oder Gleichungen mit trigonometrischen Funktionen mit Einsatz von Technologie auflösen Sinus, Kosinus und Tangens eines Winkels als Seitenverhältnisse im rechtwinkeligen Dreieck modellieren, interpretieren, argumentieren und rechtwinkelige Dreiecke auflösen x x x x x x x x x x x x x x x x x Kommentar 2.2: Die folgenden Gesetze sind gemeint: am · an = am+n ; am · bm = (a · b)m und (am)n = amn mit m,n Є Z oder Q Kommentar 2.4: Die folgenden Gesetze werden benötigt, hier einfachheitshalber mit dekadischem Logarithmus angeführt: lg(ab) = lg a +lg b, lg (a /b)=lg a – lg b, lg an = nlg a lg a = ln a/ln 10 und ln a = lg a/ lg e Kommentar 2.6: Es wird vorausgesetzt, dass die Formeln der elementaren Geometrie aus der Unterstufe bekannt sind: Ähnlichkeitssätze, Pythagoreischer Lehrsatz, Flächen und Volumsberechnungen. Kommentar 2.7: Formeln können aus allen Gebieten vorkommen z.B. aus Technik, Wirtschaft und Naturwissenschaft. Sie müssen nicht im Fachzusammenhang verstanden werden, dennoch soll die Abhängigkeit der variablen Größen voneinander interpretiert werden können und die Umformung nach einer der variablen Größen kein Problem darstellen. 3. Funktionale Zusammenhänge Inh Formulierung des Deskriptors: Inhalt + Handlung alt Die Definition der Funktion als eindeutige Zuordnung kennen und 3.1 kommunizieren Funktionen als Modelle zur Beschreibung der Abhängigkeit zwischen 3.2 Größen verstehen und erklären Eine lineare Gleichung in 2 Variablen als Beschreibung einer linearen 3.3 Funktion interpretieren (Geradengleichung: y = kx+d) s. Kommentar Eine lineare Funktion grafisch im Koordinatensystem darstellen und die 3.4 Bedeutung der Parameter k und d verstehen und interpretieren Lineare Funktionen aus verschiedenen Problemstellungen modellieren 3.5 und sie zur Lösung des Problems einsetzen, die Lösung interpretieren und argumentieren ~2~ A B C D x x x x x x x x x x x x 3.6 3.7 3.8 3.9 3.1 0 3.1 1 3.1 2 Potenzfunktionen und Polynomfunktionen (bis zum Grad 4) grafisch darstellen und ihre Eigenschaften interpretieren s. Kommentar Exponentialfunktionen grafisch darstellen, als Zu- und Abnahmemodelle interpretieren, die Begriffe "Verdopplungs- und Halbwertszeit" kennen, berechnen und im Kontext deuten, sowie den Einfluss der Parameter von Exponentialfunktionen verstehen, interpretieren und deuten s. Kommentar Lineare Funktionen und Exponentialfunktionen strukturell vergleichen, die Angemessenheit einer Beschreibung mittels linearer Funktionen oder mittels Exponentialfunktion bewerten Die Nullstelle(n) von Funktionsgraphen bestimmen und als Lösung(en) einer Gleichung interpretieren (Technologieeinsatz) Schnittpunkte zweier Funktionsgraphen bestimmen und als Lösungsmenge einer Gleichung oder eines Gleichungssystems mit 2 Variablen interpretieren (Technologieeinsatz) Praxisbezogene Problemstellungen mit geeigneten Funktionstypen beschreiben (Aufstellen einer Funktionsgleichung) Sinus-, Kosinus- und Tangensfunktionen ausgehend vom Einheitskreis mit Winkel im Grad- und im Bogenmaß grafisch darstellen und argumentieren x x x x x x x x x x x x x x x x x x 3.3 Kommentar: Mit Variablen und Parametern umgehen können, auch wenn sie nicht mit den Standardsymbolen (x für unabhängige Variable, k für Anstieg, d für Ordinatenabschnitt) bezeichnet werden! 3.6 Kommentar: Prototypische Verläufe der Graphen von Polynomfunktionen in Abhängigkeit vom Grad (bis 4) sowie den Zusammenhang zwischen dem Grad der Polynomfunktion und der Anzahl der Null-, Extrem- und Wendestellen wissen 4.6 3.7 Kommentar: die prototypischen Verläufe der Graphen von f(x) = a · bx mit b Є R+ bzw. f(x) = a · e λ·x; kennen; die Bedeutung der Parameter a und b (bzw. λ) kennen und die Parameter in unterschiedlichen Kontexten deuten können 4. Analysis Inhalt 4.1 4.2 4.3 4.4 4.5 Formulierung des Deskriptors: Inhalt +Handlung Über einen intuitiven Grenzwertbegriff und über einen intuitiven Stetigkeitsbegriff von Funktionen verfügen Differenzen- und Differentialquotient als Änderungsraten verstehen und zur Lösung von Aufgaben einsetzen, die Lösung interpretieren und argumentieren A B x ~3~ D x x Den Begriff Ableitungsfunktion kennen Elementare Grundfunktionen differenzieren und die Ableitung von aus diesen zusammengesetzten Funktionen mit Hilfe der Ableitungsregeln bestimmen s. Kommentar Eigenschaften von Funktionen wie Monotonie, lokale Extrema, Krümmungsverhalten, Wendestellen am Graphen erkennen und C x x x x x x x x x x x 4.6 4.7 4.8 4.9 4.10 mit Hilfe der Ableitung(sfunktion) modellieren, berechnen, interpretieren und argumentieren Den Zusammenhang zwischen Funktion und Ableitungsfunktion erkennen und beschreiben, in deren grafischer Darstellung interpretieren und argumentieren Den Begriff Stammfunktion kennen sowie den Zusammenhang zwischen Funktion und Stammfunktion in deren grafischer Darstellung erkennen und beschreiben Stammfunktionen von Potenz- und Polynomfunktionen mit dem unbestimmten Integral berechnen Den Begriff des bestimmten Integrals auf der Grundlage eines intuitiven Grenzwertbegriffes als Grenzwert einer Summe von Produkten deuten und beschreiben Das bestimmte Integral als orientierten Flächeninhalt deuten und die Flächen berechnen s. Kommentar x x x x x x x x x x Kommentar 4.4 Die Ableitungen von Potenz-, Polynom- und Exponentialfunktionen. Einfache Regeln des Differenzierens kennen und anwenden können: Summenregel: (f(x)+g(x))’ = f ’(x) + g’(x), Faktorregel: (k · f(x))’ = k · f’(x) Kettenregel: (f(g(x))’ = f ’(g(x)) · g’(x) Kommentar 4.10 Mit Technologieeinsatz die Fläche unter Berücksichtigung evt. Nullstellen von bekannten Funktionen bestimmen können, ohne Technologieeinsatz Flächen mit dem bestimmten Integral von Potenz- und Polynomfunktionen händisch berechnen können. 5. Stochastik Inhalt 5.1 5.2 5.3 5.4 5.5 5.6 Formulierung des Deskriptors: Inhalt +Handlung A B C D x x x x x x x x x x x x x x x x x x x Daten erheben, Häufigkeitsverteilungen (absolute, relative und prozentuelle Häufigkeiten) grafisch darstellen und interpretieren sowie die Auswahl einer bestimmten Darstellungsweise problembezogen argumentieren s. Kommentar Mittelwerte und Streuungsmaße von Häufigkeitsverteilungen berechnen, interpretieren und argumentieren Arithmetisches Mittel und Standardabweichung, Median s. Kommentar Den Wahrscheinlichkeitsbegriff kennen, verwenden und deuten Die Additions‐ und Multiplikationsregel auf einander ausschließende bzw. unabhängige Ereignisse anwenden Die Binomialverteilung kennen und im Kontext nutzen und interpretieren (Erwartungswert, Varianz, Wahrscheinlichkeits- und Verteilungsfunktion) Die Normalverteilung im Kontext nutzen und interpretieren ~4~ 5.7 Auswirkung von Erwartungswert und Standardabweichung auf die Normalverteilungskurve kennen und argumentieren x x Kommentar 5.1. Die wichtigsten Darstellungsweisen kennen: Stab, Säule, Balken, Kreis, Torte, Histogramm, Boxplot. Die Darstellungsweisen interpretieren und begründen können, für welche Art von Problemstellungen und Untersuchungen sich eine bestimmte Darstellungsweise besonders gut eignet. Dabei sollte auch die Manipulierbarkeit von Daten durch spezielle Darstellungsweisen diskutiert werden. Kommentar 5.2 Hinweis: Es werden die folgenden Bezeichnungen gewählt: Für empirisch erhobene Daten xi Mittelwert x , Standardabweichung (Grundgesamtheit, statt bei einer Vollerhebung auch ) Standardabweichung einer Stichprobe als Schätzung auf die Grundgesamtheit (bzw. für große Stichproben) In vielen Fällen wird in Lehrbüchern nicht klar zwischen den verschiedenen Formeln unterschieden, daher gilt für die Reifeprüfung (bis auf Weiteres) folgende Festsetzung: Beide Formeln für s (bzw. ) gelten als richtige Lösung, gleichgültig, ob es sich um die Standardabweichung einer Grundgesamtheit oder um die Standardabweichung einer Stichprobe handelt. ~5~

