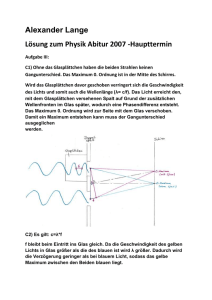
Document

0. Aufgabenstellung
1. Messen Sie die U-I-Kennlinie des Versuchsrohres für verschiedene Werte der
Kathodentemperatur und des Hg-Dampfdrucks, und ermitteln Sie die optimalen
Betriebsbedingungen !
2. Bestimmen Sie das erste Anregungsniveau von Quecksilber und geben Sie die Wellenlänge
der entsprechenden Spektrallinie an !
3. Bestimmen Sie die Kontaktspannung zwischen Katode und Gitter !
4. Diskutieren Sie den Einfluß von Katodentemperatur und Hg-Dampfdruck auf die
Meßergebnisse !
5. Bestimmen Sie die Ionisierungsspannung der Hg-Atome !
1. Theoretische Grundlagen
Ziel des Franck-Hertz-Versuches ist der Nachweis der Existenz diskreter Energieniveaus in
den Atomen. Im Mittelpunkt steht also die experimentelle Bestätigung der Bohrschen
Postulate1 :
1. In einem Atom bewegt sich ein Elektron nach den Gesetzen der klassischen Mechanik auf
diskreten Kreisbahnen mit den Energien En.
2. Die Bewegung des Elektrons erfolgt strahlungslos. Beim Übergang des Elektrons von
einem stationären Zustand mit Energie Ea in einen stationären Zustand niedrigerer Energie
Ee wird ein Photon der Frequenz ν
=
Ea − Ee
c
=
h
λ
emittiert.
3. Der Drehimpuls eines Elektrons in einem stationären Zustand nimmt nur die diskreten
Werte
m vh =
nh
2π
an, wobei n eine natürliche Zahl ist.
Die Idee zur Bestätigung der Bohrschen Theorie lag darin, Wechselwirkungen zwischen frei
beweglichen Elektronen und Atomen (bzw. Molekülen) zu beobachten.
Durch eine Katoden (Glühkatode) - Anoden - Röhre lassen sich frei bewegliche Elektronen
mittels eines elektrischen Feldes beschleunigen. Dringen diese durch ein Medium, kommt es
zu elastischen oder unelastischen Zusammenstößen mit den Atomen.
Von einem elastischem Stoß spricht man dann, wenn die gesamte kinetische Energie der
beiden Stoßpartner konstant bleibt. Im Gegensatz dazu ändert sich die Bewegungsenergie bei
einem unelastischen Stoß. Die dabei frei werdende Energie wird beim Franck-Hertz-Versuch
in innere Energie der Atome umgewandelt.
2. Meßmethoden und Meßapparatur
Verwendete Geräte :
• Franck-Hertz-Röhre
• Thermostat
• Gleichspannungsregler
(Heizung
: Typ 3203 {30 V, 10 A};
Gitterspannung : Typ 3207 {30 V, 1 A};
Gegenspannung : Tg 20/1 {20 V, 1 A})
• Vielfach-Meßgeräte
• XY-Schreiber (Meßbereich : X : 20 V; Y : 100 mV)
In einem evakuierten Glaskolben befindet sich ein Tropfen Quecksilber. Durch Erhitzen des
Glaskolbens auf etwa 373 K wird eine Quecksilberdampfatmosphäre erzeugt. Aus der
Glühkatode werden Elektronen emittiert, die durch die Beschleunigungsspannung UKG in
Richtung Gitter forciert werden.
Da die Masse der Hg-Atome um ein Vielfaches größer als die Elektronenmasse ist, wird bei
elastischen Stößen von Elektronen auf Hg-Atome praktisch keine Energie übertragen (Die
mittlere freie Weglänge ist klein gegenüber dem Abstand Katode-Gitter bei obigen
Bedingungen.). Wenn jedoch die Elektronen eine gewisse Mindestenergie erreicht haben,
können sie ein Hg-Atom bei einem Stoß anregen und die kinetische Energie des Elektrons
wird in innere Energie des Hg-Atoms umgewandelt. Wie schon unter 1. erwähnt, handelt es
sich hierbei um einen unelastischen Stoß. Die aufgenommene Energie wird kurze Zeit später
in Form eines Photons (Strahlung der Wellenlänge λ, Berechnung mit Hilfe der Beziehung im
2. Bohrschen Postulat) abgegeben.
Zwischen dem Gitter und der Auffangelektrode wird eine Gegenspannung UG von 1,5 V
angelegt. Es gelangen also nur die Elektronen zur Auffangelektrode, deren kinetische Energie
am Gitter größer als eUG ist (e - Elementarladung). Der Anodenstrom IA wird in Abhängigkeit
von der Beschleunigungsspannnung UKG gemessen. Der Verlauf der UKG - IA - Charakteristik
wird dann mittels des XY-Schreibers dargestellt.
Bei dieser Messung wird die IA(UKG)-Kennlinie periodischen Schwankungen unterliegen. Bei
einer kontinuierlichen Erhöhung der Beschleunigungsspannung wird der Stromfluß immer
dann abnehmen, wenn die Elektronen ein ganzes Vielfaches der Mindestenergie zur Anregung
eines Hg-Atoms besitzen. Ansteigen wird die gemessene Stromstärke wieder nach jedem
lokalen Minimum, da dann wieder mehr Elektronen die nötige kinetische Energie besitzen,
den Raum zwischen Gitter und Auffangelektrode zu überwinden.
K
G
A
I
U
UG
UKG
Abb. 1 Schema der Anordnung von Franck und Hertz zum Nachweis der diskreten
Energieniveaus von Atomen
(A - Auffangelektrode, G - Gitter, K - Glühkatode, I - Amperemeter, U - Voltmeter)
Der oben beschriebene Franck-Hertz-Versuch nutzt mechanische Anregung aus, um den
Nachweis der diskreten Energieniveaus zu führen.
Man kann auch durch optische Anregung zeigen, daß die Grundbehauptung der Bohrschen
Postulate richtig ist. (Optische Anregung liegt dann vor, wenn ein Atom durch Licht im
ultraroten, sichtbaren oder ultravioletten Spektralbereich angeregt wird.)
Bei der optischen Anregung schließt man aus den Emissions- und Absorptionsspektren auf die
Energieübergänge in Atomen (Spektroskopie).
Eine weitere Möglichkeit, Atome anzuregen, ist die thermische Anregung, bei der es zu
Stoßprozessen durch Wärmewirkung kommt.
Für die Bestimmung des ersten Anregungsniveaus von Quecksilber wird der Gitter-AnodenStrom gemessen. Der Verlauf der Kurve gibt dabei Auskunft, wann es zu elastischen und zu
unelastischen Stößen der Elektronen mit den Atomen kommt. Dagegen wird zur Bestimmung
der Ionisierungsspannung der Katoden-Anoden-Strom gemessen, der rapide ansteigt, wenn es
in der Röhre zu einer Gasentladung kommt.
3. Meßergebnisse
In unserem Versuch haben wir insgesamt 4 Meßdiagramme aufgenommen. Dabei haben wir
mit Röhrentemperaturen von 355 K bis 399 K (Siehe Tabelle 1 .. 4 , genaue Werte: 355, 367,
384 und 399 K) gearbeitet. Der Katodenheizstrom wurde jeweils von 3,0 bis 4,0 Ampere
(3.0 A, 3.2 A, 3.4 A, 3.6 A, 3.8 A, 4.0 A) geregelt. Mit Hilfe eines XY-Schreibers wurde der
Verlauf des Gitter-Anoden-Stromes (siehe Diagramme 2 bis 5) ermittelt.
Tabelle 1
Katodenheizstrom
in A
3,0
3,2
3,4
3,6
3,8
4,0
(Temperatur in der Franck-Hertz-Röhre: 355 K)
1. Maximum
4,9
4,8
5,0
5,1
Mittelwert
Standardabweichung
Vertrauensgrenze
Differenz der Maxima :
(Angaben in V)
Tabelle 2
Katodenheizstrom
in A
3,0
3,2
3,4
3,6
3,8
4,0
Differenz der Maxima :
(Angaben in V)
Gitterspannung in V für
2. Maximum
3. Maximum
10,1
15,0
10,1
15,0
9,8
14,7
9,8
14,7
Differenz der Maxima in V
2. - 1.
3. - 2.
5,2
4,9
5,3
4,9
4,8
4,9
4,7
4,9
4,95
0,20
0,07
(Temperatur in der Franck-Hertz-Röhre: 367 K)
1. Maximum
5,2
5,2
5,3
5,4
Gitterspannung in V für
2. Maximum
3. Maximum
10,5
15,5
10,5
15,2
10,2
15,1
9,8
14,7
Mittelwert
Standardabweichung
Vertrauensgrenze
Differenz der Maxima in V
2. - 1.
3. - 2.
5,3
5,0
5,3
4,7
4,9
4,9
4,4
4,9
4,93
0,30
0,10
Tabelle 3
Katodenheizstrom
in A
3,0
3,2
3,4
3,6
3,8
4,0
(Temperatur in der Franck-Hertz-Röhre: 384 K)
1. Maximum
5,2
5,1
4,9
5,1
Mittelwert
Standardabweichung
Vertrauensgrenze
Differenz der Maxima :
(Angaben in V)
Tabelle 4
Katodenheizstrom
in A
3,0
3,2
3,4
3,6
3,8
4,0
Differenz der Maxima :
(Angaben in V)
Gitterspannung in V für
2. Maximum
3. Maximum
10,5
15,4
10,4
15,0
9,9
15,1
9,8
15,1
Differenz der Maxima in V
2. - 1.
3. - 2.
5,3
4,9
5,3
4,6
5,0
5,2
4,7
5,3
5,04
0,28
0,10
(Temperatur in der Franck-Hertz-Röhre: 399 K)
1. Maximum
4,8
4,9
4,8
4,7
Gitterspannung in V für
2. Maximum
3. Maximum
10,2
15,2
10,1
14,9
9,8
14,8
9,9
15,0
Mittelwert
Standardabweichung
Vertrauensgrenze
Differenz der Maxima in V
2. - 1.
3. - 2.
5,4
5,0
5,2
4,8
5,0
5,0
5,2
5,1
5,09
0,18
0,06
Das erste Strom-Maximum (bei verschiedenen Temperaturen) lag etwa zwischen
4.8 und 5.2 Volt Gitterspannung, das zweite zwischen 9.8 und 10.5 Volt und das dritte
zwischen 14.8 und 15.2 Volt. Diesem Anstieg folgte ein rapider Abfall der Kurve aufgrund
der Energieübertragung vom Elektron zum Atom.
Die Anzahl der beobachteten Maxima hing empfindlich von dem Katodenheizstrom
(Steuerung der Elektronen-Emission der Katode) und von der Temperatur der Röhre ab. Die
optimalen Messungen erzielten wir bei einem Katodenheizstrom von 3.8 A bis 4.0 A und bei
einer Röhrentemperatur von 367 K. Diese Kurve liefert also die genauesten Meßwerte
(∆U=4.93 eV± 0.2 eV).
Bei zu niedriger Temperatur und damit zu geringem Hg-Dampfdruck ist die mittlere freie
Weglänge der Elektronen so groß, daß viele Elektronen vor dem ersten Stoß schon ein
Hg-Atom ionisieren können (Gasentladung). Zu hohe Temperatur führt zu einem hohen
Druck, die mittlere freie Weglänge wird klein. Es kommt zu so vielen elastischen Stößen, daß
der ein geringer Anodenstrom entsteht, bei dem Maxima und Minima schlecht auszumachen
sind.
Das Diagramm 1 stellt eine Auswertung der UKG - IA - Kennlinie dar.
Die kinetische Energie der aus der Klühkatode herausbeschleunigten Elektronen ergibt sich
aus der Gitterspannung UKG und der Elementarladung e.
EKin =
(1.)
1
mv 2 = eUKG
2
Im Diagramm 1 ist die kinetische Energie der Elektronen über die Ordnungszahl der Maxima
aufgetragen. Aus dem Anstieg der Geraden ergibt sich die Anregungsenergie der Hg-Atome.
Der Schnittpunkt mit der Ordinatenachse liefert uns die Kontaktspannung zwischen Katode
und Gitter.
16
14
kinetische Energie in eV
12
10
8
6
4
2
0
0
1
2
Ordnungszahl der Maxima
Diagramm 1: Auswertung der UKG - IA - Kennlinie zur Bestimmung der
3
Anregungsenergie der Hg-Atome
Aus dem Schnittpunkt mit der Ordinatenachse ergibt sich zwischen Katode und Gitter eine
Kontaktspannung von 0.3 eV.
Die erhaltene Anregungsenergie von (4.93 ± 0.2) eV ziehen wir jetzt zur Berechnung der
Wellenlänge der Spektrallinie heran. Nach den Formeln:
(2.)
E A − E E = h ν = hc ν =
(3.)
λ=
hc
eUKG
hc
= eU KG
λ
[Einheit in Elektronenvolt]
[Einheit in Metern ]
Nach Einsetzen der Werte:
h = 6.626176 10-34 Js
e = 1.6021892 10-19 C
c = 299792458 m/s
UKG= (4.93 ± 0.2) eV
erhalten wir für λ 251.9 nm ±10.2 nm.
Zur Bestimmung der Ionisierungspannung haben wir mit einem Heizstrom von 4 A und einer
Röhrentemperatur von 374 K gearbeitet. Bei einer Gitterspannung von 11.0 V wuchs der
Katoden-Anoden-Strom plötzlich stark an (siehe Diagramm 6).
Diese Gitterspannung entspricht also der Ionisierungspannung, da der Anstieg auf eine
Gasentladung in der Röhre hinweist.
4. Diskussion
Die von uns bestimmte Anregungsenergie von (4.93 ± 0.2) eV liegt recht nahe an dem in der
Literatur angegebenen Wert2 von 4.9 eV. Die einfache Messung mit dem XY-Schreiber fiel
also recht genau aus. Besser wäre jedoch gewesen, die Lage der Maxima mit einem
Spannungsmeßgerät explizit zu bestimmen. Genauere Meßergebnisse erhält man, wenn man
den Raum, in dem die Elektronen beschleunigt werden, von dem Raum, in dem die
Zusammenstöße zwischen den Elektronen und Hg-Atomen stattfinden, trennt. Die Elektronen
wurden im Gegensatz zu solch einer Versuchsanordnung, bei der von uns benutzten
Meßapparatur nach den Zusammenstößen durch die Katoden-Gitter-Spannung weiter
beschleunigt. Es waren hier also mehr Elektronen in der Lage, die Gegenspannung zu
überwinden, obwohl sie nicht mehr die nötige kinetische Energie besitzen dürften.
Abschließend kann man aber sagen, daß die Meßergebnisse zufriedenstellende Ergebnisse
lieferten.
5. Zusammenfassung
Mit dem Franck-Hertz-Versuch wurden das erste Anregungsniveau von Quecksilber, die
Wellenlänge der entsprechende Spektrallinie, die Kontaktspannung zwischen Katode und
Gitter der Versuchsapparatur und die Ionisierungsspannung der Hg-Atome bestimmt, in dem
gezeigt wurde, daß Atome durch Elektronenstoß nur quantenhaft Energiebeträge aufnehmen
können. Dieser Versuch ist also eine Bestätigung für die Bohrsche Theorie, der Existenz
diskreter Energieniveaus.
1
Tipler, Paul A.: Physik. (Spektrum Akademischer Verlag, Heidelberg, Berlin, Oxford 1994), S. 1208 und 1209
2
Spolski, E.W. : Atomphysik 1 (VEB Deutscher Verlag der Wissenschaften, Berlin 1979), S. 285