Objekt

Gliederung
5. Compiler
1.
2.
3.
4.
Struktur eines Compilers
Syntaxanalyse durch rekursiven Abstieg
Ausnahmebehandlung
Arrays und Strings
6. Sortieren und Suchen
1.
2.
3.
4.
5.
Grundlegende Datenstrukturen
Bäume
B-Bäume und Tries
Sortieren in Vektoren
Streuspeicherung
7. Graphen
1. Darstellung und Topologisches Sortieren
2. Kürzeste Wege
3. Fluß- und Zuordnungsprobleme
Grundlegende Datenstrukturen
Überblick
• Wie können mehrere Objekte einer gleichen Klasse in einem
Objekt zusammengefasst werden, ohne vorher die Anzahl
der Elementen festzulegen?
• Wie werden Operationen auf dynamischen Datenstrukturen
spezifiziert?
• Welche Arten dynamischer Datenstrukturen gibt es?
Abstrakte Datentypen
• Ein abstrakter Datentyp (ADT) ist eine Datenstruktur
zusammen mit darauf definierten Operationen.
• Bei der Festlegung von ADTs werden Aspekte der konkreten
Implementierung nicht berücksichtigt
• In Java können ADTs durch Definition von Interfaces
spezifiziert werden
• Beispiele von ADTs:
– Keller (engl. Stacks),
– Schlangen (engl. Queues)
– verkettete Listen.
3
Datenstruktur: Stack
Ein Stack (Stapel- oder Kellerspeicher)
• ist eine Folge von Elementen a1, ..., am
• Nur am Ende der Folgen können Elemente gelesen, gelöscht
oder hinzugefügt werden (top)
• Das zuletzt eingefügte Element wird zuerst entfernt:
LIFO-Prinzip (Last-In First-Out)
am
Oben (top)
am-1
.
.
.
a...2
a1
4
Datenstruktur: Stack
Beispiele
• Stapel
• Stapel
• Stapel
für Stack:
von Münzen
von Tellern
von Akten
5
Stack: Anwendbare Operationen (1)
• push : Stack X Objekt → Stack
Mit der Operation push legt man ein Element auf dem Stapel
ab
6
Stack: Anwendbare Operationen (2)
• pop : Stack → Stack
Mit der Operation pop entfernt man das oberste Element
eines Stapels
• top : Stack → Objekt
Mit der Operation top erhält man das oberste Element eines
Stapels
7
Stack: Anwendbare Operationen (3)
•
•
•
•
push : Stack X Objekt → Stack legt Element auf Keller
pop : Stack → Stack entfernt oberstes Element
top : Stack → Objekt liefert oberstes Element
empty : Stack → boolean liefert true, falls Keller leer ist
• Merke: Die Operationen pop und top sind nur zulässig, wenn
der Stapel nicht leer ist
8
Stack: Definition der Schnittstelle
Schnittstellendefinition
public interface Stack {
public void push (Object obj) throws StackException;
public Object pop () throws StackException;
public Object top () throws StackException;
public boolean isEmpty ();
}
9
Stack: Implementierung (1)
• Implementierung mit Hilfe eines Arrays
• Nachteil: Größe des Arrays kann nicht verändert werden
public class ArrayStack implements Stack {
private Object elements[] = null; // Array von Elementen
private int num = 0;
num: speichert die aktuelle Anzahl
von Elementen. Wird beim
push inkrementiert,
beim pop dekrementiert
public ArrayStack (int size) {
elements = new Object [size];
}
public ArrayStack () {
elements = new Object [100];
}
Konstruktor mit
vorgegebener Kapazität
Konstruktor mit Standardkapazität:
Stack wird mit einem Array
von 100 Elementen Angelegt
10
Stack: Implementierung (2)
public void push (Object obj) throws StackException {
if (num == elements.length - 1)
Ausnahme falls Kapazität
// Kapazität erschöpft
erschöpft ist:
num = elements.length
throw new StackException ();
elements[num++] = obj;
}
public Object pop () throws StackException {
if (isEmpty ())
// Stack ist leer
throw new StackException ();
Object o = elements[--num];
elements[num] = null;
return o;
}
11
Stack: Implementierung (3)
public Object top () throws StackException {
if (isEmpty ())
throw new StackException ();
return elements[num - 1];
}
public boolean isEmpty () {
return num == 0;
}
true falls num gleich 0
false fals num ungleich 0
}
12
Stack: typische Anwendungen
• Compilerbau:
– Auswertung von Postfix-Ausdrücken
– Syntaktischen Analyse von Programmen
• Umwandlung von rekursiven Programmen in nicht-rekursive
Programme
• Backtracking-Algorithmen
• Laufzeitstack bei der Speicherplatzverwaltung von
Programmen
13
Stack: Auswertung von Postfix-Ausdrücken (1)
• Beispiel: Arithmetischer Ausdruck (2+4)2/(16-7)
• Postfix-Ausdruck: 2 4 + 2 16 7 - /
• Abarbeitung mittels eines Stack von links nach rechts:
– Das gelesene Datum ist ein Operand: mit push auf dem Stack legen
– Das gelesene Datum ist ein Operator: auf die obersten n Elemente
anwenden und das Ergebnis ersetzt die n Elemente
14
Auswertung von Postfix-Ausdrücken (2)
1. 2
2.
3.
4.
5.
6.
7.
4
+
2
16
7
-
/
4
+
2
16
7
-
/
2
+
2
16
7
-
/
2
4
2
16
7
-
/
6
16
8.
7
-
/
36
7
-
/
16
36
-
/
7
16
36
9.
/
9
36
4
Ergebnis=4
15
Datenstruktur: Queue
Ein Queue (Warteschlange) ist eine Folge von Elementen
a1, ..., am mit den folgenden Eigenschaften:
• Nur am Anfang der Folge (vorne) können Elemente gelesen
und gelöscht werden können. Am anderen Ende (hinten)
können Elemente hinzugefügt werden
• Das zuerst eingefügte Element wird zuerst entfernt:
FIFO-Prinzip (First-In First-Out)
a1
Anfang
a2
...............
Am-1
am
Ende
16
Queue: anwendbare Operationen
•
•
•
•
enter : Queue X Objekt → Queue fügt Element hinten ein
leave : Schlange → Queue entfernt vorderstes Element
front : Queue → Objekt liefert vorderstes Element
empty : Queue → boolean liefert true, falls die Schlange
leer ist
17
Datenstruktur: Queue
Beispiele für Warteschlangen
• Warteschlange an der Ladenkasse
• Warteschlange in der Mensa
• Warteschlange im Stau
18
Queue: Typische Anwendungen
• Nutzung gemeinsamer Betriebsmittel (z.B.
Druckerwarteschlange, Warteschlangen für Prozessoren,
usw.)
• Bearbeitung von von Erzeuger-/Verbraucher-Problemen
• Branch-and-Bound-Algorithmen für Suchprobleme in Bäumen
und Graphen
19
Beispiel: Erzeuger / Verbraucher - Probleme
• Ein Produzent erzeugt (Waren-)Objekte, die von einem
Konsumenten weiterverarbeitet werden
• Der Produzent legt die Objekte in einem Puffer ab, der
Konsument entnimmt die benötigten Objekte aus dem
Puffer.
do {
Elem x = produce ();
while (q.IstVoll()) warte();
Q.enter(x)
} while (!fertig);
do {
if (! q.IstLeer()) {
Elem x = Q.front ();
consume(x);
}
20
Queue: Definition der Schnittstelle
• Benötigte Methoden
–
–
–
–
void enter(Object obj)
Object leave ()
Object front ()
boolean isEmpty()
• Schnittstellendefinition
public interface Queue {
public void enter (Object obj) throws QueueException;
public Object leave () throws QueueException;
public Object front () throws QueueException;
public boolean isEmpty ();
}
21
Queue: Implementierung durch ein Array (1)
• Implementierung mit Array A: Maximale
Warteschlangengröße = A.length
• Zwei Indizes markieren Anfang und Ende der
Warteschlange
– Anfang zeigt auf das vordere Element
– Ende zeigt auf die nächste freie Stelle
• Element x in Warteschlange einfügen: x wird an Position
A[Ende] gespeichert und Ende wird inkrementiert
• Element x aus Warteschlange entfernen: Anfang
inkrementieren
N
U
V
D
Y
X
A
T
E
Anfang
Ende
22
Queue: Implementierung durch ein Array (2)
• Problem: Falls Anfang und Ende nur inkrementiert werden
würden, wird Indexbereich des Arrays überschritten
• Lösungen
– Das erste Element ist immer an Position 0, nach jedem entfernen
eines Elements aus dem Array, müssen alle Elemente nach links
verschoben werden -> wenig praktikabel!
– Indexbereich des Arrays als zyklische Liste betrachten
23
Queue: Implementierung durch „zirkuläres“ Array
• Indexbereich als zyklische
Liste: das erste Element folgt
auf das letzte!
– Für jeden Index ist die nächste
Position modulo Max.
Warteschlangengröße
Anfang
Ende
• Falls Anfang= Ende kann die
Warteschlange leer oder voll sein
– Letzte Operation war enter:
Warteschlange ist voll
– Letzte Operation war leave:
Warteschlange leer
• Verwendung einer boolesche Variable
voll, um Zustand der Warteschlange
zu protokollieren
24
Queue: Implementierung durch ein Array (3)
• Implementierung auf der Basis eines Arrays
• Nachteil: Die Queue kann nicht dynamisch wachsen
public class ArrayQueue implements Queue {
private Object[] elements; // Elemente
private int Anfang =0;
private int Ende =0;
// Queue mit vorgegebener Kapazität erzeugen
public ArrayQueue (int size) {
Konstruktor mit
vorgegebener Kapazität
elements = new Object[size];
}
// Queue mit Standardkapazität erzeugen
Konstruktor mit Standardkapazität:
public ArrayQueue () {
Warteschlange wird mit einem
elements = new Object[100];
Array von 100 Elementen Angelegt
}
25
Queue: Implementierung durch ein Array (4)
public void enter (Object obj) throws QueueException {
if (istVoll()) throw new QueueException (‘‘Überlauf!“);
Objekt in Array aufnehmen
elements[Ende] = obj;
Ende = next(Ende);
Ende-Index fortschalten
voll =(Anfang == Ende);
Zustand speichern:
}
voll falls Anfang = Ende,
public Object leave () throws QueueException {
sonst nicht voll
if (isEmpty ())
throw new QueueException (‘‘Zugriff auf leere Queue!“);
Object obj = elements[Anfang];
elements[Anfang] = null;
// unteren Zeiger aktualisieren
Anfang = next(Anfang);
Anfang-Index fortschalten
voll = false;
Nach leave darf die Queue
return obj;
nicht voll sein
}
•
26
Queue: Implementierung durch ein Array (5)
public Object front () throws QueueException {
if (isEmpty ())
throw new QueueException (‘‘Zugriff auf leere Queue“);
return elements[Anfang];
}
public int next(int n){
return (n+1)%elements.length;
}
public boolean isVoll () {
return voll;
}
public boolean isEmpty () {
return ((Anfang == Ende) && (voll != false) );
}
}
Anfang kann gleich Ende sein und
true falls Anfang gleich Ende
die Queue ist voll!
False sonst
Dieser Fall wird damit abgefangen! 27
Datenstruktur: Liste
• Eine (verkettete) Liste (linked list) ist eine dynamische Folge
• von Elementen a1, ..., am mit den folgenden Eigenschaften:
– Im Gegensatz zu Arrays können Listen zur Laufzeit beliebig wachsen
und verändert werden.
– Jedes Listenelement hat zwei Komponenten
• Inhalt
– Das eigentlich zu speichernde Element. Kann ein beliebiges Objekt
oder ein primitiver Datentyp sein.
• Referenz auf das nachfolgende Element
28
Datenstruktur: Liste
• Für die Navigieren in einer Liste muss das erste Element
erreichbar sein: Der „Anker“ für den Beginn der Liste wird
mit Head bezeichnet
• Das letzte Element verweist auf null
• Für eine einfache Handhabung kann eine bestimmte Position
als "aktuell" ausgezeichnet werden. Eine solche Position wird
auch Cursor genannt.
head
Objekt 1
Objekt 2
Objekt 3
next
next
next
Cursor (2)
X
null
29
Elemente in Listen einfügen
Beim Einfügen eines neuen Elements in eine Liste gibt es drei
Möglichkeiten:
• Prepend: Einfügen vor dem ersten Listenelement
– Das erste Listenelement wird zum Nachfolger des neuen Elements
– head zeigt auf das neue Element.
• Insert: Einfügen hinter einem gegebenen Element
– next des neuen Elements übernimmt den Wert next des aktuellen
Elements.
– current.next wird auf das neue Element gesetzt.
• Append: Einfügen als letztes Element
– current.next des letzten Listenelements wird auf die Referenz des
neuen Elements gesetzt
– Ein Sonderfall von „insert“.
30
Verkettete Liste: Anwendbare Operationen
• addFirst : Liste X Objekt → Liste fügt ein Element am
Anfang der Liste ein (entspricht ‘prepend‘‘)
• addLast : Liste X Objekt → Liste fügt ein Element am
Ende der Liste ein (entspricht ‘‘append‘‘)
• removeFirst : Liste → Liste löscht das erste Element
• removeLast : Liste → Liste löscht das letzte Element
• getFirst : Liste → Objekt liefert das erste Element
• getLast : Liste → Objekt liefert das letzte Element
• empty : Liste → boolean liefert true, falls Liste leer ist
• size : Liste → int liefert Anzahl der Elementen in der Liste
31
Einfügen vor dem ersten Listenelement
• Operation AddFirst: head bekommt Referenz auf das neue
Objekt
Objekt 0
next
head
X
Objekt 1
Objekt 2
Objekt 3
next
next
next
X
null
32
Einfügen als letztes Element
•
•
Operation AddLast
1. Letzte Element finden
2. Next-Referenz auf neues Element
Aufwand ist abhängig der Anzahl der Elementen in der Liste
Objekt 4
next
head
Objekt 1
Objekt 2
Objekt 3
next
next
next
X
X
null
33
Das letzte Element löschen
•
•
Operation removeLast
1. Vorletztes Element finden
2. Next-Referenz des vorletzten Elements auf null setzten
Aufwand ist abhängig der Anzahl der Elementen in der Liste
head
Objekt 1
Objekt 2
Objekt 3
next
next
next
X
null
34
Komplexität der Listenoperationen
Operation
Komplexität
AddFirst
getFirst
removeFirst
O(1)
AddLast
getLast
removeLast
O(n)
35
Verkettete Liste: Definition der Schnittstelle
public interface Liste {
public void addFirst (Object o)
public void addLast (Object o)
public Object removeFirst ()
public Object removeLast ()
public Object getFirst ()
public Object getLast ()
public boolean isEmpty ()
public int size ()
}
36
Verkettete Liste: Definition von Listenelementen
class Node {
Object obj;
Node next;
public Node (Object o, Node n) {
obj = o;
next = n;
}
public Node () {
obj = null;
next = null;
}
public void setElement (Object o)
{
obj = o;
}
public Object getElement () {
return obj;
}
public void setNext (Node n){
next = n;
}
public Node getNext () {
return next;
}
}
37
Verkettete Liste: Implementierung
public class List {
private Node head = null;
public List () {
head = new Node ();
}
public void addFirst (Object o) {
Node n = new Node (o, head.getNext ());
head.setNext (n);
}
public void addLast (Object o) {
Node l = head;
while (l.getNext () != null)
l = l.getNext ();
Node n = new Node (o, null);
l.setNext (n);
}
public Object getFirst ()
throws ListEmptyException {
if (isEmpty ())
throw new ListEmptyException ();
return head.getNext ().getElement ();
}
public Object getLast ()
throws ListEmptyException {
if (isEmpty ())
throw new ListEmptyException ();
Node l = head;
while (l.getNext () != null)
l = l.getNext ();
return l.getElement ();
}
public Object removeFirst ()
throws ListEmptyException {
if (isEmpty ())
throw new ListEmptyException ();
Object o = head.getNext ().getElement ();
head.setNext (head.getNext ().getNext ());
return o;
}
public boolean isEmpty () {
return head.getNext () == null;
}
38
Verkettete Liste: Implementierung
public Object removeLast () throws ListEmptyException {
if (isEmpty ())
throw new ListEmptyException ();
Node l = head;
while (l.getNext ().getNext () != null)
l = l.getNext ();
Object o = l.getNext ().getElement ();
l.setNext (null);
return o;
}
public int size () {
int s = 0;
Node n = head;
while (n.getNext () != null) {
s++;
n = n.getNext ();
}
return s;
}
39
Verkettete Listen: Zusammenfassung
• Vorteile von verkettete Listen :
– Dynamische Länge
– Keine Speicherverschwendung durch Vorreservierung des
Speicherplatzes
– Einfache Einfüge- und Löschoperationen
– In den Listenelementen enthaltene Objekte können beliebige Objekte
untergebracht werden
• Nachteile:
– Zugriff erfolgt immer sequentiell
– Aufwand für Suche nach einem Listen-Element: Da es sich um eine
lineare Suche handelt, gilt
• Aufwand = O(1) im günstigsten Fall bzw.
• O(n) in den anderen Fällen.
40
Doppelt verkettete Listen
• Die doppelt verkettete Liste ist eine spezielle verkettete
Liste bei der jedes Element sowohl seinen Nachfolger als
auch seinen Vorgänger kennt
• tail zeigt auf das Ende der Liste
• Merke: Die Operationen AddLast, getLast und removeLast
sind nun mit konstantem Aufwand realisierbar!
tail
head
X
null
Objekt 1
Objekt 1
Objekt 1
next
next
next
Prev.
Prev.
Prev.
X
null
41
Komplexität der Listenoperationen
Operation
AddFirst
getFirst
removeFirst
AddLast
getLast
removeLast
Komplexität
O(1)
42
Das Iterator-Konzept (1)
• Das Durchwandern (über alle Elemente zu navigieren) einer
Kollektion ist abhängig der Implementierung
– Bei der Benutzung von Arrays für die Implementierung einer
Kollektion wird eine Indexvariable verwendet
– Bei der Benutzung von Listen für die Implementierung einer
Kollektion wird die next-Referenz verwendet
• Notwendigkeit einer einheitlichen Behandlung des
Navigierens unabhängig der internen Realisierung der
Kollektion
• Iteratoren sind Objekte zum Iterieren über Kollektionen,
deren Klasse die vordefinierte Java-Schnittstelle
java.util.Iterator implementiert
43
Das Iterator-Konzept (2)
• Ein Iterator verwaltet einen internen Zeiger auf die aktuelle
Position in der zugrunde liegende Datenstruktur
• Mehrere Iteratoren können gleichzeitig auf eine Kollektion
operieren
Iterator
über Array
Iterator
über Liste
44
Die Schnittstelle Iterator
Die Schnittstelle java.util.Iterator definiert folgende Methoden
• Boolean hasNext()
Prüft, ob noch weitere Elemente in der Kollektion verfügbar
sind
• Object next()
Liefert das aktuelle Element zurück und setzt den internen
Zeiger des Iterators auf das nächste Element
• void remove
Löscht das aktuelle Element
45
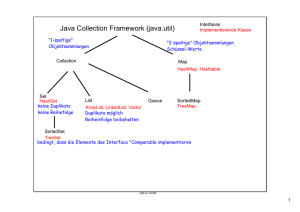
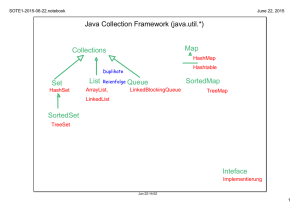
Das Java Collection Framework
• Grundlegende Datenstrukturen wie Liste, Stack und Warteschlange
müssen nicht immer neu implementiert werden
• Im Java Collection Framework sind entsprechende Klassen verfügbar
(z.B. ArrayList, Stack, Vector, ...)
• Im Java Collection Framework werden Schnittstellen und
Implementierungen angeboten (z.B. Schnittstelle List und Array-basierte
Implementierung ArrayList)
• Die Schnittstelle java.util.Collection
bildet die Basis für die spezielleren
Schnittstellen List, Set und
SortetSet
• Die Schnittstelle Map definiert
Methoden für die Verwaltung von
Schlüssel-Wert-Paare
46