Folien_Sitzung_09
Werbung

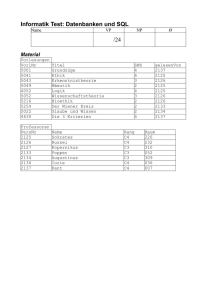
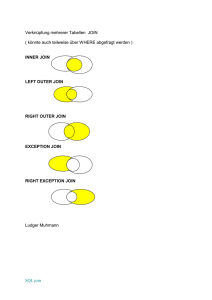
Technische Universität München Übung zur Einführung in die Informatik für Hörer anderer Fachrichtungen im Sommersemester 2010 Sitzung 8 + 9: Die relationale Algebra und Einstieg in SQL Jan Herrmann Lehrstuhl für Angewandte Informatik / Kooperative Systeme Folien nach an Prof. A. Kemper (http://www3.in.tum.de/teaching/ws0910/) Technische Universität München Überblick Sitzung 8+9 • Die relationale Algebra • Einführung in SQL 2 Studenten Professoren Rang Raum MatrNr Vorlesungen Name Semester 24002 Xenokrates 18 232 25403 Jonas 12 5001 Grundzüge 2127 Kopernikus C3 310 26120 Fichte 10 5041 Ethik 4 2125 2133 C3 52 26830 Aristoxenos 8 5043 Erkenntnistheorie 3 2126 2134 Augustinus C3 309 27550 Schopenhauer 6 5049 Mäeutik 2 2125 2136 Curie C4 36 28106 3 4052 Logik 4 2125 2137 Kant C4 7 29120 Theophrastos 2 5052 3 2126 29555 2 5216 Wissenschaftstheori e Bioethik 2 2126 5259 Der Wiener Kreis 2 2133 5022 Glaube und Wissen 2 2134 4630 Die 3 Kritiken 4 2137 PersNr Name 2125 Sokrates C4 226 2126 Russel C4 Popper voraussetzen Carnap Feuerbach hören Vorgänger Nachfolger VorlNr Titel SWS gelesenV on 4 2137 Technische Universität München 5041 MatrNr VorlNr 5001 5043 26120 5001 5001 5049 27550 5001 5041 5216 27550 4052 5043 5052 28106 5041 5041 5052 28106 5052 PerslNr Name Fachgebiet Boss 5052 5259 28106 5216 3002 Platon Ideenlehre 2125 28106 5259 3003 Aristoteles Syllogistik 2125 prüfen 29120 5001 3004 Wittgenstein Sprachtheorie 2126 MatrNr VorlNr PersNr Note 29120 5041 3005 Rhetikus Planetenbewegung 2127 28106 5001 2126 1 29120 5049 3006 Newton Keplersche Gesetze 2127 25403 5041 2125 2 29555 5022 3007 Spinoza Gott und Natur 27550 4630 2137 2 25403 5022 5001 Assistenten 3 2126 Technische Universität München Die relationale Algebra • • • • • • • • σ Selektion π Pojektion x Kreuzprodukt A Join (Verbund) ρ Umbenennung − Mengendifferenz ÷ Division ∪ Vereinigung • • • • • • • ÷ Division ∪ Vereinigung ∩ Mengendurchschnitt F Semi-Join (linker) E Semi-Join (rechter) C linker äußerer Join D rechter äußerer Join 4 Technische Universität München Die relationalen Algebra-Operatoren Selektion σSemester > 10 (Studenten) σSemester > 10 (Studenten) MatrNr Name Semester 24002 Xenokrates 18 25403 Jonas 12 ΠRang(Professoren) Projektion ΠRang(Professoren) Rang C4 C3 5 Technische Universität München Die relationalen Algebra-Operatoren Kartesisches Produkt PersNr 2125 Professoren x hören Professoren Name Rang Raum Sokrates C4 226 hören MatrNr VorlNr 26120 5001 ... ... ... ... ... ... 2125 Sokrates C4 226 29555 5001 ... ... ... ... ... ... 2137 Kant C4 7 29555 5001 • Problem: riesige Zwischenergebnisse (im BSP |P| * |h| Tupel) • Beispiel: (Professoren x hören) • "bessere" Operation: Join (siehe unten) 6 Technische Universität München Die relationalen Algebra-Operatoren Umbenennung • Umbenennung von Relationen • Beispiel: Ermittlung indirekter Vorgänger 2. Stufe der Vorlesung 5216 ΠV1. Vorgänger(σV2. Nachfolger=5216 ∧ V1.Nachfolger = V2.Vorgänger ( ρV1 (voraussetzen) x ρV2 (voraussetzen))) • Umbennung von Attributen ρVoraussetzung ← Vorgänger (voraussetzen) 7 Technische Universität München Formale Definition und Minimalität der Algebra Basisausdrücke • Relation der Datenbank Operationen • Selektion: σp (E1) • Projektion: ΠS (E1) • Kartesisches Produkt: E1 x E2 • Umbenennung: ρV (E1), ρA ← B (E1) • Vereinigung: E1 ∪ E2 • Differenz: E1 - E2 8 Technische Universität München Der natürliche Verbund (Join) Gegeben seien: (Beachte: überlappende Schemata – vgl. Bi) •R(A1,..., Am, B1,..., Bk) •S(B1,..., Bk, C1,..., Cn) R A S = ΠA1,..., Am, R.B1,..., R.Bk, C1,..., Cn(σR.B1=S. B1 A1 R−S A2 ... Am B1 RAS R∩S B2 ... ∧...∧ R.Bk = S.Bk(RxS)) Bk C1 S−R C2 ... Cn 9 Technische Universität München Drei-Wege-Join (Studenten A hören) A Vorlesungen (Studenten A hören) A Vorlesungen MatrNr Name Semester VorlNr Titel SWS gelesenVon 26120 Fichte 10 5001 Grundzüge 4 2137 27550 Jonas 12 5022 Glaube und Wissen 2 2134 28106 Carnap 3 4052 Wissenschftstheorie 3 2126 ... ... ... ... ... ... ... 10 Technische Universität München Allgemeiner Join (Theta-Join) • Gegeben seien folgende Relationen(-Schemata) – R(A1, ..., An) und – S(B1, ..., Bm) R A θ S = σθ (R x S) R Aθ S R Aθ S R A1 A2 S ... An B1 B2 ... Bm 11 Technische Universität München Andere Join-Arten • natürlicher Join A a1 a2 L B b1 b2 C c1 c2 A C c1 c3 R D d1 d2 E e1 e2 = A a1 Resultat B C D b1 c1 d1 A a1 a2 Resultat B C D b1 c1 d1 b2 c2 E e1 • linker äußerer Join A a1 a2 L B b1 b2 C c1 c2 C C c1 c3 R D d1 d2 E e1 e2 = E e1 12 Technische Universität München • rechter äußerer Join A a1 a2 L B b1 b2 C c1 c2 D C c1 c3 R D d1 d2 E e1 e2 = A a1 - Resultat B C D b1 c1 d1 c3 d2 E e1 e2 13 Technische Universität München Andere Join-Arten • äußerer Join (full outer join) A a1 a2 L B b1 b2 C c1 c2 B C c1 c3 R D d1 d2 E e1 e2 = A a1 a2 - Resultat B C D b1 c1 d1 b2 c2 c3 d2 E e1 - e2 • Semi-Join von L mit R A a1 a2 L B b1 b2 C c1 c2 E C c1 c3 R D d1 d2 E e1 e2 = Resultat A B C a1 b1 c1 14 Technische Universität München Andere Join-Arten (Forts.) • Semi-Join von R mit L A a1 a2 L B b1 b2 C c1 c2 F C c1 c3 R D d1 d2 E e1 e2 = Resultat C D E c1 d1 e1 15 Technische Universität München Die relationale Division Bsp.: Finde MatrNr der Studenten, die alle vierstündigen Vorlesungen hören L := ΠVorlNr(σSWS=4(Vorlesungen)) L hören ÷ ΠVorlNr(σSWS=4(Vorlesungen)) 16 Technische Universität München Definition der Division • t ∈ R ÷ S, falls für jedes ts ∈ S ein tr ∈ R existiert, so dass gilt: – tr.S = ts.S – tr.(R-S) = t R M m1 m1 m1 m2 m2 V v1 v2 v3 v2 v3 ÷ S V v1 v2 = R÷S M m1 • Die Division R ÷ S kann auch durch Differenz, Kreuzprodukt und Projektion ausgedrückt werden: 17 R ÷ S = Π(R − S)(R) − Π (R − S)((Π (R − S)(R) x S) − R) Technische Universität München Mengendurchschnitt Beispiel für den Mengendurchschnitt (Operatorsymbol ∩): Finde die PersNr aller C4-Professoren, die mindestens eine Vorlesung halten. ΠPersNr(ρPersNr←gelesenVon(Vorlesungen)) ∩ ΠPersNr(σRang=C4(Professoren)) • • • Mengendurchschnitt nur auf zwei Argumentrelationen mit gleichem Schema anwendbar Deshalb ist die Umbenennung des Attribute gelesenVon in PersNr in der Relation Vorlesungen notwendig Der Mengendurchschnitt zweier Relationen R ∩ S kann durch die Mengendifferenz wie folgt ausgedrückt werden: R∩S=R− (R − S) 18 Technische Universität München Weitere Beispiele • • • • Welche Professoren kennt Carnap? Wer ließt mindestens 2 Vorlesungen? Wer hört mindestens eine Vorlesung? Wer hat alle geprüften Vorlesungen auch gehört? 19