Formelsammlung Systemtheorie 2

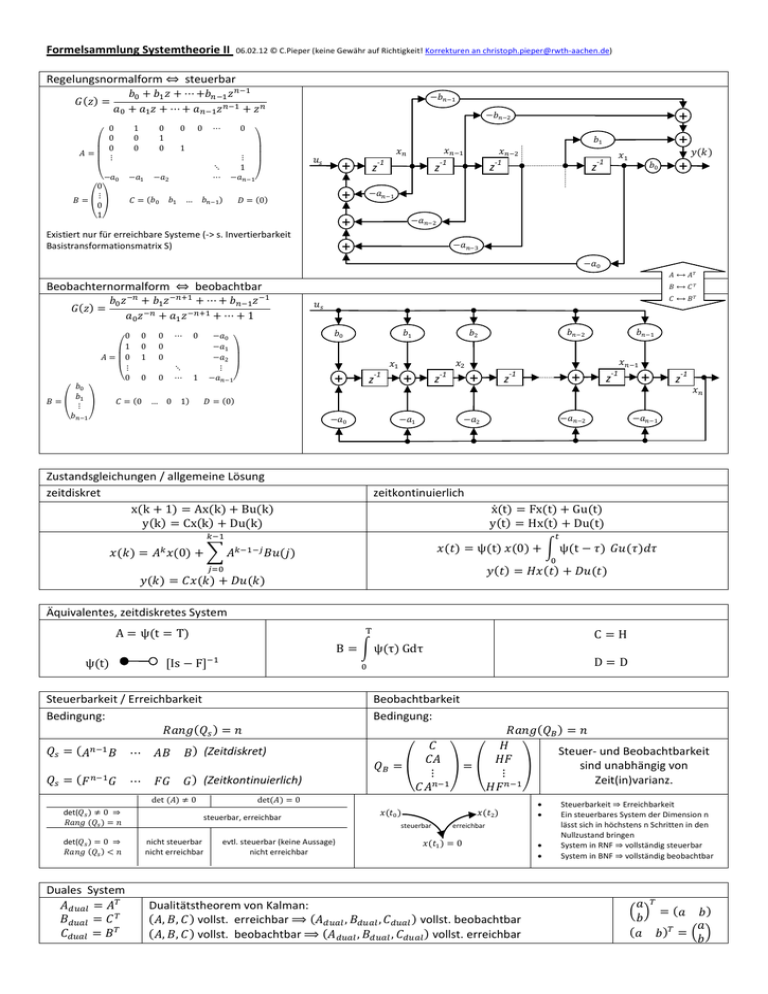
Formelsammlung Systemtheorie II
Regelungsnormalform
06.02.12 © C.Pieper (keine Gewähr auf Richtigkeit! Korrekturen an [email protected])
steuerbar
+
+
+
z
-1
z
-1
z
-1
z
-1
+
+
+
Existiert nur für erreichbare Systeme (-> s. Invertierbarkeit
Basistransformationsmatrix S)
Beobachternormalform
+
beobachtbar
+
Zustandsgleichungen / allgemeine Lösung
zeitdiskret
z
-1
+
z
-1
+
z
-1
+
z
-1
+
z
-1
zeitkontinuierlich
Äquivalentes, zeitdiskretes System
Steuerbarkeit / Erreichbarkeit
Bedingung:
Beobachtbarkeit
Bedingung:
(Zeitdiskret)
Steuer- und Beobachtbarkeit
sind unabhängig von
Zeit(in)varianz.
(Zeitkontinuierlich)
det(


steuerbar, erreichbar
steuerbar
det(
nicht steuerbar
nicht erreichbar
erreichbar
evtl. steuerbar (keine Aussage)
nicht erreichbar


Duales System
Dualitätstheorem von Kalman:
vollst. erreichbar
vollst. beobachtbar
vollst. beobachtbar
vollst. erreichbar
Steuerbarkeit Erreichbarkeit
Ein steuerbares System der Dimension n
lässt sich in höchstens n Schritten in den
Nullzustand bringen
System in RNF vollständig steuerbar
System in BNF vollständig beobachtbar
Charakteristisches Polynom von
Zustandsvektorrückführung
+
z-1
+
B
C
+
A
+
+
K
z
-1
z
-1
z
-1
z
-1
+
+
+
+
Gegeben ist System mit Matrix
mit der charakt. Gleichung:

in RNF (ZV in BSB von rechts nach links
sind letzte Zeile von
ansteigend)
aus Nenner von
(A) Errechnen von
1.
2.

Gewünschte Pole von
(B)
wenn
oder
Nachteil:
Errechnen von
1.
2.


:
schon vorhanden
wird benötigt (falls

in nicht-RNF verlangt )
Koeffizienten vergleich
praktisch, falls
Schätzung des Zustandsvektors (Luenberger Beobachter)
z-1
+
B
Festlegen des Verhaltens von
:
C
über die Eigenwerte von
A
B
-1
+
z
+
A
!
C
+


L
Bedingung für das Finden von
beobachtbar sein.
(Dead-Beat:
L
Regelung mit geschätztem Zustandsvektor
+
z-1
+
B
C
A
K
B
+
z-1
+
L
!
ALC
Dualität K-Vektorrückführung
Luenberger Beobachter
2n-dimensionale Zustandsgleichung:
:
muss
)
Äquivalenter Zustandsvektor
Ist ein Zustandsvektor von
D.h.
, dann ist
ein gültiger äquivalenter Zustandsvektor, falls gilt:
muss berechenbar sein:
Transf. auf RNF
Basistransformationsmatrix
dim
2
3
Für
Achtung! Beginn bei
muss nur
berechnet werden.
nicht bei
!
4
Damit existiert muss auch
existieren. Deswegen muss gelten: d
(nur dann ist invertierbar), also auch
Minimal äquivalentes System
Existiert, falls linear abhängige Zeilen hat.
Gegeben ist System
Gesucht ist System
Berechnung von R:
Äquivalenzgesetze:
1.
Form von
2.
3.
4.
5.
:
m
m
Koeffizienten Vergleich:
und
Die Existenz eines minimaleren Systems äußert sich durch
Kürzungen in der Übertragungsfunktion.
m
Zustandsgleichungen des gestörten Systems
+
+
!
Kalman Gleichungen
Measurement update:
rauschbehaftete Eingänge müssen
als Störgröße
modelliert werden
Time update:
Anfangsbedingungen:
Stabilität
 Asymptotische Stabilität:
alle Eigenwerte von A liegen im Einheitskreis LTI-System (A,B,C) ist asymptotisch Stabil
 BIBO-Stabilität:
- alle Pole in linker, offener Halbebene (s-Bereich)
- alle Pole innerhalb des Einheitskreis (z-Bereich)
Asymptotische Stabilität BIBO Stabilität
Dead-Beat asymptotisch stabil
Adaptive Systeme
Optimale Filterkoeffizienten:
Unbekanntes System
die den quadratische Fehler:
minimieren.
Adaptionsalgorithmus
+
Adaptives Systemmodell
(# Koeffizienten des adaptiven Systems)
Gauß-Markoff-Modell
1. Gauß-Eigenschaft
Da und
und
2. Markoff-Eigenschaft
hängt nur von
…ist gegeben, wenn
Gaußveteilt sind, sind es auch
ist weiß, mittelwertfrei
(# Koeffizienten des unbekannten Systems)
und
.
aber nicht von den vorherigen Werten ab.
in
weiß ist.
Die Aussagen beziehen sich nur auf den Zustandsvektor
, aber nicht auf den Ausgang
(kann auch von früheren Werten abhängen)
Abtastung
Abzustastendes Signal:
Abtastung (Multiplikation mit Dirac-Folge):
Fouriertransformierte in Abhängigkeit der Abtastwerte:
Für die Rekonstruktion muss ein bandbegrenztes Filter verwendet
werden, und die Skalierung mit rückgängig gemacht werden.
Halteglied nullter Ordnung:
Fouriertransformierte in Abhängigkeit der Abtastwerte:
Faltung
1. Spiegeln / Stauchen
2. Verschieben
Faltungsintegral Beispiel:
Im Frequenzbereich:
Im Zeitbereich:
Überführung in den Nullzustand
Voraussetzung System steuerbar:
für
ist die Folge, die das System in k Schritten in den Nullzustand überführt.
Oft genutzte Fourier-Transformierte
1
Matrizen
Inverse
Transponierte
Determinante eines Produkts
Stochastik

Grundlegende Eigenschaften

Stochastische Unabhängigkeit

bedingte Zähldichte

Bayes Theorem

Satz der totalen W‘keit

Erwartungswert

bedingter Erwartungswert

Varianz

Randverteilungsdichte

Verteilungsfunktion

Dichte der Summen von 2
Zufallsvariablen

Korrelation / Stochastische Abh.

Transformationssatz für Dichten
mit
Stochastisch unabhängig unkorreliert
Gaußverteilt: Stochastisch unabhängig
Rauschprozesse
Es seien
und
Zufallsprozesse. Dann gilt:

ist additives, mittelwertfreies, weißes Rauschen

ist mittelwertfrei

und
sind mit korreliert
unkorreliert
mit

und
sind unkorreliert, aber nicht
mittelwertfrei
Lineare Algebra
Bauteilgleichungen
Kondensator
Spule
Grundlegende physikalische Formeln
Kreisfrequenz
Weg-Zeit-Gesetz
Übertragungsfunktion ermitteln
Auf dem Blockschaltdiagramm
+
∑
H1(z)
H2(z)
Zustandsgleichungen ineinander einsetzen...
häufige Matrixoperationen
u(k)
h
u(k)
y(k)
y(k)
h
,
Summenformel
Vertauschen von Summen-Grenzen
,
Fourier-Transformierte: gerade/ungerade Funktion
Raised-Cosine-Filter
y
x=y
x<y
x
x>y
Winkel α
(Grad)
Bogenmaß
Sinus
Kosinus
Tangens
Polstelle
Polstelle
Scheitelpunktsform
„Vektor“ Ableitungen
Gleichverteilung (zeitkontinuierlich)
Erwartungswert
Varianz
a
b
FIR-Filter (Impulsantwort der Länge n)
-1
-1
z
z
z
+
+
FIR-Filter (unendliche Impulsantwort)
-1
z-1
+
z-1
+
Verschiebungsregeln für Blockschaltdiagramme (nur LTI)
Knotenpunkt verschieben
z-1
+
+
Additionspunkt verschieben
+
+
+
+
Indikatorfunktion
gestreckt um Faktor 2
-2
2
x
-4
4
x
-1
3
x
Halteglied nullter Ordnung
Abtastsystem
Regelstrecke G(s)
Mit
Quasikontinuierliche Regelung
Aufgeschnittener Regelkreis:
+
-
+
Einfluss von
und
Wenn die Abtastzeit
der Streckenzeitkonstanten ist, kann der Abtast-Haltevorgang bei der Dimensionierung des
Reglers vernachlässigt werden.
Beispiel Regelstrecke:
größte Streckenzeitkonstante
Idealer, kontinuierlicher PID-Regler
Aus dem Zeitkontinuierlichen:
P-Anteil:
I-Anteil:
D-Anteil:
Für Rekursionsgleichung: