Bucketsort

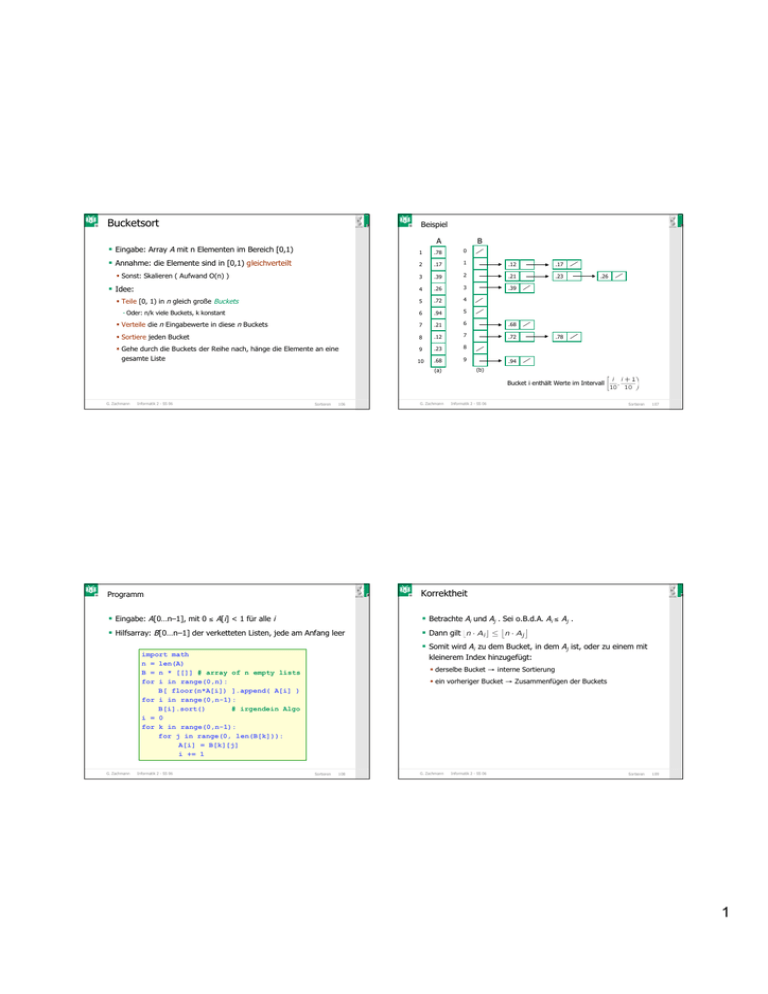
Bucketsort
C
G
C
C
G
C
Beispiel
A
B
 Eingabe: Array A mit n Elementen im Bereich [0,1)
1
.78
0
 Annahme: die Elemente sind in [0,1) gleichverteilt
2
.17
1
.12
.17
3
.39
2
.21
.23
4
.26
3
.39
5
.72
4
6
.94
5
 Verteile die n Eingabewerte in diese n Buckets
7
.21
6
.68
 Sortiere jeden Bucket
8
.12
7
.72
 Gehe durch die Buckets der Reihe nach, hänge die Elemente an eine
9
.23
8
10
.68
9
 Sonst: Skalieren ( Aufwand O(n) )
 Idee:
 Teile [0, 1) in n gleich große Buckets
- Oder: n/k viele Buckets, k konstant
gesamte Liste
.26
.78
.94
(b)
(a)
Bucket i enthält Werte im Intervall
G. Zachmann
Informatik 2 - SS 06
Sortieren
G. Zachmann
106
C
G
C
Programm
Informatik 2 - SS 06
 Betrachte Ai und Aj . Sei o.B.d.A. Ai ≤ Aj .
 Hilfsarray: B[0…n–1] der verketteten Listen, jede am Anfang leer
 Dann gilt
C
G
C
 Somit wird Ai zu dem Bucket, in dem Aj ist, oder zu einem mit
import math
n = len(A)
B = n * [[]] # array of n empty lists
for i in range(0,n):
B[ floor(n*A[i]) ].append( A[i] )
for i in range(0,n-1):
B[i].sort()
# irgendein Algo
i = 0
for k in range(0,n-1):
for j in range(0, len(B[k])):
A[i] = B[k][j]
i += 1
Informatik 2 - SS 06
107
Korrektheit
 Eingabe: A[0…n–1], mit 0 ≤ A[i] < 1 für alle i
G. Zachmann
Sortieren
kleinerem Index hinzugefügt:
 derselbe Bucket → interne Sortierung
 ein vorheriger Bucket → Zusammenfügen der Buckets
Sortieren
108
G. Zachmann
Informatik 2 - SS 06
Sortieren
109
1
C
G
C
Laufzeit
C
G
C
 ni = Anzahl der Elemente im Bucket Bi . Insertion-Sort benötigt
 Angewiesen darauf, daß kein Bucket "zu viele Werte" beinhaltet
quadratische Zeit. Damit ist die Zeitkomplexität von Bucketsort:
 Alle Zeilen außer der Bucket-Sortierung benötigen eine
Zeitkomplexität von O(n)
 Intuitiv: wenn jeder Bucket eine konstante Anzahl an Elementen
 Anwendung des Erwartungswerts auf beiden Seiten und die
bekommt, braucht man O(1) Zeit, um jeden Bucket zu sortieren →
Linearität des Erwartungswerts ergibt
O(n) für Sortieren aller Buckets
 Annahme scheint plausibel, aber sorgfältigere Analyse folgt
G. Zachmann
Informatik 2 - SS 06
Sortieren
G. Zachmann
110
Informatik 2 - SS 06
Sortieren
111
C
G
C
C
G
C
 Behauptung:

 Beweis:

 Xij ist eine Zufallsvariable


G. Zachmann
Informatik 2 - SS 06
Sortieren
112
G. Zachmann
Informatik 2 - SS 06
Sortieren
113
2
C
G
C
C
G
C
 Daraus folgt:


 wegen j ≠ k sind Xij und Xik unabhängige Zufallsvariablen
 Einsetzen liefert:
G. Zachmann
Informatik 2 - SS 06
Sortieren
Radix-Sort
Sortieren
115
C
G
C
 Beobachtung: nutze aus, daß Integers zu beliebiger Basis r
dargestellt werden können (daher der Name, "radix" = Wurzel)
 Sortieranlagen für Briefe entsprechend ihrer Postleitzahl
 Naïve (intuitive) Idee:
 Nachteile
 Sortiere alle Daten gemäß erster (höchstwertiger) Ziffer in Fächer
 Verwendet eine konkrete Zahlenrepräsentation
 Sortiere Fach 0 mittels Radix-Sort rekursiv
(typ. als Byte-Folge)
- arbeite dabei auf dem Teil-Array, das Fach 0 entspricht
 Verfahren muß in jedem Fall
an den konkreten Sortierschlüssel
 Sortiere Fach 1, etc. …
 Problem: bei jeder Rekursion muß man r-1 viele Fächer
angepasst werden
"aufbewahren" (mittels Marker-Array wie bei Counting-Sort)
→ erfordert rel. viel Zwischenspeicher: O(rd),
r = Radix, d = Anzahl Stellen der Keys
 ist also kein allgemeines
Sortierverfahren
Informatik 2 - SS 06
Informatik 2 - SS 06
C
G
C
 Vorbild
G. Zachmann
G. Zachmann
114
Sortieren
116
G. Zachmann
Informatik 2 - SS 06
Sortieren
117
3
C
G
C
 Lösung: sortiere zuerst nach letzter (niederwertigster) Stelle, dann
C
G
C
Beispiel
 12 Briefe anhand der Postleitzahl sortieren
nach zweitletzter, etc. (→ Backward Radix-Sort )
 beginne mit der letzten Ziffer
 Sei d Anzahl Digits, 0 = niederwertigstes Digit
 Ann. (oBdA): alle Keys haben gleiche Anzahl Stellen
 Definiere zr ( t,a) = t-te Stelle der Zahl a dargestellt zur Basis r,
t=0 ist niederwertigste Stelle
 Algo-Skizze:
def radix_sort( A ):
for i in range(0, d):
führe stabilen Sort auf A durch
mit zr (i,A[*]) als Key
 Da Digits in [0,r-1] sind, verwende Counting-Sort
G. Zachmann
Informatik 2 - SS 06
Sortieren
G. Zachmann
118
Informatik 2 - SS 06
Sortieren
119
C
G
C
C
G
C
 Briefe unter Beibehaltung der Ordnung wieder zusammenlegen
 nach vorletzter Ziffer sortieren, etc.
G. Zachmann
Informatik 2 - SS 06
Sortieren
120
G. Zachmann
Informatik 2 - SS 06
Sortieren
121
4
C
G
C
Ausführlicher Algorithmus
C
G
C
Korrektheit
 Zunächst "counter-intuitive", daß dieser tatsächlich funktioniert
def radix_sort( A, d ):
 funktioniert tatsächlich auch nur, wenn Sort im Inneren der Schleife
# init bins
bin = r * [[]]
# now bin = [ [], [], [], … ]
stabil ist
 Schleifeninvariante: Nach dem i -ten Durchlauf ist A bzgl. des
for i in range( 0, d ):
Schlüssels 〈zi (.), …, z0(.)〉 sortiert
# distribute a[i] on bin according to z(t,.)
for j in range(0, len(A) ):
bin[ z(i, A[j]) ].append( A[j] )
(Erinnerung: z0(.) liefert das LSD [least significant digit] einer
Zahl)
# gather bins
A = []
for j in range(0, r):
A.extend( bin[j] )
bin[j] = []
G. Zachmann
Informatik 2 - SS 06
Sortieren
G. Zachmann
122
C
G
C
Informatik 2 - SS 06
Sortieren
123
C
G
C
Analyse
 vor dem ersten Durchlauf: A ist unsortiert
 d viele Digits, also d äußere Schleifendurchläufe
 nach dem ersten Durchlauf: A ist gemäß letztem Digit sortiert
 Pro äußerem Schleifendurchlauf:
 Distribute: n Elemente in A, für jedes Element A[i] wird konstanter
Zeitaufwand betrieben (Digit t extrahieren, A[i] kopieren, …)
 im i-ten Durchlauf:
 Element A j kommt in Bin z i(A j )
 Gather: r Bins, alle Bins zusammen haben n Elemente
 für alle A k, k < j, gilt:
 Zusammen:
- zi(Ak ) = zi(Aj ) → Ak steht im selbem Bin wie Aj, aber an früherer Stelle
innerhalb dieses Bins → Reihenfolge von Ak & Aj bzgl. 〈z i-1(.), …, z0(.)〉 bleibt
gewahrt, damit ist Reihenfolge auch bzgl 〈z i (.), …, z0 (.)〉 ok
- zi(Ak ) ≠ zi(Aj ) → Ak steht in anderem Bin → Reihenfolge bzgl. 〈zi (.), …, z0(.)〉
 Spezialfall n « rd (z.B. d = 32-Bit Zahlen):
 d und r konstant → Aufwand linear, d.h., c*n
 Spezialfall möglichst "kurze" Keys:
 D.h., wähle
ist sowieso korrekt, da nur i-tes Digit relevant
 Worst-case Aufwand:
 nach Zusammenfassen der Bins ist Reihenfolge aller Schlüssel bzgl.
Digits i-1,…,0 immer noch korrekt
G. Zachmann
Informatik 2 - SS 06
Sortieren
124
G. Zachmann
Informatik 2 - SS 06
Sortieren
125
5
C
G
C
Optimale Wahl von r
C
G
C
 Beobachtung: wir haben die freie Wahl für r → ausnutzen
 Frage: für welches r (r ≤ b) wird
 Lemma:
1. Fall:
Gegeben n b-Bit Zahlen.
Radix-Sort sortiert diese Zahlen in Zeit
für jedes beliebige
.
 Dann gilt
 Wähle also r =b , d.h., 1x Counting-Sort ist optimal
2. Fall:
 Beweis: verwende Counting-Sort als stabilen Sortier-Algo
 Setze
 Wähle
, d.h., Keys pro Durchlauf haben r Bits
 Wenn
 Beispiel: b = 32, r = 8, k = 255, d = 4
gewählt wird, wächst 2r im Zähler schneller als r
im Nenner, ergibt längere Laufzeit
 Pro Durchlauf von Counting-Sort:
 Wenn
aber
 Zusammen:
Informatik 2 - SS 06
liefert Laufzeit
 Beh.: diese Wahl ist optimal
 Zahlenbereich für Digits ist
G. Zachmann
minimal?
Sortieren
G. Zachmann
126
C
G
C
Umsetzung
 normalerweise hat man keinen dezimal ausgedrückten Schlüssel
 Lösung z.B. durch Betrachtung des Sortierschlüssels als Folge von
gewählt wird, bleibt
Informatik 2 - SS 06
,
Sortieren
127
Absch(l)ießende Bemerkungen
C
G
C
 Lineare Verfahren sind O(N), es kann im Sinne der Komplexität
keine schnelleren Verfahren geben
 Aber Achtung: die "verborgene" Konstante zählt in der Praxis!
Bytes
 256 Sortierfächer werden benötigt
 Verfahren muß in jedem Fall an den konkreten Sortierschlüssel
angepaßt werden
 Anzahl der Durchgänge entspricht Anzahl der Bytes
 ist also kein allgemein anwendbares Sortierverfahren
 Achtung: Bytesortierung muß mit Ordnung des Schlüssels
übereinstimmen (kleinere Probleme bei Zweierkomplementzahlen:
.. FFFE FFFF 0000 0001 ..)
G. Zachmann
Informatik 2 - SS 06
Sortieren
128
G. Zachmann
Informatik 2 - SS 06
Sortieren
129
6
Welcher Sortieralgorithmus ist der beste?
C
G
C
C
G
C
 nicht leicht zu beantworten
 wenige Datensätze (z.B. unter 100)
 möglichst einfachen Algorithmus verwenden ⇒ Insertion-, Selectionoder Bubblesort
 Datenbestand bereits fast sortiert ⇒ Insertion- oder Bubblesort
 viele Daten, zufällig angeordnet, die man häufig sortieren muß
 Radix-Sort an das spezielle Problem anpassen (Achtung:
Neuprogrammierung = Fehlerquelle)
 will man flexibel sein und einen Standardalgorithmus verwenden
 scheut man nicht das Risiko, eine ungünstige Verteilung der
Eingabedaten zu erwischen ⇒ Quicksort
 will man sicher gehen ⇒ Mergesort, Heapsort (evtl. auch Shellsort)
G. Zachmann
Informatik 2 - SS 06
Sortieren
130
G. Zachmann
Informatik 2 - SS 06
Sortieren
131
7