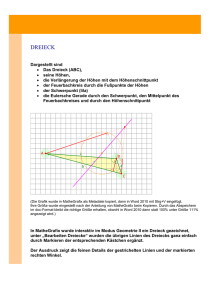
2.2C. Das allgemeine Dreieck

2.2C. Das allgemeine Dreieck
Jedes Dreieck läßt sich nach geeigneter Drehung und Verschiebung in ein Dreieck mit den
Eckpunkten
A = ( −x, 0 ), B = ( y, 0 ), C = ( 0, z ) (x, y, z > 0)
transformieren.
Die Wahl dieser Koordinaten hat den Vorteil, daß eine Seite waagerecht liegt, und die darauf
senkrecht stehende Höhe den Fußpunkt Hc = (0,0) hat.
Ein solches (fast) allgemeines Dreieck wollen wir jetzt zeichnen.
Wir tragen die Höhe auf der Grundlinie ein:
Oder stumpfwinklig:
Die Seitenvektoren des Dreiecks sind
a = (y,-z) , b = (x,z) und c = (x+y,0) , mit a+b = c.
Für die Seitenlängen ergibt sich somit:
|a| = B − C =
y2 + z2 , |b| = C − A =
x2 + z2 , |c| = B − A = x + y .
Für den Spezialfall x = 5, y = 9, z = 12 liefert das die Seitenlängen |a| = 15, |b| = 13 und |c| = 14.
Dass diese Seitenlängen alle ganzzahlig sind, ist ein glücklicher Zufall!
Für den Spezialfall x = 12, y = 4, z = 5 bekommen wir |a| = 41 , |b| = 13 und |c| = 16.
Wir zeichnen jetzt sämtliche Höhen ein:
Aus der Ähnlichkeit des grünen und gelben Dreiecks liest man ab:
x z
xy
= , also h =
.
h y
z
Mit Hilfe des Skalarproduktes geht es noch schneller: Da die bei A startende Höhe senkrecht auf
der gegenüberliegenden Seite steht, haben wir
(x, h)(−y, z) = x y − h z =0 ,
x y = h z.
Der Höhenschnittpunkt H wird daher in Koordinaten beschrieben durch
xy
H = (0, h) = (0,
).
z
Der stumpfwinklige Fall ist vielleicht etwas gewöhnungsbedürftig, weil man sich zwei Seiten und
alle drei Höhen verlängert denken muß:
Um die beiden Fußpunkte Ha und Hb der Höhen auf den Seiten a und b zu berechnen, betrachten
wir die Höhenvektoren
f = Ha − A , g = Hb − B , h = Hc − C
und machen den vektoriellen Ansatz
f + sa = c = a+b , d.h. Ha = f + A = c - sa + A = (y − s y, s z).
Da f senkrecht auf a steht, ergibt sich nach Multiplikation der Gleichung mit a:
0 + saa =(a+b)a , also s ( y2 + z2 ) = ( x + y ) y , d.h.
(x + y) y
s = 2 2 , und Einsetzen von s führt auf
y +z
y z 2 − x y2 ( x + y ) y z
Ha = (
,
).
y2 + z 2
y 2 + z2
Analog erhält man für den anderen Höhenvektor
y x2 − x z 2 ( x + y ) x z
Hb = (
,
).
x2 + z 2
x 2 + z2
Spiegelt man den Höhenschnittpunkt an der waagerechten Seite nach unten, so muß aufgrund der
Gleichung x y = h z und des Sehnensatzes der Spiegelpunkt auf dem Umkreis des Dreiecks
liegen.
Aus Analogiegründen liegen auch die Spiegelpunkte an den anderen beiden Seiten auf dem
Umkreis!
Dessen Mittelpunkt hat die Koordinaten
y−x z−h
(
,
),
2
2
und sein Radius ist
( x + y )2 + ( z − h )2
2
.
Jetzt können wir den Umkreis und die drei Spiegelpunkte konstruieren:
Eine besonders schöne Konsequenz der Kommutativität des Skalarproduktes ist der
"schiefwinklige Kathetensatz".
In diesem Bild entsprechen nun
die blauen Rechteckflächen (oben) den Skalarprodukten ab und ba
die grünen Rechteckflächen (rechts) den Skalarprodukten ac und ca
die roten Rechteckflächen (links) den Skalarprodukten bc und cb.
Daß die beiden zugehörigen Flächeninhalte jeweils gleich sind, besagt schlicht die Kommutativität
des Skalarprodukts!
Statt des Satzes von Pythagoras gilt im schiefwinkligen Dreieck mit den Seitenlängen
a = |a|, b = |b|, c = |b-a|
der Cosinussatz
für den zwischen a und b liegenden Winkel γ :
c2 = a2 − 2 a b cos( γ ) + b2.
Denn es ist ja aufgrund des Distributiv- und Kommutativgesetzes
( a − b )2 = (a-b)(a-b) = aa - 2ab + bb = a2 − 2 a b cos( γ ) + b2.
Auch diesen Satz kann man aus der obigen Figur ablesen:
Je eines der blauen Rechtecke hat den Flächeninhalt ab = a b cos( γ ). Zieht man diese Flächen von
der Summe der beiden Quadrate ab, so bleibt je ein rotes und ein grünes Rechteck, und deren
Flächen entsprechen in ihrer Summe dem unteren Quadrat.
Aufgrund des Cosinussatzes kann man z.B. bei gegebenen Seitenlängen a,b,c den Cosinus eines
Eckwinkels mit der folgenden Formel berechnen:
cos( γ ) =
a2 + b2 − c2
2ab
.
Eine geniale Entdeckung des antiken Mathematikers HERON von Alexandria (ca. 100 n.Chr.) war
eine Formel, mit der man den
Flächeninhalt eines Dreiecks
aus den Seitenlängen a,b,c berechnen kann. Bezeichnet s den halben Umfang des Dreiecks, d.h.
a+b+c
s=
,
2
so ist der Flächeninhalt des Dreiecks
F=
s (s − a) (s − b) (s − c) .
Zum Beispiel erhält man für ein Dreieck mit den Seitenlängen 13, 14 und 15:
F=
( 13 + 14 + 15 )( 13 + 14 − 15 )( 13 − 14 + 15 )( −13 + 14 + 15 ) = 84 ,
im Einklang mit der Formel "Fläche = Höhe mal halbe Grundlinie" (siehe oben):
( 5 + 9 ) 12
F=
= 84 .
2
Ein eleganter algebraischer Beweis für Herons Formel benutzt den Cosinussatz, die Gleichung
x2 − y2 = ( x + y ) ( x − y ) ,
und die
Dreiecks-Flächenformel
a b sin( γ )
a ha =
,
2
wobei ha = b sin( γ ) die Länge der Höhe auf der Seite der Länge a ist.
2
( 4 F )2 = ( 2 a b sin( γ ) )2 = ( 2 a b )2 ( 1 − cos( γ )2 ) = ( 2 a b )2 − ( a2 + b2 − c2 ) =
( 2 a b + a2 + b2 − c2 ) ( 2 a b − a2 − b2 + c2 ) = ( ( a + b )2 − c2 )( c2 − ( a − b )2 ) =
( a + b + c ) ( a + b − c ) ( a − b + c ) ( −a + b + c ) = 2 s ( 2 s − 2 c ) ( 2 s − 2 b ) ( 2 s − 2 a ).
Division durch 16 und Wurzelziehen ergibt die Behauptung!
Beenden wir unsere Untersuchungen des allgemeinen Dreiecks mit einem der schönsten Sätze der
ebenen Geometrie, der von LEONHARD EULER (1763) stammt:
Der Höhenschnittpunkt H, der Umkreismittelpunkt M und der Schwerpunkt S eines Dreiecks liegen
auf einer Geraden, der sogenannten Eulerschen Geraden.
Der Schwerpunkt teilt die Verbindungsstrecke der beiden anderen Punkte im Verhältnis 2:1.
Für den Höhenschnittpunkt H haben wir in der oben gewählten Position die Koordinaten
xy
0 und h =
,
z
für den Umkreismittelpunkt M
y−x
z−h
und
,
2
2
und der Schwerpunktvektor S ist natürlich das arithmetische Mittel (A+B+C)/3 der Eckvektoren,
hat also die Koordinaten
y−x
z
2 (z − h)
und
= (h +
)/3.
3
3
2
Somit wird die Strecke zwischen Höhenschnittpunkt und Umkreismittelpunkt tatsächlich vom
Schwerpunkt im Verhältnis 2:1 geteilt.
Wir betrachten wieder ein allgemeines Dreieck mit den Ecken A, B, C.
Im Beispiel wählen wir A = (-x,0), B = (0,y) und C = (0,z).
Zuerst die Seitenhalbierenden und ihr Schnittpunkt (der Schwerpunkt des Dreiecks):
Als nächstes die Mittelsenkrechten der drei Seiten und ihren Schnittpunkt.
Das ist der Mittelpunkt des Umkreises.
Nun die drei Höhen und ihr Schnittpunkt.
Jetzt die Strecke zwischen Umkreismittelpunkt und Höhenschnittpunkt:
Und alles zusammen:
Legt man nicht einen Höhenfußpunkt, sondern den Umkreismittelpunkt in den Ursprung, so erhält
man einen besonders kurzen Beweis für den Eulerschen Satz, der auch in beliebiger Lage klappt:
Es ist dann M = 0 und |A|=|B|=|C|. Wegen
(3 S − C) (A − B) = (A + B) (A − B) = A A − B B = A 2 − B 2 = 0
efüllt 3 S die Gleichung der Höhe auf der Seite AB, und ebenso die der Höhen auf AC und auf BC.
Damit ist 3S der Höhenschnittpunkt H, d.h. 3 S = H + 2 M (wegen M = 0).