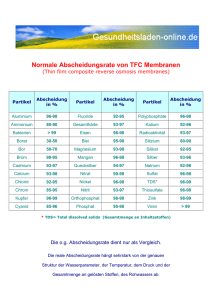
Deformable Bodies

Proseminar – Deformable Bodies
Deformable Bodies
Volker Jacht
1 Motivation
In der realen Welt ist praktisch jeder Körper durch äußere Krafteinwirkung deformierbar. Deshalb ist
die Simulation und Animation deformierbarer Körper ein wichtiger Bestandteil in der Informatik, um
eine glaubhafte Visualisierung realer und fiktiver Geschehen zu ermöglichen.
Im Folgenden gibt es eine Einführung in das Konzept von Masse-Feder-Systemen, das für die einfache
Repräsentation und Simulation von deformierbaren Körpern einsetzbar ist.
2 Masse-Feder-Systeme
Masse-Feder-Systeme bestehen aus einer Menge von Federn (Kanten) und Partikeln (Knoten). Jede
Feder muss dabei mit genau zwei Partikeln verbunden sein und ist über diese jeweils frei drehbar.
Damit elastische Körper visuell plausibel dargestellt werden können, müssen Partikel und Federn zu
einer Gitterstruktur zusammengesetzt werden, die jegliche Verformung in elastische Energie umwandelt. Somit kann der Körper nach Wegfall der äußeren Krafteinwirkung zu seiner Ursprungsform
zurückkehren.
Abb. 1: stabiles Gitter, bestehend aus Federn und Partikel
Zur Darstellung und späteren Berechnung des Systems, werden jedem Partikel folgende Eigenschaften zugeschrieben:



Masse
Geschwindigkeit
Position
Jede Feder
( )
ist mit dem Partikel und dem Partikel verbunden. Wichtige Eigenschaften sind
dabei:



⃗
⃗
Normalauslenkung
Federkonstante
Dämpfungskoeffizient
1
Proseminar – Deformable Bodies
3 Simulation
3.1 Berechnung der Kräfte
Die Federkraft, die auf Partikel aufgrund der Federverbindung
Hilfe des Hookeschen Gesetzes berechnet werden.
⃗
(‖ ‖
)
mit dem Partikel wirkt, kann mit
(1)
‖‖
Da der Energieerhaltungssatz gilt, würde sich ein Körper nach einer äußeren Krafteinwirkung in einen
endlosen oszillierenden Verformungsprozess begeben. Um in kurzer Zeit nach einem erfolgten Stoß
wieder einen beruhigten stabilen Zustand zu erreichen, muss die Stoßenergie mit Hilfe eines Dämpfungsprozesses absorbiert werden. Die Dämpfungskraft auf Partikel ist abhängig von dessen relativer Geschwindigkeit zum benachbarten Partikel , die durch die Feder miteinander verbunden sind.
Diese Kraft wirkt stets in Federrichtung und ist entgegengesetzt zur relativen Geschwindigkeit.
(2)
⃗
((⃗
⃗ )
‖‖
)
‖‖
Aus dem 3. Newtonschen Gesetz folgt die Formel:
⃗
⃗
und ⃗
⃗
(3)
Die resultierende Kraft auf Partikel ist die Summe aller Feder- und Dämpfungskräfte durch benachbarte Partikel, sowie der externen Kräfte.
⃗
∑(⃗
⃗
)
(4)
⃗
Externe Kräfte setzen sich zum Beispiel aus der Gravitationskraft, der Luftreibung, aus Kräften, die
durch Kollisionen mit anderen Objekten verursacht werden, etc. zusammen.
⃗
⃗
⃗
⃗
(5)
…
3.2 Differentialgleichung
Die Positions-, Geschwindigkeits-, Kraftvektoren und Massen aller Partikel werden in Matrizen zusammengefasst.
(
)
(
)
(6)
(
)
(7)
(
)
(8)
2
Proseminar – Deformable Bodies
(9)
M
(
)
Mit Hilfe des 2. Newtonschen Gesetzes kann nun folgende Differentialgleichung aufgestellt werden,
die das Verhalten des Masse-Feder-Systems beschreibt.
(10)
( ̇)
̈
Da zur visuellen Darstellung Masse-Feder-Systeme nur das von Bedeutung ist, und sich dieses nicht
analytisch aus ̈ herleiten lässt, muss unter Einsatz von numerischen Lösungsverfahren approximiert werden.
3.3 Numerische Lösungsverfahren
3.3.1 Explizites Eulerverfahren
Ein mögliches numerisches Lösungsverfahren ist das explizite Eulerverfahren. Dieses gehört zu den
einfachsten aller numerischen Verfahren zur Annährung von Differentialgleichungen. Es approximiert
die neue Position durch Linearisierung mit Hilfe der ersten Ableitung, also der Geschwindigkeit, am
Anfang des Zeitschritts
.
(
)
( )
( )
(11)
Die geforderte Geschwindigkeit lässt sich analog über die Beschleunigung zu Beginn des Zeitschritts
approximieren. Die Beschleunigung ist als ̈ über die Differentialgleichung (10) gegeben.
(
)
( )
( ( ) ( ))
(12)
Je kleiner gewählt wird, umso genauer wird das Ergebnis. Bei steifen Systemen muss zusätzlich
darauf geachtet werden, dass ein großes nicht nur Ungenauigkeit verursacht, sondern das System
zunehmend instabiler wird, bis das Resultat letztendlich unbrauchbar ist.
Abb. 2: Numerische Approximation mit unterschiedlichen Zeitschritten
Der große Vorteil des expliziten Eulerverfahrens besteht darin, dass es leicht zu Implementieren und
für einfache Systeme völlig ausreichend ist.
3
Proseminar – Deformable Bodies
Die Durchführung einer Simulation unter Verwendung des expliziten Eulerverfahrens sieht im Kern
wie folgt aus:
forever (
) {
forall Particles p {
p.setForce(⃗ )
}
// compute spring and damping forces for each
particle
forall Springs s {
⃗
s.getI().addForce(⃗
);
s.getJ().addForce(⃗
⃗
);
}
// Euler with stepsize
forall Particles p {
p.addVelocity(
p.getForce() *
/p.getMass()
);
p.addPosition(p.getVelocity *
);
}
}
Zuerst wird in der Hauptschleife
des jeweiligen Renderframes gesetzt.
Danach werden die wirkenden Kräfte aller Partikel mit den wirkenden externen Kräften initialisiert.
Diese sind durch Gleichung (5) beschrieben.
Im nächsten Bereich werden die Feder- (1) und Dämpfungskräfte (2) beider Partikel jeder Feder ausgewertet und nach Gleichung (4) zu diesen hinzu addiert.
Zuletzt wird für alle Partikel der explizite Eulerschritt zur Berechnung der Geschwindigkeit nach (12)
und der neuen Position nach (11) verwendet.
4
Proseminar – Deformable Bodies
Ein Nachteil des expliziten Eulerverfahrens ist die Instabilität, die insbesondere bei steifen Systemen
auftritt. Zur Veranschaulichung wird im Folgenden ein Dämpfungssystem betrachtet, welches abhängig von der Anfangsbedingung sehr schnell gegen 0 konvergiert. Wird diese Differentialgleichung wie
in Abb. 3 als Richtungsfeld dargestellt, zeigen sich die unterschiedlichen Verhaltensweisen, abhängig
von der Schrittgröße
Abb. 3: Richtungsfeld eines steifen Dämpfungssystems mit unterschiedlich großen Zeitschritten
Je kleiner die Schrittgröße ist, umso mehr stimmt die Approximation mit der exakten Lösung überein.
Wird jedoch ein zu großes gewählt, so schaukelt sich das System hoch, bis es endgültig unbrauchbare Ergebnisse liefert und „explodiert“.
3.3.2 Bessere Verfahren
Neben dem expliziten Eulerverfahren gibt es eine ganze Reihe anderer Verfahren, die eine erhebliche
Vielfalt an Verbesserungsmöglichkeiten bieten.
Das Eulerverfahren entspricht der Taylor-Reihenentwicklung ersten Grades. Um eine höhere
Genauigkeit zu erzielen, kann durch weiteres Ableiten der Grad erhöht werden. Dies bringt einen
größeren Rechenaufwand mit sich, ist dafür aber im Ergebnis effektiver als das simple Eulerverfahren. In der Praxis sind Verfahren bis zum vierten Grad, z.B. das klassische Runge-Kutta-Verfahren,
üblich.
All diese expliziten Verfahren mit unterschiedlicher Genauigkeit besitzen nach wie vor die negative
Eigenschaft, dass sie ab einer zu großen Schrittgröße instabil werden und keine brauchbaren Ergebnisse mehr liefern können. Dieses Problem kann unter Einsatz von impliziten Verfahren behoben
werden. Implizite Verfahren sind wesentlich schwieriger zu implementieren und sind ziemlich rechenintensiv, aber dafür, zumindest theoretisch, selbst bei beliebig großen Zeitschritten stabil.
5