2. Messverfahren für elektrische Größen
Werbung
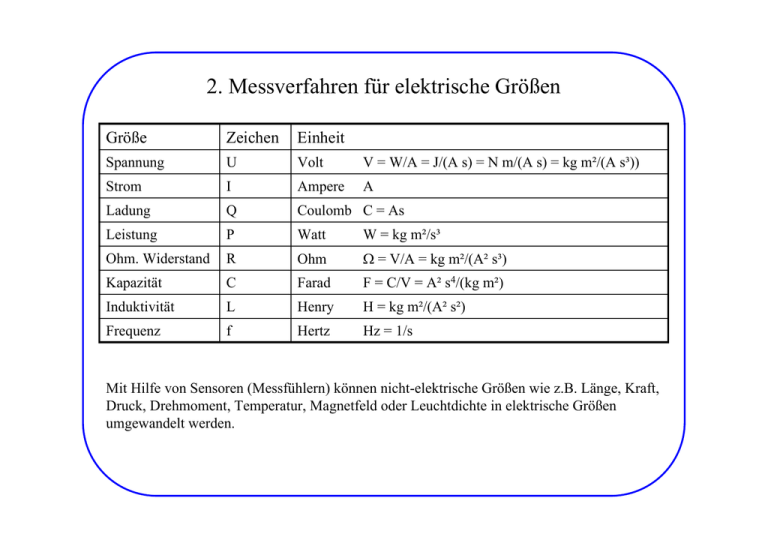
2. Messverfahren für elektrische Größen Größe Zeichen Einheit Spannung U Volt V = W/A = J/(A s) = N m/(A s) = kg m²/(A s³)) Strom I Ampere A Ladung Q Coulomb C = As Leistung P Watt W = kg m²/s³ Ohm. Widerstand R Ohm Ω = V/A = kg m²/(A² s³) Kapazität C Farad F = C/V = A² s4/(kg m²) Induktivität L Henry H = kg m²/(A² s²) Frequenz f Hertz Hz = 1/s Mit Hilfe von Sensoren (Messfühlern) können nicht-elektrische Größen wie z.B. Länge, Kraft, Druck, Drehmoment, Temperatur, Magnetfeld oder Leuchtdichte in elektrische Größen umgewandelt werden. Spezielle Begriffe bei elektrischen Größen Gleichgröße Wechselgröße Gleichrichtwert Effektivwert, RMS (root mean square value) Dezibel, dB x eff = X = 1 T 2 x dt T ∫0 Das Dezibel ist als "unechte Sondereinheit" ein Logarithmisches Maß für Leistungsverhältnisse. Hiervon abgeleitet wird es auch für Spannungs- und Stromverhältnisse benutzt (Gleichheit der Widerstände vorausgesetzt). Definition: ⎛P⎞ a = 10 ⋅ lg⎜ 1 ⎟ in dB ⎝ P2 ⎠ Mit P = U² bzw. P = I² ⋅ R und R1 = R 2 = R R fo lg t: ⎛U ⎞ a = 20 ⋅ lg⎜ 2 ⎟ in dB ⎝ U1 ⎠ ⎛I ⎞ a = 20 ⋅ lg⎜ 2 ⎟ in dB ⎝ I1 ⎠ Beispiele: U2 U1 U2 U1 U2 U1 U2 U1 1 1 P ⇒ 2 = : a = -3dB P1 2 2 P =1 ⇒ 2 = 1 : a = 0dB P1 P =2 ⇒ 2 = 4 : a = 6dB P1 P = 10 ⇒ 2 = 100 : a = -3dB P1 = Kirchhoffsche Regeln Knotenregel: In einem Verzweigungspunkt ist die Summe der hin fließenden Ströme gleich der Summe der abfließenden Ströme. n ∑I i =1 i =0 Maschenregel: Die Summe der Quellspannungen ist dem Betrag nach gleich der Summe aller Spannungen an den Widerständen. m n ∑ E +∑ I R k =1 k i =1 i i =0 Schaltung von Widerständen R= Ohmsches Gesetz: Reihenschaltung: U I n R1 R2 Rn R = ∑ Ri i =1 Folge der Kirchhoffschen Regeln Parallelschaltung: R1 n 1 1 =∑ R i =1 Ri R2 Rn Der Gesamtwiderstand ist bei der Parallelschaltung kleiner als der kleinste Teilwiderstand ! Analoge Messgeräte Strom- und Spannungsmesser nutzen die Wirkung des elektrischen Stromes ! z.B. Heizdrahtinstrument; Heizdraht verlängert sich durch Erwärmung verursacht durch Stromfluss. Anmerkung: Ampère hat die Stromrichtung vom Pluspol zum Minuspol festgelegt (technische Stromrichtung). Die Elektronen in metallischen Leitern fließen vom Minuspol zum Pluspol (Elektronenstromrichtung). Dreheiseninstrument Im Magnetfeld der Spule werden die beiden Weicheisenstäbe gleichartig magnetisiert, es liegen sich also jeweils zwei gleichartige Pole gegenüber. Daher kommt es zur Abstoßung. Drehspulinstrument Fließt Strom durch die Spule, so findet eine Wechselwirkung des "Spulenmagneten" mit den Polen des Hufeisenmagneten statt. Es kommt je nach Stromrichtung zu einer Links- bzw. Rechtsdrehung der Spule. Bei der Drehung der Spule werden die Zuleitungsbänder (Spiralfeder) verdrillt. Die Spule dreht sich soweit bis das durch den Strom bewirkte auslenkende Drehmoment gleich dem durch die Spiralfeder entstehenden rücktreibenden Drehmoment ist. Die Drehspule ist in der Praxis auf einen Eisenkern gewickelt. Fließt Strom, so wird auch dieser Eisenkern zum Magneten, die Kräfte auf die Drehspule und damit das Drehmoment werden größer (damit wird das Messgerät empfindlicher). Strom- und Spannungsmessung Rst Rst Rsp Rsp Damit die Messwerte durch die Instrumente möglichst wenig beeinflusst werden, besitzen Strommesser (Amperemeter) im Vergleich zum Widerstand des Messkreises Rx einen kleinen Innenwiderstand Rst, Spannungsmesser (Voltmeter) dagegen einen vergleichsweise hohen Innenwiderstand Rsp. In der stromrichtigen Schaltung verfälscht der Spannungsabfall Ust am Widerstand Rst das Ergebnis. Es gilt hier: U − U st U 0 − IRst = Rx = 0 I I In der spannungsrichtigen Schaltung wird der Teilstrom Isp über Rsp mit gemessen. Es gilt hier: U0 U0 Rx = = I − I sp I − U R sp Im Allgemeinen gilt: bei kleinen Rx die spannungsrichtige Schaltung verwenden bei großen Rx die stromrichtige Schaltung verwenden Messbereichserweiterung Strommesser Zur n-fachen Erweiterung des Messbereiches eines Strommessers schaltet man parallel zum Instrument (Innenwiderstand Ri) einen Widerstand Rsh (Shunt/Beipass), über den bei Vollausschlag der (n-1)-fache Strom fließen muss. Rsh = Ri n −1 Spannungsmesser Zur n-fachen Erweiterung des Messbereiches eines Spannungsmessers schaltet man zum Instrument (Innenwiderstand Ri) einen Widerstand Rv in Reihe. An diesem Vorwiderstand tritt bei Vollausschlag ein (n1)-facher Spannungsabfall auf. Rv = (n − 1) Ri Widerstandsmessung durch Strom- und Spannungsmessung Vierdrahtmessung Vielfachmessgeräte: Vielfachmessgeräte sind so ausgelegt, dass man mit ein und demselben Gerät Spannung und Strom messen kann. Durch den Einbau geeigneter Parallelwiderstände für die Strommessung und Vorwiderstände für die Spannungsmessung lässt sich der Messbereich erweitern. Widerstandsmessung mit Messbrücken Wheatstone-Messbrücke Zwischen den Punkten A und B befindet sich eine Spannungsquelle U. Zwischen den Punkten C und D ein Galvanometer G. Ziel ist es, die Brücke durch geeignete Wahl der Widerstände R1, R2, RN und RX „abzugleichen“ (Galvanometer stromlos!). Somit liegen die Punkte C und D auf gleichem Potential und es gilt: R1 I1 = RX I X R2 I 2 = RN I N Außerdem gilt: I1 = I2 und IX = IN Nach Division erhält man: R X = RN R1 R2 Thomson-Messbrücke Doppelbrücke. Geeigneter als Wheatstone-Brücke bei sehr kleinen RX und langen Leitungsdrähten. Widerstandskennlinie Spezifischer Widerstand (Materialgröße, [Ωm] R=ρ l A Widerstand eines homogenen zylindrischen Leiters Erklärung: Nach der klassischen Theorie der elektrischen Leitung bilden die Leitungselektronen in einem Metall ein „Elektronengas“ mit ungeordneter thermischer Bewegung. Durch einen elektrische Spannung werden die Elektronen in der Richtung beschleunigt, die der elektrischen Feldstärke entgegengesetzt ist (elektrische Feldkraft). Durch Stöße mit den Metallionen werden sie abgebremst (Reibungskraft). Æ mittlere Geschwindigkeit (materialabhängig) stellt sich ein Temperaturabhängigkeit des Widerstandes Die Temperaturabhängigkeit des elektrischen Widerstandes kann vor allem für metallische Stoffe wie folgt beschrieben werden: (β und γ sind Temperaturkoeffizienten, R0 ist der Widerstand am Eispunkt 0°C) Rt = R0 (1 + βt + γt 2 ) Für kleine Temperaturintervalle gilt mit hinreichender Genauigkeit der lineare Zusammenhang: Rt = R0 (1 + βt ) Durch Messung bei zwei Temperaturen erhält man β: Rt1 − Rt 2 β= t1 Rt 2 − t 2 Rt1 Für metallische Stoffe ist β positiv (der Widerstand steigt mit der Temperatur). Für spezielle Legierungen erreicht man β ≈ 0 (Eignung für Normal- und Messwiderstände). Elektrolyte und Halbleiter weisen ein negatives β auf (Ursache: Zunahme der Ladungsträgerkonzentration) Wechselstromkreis Widerstand Kondensator Spule Bei einem idealen Kondensator eilt der Strom der angelegten Spannung um den Phasenwinkel ϕ=90° voraus. Einen realen Kondensator kann man Reihen- oder Parallelschaltung einer verlustfreien Kapazität C und eines Wirkwiderstandes R ersetzen. Bei einer idealen Spule eilt der Strom der Spannung um ϕ=90° nach. Auch eine reale Spule lässt sich durch einen Wirkwiderstand R und eine verlustfreie Induktivität L darstellen. Bei realen Kondensatoren und Spulen treten Verluste auf. Diese Verluste werden erzeugt durch das Dielektrikum bei Kondensatoren und durch Wirbelstrom- und Magnetisierungsverlusten bei Spulen. Infolge dieser Verluste ist der Phasenwinkel ϕ des komplexen Widerstandes kleiner als 90°. Als Verlustwinkel bezeichnet man δ=90°-ϕ, als Verlustfaktor tan δ. Wechselstromwiderstände Zeigerdiagramme Leitwert eines Kondensators Widerstand einer Spule Übungsaufgabe Eine Glühlampe mit einer Leistung P = 100 W, die für eine Betriebsspannung von U1 = 100 V vorgesehen ist, soll an die Netzspannung U2 = 220 V, f = 50 Hz angeschlossen werden. Wie groß muss entweder 1. die Kapazität eines zur Glühlampe in Reihe geschalteten Kondensators oder 2. ein ebenfalls in Reihe geschalteter Ohmscher Widerstand Sein, um die Wirkleistung P an der Glühlampe zu erbringen ? Wie groß ist die dem Netz entnommene Wirkleistung für 1. und 2. ?