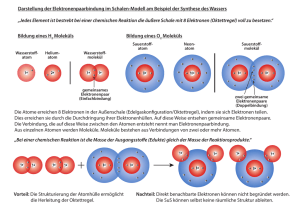
Stoffe – Valenzelektronen – Struktur

Stoffe – Valenzelektronen – Struktur
Chemiker teilen Materie, die ihnen in die Hände gerät, in verschiedene Kategorien ein:
•
Gemische
o Heterogene Gemische (Mischung auf makroskopischer Ebene)
o Homogene Gemische (Mischung auf molekularer Ebene, Beispiel: Lösung)
•
Reine Stoffe
o Verbindungen
o Elementare Verbindungen (z.B. Cl2)
o Atomare Elemente (z.B. Edelgase)
•
Heterogene Gemische können Komponenten in verschiedenen Aggregatzuständen
•
Homogene Gemische und reine Substanzen können auch simultan in mehreren
(flüssig, fest, gasförmig) enthalten.
Aggregatzuständen vorliegen, man spricht dann von Phasen des jeweiligen
Aggregatzustands (Beispiel: In Wasser schwimmendes Eis mit Wasserdampf darüber).
Reine Stoffe lassen sich grob in 3 Kategorien einteilen:
•
Molekulare Substanzen
o Eine relativ geringe Anzahl Atome ist fest miteinander über untereinander
geteilte Valenzelektronen verbunden. Diese Bindung nennt man kovalent. Die
Moleküle wiederum bilden mehr oder weniger feste Verbunde als weiche
Festkörper, Flüssigkeiten oder Gase. Beispiele: Wasser, Ammoniak, Glucose,
Octan, Kohlendioxid
•
Salze
o Valenzelektronen sind praktisch vollständig von einer Atom- oder Molekülart
auf den Bindungspartner übergegangen. Es herrschen grosse elektrische
Potentiale zwischen den Komponenten, Kationen (Elektronenverlust, positiv
geladen) und Anionen (Elektronengewinn, negativ geladen). Die starken
1
elektrostatischen Kräfte sorgen dafür, dass der Stoff meist fest oder höchstens
flüssig ist. Beisiele: Natriumchlorid (Kochsalz), Titandioxid, Kaliumacetat
•
Metalle
o Ein Teil oder auch alle Valenzelektronen sind von den Atomen gelöst und
bewegen sich einigermassen frei zwischen den verbliebenen Kationen. Diese
werden durch die bewegliche Ladungswolke ziemlich fest zusammengehalten.
Solche Stoffe sind meist fest oder auch flüssig. Durch die beweglichen
Elektronen leiten Metalle Wärme und elektrischen Strom. Beispiele: Eisen,
Quecksilber, Natrium
Selbstverständlich gibt es Grenzfälle und Mischformen. Salze, bei denen die Elektronen nicht
so vollständig zwischen Kation und Anion ausgetauscht sind, haben einen gewissen
kovalenten Anteil. Ebenso existieren Salze mit Metallcharakter, bei denen einige Elektronen
nicht auf das Anion übergehen, sondern sich frei im Kristall bewegen.
Ein Salz muss nicht notwendigerweise aus ionisierten Atomen bestehen, es kann sich auch
aus geladenen molekularen Gruppierungen zusammensetzen, die in sich kovalent gebunden
sind. Beispiel: Ammoniumnitrat.
Schalenbau – Konsequenzen: Aufbauprinzip und Elektronegativität
Metalle sind Elemente, deren Atome die Valenzelektronen eher schlecht binden. Sie sind im
Periodensystem auf der linken Seite konzentriert. Der Grund dafür ist die gute Abschirmung
der Kernladung durch die tiefer liegende Elektronenschalen bei Beginn einer neuen Schale.
Mit steigender Kernladung in der Periode wird die Wirkung der Kernladung auf derselben
Schale grösser, die Elektronen werden fester gebunden. Erst durch den Übergang zur nächsten
Hauptquantenzahl vergrössert sich der mittlere Abstand der äusseren Elektronen zum Kern
wieder so, dass die Abschirmung grösser wird. Eine Durchmischung der Schalen tritt
allerdings ab der 3. Periode auf. Die 3d-Orbitalfunktionen sind besser abgeschirmt vom Kern
als die 4s-Funktion, weil ihre grösste Elektronendichte relativ weit vom Kern liegt, während
s-Funktionen immer eine hohe Dichte in Kernnähe aufweisen. Deshalb gehen 2
Valenzelektronen zuerst in den 4s-Zustand, bevor 3d-Zustände auftreten. Die Elemente mit
Auffüllung der 3d-Zustände gehören deshalb zur 4. Periode, die mit 4d-Zuständen zur 5.
2
Periode etc. Für ein Atom mit nur einem Elektron (H, He+, Li2+ etc.) gilt allerdings das ideale
Orbitalschema, weil es in einem solchen Atom keine Elektron-Elektron Abstossung gibt. Das
lässt sich durch Anregung solcher Atome mit Licht (Spektroskopie) verifizieren,
Die abnehmende Abschirmung nach rechts im Periodensystem hat auch zur Folge, dass die
Elektronen von Bindungspartnern stärker gebunden werden. Damit wird die kovalente
Bindung unsymmetrisch, ein statischer elektrischer Dipol entsteht: µ = qd , wobei q der
Betrag der partiellen Ladung auf den Enden des Dipols ist und d der Abstand, hier gerichtet
als Vektor.
q+
q−
d
Diese Art Moleküle trägt immer ein kleines elektrisches Feld mit sich, das die gegenseitige
Anziehung verstärkt. Stoffe dieser Art nennt man in der Chemie polar. Die Teilladungen q+
und q- sind stets kleiner als die Elementarladung, welche das kleinste freie Ladungsquant
repräsentiert, und eine Eigenschaft der Elektronen und Protonen (Wasserstoff-Kerne) ist.
Die Eigenschaft, Partnerelektronen stark zu binden, wird semiquantitativ durch die so
genannte Elektronegativität beschrieben. Es gibt davon 5 Definitionen, gebräuchlich ist die
des Amerikaners Linus Pauling, der ein fundamentales Werk der Chemie verfasst hat: The
Nature of the Chemical Bond. Obwohl 1939 erschienen, ist es immer noch aktuell! Das
Paulingsche Mass wird aus der Differenz von Bindungsenergien zweier Atomarten A und B
bestimmt, wofür man die Dissoziationsenergien von A-B, A-A und B-B in die Atome misst.
Als Referenzelement dient das Fluor, das am stärksten elektronenziehende Element, dem
willkürlich der Wert 3.98 zugeordnet wird. In Molekülen, die mehr als zwei Atome enthalten,
kann man das gesamte Dipolmoment durch Vektor-Addition der Bindungsdipolmomente der
verbundenen atomaren Nachbarn darstellen. Das führt dazu, dass z.B. das gesamte
Dipolmoment von BF3 gleich Null ist, weil die Fluoratome ein gleichseitiges Dreieck um das
Bor bilden. Die Bindungsdipole sind stark, die EN von F ist 3.98, während Bor nur den Wert
2.04 aufweist. NH3 hingegen hat ein Netto-Dipolmoment, weil das N nicht in der Ebene der
3 H liegt. Der Grund für die andersartige Geometrie sind nicht gebundene Elektronen in der
Valenzschale des N.
3
Chemischer Formalismus
Die Elemente einer Verbindung werden in Formeln durch die im Periodensystem
zugeordneten Abkürzungen repräsentiert. Die Anzahl der Atome einer Art wird durch einen
nach und tief gestellten Index angegeben. Bei Salzen und metallischen Verbindungen gibt
man die kleinste Einheit mit ganzzahligen Verhältnissen an, da sich diese Fragmente im
Kristallgitter fortwährend wiederholen.
Bei molekularen Verbindungen baut man etwas lokale Strukturinformation ein. Beispiel:
Wasserstoffperoxid kann man stöchiometrisch als HO angeben, also eine Verbindung aus
gleichviel Wasserstoff und Sauerstoff. In einem Wasserstoffperoxid-Molekül sind jedoch 2
Wasserstoffatome mit 2 Sauerstoffatomen verbunden, deshalb schreibt man H2O2. Man kann
auch HOOH angeben, was die Lage der Bindungen zwischen den Atomen verdeutlicht. Die
Brutto- oder Summenformeln sind nützlich, um aus den relativen Atommassen bequem die
relative Molekülmasse zu berechnen, oder um einen Überblick über die Zusammensetzung zu
bekommen.
Strukturformeln
Um die tatsächlichen Verhältnisse in einem Molekül oder Kristall genauer zu beschreiben,
brauchen wir jedoch Strukturformeln. Dafür gibt es einfache Modelle, bei denen die
Valenzelektronen durch Punkte und Striche symbolisiert werden, oder komplexe, die
Orbtitaldiagramme verwenden.
Wasser, brutto H2O, sieht dann so aus: H
O
H Die zwei Striche repräsentieren je ein
Paar Elektronen die zwischen H und O geteilt werden. Jedes H steuert ein Elektron bei (mehr
kann es nicht bieten), das O 2 Stück von den 6, die es besitzt (laut Ordnungszahl). Die
Bindungselektronen gehören immer zu beiden Partneratomen. Also haben die beiden H nun 2
Elektronen, der Sauerstoff 8. Das ist die jeweilige maximale Elektronenzahl für die
Hauptquantenzahl ihrer Valenzschalen. Beide Atomarten haben so die
Elektronenkonfiguration ihres zugehörigen Edelgases, H die von He und O die von Ne. Dieser
Zustand wird angestrebt, weil er die elektrostatische Energie für die Valenzschalen minimiert.
Für Atome der zweiten Periode ist dies immer erfüllt, wenn sie 8 Elektronen in der
Valenzschale tragen, man nennt dies auch Oktettregel. Für Wasserstoff mit seiner Mini-
Schale ist es eine Duett-Regel. Ab der dritten Periode wird es kompliziert, weil die Schalen zu
mischen beginnen. Es bleibt noch die kleine Frage, warum das H2O oben gewinkelt
abgebildet wird und nicht etwa linear. Die Antwort liegt bei den 4 Elektronen des O, die nicht
4
für die Bindung verwendet wurden. Wohin damit? Elektronen stossen sich gegenseitig ab, so
sehr sie sich auch vom Kern angezogen fühlen. Damit wandert wegen der Elektronendichte
zwischen O und H, den Bindungen, die sich gegenseitig abstossen, Elektronenladungsdichte
der Valenzschale des O möglichst weit davon weg. Elektronen bleiben dabei gepaart im
nahezu gleichen Quantenzustand, sie unterscheiden sich nur durch ihre Spinquantenzahlen
von + ½ und – ½. Diese Paare verhalten sich ähnlich wie Bindungen und stossen sich auch
gegenseitig ab. Damit sich alle 4 Elektronenpaare möglichst weit voneinander entfernen und
so die elektrostatische Abstossung minimieren, bildet sich ungefähr die Geometrie eines
Tetraeders aus, wobei an 2 Ecken H sitzen und an den beiden andern ungebundene
O
:
:
Elektronenpaare. Man symbolisiert das einfach als H
H
wobei die Punkte die
ungebundenen Elektronen darstellen, oder pseudo-dreidimensional H
O
Hier werden
H
die ungebundenen Elektronenpaare durch die Bindungsstriche ohne Atom repräsentiert. Die
Geometrie erklärt denn auch zusammen mit den Elektronegativitätsdifferenzen, warum H2O
eine polare Substanz ist.
Beispiele mit komplexeren Bindungsverhältnissen:
Nitrit NO2−: N hat 5 Valenzelektronen (VE), jedes O hat 6. Dazu kommt ein extra Elektron
wegen der negativen Ladung, total 18 VE.
O
O
O
O
N
N
Die negative Ladung ist aufgrund der 2 gleichwertigen Formeln auf beide O gleichmässig
verteilt. Die ungebundenen Valenzelektronen am N sorgen dafür, dass es gewinkelt ist. Ein
Dipolmoment hat es hingegen nicht: Geladene Moleküle (= Ionen) haben kein
Dipolmoment, sondern einfach eine Ladung.
Mit einem weiteren O gelangt man zum Nitrat, das dann kein ungebundenes Elektronenpaar
am N besitzt.
O
O
O
O
+
O
+
N
N
N
O
O
O
+
O
Die Repräsentation von Elektronen durch Punkte und von gepaarten Elektronen durch Striche
ist die Notation nach Lewis. Die Ableitung der räumlichen Molekülstruktur aus der
gegenseitigen Abstossung der Bindungselektronen und der ungebundenen Elektronen heisst
5
VSEPR-Modell (valence shell electron pair repulsion). Bisher haben wir Moleküle bzw. Ionen
betrachtet, die Elemente der 1. und 2. Periode enthalten und die Oktettregel erfüllen. Beim
Übergang zur 3. Periode können auch Bindungen aufgrund der Besetzung von d-Zuständen
gebildet werden, z.B. im Sulfat:
O O
O
S
O
Der Schwefel hat hier 10 Valenzelektronen, der Sauerstoff jedoch 8, wie es strikt für die 2.
Periode gilt. Interessant ist, dass d-Zustände in einem Molekül schon in der 3. Periode besetzt
werden können, in den freien Atomen aber nicht.
Elemente können auch weniger als 8 Valenzelektronen tragen. Eine Variante ist der Verlust
aller Valenzelektronen bei den Elementen niedriger Elektronegativität, wenn sie mit einem
Element hoher Elektronegativität eine ionische Verbindung (Salz) eingehen. Die
Valenzelektronen des schwach elektronegativen Elements werden gänzlich in die
Valenzschale der stark elektronegativen Elements transferiert, da dann zu einem Anion mit
entsprechender Edelgaskonfiguration wird. Das „Spenderatom“ wird zum Kation und trägt
nun die Edelgaskonfiguration der vorgehenden Periode. Die Edelgaskonfiguration ist die
energetisch am tiefsten liegende Besetzung einer Periode, deshalb streben molekül- oder
ionenbildende Systeme dorthin. Beispiel: NaCl = [Ne]+ [Ar]–. Der andere Fall ist die
Verbindung von Elementen ähnlicher Elektronegativität mit wenigen Valenzelektronen, z.B.
BH3:
H
H
B
H
Solche Verbindungen können ein Molekül mit einem ungebundenen Elektronenpaar durch
dieses binden, indem sie es in ihre eigene Valenzschale einbauen.
Lösungen
Zur Durchführung einer Reaktion lieben die Chemiker nichts mehr als eine Lösung (die eines
Problems sowieso). Lösungen sind homogene Mischungen und bieten deshalb einige Vorteile
gegenüber Festkörpern oder Gasen als Reaktionsmedium, wobei der Nachteil der Festkörper
schwerer wiegt. In Festkörpern sind Moleküle, Ionen oder Atome auf einer
menschenkompatiblen Zeitskala ortsfest. Wenn man zwei Festkörperoberflächen
6
zusammenpresst, wird eine Reaktion dort höchstens sehr langsam ablaufen, und die
Ansammlung der Produkte wird den Prozess zu Erliegen bringen. In Gasen ist die
Vermischung von Reaktanden kein Problem, es kann sogar zu schnell gehen, so dass
exotherme (wärmeproduzierende) Reaktionen explosionsartig verlaufen können. Eher
Schwierigkeiten bieten die Behälter, die dicht sein müssen, weil die Reaktionsmischung sonst
entweicht. Nachteilig ist auch, dass nur wenige Stoffe bei unsern Umweltbedingungen
gasförmig sind, und dass das Verdampfen normalerweise flüssiger oder gar fester Stoffe viel
Energie benötigt und dabei auch zur Zersetzung führen kann, bevor die erwünschte Reaktion
eintritt.
Lösungen lösen all diese Probleme: Die Moleküle sind mobil und können sich treffen, somit
reagieren. In einer Lösung können Festkörper bzw. ihre Komponenten vorliegen, aber auch
Gase, alle molekular verteilt. Im Falle heftiger exothermer Reaktion dient das Lösungsmittel
als Moderator, es kann Energie absorbieren und durch Verdünnung die Reaktionsrate
absenken. Nicht zuletzt ist auch die Sache mit dem Behälter viel einfacher als bei Gasen: Im
einfachsten Fall genügt ein Becherglas, es braucht kein geschlossenes System mit
Überdrucksicherung.
Deshalb beginnen sehr viele chemische Arbeitsvorschriften mit: Man löst …
In unserer nicht so perfekten Welt (eigentlich ist sie perfekt, wir sind nur zu ungeschickt) gibt
es natürlich auch ein paar Haken bei der Nutzung von Lösungen. Es gibt z.B. Stoffe, die sich
partout kaum in irgendeiner Flüssigkeit lösen. Es gibt Stoffe, die sind so reaktionsfreudig,
dass sie mit allen bekannten Lösungsmitteln reagieren (oder zumindest mit denen, in denen
sich der zweite gewählte Reaktand wohlfühlt). Aus diesen Gründen gibt es dann auch
exotischere Arbeitsvorschriften, in denen Lösungen mit Festkörpern, Gase mit Festkörpern
oder Gase mit Gasen zur Reaktion gebracht werden. Als besonders harte Methode bietet es
sich auch an, zwei Festkörper zusammen zu schmelzen.
Der Lösungsprozess
Wenn man mit Lösungen arbeiten will, lohnt es sich, einmal den Lösungsprozess für
Festkörper und Gase in unterschiedlichen Lösungsmitteln näher zu betrachten, ebenso den
Zustand des gelösten Materials. Bei der Lösung von Gasen oder eines flüssigen Stoffs in
Flüssigkeit handelt es sich um einen Transfer zwischen Phasen mit hoher Mobilität der
Moleküle. Dieser geht ziemlich zwanglos per Diffusion vonstatten, wogegen das Aufbrechen
eines Festkörpers ein komplexer Vorgang ist. Man muss hier zwischen dem Lösen polarer
und apolarer Stoffe unterscheiden. Apolare Substanzen haben schwache nicht-kovalente
7
Bindungen zwischen den Molekülen in einem Kristall, diese Kristalle sind entsprechend
weich. Moleküle treten relativ leicht aus der Oberfläche aus, viele solche Stoffe haben sogar
einen deutlichen Dampfdruck (Iod, Naphthalin etc.). Kommt ein solches Material mit dem
Lösungsmittel in Berührung, so treten Moleküle in die flüssige Phase über und verteilen sich
darin. Gleichzeitig wird die „Lücke“ an der Kristalloberfläche mit Lösungsmittel „gestopft“,
so dass eine Rückkehr sehr unwahrscheinlich ist. Der Vorgang setzt sich immer weiter fort,
bis die Lösung gesättigt ist. Diese Bedingung umschreibt, dass die Dichte (Konzentration) des
gelösten Stoffs so gross geworden ist, dass er wieder Aggregate bildet, d.h. kristallisiert. Dies
ist das Lösungsgleichgewicht. Seine Lage hängt vom Verhältnis der Bindungskräfte zwischen
zwei Stoffmolekülen zu denjenigen zwischen Stoffmolekülen und Lösungsmittelmolekülen
ab.
Hier sei kurz angemerkt, dass es dazu keine statischen Dipole braucht. Symmetrische
Moleküle wie I2 lösen sich sehr gut in symmetrischen Lösungsmitteln wie CCl4. Die Kraft
zwischen zwei solchen Partnern ist zwar schwach, doch immer anziehend, und wird
Londonsche Dispersionskraft genannt. Dies ist nicht die van der Waals Kraft, sondern nur ein
Teil davon! Sie kommt dadurch zustande, dass die Verteilung der Elektronen in einem
Molekül (oder Atom) zeitlich nicht konstant ist. Es besteht ein zeitlich variables elektrisches
Feld, das sich mit dem entsprechenden Feld des Nachbarmoleküls synchronisiert (grob
vergleichbar mit dem makroskopischen Phänomen der elektrostatischen Influenz).
Bei polaren Stoffen ist das Lösen mehr von den zwischenmolekularen Kräften abhängig, am
extremsten wird das beim Lösen von Salzen oder starken Säuren unter elektrolytischer
Dissoziation. Aus der Oberfläche eines Ionenkristalls treten praktisch keine Teilchen bei
Raumtemperatur aus, zu gross sind die elektrostatischen Kräfte zwischen Kationen und
Anionen. Ein Lösungsmittel, dessen Moleküle ein kräftiges statisches Dipolmoment besitzen,
kann die Struktur jedoch aufbrechen. Man kann sich das wie folgt vorstellen:
8
Die Lösungsmitteldipole werden zunächst an der Oberfläche des Kristalls adsorbiert. Dabei
richten sie sich antiparallel zu benachbarten Kationen und Anionen aus, was das lokale
elektrische Feld eines solchen Paars schwächt. Die gesamte Bindungskraft an der Oberfläche
wird vermindert. Durch die Schwingungen der Ionen im Kristallgitter können jetzt einzelne
von ihnen austreten und werden sofort von Lösungsmitteldipolen eingehüllt. Verlässt ein
Kation den Kristall oder umgekehrt ein Anion, muss wegen der Elektroneutralität gleich ein
Gegenion austreten. Die Lücke wird mit einem Lösungsmitteldipol gefüllt, und der
Abbauprozess geht weiter. Die bereits gelösten Ionen werden durch Dipole so eingehüllt, dass
ihre wechselseitigen elektrostatischen Kräfte sehr gering werden: Wir haben eine
Elektrolytlösung. Die Ionen sind zu einem grossen Grad gegeneinander beweglich, die
Lösung leitet elektrischen Strom. Die Grenze der Löslichkeit wird auch hier erreicht, wenn
die Konzentration der Ionen so gross wird, dass wieder Kristalle gebildet werden. Dies
wiederum hängt davon ab, wie stark die Bindungskraft im Kristall im Vergleich zur Bindung
der Ionen durch die Lösungsmitteldipole ist. Die Auflösung von polaren molekularen Stoffen
in polaren Lösungsmitteln verläuft ähnlich, nur sind die Kräfte geringer.
Die schlechte Löslichkeit von apolaren Gasen oder Flüssigkeiten in polaren Lösungsmitteln
erklärt das auf den zwischenmolekularen Bindungskräften beruhende Modell ebenfalls: Im
polaren Lösungsmittel herrschen stärkere Kräfte zwischen den Lösungsmittelmolekülen als
die, die zwischen Gelöstem und Lösungsmittel möglich sind. Die Lösungsmittelmoleküle
„kleben“ also zusammen und lassen das zu Lösende nicht herein. Die Löslichkeit ist also
immer eine Frage der relativen Bindungskräfte zwischen und innerhalb von zwei Phasen.
Lösung und Energie
Lösungsvorgänge sind Zustandsänderungen und damit auch Energieumsatz begleitet. Die
Energieänderung, gemessen in einem Kalorimeter mit Druckausgleich (p = const.) nennt man
Enthalpie ∆H. Die Lösungsenthalpie ∆SH° für ein Salz setzt sich additiv zusammen aus der
Gitterenergie ∆sublH°, die die Bindungsenergie des Kristalls darstellt, und der
Solvatationsenthalpie ∆solvH°, die die Bindung der Lösungsmitteldipole an die Ionen
repräsentiert. ∆sublH° steht bei Lösung eines Salze wie KCl(s) in H2O für
KCl(s) →
Der Vorgang für ∆solvH° ist
Total ergibt sich
K+(g) + Cl–(g)
K+(g) + Cl–(g) →
KCl(s) →
K+(solv, l) + Cl–(solv, l)
K+(solv, l) + Cl–(solv, l)
∆sublH° = 701.2 kJ/mol
∆solvH° = -684.1 kJ/mol
∆SH° = 17.1 kJ/mol
9
Hier sei noch angemerkt, dass ∆solvH° nicht nur die Energie beinhaltet, die beim Binden des
Lösungsmittels an die Ionen frei wird, sondern auch den Energieverbrauch, um die an die
Ionen zu bindenden Moleküle dem Lösungsmittelverband zu entziehen. Der zweite Anteil ist
einiges kleiner als der erste, weil Dipol-Dipol Wechselwirkungen schwächer als Ion-Dipol
Wechselwirkungen oder gar Ion-Ion Wechselwirkungen sind.
Die Vorzeichen der ∆H-Werte sind systemegoistisch zu interpretieren: Negative Werte
bedeuten, dass Wärme freigesetzt wird, positive, dass Wärme aufgenommen wird, d.h. das
System Gelöstes - Lösungsmittel sich abkühlt. Obwohl der Lösungsvorgang für KCl externe
Energie benötigt, läuft er spontan ab. Der Grund dafür ist der Gewinn an Beweglichkeit für
die Ionen des Festkörpers, der durch die Entropieänderung ∆S ausgedrückt wird. Die Entropie
ist eine Funktion, die die Freiheitsgrade der Bewegung in einem molekularen System
repräsentiert bzw. im invertierten Sinn seinen Ordnungsgrad. Die Funktion, die beides, ∆H
und ∆S zusammenfasst, ist ∆G = ∆H - T ∆S, genannt Gibbs-Energie. Damit ein Vorgang
spontan abläuft, muss sein ∆G negativ sein.
Im Gegensatz zur Lösung von Festkörpern oder Flüssigkeiten in Flüssigkeiten ist die Lösung
von Gasen in Flüssigkeiten (oder Festkörpern) immer exotherm, d.h. ∆H ist negativ, weil der
Übergang stets von schwach bis gar nicht gebundenem Zustand zu einem stärker gebundenen
verläuft.
Der gelöste Zustand
Der flüssige Aggregatzustand ist der komplexeste, weil Ordnung und Chaos zugleich
herrschen, und auch die strukturelle Komplexität verschiedener Flüssigkeiten ist sehr variabel.
Apolare Flüssigkeiten gleichen einem sehr dichten Gas, gelöste Stoffe darin sind einfach
dispergiert. Die Moleküle des Gelösten sind kaum stärker an die Lösungsmittelmoleküle
gebunden als diese untereinander. Mit zunehmender Polarität erhöht sich die Ordnung im
Lösungsmittel selbst, die Moleküle sind zwar immer noch sehr beweglich, aber es gibt
bevorzugte gegenseitige Ausrichtungen. Im Extremfall treten so genannte
„Wasserstoffbrücken“ auf. Diese Bedingung ist immer gegeben, wenn das
Lösungsmittelmolekül ein sehr elektronegatives Element, an das H direkt gebunden ist,
enthält, und das elektronegative Element mindestens ein ungebundenes Valenzelektronenpaar
besitzt. Der Klassiker ist Wasser, H2O. Organische Abkömmlinge von H2O, die Alkohole,
besitzen diese Eigenschaft ebenfalls, dazu kann man NH3(l) und seine organischen Derivate,
die Amine, sowie HF und HCN(l) nennen. HF und HCN(l) gehören wie H2O zu den polarsten
aller Lösungsmittel, allerdings sind die ersteren aus anderweitigen Gründen höchst unpopulär.
10
Die Wasserstoffbrücke ist eine Bindung zwischen einem der H-Atome eines Moleküls und
dem ungebundenen Valenzelektronenpaar des elektronegativen Elements eines andern
Moleküls. Diese Bindung ist stark gerichtet und praktisch linear. Sie sorgt dafür, dass
Lösungsmittel, die sie bilden, stark strukturiert sind und hohe Siedepunkte haben. Beispiel
H2O:
O
H
O
H
O
H
H
O
H
H
O
H
H
O
H
H
O
H
H
H
H
O
H
H
Die Wasserstruktur ist natürlich in Wirklichkeit dreidimensional, mit den O-Atomen in
Zentren von Tetraedern, die durch die H gebildet werden. Stoffe mit niedrigem Dipolmoment
werden kaum eingelassen, weil das zu einer Erhöhung der Gesamtenergie führen würde, sie
sind schlecht löslich in Wasser.
Die Struktur wird gebrochen, wenn Ionen in sie eingebaut werden, weil die elektrostatische
Kraft zwischen Ionen und Dipolen grösser ist als zwischen Dipolen allein. Sie wird auch
gestört, wenn polare Substanzen mit ähnlichem Dipolmoment wie H2O eingefügt werden.
Durch das Lösen von Ionen wird die Flüssigkeit lokal inhomogen. Die direkt am Ion
liegenden Wassermoleküle sind in seinem elektrostatischen Feld ausgerichtet:
H2O
H2O
OH2
H2O
OH2
H2O
eigentlich 3-D
1. Solvathülle
1. + 2. Solvathülle
Für Anionen liegen die Wasser-Dipole natürlich umgekehrt. Wie dick die
Lösungsmittelschicht, die durch die Ionen ausgerichtet wird, tatsächlich ist, hängt von der Art
11
der Ionen selbst ab. Je kleiner der Radius und je grösser die Ladung, desto grösser die
Ladungsdichte an der „Oberfläche“ eines Ions, und desto stärker die Solvatationsbindung.
Dies führt zum nur scheinbar paradoxen Effekt, dass Ionen, die im Kristallgitter wenig Raum
einnehmen, in Messungen an Lösungen grösser erscheinen als Ionen, die im Kristall viel Platz
brauchen. Eine solche Messung betrifft z.B. die elektrische Leitfähigkeit, bei der die Ionen
durch ein externes elektrisches Feld zur Wanderung gezwungen werden. Anionen haben bei
gleicher Ladung meist eine kleinere Ladungsdichte als Kationen, weil der negative
Ladungsüberschuss auf Grund der gegenseitigen Elektronen-Abstossung die Elektronenhülle
aufbläht, während in Kationen der positive Ladungsüberschuss die Elektronenhülle
kontrahiert. Die Folge davon ist, dass die partielle Solvatationsenthalpie des Kations die
Löslichkeit von Salzen stark beeinflusst.
Konzentrationsbegriff
Um die Präsenz eines gelösten Stoffs im Lösungsmittel zu charakterisieren, genügt eine
einfache Mengenangabe, auch als sehr praktischer Wert in Mol, nicht mehr. Etwas
geschickter ist es, die Zahl der Mole auf eine bestimmte Masse des Lösungsmittels
anzugeben. Die Zahl der Mole pro kg Lösungsmittel heisst Molalität. Das hat den Vorteil,
dass die Zahl Lösungsmittelmoleküle pro Mol Gelöstes temperaturunabhängig ist, im
Gegensatz zum Mass der Molarität, das als Mole pro Liter Lösungsmittel definiert ist. Die
Zahl der Lösungsmittelmoleküle pro Volumen ist temperaturabhängig, weil die Massendichte
der meisten Stoffe sich stark mit der Temperatur ändert. Eine sehr clevere
Konzentrationsdefinition ist der Molenbruch: Er ist bestimmt als die Molzahl der
anzugebenden Komponente im Verhältnis zur Summe der Mole aller Komponenten eines
Lösungs- oder Gasgemischs.
Für Arbeiten in wässriger Lösung hat sich die Molarität eingebürgert, trotz der Schwäche mit
der Temperaturabhängigkeit. Man behilft sich, indem man thermochemische oder kinetische
Werte auf so genannte Standardbedingungen, in diesem Fall T = 298.15 K (25°C) und
p = 101.3 kPa (1 atm), bezieht. Bei physikalisch-chemischen Bestimmungen wird eher die
Molalität bzw. der Molenbruch verwendet.
Allen Konzentrationsmassen ist gemeinsam, dass sie beschreiben, wie wahrscheinlich man
eine bestimmte Molekülart in einer normierten Teilmenge eines Gemischs antrifft. Diese
Eigenschaft ordnet die Konzentrationsmasse allgemeiner als Masse einer Dichte im
physikalischen Sinn ein. In Gasen kann man als Konzentrationsmass den Partialdruck
verwenden: Der Gesamtdruck eines Gasgemischs setzt sich additiv aus den Mol-Anteilen der
12
Komponenten zusammen, was direkt aus Avogadros Befunden hervorgeht. Der Teildruck
entspricht also genau dem Molanteil, gleicht somit als Mass dem Molenbruch.
In den folgenden Betrachtungen werden wir als Konzentrationsmasse die Molarität M der
Dimension [M] = mol l-1 und den Partialdruck p (Pa) verwenden. Da die Definition der
Konzentration c=
n
für die Molarität ist, ist die Menge leicht als n=cV zu errechnen. Molare
V
Konzentrationen während einer Reaktion
A+B
→
C
werden als [A], [B] und [C] symbolisiert. Die totalen analytischen
Anfangskonzentrationen werden mit cA und cB bezeichnet. cC ist gleich Null. Verläuft die
Reaktion genau wie notiert, so gilt die ganze Zeit [A] + [C] = cA und [B] + [C] = cB wegen der
Massenerhaltung.
Konzentrationsabhängige Phänomene in der Chemie: Reaktionsraten
Anstelle des Begriffs Reaktionsrate ist im deutschsprachigen Raum auch
„Reaktionsgeschwindigkeit“ üblich. „Geschwindigkeit“ ist aber intuitiv so sehr an
mechanische Ortsveränderungen gebunden, dass Reaktionsrate eher der Beobachtung gerecht
wird, wenn ein Stoffumsatz gerade abläuft. Im Englischen heisst es denn auch „reaction rate“.
Definieren kann man das auf zwei Arten: Entweder ist es der Mengenumsatz pro Zeiteinheit,
oder ein Konzentrationsumsatz pro Zeiteinheit. Es stellte sich empirisch früh heraus, dass sich
die mathematische Beschreibung des Mengenumsatzes schlecht zur Verallgemeinerung und
zur Übertragung auf Messgrössen eignet. Im Gegensatz dazu haben sich
konzentrationsbasierte Beschreibungen sehr bewährt.
Die Pioniere der chemischen Kinetik sind heute ziemlich vergessen: Der Erste, der den
zeitlichen Verlauf einer chemischen Reaktion beschrieb, war Ludwig Wilhelmy. Er leitete
schon 1850 auch die korrekte mathematische Beschreibung her. Diese Arbeit wurde bestätigt
durch die gemeinsamen Studien von Augustus Harcourt und William Esson. Für eine
Reaktion wie oben beschrieben,
wurde gefunden, dass
A+B →
C
∆[C]
= k[A][B] , wenn man [A], [B] und [C] in regelmässigen, im
∆t
Vergleich zur gesamten Reaktionszeit kurzen Zeitintervallen bestimmte. Das funktionierte
natürlich nur mit recht langsamen Reaktionen, war aber dennoch eine sehr wichtige
Erkenntnis. Aus der Abhängigkeit vom Produkt der Konzentrationen der Reaktanden wurde
durch Max Trautz die Kollisionstheorie der chemischen Reaktionen entwickelt, welche auch
13
auf der statistischen Mechanik von Ludwig Boltzmann basiert. Die Konzentration beschreibt,
wie wahrscheinlich es ist, eine bestimmte Molekülart in einem normierten Volumen
anzutreffen. Das Produkt zweier Konzentrationen beschreibt deshalb die Anzahl aller
möglichen Kontakte zweier Molekülarten im Einheitsvolumen. Man kann das aus der
Kombinatorik ableiten: Haben wir ein geschlossenes Gefäss (das Einheitsvolumen) und darin
beispielsweise 6 rote und 3 blaue Kugeln, so berechnet sich die Anzahl aller möglichen
Berührungen zwischen roten und blauen Kugeln, falls wir das Gefäss bewegen, zu 6 x 3.
Diese Zahlen repräsentieren aber gerade auch die „Konzentration“ roter und blauer Kugeln im
Einheitsvolumen. Der Faktor k ist die so genannte Geschwindigkeitskonstante. Wie schon
Wilhelmy fand, hängt sie von der Temperatur (und auch vom Druck) ab. Gemäss
Kollisionstheorie ist k eine Erfolgswahrscheinlichkeit. Um eine Kollision von A mit B
erfolgreich zum Produkt C zu bringen, müssen noch mehr Bedingungen als die schlichte
Tatsache der Begegnung von A und B erfüllt sein. Die kinetische Bewegungsenergie der
Moleküle muss einen Mindestwert besitzen, und nicht alle räumlich verschiedenen
Begegnungen führen zum Erfolg, weil Moleküle stark strukturiert sein können. Wilhelmy hat
sein Gesetz auch richtigerweise in eine Differentialgleichung überführt:
d [C]
d [A]
d [B]
=−
=−
= k[A][B]
dt
dt
dt
Dies ist die noch heute übliche Art, Gesetze für Reaktionsraten zu notieren. Die
Differentialquotienten stehen für die Rate, der Term k[A][B] für die
Konzentrationsabhängigkeit der Rate. Die Zeitabhängigkeit lässt sich durch Integration
erhalten, dazu jedoch später.
Das chemische Gleichgewicht
Es gibt Reaktionen, die nie im Sinne von
A+B →
C
A und B gänzlich zu C umwandeln. Die Reaktion scheint „abzubrechen“ doch das kann nicht
sein, weil es keine physikalischen Gründe für einen Stopp gibt (Magie wäre noch möglich).
Die einzige rationale Erklärung besteht darin, eine Gegenreaktion
C
→
A+B
in Betracht zu ziehen. Nach einem gewissen Umsatz von A und B zu C steigt die
Konzentration von C so sehr, dass sie die Rate der Gegenreaktion die Bildungsrate von C
kompensiert: Wir haben Gleichgewicht, genau genommen dynamisches Gleichgewicht, die
einzige Form in der Chemie, denn statische Gleichgewichte wurden bis heute nicht gefunden.
14
Man könnte so ein dynamisches Gleichgewicht auch mit „rasendem Stillstand“ umschreiben,
weil die Stoffumsätze in beiden Richtungen sehr hoch sein können, ohne dass äusserlich
etwas geschieht. Wir schreiben jetzt
d [C]
= 0 = k f [A][B] − kr [C]
dt
um auszudrücken, dass sich [C] nicht mehr ändert. –kr stammt vom Gesetz für die
Rückreaktion,
d [C]
= − kr [C] , das den Zerfall von C beschreibt. kf ist das k aus der
dt
ursprünglichen Formulierung, da wir jetzt zwei Reaktionen betrachten, müssen wir ihre kFaktoren unterscheiden. f steht für forward und r für reverse.
0 = k f [A][B] − kr [C]
kann man umformen zu
k
[C]
= f = K eq
[A][B] kr
Das ist das Massenwirkungsgesetz (MWG, Law of Mass Action), wie es zuerst 1864 von
Guldberg und Waage formuliert wurde. Es besagt, in welchem Verhältnis [A], [B] und [C] für
konstante Umgebungsbedingungen (Temperatur, Druck) zueinander stehen, sobald
Gleichgewicht erreicht ist. Die Reaktionsgleichung wird jetzt auch entsprechend
⇀ C
A+B ↽
geschrieben. Die Gleichgewichtskonstante Keq ist keine echte Konstante, sondern eigentlich
eine Funktion der Temperatur und des Drucks, genauso wie die Geschwindigkeitskonstanten,
aus denen sie errechnet wird.
Das Massenwirkungsgesetz ist auch die exakte Form, mit der sich die
Konzentrationsabhängigkeit des Prinzips von Le Châtelier begründen lässt. Dieses besagt,
dass ein chemisches Gleichgewichtssystem immer auf einen ausgeübten Zwang hin
ausweicht. Erhöhung der Temperatur verschiebt ein Gleichgewicht in Richtung der
endothermen Teilreaktion, Abkühlen in Richtung der exothermen. Bei Gasreaktionen treibt
Erhöhung des Drucks das Gleichgewicht auf die Seite mit der kleineren Anzahl Moleküle,
weil dann das Volumen abnimmt. Bei gleicher Zahl Moleküle geschieht nichts. Die Wirkung
von Konzentrationsänderungen lässt sich mit dem Massenwirkungsgesetz illustrieren:
Für
[C]
= K eq erhöht die Zugabe von A die Konzentration [C], und [B] nimmt ab. Gibt
[A][B]
man C zu, steigen [A] und [B].
15
Heterogene Gleichgewichte
Dieser Fall liegt vor, wenn bei einer Reaktion Moleküle, Atome oder Ionen zwischen Phasen
bzw. Aggregatzuständen übertreten. Typische Fälle sind Bildung oder Zersetzung von
Festkörpern in Lösung, Austausch zwischen Gas und Festkörper oder Gas und Lösung. In der
Lösung können wir unser normales Konzentrationsmass verwenden, in der Gasphase den
Partialdruck. Ein sehr praktischer Zusammenhang besteht auch darin, dass die gelöste
Konzentration eines Gases in einer Flüssigkeit oder einem Festkörper in erster Näherung
proportional zu seinem Partialdruck ist. Die schwierigere Frage ist die nach der Konzentration
eines Festkörpers. Dazu kann man feststellen, dass, weil ein Festkörper nur
Austauschreaktionen an der Grenzfläche zu einer Lösung oder einem Gas eingehen kann, sich
die Konzentration innerhalb der festen Phase nicht ändert, bis der Festkörper aufgebraucht
ist. Das ist anders für Gas in Kontakt mit Lösung oder Kontakt zwischen zwei nicht
mischbaren Lösungen. Dort führt die molekulare Bewegung zu einem ständigen
Konzentrationsausgleich in den Phasen, wenn etwas über die Grenzfläche ein- oder
auswandert. Eine Lösung oder ein Gas über einem Festkörper „sieht“ hingegen immer eine
konstante Konzentration des Feststoffs. Das schlägt sich dann in einer einfacheren
Schreibweise des MWG nieder. Beispiel: Die Auflösung von CaCO3 in CO2-haltigem Wasser.
Das ist das Phänomen, das zur Wasserhärte führt und zur Bildung von Karst-Erscheinungen.
Das Gleichgewicht besteht zwischen 3 Phasen.
⇀ Ca2+ + 2 HCO3–
CaCO3 + H2O + CO2 ↽
[Ca 2+ ][HCO3− ]2
K=
[CO 2 ][H 2O]
Man sieht hier, dass CaCO3 gar nicht im MWG auftaucht. Da seine „Konzentration“ nicht
variiert, solange festes Material da ist, wurde es gleich in die Konstante einbezogen. Manche
Lehrbücher schreiben, die Konzentration eines Festkörpers sei immer gleich 1, was aber so
nicht stimmt (Mortimer hat’s richtig). Weil Chemiker gern vereinfachen, kann man an diesem
MWG noch weiter basteln. Falls H2O das Lösungsmittel ist, ist seine Konzentration im
Gegensatz zum Gelösten so gross, dass sie selbst bei einem gewissen Umsatz nahezu konstant
bleibt. Also weg damit und rein in die Konstante
[Ca 2+ ][HCO3− ]2
K'=
[CO 2 ]
Wie schon erwähnt, ist die Konzentration eines gelösten Gases etwa proportional zum
Partialdruck, und CO2 ist ein Gas, darum endet man bei
16
[Ca 2+ ][HCO3− ]2
pCO 2
K"=
Ein Beispiel für ein Festkörper-Gasphase Gleichgewicht ist das Exponieren von NH4HS in
einer Vakuumkammer. Dabei treten NH3 und H2S aus dem Festkörper in die Gasphase über:
⇀ NH3(g) + H2S(g)
NH4HS(s) ↽
MWG:
K p = pNH3 pH 2 S
Gibt man NH3 und H2S gleichmässig zu (entspricht Kompression der Gasphase), so bildet
sich einfach mehr NH4HS, bis die Partialdrucke wieder gleich sind wie vorher. Gibt man NH3
allein zu, so wird so lange NH4HS gebildet, bis die Partialdrucke wieder Kp erfüllen, dabei ist
dann pNH 3 > pH 2 S . Zugabe von nicht reagierenden Gasen oder NH4HS ändert nichts an den
Partialdrucken. Wegnahme von NH3 oder H2S bewirkt Verdampfen von NH4HS, bis das
Produkt der Partialdrucke wieder Kp erfüllt. Temperaturerhöhung verstärkt die Verdampfung,
Kp und damit die Partialdrucke werden grösser, weil Kp bezüglich Temperatur eben keine
Konstante ist!
Die Konstante des Lösungsgleichgewichts von in Wasser schwerlöslichen Salzen besitzt eine
spezielle Bezeichnung: Löslichkeitsprodukt. Der Name rührt daher, dass der Nenner des
MWG eigentlich nur die „Festkörperkonzentration“ enthält, die aber in der Konstante
verschwindet und somit immer ein Produkt verbleibt. Beispiele:
⇀ Ba2+ + SO42−
BaSO4 ↽
⇀ 2 Ag+ + CrO42−
Ag2CrO4 ↽
L(BaSO4 )=[Ba 2+ ][SO 2-4 ]
L(Ag 2CrO 4 )=[Ag + ]2 [CrO 2-4 ]
Das Löslichkeitsgleichgewicht spielt nur, solange Festkörper vorhanden ist! Ist die
Verdünnung so gross, dass kein Salz ausfällt, ist das Löslichkeitsprodukt bedeutungslos.
Gekoppelte Gleichgewichte
Falls für eine Molekül- oder Ionenart in einer Lösung 2 (oder gar mehr) unterschiedliche
Reaktionen möglich sind, so sind die dazugehörigen Gleichgewichte gekoppelt. Beispiel:
⇀
NH3 + B(OH)3 ↽
NH3 + H+
⇀
↽
H
+
HN
H
O
H
-
B O
O
NH4+
H
(H3NB(OH)3)
K1 =
[H 3 NB(OH)3 ]
[NH 3 ][B(OH)3 ]
K2 =
[NH +4 ]
[NH 3 ][H + ]
H
17
Beide MWGs enthalten die Konzentration [NH3] und können somit unter Elimination dieser
Variablen ineinander eingesetzt werden:
K1 [H 3 NB(OH)3 ][H + ]
=
= K3
[NH +4 ][B(OH)3 ]
K2
Dieses Gleichgewicht ist zentral für die Bestimmung von Amin-Stickstoff in organischem
Material nach Kjeldahl.
18