PDF file - IDB - Universität Bonn

Rheinische Friedrich-Wilhelms-Universität Bonn
Institut für Informatik III
Diplomarbeit
Änderungspropagierung zur regelbasierten
Analyse von Finanz-Datenströmen in
TInTo
Gereon Schüller
September 2007
Erstgutachter: Prof. Dr. Rainer Manthey
Danksagung
An dieser Stelle möchte ich zunächst Herrn Prof. Dr. Rainer Manthey und Herrn
Dr. Andreas Behrend für die ausgezeichnete Betreuung meiner Diplomarbeit sowie
für die hilfreichen Verbesserungsvorschläge danken. Ferner möchte ich mich bei den
Hörerinnen und Hörern der Vorlesungen Deduktive Datenbanken und Event Monitoring Systems bedanken, deren Anmerkungen während der Übungsgruppen zur
Verbesserung des Systems TInTo beigetragen haben.
Meinen Eltern und meiner Schwester danke ich für die fortlaufende Unterstützung
und die manchmal aufzubringende Geduld während meines Studiums.
Ein ganz besonderer Dank gilt meiner Kommilitonin und besten Freundin Maria
Klodt, die mir während meines gesamten Studiums stets mit fachlichem und vor allem
mit menschlichem Rat zur Seite gestanden hat.
Bonn am Rhein, im September 2007
iii
iv
Inhaltsverzeichnis
1. Einleitung
1
2. Grundlagen
5
2.1.
Grundlagen relationaler Datenbanken
2.2.
Relationale Algebra und Relationenkalkül
. . . . . . . . . . . . . . . . . .
2.3.
SQL
2.4.
Access
. . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3. Grundlagen der technischen Analyse
5
7
11
16
19
3.1.
Wertpapiere . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.
Kurse
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
3.3.
Technische Indikatoren . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
4. TInTo
19
27
4.1.
Systemarchitektur von TInTo
. . . . . . . . . . . . . . . . . . . . . . .
27
4.2.
Spezikation von technischen Indikatoren in TInTo . . . . . . . . . . .
32
4.3.
Diskussion des bestehenden Systems
35
. . . . . . . . . . . . . . . . . . .
5. Grundlagen der Änderungspropagierung
39
5.1.
Inkrementelle Regeln für die RA
. . . . . . . . . . . . . . . . . . . . .
40
5.2.
Auswertungsstrategien . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
6. Erweiterungen von TInTo
45
6.1.
Änderungen an der Benutzeroberäche . . . . . . . . . . . . . . . . . .
45
6.2.
Umstellung des HTTP-Abrufs auf ActiveX . . . . . . . . . . . . . . . .
52
6.3.
Wertpapiersymbolsuche mittels XML . . . . . . . . . . . . . . . . . . .
53
6.4.
Erweiterung um Intradaykurs-Daten
. . . . . . . . . . . . . . . . . . .
55
6.5.
Korrektur der Indikatorberechnungen . . . . . . . . . . . . . . . . . . .
57
7. Spezialisierung von SQL-Views
61
7.1.
Relevante Unterschiede zwischen SQL und der RA
. . . . . . . . . . .
61
7.2.
Delta-Regeln in SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . .
63
7.2.1.
Delta-Regeln für Operatoren aus der RA . . . . . . . . . . . . .
63
7.2.2.
Delta-Regeln für Aggregationen . . . . . . . . . . . . . . . . . .
65
7.3.
Mögliche Implementierungen der Änderungspropagierung
. . . . . . .
71
v
Inhaltsverzeichnis
8. Änderungspropagierung zur Indikatorberechnung in TInTo
. . . . . . . . . . . . . . . . . . . . .
73
8.1.
Materialisierte Sichten in TInTo
8.2.
Verwaltung spezialisierter Änderungsanweisungen . . . . . . . . . . . .
74
77
8.3.
Timer-gesteuertes Pulling neuer Kursdaten
. . . . . . . . . . . . . . .
78
8.4.
Abarbeitung der Delta-Regeln . . . . . . . . . . . . . . . . . . . . . . .
79
8.5.
Aufbau der Delta-Regeln . . . . . . . . . . . . . . . . . . . . . . . . . .
81
9. Perfomanceanalyse für verschiedene Indikatorklassen
93
10. Zusammenfassung und Ausblick
99
Literaturverzeichnis
101
A. Anhang
105
A.1. Abkürzungsverzeichnis . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
A.2. Hinweis zu Markennamen
. . . . . . . . . . . . . . . . . . . . . . . . . 106
A.3. Hinweise zur beiliegenden CD-ROM
vi
. . . . . . . . . . . . . . . . . . . 106
1. Einleitung
Heutige Datenbankmanagementsysteme erlauben neben der reinen Speicherung von
Daten auch die Ableitung von Daten aus den abgespeicherten Daten. Dabei können
die Basisdaten üblicherweise mit Mengenoperationen untereinander verknüpft, sowie
mathematische Berechnungen auf den Daten durchgeführt werden. Die Ableitungsvorschriften können in sogenannten Sichten abgespeichert werden. In den meisten
Datenbankmanagementsystemen wird dabei nur die Denition selbst, nicht jedoch
die abgeleiteten Daten abgespeichert, so dass bei jedem Neuabruf der Daten die
Berechnungen erneut durchgeführt werden. Werden daneben auch die Daten abgespeichert, so spricht man von einer materialisierten Sicht. Sobald jedoch die zu
Grunde liegenden Daten geändert werden, müssen auch die davon abgeleiteten materialisierten Sichten geändert werden. Basieren Sichten aufeinander, so muss diese
Aktualisierung entlang der sich so ergebenden Hierarchie (Sichtenhierarchie ), ausgehend von der untersten Ebene, durchgeführt werden. In der Datenbanktheorie werden
Datenbanksysteme, die Sichtdenitionen erlauben, als
deduktive Datenbanksysteme
bezeichnet und Verfahren, die die Sichten nach Basisdatenänderungen aktualisieren,
werden als
Änderungspropagierung
bezeichnet. Als einfachstes Verfahren der Ände-
rungspropagierung ist dabei die vollständige Neuberechnung zu nennen. In vielen
Fällen kann jedoch die
inkrementelle Änderungspropagierung
eektiver sein. Dieses
Verfahren aktualisiert nur diejenigen Daten, die aufgrund der Basisdatenänderungen
auch geändert werden müssen. Die Schwierigkeit dieser Verfahren liegt darin, die Daten zu identizieren, die zur Aktualisierung benötigt werden, ohne Rechenschritte
durchzuführen, die nichts zur Änderung beitragen.
Eine weitere Grundlage dieser Arbeit bilden
Datenströme.
Unter Datenströmen
versteht man eine Abfolge von Daten, die zeitlich geordnet in ein Datenverarbeitungssystem eingegeben werden, das diese Daten dann verarbeitet. Oft wird dabei
von einer gewissen Frequenz der Dateneingabe ausgegangen, auch wenn hierbei keine quantizierbare Grenzziehung möglich ist. Zur Verarbeitung von Datenströmen
existieren zwei generelle Ansätze. Einerseits können die Daten von auÿen in das System eingegeben werden, wobei das System erst bei der Eingabe auf die neuen Daten
reagiert. Das System ist in diesem Fall passiv, während die Auÿenwelt die aktive
Seite übernimmt. Andererseits kann auch das System die aktive Seite übernehmen
und selbst die Daten aus einer Quelle abfragen, die ihrerseits auf die Datenanfrage
reagiert.
Kombiniert man ein Datenbanksystem mit Datenstromverarbeitung, so erhält man
ein
Datenstromsystem.
In einem solchen System ist es wünschenswert, abgeleitete
Daten schneller zu berechnen, als neue Daten eintreen. Viele Sichtneuberechnungen benötigen jedoch überlineare Laufzeit, so dass die Berechnungszeit Zeitgrenzen
1
1. Einleitung
schnell überschreitet. Mittels inkrementeller Änderungspropagierung kann jedoch in
vielen Fällen die Laufzeit auf eine lineare oder sogar sublineare Laufzeit verbessert
werden.
In den vergangenen Jahren wurden sowohl in der Arbeitsgruppe Intelligente Datenbanken des Instituts für Informatik III der Universität Bonn als auch an anderen Instituten etliche Arbeiten zum Thema inkrementelle Änderungspropagierung
veröentlicht. Diese Arbeiten beziehen sich jedoch fast ausschlieÿlich auf Elementaroperationen der relationalen Algebra, wie Vereinigung, Dierenz und Join, jedoch
nicht auf mathematische Berechnungen auf Relationen. Die meisten Veröentlichungen verwenden als Datenbankanfragesprache zudem die theoretische Sprache
Datalog,
die jedoch in kommerziellen Datenbankmanagementsystemen keine Verwendung ndet. Nahezu alle Datenbankmanagementsysteme verwenden die Datenbankanfragesprache SQL. Somit existiert bisher keine Implementierung eines Datenstromsystems,
welches durch Datenströme induzierte Änderungen entgegennimmt und dann eine inkrementelle Änderungspropagierung auf Sichten mit mathematischen Berechnungen
durchführt.
In dieser Diplomarbeit wurde ein bestehendes Datenbanksystem, welches Kursdaten von Wertpapieren speichert und eine Berechnung sogenannter
toren
technischer Indika-
mittels SQL-Sichten durchführt, derart erweitert, dass es Kursdaten selbsttätig
in einer vorgegebenen Frequenz von einem Kursanbieter aus dem Internet abruft und
mittels der neuen Daten eine inkrementelle Änderungspropagierung auf den materialisierten Indikatorwerten durchführt. Ziel war dabei, die Berechnungsperformance zu
verbessern. Die gesamte Änderungspropagierung soll dabei mittels SQL-Anweisungen durchgeführt werden. Die dafür nötigen Änderungspropagierungsregeln wurden
dabei für alle Indikatoren von Hand erstellt, ohne dass es dafür bereits entsprechende Vorarbeiten gab. Zuerst wurden für die mathematischen Berechnungen Regeln
aufgestellt, die unter Ausnutzung der bereits errechneten Werte und Hinzunahme
der neuen Werte inkrementell das neue Berechnungsergebnis errechnen. Anschlieÿend wurden diese Berechnungsvorschriften in SQL umgesetzt. Daneben wurde der
zeitgesteuerte Datenabruf aus dem Internet realisiert. Die Implementierung erfolgte dabei unter dem Datenbankmanagementsystem
Microsoft Access,
das von Haus
aus weder über ein Konzept für materialisierte Sichten, eine prozedurale Umgebung
für SQL-Anweisungen noch über eine Datenstromkomponente verfügt. Die nötigen
Verfahren wurden daher ebenfalls neu unter der Access-eigenen Programmiersprache
Visual Basic for Applications
programmiert bzw. die SQL-Anweisungen wurden
derart gestaltet, dass diese auch ohne eine prozedurale Umgebung und somit ohne
Fallunterscheidung ausführbar waren.
Bei Messungen zeigte sich, dass durch den Einsatz der in dieser Diplomarbeit
aufgestellten Änderungsregeln (Delta-Regeln ) die Berechnungszeit deutlich gesenkt
werden kann. So konnte für einen technischen Indikator die Berechnungszeit von elf
Sekunden auf eine halbe Sekunde gesenkt werden. Dadurch konnte die Abrurequenz
wesentlich erhöht werden.
Diese Arbeit setzt eine Reihe vorhergehender Diplomarbeiten fort, die die Modellierung und Berechnung von Wertpapierkenndaten in relationalen Datenbankmana-
2
gementsystemen behandeln. Andreas Krumme hat in seiner Diplomarbeit [Kru05]
eine ob jektorientierte und regelbasierte Modellierung von Wertpapieren und Kursverläufen entwickelt. Alexander Geppert stellte in seiner Diplomarbeit [Gep05] einen
regelbasierte[n] Ansatz zur Modellierung der technischen Analyse von Wertpapierkursen vor. Christian Hübel [Hüb07] entwickelte dann das in dieser Arbeit weiterentwickelte System TInTo.
Die weitere Arbeit ist wie folgt aufgebaut: In Kapitel 2 werden zunächst die Grundlagen relationaler Datenbanken, der relationalen Algebra, der Datenbankanfragesprache SQL und die von Access vorgestellt. Kapitel 3 gibt einen kurzen Überblick
über Grundlagen aus der Finanzwelt und über technische Indikatoren. In Kapitel 4
wird das vorhandene TInTo-System vorgestellt und diskutiert. Kapitel 5 führt in die
Grundlagen der Änderungspropagierung im Kontext der relationalen Algebra ein.
In Kapitel 6 werden allgemeine Erweiterungen des TInTo-Systems vorgestellt, die
nicht direkt mit der Änderungspropagierung zusammenhängen. In Kapitel 7 wird gezeigt, wie die Änderungspropagierung in Datenbanksystemen unter SQL umgesetzt
werden kann, wobei auch Propagierungsregeln für Aggregationen entwickelt werden.
Kapitel 8 beschreibt, wie die Änderungspropagierung konkret in TInTo umgesetzt
wurde. In Kapitel 9 werden die Ergebnisse von Testläufen des Systems gezeigt und
analysiert.
3
1. Einleitung
4
2. Grundlagen
relationalen Datenbanken,
In diesem Kapitel werden zunächst einige Grundlagen zu
zur
relationalen Algebra
sowie zu den
die Grundzüge der Datenbanksprache
nagmentsystem
Microsoft Access
Relationenkalkülen
SQL
vorgestellt. Danach werden
gegeben. Zuletzt wird das Datenbankma-
vorgestellt.
2.1. Grundlagen relationaler Datenbanken
Im Folgenden werden die Grundlagen zu relationalen Datenbanken dargelegt. Die
meisten davon beruhen auf dem im Jahr 1970 erschienenen Artikel von Edgar F.
Codd [Cod70]. Ergänzungen hierzu, insbesondere zur relationalen Algebra und zum
Relationenkalkül, entstammen [KE01].
Eine
Relation R ist eine Teilmenge des kartesischen Produkts von nicht notwendig
verschiedenen Mengen:
R ⊆ A1 × A2 × . . . × An
(2.1)
Jedes Element einer Relation wird Tupel genannt, die
wird
j -tes
Attribut genannt, die Menge
Aj
j -te
Wertebereich
Komponente eines Tupels
oder
Domäne
des Attributs
j . Als Wertebereich sind im Kontext relationaler Datenbanken nur solche Mengen als
Wertebereich zulässig, die
atomare
Werte enthalten, nicht jedoch solche, die wieder-
um strukturierte Elemente enthalten.
Üblicherweise wird von Duplikatfreiheit der Relationen ausgegangen. In Codds
Entwurf wurde auch der Reihenfolge der Attribute Unterscheidungskraft zugeteilt,
obwohl jedes Attribut auch mit einem Namen versehen werden sollte. Somit wäre
es möglich, in einer Relation zwei Attribute gleichen Namens zu verwenden. Um
diesen Zustand zu vermeiden, denierte er den Begri relationship , eine Relation
ohne Ordnung der Attribute, aber mit eindeutigen Namen, die gegebenenfalls durch
vorangestellte
Rollenbezeichner
gekennzeichnet werden. Im Laufe der Zeit ist diese
Unterscheidung jedoch verloren gegangen, und so werden beide Begrie heute meist
synonym verwendet.
Die Struktur und der Name einer Relation werden als
einer Relationen enthaltenen Tupel als
Schema
bezeichnet, die in
Zustand.
Für die hier angesprochenen Grundkonzepte existieren verschiedene Begrie. Während in der Theorie von
in der Praxis oft von
Relation, Tupel, Attribut
Tabelle, Zeile, Spalte
oberäche von Access hingegen verwendet
Felddatentyp.
und
und
Wertebereich
Datentyp
die Rede ist, wird
gesprochen. Die Benutzer-
Datenblatt, Datensatz, Feldbezeichner
und
Es ist empfehlenswert, nur die Begrie aus einem Bereich zu verwenden.
5
2. Grundlagen
In dieser Arbeit werden dabei vornehmlich die Begrie aus der Theorie Verwendung
nden. Allerdings erscheint es bei der Beschreibung der Implementierung angebracht,
die Begrie zu benutzen, die auch im verwendeten DBMS verwendet werden, um die
Implementierung leichter nachvollziehbar zu beschreiben. Auch im Zusammenhang
mit SQL ist die Kenntnis der praktischen Begrie nützlich, da die Schlüsselwörter
aus diesem Bereich entlehnt sind.
Der Begri
Tabelle
unterscheidet sich von der
Relation
auch in der Semantik,
da eine Relation stets duplikatfrei ist, eine Tabelle dies jedoch nicht zwingend sein
muss. Praktische DBMS erlauben auch meist Duplikate innerhalb von Tabellen, was
in dieser Arbeit aus Vereinfachungsgründen ausgeschlossen sein soll.
Codd hat auch das Prinzip des
Schlüssels beschrieben. Ein Schlüssel einer Rela-
tion ist ein Attribut oder eine Kombination von Attributen, aus dem alle anderen
Attribute des jeweiligen Tupels folgen. Eine Relation kann dabei mehrere Attribute
aufweisen, die als Schlüssel in Frage kommen. Man wählt dann einen Schlüssel als
Primärschlüssel
ten
aus, alle anderen geeigneten Attribute werden als
Schlüsselkandida-
bezeichnet. Da den Primärschlüsseln eine wichtige Rolle zukommt, werden ihre
Namen meist unterstrichen dargestellt
Daneben gibt es die
Fremdschlüssel. Fremdschlüssel sind Schlüssel einer Relati-
on, die in einer anderen Relation referenziert werden. Angenommen, jedem Professor
an einer Universität sei eine Personalnummer zugeordnet, und jede Vorlesung werde
von einem Professor gehalten. Statt in einer Relation
Vorlesungen
alle Angaben
einem Professor zu speichern, reicht es aus, dessen Personalnummer zu speichern,
sofern alle sonstigen Angaben zu diesem Professor in einer eigenen Relation abgelegt
sind, die wiederum
Personalnummer
als Schlüssel hat. Wie man aus zwei solchen
Relationen eine Antwort erhalten kann, wird im folgenden Abschnitt beschrieben.
Schlüssel sind zur physischen Organisation einer Datenbank sehr nützlich. Mittels
geeigneter Datenstrukturen, wie etwa Such- oder Bayerbäumen, ist es möglich, die
Schlüsselattribute so abzulegen, dass bei Kenntnis des Schlüssels die Datensätze in
sehr kurzer (z. B. logarithmischer) Zeit gefunden werden können.
Von relationalen Datenbanken wird erwartet, dass sie zu jedem Zeitpunkt
tent
(stimmig)
konsis-
sind. Insbesondere beinhaltet diese Forderung, dass Schlüssel- und
Fremdschlüsselbedingungen nicht verletzt werden und Wertebereiche stets eingehalten werden. Daneben treten in späteren Betrachtungen auch noch die benutzerdenierten
Integritätsbedingungen auf, die im Prinzip jede boolesche Bedingung auf
Relationen sein können. Auch diese müssen zu jedem Zeitpunkt erfüllt sein. Da es
teils unmöglich sein kann, die Forderung zu allen Zeitpunkten zu erfüllen, z. B. bei
zyklischen Abhängigkeiten, gibt es das Konzept der
sen mehrere Änderungen zu einer sogenannten
Transaktion.
atomaren
Transaktionen fas-
Änderung zusammen, die
entweder ganz oder gar nicht ausgeführt wird. Auch bei Störungen von auÿen, beispielsweise Rechnerausfällen, muss sich die Datenbank wieder in einem konsistenten
Zustand benden. Tatsächlich sind Transaktionen ein sehr weites Forschungsfeld, auf
das im Rahmen dieser Arbeit nicht weiter eingegangen werden kann.
Eine der Hauptforderungen Codds war es, dass Daten
unabhängig von ihrer phy-
sischen Speicherstruktur sein sollen. Damalige Systeme setzten voraus, dass der Be-
6
2.2. Relationale Algebra und Relationenkalkül
nutzer bzw. ein Anwendungsprogramm, welches auf die Datenbank zugreifen wollte,
über deren Struktur genau Bescheid wusste. Im Prinzip war dieses Vorgehen nichts
weiter als ein direktes Schreiben und Lesen von Dateien auf dem Rechner. Um diesen Missstand auszugleichen, wurde das Konzept des Datenbankmanagementsystems,
kurz DBMS, als weitere Ebene zwischen Datenbank und Benutzer eingeführt. Der
Benutzer richtet seine Anfragen nunmehr nur an das DBMS, und dieses entscheidet,
wie es zu einer Antwort oder Änderung gelangt. Da das DBMS stets die Kontrolle
behält, wird auch die Gefahr inkonsistenter Zustände drastisch reduziert.
physischen Datenunabhängigkeit wird noch die logische Datenunabhängigkeit gefordert. Treten im Schema, welches der Datenbank zugrunde
Neben der
liegt, Änderungen auf, so sollten externe Subschemata, das sind die Schemata, welche dem Benutzer präsentiert werden, davon nicht berührt sein.
2.2. Relationale Algebra und Relationenkalkül
Ein Datenbanksystem dient nicht nur der Abspeicherung und dem Aunden von
Daten. Es ist ebenfalls Zweck eines Datenbanksystems, Operationen auf den vorhandenen Daten ausführen zu können. Angenommen, eine relationale Datenbank habe
folgende Relationen:
Studenten:
Professoren:
Vorlesungen:
{MatrNr, Name, Vorname, Wohnort}
{PersNr, Name, Vorname, Wohnort, Gehalt}
(2.2)
{VorlNr, Titel, Raum, PersNr}
Es sollten sich nunmehr Fragestellungen beantworten lassen wie
•
Welcher Professor hält die Vorlesung Informationssysteme?
•
Wie lauten die Anschriften aller Professoren und Studenten?
•
Welcher Professor hält keine Vorlesung?
•
Wie lauten die Titel aller Vorlesungen?
Zu diesem Zweck wurde die
relationale Algebra (RA) entwickelt. Die relationale
Algebra bildet Relationen auf Relationen ab. Sie ist stark mit der Mengenalgebra aus
der Mathematik verwandt. Charakteristisch für die relationale Algebra ist, dass sie
nur die Antwortrelation speziziert, jedoch keinerlei Auswertungsplan impliziert.
Zunächst ist man versucht anzunehmen, dass alle aus der Mathematik bekannten
Operatoren, die auf Mengen arbeiten können, auch auf Relationen angewendet werden könnten. Dies ist aber nicht uneingeschränkt der Fall. Versucht man Relationen
zu vereinigen, die nicht die gleiche Stelligkeit (d. h. die gleiche Anzahl an Attributen) aufweisen, so erhält man zwar eine Menge, aber keine Relation mehr, da in
einer Relation die Gleichstelligkeit aller Tupel verlangt wird. Ähnliches gilt, wenn
zwei Relationen unterschiedliche Wertebereiche in ihren Attributen aufweisen. Man
7
2. Grundlagen
erhielte zwar im strengen Sinne wieder eine Relation, in der ein Wertebereich ver-
1
gröÿert würde, allerdings wäre diese nur noch schwer im Rechner darstellbar.
diesem Grund wurde der Begri der
Vereinigungsverträglichkeit
Aus
deniert. Nur Rela-
tionen, die vereinigungsverträglich sind, dürfen in der relationalen Algebra vereinigt
vereinigungsverträglich,
werden. Zwei Relationen heiÿen
wenn sie die gleiche Anzahl
an Attributen haben und die Attribute, die an der gleichen Stelle stehen, den gleichen
Wertebereich haben. Oft wird auch Namensgleichheit verlangt, was aber durch eine
Benennungskonvention ausgeglichen werden kann.
Eine Sonderrolle unter den Mengenoperatoren nimmt das Kreuzprodukt
×
ein.
Für dieses ist keine Vereinigungsverträglichkeit Voraussetzung. Mathematisch gesehen würde das Kreuzprodukt zweier Relationen ein Paar zweier Tupel liefern. Aus
diesem Grund deniert man in der relationalen Algebra das Kreuzprodukt so um,
dass die Tupel aus beiden Relationen zu einem Tupel vereinigt werden:
{(a1 , a2 , . . . , an )} × {(b1 , b2 , . . . , bm )} 7→ {(a1 , a2 , . . . , an , b1 , b2 , . . . , bm )}
(2.3)
Neben den klassischen Mengenoperatoren stehen noch weitere Operatoren zur Verfügung. Sehr wichtig ist die
Selektion
σ.
Diese wählt aus einer Relation diejenigen
Tupel aus, die eine angegebene Bedingung erfüllen:
σc (R) = {t ∈ R | c}
c
(2.4)
ist dabei eine Prädikat, welches Attribute der jeweiligen Relation, Konstanten und
logische Operatoren enthalten darf.
Die
Projektion
πa1 ,a2 ,...,am (R)
entfernt Attribute aus Relationen und lässt nur die
a1 , a2 , . . . , am stehen.
ρa←b (R) benennt das Attribut rechts des Pfeils in den
im Subskript angegebenen Attribute
Der
Umbenennungsoperator
links des Pfeils stehenden Namen um. Der Umbenennungsoperator ist überladen und
darf auch auf Relationsnamen angewendet werden.
Aus der Komposition von Kreuzprodukt und Selektion lässt sich der
Der
Natural Join
(Symbol
Join
ableiten.
1) verknüpft zwei Relationen, indem er aus dem Kreuzpro-
dukt die Tupel auswählt, die in gleichnamigen Attributen gleiche Werte haben. Die
dabei entstehenden doppelten Attribute werden aus dem Ergebnis herausprojiziert.
Der Theta-Join (Symbol
1θ )
arbeitet ganz ähnlich, nur werden die Tupel aus bei-
den Relationen mittels des Prädikats
θ
verglichen. Eine anschlieÿende Projektion
ndet dabei nicht statt.
Die Outer-Joins führen auch Tupel auf, die keinen Join-Partner besitzen. Die dabei
aufgrund fehlender Join-Partner nicht besetzten Attribute werden mit einem speziellen Wert, dem sogenannten
tebereichen erlaubt ist. Beim
Null-Wert aufgefüllt, der per Denition in allen WerFull-Outer-Join
werden Tupel aus beiden Relationen
aufgeführt, die keinen Join-Partner besitzen, beim
der linken Relation, entsprechend ist der
1
nur diejenigen aus
deniert.
Dass es natürlich möglich wäre, mittels geeigneter Konvertierungen Wertebereiche zu vereinigen,
soll hier auÿer Acht gelassen werden.
8
Left-Outer-Join
Right-Outer-Join
2.2. Relationale Algebra und Relationenkalkül
Die
Semi-Joins
führen zwar den Join aus, geben aber nur die Attribute einer
Relation zurück. Sie nden gewissermaÿen diejenigen Tupel, die einen Join-Partner
besitzen. Daraus lässt sich noch der
Complement-Semi-Join
ableiten, der diejenigen
Tupel zurückgibt, die keinen Join-Partner besitzen.
Jedes andere Relationenkalkül, welches gleichmächtig zur relationalen Algebra ist,
wird relational
vollständig genannt.
Man kann die relationale Algebra um
Regeldenitionen
erweitern. Dazu wird
eine Regelmenge der Form
= Regelrumpf1
Regelkopf1
.
.
.
Regelkopfn
(2.5)
= Regelrumpfn
angegeben. Auf den linken Seiten (als Regelkopf ) ist dabei ein Literal anzugeben. Auf
den rechten Seiten (als Regelrumpf ) steht jeweils ein RA-Ausdruck. Innerhalb dieser
RA-Ausdrücke dürfen dabei die denierten Regelköpfe in gleicher Weise wie Relationennamen verwendet werden. Insbesondere ist es zulässig, auf diese Weise Regelmengen mit direkter oder indirekter Rekursion anzugeben. Treten mehrere verschiedene
Regeln mit gleichem Kopf auf, so werden die Rümpfe dieser Regeln vereinigt. Die
Regelmenge
R = A; R = B
ist somit gleichbedeutend mit
R = A ∪ B.
Eine mögliche Regelmenge wäre also beispielsweise:
R=S∪T
T = πX,Y (T 1T.Y =V.X V )
(2.6)
T = πX,Y (V )
S = W \V
Ein Datenbanksystem, das ein solches Regelkonzept unterstützt, wird auch
duktives Datenbanksystem
niert wird, wird als
Sicht
de-
genannt. Eine Relation, die durch eine Regel de-
(engl. view) oder
abgeleitete Relation
bezeichnet. Als
Unterscheidung werden Relationen, die nicht durch eine Regel deniert werden, als
Basisrelationen
bezeichnet.
Wie man an der Regelmenge 2.6 sieht, wird eine Regelmenge schnell unübersichtlich, insbesondere wenn man erkennen möchte, welche Relation aus welcher entsteht.
Man deniert daher den
Abhängigkeitsgraphen einer Regelmenge. Der Abhängig-
keitsgraph ist ein gerichteter Graph, dessen Knoten jeweils für die in einer Regelmenge
denierten abgeleiteten Relationen und die verwendeten Basisrelationen stehen (also
für die in der Menge vorkommenden Literale in Regelköpfen und Regelrümpfen). Zwei
Knoten
wenn
R
R
und
S
sind genau dann mit einer gerichteten Kante
für einen Regelkopf steht und das Literal von
auftritt. Ferner werden alle Kanten
fern in der entsprechenden Regel
R
R←S
S
R←S
verbunden,
im zugehörigen Regelrumpf
mit der Beschriftung neg versehen, so-
als Regelkopf und
S
innerhalb des Regelrumpfs
im Subtrahenden auftaucht. Abbildung 2.1 zeigt den Abhängigkeitsgraphen für die
Regelmenge 2.6.
9
2. Grundlagen
Abbildung 2.1.: Der Abhängigkeitsgraph der Regelmenge 2.6
Neben der relationalen Algebra existieren auch noch andere Kalküle auf Relationen. Gebräuchlich sind hier vor allem das Tupelkalkül, das Domänenkalkül und
Datalog.
Im
Tupelkalkül
wird für eine Relation das Aussehen des Zieltupel-Schemas an-
gegeben sowie Bedingungen, die an dieses Schema gestellt werden. Die Grundform
einer Anfrage lautet:
{t | P (t)}
(2.7)
|
wobei links vom -Zeichen das Aussehen der Zieltupel festgelegt wird, rechts davon die
Bedingung als Prädikat, welches das links stehende Tupel (oder dessen Attribute) als
freie Variablen enthält. Nicht im Zieltupel angegebene Attribute und Tupel müssen
durch die Quantoren
∃, ∀
gebunden werden. Der Zugri auf einzelne Tupelattribute
erfolgt mit der Punktschreibweise
Tupel.Attribut,
eckige Klammern begrenzen das
Tupel. Eine Abfrage im Tupelkalkül könnte etwa wie folgt aussehen:
{[p.Name] | ∃p ∈ Professoren ∧ ∃v ∈ Vorlesungen
∧v.PersNr = p.PersNr ∧ v.Raum = 'A207'}
(2.8)
Das Ergebnis ist eine einstellige Relation mit den Namen aller Professoren, die eine
Vorlesung im Raum A207 halten.
Ein anderes Relationenkalkül ist das
Domänenkalkül. Der Name stammt daher,
dass hier über die einzelnen Domänen, also die Wertebereiche der Attribute, quantiziert wird. Ein Ausdruck im Domänenbereichskalkül ist wie folgt aufgebaut:
{[a1 , a2 . . . , an ]|P (a1 , . . . , an )}
(2.9)
Die Domänen sind dabei nicht mehr automatisch an Relationen gebunden, diese
Bindung muss in der Formel vorgenommen werden. Die Beispielanfrage aus 2.8 sieht
im Domänenkalkül so aus:
{[n] | ∃p, v, w, g : Professoren([p, n, v, w, g])
∧∃vl, t, r : Vorlesungen([vl, t, r, p]) ∧ r = 'A207'))}
10
(2.10)
2.3. SQL
Für die Behandlung deduktiver Datenbanken wird oft die Sprache
Datalog
ver-
wendet, die mit dem Domänenkalkül verwandt ist. Der Existenzquantor wird hier
nicht explizit angegeben, alle nicht gebundenen Variablen werden implizit mit dem
Existenzquanto ∃
quantiziert. Relationennamen werden vor den in runden Klam-
mern stehenden Tupelspezikationen angegeben. Datalog ist regelorientiert, ähnlich
der weiter oben defnierten erweiterten RA. Statt des Gleichheitszeichens wird hier
ein Pfeil verwendet. Statt des Symbols ∧
aus der booleschen Algebra wird oft auch
das Komma verwendet. Zusätzlich enthält Datalog den Negationsoperator rend das logische Oder ∨
¬,
wäh-
entfällt. Mehrere Regeln mit gleichem Kopf werden wie
in der erweiterten RA vereinigt. Die Anfrage aus 2.8 lautet somit in Datalog:
ergebnis
(n) ← Professoren(p, n, v, w, g), Vorlesungen(vl, t,0 A2070 , p)
(2.11)
2.3. SQL
Nach dem konzeptuellen Entwurf kann nun die Umsetzung im Rechner erfolgen.
Dazu ist es nötig, eine Möglichkeit zu haben, Datenbanken und Relationen im DBMS
anzulegen, zu ändern und abzufragen. Die Kommunikation zwischen Benutzer und
DBMS erfolgt dabei mittels einer so genannten
Die heute meist verwendete Sprache ist
Datenbanksprache.
SQL.
Die Urform dieser Sprache wurde
Anfang der 70er Jahre von IBM entwickelt und unter dem Namen SEQUEL, einem
sprechenden Akronym für
Structured English Query Language
geführt, später aber in
SQL umbenannt. Nachdem die Sprache auch von anderen Herstellern übernommen
worden war, wurde die Notwendigkeit einer Normierung erkannt. Die erste genormte
Version wurde 1986 vom
American National Standards Institute (ANSI)
licht und wird als SQL-86 bezeichnet. Spätere Normen wurden von der
Standards Organisation
veröent-
International
genormt und als SQL-89 (1989), SQL-92 bzw. SQL2 (1992),
SQL:1999 bzw. SQL3 (1999) und SQL:2003 (2003) veröentlicht. Seit SQL3 sind
dabei auch
objektrelationale
Aspekte enthalten. Daneben haben die Hersteller von
Datenbankmanagementsystem auch noch eigene Erweiterungen zur Sprache hinzugefügt, andere Teile der Norm hingegen nicht implementiert.
In dieser Arbeit wird SQL-92 nebst einigen wenigen Erweiterung des DBMS
crosoft Access
Mi-
Verwendung nden. Alle Erweiterungen sollten aber wenn auch in
anderer Form in anderen DBMS oder im normierten SQL zu nden sein. SQL
gliedert sich in verschiedene Teile. Wichtig sind hier die
guage )
zur Denition und Änderung von Relationen-Schemata und die
Manipulation Language
Die
DDL (Data Denition Lan-
DDL
DML
(Data
zur Änderung und Abfrage von Daten.
dient dazu, Relationen anzulegen, zu ändern und zu löschen. Um eine
Datenbank anzulegen, genügt die Anweisung
CREATE DATABASE DatenbankName;
11
2. Grundlagen
Anschlieÿend können Relationen (=Tabellen) mit der Anweisung
Create Table
angelegt werden:
CREATE TABLE Tabellenname(
Spaltenname1 TYP [Spaltenbeschränkungen],
Spaltenname2 TYP [Spaltenbeschränkungen]
[Tabellenbeschränkungen]
);
Typ ein unterstützter Datentyp angegeben werden muss. Als Spaltenbeschränkungen können Primärschlüssel (Primary Key), Einschränkungen des Wertebereichs (Check), Eindeutigkeitsbedingungen (Unique), Fremdschlüssel (Foreign
Key) und Verbot von Nullwerten (Not Null) verwendet werden. Für Bedingungen,
wobei statt
die über mehrere Spalten gehen, können
Tabellenbeschränkungen
verwendet werden.
Um das Beispiel aus 2.2 in SQL umzusetzen, kann somit folgende Anweisung verwendet werden:
CREATE TABLE Professoren(
PersNr INTEGER
PRIMARY KEY,
Name
VARCHAR(20) NOT NULL,
Vorname VARCHAR(20) NOT NULL,
Wohnort VARCHAR(20)
Gehalt CURRENCY
);
CREATE TABLE Studenten ...
CREATE TABLE Vorlesungen(
VorlNr INTEGER
PRIMARY KEY,
Titel VARCHAR(50)
UNIQUE,
Raum
VARCHAR(4)
CHECK (<’Z999’),
PersNr INTEGER
REFERENCES Professoren
);
Eine ganz ähnliche Syntax verwendet die
ALTER TABLE-Anweisung,
mit der be-
stehende Tabellen geändert werden können.
Die
DML
dient dazu, in der Datenbank gespeicherte Daten anzufragen oder zu
verändern. Die sicherlich häugste Anweisung ist die
SELECT
FROM
[WHERE
SELECT-Anweisung:
Zielliste
Quelltabellen
Bedingung];
In der Zielliste werden diejenigen Spalten (=Attribute) angegeben, welche in der Ausgabe zurückgegeben werden sollen. Die Spaltennamen können dabei direkt angegeben
werden oder bei Mehrdeutigkeiten durch die Syntax
Tabellenname.Spaltenname
näher qualiziert werden. Auÿerdem dürfen Attribute durch vordenierte Funktionen
miteinander verknüpft werden. Als Sonderzeichen ist das Symbol
alle Spalten zurückgibt.
12
∗
zugelassen, das
2.3. SQL
Im
From-Teil
können eine oder mehrere Tabellen der Datenbank angegeben wer-
den. Diese werden entweder durch ein Kreuzprodukt verknüpft, sofern die Tabellennamen durch Kommata getrennt sind, oder mit einem Join verbunden, der durch
sein Schlüsselwort anzugeben ist. Mögliche Joins sind:
{Natural {{Inner | Left | Right | Full} [Outer]} Join}.
Join-Bedingungen können nach der Tabellenliste mit der
den.
Im
ON-Klausel angegeben wer-
Where-Teil kann eine Bedingung angegeben werden, die die zurückgegebenen
2
Datensätze (Tupel) einschränkt .
SQL unterstützt daneben noch die Verwendung der Mengenoperationen
Except, Intersect
Blöcke)
für
∪, \, ∩,
die ganze
Select-From-Where-Blöcke
Union,
(SFW-
miteinander verbinden.
Daneben gibt es noch einige Sonderregeln: Statt Tabellennamen können auch Unteranfragen (das sind wiederum einzelne SFW-Blöcke, die in runde Klammern eingeschlossen sind), angegeben werden. Unteranfragen, die nur eine Spalte und einen
Datensatz zurückgeben, können auch anstatt eines beliebigen Skalars in Bedingungen
angegeben werden.
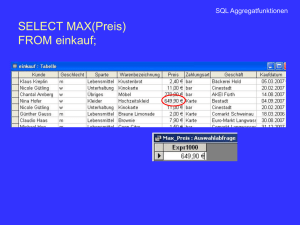
Neben den einfachen Selektionsabfragen, die lediglich Datensätze auswählen und
modizieren, kennt SQL auch noch so genannte
Aggregationsabfragen. Diese fas-
sen mehrere Datensätze einer Tabelle zusammen und berechnen aus den Spaltenwerten der zusammengefassten Datensätze mathematische Funktionen. Die Syntax für
eine Aggregationsabfrage lautet:
SELECT
FROM
[WHERE
[GROUP BY
[HAVING
Ist ein
Zielliste
Quelltabellen
Bedingung]
{Gruppenliste}]
Bedingung];
Group By-Teil
angegeben, so werden diejenigen Datensätze zusammenge-
fasst, gleiche Werte in den Spalten, die in der Gruppenliste angegeben sind, enthalten. Ohne Angabe eines
Group By-Teils
bilden alle Datensätze eine Gruppe.
Spalten, die in der Ziel-, nicht jedoch in der Gruppenliste angegeben werden, dürfen nur als Argument einer sogenannten
Aggregierungsfunktion
enthalten sein. Eine
Aggregierungsfunktion erhält als Argument einen Spaltennamen und führt auf diesen Spalten eine mathematische Funktion aus. Aggregierungsfunktionen sind z. B.
Sum, Count, Avg, Min oder Max, die Summe, Anzahl, arithmetisches Mittel, Minimum und Maximum zurückliefern. Anschlieÿend werden die Gruppierungsattribute
und die Ergebnisse der Aggregierungsfunktionen auf einen Datensatz abgebildet. Da-
Having-Bedingung geWhere- und dem Having-
bei werden diejenigen Datensätze ausgeltert, die nicht der
nügen. Hervorzuheben ist der Unterschied zwischen dem
Teil: Der
2
Where-Teil
operiert auf den Datensätzen vor der Zusammenfassung, der
In dieser Hinsicht ist die Bezeichnung SELECT unglücklich gewählt, da sie nicht dem Begri
aus der Relationen Algebra entspricht.
13
2. Grundlagen
Having-Teil
auf den Gruppen nach der Zusammenfassung und Berechnung der Ag-
gregatfunktion.
Soll z. B. in der Datenbank aus dem Beispiel 2.2 das Durchschnittsgehalt aller
Professoren berechnet werden, so liefert folgende Anfrage das gewünschte Ergebnis:
SELECT AVG(Gehalt) AS Durchschnittsgehalt
FROM Professoren
Die Rückgabe ist ein Tupel mit einem Attribut, welches das Durchschnittsgehalt
enthält. Soll hingegen berechnet werden, wie das Durchschnittsgehalt der Professoren
nach Wohnort lautet, aber nur diejenigen Wohnorte ausgegeben werden, in denen das
Durchschnittsgehalt 3000
SELECT
FROM
GROUP BY
HAVING
e
übersteigt, so lautet die Abfrage:
Wohnort, AVG(Gehalt) AS Durchschnittsgehalt
Professoren
Wohnort
Durchschnittsgehalt > 3000
In SQL ist es möglich,
Sichten zu denieren. Diese entsprechen den Regeldeni-
tionen der relationalen Algebra. Eine Sicht (englisch
speicherte Anfragedenition. Sie wird mit der
View )
ist eine im DBMS vorge-
Create View-Anweisung
angelegt:
CREATE VIEW Angehoerige AS (
(SELECT Name, Vorname, Wohnort FROM Studenten)
UNION
(SELECT Name, Vorname, Wohnort FROM Professoren))
Der Name eines Views kann an jeder Stelle verwendet werden, an der auch eine Basis-Relation verwendet werden kann, z. B. im
From-Teil
eines SFW-Blocks. Es ist
jedoch zu beachten, dass ein View nur dann als Ziel einer Datenänderungsanweisung vorkommen darf, sofern der View
änderbar
ist. Im SQL-Standard existieren
dafür strikte Regeln. So darf in der View-Denition kein
Having
Distinct, Group By oder
enthalten sein, in der Zielliste dürfen nur eindeutige Spaltennamen stehen
und mindestens ein Schlüssel enthalten sein, und es darf eine Tabelle, die ebenfalls
änderbar sein muss, referenziert werden [KE01].
Änderungen an Tabellen können mit den Anweisungen
vorgenommen werden. Die Syntax für
Insert Into
Insert Into und Update
lautet
INSERT INTO Tabellenname(Spaltennamen) {VALUES
Werteliste|(SFW-Block)};
wobei mit
Values
Werte direkt angegeben werden können, bei Verwendung einer
Unteranfrage werden die von ihr zurückgegebenen Tupel angefügt.
Änderungen können mit der Anweisung
UPDATE Tabellenname
SET Spaltenname = Wert,
...
[WHERE Bedingung];
14
2.3. SQL
vorgenommen werden. Die Zuweisung der Ausdrücke erfolgt dabei simultan, was zur
Folge hat, dass die auf der rechten Seite stehenden Attribute stets auf dem alten
Zustand ausgewertet werden (vgl. [KE01] S. 129).
Aufgrund der Unterstützung der Mengenoperationen einerseits als auch der Operationen aus dem Tupelkalkül andererseits ist der Sprachumfang von SQL sehr umfangreich. Es lässt sich jedoch ein Kern
von SQL ausmachen, der direkt in die
relationale Algebra übersetzbar ist und in den alle aufwendigeren Formen übersetzt
werden können. Voraussetzung ist allerdings, dass man keine Duplikate in SQL zulässt, wie dies in der relationalen Algebra stets angenommen wird. Pieper hat in
ihrer Doktorarbeit ein Basis-SQL
im Kontext von Datalog entwickelt. Manthey
hat dieses in seiner Vorlesung Deduktive Datenbanken [Man05] für die Relationale
weiterentwicklt. Dieses Konzept soll hier vorgestellt werden:
•
Union-Operator ist unverzichtbar, aber das Or
dieses immer durch Union ersetzt werden kann:
Der
da
in
Where-Teilen nicht,
SELECT r.A
FROM r
WHERE r.B=0 OR r.C=0
wird somit zu
(SELECT r.A FROM r
UNION
(SELECT r.A FROM r
WHERE r.B=0)
WHERE r.C=0)
Die Gegenrichtung ist hingegen nicht möglich, falls die Operanden aus verschiedenen Relationen stammen.
•
Eine entsprechende Argumentation trit auf das Verhältnis von
und
•
And
Negation vor Vergleichsliteralen lässt sich durch Umkehren des Vergleichsoperators ersetzen. Somit entspricht •
Intersect
zu.
Ein
Not
r.C=0 der Bedingung r.C<>0.
Not vor Exists lässt sich durch Minus und Exists äquivalent ausdrücken:
SELECT r.A FROM r
WHERE r.B=0
AND NOT EXISTS (SELECT * FROM s WHERE r.B=s.D)
wird zu
(SELECT r.A FROM r WHERE r.B=0)
MINUS
(SELECT r.A FROM r WHERE EXISTS
(SELECT * FROM s WHERE r.B=s.D)
15
2. Grundlagen
•
Über den Umweg des Semi-Joins wird auch das
vor
Exists
Not
als einstelliger Operator
überüssig. Aus
SELECT r.A
FROM r
WHERE NOT EXISTS
(SELECT * FROM s WHERE r.B>s.D)
wird
(SELECT r.A FROM r)
MINUS
(SELECT r.A FROM r,s WHERE r.B>s.D)
In
•
ist ein Spezialfall von
Exsits
mit Gleichheitsbedingung
Join
•
-Varianten lassen sich auf Selektion, Mengenvereinigung und Kreuzprodukt zurückführen
Intersect
•
lässt sich durch zweifache Dierenzbildung ausdrücken:
R ∩ S = R\(R\S)
(2.12)
Or, And, Intersect, Not, Exists, In, Join
Blöcken verzichtbar. Lediglich Union, Minus und die
Diesen Überlegungen zufolge sind
und die Schachtelung von
Produktbildung im
From-Teil
sind unverzichtbar.
Diese Überlegungen tragen dazu bei, die Änderungspropagierung im Kontext von
SQL, die im Kapitel 7 behandelt wird, zu vereinfachen.
2.4. Access
Das in dieser Diplomarbeit erweiterte Datenbanksystem verwendet das relationale
Datenbankmanagementsystem
Access.
Access, das von der Firma Microsoft vertrie-
ben wird, ist Teil des Oce-Pakets, zu dem auÿerdem auch die Tabellenkalkulation
Excel
und das bekannte Textverarbeitungssystem
Word
gehören. Während die meis-
ten anderen heute verwendeten Datenbankmanagementsysteme auf eine Client-/Serverstruktur setzen, bei der ein Datenbankserver mittels einer Netzwerkschnittstelle
von einem Client-Programm angesprochen werden kann, ist Access als Programm
aus einem Stück aufgebaut. Eine komplette Datenbank wird von Access in einer
einzigen Datei verwaltet, die neben dem Datenbankschema und dem Datenbankzustand auch die Benutzeroberäche, wie Formulare (zur Dateneingabe) und Berichte
(zur Datenausgabe auf Drucker) enthält. Access unterstützt die Verwendung von
Abfragen (Views) unter Verwendung von SQL-92. Dabei lassen sich sowohl
16
Select-
2.4. Access
Anfragen, als auch Anweisungen mittels
Insert, Update
oder
Delete
ausführen.
Einmal abgespeicherte Views können selbst wieder als Quellen in anderen Viewdenition verwendet werden. Views werden nur als Denition abgespeichert und bei
jedem Aufruf neu berechnet. Neben Viewdenitionen per SQL unterstützt Access
auch einen so genannten Entwurfseditor, mit dem sich Abfragen grasch erzeugen
lassen. Von diesem kann auch in die SQL-Ansicht umgeschaltet werden, so dass sich
das System im gewissen Maÿe auch zum anfänglichen Lernen der Sprache SQL nutzen
lässt.
Der Funktionsumfang des reinen Access-Systems beschränkt sich neben den Funktionen zum Entwurf auf relativ einfach gehaltene Funktionen zur Dateneingabe und
Darstellung. So kann in Formularen festgelegt werden, dass bestimmte Eingabeformate eingehalten werden müssen, oder es können zu Tabellen diejenigen Tabellen angezeigt werden, die über Fremdschlüssel in Beziehung stehen, wobei die in Beziehung
stehenden Datensätze automatisch angezeigt werden. Der Funktionsumfang lässt sich
jedoch durch die Verwendung der integrierten Programmiersprache
Applications
Visual Basic for
(VBA) fast beliebig erweitern. Diese Sprache lehnt sich zum Teil an
BASIC an, übernimmt andererseits aber auch objektorientierte Konstrukte, wie sie
aus anderen Sprachen wie C++ bekannt sind. Bereits mit dem Standardumfang von
VBA ist es möglich, Dateien zeilen- oder byteweise einzulesen, andere Anwendungen zu starten oder einfache Benutzereingaben einzulesen. Daneben ermöglicht die
Sprache Zugri auf praktisch jede Komponente des Access-Systems. So lassen sich
Berichte aufrufen, Formulare önen, Werte aus Formularen abfragen oder auch SQLAnweisungen ausführen. Umgekehrt ist es möglich, aus der Benutzeroberäche heraus VBA-Code aufzurufen. In Formularen sind jedem Steuerelement wie Textboxen
oder Schaltächen
Ereignisse
zugeordnet, bei deren Eintritt Unterprogramme (Subs)
aufgerufen werden können. Eine Besonderheit in der Zusammenarbeit von VBA und
Access besteht darin, dass es ebenfalls möglich ist, benutzerdenierte Funktionen
im SQL-Code zu verwenden. Auf diese Weise können zum Beispiel mathematische
Funktionen, die nicht in Access integriert sind, selbst in VBA geschrieben und die
Berechnung anschlieÿend auf Attributwerte angewendet werden. Diese Erweiterbarkeit bezieht sich allerdings nur auf Skalarfunktionen, Aggregatfunktionen können in
VBA nicht programmiert werden.
VBA lässt sich wiederum durch das Einbinden von sogenannten
ActiveX -Kompo-
nenten erweitern. Dies sind spezielle Programmbibliotheken, die ihrerseits prinzipiell in einer beliebigen Programmiersprache geschrieben sein können. In VBA lassen
sich diese Komponenten als Ob jekte (ähnlich wie Klassen) verwenden. Die in TInTo
verwendete Visualisierung der Kursdaten beruht auf der Verwendung einer solchen
Komponente. Eine weitere wichtige Komponente ist das
Data Access Object,
das das
satzweise Einlesen und Schreiben von Daten in Access-Tabellen ermöglicht. Schlieÿlich kann VBA auch DLL-Dateien (Dynamic Link Libraries) ansprechen, womit insbesondere die Verwendung von Aufrufen der Windows-API möglich ist. Letztendlich
ist VBA somit anderen Programmiersprachen unter Windows hinsichtlich des Funktionsumfangs ebenbürtig. Hauptnachteil von VBA unter Access ist jedoch, dass die
Programme bei jeder Ausführung neu interpretiert werden, wodurch die Geschwindig-
17
2. Grundlagen
keit zum Teil deutlich geringer ist als bei kompilierten Programmen. Dieses Problem
lässt sich gegebenenfalls durch die Auslagerung von Code in externe Komponenten
verbessern.
Obwohl im System TInTo (noch nicht) verwendet, ist noch die Mehrbenutzer- und
Netzwerkfähigkeit von Access zu nennen. Die Verwendung in Netzwerken kann zum
einen dadurch erfolgen, dass eine Access-Datenbank auf einem Netzlaufwerk in einem Windows-Netzwerk gespeichert wird. Gängige Praxis ist es dabei, die Oberäche
von den eigentlichen Daten zu trennen, indem alle Tabellen in einer eigenen Datei
gespeichert werden und über eine Verknüpfung wieder in die übrige Datenbankdatei eingebunden werden. Die Oberäche verbleibt dann auf den Client-Rechnern,
während die Datendatei im Netzwerk zur Verfügung gestellt wird. Dabei werden alle
Zugrie von den Access-Instanzen auf den Client-Rechnern kontrolliert, auf dem Server muss Access nicht vorhanden sein. Eine andere Art der Anbindung kann über die
Datenbankschnittstelle ODBC erfolgen. Dabei kann statt der Access-eigenen Datenbankkomponente ein anderes DBMS angebunden werden. Mittels sogenannten
Through-Abfragen
Pass-
ist es dann möglich, auch die SQL-Abfragen von dem angebun-
denen DBMS durchführen zu lassen, so dass Access nur noch die Oberäche zur
Verfügung stellt.
18
3. Grundlagen der technischen Analyse
Die Grundlagen des Wertpapierhandels wurden bereits in den vorhergehenden Diplomarbeiten von Krumme [Kru05], Geppert [Gep05] und Hübel [Hüb07] behandelt.
Aus diesem Grund wurde diese Kapitel bewusst etwas kürzer gehalten. Da aber die
Kenntnis einiger Grundbegrie auch im Zusammenhang mit den Erweiterungen an
TInTo wichtig sind, soll an dieser Stelle nun ein kurzer Ausug in die Welt des
Wertpapierhandels unternommen werden.
In diesem Kapitel wird zunächst erklärt, was ein Wertpapier ist, was ein Kurs ist
und welche verschiedenen Kurse eines Wertpapiers wichtig sind. Danach folgt eine
Einführung in die Thematik der Charts, bevor dann über die technische Analyse zum
Begri des technischen Indikators übergangen wird. Einige Indikatoren werden dann
noch näher vorgestellt.
Neben den erwähnten Arbeiten gibt es zu dem Thema vertiefende Literatur, auf
die auch in diesem Kapitel Bezug genommen wird. So gibt die Broschüre [Ban05]
des deutschen Bankverlags eine grundlegende Einführung in das Thema Wertpapierhandel. Sie stellt die verschiedenen Arten von Wertpapieren vor, erklärt deren
Grundbegrie und gibt Hinweise, wie das Kaufen und Verkaufen von Wertpapieren
über eine Bank möglich ist. Eine sehr ausführliche Referenz zum Thema technische
Analyse ist das Buch von Murphy [Mur00]. Eine Beschreibung sehr vieler technischer Indikatoren ndet sich im Buch von Paesler [Pae06], welches auch Anleitungen
zum Arbeiten mit diesen Indikatoren gibt und ferner eine Formelsammlung enthält.
Es sei noch angemerkt, dass die folgenden Ausführungen sich auf das deutsche
Wertpapierrecht beziehen und in anderen Ländern zum Teil deutlich andere Regelungen gelten.
3.1. Wertpapiere
Zunächst einmal ist ein
Wertpapier eine Urkunde, die ein privates Recht, beispiels-
weise eine Forderung oder eine Beteiligung an einer Kapitalgesellschaft, verbrieft
[Wik07b]. Beispiele für Wertpapiere sind z. B. Aktien oder Inhaberschuldverschrei-
1
bungen .
Bei auf den Inhaber lautenden Wertpapieren ergibt sich bereits aus dem Besitz des
Wertpapiers das private Recht des Besitzers. So ist bei einer Inhaberschuldverschreibung der jeweilige Inhaber des Papiers zur Forderung berechtigt (Ÿ 793 BGB). Auch
1
Vgl. Ÿ1 Abs. 1 DepotG: Wertpapiere im Sinne dieses Gesetzes sind Aktien, Kuxe, Zwischenscheine,
Reichsbankanteilscheine, Zins-, Gewinnanteil- und Erneuerungsscheine, auf den Inhaber lautende
oder durch Indossament übertragbare Schuldverschreibungen, ferner andere Wertpapiere, wenn
diese vertretbar sind, mit Ausnahme von Banknoten und Papiergeld.
19
3. Grundlagen der technischen Analyse
Aktien können auf den Inhaber lauten (Ÿ 10 Abs. 1 AktG). Neben den Inhaberpapieren können Wertpapiere auch auf den Namen lauten, d. h. nur die Person mit dem
eingetragenen Namen ist zur Ausübung des Rechts berechtigt. Auch solche Papiere
können durch Indossament (schriftlicher Vermerk des bisherigen Berechtigten, dass
das Recht auf eine andere Person übergangen ist) oder durch Übertragung (entsprechender Vermerk durch den Aussteller) auf andere Personen übertragen werden.
Der in früheren Zeiten durchaus übliche Fall, dass sich die Wertpapiere auch tatsächlich im physischen Besitz des Inhabers benden, ist heute kaum noch anzutreffen. Die meisten Wertpapiere werden heute in speziellen Lagern
(Depots)
verwahrt
und auch nur noch virtuell übertragen, d. h. es wird notiert, welche und wie viele Wertpapiere dem jeweiligen Inhaber gehören. Mehrere Wertpapiere können dabei
zu Sammelurkunden zusammengefasst werden, die nur noch beschreiben, wie viele
Exemplare eines Wertpapiers zur Verfügung stehen. Trotz der also weitgehend eingetretenen Trennung zwischen physischer Repräsentation und Recht ist der Begri
Wertpapier beibehalten worden.
Frei handelbare Wertpapiere können wie bewegliche Sachen ge- und verkauft werden. Üblicherweise geschieht dies an einer Wertpapierbörse. Bekannte Wertpapierbörsen sind beispielsweise die Deutsche Börse in Frankfurt oder die New York Stock
Exchange.
In TInTo werden hauptsächlich Aktien sowie Aktien-Indexe, also eine Kennzahl,
die sich aus den Kursen bestimmter Aktien zusammensetzt, betrachtet.
Aktien sind Wertpapiere, die eine Beteiligung an einem Unternehmen, einer Ak-
tiengesellschaft, verbriefen. Jeder Inhaber einer Aktie ist an dem jeweiligen Unternehmer beteiligt, und zwar mit dem Anteil, der sich aus dem Anteil einer Aktie am
Stammkapital der Gesellschaft ergibt. Das Stammkapital wird dabei entweder durch
Stückaktien zerlegt (werden z. B. 10.000 Stückaktien ausgegeben, so ist jeder Aktionär pro Aktie zu einem Zehntausendstel am Unternehmen beteiligt), oder durch
Nennwertaktien (beträgt der Nennwert 5
e
und das Stammkapital 100.000
e,
so ist
jeder Aktionär pro Aktie zu einem Zwanzigtausendstel am Unternehmen beteiligt).
Aus der Beteiligung ergibt sich zum einen die Picht, die nötige Einlage in das
Stammkapital zu leisten, andererseits das Recht, an Gewinnausschüttungen
denden)
(Divi-
beteiligt zu sein und an der Hauptversammlung teilnehmen und abstimmen
zu dürfen; nur bei sogenannten Vorzugsaktien entfällt das Recht zur Teilnahme an
der Hauptversammlung, dafür erhöht sich üblicherweise der Dividendenanteil. Auÿerdem ist die Gesellschaft den Aktionären gegenüber zur Rechenschaft verpichtet.
Eine geschäftsführende Tätigkeit übernimmt ein Aktionär dabei nicht, er kann also nicht in Geschäftsprozesse eingreifen. Hierfür ist der von der Hauptversammlung
gewählte Vorstand zuständig, der vom Aufsichtsrat überwacht wird. Für Aktionäre
besteht keine Nachschusspicht, d. h. sie müssen auch bei Verlust des Stammkapitals
des Unternehmens kein Geld nachzahlen, woraus sich als Konsequenz auch ergibt,
dass die Haftung einer Aktiengesellschaft durch das Stammkapital beschränkt wird.
Einzelne Aktienkurse spiegeln nicht zwangsläug die gesamte Marktlage wieder. So
kann es auch zu Zeiten, in denen der Aktienmarkt ein hohes Kursniveau erreicht hat,
vorkommen, dass ein einzelnes Unternehmen schlechte Geschäftszahlen liefert oder
20
3.2. Kurse
ähnliches. In diesem Fall würde die Bewegung des Kurses von der des Gesamtmarktes
abweichen. Charles Dow veröentlichte 1884 den ersten
Aktienindex
[Mur00]. Er
fasste 9 Eisenbahngesellschaften und 2 produzierende Firmen zusammen, um die
wirtschaftliche Gesundheit des Landes darzustellen. 1897 entstanden daraus zwei
Indizes, einer für Industrie- und einer für Eisenbahnaktien. Der
Average
Dow Jones Industrial
gilt heute noch als ...lebenswichtiges Instrument für die Markttechniker`
(Market Technicans Associaton, zitiert nach [Mur00]).
Der wohl bekannteste Aktienindex in Deutschland ist der DAX, ein Aktienindex, der sich aus 30 der 35 gröÿten deutschen Aktiengesellschaften zusammensetzt.
Die Gröÿe wird dabei nach Marktkapitalisierung und Orderbuchumsatz berechnet
[Wik07a].
Der Berechnung der Aktienindexe erfolgt üblicherweise als gewichtete Summe der
zu Grunde liegenden Aktienkurse.
3.2. Kurse
Ein Börsenhandel mit Wertpapieren ist während eines Handelstages fortlaufend möglich. Dabei können sowohl Verkaufs- als auch Kaufaufträge an die Börsenmakler oder
an ein automatisiertes Computersystem übergeben werden. Üblicherweise wird dabei
eine Preisspanne angegeben, zu der der Auftrag ausgeführt werden darf. Kann zwischen einer Kauf- und einer Verkaufsspanne eine Übereinstimmung erzielt werden, so
wird der Handel durchgeführt. Der dabei erzielte Preis wird von der Börse zusammen
mit dem Zeitpunkt des Handels veröentlicht und als
Kurs
bezeichnet. Die Mittei-
lung erfolgt in regelmäÿigen Intervallen, meist sind dies wenige Sekunden. Aus den
veröentlichten Kursen werden noch vier Kennzahlen für eine bestimmte Zeitspanne
abgeleitet:
•
Der
Erönungskurs
•
Der
Schlusskurs
•
Der
Tiefstkurs
•
Der
Höchstkurs
(engl. Open) gibt den ersten Kurs für die Zeitspanne an.
(engl. Close) gibt den letzten Kurs für die Zeitspanne an.
(engl. Low) gibt den tiefsten Kurs der Zeitspanne an.
(engl. High) gibt den höchsten Kurse der Zeitspanne an.
Die gewählte Zeitspanne ist dabei prinzipiell beliebig. Oft verwendet wird vor allem der Zeitraum des Handelstags, von seiner Erönung am Morgen bis zu seiner
Schlieÿung am Abend (diese Daten werden als End-Of-Day-Daten bezeichnet), aber
auch die Zeitspanne von einer Stunde. Daten, die niedrigere Zeitspannen als einen
Tag verwenden, werden auch als
das
Volumen,
Intraday-Daten
bezeichnet. Daneben wird oft noch
also die Anzahl der in einem Handelszeitraum gehandelten Exemplare
eines Wertpapiers, angegeben. Eine graphische Darstellung des Kurses eines Wertpapiers gegen die Zeit wird als
Chart
bezeichnet. Dabei wird die Zeit auf der x-
Achse aufgetragen, der Kurs auf der y-Achse. Somit ist ein direkter Überblick über
den Kursverlauf des Wertpapiers möglich. In der Praxis haben sich mehrere ChartDarstellungen etabliert:
21
3. Grundlagen der technischen Analyse
•
Der Linienchart (Abb. 3.1 oben) ist die einfachste Darstellung. Zu jedem Zeitpunkt auf der x-Achse wird der Kurs (üblicherweise der Schlusskurs) auf der
y-Achse aufgetragen. Die Punkte werden dann als Linienzug miteinander verbunden. Auf diese Weise ähnelt der Chart einem Funktionsgraphen
•
Der einfache Balkenchart oder auch OHLC-Chart (Abb. 3.1 mitte) stellt für
jeden Zeitpunkt auf der x-Achse Erönungs-, Schluss-, Höchst- und Tiefstkurs
dar. Für jeden Zeitpunkt wird ein senkrechter Balken gezeichnet, dessen oberes Ende beim y-Wert des Höchstkurses endet, während das untere Ende den
Tiefstkurs markiert. An diesen Balken werden zwei kleine waagrechte Striche
angeschlossen, die in sich in Höhe des Schluss- und des Erönungskurses benden. Der Strich des Erönungskurs wird dabei links angeschlossen, der Strich
des Schlusskurses rechts.
•
Der Kerzenchart (Abb. 3.1 unten) ist in seiner Idee dem Balkenchart ähnlich.
Statt eines Balkens wird ein schmales Rechteck gezeichnet. Die waagerechten
Kanten des Rechtecks auch Kerzenkörper genannt geben dabei Erönungsund Schlusskurs an, zwei Linien
(Dochte),
die aus dem Körper herausragen,
geben den Höchst- und Tiefstkurs an. Da aus der Form einer Kerze nicht erkennbar ist, welches der Erönungs- und welches der Schlusskurs ist, nimmt
der Kerzenkörper zwei Farben an: Liegt der Schlusskurs über dem Erönungskurs, ist der Körper grün gefärbt (bei schwarz-weiÿ-Darstellungen weiÿ), im
umgekehrten Fall rot (bzw. schwarz).
Neben der grundsätzlichen Kursrepräsentation ist eine weitere Variation, eine lineare (arithmetische) Skalierung der y-Achse zu verwenden oder eine logarithmische.
Bei der arithmetischen Skala entsprechen gleiche Abstände gleichen Abständen im
Kurswert, während bei der logarithmischen Skala gleiche Abstände gleichen prozentualen Wertzuwächsen entsprechen: Der Abstand zwischen 1 und 2 sowie der zwischen
5 und 10 ist gleich groÿ, da beides einem Kurszuwachs von 100% entspricht.
Neben den Kursen wird in Chartdarstellungen auch oft das Volumen angegeben.
Dieses weist eine eigene Skalierung auf, die üblicherweise auf einer zweiten y-Achse
aufgetragen wird. Das Volumen wird beim Kerzenchart ebenfalls durch kleine schmale
Rechtecke symbolisiert und so gefärbt wie der zugehörige Kerzenkörper, oder als
kleine senkrechte Balken. Beide Male entspricht die Höhe der Darstellung der Höhe
des Umsatzes.
Weiterhin ist für den Chart zu wählen, über welchen Zeitraum er dargestellt werden soll und wie hoch die Granularität (zeitliche Auösung) sein soll. Sehr verbreitet
ist der Tageschart, der über einen mittleren Zeitraum (z. B. mehrere Monate) dargestellt wird und in dem jeder Balken oder jede Kerze einem Tag entspricht. Geht
man zu einem höheren Zeitraum über, so werden die Kerzen so schmal, dass sie kaum
noch erkennbar sind. In diesem Fall können mehrere Tage zu einer Kerze zusammengefasst werden. In anderer Richtung ist es für einen Chart, der nur den aktuellen
Tag darstellen soll, nützlich, nur eine Stunde zu einer Kerze zusammenzufassen. Die
22
3.2. Kurse
Abbildung 3.1.: Drei verschiedene Darstellungen eines Kursverlaufes: Oben der Linienchart des Schlusskurses, in der Mitte der Balkenchart und unten
der Kerzenchart. Alle drei Charts wurden mittels TInTo erzeugt.
23
3. Grundlagen der technischen Analyse
vier Kurse sind dann natürlich auch anzupassen, der Erönungs- und der Schlusskurs
werden dann zum ersten bzw. letzten Kurs des gewählten Zeitraums, entsprechend
verhält es sich mit den Höchst- und Tiefstkursen.
3.3. Technische Indikatoren
Da der Anleger im Allgemeinen daran interessiert ist, z. B. zu einem möglichst billi-
2
gen Kurs zu kaufen und zu einem möglichst hohen Kurs zu verkaufen , wurden Wege
gesucht, Kurse vorherzusagen. Eine Möglichkeit ist die
Fundamentalanalyse,
die
untersucht, welche Zukunftsaussichten eine Aktiengesellschaft hat, welche Betriebsänderungen zu erwarten sind, welche Nachfrage nach den produzierten Gütern besteht etc. Der andere groÿe Bereich ist der Bereich der
technischen Analyse.
Anhand
von Kursdaten der Vergangenheit soll hierbei auf die Entwicklungen in der Zukunft
geschlossen werden. Hintergrund ist die Annahme, dass der Kurs eines Wertpapiers
auch dessen
inneren
3
Wert
aufgrund von Angebot und Nachfrage widerspiegelt. Mur-
phy [Mur00] beschreibt die Situation so: Der Fundamentalist studiert die Ursachen
von Marktbewegungen, während der Techniker die Auswirkungen untersucht.
Technische Indikatoren sind aus dem Kursverlauf abgeleitete Kenngröÿen, die
durch bestimmte Werte oder Wertveränderungen die aktuelle Marktsituation beschreiben sollen. Viele Indikatoren geben dabei auch Verkauf- und Kaufsignale, d. h.
bei Erreichen oder Unterschreiten eines bestimmten Wertes oder beim Kreuzen von
zwei Indikatoren wird dem Anleger signalisiert, dass er ein Wertpapier kaufen oder
verkaufen sollte.
Mathematisch gesehen handelt es sich bei den technischen Indikatoren um mathematische Funktionen auf den Kurswerten (und eventuell dem Volumen) der Vergangenheit und der Gegenwart:
T (t) = f (Kurs(t), Kurs(t − 1), . . . , Kurs(t − i), . . . , Kurs(t − n))
(3.1)
Dabei bezeichnet t den Handelstag, dessen Indikatorwert berechnet werden soll,
Kurs(t) einen oder mehrere der vier oben angeführten Kenn-Kurse eines Wertpapiers
am Tag t und f eine Funktion auf deren Werten. Die Variable n wird Berechnungs-
periode
oder
Berechnungszeitraum
des Indikators genannt.
Dehnt man nun die Berechnungsbasis von technischen Indikatoren auf andere Kurse als die Tageskurse aus, so können an die Stelle von Handelstagen Handelszeiträume
treten, und die Hoch-, Tief-, Erönungs- und Schlusskurse beziehen sich dann auf
diesen Handelszeitraum, z. B. eine Stunde oder einen Monat.
Im Folgenden werden einige Indikatoren vorgestellt, die jeweils eine bestimmte
Klasse von Berechnungskomplexitäten repräsentieren. Auf die hier vorgestellten Indikatoren wird im Kapitel 9 Bezug genommen. Die Interpretation der Indikatoren
ADO, SMA und MACD wurde der Diplomarbeit von Hübel [Hüb07] entnom-
2
3
Im Derivate-Handel kann dies auch umgekehrt sein, was hier aber nicht thematisiert werden soll.
Wert, der sich aus dem Betriebsvermögen und änhlichem ergibt
24
3.3. Technische Indikatoren
men. Die Interpretation des Indikators CCI wurden den Ausführungen auf der Website [Sto] entnommen.
Der
Accumulation/Distribution Oszillator,
abgekürzt ADO, beschreibt die
beiden Kräfte Accumulation und Distribution. Unter
Accumulation
die Stärke der Käufer, in einem Markt Wertpapiere zu kaufen, unter
versteht man
Distribution
die
Stärke der Verkäufer, zu verkaufen. Der ADO wird wie folgt berechnet:
(t) = (High(t) − Open(t)) +
ADO
Close(t) − Low(t)
2 · (High(t) − Low(t))
(3.2)
Der Indikator kommt somit ohne Aggregation aus.
Der A/D Oszillator misst die vorherrschenden Marktkräfte [Hüb07] und zeigt
Kauf- und Verkaufsdruck an, wobei steigende Werte einen zunehmenden Kaufdruck
anzeigen. Üblicherweise werden zur Signalisierung Schwellenwerte eingesetzt.
Der
gleitende Durchschnitt
oder SMA (simple moving average) ist ein in der
technischen Analyse häug verwendeter Indikator. Er gibt den Durchschnitt des
Schlusskurses der letzten
n
Handelszeiträume an:
Pn−1
SMAn
Dabei gibt
t
i=0
(t) =
Close
(t − i)
(3.3)
n
die fortlaufende Nummer des Handelszeitraums an und
n
die Berech-
nungsperiode. Der SMA bewirkt eine Glättung der Kursverläufe und dient ebenfalls
als Widerstands- und Unterstützungslinie [Hüb07]. Überschreitet ein kurzfristiger
Durchschnitt einen längerfristigen, so gilt dies als Signal für einen Aufwärtstrend,
die umgekehrte Situation als Signal für einen Abwärtstrend. Der SMA reagiert dabei
träge, da alle Kurswerte gleich gewichtet werden, ungeachtet, wie lange sie schon
zurückliegen.
Der SMA gehört zur Klasse der Indikatoren mit einfacher Aggregation, da nur für
die Berechnung der Summe eine Aggregation durchzuführen ist.
Der
Commodity Channel Index (CCI) wurde von Donald Lambert zur Identi-
zierung von Handelszyklen entworfen [Sto]. Die Annahme für diesen Indikator geht
dahin, dass Handelswaren (oder auch Wertpapiere) sich in Zyklen bewegen, wobei als
Berechnungsperiode möglichst ein Drittel der Zyklenlänge verwendet werden sollte.
Die Berechnungsvorschrift des CCI lautet:
CCI
Hierbei ist TP
=
High
(t) =
(t) − SMATPn (t)
0, 015 · MDn (t)
TP
+ Low + Close
(3.4)
der typische Preis des Wertpapiers am je-
weiligen Handelstag, SMATP der gleitende Durchschnitt des typischen Preises über
n
Handelszeiträume und MD die mittlere Abweichung, der Durchschnitt aus der
absoluten Dierenz zwischen dem SMATP des letzten Handelszeitraums und des
n Handelszeiträume:
Pn−1
i=0 |TP(t − 1) − SMATPn (t − i)|
MDn (t) =
n
typischen Preises der letzten
(3.5)
25
3. Grundlagen der technischen Analyse
Der Wert
0,015
schlieÿlich ist ein Normierungsfaktor, der gewährleisten soll, dass 70
bis 80% aller Indikatorwerte zwischen
+100,
−100 und +100 liegen. Liegt der Wert über
−100 als Verkaufssignal gewertet. Durch die
so wird dies als Kaufsignal, unter
Notwendigkeit, SMATP und MD zu berechnen, fällt dieser Indikator in die Klasse
der Indikatoren mit mehrfacher Aggregation.
Die
Moving Average Convergence/Divergence (MACD) ist ein Indikator, der
sowohl die Trendrichtung als auch die Trendstärke anzeigt. Er verbindet Trendfolgeund Oszillator-Eigenschaften. Berechnet wird er mittels zweier exponentieller gleitender Durchschnitte. Zur Berechnung des MACD wird zunächst der exponentielle
Durchschnitt EMA berechnet:
EMA
wobei Ew
(t)
(t) = (Close(t) − EMA(t − 1)) · Ew(t) + EMA(t − 1)
(3.6)
ein Gewichtungsfaktor ist, der als
Ew
(t) =
2
n+1
(3.7)
deniert ist. Aus dem EMA kann dann der MACD berechnet werden:
MACD
(t) = EMA12 (t) − EMA26 (t)
(3.8)
wobei EMA12 der EMA über 12 Tage, der EMA26 der EMA über 26 Tage ist. Diese Werte wurden aufgrund der von dem Ernder des EMA, G. Appel, beobachteten
Marktzyklen gewählt [Pae06]. Schlieÿlich wird als dritte Komponente noch eine Glättung der Signallinie von 9 Tagen berechnet.
In seiner Diplomarbeit [Hüb07] listet Hübel mehrere Interpretationen des MACD
auf: Der Indikator vollzieht die Bewegung des Kurses nach. Dsie Lage zur Mittellinie
zeigt den Trend an. Ein steigender MACD über der Mittellinie zeigt ein steigendes Momentum im Aufwärtstrend an, ein fallender eine nachlassende Intensität des
Aufwärtstrends (entsprechendes gilt für die Gegenrichtung). Divergenzen zwischen
MACD und Kursverlauf weisen auf Schwächen im Trend hin und signalisieren wie
auch Schnittpunkte mit der Mittellinie oder der Signallinie Trendwechsel.
Der MACD ist aufgrund der rekursiven Denition des EMA ein rekursiver Indikator. Prinzipiell lassen sich mit der in TInTo verwendeten SQL-Version SQL-92 keine
rekursiven Sichten denieren. Hübel hat jedoch in seiner Diplomarbeit ebenfalls ein
Verfahren vorgestellt, mit dem sich der MACD auch mittels SQL (über den Umweg
einer Folge von Änderungsanweisungen) berechnen lässt.
26
4. TInTo
TInTo die Abkürzung steht für Technical Indicator Tool ist eine von Christian
Hübel im Zusammenhang mit seiner Diplomarbeit [Hüb07] erstellte Access-Applikation zur regelbasierten Wertpapieranalyse. Das System dient dazu, Kurse von Wertpapieren und zugehörige technische Indikatoren auf diesen Kursen zu berechnen und
grasch als Chart anzuzeigen. Ein wichtiges Merkmal von TInTo liegt darin, dass es
möglich ist, die Berechnungsvorschriften technischer Indikatoren selbst in SQL zu denieren, während in den herkömmlichen Anwendungen die Berechnungsvorschriften
meist vorgegeben sind oder in seltenen Fällen nur mittels einer eingebauten, proprietären Skriptsprache denierbar sind. Einmal denierte Indikatordenitionen werden
abgespeichert und sind später immer wieder verwendbar.
Um möglichst aktuelle Kursdaten zur Verfügung zu haben, werden die Kursdaten
mittels Abruf aus dem Internet in das System eingelesen und in der Datenbank abgespeichert. Bei jeder Auswahl des Wertpapiers werden dabei die abgespeicherten Daten
aktualisiert. Im bestehenden System werden dabei ausschlieÿlich Tagesenddaten verwendet. Der Benutzer hat dabei alle ihm zur Verfügung stehenden Bedienelemente
auf einen Blick zur Verfügung. Als Konsequenz sind in TInTo bis auf die Denition
der Indikatoren alle Funktionen direkt im Hauptfenster erreichbar.
4.1. Systemarchitektur von TInTo
Die Funktionalitäten des Systems sind auf verschiedene Komponenten verteilt. Die
Daten werden mittels des DBMS in der Datenbank abgespeichert und abgefragt.
Weitere Funktionalitäten, die nicht in Microsoft Access direkt verfügbar waren, wurden mittels Visual Basic for Applications selbst implementiert. Für die grasche
Darstellung der Indikatoren wurde das von der Firma
ring
Advanced Software Enginee-
vertriebene ActiveX-Ob jekt ChartDirector verwendet, das alle Zeichenfunktio-
nen übernimmt und lediglich ein Array mit den darzustellenden Werten erwartet.
Es kann zwischen vier verschiedenen Hauptkomponenten des Systems unterschieden werden:
1. der Benutzeroberäche zur Interaktion mit dem Benutzer, insbesondere zur
Eingabe von Steuerungsanweisungen an das System,
2. der Wertpapierverwaltung zum Abruf und zur Verwaltung von Wertpapierstammdaten und Kursen,
27
4. TInTo
3. der Indikatorverwaltung mit Berechnungsmodul, welche die Berechnungsvorschriften für die verschiedenen Indikatoren verwaltet und Abhängigkeiten zwischen den Indikatordenitionen behandelt und
4. der graschen Anzeige, die die berechneten Ergebnisse als Chart ausgibt.
Diese vier Komponenten und ihr grundsätzlicher Aufbau sollen in diesem Abschnitt
kurz vorgestellt werden.
Einen Überblick über die Systemarchitektur und die Interaktionen zwischen den
verschiedenen Komponenten von TInTo gibt die Abbildung 4.2.
Die
Benutzeroberäche
(Abb. 4.1) besteht aus mehreren Access-Formularen.
Hauptformular ist das Formular
Main. Es erlaubt den Zugri auf die grundlegenden
Funktionen von TInTo. Der Benutzer kann hier auswählen, welches Wertpapier er
anzeigen möchte, welcher Indikator berechnet werden soll etc.
Links oben im Hauptfenster bendet sich zunächst ein Kombinationsfeld zur Auswahl des anzuzeigenden Wertpapiers. Aus einer Liste kann der Benutzer das Wertpapierkürzel auswählen. Die Kürzel werden aus der Tabelle
TWertpapier bezogen.
Nach einem Klick auf die Schaltäche neben dem Kombinationsfeld wird die Prozedur
zur Chartanzeige gestartet. Zuerst werden neue Daten aus dem Internet abgerufen
und in der Kurstabelle abgespeichert. Anschlieÿend wird die Funktion
ChartShow,
die die Daten aus der Kurstabelle abruft, aufgerufen. Gibt der Benutzer ein unbekanntes Kürzel ein, wird vom Kursanbieter
Yahoo! (www.yahoo.com)
eine Liste
abgerufen, die auf den Suchbegri passende Wertpapiere zur Auswahl enthält. Dem
Benutzer wird diese Liste als Auswahlmöglichkeit angezeigt, das entsprechende Wertpapier in der Tabelle
TWertpapier angelegt und die Kurse seit dem 1. Januar 2001
aus dem Internet abgerufen.
Unter dem Auswahlfeld für das Wertpapier bendet sich der Bereich, in dem das
Aussehen des Charts bestimmt werden kann. Zum einen kann der Benutzer die Art
des Charts auswählen, wobei Candlestick, OHLC, Schlusskurs, Typischer Kurs,
Gewichteter Kurs und Mittlerer Kurs zur Verfügung stehen. Die ersten beiden
Charttypen wurden bereits im Abschnitt 3.2 beschrieben, die weiteren Auswahlen
führen jeweils zu einem Linienchart mit dem entsprechenden Kurs. Darunter benden sich zwei Kontrollkästchen, mit denen der Benutzer festlegen kann, ob im
Chart Volumenbalken angezeigt werden sollen und ob die Skalierung logarithmisch
sein soll. Wird keine logarithmische Skalierung gewählt, so wird stattdessen die lineare Skalierung gewählt. In einer darunter bendlichen Auswahlliste lässt sich ein
ChartDirector-interner Indikator auswählen. Die Visualisierungskomponente ChartDirector verfügt selbst über die Fähigkeit, bestimmte Indikatoren zu berechnen. Ist
in der Liste ein Indikator ausgewählt, so wird der Indikator unmittelbar unter dem
Kurschart angezeigt, sobald die oben an der Liste bendliche Schaltäche betätigt
wird. Ähnlich aufgebaut ist die unterste Liste, die die Auswahl eines selbstdenierten Indikators erlaubt. Die Liste wird mittels der Indikatornamen aus der Tabelle
TView
gefüllt. Oberhalb der Liste benden sich vier Schaltächen, die zum Einfü-
gen, Bearbeiten, Löschen und Anzeigen der Indikatoren dienen. Die selbstdenierten
Indikatoren werden jeweils als unterstes im Chart angezeigt, wobei das Aussehen der
28
4.1. Systemarchitektur von TInTo
Darstellung in der Indikatordenition hinterlegt werden kann. Unter der Liste bendet sich noch die Schaltäche Access ein-/ausblenden, mit der das Hauptfenster
von Access eingeblendet werden kann. Standardmäÿig wird dieses beim Start ausgeblendet. Oben rechts im Fenster benden sich fünf Schaltächen, mit denen der
Zeitraum ausgewählt werden kann, für den die Berechnung durchgeführt werden soll.
Bei Betätigung der Schaltäche Indikator bearbeiten (gekennzeichnet durch gekreuzten Schraubenschlüssel und Hammer) önet sich das
Indikatordenitionsfenster.
In diesem lässt sich in den oberen drei Eingabefeldern der Name (als Kurzbezeichnung), die Caption (Langbezeichnung) sowie eine Sortierpriorität zum Ausblenden
selten genutzter Indikatoren eingeben. Darunter bendet sich ein groÿes Textfeld, in
dem die SQL-Denition eingegeben werden kann. Wie diese formuliert werden muss
wird im Abschnitt 4.2 beschrieben. Rechts benden sich Eingabefelder, in denen das
Aussehen der drei gleichzeitig möglichen Indikatorlinien eingestellt werden kann. In
der ersten Spalte kann ein Name für die Indikatorlinie angegeben werden. Die Linie
wird dann durch eine kleine Legende oberhalb des Graphen gekennzeichnet. Daneben
kann die Farbe angegeben werden. Möglich sind hier
2563 = 16.777.216 Farben, die als
Hexadezimalzahl angegeben werden können. Dabei stehen jeweils zwei Stellen für rot,
grün und blau. Somit steht beispielsweise die Zahl &HFF00FF für lila (rot und blau).
Rechts daneben kann eine Zeichenfolge angegeben werden, die Schwellenwerte für die
T:Höchstwert, Farbe,
T:70,&Hff8080,30,&H8080FF
Indikatoren festlegt. Die Zeichenfolge muss das Format
Tiefstwert, Farbe
haben. Die Zeichenfolge
führt dazu, dass die Marke von 30 mit einer hellblauen Linie und die Marke von 70
mit einer roten Linien gekennzeichnet wird. Zusätzlich färbt die Visualisierungskomponente die von der Schwellenlinie und dem Kurvenverlauf eingeschlossene Fläche
ebenfalls ein. Im Denitionsfenster bendet sich unten links eine Schaltäche, mit
der eine
Die
Kurstabelle
aufgerufen werden kann.
Wertpapierverwaltung initiiert den Kursabruf aus dem Internet und spei-
chert die Kurse in der Tabelle
TKurs
ab. Ferner sucht sie nach neuen Wertpa-
1
pierkürzeln und speichert die Stammdaten wie Kürzel, Name, ISIN
TWertpapier
in der Tabelle
ab.
Der Kursabruf erfolgt, indem eine Anfrage über die Internet-Schnittstelle an den
Dienstleister
Yahoo! gesendet
wird. Die gewünschten Daten sind dabei in der URL des
Abrufs einkodiert. Um beispielsweise die Daten für die Aktie von Microsoft (Kürzel
MSFT) vom 5.6.2007 bis 7.6.2007 abzurufen, wird die URL
http://ichart.finance.yahoo.com/table.csv?s=MSFT
&a=5&b=4&c=2007&d=5&e=6&f=2007&g=d&ignore=.csv
an die Internet-Schnittstelle übergeben. Dabei steht der Parameter hinter
s=
für
das jeweilige Wertpapierkürzel, die nachfolgenden Parameter kodieren die Datumsgrenzen, wobei sowohl Monat als auch Tag jeweils um eins vermindert anzugeben
sind, so dass die Zählung bei null beginnt. Der letzte Parameter gibt das Datenfor-
1
International Securities Identication Number, eine weltweit eindeutige Identikationsnummer für
Wertpapiere
29
4. TInTo
Abbildung 4.1.: Die Benutzeroberäche der ursprünglichen TInTo-Version
mat .csv an.
2
3
Als Rückgabe sendet der Server eine sogenannte CSV-Datei , die für
jeden angefragten Handelstag eine Zeile enthält, deren Einträge jeweils durch Kommata separiert sind. Zusätzlich ist eine Überschriften-Zeile angegeben. Die Rückgabe
für den oben angegebenen Aufruf ist dann
Date,Open,High,Low,Close,Volume,Adj Close
2007-06-06,30.37,30.53,30.25,30.29,38217500,30.29
2007-06-05,30.62,30.63,30.33,30.58,44265000,30.58
2007-06-04,30.42,30.76,30.40,30.72,41434500,30.72
Diese Rückgabe wird in einem String abgelegt und von der Funktion
DataLoad
weiterverarbeitet. Zunächst wird die erste Zeile aus dem String entfernt, da sie keine
für das Programm nutzbaren Informationen enthält (die Zeile ist immer gleich). Dann
wird die Tabelle
TKurs
mittels des DAO-Ob jekts geönet. In einer Schleife wird
dann der String zeilenweise ausgewertet. Dazu wird der letzte Zeilenumbruch (ASCIIZeichen 10) im String gesucht. Alle Zeichen von dieser Position bis zu Ende des Strings
stellen die letzte Zeile und somit den ersten Datensatz dar (auf diese Weise werden
die Datensätze passend umsortiert). Danach wird in dieser Zeile wiederum das erste
Komma gesucht und der String vom Anfang der Zeile bis zum ersten Komma in das
2
3
Die Syntax entstammt der Syntax der Skriptsprache PHP.
Comma seperated values
30
4.1. Systemarchitektur von TInTo
Access-Datumsformat konvertiert und das Datumsattribut der Tabelle entsprechend
gesetzt. Ganz ähnlich wird in einer inneren Schleife mit den weiteren Kurswerten
verfahren. Nach Ende der Zeile wird der nächste Datensatz angelegt und die nächste
Zeile verarbeitet. Die Verarbeitung endet, sobald das Ende des Strings erreicht ist.
Die
Indikatorverwaltung verwaltet die verschiedenen Indikatordenitionen, die
vom Benutzer eingegeben werden können. Die Abfragedenition, also der SQL-Ausdruck, der für die Berechnung des Indikators benötigt wird (s. Abschnitt 4.2) wird
als String in der Tabelle
TView
abgespeichert. Bei jeder Berechnung wird dieser
SQL-String abgefragt. Ferner sorgt die Indikatorverwaltung dafür, dass Abhängigkeiten zu anderen Denitionen berücksichtigt werden. Dazu wird mittels der Funktion
ChartAddQuery
überprüft, welche Relationen im
werden. Dazu wird das Schlüsselwort From
TKurs
sind. Wir im
referenziert
im Ausdruck gesucht und alle danach
auftretenden Strings, die weder die Schlüsselwörter der Basistabelle FROM-Teil
From-Teil
Join, Inner
noch der Name
die Basisrelation
TKurs
refe-
renziert, so wird mit der Auswertung des SQL-Ausdrucks fortgefahren. Andernfalls
werden zunächst rekursiv die referenzierten Indikatordenitionen ausgewertet, im
Access-System die entsprechenden Abfragen angelegt und dann erst die Berechnung
der Indikatordenition fortgesetzt. Auf diese Weise wird gewissermaÿen eine Abhängigkeitshierarchie, die zwischen verschiedenen Indikatordenitionen besteht, in einem
Top-Down-Ansatz aufgebaut, so dass jeweils benötigte Indikatordenitionen zur Verfügung stehen. In der Tabelle
TView werden auÿerdem auch die Ausgabeparameter
wie Ausgabefarbe, farbliche Markierungen etc. abgespeichert.
Die
Schnittstelle zum Internet
wird über eine Klasse namens
clsHTTP
be-
reitgestellt. Diese Klasse beinhaltet verschiedene Visual-Basic-Methoden, die ihrerseits Funktionen der Windows-API aufrufen. TInTo benutzt hier hauptsächlich die
Methode
WriteHTTPDataToString, die einen URL-String als Parameter entge-
gennimmt und die über diese URL abgerufenen Daten als String zurückgibt. Tritt
ein Fehler beim Datenabruf auf, löst die Klasse ein Fehler-Ereignis aus. Diese Klasse
wurde ausweislich des Copyright-Hinweises im Quellcode aus einer fremden Quelle
fertig übernommen. Die Beschreibung der Funktionsweise im Einzelnen würde hier
den Rahmen sprengen, zumal nur ein geringer Teil der Funktionalität tatsächlich
verwendet wird. Im Prinzip werden hierfür mittels des Windows-Sockets zunächst
HTTP-Anfragen an einen Server versendet, und anschlieÿend blockweise die zurückerhaltenen Daten ausgelesen. Diese können dann z. B. als String abgelegt und weiterverarbeitet werden.
Herzstück der Anwendung ist die
grasche Anzeige.
Während die eigentliche
grasche Darstellung auf dem Bildschirm der COM-Komponente
ChartDirector
über-
lassen wird, so wird die Vorbereitung der Daten vom TInTo-System übernommen.
Fordert der Benutzer die Zeichnung des Charts an, so wird die Funktion
ChartShow
aufgerufen, die die Vorbereitung übernimmt und schlieÿlich die Neuzeichnung des
Charts durch einen Methodenaufruf an den ChartDirector initiiert. Zuerst wird die
aktuelle Gröÿe des Hauptfensters festgestellt und daraus die Gröÿe des zu zeichnenden Charts berechnet. Danach wird in Abhängigkeit von dem darzustellenden Intervall (der Datumsgrenzen) berechnet, welches die kleinste Datensatznummer und
31
4. TInTo
welches die maximale Datensatznummer in der Kurstabelle ist. Anschlieÿend werden aus der Indikatortabelle
TView die SQL-Denition des ausgewählten Indikators
abgefragt und wie oben beschrieben mittels der Indikatorverwaltung gegebenenfalls
weitere Abfragen angelegt. Dann wird mittels des DAO-Ob jekts die Indikatorsicht
geönet und zeilenweise in ein Array eingelesen. Auftretende NULL-Werte werden
dabei speziell behandelt und gegebenenfalls in eine arithmetische 0 konvertiert. In einer inneren Schleife werden dabei Höchst- und Tiefstkurs für eine Gruppe bestimmt.
Die Daten werden nach ihrer Anzahl gruppiert, wobei die Anzahl der in einer Gruppe
bendlichen Werte in Abhängigkeit vom gewählten Intervall bestimmt werden. Als
Indikatorwert wird dabei das arithmetische Mittel der Indikatorwerte der Gruppe
4
verwendet.
In einer weiteren Schleife werden anschlieÿend die soeben gefüllten Arrays in umgekehrter Reihenfolge in ein weiteres Array kopiert. Mittels eines Methodenaufrufs
werden anschlieÿend die Ausmaÿe des zu zeichnenden Charts festgelegt, die Skalierung gewählt und falls gewünscht die ChartDirector-internen Indikatoren hinzugefügt. Danach werden die selbstdenierten Indikatoren hinzugefügt, wobei die Arrays
als Parameter übergeben werden. Schlieÿlich wird der Zeichenmethode des ChartDirectors aufgerufen.
4.2. Spezikation von technischen Indikatoren in TInTo
In TInTo werden, wie bereits erwähnt, technische Indikatoren als SQL-Abfrage hinterlegt. Der Benutzer kann in einem Fenster einen SQL-Ausdruck eingeben, dessen
Rückgabe dann im Chart angezeigt wird.
Als Quelle für Kursdaten kann der Benutzer die Relation
Relation enthält die Attribute
TKurs verwenden. Diese
ID, n, Date, Open, High, Low, Close
und
n
dabei eine Kennzahl, die für das jeweilige Wertpapier vergeben wird,
fende Zahl des Kurses,
Date
das Datum.
Open, Close, High
und
Low
Erönungs-, Schluss-, Höchst- und Tiefstkurs des jeweiligen Tages,
Als Hilfsmittel stehen dem Benutzer ferner die Funktionen
spGetID()
und
spGetN()
zur Verfügung.
spGetPar
Vol. ID
ist
eine fortlau-
beinhalten den
Vol
das Volumen.
spGetPar(Prompt),
zeigt dem Benutzer bei Aufruf
ein Fenster an, in dem er einen Wert eingeben kann.
spGetID()
im TInTo-Fensters ausgewählten Wertpapiers zurück und
spGetN()
gibt die ID des
gibt die kleinste
Kursnummer zurück, die innerhalb des ausgewählten Zeitraums liegt.
Das Verfahren, um mittels SQL Indikatorwerte zu berechnen, ist nicht auf den
ersten Blick oensichtlich. Eine Möglichkeit bestünde darin, die einzelnen Kurswerte zu durchlaufen und die Indikatorwerte aus den zurückerhaltenen Tupeln mittels
selbst programmiertem Code zu berechnen. Dieses Verfahren würde jedoch der Idee
widersprechen, die Indikatoren nur mittels SQL zu berechnen. Hübel wählte einen
anderen Ansatz, den bereits Geppert in seiner Diplomarbeit [Gep05] vorschlug: Er
verknüpfte die Tabelle
4
TKurs
mittels eines Theta-Joins mit sich selbst. Die Theta-
Dieses Verfahren wird im Abschnitt 6.5 noch diskutiert werden.
32
4.2. Spezikation von technischen Indikatoren in TInTo
Eingabe
Wertpapiersuche
Wertpapierverwaltung
Rückgabe
Anfragen
Grafik
Berechnungsaufforderung
Kurse und
Stammdaten
Kurse und
Stammdaten
ChartDirector
Werte
Berechnungsmodul
Kurse
DB
Internetschnittstelle
HTTP-Abfragen
CSV-Daten
Abbildung 4.2.: Die Komponenten des TInTo-Systems
Bedingung besteht darin, dass die fortlaufend vergebene Nummer der zu betrachtenden Kurswerte zwischen der Nummer des aktuellen Kurswertes
t
und
t−n
liegen
muss. Anschlieÿend werden mittels Aggregation die mit einem Kurswert verknüpften
anderen
n+1
Kurswerte zusammengefasst und dann eine Aggregatfunktion auf die
zusammengefassten Kurswerte angewendet.
Als Beispiel soll hier der gleitende Durchschnitt dienen, dessen Denition in der
Gleichung 3.3 angegeben wurde. Die entsprechende SQL-Abfrage lautet:
TKurs.n, TKurs.Date, TKurs.Open, TKurs.Close,
TKurs.High, TKurs.Low, AVG(TK1.Close) AS Ind
FROM
TKurs INNER JOIN TKurs AS TK1
ON (TKurs.n>=TK1.n
AND TKurs.n-spGetPar("Periodenvorgabe=10")<=TK1.n
AND TKurs.ID=TK1.ID)
GROUP BY TKurs.n, TKurs.Date, TKurs.Open, TKurs.Close,
TKurs.High, TKurs.Low
WHERE TKurs.ID=spGetID() AND TKurs.n>spGetN()
SELECT
Zuerst werden also die Attribute aus TKurs selektiert. Diese dienen später dazu,
den Chart, also den eigentlichen Kursverlauf, zu zeichnen. Es folgt der arithmeti-
33
4. TInTo
sche Durchschnitt der Schlusskurse aus TK1. Im
From-Teil
wird die Kurstabelle
mit sich selbst per Join verbunden, so dass der Wert von TK1.n zwischen
und
Tkurs.n-spGetPar("Periodenvorgabe=10")
Tkurs.n
liegen muss. Damit wirklich
nur die Kurse des selben Wertpapiers verglichen werden, müssen auch die ID-Werte
Group By-Teil fasst hinterher die Werte, die einem Kurswert
TKurs zugeordnet wurden, zusammen. Aus diesen wird dann der Mittelwert,
wie im Select-Teil angegeben, errechnet. Im WHERE-Teil werden die Werte dann
übereinstimmen. Der
aus
noch auf das ausgewählte Wertpapier und den ausgewählten Zeitraum eingeschränkt.
Die Berechnung des Rückgabewertes von
spGetN()
erfolgt dabei mittels einer VBA-
Routine. Auch Indikatoren mit mehrstuger Aggregation sind in TInTo möglich. Dazu wird in für jede Aggregationsstufe ein eigener Hilfsindikator angelegt. In den
höheren Aggregationsstufen wird dieser Hilfsindikator dann über seinen Namen angesprochen. So ist beispielsweise für den CCI der Hilfsindikator CCI0 angelegt worden. In der Denition des CCI selbst wird der Indikator dann im
From-Teil
des
SQL-Ausdrucks referenziert. Die Wertpapierverwaltung (s.o.) sorgt dafür, dass die
so referenzierte Sicht automatisch angelegt wird. Schlieÿlich hat Hübel auch ein Verfahren entwickelt, rekursive Indikatoren in TInTo anlegen zu können. Dabei wird die
Rekursion, die in Access-SQL nicht direkt unterstützt wird, simuliert. Kern dieser
Simulation ist eine Folge von Update-Anweisungen. Wie man an den Gleichungen
3.6 und 3.8 sieht, sind sowohl der EMA (exponentieller Durchschnitt) als auch der
MACD selbst rekursiv deniert. Die Simulation erfolgt nun wie folgt: In der Kurstabelle sind drei Hilfsattribute
v1 , v2 , v3
enthalten. Diese werden zu Beginn mit den
Schlusskursen des jeweiligen Datensatzes gefüllt:
UPDATE tmpAggregation
SET v1=Close, v2=Close
WHERE tmpAggregation.ID=spGetID()
AND tmpAggregation.n>2
Danach wird mit einer zweiten Updateanweisung der EMA berechnet. Dazu wird die
Kurstabelle mit sich selbst verknüpft und die Werte entsprechend zugewiesen:
UPDATE tmpAggregation AS TK1 INNER JOIN tmpAggregation AS TK0
ON (TK1.ID=TK0.ID AND (TK1.n-1)=TK0.n) SET
TK1.v1=((TK1.v1-TK0.v1)*2/(26+1))+TK0.v1,
TK1.v2=((TK1.v2-TK0.v2)*2/(12+1))+TK0.v2,
TK1.v3=((((TK1.v2-TK0.v2)*2/(12+1))+TK0.v2)(((TK1.v1-TK0.v1)*2/(26+1))+TK0.v1))
WHERE TK1.ID=spGetID() AND TK1.n>1
Die Berechnung erfolgt aufgrund der Sortierung der Kurstabelle in Reihenfolge der
Datumswerte. Bei der Aktualisierungszuweisung enthält die rechts referenzierte Kopie
TK0 der Tabelle bereits den aktualisierten Wert des EMA, so dass hierüber der
rekursive Zugri möglich ist. In einem weiteren Schritt wird dieses Verfahren so
wiederholt, dass der MACD selbst berechnet wird:
34
4.3. Diskussion des bestehenden Systems
UPDATE tmpAggregation AS TK1 INNER JOIN tmpAggregation AS TK0
ON (TK1.ID=TK0.ID AND (TK1.n-1)=TK0.n)
SET TK1.v3=((TK1.v3-TK0.v3)*2/(9+1))+TK0.v3
WHERE TK1.ID=spGetID()
Die eigentliche Indikatorsicht selektiert dann nur noch die Werte aus den Hilfsattributen, wobei aus diesen noch Dierenzen gebildet werden, um Signallinien für den
jeweiligen Indikator zu erhalten:
SELECT ID, n, Date, High, Low,
Open, Close, Vol, (v2-v1)-v3 AS Ind1,
(v2-v1) AS Ind3, v3 AS Ind2, Volstart
FROM tmpAggregation
WHERE TK1.ID=spGetID()
ORDER BY ID DESC, Date DESC
Die einzelnen Update-Anweisungen sind durch Paragrafenzeichen (Ÿ) getrennt. Bei
der Indikatorberechnung werden die Anweisungen an diesem Zeichen zerlegt. Aktionsabfragen werden dann ausgeführt,
Select-Ausdrücke
werden zum Zeichnen des
Indikators verwendet.
4.3. Diskussion des bestehenden Systems
Dem Anspruch, ein Tool für die technische Indikatoranalyse zu sein, wird das Programm gerecht. Besonders interessant ist die Möglichkeit, Indikatoren selbst zu denieren. Allerdings muss der Anwender für diese Möglichkeit mit SQL vertraut sein.
Dies mag auf der einen Seite ein Nachteil gegenüber proprietären Skriptsprachen sein,
andererseits ist die Literaturlage zum Thema SQL auch für den Einsteiger sehr gut
und die Sprache standardisiert. Die bereits vordenierten Indikatoren können dabei
dem Anwender als Vorlage dienen.
Die Verwendung eines (relationalen) DBMS für die Berechnung technischer Indikatoren einige unbestreitbare Vorteile. Da in dieser Anwendung groÿe Datenmengen vorhanden sind, kann ein DBMS hier seine Fähigkeiten hinsichtlich der physischen Datenmodellierung ausspielen, beispielsweise durch die Verwendung von Indizes, Suchbäumen oder ähnlichem. Man könnte dagegen einwenden, dass es bei einer
Berechnung aller Indikatorwerte für einen Zeitraum lineare Laufzeit nicht unterschritten werden kann. Da aber auch ein viel kleineres Intervall für die Berechnung verwendet werden kann, als der Zeitraum, für den Daten zur Verfügung stehen und
auch nach Wertpapieren geltert werden muss, sind die Selektionsmechanismen für
die Indikatorberechnung sehr nützlich.
Eine prinzipielle Frage ist, ob Access für eine solche Anwendung eine geeignete
Grundlage ist. Access besitzt im Vergleich zu anderen DBMS einige Nachteile. So
fehlt in Access eine prozedurale Erweiterung wie SQL/PL, die zur Hintereinanderausführung von SQL-Anweisungen geeignet wäre. Christian Hübel hat dieses Manko
durch eine selbsterstellte Erweiterung ausgeglichen. Ein weiteres technisches Pro-
35
4. TInTo
blem, das bei allen Access-Anwendungen gegeben ist, liegt darin, dass Access immer
sein eigenes Hauptfenster im Hintergrund anzeigt, was bei Benutzern, die mit der
Verwendung von Access nicht vertraut sind, zu Verwirrungen und Fehlbedienungen
führen kann. Es wurde versucht, das Problem dadurch zu umgehen, dass mittels
eines API-Aufrufs das Access-Fenster ausgeblendet wird. Dies führte im Test dann
zu Problemen, wenn Fehler auftraten und Access in das nun nicht mehr sichtbare
Access-Fenster springen wollte. Oft blieb dann nur noch das Beenden des Prozesses mittels des Windows-Taskmanagers. Auch ist Access in der Abarbeitung von
Anfragen oft langsamer als andere Produkte. Eine alternative Implementierung hätte eventuell darin bestanden, die Benutzeroberäche als eigenständige Anwendung
in einer herkömmlichen Programmiersprache zu erstellen und diese an ein groÿes
DBMS, beispielsweise Oracle, anzubinden. Diese Lösung setzt allerdings einen beträchtlichen Aufwand voraus, entweder einen Datenbankserver bereitzuhalten oder
ein solches DBMS zu installieren. Auÿerdem dürften die meisten solcher Lösungen
auch mit gröÿeren nanziellen Kosten verbunden sein, selbst wenn man den Kaufpreis
für Microsoft Access hinzuzählt.
Auf Seite der Benutzerinteraktion muss hervorgehoben werden, dass die Oberäche
sehr übersichtlich ist. Während sich der Benutzer bei vielen heute erhältlichen Anwendungen durch mehrere Menüs begeben muss, um allein die Standardeinstellungen
festzulegen, so ist es in TInTo möglich, alle Grundfunktionen aus dem Hauptfenster
heraus zu erledigen. Dem Einsteiger kommt zudem entgegen, dass viele Indikatoren bereits vordeniert sind. Bei der Neudenition von Indikatoren ist die Angabe
des Formatierungsstrings etwas kompliziert. Auch muss der Benutzer selbst für eine ordnungsgemäÿe Installation des ChartDirectors sorgen, bevor er das Programm
erstmals verwendet, ansonsten kommt es zu Fehlermeldungen. Die Symbolsuche in
TInTo ist nur schwer zu nden: Bei freier Eingabe eines noch unbekannten Kürzels
wird dem Benutzer ein Auswahlfenster angezeigt, aus dem er das passende Wertpapier auswählen kann.
Dafür muss sich der Benutzer nach Anlage des Wertpapiers in der Datenbank
nicht mehr um den erneuten Abruf von neuen Daten kümmern, da dieser Abruf automatisch bei Neuzeichnung des Charts durchgeführt wird. Hier wirkt verwirrend,
dass das System die Daten im Hintergrund abruft, ohne dass der Benutzer davon
erfährt. Gerade bei einer langsamen Internetverbindung hält das System somit ohne
Erklärung an. Bei Fehlern im Datenabruf, die schon durch eine restriktiv eingestellte Firewall entstehen können, erhält der Benutzer eine Fehlermeldung, eine weitere
Fehlerbehandlung ndet jedoch nicht statt. Es sollte erwähnt werden, dass die Fehlerbehandlung in Access kompliziert ist, da diese nur über GoTo-Befehle, die dann für
die gesamte Prozedur gelten, möglich ist und eine gezielte Fehlerkorrektur nicht so
einfach durchführbar ist, wie das mittels try. . . catch-Konstrukten in Programmiersprachen wie C++ oder Java möglich wäre.
Besonders hervorzuheben ist der Ansatz, referenzierte Abfragen automatisch anzulegen. Auf diese Weise ist es möglich, praktisch unbegrenzt Sichthierarchien in
Indikatordenitionen zu verwenden, ohne dass sich der Benutzer darum gesondert
kümmern müsste. Diese Technik könnte durchaus auch in anderen Systemen, die mit
36
4.3. Diskussion des bestehenden Systems
vorgespeicherten SQL-Views arbeiten, nützlich eingesetzt werden. Eventuell könnte
man noch abfragen, ob unter einem verwendeten Namen bereits eine Basistabelle
vorhanden ist, dann könnte man diese Subroutine universell einsetzen.
Auf Seiten der Darstellung gibt es einige Erweiterungsmöglichkeiten. So wäre es
wünschenswert, Indikatoren direkt mit dem Kursverlauf überlagern zu können. Falls
man TInTo auch zur Kaufauswahl von Wertpapieren benutzen möchte, müssten auch
mehrere Wertpapiere miteinander verglichen werden können. Die Erweiterung auf
weitere Intervalle setzt in jedem Fall eine Änderung des Quellcodes und der Benutzeroberäche voraus. Daten, die auÿerhalb der möglichen Intervallgrenzen liegen,
werden aus der Kurstabelle nicht mehr entfernt. Weiterhin wirkt sich einschränkend
aus, dass die Anzahl der darstellbaren Kurswerte auf 300 beschränkt ist. Bei mehr
Werten werden aus den einzelnen Werten Mittelwerte gebildet, wobei sich die Frage
stellt, ob dies für alle Indikatoren zweckmäÿig ist. Diese Frage wird in Abschnitt 6.5
nochmals behandelt. Zudem liegt hier ein
impedance mismatch
vor, da die Daten
mittels VBA aggregiert werden, anstatt mit einer SQL-Anfrage.
Das bisherige System ist zudem verhältnismäÿig statisch. Zwar werden die Tageskursdaten automatisch bei Auswahl eines Wertpapiers aus dem Internet abgerufen,
ein neuer Kurs tritt dabei aber nur an jedem Tag auf. Somit entsteht zwar ein Datenstrom, aber mit einer so geringen Frequenz, dass die Eekte, die bei der Verarbeitung
von Datenströmen auftreten, nicht zu beobachten sind. So steht ein sehr groÿer Zeitraum zur Berechnung der Indikatoren zur Verfügung.
Die Erweiterung um Intraday-Daten und einen automatischen Datenabruf stellt
daher einige neue Anforderungen. Einige der oben genannten Verbesserungsmöglichkeiten wurden unabhängig von der engeren Aufgabenstellung umgesetzt, um das
System noch besser nutzbar zu machen. Diese Erweiterungen werden im Kapitel 6
beschrieben.
37
4. TInTo
38
5. Grundlagen der
Änderungspropagierung
Sobald in einer Datenbank Sichten deniert sind, stellt sich die Frage, welche Auswirkungen Änderungen der Basisrelationen auf die abgeleiteten Sichten haben. Solange
die Sichten bei jedem Aufruf neu berechnet werden, besteht kein Problem, da Änderungen jedes Mal automatisch berücksichtigt werden. Häug ist es jedoch nützlich,
einmal berechnete Ergebnisse auf Datenträgern abzuspeichern, um diese nicht jedes
Mal neu berechnen zu müssen. Auf diese Weise kann insbesondere bei rechenintensiven Abfragen eine erhebliche Zeiteinsparung, natürlich auf Kosten von Speicherverbrauch, erreicht werden. In diesem Fall ist es aber notwendig, die abgespeicherten Daten jeweils zu aktualisieren, sobald Änderungen der Basisrelationen auftreten.
Verfahren, die solche Aktualisierungen durchführen, werden als Änderungspropagierung bezeichnet. Am einfachsten ist es, eine naive Änderungspropagierung durchzuführen, d. h. bei jeder Änderung der Basisrelationen alle materialisierten Sichten
neu zu berechnen. Dieses Verfahren ist jedoch sehr aufwendig. Eine erste Optimierung lässt sich dadurch erreichen, dass man für jede materialisierte Sicht eine Analyse
durchführt, die feststellt, von welchen Basisrelationen eine Sicht abhängt. Ein solches
Verfahren, das auch als
Relevanzanalyse
bezeichnet wird, lässt sich durch eine Top-
Down-Analyse des Abhängigkeitsgraphen durchführen. Bereits solche Verfahren werfen das Problem auf, die Änderungspropagierung automatisch nach jeder relevanten
Änderung starten zu müssen.
Doch auch eine solche optimierte naive Änderungspropagierung führt sehr häug
überüssige Rechenschritte durch. Angenommen, eine Sicht hängt nur von einer Relation ab und führt eine Pro jektion durch. Eine Änderung auspro jizierter Tupel hat
in diesem Fall überhaupt keine Auswirkung auf die abgeleitete Sicht und eine Neuberechnung ist deshalb überüssiger Rechenaufwand. Ein ähnlicher Fall liegt vor,
wenn bei einer Relation mit mehreren tausend Einträgen ein Tupel gelöscht wird.
Auch in diesem Fall wird die gesamte abgeleitete Relation, die möglicherweise genauso viele Tupel enthält, neu berechnet. Hier ist der Rechenaufwand viel höher als
benötigt. Aus diesem Grund wurden in den vergangenen rund 20 Jahren Verfahren
entwickelt, die bestrebt sind, nur die tatsächlich nötigen Änderungen durchzuführen.
Solche Verfahren werden als
inkrementelle Änderungspropagierung bezeichnet.
Die gleichen Probleme stellen sich auch bei Integritätsbedingungen, die Bedingungen
auf Basisrelationen überprüfen. Die Techniken hierfür weichen nicht wesentlich voneinander ab. Da Integritätsbedingungen jedoch im Rahmen dieser Diplomarbeit keine
Rolle spielen, wird im Folgenden auf deren Behandlung verzichtet. Eine sehr ausführliche Behandlung des Themas (allerdings unter Verwendung von Datalog anstelle der
39
5. Grundlagen der Änderungspropagierung
relationalen Algebra) ndet sich in der Dissertation von Birgit Pieper [Pie01], auf
der auch die folgenden Ausführen im Wesentlichen beruhen. Spezische Hinweise
zur relationalen Algebra wurden weiterhin den Ausarbeitungen zur Vorlesung Event
Monitoring Systems [MB07] entnommen.
Zum Thema inkrementelle Änderungspropagierung ist eine Vielzahl von Veröffentlichungen erschienen. Als Beispiele seien hier [BLT86], [CW91],[QW91], [GMS93],
[CLS00] und [BM04] genannt. Die Erforschung dieses Themas ist seit vielen Jahren
auch ein Schwerpunkt der Arbeitsgruppe intelligente Datenbanken am Institut für
Informatik der Universität Bonn und daher Inhalt mehrerer Diplomarbeiten und Dissertation dieser Arbeitsgruppe, wobei hier neben [Pie01] unter anderem auch [Gri97]
und [Beh04] zu nennen sind.
5.1. Inkrementelle Regeln für die RA
Eine grundlegende Überlegung zur inkrementellen Änderungspropagierung ist, durch
Analyse der Denitionsregeln von Views festzustellen, welche Änderungen durchgeführt werden müssen. Zunächst führt man dazu Hilfsrelationen bzw. -sichten ein, die
als
Delta-Relationen
bzw.
Delta-Sichten
bezeichnet werden und genau diejeni-
gen Tupel enthalten, die entfernt oder hinzugefügt werden müssen. Zu jedem Literal
R
im Rumpf einer Regel sind Delta-Relationen für Einfügungen und Löschungen zu
erstellen, die als
R−
und
R+
bezeichnet werden. Diese Sichten lassen sich wiederum
Delta-Regeln bezeichnet werden.
mittels Regeln denieren, die als
Ist beispielsweise eine Sicht
S
für eine Selektion aus
R
deniert durch
S = σcond (R)
(5.1)
dann kann man Delta-Sichten zu dieser Regel erstellen, die Einfügungen und Löschungen in
S
R
berücksichtigen. Man stellt fest, dass ein Tupel aus
eingefügt wird, wenn es die Bedingung
cond
R
genau dann in
erfüllt, ebenso kann ein Tupel aus
S
nur dann entfernt werden, wenn es diese Bedingung schon erfüllt hatte. Somit lauten
die entsprechenden Delta-Regeln:
S + = σcond (R+ )
(5.2)
S − = σcond (R− )
Wobei
S+
die in
S
einzufügenden und
S−
die aus
S
zu löschenden Tupel enthält.
Die Delta-Regeln für die Selektion gehören dabei zu den einfachsten Regeln, da die
Selektion keine Duplikate erzeugen kann und zudem ein unärer Operator ist, der sich
nur auf eine Relation bezieht.
Sobald sich ein Operator auf zwei Relationen bezieht, also binär ist, dann tritt
ein weiteres Problem auf: Jede Delta-Regel bezieht sich auf ein Literal, welches als
R±
referenziert wird. Alle anderen Literale werden aber ebenso benötigt, da nur im
Zusammenhang mit diesen die Berechnung durchgeführt werden kann. Sei beispielsweise die Denition einer Sicht
40
S
gegeben, die den Schnitt zweier Relationen
Q
und
5.1. Inkrementelle Regeln für die RA
R
berechnet:
S =Q∩R
Wird nun ein Tupel in
(5.3)
Q eingefügt, dann wird dieses nur dann in S eingefügt, wenn
R bereits vorhanden ist. Während ein Tupel in Q eingefügt
das selbe Tupel auch in
wird, kann aber auch zum gleichen Zeitpunkt (in der gleichen Transaktion) ein Tupel
in
R
eingefügt werden, dass berücksichtigt werden müsste, es kann aber ebenso gut
gleichzeitig ein Tupel aus
R
R
gelöscht werden. Es wird also der neue Zustand von
benötigt, der aber zu diesem Zeitpunkt noch gar nicht vorliegen kann, da der
neue Datenbankzustand gerade erst berechnet wird. Diese Situation lässt sich jedoch
durch eine Simulation des neuen Zustands mittels Regeln beheben. Für jede Relation
R
wird dafür eine sogenannte
Transitionsregel eingeführt:
Rnew = R\R− ∪ R+
Möchte in den Delta-Regeln sowohl Änderungen in
R
(5.4)
als auch in
Q
berücksichtigen,
so muss stets der Schnitt mit der neuen Relation erfolgen:
S + = Q+ ∩ Rnew
S + = Qnew ∩ R+
(5.5)
S − = Q− ∩ Rnew
S − = Qnew ∩ R−
Setzt man in diese Regeln die Denition der Transitionsregel ein, löst die Vereinigungssemantik auf und wendet das Distributivgesetz an, dann erhält man zwei
äquivalente Regeln:
S + = Q+ ∩ R\R−
∪ R+ ∩ Q\Q−
∪ Q+ ∩ R+
S − = Q− ∩ R\R−
∪ R− ∩ Q\Q−
∪ Q− ∩ R−
Eine weitere Schwierigkeit liegt dann vor, wenn ein Operator
duplikaterzeugend
(5.6)
wir-
ken kann, das heiÿt er kann aus einer zunächst duplikatfreien Menge eine Menge,
∪ Duplikate, falls
Pro jektion π erzeugt
die Duplikate enthält, erzeugen. So erzeugt die Mengenvereinigung
ein Tupel in beiden vereinigten Relationen vorliegt. Auch die
Duplikate, falls mehrere Tupel in herausprojizierten Attributen unterschiedlich, in
verbleibenden Attributen aber gleich sind. In den Delta-Regeln ist sicherzustellen,
dass keine Fakten eingefügt oder gelöscht werden, die bereits in der jeweiligen Sicht
vorhanden sind oder noch über einen alternativen Ableitungsweg verfügen. Für Einfügungen kann dies mittels einer nachgeschalteten Duplikate-Eliminierung erfolgen,
die bei Datenbanksystemen ohnehin aufgrund der duplikaterzeugenden Operationen
erforderlich ist. Bei Löschungen jedoch reicht dies nicht aus, da festgestellt werden
muss, ob ein Tupel über mehrere Ableitungswege verfügt. Gupta et al. [GMS93] haben hierzu einen
Counting-Algorithmus vorgeschlagen. Bei diesem Verfahren wird
jede Relation um ein Zählattribut ergänzt, das für jeden Ableitungsweg um eins erhöht wird. Bei Löschungen wird dieses Attribut um eins dekrementiert. Erst wenn
41
5. Grundlagen der Änderungspropagierung
der Zähler null ist, wird das Tupel physisch gelöscht. Es ist aber auch möglich, durch
Überprüfung des neuen Zustandes mittels der Transitionsregeln alternative Ableitungswege zu nden. So lautet dann die Delta-Regel für die Regel
P = Q∪R
wie
folgt:
P − = Q− \ R ∪ R+
∪ R− \ Q ∪ Q+
∪ R− ∩ Q−
Durch die Mengendierenzen ist jeweils sichergestellt, dass ein aus
nicht auch noch gleichzeitig in
R
oder
R+
(5.7)
Q gelöschtes Tupel
vorhanden ist. Der Mengenschnitt im
letzten Term berücksichtigt dann noch diejenigen Tupel, die aus beiden Relationen
gleichzeitig gelöscht werden, so dass nicht zu wenig Tupel gelöscht werden.
Liegen in einer Regelmenge Regeln vor, die aus mehreren Operationen zusammengesetzt sind, so kann die Delta-Regelmenge dadurch erstellt werden, dass zunächst
die einzelnen Regeln in Regeln mit einem Grundoperator zerlegt werden. Dadurch
erhält man eine Regelmenge, die in den Regelrümpfen jeweils nur einen Operator
enthält. Auf diese lassen sich dann die Transformationen für die Grundoperatoren
anwenden. Die Menge der Regeln lässt sich anschlieÿend wieder durch Einsetzen und
Äquivalenztransformation reduzieren.
Auch für Sichten mit Aggregationen sind Delta-Regeln möglich. Obwohl bereits
viele Publikationen zur inkrementellen Änderungspropagierung erschienen sind, sind
bisher erst wenige Publikationen zum Thema Änderungspropagierung für Aggregatfunktionen erschienen. Zu erwähnen ist hier der Artikel von Gupta et al. [GMS93],
in dem bereits erste Ansätze geliefert werden. Insbesondere wird der oben bereits
erwähnte Zählalgorithmus dazu eingesetzt, leere und somit zu löschende Gruppen
zu erkennen. Die Behandlung der Änderungen von Aggregatfunktionen beschränkt
sich jedoch im Wesentlichen auf die Summen und die Zählfunktion selbst. Eine ausführliche Behandlung dieses Themas ist ein Ziel dieser Arbeit und wird im Abschnitt
7.2.2 durchgeführt.
5.2. Auswertungsstrategien
Die Delta-Regeln geben lediglich an, welche Änderungen durchzuführen sind, führen
diese aber nicht aus. Zur Ausführung der eigentlichen Änderungen sind Auswertungsstrategien erforderlich. Es lassen sich zwei grundlegende Strategien identizieren:
•
Bei der
Pulling- oder Top-Down-Strategie werden für jede Sicht die Del-
ta-Regeln aufgestellt und so lange die Regeldenitionen ineinander eingesetzt
(expandiert), bis sich jede Delta-Sichtdenition nur noch auf Basisrelationen
und die Delta-Relationen dieser Basisrelationen bezieht. Anschlieÿend liegen
die Delta-Mengen für jede Sicht vor, so dass die in Delta-Mengen enthaltenen
Tupel aus der jeweiligen Sicht entfernt oder in diese eingefügt werden können.
•
Bei der
Pushing- oder Bottom-Up-Strategie wird der Propagierungspro-
zess von unten durchgeführt, beginnend mit den untersten Sichten im Abhängigkeitsgraph, die direkt von den Basisrelationen abhängen.
42
5.2. Auswertungsstrategien
Der Vorteil der Pulling-Strategie liegt darin, dass diese zielgerichtet für benötigte
Sichten durchgeführt wird. Allerdings ist es wichtig, dass die Anfragekomponente der
Datenbank erkennen kann, ob mehrfach Zugrie auf die selben Zwischenergebnisse
erfolgen, da sonst Ableitungen wiederholt werden.
Bei der Bottom-Up-Strategie fällt das Problem der Mehrfachberechnung weg, sofern die Berechnungsergebnisse gespeichert werden. Jedoch werden bei dieser Methode möglicherweise Änderungen für irrelevante Sichten durchgeführt. Diesem Umstand
kann durch eine geeignete Relevanzanalyse abgeholfen werden.
Bei der Verwendung der Bottom-Up-Strategie ist darauf zu achten, dass der Abhängigkeitsgraph so von unten nach oben durchlaufen wird, dass verwendete DeltaRelationen stets vollständig vorliegen, bevor sie als Quellrelationen in höheren Ebenen der Sichtenhierarchie verwendet werden. Dies wirft dann Probleme auf, wenn
rekursive Sichtdenitionen auftreten, die allerdings hier nicht behandelt werden sollen.
Eine Mischung aus beiden Verfahren stellen die von Griefahn sowie Behrend und
Manthey entwickelten Methoden auf der Grundlage von Magic Sets, einer Methode
zur Regeloptimierung, dar ([Gri97], [Beh04], [BM04]).
Wesentlich ist die Frage, wie diese Strategien implementiert werden können. Bei der
Top-Down-Strategie kann die Implementierung beispielsweise dadurch erfolgen, dass
in festgelegten Zeitintervallen die jeweiligen Sichtaktualisierungen abgefragt werden.
Eine andere Möglichkeit, die sich für die Bottom-Up-Strategie unmittelbar anbietet, aber in abgewandelter Form auch für Top-Down-Strategie anwendbar ist, besteht in der Verwendung von
Triggern. Als Trigger 1
bezeichnet man Aktionen, die
automatisch nach Ereignissen, wie Einfügungen, Löschungen oder auch nach Zeitintervallen in der Datenbank ausgelöst werden. In diesem Zusammenhang hat sich
das Konzept
eignis
ECA, eventconditionaction
(event)
durchgesetzt: Ausgehend von einem Er-
wird bei Erfüllung einer Bedingung
(condition)
eine Aktion
(action)
durchgeführt. Eine einfache, prototypische Triggerspezikation wäre also:
ON +r_plus(a1,...,an)
IF t(a1,...an,b1,...,bm)
DO -s(a1,....an)
Diese Schreibweise ist an das DRC angelehnt, wobei der Bezeichner vor der Klammer die Relationen und die Argumente in den Klammern die Attribute bezeichnen
R+ ein
in T mit
soll. Die obige Triggerdenition bedeutet also: Sobald in
Tupel mit den
a1 , . . . , an eingefügt wird, prüfe, ob ein Tupel
a1 , . . . , an , b1 , . . . , bm existiert. Wenn dies der Fall ist, so lösche das
den Attributen a1 , . . . , an . Die Attribute bj sollen in diesem Fall
den Attributen
Attributen
Tupel aus
S
mit
für die Attribu-
te stehen, welche nicht im eingefügten Tupel enthalten sind, aber zur Prüfung der
Bedingung nötig sind.
Es ist nun leicht, für jede Delta-Sicht einen solchen Trigger zu denieren: Der Regelkopf wird dabei in den
1
DO-Teil, R−
und
R+
in den
ON-Teil
und die Residuen
engl.: Auslöser, auch Abzug von einer Schusswae
43
5. Grundlagen der Änderungspropagierung
in den
IF-Teil
übernommen. Da ein Trigger automatisch den nächsten Trigger in
einer Art Kettenreaktion auslösen kann, wird damit automatisch eine Bottom-UpPropagierung erreicht. Bei der Verwendung von Triggern ist darauf zu achten, in
welchem Zustand die referenzierten Relationen vorliegen. Wurde der Trigger für eine referenzierte Relation bereits ausgelöst, so liegt diese bereits im neuen Zustand
vor. Eventuell kann es dann notwendig sein, den alten Zustand zu simulieren, was
wiederum durch eine Transitionsregel möglich ist. Weitere Probleme können bei rekursiven und insbesondere negativ rekursiven Sichtdenitionen der Form
R = S\R−
auftreten. Diese Problematik wird ausführlich in der Dissertation von Pieper [Pie01]
behandelt.
Zuletzt ist es noch notwendig, dafür Sorge zu tragen, dass bei Integritätsverletzungen die Änderungspropagierung abgebrochen wird und der alte Zustand wieder
hergestellt wird. Zu diesem Zweck müssen die Trigger noch in einer gemeinsamen
Transaktion ausgeführt werden, die bei Integritätsverletzungen abgebrochen wird.
Dies kann wiederum durch eigene Trigger erreicht werden, die die Integritätsregeln
prüfen und den Transaktionsabbruch im Aktionsteil enthalten.
Aus diesen Ausführungen erkennt man bereits, dass es sich bei der Änderungspropagierung um ein kompliziertes Thema handelt. Nützlich wäre zur Vereinfachung des
Verfahrens ein automatischer Regelcompiler, der die Regeln zur Änderungspropagierung sowie die Trigger automatisch erstellt.
Tatsächlich wird die Behandlung der Änderungspropagierung auf Finanzdatenströmen wieder einfacher, da hier keine Löschungen in den Basistabellen auftreten werden. Die Durchführung der Änderungspropagierung wird in TInTo dadurch gesteuert,
dass die Pulling-Komponente auch gleich die Änderungspropagierung anstöÿt. Das
genaue Verfahren wird in Kapitel 8 beschrieben.
44
6. Erweiterungen von TInTo
Neben der eigentlichen Aufgabe dieser Diplomarbeit, ein inkrementelle Änderungspropagierung in das bestehende System zu integrieren, wurden zunächst einige davon
unabhängige Erweiterungen vorgenommen, die den Bedienkomfort, die Geschwindigkeit und die Korrektheit der Indikatorberechnung verbessern sollten. Im Folgenden
werden die wichtigsten durchgeführten Änderungen skizziert.
6.1. Änderungen an der Benutzeroberäche
Zunächst wurden alle Beschriftungen der Benutzeroberäche ins Englische übersetzt.
Dies war dadurch motiviert, dass das System auch einem internationalen Publikum
vorgestellt wurde (s. [BD07]).
Inhaltliche Änderungen betrafen zunächst Kombinationsfelder zur Auswahl von
Auösung und Zeitraum. Im existierenden TInTo-System waren zur Auswahl von
Gruppierung und Zeitraum nur die Befehlsschaltächen monatlich, Quartal sowie 1, 3 und 5 Jahre vorgesehen. Über die Auswahl der entsprechende Schaltäche
wurden sowohl der Zeitraum, aus dem die Kursdaten angezeigt wurden, als auch
die Auösung festgelegt, also die Anzahl der Werte, die eine Kerze im Diagramm
bilden. So wurden beispielsweise für einen Zeitraum von einem Jahr stets die Werte eines Monats zu einer Kerze zusammengefasst. Für den Benutzer kann es aber
auch durchaus wünschenswert sein, beide Werte getrennt einzustellen, beispielsweise
um die Volatilität
1
besser einzuschätzen zu können. Zudem erschwert die Verwen-
dung von Befehlsschaltächen Erweiterungen der Auswahlmöglichkeiten, da für jede
Auswahlmöglichkeit eine zusätzliche Schaltäche hinzugefügt werden müsste. Dies
wiederum ist durch den zur Verfügung stehenden Platz deutlich eingeschränkt.
Um eine getrennte Auswahl für Zeitraum und Frequenz zu ermöglichen, wurden im
Hauptfenster zwei sogenannte
Kombinationsfelder angelegt, aus denen der Benut-
zer seine Auswahl treen kann. Der Name Kombinationsfeld (engl. textbfdropdownbox) rührt daher, dass sich in diese Felder sowohl freier Text eintragen lässt, sich aber
auch durch Anklicken eines rechts angezeigten Pfeils eine Liste önet, die die Auswahl aus einer vorgegebenen Werteliste ermöglicht. Der Vorteil der freien Texteingabe
konnte in dieser Anwendung zwar nicht genutzt werden (und wurde daher auch deaktiviert), es blieb jedoch der Vorteil, ein Steuerelement zur Verfügung zu haben, das
bei Nichtbenutzung nur einen geringen Platz einnimmt, im Bedarfsfall jedoch eine
groÿe Anzahl von Auswahlmöglichkeiten zur Verfügung stellt.
1
Schwankungsbreite eines Wertpapiers
45
6. Erweiterungen von TInTo
Ein weiterer Vorteil bestand darin, dass Kombinationsfelder in Access Daten direkt aus Tabellen oder Abfragen beziehen können, was die zukünftige Erweiterbarkeit erheblich vereinfacht: Statt wie in der ursprünglichen Version die Anzahl der
zu lesenden Kurse für eine Auswahl im Quellcode eines Moduls festzulegen, werden
nun die entsprechenden Zahlen in einer Tabelle hinterlegt. So wurden in der Tabelle
TTimeRange (Abb. 6.1) sowohl die Auswahlmöglichkeiten an Zeiträumen nebst der
Anzahl der zu berücksichtigenden Kurswerte hinterlegt, als auch ein boolescher Wert,
der angibt, ob es sich bei dem ausgewählten Zeitraum um einen Intraday- oder einen
Tageskurs-Bereich handelt (siehe auch Abschnitt 6.4). In der Tabelle
TResolution
(Abb. 6.2) wurden die verschiedenen Auösungen nebst dem entsprechenden SQLGROUP-BY-Ausdruck hinterlegt. Zum Einfügen weiterer Zeiträume genügt es, die
entsprechenden Datensätze in die Tabellen einzufügen. Die zur Verfügung stehenden
Auösungen werden in Abhängigkeit von den Zeiträumen festgelegt. Bei Auswahl
eines Zeitraums aus dem entsprechenden Kombinationsfeld wird mittels einer Ereignisaktion auch die Auswahlmöglichkeit des anderen Kombinationsfelds neu gesetzt:
1
2
3
4
5
6
7
8
9
10
11
Private Sub TimeRange_AfterUpdate()
If Me.TimeRange.Column(2) Then
Me.Frequency.RowSource = "SELECT FriendlyName," & _
"GroupDays, Intraday, GroupBy FROM TResolution" & _
"WHERE Intraday = True;"
Else
Me.Frequency.RowSource = "SELECT ... "‘ & _
"WHERE Intraday = False;"
End If
Me.Frequency.Requery
End Sub
Ob es sich bei dem ausgewählten Zeitraum um einen Tageskurs- oder EOD-Zeitraum
handelt, kann mittels der zweiten Spalte des Kombinationsfelds festgelegt werden
(Abfrage in Zeile 2). Wie man sieht, wird in Access als Datenquelle einfach ein SQLAusdruck übergeben. Dessen Ergebnis wird dann im Kombinationsfeld angezeigt.
Über das Optionsformular und die Registerkarten Resolution und Time range
kann der Benutzer Änderungen der Auösungen und Zeiträume auch selbst durchführen, ohne in den Quellcode eingreifen zu müssen (s. Abb. 6.4).
In der bisherigen Version war der aktuelle Schlusskurs lediglich aus der letzten
angezeigten Kerze des Charts oder über die Kurstabelle, welche im Indikatordenitions-Fenster aufgerufen werden kann, ersichtlich. Für ein dynamisches System,
welches fortlaufend aktuelle Kursdaten abfragt, ist aber eine genaue Kursanzeige
wünschenswert. Auf vielen Webseiten, die technische Charts zur Verfügung stellen,
wird der jeweils letzte Kurs durch einen zusätzlichen
Eintrag auf der Skala
der
y-Achse markiert, auch wenn dieser nicht dem Raster der Skala entspricht. Diese
Anzeige wurde auch in TInTo eingebaut. Auf der y-Skala wandert praktisch der
aktuelle Wert auf und ab. Die Anzeige wurde mittels der ChartDirector-Methode
addLabel implementiert. Im Verlauf der Chart-Neuzeichnung der Änderungspropa-
46
6.1. Änderungen an der Benutzeroberäche
Abbildung 6.1.: Die Tabelle TTimeRange
Abbildung 6.2.: Die Tabelle TResolution
gierung (mehr dazu in Kap. 8) wird die Methode
mc.yAxis().addLabel last, last
aufgerufen, wobei
mc
das ChartDirector-Ob jekt ist. Die beiden Parameter geben die
Position an der Skala und die Beschriftung der Marke an. In diesem Fall sind beide
Parameter deshalb identisch.
Zusätzlich wurde noch eine rein
textuelle Anzeige
im linken Teil des TInTo-
Hauptformulars eingefügt: In einer tabellarischen Darstellung sind die jeweils letzten
abgefragten Kurse abzulesen. Die Anzeige wird bei jedem neuen Datenabruf aktualisiert und gibt so dem Benutzer ein Feedback, dass die Kursabfrage erfolgte, auch
dann, wenn dies nicht aus dem Chart ersichtlich ist, beispielsweise wenn der Handel
bereits beendet wurde. Angezeigt werden jeweils die letzten acht Kurswerte nebst
Abrufzeit. Da
Yahoo! zwar
sekundengenaue Werte, aber die Zeit ohne Sekunden zu-
rückgibt, werden diese aus der Systemzeit entnommen. Während jedes Datenabrufs
wird also innerhalb der Routine
saveRTQuote
folgende Anweisung durchgeführt:
47
6. Erweiterungen von TInTo
With Forms.main.Controls("LastQuotes")
.AddItem symbol & ";" & CDate(Replace(sTime, ".", ",")) &_
":" & Format(Second(Now()), "00") & ";" & sLast, 0
If .ListCount > 8 Then .RemoveItem 8
End With
Aus den zur Verfügung stehenden Variablen für Symbol, Zeit und Kurswert wird ein
Semikolon-separierter String erstellt, der dann als Eintrag in das Listenfeld übergeben wird. Enthält das Listenfeld schon mehr als acht Einträge, so wird der älteste
Eintrag entfernt. Leider wird bei jeder Aktualisierung die Anzeige vollständig neu
auf den Bildschirm gezeichnet, was auf einigen Rechnern und einer hohen PollingFrequenz ein unangenehmes Flackern hervorruft. An dieser Stelle besteht derzeitig
noch Verbesserungsbedarf.
Eine ebenfalls von verschiedenen Webseiten angebotene Möglichkeit besteht darin,
in einen angezeigten Chart
Linien von Hand (mittels der Maus) einzeichnen zu kön-
nen. Diese Möglichkeit ist dann wichtig, wenn Trendkanäle und andere Formationen,
die eher dem menschlichen Auge auallen, als dass sie einfach mathematisch fassbar
sind, gekennzeichnet werden sollen. Zu diesem Zweck wurde eine Befehlschaltäche,
die durch das Symbol einer diagonalen Linie gekennzeichnet ist, eingefügt. Wird diese Schaltäche betätigt, so wird der erste Mausklick im Chartfenster als Startpunkt
einer Linie gesetzt, der zweite als deren Endpunkt. Auf diese Weise können mehrere Linien in den bestehenden Chart eingefügt werden. Bei jeder Aktualisierung des
Charts werden die Linien wieder aus dem Chart entfernt. Das Zeichnen der Linie
geschieht mittels des MouseDown und des MouseUp-Ereignisses des ChartDirectors:
Private Sub ChartViewer_MouseDown(
Button As Integer, Shift As Integer,
x As Single, Y As Single)
startX = x
startY = Y
End Sub
Private Sub ChartViewer_MouseUp(...)
If Me.DrawModeOnOff Then
Chart.DrawLine startX, startY, (x), (Y)
End If
End Sub
Bei Betätigung der Maustaste im ChartDirector-Fenster wird das erste Ereignis ausgelöst. Dieses speichert in zwei globalen Variablen die aktuelle Position der Maus.
Wird die Maustaste wieder losgelassen, so wird von der Startposition bis zur aktuellen Position die Linie in den Chart gezeichnet. Vorher wird die boolesche Variable
DrawModeOnOff
abgefragt, die durch die Schaltäche umgeschaltet wird.
Daneben steht dem Benutzer nun die Möglichkeit oen, den angezeigten Chart
nebst eventuell angezeigter Indikatoren als
Grak abzuspeichern. Diese Option ist
dann nützlich, wenn man Charts für die spätere Verwendung sichern möchte oder sie
48
6.1. Änderungen an der Benutzeroberäche
anderen zugänglich machen möchte, die nicht über das TInTo-System verfügen. Die
Funktion ist über die Schaltäche Save Picture... verfügbar. Wird die Schaltäche
betätigt, so önet sich ein Dialog, in welchem der Benutzer den Dateinamen angeben
kann. Vorgegeben wird hier das Wertpapierkürzel nebst dem aktuellen Datum und
Uhrzeit, es kann aber auch jeder andere Name angegeben werden. Mögliche Grakformate sind JPEG oder PNG. Die Methode zum Abspeichern ist im ChartDirector
bereits eingebaut und muss nur noch über die ChartDirector-Methode
DateiName
makeChart
aufgerufen werden. Den Dateityp bestimmt der ChartDirector anhand
der Dateiendung. Der Datei-Speichern-Dialog hingegen fehlt in Access. Da er aber oft
benötigt wird, existieren im Internet zahlreiche Beispiele für eine Klasse, die mittels
2
API-Aufrufen dieses Fenster aufruft.
Der Code hierfür ist sehr umfangreich, so dass
hier vom Abdruck abgesehen wird.
Im Zusammenhang mit dem automatischen Abruf von Intraday-Daten sollte der
Benutzer die Möglichkeit haben, die Häugkeit des Abrufs einzustellen und festzulegen, wie lange die abgerufenen Daten gespeichert bleiben sollen. Daneben kann es
aufgrund von Systemabstürzen, Übertragungsfehlern bei der Kursabfrage und ähnlichen Ereignissen dazu kommen, dass die Kursdaten in einem fehlerhaften Zustand in
der Datenbank gespeichert werden. Daher sollte es für den Benutzer die Möglichkeit
geben, das System wieder in den Ursprungszustand zurücksetzen zu können.
Um den Aufruf dieser Funktionen zu ermöglichen, gleichzeitig aber die Übersichtlichkeit im Hauptfenster zu wahren, wurde ein
Optionsformular
(Abb. 6.4) ein-
geführt. Es ist unter der Schaltäche Optionen im Hauptfenster aufrufbar. Das
Optionsformular wiederum ist durch
Registerkarten
strukturiert. Es umfasst folgen-
de Funktionen:
•
Festlegung der Abruffrequenz
(Polling frequency),
mit der die Daten aus dem
Internet abgerufen werden können. Vorgegeben sind hier 10, 30, 60, 120 und
3
240 Sekunden, es können aber auch andere Werte frei eingegeben werden.
•
Festlegung des Zeitraums, nach dem die Intraday-Daten wieder aus der Datenbank gelöscht werden. Die Angabe erfolgt in Tagen, kann aber auch auf den
Wert Never eingestellt werden, so dass die Daten nie aus der Datenbank gelöscht werden. Bei Abruf neuer Daten aus dem Internet wird aus der Kongurationstabelle abgefragt, nach welcher Zeit die Daten gelöscht werden sollen. Anschlieÿend wird dementsprechend die Löschabfrage
DeleteOldQuotes
aus-
geführt.
•
Rücksetzen der Datenbank in den ursprünglichen Zustand: Nach Betätigen der
Schaltäche Reset TInTo werden alle Kursdaten, Wertpapierkürzel und Suchergebnisse der Wertpapiersuche entfernt. Vorher erscheint eine Sicherheitsabfrage.
2
3
z. B.:
http://www.activevb.de/tipps/vb6tipps/tipp0368.html
Solange diese dem Wertebereich des Long Integer genügen, dies sollte aber in der Praxis stets der
Fall sein.
49
6. Erweiterungen von TInTo
Abbildung 6.3.: Das neue TInTo-Fenster mit Erweiterungen: 1) Die Kombinationsfelder zur Auswahl von Zeitraum und -auösung, 2) Die textuelle
Kursanzeige, 3) Die Anzeige des aktuellen Kurses an der zweiten yAchse, 4) Die Zeichenmöglichkeit für Linien, 5) Die Schaltäche zum
Abspeichern der Grak, 6) Schaltäche für das Optionsmenü
50
6.1. Änderungen an der Benutzeroberäche
•
Initialisieren des Hauptfensters: Nachdem ein Fehler beim Zeichnen des Charts
aufgetreten ist (z. B. durch eine fehlerhafte Indikatordenition) wird bisweilen
das Hauptfenster nicht mehr korrekt aufgebaut. Um TInTo deswegen nicht neu
starten zu müssen, kann über Init TInTo das Fenster neu initialisiert werden.
•
Leeren der während der Indikatorberechnung erzeugten materialisierten Sichten: Für das Leeren der temporären Tabellen (materialisierte Sichten) werden
alle Tabellen der Datenbank durchlaufen, die mit dem Präx tmp beginnen
und eine Löschabfrage darauf durchgeführt. Dies ist insbesondere dann nützlich, wenn man die Datenbank komprimieren möchte.
•
Rücksetzen der Simulation: In der Simulationsversion von TInTo werden alle
Simulationsdaten als unbenutzt markiert.
•
Einlesen historischer Intraday-Kurse: Hiermit können aus einer speziellen Datei
historische Intraday-Kurse eingelesen werden. Die Datei muss dazu genauso
aufgebaut sein, wie der von
Yahoo! gelieferte
String für den Intraday-Abruf.
Die einzelnen Rückgabestrings sind dabei durch Zeilenumbrüche zu trennen.
Die Datei wird zeilenweise eingelesen und mit der gleichen Methode wie beim
Internet-Abruf geparst und abgespeichert.
•
Hinzufügen und Ändern von Zeiträumen und Frequenzen für die Auswahlfelder
des Hauptfensters mittels der Registerkarten Resolution und Time range.
Auf diesen Registerkarten benden sich Listenfelder mit den entsprechenden
Tabellen, so dass der Benutzer die Daten hier sehr einfach ändern kann.
Die Einstellungen des Optionsfensters werden in der Tabelle
TConfig
gespeichert.
Dort wird auch beim Schlieÿen des Systems die aktuelle Fenstergröÿe abgespeichert.
Beim nächsten Start wird diese ausgelesen und das Hauptfenster entsprechend dimensioniert.
Die Verwendung eines eigenen Optionsfensters entspricht dabei weiterhin Hübels
Alles-auf-einen-Blick` Ansatz (sic!), demzufolge möglichst alle Funktionen in einem
Fenster untergebracht werden sollen ([Hüb07], S.70), ausgenommen administrative
und Sonderfunktionen, die in diesem Fall jedoch vorliegen. Gerade die Tatsache,
dass diese Funktionen im Allgemeinen nur selten benutzt werden, rechtfertigt deren
Auslagerung.
Um Tests von TInTo auch auÿerhalb der Börsenzeiten oder ohne Internetanschluss
TSimulation angelegt. Diese enthält
getRTQuote in der Timer-Routine
des Formulars TIntradayTimer in getSimulatedQuote um, so werden die Daten
zu ermöglichen, wurde eine Simulationstabelle
einige Testdatensätze. Ändert man den Aufruf
statt aus dem Internet aus dieser Tabelle eingelesen. Einmal verwendete Datensätze
werden im Attribut
used
als benutzt markiert. Mittels des Optionsfensters lassen
sich alle Testdaten als unbenutzt markieren.
51
6. Erweiterungen von TInTo
Abbildung 6.4.: Das Optionsfenster von TInTo, hier mit der Registerkarte Intraday
6.2. Umstellung des HTTP-Abrufs auf ActiveX
Der HTTP-Abruf, also der Abruf von Daten aus dem Internet mittels des HypertextTransfer-Protokolls, war in der bisherigen Version in einer selbst geschriebenen Klasse
clsHTTP implementiert. Diese verwendete Aufrufe der API (Application Programming Interface) von Windows. Obwohl die Klasse sehr sorgfältig programmiert war
und auch Fehler abng, so lag doch ein Nachteil darin, dass die Klasse in Visual Basic
for Applications implementiert war und bei jedem Aufruf neu interpretiert wurde.
Bei einer erhöhten Polling-Frequenz kam es dabei immer wieder zu Fehlermeldungen,
insbesondere zum Fehler Proxy-Error. Auÿerdem dauerte der Abruf recht lange.
Als Alternative bot sich das Windows-HTTP-Ob jekt an. Dieses kapselt bereits
den kompletten HTTP-Abruf und liegt schon fertig kompiliert vor. An allen entsprechenden Programmstellen wurde nun der Aufruf der Klasse
clsHTTP
durch einen
Aufruf des Windows-HTTP-Objekts ersetzt. Aus
cHTTP.HttpURL = "http://finance.yahoo.com..."
cHTTP.ConnectToHTTPHost
c = cHTTP.WriteHTTPDataToString
wurde
wHTTP.Open "GET", "http://finance.yahoo.com..."
wHTTP.send
c = wHTTP.responseText
Dadurch wurde der Abruf beschleunigt und die genannten Fehlermeldungen traten
nicht mehr auf.
Allerdings muss das Ob jekt (bzw. seine Datei winhttp.dll) auf dem Rechner vorhanden und registriert sein, um die neue Funktionalität nutzen zu können. Bei den
neueren Windows-Versionen wird dieses Ob jekt bereits mitgeliefert.
52
6.3. Wertpapiersymbolsuche mittels XML
6.3. Wertpapiersymbolsuche mittels XML
Möchte der Benutzer ein neues Wertpapier zu seinem Portofolio in TInTo hinzufügen, so sucht das Programm erst nach einer Liste der Wertpapierkürzel, die auf
das jeweilige Wertpapier zutreen. Dies ist schon deshalb nötig, da der Kursanbieter
Yahoo! verschiedene
Börsenplätze anbietet, an denen ein Wertpapier gehandelt wer-
den kann. Je nach Börsenplatz können sich die Kurse unterscheiden. Den einzelnen
Wertpapierkürzeln werden dabei Suxe angehängt, die den jeweiligen Börsenplatz
kennzeichnen. Somit können die Wertpapierkürzel kaum anders in das System eingegeben werden. Bisher erfolgte dieser Abruf dergestalt, dass per HTTP-Aufruf eine
Webseite im HTML-Format heruntergeladen wurde. Dieses HTML-Dokument wurde
anschlieÿend in einen selbst programmierten Parser geleitet und so die Wertpapierinformationen extrahiert. Da sich die Struktur der HTML-Datei rasch ändern kann,
z. B. aus reinen Designgründen (die HTML-Datei ist ja auch eher für die direkte Anzeige im Browser vorgesehen), birgt diese Methode Unsicherheiten. Auÿerdem
kann die Suche bisweilen so viele Suchkürzel zurückliefern, dass das Ergebnis auf
mehrere Seiten verteilt wird. Programme wie beispielsweise der
Yahoo! Widget,
ein
kleines Tool zur textuellen Anzeige von Kursen, beziehen daher ihre Suchergebnisse
als XML-Dokument. XML ist ein Standard für ein strukturiertes Dateiformat, in dem
die Daten hierarchisch in Elementen abgelegt werden. Auf die einzelnen Einträge
kann über geeignete Programmbibliotheken zugegrien werden.
In TInTo wurde nun der HTTP-Aufruf entsprechend verändert. Der dabei zurückerhaltene String stellt ein komplettes XML-Dokument dar, ein Beispiel ist im Listing
6.1 dargestellt. Der String wird einer Ob jektinstanz der Programmbibliothek
soft XML 4.0
Micro-
übergeben. Diese parst den String und baut einen internen Baum auf.
Dieser wird im Programm durchlaufen und die einzelnen Kürzel abgefragt:
Set xmlRoot = xmlDoc.documentElement
Set xmlFIList = xmlRoot.selectNodes(strNode)
For Each xmlFinNodes In xmlFIList.
If xmlFinNodes.selectNodes("./name/short").length > 0 Then
DoCmd.RunSQL "INSERT INTO tmpSearchResults VALUES(’" & _
cSQL(xmlFinNodes.Attributes(0).Text) & "’, ’" & _
cSQL(xmlFinNodes.selectSingleNode("./exchange").Text) & "’, ’" & _
cSQL(xmlFinNodes.selectSingleNode("./name/short").Text) & "’);"
End If
Next
’Gibt es noch weitere Seiten? Wenn ja neue Iteration
If xmlRoot.selectSingleNode("./symLookup/navlink").hasChildNodes Then
i = Val(xmlRoot.selectSingleNode("./symLookup/navlink/currentPage")._
Attributes(0).Text)
j = Val(xmlRoot.selectSingleNode("./symLookup/navlink/currentPage")._
Attributes(1).Text)
If i > j Then intPage = intPage + 1
End If
53
6. Erweiterungen von TInTo
Listing 6.1: Ein Ausschnitt aus der XML-Rückgabe für die Suche nach Microsoft
<page>
<settings page="symlookup">
<experiment id="NULL"/> <ip/>
<FreeRTQuotes>
<enableFreeRTQuotes>no</enableFreeRTQuotes>
<enableFreeRTQuotesExtHours>no</enableFreeRTQuotesExtHours>
</FreeRTQuotes>
<chartpref mode="classic"/>
<marketIndices>
<entry>
<symbol>^DJI</symbol>
<display>Dow</display>
</entry>
<entry>
<symbol>^IXIC</symbol>
<display>Nasdaq</display>
</entry>
</marketIndices>
<sections/>
</settings>
<financialInstruments>
<index symbol="^DJI">
<symbol datum_id="s00">^DJI</symbol>
<displaySymbol datum_id="s20">^DJI</displaySymbol>
<exchange datum_id="x00">DJI</exchange>
<priceFormat>#,##0.00</priceFormat>
<currency datum_id="c01">USD</currency>
<quote>
<change datum_id="c00">
<absolute datum_id="c10">47.070000</absolute>
<percent datum_id="p20">0.338190</percent>
</change>
<last contributor="rts" datum_id="l00">
<size datum_id="k30">0</size>
<value datum_id="l10">13965.290039</value>
<nvalue>13965.290039</nvalue>
<time datum_id="t10" display0="10:57am ET"
display1="Jul 19" display2="Jul 19, 2007">
2007-07-19T10:57:12-04:00
</time>
</last>
</quote>
</index>
...
</financialInstruments>
</page>
54
6.4. Erweiterung um Intradaykurs-Daten
Abbildung 6.5.: Das Auswahlfenster für Wertpapiere
Beim Baumdurchlauf wird als Letztes geprüft, ob es noch weitere Kürzel auf weiteren
Seiten (also anderen XML-Dokumenten) gibt. Dies wird durch ein spezielles XMLElement
<currentpage> signalisiert, das als Attribute die aktuelle Seitennummer
und die Gesamtzahl an Seiten enthält. Weitere Seiten werden dann gegebenenfalls
nachgefordert. Wie man sieht, kann auf die Elemente eines XML-Dokuments mittels
einer Pfadangabe zugegrien werden, die Attribute sind Elemente der XML-Klasse.
Die so ermittelten Daten werden dann in die Tabelle
TSuchergebnisse geschrieben,
die dem Benutzer zur Auswahl als Liste in einem Formular präsentiert wird (Abb.
6.5).
In Tests verlief der Abruf der Kürzel stets problemlos. Es ist zu erwarten, dass sich
die Struktur der XML-Ausgabe nicht ändert, was dann gegebenenfalls Anpassungen
des Programms erfordern würde. Nachteilig ist, dass nun zum Betrieb von TInTo
Microsoft XML in einer Version ab 4.0 installiert sein muss, was aber bei neueren
Windows-Versionen standardmäÿig der Fall ist.
6.4. Erweiterung um Intradaykurs-Daten
Eine wichtiger Schritt in Richtung eines Systems, das auch Datenströme verwalten
kann, war die Erweiterung um die Fähigkeit, Intraday-Daten zu verwalten. Das von
Hübel ursprünglich entwickelte System verwaltete nur Tagesenddaten
EOD),
(End-Of-Day,
also diejenigen Kurse, welche am Ende eines Handelstages festgestellt werden.
Zwar ergibt sich somit in gewisser Weise auch ein Datenstrom, allerdings nur mit
einer Periode von einem Tag.
Hübel [Hüb07] verweist bereits auf die prinzipielle Möglichkeit, TInTo um IntradayFähigkeiten zu erweitern, verweist aber auch auf die Schwierigkeit, entweder alle
EOD- und Intraday-Daten in einer Tabelle abspeichern zu müssen, oder aber zwei
getrennte Tabellen anlegen zu müssen, was doppelte Sichtdenitionen der Indikatoren
verlangt.
Der erste Weg einer gemeinsamen Tabelle weist die Schwierigkeit auf, dass die
EOD-Daten ganz anderer Natur sind als die Intraday-Daten. Die EOD-Daten sind
bereits bei ihrem Abruf aus dem Internet vor-aggregiert, d. h. es existiert zu jedem
Tag ein Hoch-, Tief-, Erönungs- und Schlusskurs, die auch direkt vom Kursanbie-
55
6. Erweiterungen von TInTo
ter mitgeliefert werden. Die Kurse müssen nur noch in der Datenbank zur späteren
Verwendung abgespeichert werden. Bei den Intraday-Daten lassen sich zwar auch
Höchst- und Tiefst-Kurse abrufen, diese beziehen sich aber auf den bisher erfolgten
Handelstag und nicht auf den Zeitraum, den der einzelne Datensatz repräsentiert. Ein
echter Schlusskurs ist bei Intraday-Daten auch nicht feststellbar, stattdessen nimmt
der momentan letzte Kurs, zu dem ein Handel erfolgt ist, dessen Stelle ein. Schlieÿlich
müssten dann auch noch am Ende eines jeden Tages die Intraday-Daten gelöscht und
durch die Tagesenddaten ersetzt werden.
Um diese Probleme zu vermeiden, wurde der zweite Ansatz gewählt, bei dem Intraday-Daten und Tagesenddaten in getrennten Tabellen gehalten werden. Das Problem,
zwei Abfragendenitionen erstellen zu müssen, wurde dabei wie folgt gelöst:
In der Tabelle
TTimeRange wurde ein boolesches Attribut Intraday
angelegt (sie-
he Abb. 6.1). Wählt der Benutzer einen Zeitraum aus, der sich nur mit IntradayDaten darstellen lässt, z. B. einen Tag oder 60 Minuten, so wird dieses Attribut
ChartShow abgefragt und bei positivem Wert die temporäre TatmpAggregation (als Ersatz für eine materialisierte Sicht) aus der Tabelle
TIntraday erstellt, andernfalls aus der Tabelle TKurs. Alle Indikatordenitionen
von der Funktion
belle
greifen ohnehin wegen der Korrektur der Indikatorberechnung nur auf die Werte aus
der Tabelle
tmpAggregation
zu, so dass hier keine Anpassungen mehr notwendig
sind.
Ein weiterer Unterschied besteht in den von
Yahoo! !
zur Verfügung gestellten Vo-
lumendaten. Für die Tagesenddaten wird als Volumen jeweils das Handelsvolumen
des gesamten Handelstages angegeben, während bei den Intraday-Daten jeweils das
kumulierte Handelsvolumen seit Tagesbeginn geliefert wird. Aus diesem Grund unterscheidet sich im neuen TInTo-System die Aggregierung für Tagesend- und Intradaydaten dahin gehend, dass für die Tagesenddaten jeweils die Volumina einzelner
Tage summiert werden, während bei den Intradaydaten jeweils die Dierenz zwischen
Volumen-Minimum und -Maximum für die Gruppen berechnet wird. Der jeweilige
Minimalwert für eine Gruppe wird zwischengespeichert und später bei den Updates
wieder abgezogen, da dieser den Startwert für die jeweilige Gruppe darstellt.
Obwohl die Intraday-Daten während des Betriebs von TInTo automatisch nachgeladen werden (siehe auch Abschnitt 8.3), so fehlen doch die Daten für die Zeiträume,
in denen TInTo nicht läuft. Aus technischer Sicht wäre es kein Problem, auch historische Intraday-Daten zu beziehen. Jedoch stehen diese nur zu verhältnismäÿig hohen
Preisen kostenpichtig zur Verfügung. Andererseits war es für die Tests notwendig,
historische Intradaydaten zur Verfügung zu haben. Aus diesem Grund wurde auf einem Linux-Rechner ein sog.
cron-job
eingerichtet, dies ist ein Prozess, welcher vom
System nach einer gewissen Zeit selbsttätig wiederholt ausgeführt wird. Dieser wird
in einer sogenannten
crontable
eingetragen, wobei erst die Minuten, zu denen der Job
aufgerufen werden soll, und anschlieÿend der Befehl anzugeben ist. Für den Abruf
lautet er:
0,5,10,15,20,25,30,35,40,45,50,55 * * * * /home/gereon/dax.sh
56
6.5. Korrektur der Indikatorberechnungen
Inhalt von dax.sh:
lynx --dump "http://finance.yahoo.com/
d?s=^DJI&f=sl1opd1t1vgh" >> /var/log/dax
Mit diesem Rechner wurden also unter Verwendung des textbasierten Browsers
lynx
im Abstand von 5 Minuten die Intraday-Daten des Dow-Jones-Indexes und des DAX
heruntergeladen. Die Daten wurden zur späteren Verwendung in einer Datei abgespeichert. So wurden ab dem 22.02.2007 bis zum 22.07.2007 Intraday-Daten heruntergeladen und gespeichert. Die Daten konnten dann über das Optionsfenster von
TInTo unter dem Programmpunkt Import Intraday Quotes eingelesen werden.
6.5. Korrektur der Indikatorberechnungen
Die vielleicht bis dahin wichtigste und auch nicht auf den ersten Blick oensichtliche
Änderung betraf die Berechnung der Indikatoren. In der ursprünglichen Version el
auf, dass teilweise Dierenzen zwischen denjenigen Indikatorcharts bestanden, die
vom ChartDirector selbst erstellt wurden und denen, die mittels SQL-Ausdrücken
von TInTo erzeugt wurden.
Ein Indikator, an dem man den Unterschied besonders gut sehen kann, ist der
Aroon-Up/Down.
Dieser Indikator misst die Anzahl der seit dem letzten Kursma-
ximum oder -minimum vergangenen Tage. Der Indikatorwert wird dabei auf Werte
zwischen 0 und 100 normiert. Die Berechnungsvorschrift lautet
Aroonup (t) =
wobei
t
(n − (t − tmax ))
· 100
n
(6.1)
wieder die Nummer des aktuellen Handelstages angibt,
die der Indikatorwert berechnet werden soll und
tmax
n
die Periode, über
die Nummer des Tages des
vorhergegangenen letzten Maximums dieser Periode. Die Division durch die Periodenlänge und die anschlieÿende Multiplikation mit 100 normiert den Indikator auf
einen Wert zwischen 0 und 100. Für den Aroon-Down-Wert verläuft die Berechnung
analog über das Maximum. Ein Wert von
Aroonup = 100
besagt demnach, dass seit
dem letzten Maximum 0 Tage vergangen sind, der entsprechende Tag also selbst das
Maximum ist. Der Kurvenverlauf dieses Indikators ergibt ein Sägezahnmuster, welches schnell ansteigt, auf einem Wert von 0 oder 100 verweilt und dann linear abfällt.
Aus dem Indikatorverlauf lässt sich beispielsweise ein Aufwärtstrend ablesen, wenn
der
Aroonup
einen Wert von 70 übersteigt und über dem des
Aroondown
liegt, wobei
der Trend umso stabiler ist, je länger der Indikator auf einem hohen Niveau bleibt
[Pae06].
Berechnete man den Aroon-Up/Down jedoch mit dem vorliegenden TInTo-System
über einen längeren Zeitraum (z. B. 3 Jahre), so verschwand dieses Muster, der Wert
stieg immer wieder langsam an und el ebenso langsam ab, ein längeres Verweilen
auf den Extremwerten war nicht mehr gegeben. Die Berechnung des ChartDirectors
hingegen zeigte weiterhin den charakteristischen Verlauf. Dieser Unterschied ist in
Abb. 6.7 dargestellt
57
6. Erweiterungen von TInTo
Bei näherer Betrachtung stellte sich heraus, dass zuerst die Indikatorwerte aus den
Tageskursen des gewählten Zeitraums berechnet wurden und erst dann die Aggregierung nach der vorgesehenen Auösung erfolgte. Aus den zuvor entstandenen Indikatorwerten wurde das arithmetische Mittel errechnet und als Indikatorwert der Gruppe
angegeben. Erst dann wurden die schon gruppierten Daten dem ChartDirector übergeben, zum einen um die Werte zu zeichnen und zum anderen den ChartDirectorinternen Indikator zu berechnen.
Somit wichen sowohl die Berechungsmethode als auch die zugrunde gelegte Berechnungsperiode in beiden Fällen voneinander ab. Es erschien dabei logischer, zuerst die
Aggregation durchzuführen und erst dann in einem weiteren Schritt den Indikator zu
berechnen. Die Periodendauer würde sich auch dann nicht mehr auf die Anzahl der
zugrunde liegenden Tageskurse beziehen, sondern auf die Anzahl der Kerzen gemäÿ
gewählter Auösung. Auÿerdem schien die Verwendung des arithmetischen Mittels
nicht gerechtfertigt: Im Falle des Aroon-Up/Down sorgte die Mittelwertbildung dafür, dass die Extrema abgemindert wurden und der steile Anstieg wurde zu einem
langsamen. Dies ist besonders dann bedenklich, wenn man wie oben angesprochen ein Signal aus dem Indikator ablesen möchte, und sich auf Indikatorwerte über 70
konzentriert, die aber durch die Berechnungsmethode gar nicht erreicht werden.
Es wurde daher eine Tabelle
tmpAggregation
(s. a. Abb. 6.6) angelegt, die die
aggregierten Werte aus der Tageskurs- oder Intraday-Tabelle zwischenspeichert. Die
Indikatorberechnung erfolgt dann nur noch auf Grundlage dieser Tabelle. Auf die
eigentlichen Kurstabellen wird dabei nicht mehr zugegrien. Die Durchführung der
Aggregation erfolgt bei der Neuzeichnung eines Indikators innerhalb der Funktion
ChartShow:
If Forms![main]!TimeRange.Column(2) Then
AggrSQL = "INSERT INTO tmpAggregation SELECT First(ID) AS ID, " & _
"$ AS [Date], AutoIncrement($) AS n, First(Last) AS Open, " & _
"Max(Last) AS High, Min(Last) AS Low, Last(Last) AS Close, " &_
Max(Vol)-Min(Vol) AS Vol, Count(n) As Anzahl, Min(Vol) AS VolStart " & _
FROM [TIntraday] WHERE ((([ID])=spGetID()) AND (([n])>spGetN())) " & _
"GROUP BY $ ORDER BY $ ;"
Else
AggrSQL = _
"INSERT INTO tmpAggregation SELECT First(TKurs.ID)...FROM TKurs...
GROUP BY $ ORDER BY $ ;"
End If
’$ durch Aggregierungsstring ersetzen
AggrSQL = Replace(AggrSQL, "$", Forms.main.Frequency.Column(3))
CurrentDb.Execute "DELETE * FROM tmpAggregation"
CurrentDb.Execute AggrSQL
Wie man sieht, wurde in dem String zuerst das Dollarzeichen als Platzhalter für
den eigentlichen Aggregierungsstring eingesetzt. Dann wird ausgewählt, ob die Kursoder die Intradaytabelle als Quelle gewählt wird, je nach ausgewähltem Zeitraum im
Hauptfenster. Danach wird das Dollarzeichen durch den Aggregierungsterm aus der
Auösungstabelle ersetzt, die Aggregationstabelle gelöscht und die Anweisung ausgeführt. Aufgrund dieser Änderung mussten auch alle Indikatordenitionen abgeändert
58
6.5. Korrektur der Indikatorberechnungen
Abbildung 6.6.: Die Tabelle
tmpAggregation
werden. Die bisher referenzierte Tabelle
TKurs
mit Beispieldaten
wurde durch
tmpAggregation
ersetzt. Eine Einschränkung nach Wertpapier-ID fand nun bereits durch die Aggregation statt, so dass die in allen Denitionen anzutreende Bedingung ID=spGetID
WHERE
entfallen konnte, ebenso die Einschränkung des betrachteten Zeit-
raums.
Im Test zeigte sich dann, dass die Indikatorformationen von TInTo und ChartDirector nur noch geringfügig voneinander abwichen. Die noch vorhandenen Abweichungen
können auf verschiedenen Eekten beruhen. So ist es möglich, die Indikatoren mit
dem typischen Preis (Mittel aus Höchst-, Tiefst- und Schlusskurs) zu berechnen,
oder nur aus dem Schlusskurs.
Der Aroon-Up/Down gab auch hierfür ein gutes Beispiel ab: Auch nach der Korrektur zeigten die Charts noch geringfügige Unterschiede. Nachdem die Indikatordenition jedoch so abgeändert wurde, dass
tmax
nicht mehr als der Tag mit dem höchsten
Schlusskurs, sondern als der Tag mit dem höchsten Höchstkurs berechnet wurde
sprechend für
tmin ),
(ent-
traten im Chart praktisch keine Abweichungen mehr auf, Abb.
4
6.8 zeigt das Ergebnis.
Weitere Variationen ergeben sich aus anderen Koezienten
für gewichtete Mittel oder die Verwendung eines exponentiellen Durchschnitts statt
eines ungewichteten arithmetischen Durchschnitts, z. B. für den Indikator RSI (vgl.
[Pae06, S.77]). Dies stellt jedoch keine Verbesserung des TInTo-System selbst mehr
dar, da die Indikatordenitionen durch den Anwender frei denierbar sind.
4
Eine kleine Abweichung zeigt sich noch beim ersten Wert im Februar 2005. Ursache hierfür ist,
dass hier zweimal der gleiche Tiefstkurs auftrat, und ein Unentschieden unterschiedlich aufgelöst
wird. Dies ist letztlich Geschmackssache.
59
6. Erweiterungen von TInTo
Abbildung 6.7.: Der Chart des Aroon Up/Down-Indikators für die Aktie von Microsoft über 3 Jahre im existierenden TInTo-System. Oben der von
ChartDirector berechnete Chart, unten der von TInTo berechnete.
Man erkennt, dass in der TInTo-Berechnung das Ergebnis deutlich
verändert ist, die für den Aroon-Indikator charakteristische Sägezahn-Kurve geht verloren
Abbildung 6.8.: Der Chart des Aroon Up/Down-Indikators für die Aktie von Microsoft über 3 Jahre mit der korrigierten TInTo-Version und einer angepassten Indikatordenition, die statt des Schlusskurses den Hochund den Tiefstkurs verwendet. Oben der von ChartDirector, unten
der von TInTo berechnete Chart. Die beiden Charts sind praktisch
identisch, die einzige Abweichung im Februar 2005 rührt von einem
Unentschieden zwischen zwei Kurswerten her.
60
7. Spezialisierung von SQL-Views
In Kapitel 5 wurden die Grundlagen der Änderungspropagierung im Kontext der relationalen Algebra behandelt. Auch die meisten Veröentlichungen zu diesem Thema
verwenden meist die relationale Algebra oder Datalog, während nahezu alle heute verwendeten kommerziellen Datenbanksysteme SQL verwenden. Bevor die Änderungspropagierung in einem kommerziellen Datenbanksystem wie Access umgesetzt werden
kann, müssen die Regeln zur Änderungspropagierung in eine Sprache übersetzt werden, die das DBMS versteht, was meist eine Umsetzung in SQL bedeutet. Dazu muss
festgestellt werden, welche Probleme bei Verwendung von SQL auftreten können, die
aber im Kontext der RA oder von Datalog noch nicht berücksichtigt wurden. So ist es
möglich, dass hier Einschränkungen gemacht wurden, die in der Semantik von SQL
nicht garantiert werden, andererseits kann aber auch SQL Einschränkungen vorsehen. Zunächst werden hierzu einige wichtige Unterschiede zwischen der relationalen
Algebra und SQL herausgearbeitet. Ein wichtiger Punkt ist die Änderungspropagierung auf Aggregationen. Obwohl in der Vergangenheit sehr viele Veröentlichungen
zur inkrementellen Änderungspropagierung erschienen sind, ist nur in sehr wenigen
Veröentlichungen die Behandlung von Aggregationen berücksichtigt. Gupta et al.
beschäftigen sich im Rahmen ihres Count-Algorithmus mit Aggregationen [GMS93],
der Artikel von Chan et al. [CLS00] beschäftigt sich ausschlieÿlich damit. Einige der
Ergebnisse aus diesen Artikeln werden im Abschnitt 7.2.2 aufgegrien und um eigene
ergänzt. Insbesondere wird ein ezienter Ansatz zur inkrementellen Aktualisierung
des arithmetischen Mittels vorgestellt. Schlieÿlich werden mögliche Implementierungen der Änderungspropagierung in SQL-Datenbanksystemen diskutiert.
7.1. Relevante Unterschiede zwischen SQL und der RA
Im Abschnitt 2.3 wurde ein Basis-SQL vorgestellt, das einen Kern von SQL darstellt, der direkt in die relationale Algebra übersetzbar ist. Allerdings wurden dazu
Einschränkungen hinsichtlich der Verwendung von Duplikaten, NULL-Werten und
Aggregationen gemacht. Dies liegt daran, dass die Ausdrucksstärke beider Sprachen
nicht identisch ist. Tatsächlich bestehen zwischen beiden Sprachen wichtige Unterschiede. Hier seien die für die Änderungspropagierung wichtigsten genannt:
1. In SQL dürfen (bis zur Version 1999) Sichtdenitionen nicht rekursiv sein, weder direkt rekursiv noch indirekt rekursiv. Es dürfen also nur hierarchische
Regelmengen deniert werden, der Abhängigkeitsgraph bleibt somit stets zyklenfrei.
61
7. Spezialisierung von SQL-Views
2. SQL erlaubt Multimengen, es dürfen also mehrere Tupel den gleichen Inhalt
in allen Attributen haben. Die relationale Algebra ist stets mengenorientiert,
doppelte Tupel sind ausgeschlossen.
3. SQL erlaubt sehr viele verschiedene Formulierungen für dieselben Abfragen.
4. SQL enthält ein Aggregierungskonzept, mit dem Tupel gruppiert werden können und das Berechnungen auf den gruppierten Tupeln erlaubt.
Der erste Punkt ist im Hinblick auf die Änderungspropagierung eine Vereinfachung,
1
da die Herleitung von Daten aus rekursiven Sichten erheblich schwieriger ist.
Der
zweite Punkt wird bei Löschungen und Vereinigungen relevant. Wird ein doppeltes Tupel gelöscht, ist zu klären, ob beide Exemplare eines Tupels gelöscht werden
müssen oder nur eines. Weiterhin ist bei Einfügungen, die in der Theorie eektlos
wären, eine weitere Einfügung möglich. Der dritte Punkt wurde bereits bei der Behandlung von Basis-SQL im Abschnitt 2.3 behandelt, d. h. es lassen sich für alle
SQL-Abfragen ohne Aggregation entsprechende Formulierungen erreichen, die direkt
in die relationale Algebra transformiert werden können und somit auch gemäÿ den
im Kapitel 5 behandelten Änderungsregeln behandelt werden können. Sehr wichtig
gerade im Hinblick auf das Thema Finanzdatenströme und technische Indikatoren
ist die Aggregation. Hierfür mussten zunächst eigene Methoden entwickelt werden,
die die Änderungspropagierung ermöglichen.
Materialisierte Sichten,
wie sie in der relationalen Algebra deniert wurden,
sind im SQL-Standard noch nicht vorgesehen. Das DBMS Oracle unterstützt materialisierte Sichten, die mit dem Statement
Create Materialized View
erzeugt
werden können. Oracle ermöglicht es, eine (interne) Änderungspropagierung durchführen zu lassen.
Da die Änderungspropagierung im TInTo-System einerseits standardkonform sein
soll und andererseits auch unter Access laufen soll, muss für diesen Fall eine andere
Möglichkeit gefunden werden. Es ist mittels Standard-SQL möglich, materialisierte
Sichten zu simulieren. Dazu wird mittels der
INSERT INTO-Anweisung
eine neue
Relation, basierend auf der Rückgabe einer Abfrage, erzeugt. Um die Sicht
rend auf einer Relation
t,
basie-
r zu materialisieren, kann folgende Anweisungsfolge verwendet
werden:
CREATE VIEW t AS
SELECT a,b,c FROM r;
INSERT INTO t_materialized
SELECT * FROM t;
Es ist zu beachten, dass
t_materialized nur eine Simulation einer materialisierten
Sicht ist, da keinerlei Verbindung mehr zur ursprünglichen Sicht besteht. Änderungen
an der materialisierten Relation
1
wirken sich nicht auf die zu Grunde liegenden
In diesem Fall ist eine sogenannte Fixpunktiteration notwendig.
62
7.2. Delta-Regeln in SQL
Relationen aus, und andersherum. Für das DBMS stellen beide Relationen getrennte
Basisrelationen dar.
Ebenfalls zu simulieren sind die
Seed-Fakten, also diejenigen Fakten, deren Ein-
fügung oder Löschung die Änderungen darstellen und somit die Änderungspropagierung erforderlich machen. Es ist möglich, diese Fakten direkt in den Basisrelationen
zu löschen oder einzufügen. Es stellt sich dann das Problem, dass die ursprüngliche
Relation nicht mehr zur Verfügung steht. Es bieten sich hier zwei Möglichkeiten der
Simulation an: Als erste Möglichkeit könnten die Fakten durch ein spezielles Attribut
als neu eingefügt oder als zum Löschen markiert gekennzeichnet werden. Durch
entsprechende Selektion lieÿen sich dann
Möglichkeit besteht darin, für
R+
und
R+ , R−
R−
und
Rold
simulieren.
2
Die andere
getrennte Relationen zu verwenden, die
die gleiche Attributstruktur wie die zu Grunde liegende Relation aufweisen. Diese
Umsetzung hat den Vorteil, dass die entsprechenden Tupel nicht erst gesucht werden müssten, sondern direkt zur Verfügung stehen. Aufgrund dieses Vorteils wird im
Folgenden letztere Möglichkeit gewählt.
7.2. Delta-Regeln in SQL
Für Sichten, die direkt in die RA überführbar sind, wie Vereinigung, Pro jektion,
Selektion etc., können die Regeln analog zu denen der relationalen Algebra erstellt
werden. Die Regeln können direkt als Änderungsanweisungen übernommen werden.
Es ist aber auch möglich, die Delta-Views erst als Sichtdenitionen zu denieren und
diese Sichten dann in Änderungsanweisungen zu verwenden. Eine weitere mögliche
Änderung stellen die Updates in SQL dar, deren Propagierung ebenfalls behandelt
werden muss. Eine weitere Klasse von Abfragen stellen Aggregationen dar. Diese
Klasse ist für TInTo sehr wichtig, da die meisten Indikatordenitionen Aggregierungen verwenden. Die Möglichkeiten zur Änderungspropagierung auf Aggregationen
werden im Abschnitt 7.2.2 besprochen.
7.2.1. Delta-Regeln für Operatoren aus der RA
Bis auf die Änderungen im Subtrahenden einer Mengendierenz sind alle Änderungsregeln monoton, d. h. bei Einfügungen in den Basisrelationen werden auch (höchstens) Einfügungen in den abgeleiteten Relationen durchgeführt, entsprechendes gilt
3
für Löschungen.
Die mit Einfügungen induzierten Änderungen lassen sich also bis
auf den Fall der Mengendierenz mit
Insert-Anweisungen
durchführen. Lautet die
Denition für eine Sicht beispielsweise
CREATE VIEW s AS
(SELECT * FROM r) INTERSECT (SELECT * FROM t)
so kann die davon abgeleitete, materialisierte Sicht mit der Einfüge-Anweisung
2
3
In SQL werden im Folgenden die entsprechenden Relationen mit
R_plus, R_minus und R_old
bezeichnet, um nur die erlaubten Zeichen in SQL zu verwenden.
Die Regeln sind nicht strikt monoton, da es auch eektlose Änderungen geben kann.
63
7. Spezialisierung von SQL-Views
INSERT INTO S_materialized
((SELECT * FROM t_plus)
INTERSECT
((SELECT * FROM r) EXCEPT (SELECT * FROM r_minus)))
UNION
((SELECT * FROM r_plus)
INTERSECT
((SELECT * FROM t) EXCEPT (SELECT * FROM t_minus)))
UNION
(SELECT * FROM t_plus) INTERSECT (SELECT * FROM r_plus)
aktualisiert werden. Der zusammengesetzte
Select-From-Where-Block
ternativ hierzu auch als Sichtdenition für eine Sicht
S_plus
kann al-
verwendet werden
Wie bereits erwähnt, müssen für die Einfügungen in den Subtrahenden einer Mengendierenz Löschungen durchgeführt werden. Lautet die Denition für eine Mengendierenz
CREATE VIEW D AS
(SELECT * FROM R)
MINUS
(SELECT * FROM S);
so muss die entsprechende Regel für Einfügungen in S als Löschaktion umgesetzt
werden (Einfügungen in
R
sind der Übersichtlichkeit halber fortgelassen):
DELETE * FROM D_materialized
WHERE EXISTS (SELECT *
FROM S_plus
WHERE D.a=S.a AND D.b=S.b ...)
wobei
D.a
und
S.a
Schlüsselattribute sind.
Wie bereits im letzten Beispiel des vorhergehenden Unterabschnitts zu sehen, ist
die Syntax für
Löschungen etwas anderes zu gestalten als die für Einfügungen. Das
syntaktische Problem für SQL liegt in diesem Fall darin, dass kein Konstrukt der
Delete. . . From. . . Select. . . existiert. Eine mögliche Syntax führt über die
Exists-Klausel. Dabei müssen nur die Schlüsselattribute der beiden Relationen auf
Form
Gleichheit geprüft werden. Sei für eine Sicht
S
bereits eine Delta-Sicht
S−
deniert,
dann lautet die zugehörige Löschanweisung:
DELETE * FROM S
WHERE EXISTS (SELECT * FROM S_minus
WHERE S.a1=S_minus.a1,..., S.am=S_minus.m,...)
wobei die Attribute
a1 , . . . am
(zumindest) die Schlüsselattribute der Relation sind.
Zusätzlich zu dem im vorigen Kapitel Besprochenen sind in SQL neben Einfügungen und Löschungen auch
Updates
möglich. Eine Umsetzungsmöglichkeit ist,
Updates als Löschung, gefolgt von einer Einfügung zu propagieren. Es lassen sich
aber auch direkte Delta-Regeln aufstellen:
64
7.2. Delta-Regeln in SQL
1. Für die Selektion ist lediglich das Update zu propagieren, falls sich die Änderungen ausschlieÿlich auf die Attribute beziehen, die nicht Bestandteil der
Selektionsbedingung sind. Ansonsten ist die Selektionsbedingung auf den veränderten Tupeln zu überprüfen. Je nach Ergebnis der Prüfung ist das Tupel
einzufügen, zu löschen oder in der Selektion zu belassen.
2. Für die Projektion ist bei Updates der auspro jizierten Attribute nichts zu tun,
bei Änderung der verbliebenen Attribute ist zusätzlich zur Änderung zu prüfen, ob dies Duplikate erzeugt oder den Wegfall einer Duplikate-Eliminierung
verursacht.
3. Beim Kreuzprodukt sind die Tupel zu ändern, die das geänderte Quelltupel
enthalten.
4. Bei der Vereinigung ist wieder zu prüfen, ob Duplikate-Eliminierungen durchzuführen oder rückgängig zu machen sind. Gleiches gilt für Mengendierenz
und Schnitt.
5. Da der Join eine Zusammensetzung von Kreuzprodukt und Selektion ist, sind
auch die Änderungsregeln recht ähnlich. Zum einen ist zu prüfen, ob sich die
Join-Bedingungen geändert haben, andererseits sind aber auch die Tupel zu
aktualisieren, die als Joinpartner ein geändertes Attribut enthalten UpdateRegeln für Aggregationen sind ebenfalls möglich, diese werden im folgenden
Abschnitt behandelt.
7.2.2. Delta-Regeln für Aggregationen
In Kapitel 5 wurden nur Regeln für Änderungen berücksichtigt, die elementare Funktionen der relationalen Algebra enthalten.
SQL ist ausdrucksmächtiger als die relationale Algebra, da in SQL auch Aggregationen möglich sind. Obwohl Aggregate eine wichtige Anwendungsmöglichkeit für
Datenbanksysteme darstellen, z. B. bei der Erstellung von Statistiken, Bilanzen, der
Auswertung von Meinungsumfragen oder eben auch von Börsendaten, beschränkt
sich die Behandlung dieses Themas im Kontext der inkrementellen Änderungspropagierung auf wenige Veröentlichungen. Auch aus Gründen der Vollständigkeit ist
aber die Behandlung von Aggregationen ein wichtiger Punkt: unterstützt ein Verfahren zur automatischen Erzeugung von Delta-Regeln alle SQL-Sichtdenitionen,
so könnte im Hintergrund aus jeder Sichtdenition automatisch eine Delta-Regel
erzeugt werden, ohne dass sich der Benutzer darum weiter kümmern müsste. Die
Änderungspropagierung könnte also unsichtbar im Hintergrund ablaufen.
Im Folgenden werden nun Änderungsregeln für solche Sichten eingeführt, welche
Aggregatfunktionen, also mathematische Berechnungen auf Attributwerten der Relationen, einschlieÿen. Es wird dann untersucht, inwieweit Rechenoperationen bei
Einfügungen, Löschungen und Änderungen eingespart werden können. Ziel ist es
dabei, die Laufzeit unter Zuhilfenahme schon vorhandener, materialisierter Sichten
65
7. Spezialisierung von SQL-Views
zu verbessern. Dieser Zeitvorteil wird durch einen gegebenenfalls höheren Speicherplatzbedarf erkauft. Das prinzipielle Vorgehen ndet sich in einer formalen Sichtweise
bereits in [GMS93], soll jedoch hier ausschlieÿlich im Kontext von SQL erläutert werden.
Sei folgende SQL-Sicht mit Aggregierung gegeben:
CREATE VIEW m AS (
SELECT a, f(x) as v
FROM t
GROUP BY a
)
wobei
f (x)
eine Aggregierungsfunktion ist. Zu Erinnerung: Die Aggregierung wählt
t aus, gruppiert alle Tupel mit gleichem a-Attributwert
x-Attributwerte jeder Gruppe die Aggregierungsfunktion an.
alle Tupel aus der Relation
und wendet auf die
Wird diese Sicht materialisiert, so ist die Rückgabe wiederum eine Relation, die die
jeweiligen Gruppierungsattribute und die Werte der Aggregierungsfunktion erhält.
Möchte man nun ein Tupel in die Relation
t
einfügen, so muss ebenfalls die mate-
rialisierte Sicht geändert werden. Dabei sind folgende Fälle denkbar:
•
Das neue Tupel besitzt einen
a-Wert,
der noch nicht in der materialisierten
Sicht vorhanden ist. In diesem Fall ist die Aggregierungsfunktion lediglich auf
den
x-Wert
des Tupels anzuwenden und das Resultat als neues Tupel in die
materialisierte Sicht einzufügen.
•
Das neue Tupel besitzt einen
a-Wert,
der bereits in der materialisierten Sicht
vorhanden ist. Dann ist der Funktionswert
v
des passenden
a-Werts
gemäÿ
einer bestimmten Berechnungsvorschrift zu aktualisieren. Im Folgenden wird
diese Vorschrift
δf±
genannt.
Diese zwei Fälle können in zwei SQL-Anweisungen umgesetzt werden:
UPDATE m SET
v = delta_p(...)
WHERE a IN
(SELECT t_plus.a FROM t_plus)
INSERT INTO m(a, v)
SELECT a, f(x) as v
FROM
t_plus
WHERE a NOT IN
(SELECT m.a FROM m)
Dadurch, dass sich beide
Where-Klauseln
gegenseitig ausschlieÿen, können beide
Anweisungen unabhängig voneinander ausgeführt werden, so dass Fallunterscheidungen im Programm-Code überüssig sind. Die Ausführungsreihenfolge der Anweisungen ist wichtig, denn ordnet man die beiden Anweisungen in umgekehrter Reihenfolge
66
7.2. Delta-Regeln in SQL
an, so wird die Änderung doppelt durchgeführt, und das Ergebnis ist falsch. Einen
eleganteren Weg bietet die SQL-Erweiterung SQL/PL (SQL Procedural Language),
die mittels eines
If-Else-Konstrukts
Bei Löschungen stimmt der
a-Wert
eine Fallunterscheidung erlaubt.
stets überein, falls es sich um eine eektvolle
Löschung handelt, auch hier sind zwei Fälle zu unterscheiden:
•
In der Quellrelation
t
existieren noch weitere Tupel mit gleichem
diesem Fall ist unter Verwendung der Änderungsfunktion
δf−
a-Wert.
In
der Wert zu ak-
tualisieren.
•
In der Quellrelation
t
war das gelöschte Tupel das einzige mit diesem
Somit fällt die gesamte Gruppe weg, und in
m
a-Wert.
ist damit auch das gesamte
Tupel zu löschen.
Eine mögliche Umsetzung in SQL sieht so aus:
DELETE FROM m
WHERE a
NOT IN
(SELECT a FROM t_new)
UPDATE m SET
v = delta_m(...)
WHERE a IN
(SELECT t_minus.a FROM t_minus)
Eine andere möglichkeit besteht darin, die Anzahl der ursprünglichen Tupel vor der
Aggregierung zu zählen (vgl. [GMS93]). Sollten in den jeweiligen Aggregierungen
auch
Having-Anweisung
vorkommen, so können diese durch
Where-Klauseln
in
den Propagierungsregeln umgesetzt werden.
Updates der Basisrelationen können als Löschung und anschlieÿende Einfügung
modelliert werden oder bleiben im Falle der
Count-Funktion
sogar ganz folgenlos.
Änderungsregeln für einfache Aggregatfunktionen
Für viele Aggregatfunktionen sind die Änderungen einfach inkrementell zu berechnen:
•
Für
Count,
was die Anzahl vorhandener Tupel zurückliefert, ist lediglich der
Wert um die Anzahl der eingefügten Tupel zu erhöhen bzw. um die der gelöschten zu erniedrigen. Für Updates werden keine Änderungen notwendig.
•
Für
Sum
ist die Summe der neu eingefügten Wert zu addieren bzw. bei Lö-
schungen zu subtrahieren, bei Updates kann der gelöschte Wert subtrahiert
und anschlieÿend der neue Wert addiert werden.
Für
Count und Sum können die Änderungen allein aus dem bisherigen Wert der
Aggregierungsfunktion und dem Wert der Aggregierungsfunktion auf den Seedfakten
berechnet werden. Eine wichtige Frage ist, ob dies auch für alle Funktionen, die auf
67
7. Spezialisierung von SQL-Views
Wertemengen operieren, möglich ist. Entscheidend hierfür ist, ob diese Funktionen
mit der Mengenvereinigung und der Mengendierenz verträglich sind, da diese beiden
Operationen bei Verwendung der Delta-Mengen angewendet werden. Mathematisch
gesehen handelt es sich dabei um die Frage, ob die Funktionen bezüglich der Mengenvereinigung und des Mengenschnitts einen Homomorphismus bilden. Nützlich ist
es hierzu, Einfüge- und Löschhomomorphismen zu denieren:
Denition 7.1.
Eine Aggregierungsfunktion
f
ist ein Homomorphismus unter Ein-
fügung, falls gilt:
∃
mit
P, P +
Funktion
h (·) ∀P, P + : f P ∪ P + = h f (P ) , f P +
(7.1)
vereinigungsverträglich.
Analog lässt sich der Homomorphismus unter Löschung denieren:
Denition 7.2.
Eine Aggregierungsfunktion
f
ist ein Homomorphismus unter Lö-
schung, falls gilt:
∃
mit
P, P −
Funktion
h (·) ∀P, P − : f P \P − = h f (P ) , f P −
(7.2)
vereinigungsverträglich
Die Frage ist also, ob aus zwei Teilergebnissen für Teilmengen mittels einer weiteren Funktion, die allein auf diesen Teilergebnissen operiert, das Ergebnis für die
gesamte Menge errechnet werden kann. Tatsächlich stellen nicht alle Aggregatfunktionen solche Homomorphismen dar. So sind die Funktionen
Min
und
Max
zwar
Homomorphismen unter Einfügung, aber nicht unter Löschung.
Die inkrementelle Änderungspropagierung kann auf Homomorphismen sehr viele
Rechenschritte einsparen. Sei
gen Neuberechnung
nung sind hingegen
|R| = n
und
|R+ | = m,
so müssen bei einer vollständi-
m + n Tupel betrachtet werden. Bei inkrementeller Neuberechm Tupel für die Berechnung zu betrachten, hinzu kommen noch
die Kosten für die Suche nach dem bisherigen Wert, was bei geschickter Indexwahl in
logarithmischer Zeit geschehen kann. Insbesondere für den in der Praxis oft auftretenden Fall, dass
mn
ist, wirkt sich die inkrementelle Berechnung rechenzeitsparend
aus.
Änderungsregeln für zerlegbare Aggregatfunktionen
Auch Funktionen, die selbst keine Homomorphismen sind, können dann immer noch
sehr einfach berechnet werden, wenn sie in solche zerlegbar sind. In diesem Fall kann
unter Abspeicherung der Teilergebnisse die Änderung durchgeführt werden. Neben
einem erhöhten Speicherplatzverbrauch fallen noch die Kosten für die Zusammensetzung der Teilergebnisse an. Zur Klasse dieser Funktionen gehört die Mittelwertsfunktion
Avg.
Diese kann sehr einfach unter Abspeicherung der Summe und der Anzahl
der Argumente berechnet werden, indem zunächst die Summe und dann die Anzahl
aktualisiert wird und anschlieÿend die neue Summe durch die neue Anzahl dividiert
68
7.2. Delta-Regeln in SQL
wird. Im Rahmen dieser Diplomarbeit wurde eine Formel entwickelt, mit der es möglich ist, auch ohne Abspeicherung der Summe, nur mit Kenntnis der Mittelwerte und
der Anzahlen, den neuen Mittelwert zu berechnen. Auf diese Weise kann der Speicherplatz, der sonst zur Speicherung der neuen Summe notwendig wäre, eingespart
werden. Daneben war es eine Beobachtung, dass in TInTo die Anzahl der Tupel in
einer Gruppe für jede Indikatorberechnung konstant ist und somit auch nicht mehr
errechnet werden muss. In den Delta-Mengen ist jeweils nur ein Tupel enthalten, so
dass im Endeekt nur aus der Kenntnis des alten Mittelwertes der neue Mittelwert
berechnet werden kann. Zunächst aber soll hier die allgemeine Form dieser Formel
vorgestellt werden.
Das arithmetische Mittel ist deniert als
n
AVG
(x1 , . . . , xn ) =
1X
xi
n
(7.3)
i=1
Falls nun
m
Tupel der Relation hinzugefügt werden, so wird sich das arithmetische
Mittel ändern. Die Änderung kann wie folgt angegeben werden:
+
δ 0 AVG = AVG(x1 , . . . , xn , xn+m ) − AVG(x1 , . . . , xn )
x1 + . . . + xn + xn+m x1 + . . . + xn
=
−
n+m
n
n (x1 + . . . + xn + . . . + xn+m ) (n + m) (x1 + . . . + xn )
−
=
n (n + m)
n (n + m)
n (x1 + . . . + xn ) + n (xn+1 + . . . + xn+m ) − n (x1 + . . . + xn ) − m (x1 + . . . + xn )
=
n (n + m)
(xn+1 + . . . + xn+m ) m (x1 + . . . + xn )
=
−
n+m
n (n + m)
m
= AVG(xn+1 , . . . , xn+m ) − AVG(x1 , . . . , xn ) ·
n+m
(7.4)
Wobei
+
+
δAVG
= AVG(x1 , . . . , xn ) + δ 0 AVG
(7.5)
und aus einer entsprechenden Rechnung ergibt sich
−
δAVG
=
m
xn−m+1 + xn
AVG(x1 , . . . , xn ) −
n−m
n−m
(7.6)
Unter Zuhilfenahme des bereits berechneten arithmetischen Mittels für den alten
Datenbankzustand kann also auch das arithmetische Mittel für den neuen Zustand
berechnet werden, wofür nur konstante Zeit benötigt wird, sofern die Anzahl der Datensätze ebenfalls in konstanter Zeit erhalten werden kann. Dies kann durch die Einführung eines Hilfsattributs erreicht werden, welches den Rückgabewert der
Count-
Funktion enthält.
Die Tabelle 7.1 fasst die Delta-Regeln der gängigsten Aggregierungsfunktionen
zusammen.
69
7. Spezialisierung von SQL-Views
Funktion
1.
SU M (R)
2.
3.
COU N T (R)
4.
5.
AV G(R)
6.
7.
M AX(R)
8.
9.
M IN (R)
10.
Naive Neuberechnung
R+ )
inkrementelle Berechnung
SU M (R ∪
SU M (R\R− )
COU N T (R ∪ R+ )
COU N T (R\R− )
SU M (R) + SU M (R+ )
SU M (R) − SU M (R− )
COU N T (R) + COU N T (R+ )
COU N T (R) − COU N T (R− )
AV G(R ∪ R+ )
AV G(R\R− )
M AX(R ∪ R+ )
M AX(R\R+ )
M IN (R ∪ R+ )
M IN (R\R+ )
SU M (P )−AV G(P )
AV G(R) + COU
N T (P )+COU N T (P − )
···
M AX(M AX(R), M AX(R+ ))
+
nicht inkrementell berechenbar
M IN (M IN (R), M IN (R+ ))
nicht inkrementell berechenbar
Tabelle 7.1.: Regeln für die inkrementelle Berechnung gängiger Aggregierungsfunktionen
Nicht inkrementell berechenbare Aggregatfunktionen
Die Aggregatfunktionen
min und max sind zwar Homomorphismen unter Einfügung,
jedoch keine unter Löschung, da beim Löschen des minimalen Wertes nicht bekannt
ist, welches der zweit-minimalste Wert ist. Somit können diese Funktionen bei Löschungen auch nicht inkrementell nur durch Kenntnis des alten Wertes berechnet
werden. Diese Funktionen lassen sich auch nicht in inkrementell berechenbare Funktionen zerlegen. Es lässt sich zwar überprüfen, ob ein zu löschender Wert überhaupt
das bisherige Minimum oder Maximum ist, dies schat jedoch keine Abhilfe, da der
selbe Extremwert mehrmals auftreten kann. Es sind jedoch seit langem Datenstrukturen bekannt, welche zur schnellen Berechnung des nächstbesten Minimums oder
Maximums verwendet werden können. So bietet sich beispielsweise ein
Heap
an. Es
handelt sich dabei um einen linksvollständigen (und dadurch balancierten) Binärbaum, dessen Pfade von der Wurzel ausgehend sortiert sind. Es ist möglich, einen
Heap auf eine Relation abzubilden, indem die Knoten derart durchnummeriert werden, dass der Knoten
Knoten
2i + 1
i
als linken Sohn den Knoten
2i
und als rechten Sohn den
besitzt [Sed03]. Diese Nummerierung kann als Schlüssel in einem At-
tribut gespeichert werden, während in einem anderen Attribut der jeweilige Wert
gespeichert wird.
Eine weitere Möglichkeit besteht darin, eine Hilfstabelle anzulegen, die wie folgt
aufgebaut ist: In einem Attribut werden die Werte gespeichert, über die aggregiert
werden soll. In einem weiteren Attribut wird der jeweils nächstkleinere (bzw. nächstgröÿere) Wert gespeichert. Bei einer Löschung wird auch das entsprechende Tupel
aus der Hilfsrelation entfernt und der Zeiger des vorhergehenden Tupels auf das
nachfolgende Tupel umgesetzt. Die Tabelle 7.2 veranschaulicht das Verfahren. Ein
weiteres Verfahren, welches ebenfalls mit einer Art Cache arbeitet, wird in [CLS00]
vorgestellt. Aufgrund des relativ hohen Verwaltungsaufwands für diese Datenstruk-
70
7.3. Mögliche Implementierungen der Änderungspropagierung
500
400
500
300
400
300
400
300
300
200
300
200
200
100
200
100
Tabelle 7.2.: Ein Verfahren zur ezienten Min/Max-Suche bei Löschungen. Links der
Zustand vor der Löschung des Wertes 400, rechts der nach der Löschung
tur wurde jedoch im TInTo-System auf die inkrementelle Berechnung des Minimums
und des Maximums unter Löschung verzichtet, da hier die Anzahl der Tupel pro
Gruppe meist relativ gering bleibt.
Schlieÿlich sind auch auf Aggregationen Updates möglich. Die Vorgehensweise
hängt hier wesentlich davon ab, ob sich die Gruppierungsattribute ändern oder nicht.
Ändert sich ein Gruppierungsattribut, so ist das geänderte Tupel aus der alten Gruppe zu entfernen, wie dies auch bei einer Löschung geschehen würde. Auÿerdem ist das
geänderte Tupel wie bei einer Einfügung in die neue Gruppe einzufügen. Gegebenenfalls kann es dabei erforderlich sein, Gruppen ganz zu löschen oder neu einzufügen.
Ändern sich hingegen die Gruppenattribute nicht, so stellt die gesonderte Behandlung
von Updates anstelle der Behandlung als getrennte Einfügung/Löschung möglicherweise eine Vereinfachung dar. Für die
nichts zu ändern, für
Sum
Count-Funktion ist in diesem Falle überhaupt
ist der bisherige Wert zu subtrahieren und der neue zu
addieren. Beim Mittelwert ändert sich die Anzahl der Argumente nicht, so dass sich
die oben angegebene Formel um einen Summanden im Nenner vereinfacht.
7.3. Mögliche Implementierungen der
Änderungspropagierung
Mit einer Menge von Delta-Regeln, in den vorherigen Abschnitten eher Delta-Anweisungen, ist es möglich, ein Verfahren zur Änderungspropagierung in SQL-Datenbanken zu implementieren. Auch der SQL-Standard unterstützt mittlerweile Trigger.
Diese werden mittels der
Create Trigger-Anweisung deniert. Sei in einer Daten-
bank eine Sicht deniert, die den Mengenschnitt zweier Basisrelationen darstellt:
CREATE VIEW s AS
(SELECT * FROM q)
INTERSECT
(SELECT * FROM r)
Es sei an die Denition der Delta-Regeln für den Durchschnitt in Gleichung 5.6
erinnert:
S + = Q+ ∩ R\R−
∪ R+ ∩ Q\Q−
∪ Q+ ∩ R+
S − = Q− ∩ R\R−
∪ R− ∩ Q\Q−
∪ Q− ∩ R−
71
7. Spezialisierung von SQL-Views
Ein möglicher Trigger, der die Änderungspropagierung auf
s
für Einfügungen aus-
führt, kann wie folgt deniert werden:
CREATE TRIGGER Delta_plus_S
AFTER INSERT OF q_plus
FOR EACH STATEMENT
BEGIN ATOMIC
INSERT INTO s_plus
((SELECT * FROM q_plus)
INTERSECT
((SELECT * FROM R) EXCEPT (SELECT * FROM R_minus)))
UNION
((SELECT * FROM r_plus)
INTERSECT
((SELECT * FROM q) EXCEPT (SELECT * FROM q_minus)))
UNION
(SELECT * FROM q_plus) INTERSECT (SELECT * FROM r_plus)
END;
Dieser Trigger wird also bei Einfügungen auf
S+
ein. Die Anweisungen sind in einen
Q+
ausgeführt und fügt dann Tupel in
Atomic-Block eingeschlossen, der die Ände-
rungen als Transaktion verwaltet, d. h. entweder werden alle Anweisungen ausgeführt
oder überhaupt keine, falls die Anweisung fehlschlagen sollte.
Auch eine Implementierung, die der Pull-Strategie entspricht, ist möglich. Dazu
werden zunächst für alle Relationen Delta-Sichtdenitionen, die sich ihrerseits wieder
aufeinander beziehen, angelegt. Die physische Änderung wird dann wiederum mit
Triggern auf allen Basisrelationen durchgeführt oder zeitgesteuert gestartet.
In Datenbankmanagementsystemen, die keine Trigger unterstützen, kann mit anderen Methoden eine Ausführungsreihenfolgen für die verschiedenen Anweisungen
erzeugt werden. Dies kann im einfachsten Fall von Hand geschehen, aber auch die
vorherige Vor-Kompilierung mittels eines Programms, welches den Abhängigkeitsgraphen untersucht, wäre möglich. Der Aufruf der Änderungsanweisungen kann dann
beispielsweise dadurch erfolgen, dass direkte Änderungen des Datenbankzustandes
unterbunden werden und eine Isolationsschicht zwischen Benutzer und DBMS eingeführt wird, die eingegebene Daten analysiert und dann die Änderungspropagierung
aufruft. Auch eine zeitgesteuerte Propagierung wäre möglich. In Access existieren
keine Trigger, aber eine Möglichkeit, Anweisungen zeitgesteuert ausführen zu lassen.
Mit dieser Möglichkeit wurde eine zeitgesteuerte Bottom-Up-Propagierung implementiert, die im Kapitel 8 vorgestellt wird.
72
8. Änderungspropagierung zur
Indikatorberechnung in TInTo
Aufbauend auf den in den vorigen Kapiteln vorgestellten Grundlagen der Änderungspropagierung sowie den Überlegungen zur Umsetzung in SQL wird nun die
Erweiterung von TInTo um Änderungspropagierung auf Datenströmen vorgestellt.
Auÿerdem wird die Implementierung des automatischen, Timer-gesteuerten Abrufs
der Kursdaten beschrieben.
Für die Umsetzung der Änderungspropagierung wurden einige Grundüberlegungen
angestellt, inwieweit die in den vorigen Kapiteln beschriebenen Grundlagen umgesetzt werden können und welche Besonderheiten im Hinblick auf das Anwendungsgebiet zu beachten sind:
1. Das Ziel muss die möglichst schnelle Aktualisierung des Indikatorcharts sein.
Dabei sollen alle neuen Kurse nach dem Eintreen angezeigt werden, es sollen
keine Kurse gesammelt und dann gemeinsam angezeigt werden.
2. Es ist nur nötig, die Kurse des gerade angezeigten Wertpapiers zu aktualisieren,
auch wenn sich andere Wertpapiere im Portfolio benden. Möchte der Benutzer
jedoch das angezeigte Wertpapier wechseln, so sollte er auch für dieses die Intradaydaten zu Verfügung haben, diese sollten also ebenfalls abgerufen werden.
3. Es ist wünschenswert, dass sich bei Fehlschlagen der Änderungspropagierung
die Datenbank nach dem Fehlschlag weiterhin in einem konsistenten Zustand
bendet, der es zumindest erlaubt, beim nächsten Kursabruf die Änderungspropagierung erneut durchführen zu können.
4. Falls die technischen Indikatoren nicht so schnell berechnet werden können, dass
die Berechnung vor Abruf des nächsten Kurses abgeschlossen ist, soll der Abruf verzögert werden, um nicht die nächste Änderungspropagierung auf einem
veralteten Kurs durchführen zu müssen. In der Zwischenzeit nicht abgerufene
Kurse werden dabei verworfen.
5. Dem Benutzer soll ein sliding window präsentiert werden, d. h. sobald im
Chart am Ende ein neuer Wert hinzukommt, soll der erste Wert aus dem Chart
entfernt werden. Somit schiebt sich der Chart mit der Zeit immer weiter vor.
6. Für technische Indikatoren ist festzustellen, dass diese nur auf dem aktuellen Wert und Werten der Vergangenheit arbeiten und somit zukünftige Werte
den Indikatorwert einer abgeschlossenen Zeitperiode nicht mehr ändern werden.
73
8. Änderungspropagierung zur Indikatorberechnung in TInTo
Dies ist damit zu begründen, dass die Grundidee von technischen Indikatoren
darin besteht, Kaufs- und Verkaufssignale in der Gegenwart zu geben. Signale
für die Vergangenheit zu geben erscheint wenig sinnvoll, da zukünftige Kurse
stets unbekannt sind.
8.1. Materialisierte Sichten in TInTo
Um eine möglichste schnelle Anzeige der Kurswerte zu erreichen, lag die Idee nahe, die
berechneten Indikatorwerte zu materialisieren und bei Aktualisierungen die Sichten
inkrementell zu ändern. Da Access materialisierte Sichten nicht direkt unterstützt,
werden die materialisierten Sichten mittels zusätzlichen Tabellen simuliert, in die die
Ergebnisse der Sichten eingefügt werden. Eine Schwierigkeit, die sich dabei ergibt,
ist die Tatsache, dass die so erzeugten Tabellen von der zu Grunde liegenden Sicht
entkoppelt sind, es können also Änderungen an den Kursdaten vorgenommen werden,
ohne dass die Sichten aktualisiert werden, und es können auch Änderungen an den
so erzeugten Tabellen ohne Einschränkung vorgenommen werden. Dadurch, dass für
den Benutzer das Access-Fenster ausgeblendet wird und so die Tabellen nicht direkt
erreichbar sind, wird die Gefahr einer zufälligen Änderung gemindert. Die für die Materialisierung verwendeten Tabellen wurden zur Entwicklungszeit von Hand erstellt.
Auf Dauer wäre es wünschenswert, diese direkt bei Anlage einer Indikatordenition
automatisch zu erstellen.
Für diejenigen Indikatoren, die nur mittels einfacher Aggregation oder ohne Aggregation zu berechnen sind, genügt die Verwendung einer einzigen materialisierten
Sicht, die die jeweiligen Indikatorwerte abspeichert. Anders ausgedrückt enthält der
Abhängigkeitsgraph nur eine Ebene oberhalb der Tabelle
tmpAggregation, die die
aggregierten Kurswerte abspeichert. Die Tabelle, die die Materialisierung der obersten Ebene der Indikatorberechnung enthält, wurde
die Attribute
Die Attribute
tmpChart
genannt. Sie enthält
n, Date, High, Low, Open, Close, Vol, Ind, In2, In3, tmp1
Ind, In2
und
In3
und
tmp2
enthalten die Werte für die drei zur Verfügung ste-
henden Indikatorlinien. Ferner wurden die Hilfsattribute
tmp1
und
tmp2
angelegt,
die im folgenden Abschnitt beschrieben werden.
Die gewählte Simulation materialisierter Sichten hat zusätzlich den Vorteil, dass
in den erzeugten Tabellen Indizes angelegt werden können. Ein solcher Index wurde in der Tabelle
tmpChart
auf das Attribut
n
gesetzt. Dadurch können einzelne
Kurswerte schneller wiedergefunden werden. Da in den Indikatordenition sehr häug der Theta-Join mit Intervalleinschränkung der fortlaufenden Kursnummer auftritt
(
WHERE n<=spGetN() AND n>spGetN()-14),
können die Anfragen hiermit be-
schleunigt werden. Im besten Fall ergibt sich nur noch logarithmische Suchzeit zum
Aunden der Joinpartner, wenn Verfahren wie Index- oder Hash-Join verwendet
werden. Diese Operatoren aus der physischen Datenverwaltung nden Join-Partner,
indem sie in einem Suchbaum nach einem Indexwert suchen oder in dem sie in einer
geordneten Liste die als Index verwendeten Attribute linear durchlaufen.
Für Indikatoren mit mehrfacher Aggregation werden mehrere materialisierte Sich-
74
8.1. Materialisierte Sichten in TInTo
Name
Zweck
tmpADX0
Zwischen-Aggregation des ADX-Indikators
tmpAggregation
Vor-Aggregation der Werte gemäÿ gewählter Chart-Auösung
tmpCCI_MD
Abspeicherung der bisherigen mittleren Abweichung
(Mean Deviation) für den CCI
tmpCCI_MD_p
Abspeicherung der Änderung der bisherigen
mittleren Abweichung
tmpCCI0
Zwischen-Aggregation des CCI
tmpCCI0_Seed
Neue Daten in der Zwischenaggregation des CCI
tmpChart
Abspeicherung der berechneten Indikatorwerte
tmpFSTOC
2. Stufe der Zwischen-Aggregation des FSTOC
tmpFSTOC0
1. Stufe der Zwischen-Aggregation des FSTOC
tmpTHLR
Berechnung der True-High-Low-Range
Tabelle 8.1.: Materialisierte Sichten und Hilfsrelationen in TInTo
ten erforderlich, für jede Aggregationsschicht ist jeweils eine materialisierte Sicht
erforderlich. In der Ur-Version von TInTo wurden diese Sichten durch eine angehängte Zier bezeichnet, so wird beispielsweise die Zwischensicht des CCI mit CCI0
bezeichnet. Die Tabellen, in denen diese Sichten gespeichert werden, wurden nun
der besseren Erkennbarkeit halber mit dem Sichtennamen und dem Präx tmp
bezeichnet. Tabelle 8.1 gibt eine Übersicht über die angelegten Hilfsrelationen und
materialisierten Sichten.
Weiterhin wurden in der Tabelle
tmpChart
Hilfsattribute angelegt, die für die
Berechnung zusammengesetzter Aggregierungsfunktionen benötigt werden, d. h. für
Aggregierungsfunktionen, die selbst durch mathematische Operationen wieder miteinander verbunden sind. In den Hilfsattributen lassen sich dann die einzelnen Terme
so abspeichern, so dass die inkrementelle Neuberechnung dieser Teilterme erfolgen
kann. Anschlieÿend werden die aktualisierten Terme neu miteinander verrechnet.
Neben den Hilfsrelationen wurden auch einige
griert. Die ersten beiden Funktionen
myMin
und
Hilfsfunktionen
myMax
in TInTo inte-
dienen dabei dazu, das
Maximum bzw. das Minimum von zwei Zahlen zu nden:
Public Function myMax(x1, x2) As Variant
If x1 > x2 Then myMax = x1 Else myMax = x2
End Function
Die
Funktion
kürzt
somit
die
im
Access-SQL-Dialekt
IIF(Wenn, Dann, Sonst) ab. Standard-SQL bietet
myMin ist analog deniert.
verwendete
Schreibweise
hierfür ferner das
Case-Kon-
strukt an. Die Funktion
Eine weitere Funktion löst das Problem, dass es in Access nicht möglich ist, fortlaufende Nummern zu vergeben. Diese werden aber anstatt eines AutoWerts in
den materialisierten Sichten benötigt. Die Funktion
AutoIncrement
ist wie folgt
programmiert:
75
8. Änderungspropagierung zur Indikatorberechnung in TInTo
Public Function AutoIncrement(Dummy As Variant,
Optional Reset As Boolean) As Long
Static x
x = x + 1
If Reset Then x = 0
AutoIncrement = x
End Function
Die Funktion inkrementiert einen statischen Zähler
wird. Falls das Argument
Die Variable
Dummy
Reset
x,
dessen Wert zurückgegeben
wahr ist, wird der Zähler auf Null zurückgesetzt.
ist notwendig, da einmal ausgewertete Funktionen von Access
nicht erneut für ein Tupel aufgerufen werden, sofern die Argumente übereinstimmen.
Übergibt man nun ein Attribut als Parameter, so wird das DBMS getäuscht und
wertet die Funktion erneut aus. Falls das optionale Argument
Reset
auf True
gesetzt ist, so wird der Zähler zurückgesetzt.
Die Funktion
getVolStart() liefert den Attributwert VolStart des neuesten
tmpChart, falls im Hauptfenster ein Intraday-Zeitraum aus-
Tupels aus der Tabelle
gewählt ist:
Public Function GetVolStart() As Double
GetVolStart = 0
On Error GoTo error_Get_Vol_Start
Dim r As Recordset
Set r = CurrentDb.OpenRecordset("SELECT Vol FROM " & _
"tmpChart WHERE n = (SELECT MAX(n) FROM tmpChart)")
GetVolStart = r!Vol
Set r = Nothing
If Forms.main.TimeRange.Column(2) = False Then _
GetVolStart = 0
error_Get_Vol_Start:
End Function
Ob
ein
Bereich
mit
frage
am
Ende
durch
fragt.
Die
Funktion
Intradaydaten
Abfrage
kürzt
unter
des
ausgewählt
ist,
Steuerelements
Verwendung
des
wird
im
in
der
Hauptfenster
DAO-Ob jekts
den
IF-Ababge-
SQL-Aus-
IIF(Forms.Main.TimeRange.Column(2)=TRUE,(SELECT Volstart
FROM tmpChart WHERE n=(SELECT MAX(n) FROM tmpChart)),0) ab, der
druck
genauso verwendbar wäre, aber den Code aufblähen würde. Bei Verwendung eines
automatischen Regelcompilers würde man dem sicher den Vorzug geben. Der Volumen-Wert wird benötigt, um bei Beginn einer neuen Periode das Handelsvolumen,
mit dem die letzte Periode endete, festzustellen, da
Yahoo! kumulierte
Daten liefert
(siehe auch Abschnitt 6.4).
Der Kurswert, welcher die Änderungspropagierung auslöst, wird in einer speziellen
Hilfsrelation
TSeed gespeichert. Diese kann von den Delta-Regeln während der Abar-
beitung abgefragt werden. Somit erübrigt sich eine Suche nach dem neuen Kurswert.
Die Kurswerte werden bereits vor der Indikatorberechnung aggregiert. Wie in der
76
8.2. Verwaltung spezialisierter Änderungsanweisungen
Tabelle 6.2 auf S. 47 zu sehen, werden dafür die Zeitwerte der Kurse auf bestimmte
Werte gerundet. So wird für die wochenweise Aggregierung der Datumswert durch 7
integer-dividiert und anschlieÿend wieder mit 7 multipliziert, so dass von einem 7-Tage-Intervall immer der erste Tag als Datumswert in der Aggregation gespeichert wird.
Die gleiche Rundung muss auch für den abgerufenen Zeitwert durchgeführt werden,
damit die passende Aggregierungsgruppe gefunden werden kann. Aus diesem Grund
wird der Datumswert mit der gleichen Funktion gerundet, die auch in der Aggregation verwendet wurde. Die Rundung wird durch die Funktion
Aggregate_New
übernommen:
Public Function Aggregate_New(Ti As Date) As Date
Dim AggrStr As String
If IsNull(Forms.main.Frequency.Column(3)) Then Exit Function
If Forms![main]!TimeRange.Column(2) Then
AggrStr = Replace(Forms.main.Frequency.Column(3), _
"TIntraday.[Date]","#" & _
Format(Ti,"mm\/dd\/yyyy hh:mm") & "#")
Else
AggrStr = Replace(Forms.main.Frequency.Column(3),_
"TKurs.[Date]", "#" & Format(Ti, "mm\/dd\/yyyy") & "#")
End If
Aggregate_New = Eval(AggrStr)
End Function
Dazu wird zunächst aus dem Kombinationsfeld, in dem die Auösung ausgewählt
werden kann, der zugehörige Aggregierungsstring abgefragt. Dieser kann zum Beispiel
CDate(Fix(TIntraday.[date])+Hour(TIntraday.[Date])/24)
für die Aggregierung pro Stunde lauten. Die Referenz auf die Kurstabelle wird dann
durch das jeweilige Datum, das der Funktion übergeben wurde, ersetzt, wobei das
Datum noch passend formatiert wird. Dadurch entsteht ein String, der eine Formel
enthält. Mittels der VBA-eigenen Funktion
eval,
die das mathematische Ergebnis
eines solchen Strings zurückgibt, wird dann das Ergebnis berechnet, mit dem das
Datum auch bei der Neuberechnung aggregiert würde.
8.2. Verwaltung spezialisierter Änderungsanweisungen
Die spezialisierten Änderungsanweisungen wurden in der selben Tabelle
TView
ab-
gespeichert, die auch die Indikatordenitionen aufnimmt. Bereits in der Vorversion
war es möglich, beispielsweise für mehrstuge Aggregationen und rekursive Indikatoren, mehrere SQL-Ausdrücke zu hinterlegen. Diese wurden durch das in SQL sonst
nicht auftretenden Paragraphen-Zeichen (Ÿ) getrennt. Diese Kodierung wurde auch
für die Änderungsregeln übernommen. Somit ist nun zu jedem Indikator ein Satz von
Änderungsanweisungen, getrennt durch Ÿ-Zeichen, im Attribut
SQLUpdate hinter-
legt. In den Änderungsanweisungen kann prinzipiell jedes gültige SQL-Statement
77
8. Änderungspropagierung zur Indikatorberechnung in TInTo
hinterlegt werden. Sofern für einen Indikator noch kein Satz von Änderungsanweisungen hinterlegt ist, stellt das System dies ebenfalls fest und bricht in diesem Fall
die Änderungspropagierung mit einer Fehlermeldung ab.
8.3. Timer-gesteuertes Pulling neuer Kursdaten
Bei der Verarbeitung von Datenströmen kommen grundsätzlich zwei Verfahren in Betracht [BFO04]: Die Daten können aktiv von auÿen in ein System eingespeist werden,
welches auf das Ereignis der Datenankunft reagiert (Push-Ansatz) oder das System
fragt selbst die Daten ab (Pull-Ansatz). Da
Yahoo! zwar
Daten zur Verfügung stellt,
aber keine Ereignisse liefert, verblieb nur der Pull-Ansatz. Da die Kurse fortlaufend
und von selbst angezeigt werden sollten, el die Wahl auf ein Timer-gesteuertes Pulling. In Access kann ein Timer über ein besonderes Verfahren realisiert werden: Jedes
Formular besitzt eine Eigenschaft Zeitgeberintervall und das Ereignis Bei Zeitgeber. Nach Ablauf des eingestellten Zeitintervalls kann eine Visual Basic-Prozedur
aufgerufen werden, die dann wiederum weitere Aktionen auslösen kann. Wird die
Ereignisroutine nicht beendet, bevor das nächste Zeitereignis ausgelöst wird, so wird
das Ereignis direkt nach Abschluss der vorherigen Ereignisroutine ausgelöst.
Es wurde also ein Formular IntradayTimer angelegt. Das Zeitgeberintervall wurde zunächst auf 10 000 ms gesetzt. Der Benutzer hat über das Optionsformular die
Möglichkeit, die Aktualisierungsfrequenz einzustellen. Mittels eines Kombinationsfelds werden ihm dazu verschiedene Auswahlmöglichkeiten zur Verfügung gestellt,
es besteht jedoch auch die Möglichkeit zu einer freien Eingabe. Der Timer ist beim
Start von TInTo deaktiviert, da während des Datenabrufs das System verlangsamt
wird, so dass der Benutzer Schwierigkeiten hat, Einstellungen vorzunehmen. Erst
bei Betätigung der Schaltäche Start/Stop Polling wird der Datenabruf aktiviert.
Über einen erneuten Klick auf die Schaltäche wird der Datenabruf wieder beendet. In der Ereignisroutine des Timers wurde der Datenabruf und die Auslösung der
Änderungspropagierung implementiert:
1
2
3
4
5
6
7
8
9
10
Private Sub Form_Timer()
Dim r As Recordset
Set r = CurrentDb.OpenRecordset("TWertpapier")
r.MoveFirst
While Not r.EOF
saveRTQuote getRTQuote(r.Fields("Symbol"))
r.MoveNext
Wend
’... (ab hier Löschung alter Daten)
End Sub
Zunächst wird also die Tabelle
TWertpapier,
die die Kürzel der Wertpapiere des
Portfolios erhält, durchlaufen. Der Aufruf in Zeile 6, ruft die Daten aus dem Internet
über die Funktion
78
getRTQuote ab und sichert den zurückerhaltenen String mittels
8.4. Abarbeitung der Delta-Regeln
saveRTQuote in der Datenbank
mittels der Split-Funktion:
ab. Letztere Funktion zerlegt dabei den String
quoteString = Replace(quoteString, ",", ".")
v = Split(quoteString, ";")
v
ist eine Variant-Variable, die in VBA auch als dynamisches Array fungiert. Dieses
Array enthält nach Aufruf der
Split-Funktion
alle Stringbestandteile als Einträge.
Aus diesen wird dann ein String mit einer SQL-Insert-Anweisung erstellt. Diese Anweisung wird dann ausgeführt und speichert so die Daten in der Intraday-Tabelle
ab. Die Funktion schreibt dann den String in die textuelle Anzeige des Hauptfensters. Sofern es sich um den Kurs des gerade angezeigten Wertpapiers handelt, wird
die Tabelle
TSeed
gelöscht und der soeben abgerufene Kurs in diese geschrieben.
Zuletzt wird dann die Unterroutine aufgerufen, die für die Änderungspropagierung
selbst und das Neuzeichnen der Chartdarstellung verantwortlich ist.
Sollte der zu zerlegende Rückgabestring fehlerhaft sein, weil beispielsweise der
Yahoo! -Server
ausgefallen ist, wird die Funktion abgebrochen. Die Funktion wurde
bewusst so angelegt, dass die abgefragten Daten schon vor Durchführung der Änderungspropagierung in der Tabelle
TIntraday abgespeichert sind. Da die in der
tmpAggregation schon bei der ersten
Änderungspropagierung verwendete Tabelle
Berechnung des Charts von der Intraday-Tabelle entkoppelt wurde, stört dies die
Änderungspropagierung nicht, jedoch ist der Kurs schon gesichert, falls die Änderungspropagierung fehlschlagen sollte.
8.4. Abarbeitung der Delta-Regeln
AddValue wurde der Funktion
ChartShow nachgebildet, die seit der ursprünglichen TInTo-Version zum erstmali-
Die vom Timer als letztes aufgerufene Unterroutine
gen Zeichnen des Charts dient. Zunächst werden einige Parameter gesetzt, beispielsweise die Skalierung und ob ein interner Indikator verwendet werden soll oder nicht.
Dann wird für den im Hauptfenster ausgewählten Indikator abgefragt, ob bereits
Delta-Regeln eingegeben worden sind. Falls dies nicht der Fall ist, wird die Funktion an dieser Stelle mit einer Fehlermeldung abgebrochen. Anschlieÿend ndet das
eigentliche Bottom-Up-Verfahren zur Änderungspropagierung statt:
sqlStatements = Split(DLookup("SQLUpdate", "TView", _
"[Name] = ’" & sInd & "’"), "§")
If IsNull(sqlStatements(0)) Then
MsgBox "No SQL-Update statements available. Exiting.", _
vbCritical
Exit Function
End If
. . . Spaltenprüfung, nicht abgedruckt. . .
Workspaces(0).BeginTrans
blnTrans = True
79
8. Änderungspropagierung zur Indikatorberechnung in TInTo
For sqlI = 0 To UBound(sqlStatements)
CurrentDb.Execute sqlStatements(sqlI)
Next sqlI
Workspaces(0).CommitTrans
blnTrans = False
Die Regeln werden zunächst am Ÿ-Zeichen aufgebrochen und in ein Variant-Feld
sqlStatements
geschrieben, wobei jeder Feldinhalt einer Regel entspricht. Sollte
dieses Feld leer sein, wurden für den Indikator noch keine Delta-Regeln eingegeben
und die Funktion wird daher abgebrochen. Anschlieÿend wird mit dem Methodenaufruf
BeginTrans des Workspace-Objekts eine Transaktion begonnen. In einer For-
Schleife wird nun jede einzelne Delta-Regel ausgeführt. Nach Ende der Schleife wird
die Transaktion mit
CommitTrans beendet. Sollte während des Schleifenablaufs ein
Fehler auftreten, so wird die Transaktion abgebrochen, der Benutzer per Dialogbox
informiert und die Funktion verlassen. Fehler, die zum Abbruch der Transaktion führen, treten z. B. dann auf, wenn in den Delta-Regeln Syntaxfehler vorhanden sind. Da
die eigentlichen Intraday-Daten schon vorher in die Tabelle
TIntraday geschrieben
wurden, gehen auch bei einem Fehlschlag der Änderungspropagierung die abgerufenen Kursdaten nicht verloren. Nach einem Fehler kann der Benutzer den Chart
nochmals neu zeichnen, wobei alle materialisierten Tabellen komplett neu berechnet
werden und somit der Chart wieder korrekt ist. Die Variable
blnTrans dient dazu,
sich zu merken, ob gerade eine Transaktion läuft oder nicht, da man dies in Access
nicht explizit abfragen kann. Andererseits tritt aber bei einem Rollback ohne laufende Transaktion ebenfalls ein Fehler auf. Die Fehlerbehandlung fragt daher diese
Variable ab:
errChartShow:
MsgBox Err.Description
If blnTrans Then Workspaces(0).Rollback
Im obigen Listing nicht abgedruckt wurde die Prüfung, wie viele Spalten in der ursprünglichen Indikatordenition angegeben wurden. Dies ist vonnöten, um die richtige Anzahl an Arrays an den ChartDirector übergeben zu können, für die eigentliche
Änderungspropagierung ist dies aber nicht wesentlich.
Nach Abschluss der Änderungspropagierung werden die Indikatorwerte aus der
materialisierten Sicht
tmpChart mittels DAO eingelesen, in Arrays geschrieben und
diese anschlieÿend an das ChartDirector-Ob jekt übergeben. Anschlieÿend wird gegebenenfalls noch festgelegt, welcher interne Indikator gezeichnet werden soll, und die
Methode zur Neuzeichnung aufgerufen.
Abbildung 8.1 zeigt schematisch die Verarbeitung der abgefragten Kurswerte.
80
8.5. Aufbau der Delta-Regeln
Yahoo!-Server im Internet
Parser
Anzeige
TSeed
TIntraday
Zwischenaggregation
tmpChart
Array im RAM
ChartDirector
Abbildung 8.1.: Schema der Verarbeitung neu eintreender Kurswerte vom Internetabruf bis zur Anzeige
8.5. Aufbau der Delta-Regeln
Eine der Hauptaufgaben bei der Erweiterung um die Änderungspropagierung lag in
der Erstellung der Delta-Regeln. Da die bisherigen Arbeiten zum Thema UpdatePropagierung Delta-Regeln meist in einer theoretischen Sprache wie Datalog oder
auch der relationalen Algebra beschreiben, wurde die gesamte Umsetzung in eine
Folge von SQL-Anweisungen erstmalig erarbeitet. Zusätzlich wurden auch noch die
selbstentwickelten mathematischen Berechnungen, die für Änderungen auf Aggregationsfunktionen erforderlich sind, implementiert. Dabei stellten die Einschränkungen
des Access-Systems noch einige Hindernisse dar. Zunächst war klar, dass es, wie
in Kapitel 7 angedeutet, bei Updates auf aggregierten Daten Fallunterscheidungen
geben muss, da eine Einfügung in neue oder existierende Gruppen möglich ist. Aufgrund der speziellen Tatsache, dass Indikatorwerte aus Gruppen nicht mehr gelöscht
werden, war zudem klar, dass nicht überprüft werden muss, ob eine Gruppe aufgrund von Löschungen wegfallen muss oder nicht. Dafür ist es aber notwendig, dass
bei Hinzukommen einer neuen Aggregationsgruppe die älteste Aggregationsgruppe
aus dem Indikatorchart zu entfernen ist, damit die Fenstergröÿe der Chartdarstellung immer gleich bleibt. Auf diese Weise entsteht dann gewissermaÿen ein sliding
window, welches sich bei jeder neuen Aggregationsgruppe um eine Einheit in die
Zukunft schiebt. Hierfür ist es notwendig, unterscheiden zu können, ob eine Gruppe
81
8. Änderungspropagierung zur Indikatorberechnung in TInTo
hinzugekommen war, bevor die Löschung durchgeführt wird. Im umgekehrten Fall
kann es sonst zu Problemen kommen, wenn die Berechnungsperiode gröÿer ist als die
Anzahl der vorhandenen Gruppen und so eine noch benötigte Gruppe zu früh aus
der Berechnungsgrundlage entfernt wird.
Die Delta-Regeln wurden schrittweise für einige Indikatoren erstellt. Dabei wurden
beispielsweise für den Indikator SMA (gleitender Durchschnitt), der zur Klasse der
Indikatoren mit einfacher Aggregation zählt, zunächst die Regeln für die Einfügung in
eine vorhandene Gruppe implementiert, die somit zu einer Update-Anweisung wird.
Zur Erinnerung sei hier noch einmal die Berechnungsvorschrift aus Gleichung 3.3 für
den SMA aufgeführt:
Pn−1
SMAn
(t) =
i=0
Close
(t − i)
n
Die im TInTo-System nunmehr verwendete Abfrage für den SMA lautete:
SELECT TK.ID, TK.n, TK.Date, TK.High, TK.Low,
TK.Open, TK.Close, TK.Vol, AVG(TK1.Close) AS Ind1
FROM tmpAggregation AS TK
INNER JOIN
tmpAggregation AS TK1 ON (TK.ID=TK1.ID)
WHERE TK.ID=spGetID()
AND TK1.n<=TK.n
AND TK1.n>=TK.n-spGetPar("Periodenvorgabe Glättung=10")
GROUP BY TK.ID, TK.n, TK.Date, TK.High, TK.Low,
TK.Open, TK.Close, TK.Vol
ORDER BY TK.ID DESC, TK.Date DESC
Es wird hier also für jeden Wert der Mittelwert über die vorausgegangenen
n+1
Schlusskurse gebildet. Wie bereits im Kapitel 7 beschrieben, lässt sich die Mittelwertsfunktion
Avg
inkrementell durch Zerlegung aktualisieren. Bei Update einer
Aggregationsgruppe wird sich stets der Schlusskurs der letzten (jüngsten) Aggregationsgruppe ändern. Somit muss auch der für diese Aggregationsgruppe errechnete
Mittelwert geändert werden. Da sich die Anzahl der Werte, über die der Mittelwert
berechnet wird, nicht ändert, vereinfacht sich die Aktualisierung gegenüber der vorgestellten allgemeinen Formel 7.4 erheblich. Der neue Mittelwert kann demnach einfach
mit der Formel
AVGnew
= AVGold +
xnew − xold
n+1
errechnet werden. Da sich der neue Schlusswert in der Hilfsrelation
but
Last
(8.1)
TSeed im Attri-
bendet, lautet somit die Update-Anweisung:
UPDATE tmpChart, Tseed SET tmpChart.Ind = tmpChart.Ind
-tmpChart.Close/
(SpGetPar("Periodenvorgabe=10")+1)
+Tseed.Last/
(SpGetPar("Periodenvorgabe=10")+1),
...
82
8.5. Aufbau der Delta-Regeln
Dabei ist zu beachten, dass aufgrund des Vergleichs mit ≤
und ≥
im ursprüngli-
chen SQL-Ausdruck der Divisor noch um eins erhöht werden muss, um den richtigen
Wert zu erhalten. Neben den Indikatorwerten müssen auch noch die Werte für den
Kurschart aktualisiert werden. Für ein Gruppen-Update ist dabei folgendes zu tun:
•
Ist der neue Kurswert höher als der bisherige Höchstwert, so ist der Höchstwert
auf den neuen Kurswert zu setzen.
•
Ist der neue Kurswert niedriger als der bisherige Tiefstwert, so ist der Tiefstwert
auf den neuen Tiefstwert zu setzen.
•
Der Schlusskurs ist stets auf den letzten Wert zu setzen.
•
Der Erönungskurs bleibt stets gleich.
•
Das Volumen ist auf das aktuelle Handelsvolumen seit Beginn des Handelstages,
abzüglich des Handelsvolumens bei Beginn der Gruppe zu setzen.
Die ersten beiden Aktualisierungen sind im Access-Dialekt von SQL durch die
IIF-
Funktion durchführbar. Deren Syntax lautet
IIF(Bedingung, Wenn, Sonst)
und liefert bei wahrer Bedingung den Wenn-Wert, bei unwahrer Bedingung den
Sonst-Wert. Somit lautet eine Updatezuweisung für den Höchstwert:
tmpChart.High=
IIF(Tseed.Last>tmpChart.High, TSeed.Last, tmpChart.High),
Da der Höchstwert in den Delta-Regeln öfters verwendet wird, wird bei Verwendung
dieser Funktion der SQL-Code schnell unübersichtlich. Daher wurde eine benutzerdenierte Funktion
myMax
angelegt, die jeweils das Maximum beider Argumente
zurückgibt. Somit lautet die Zuweisung:
tmpChart.High=myMax(Tseed.Last, tmpChart.High),
Für den Tiefstkurs läuft die Aktualisierung entsprechend ab. Die Aktualisierung des
Schlusskurses erfolgt einfach durch Zuweisung von
dient gesonderte Beachtung, da
Yahoo! jeweils
TSeed.Last.
Das Volumen ver-
das Volumen seit Beginn des Handels-
tages liefert. Für eine Gruppierung, die feiner als einen Tag gruppiert, muss daher
das Volumen zu Gruppenbeginn abgezogen werden. Dieses wird bei der Aggregierung
für jede Gruppe im Attribut
VolStart
abgespeichert. Somit lautet die Zuweisung
für das Volumen:
tmpChart.Vol = Tseed.Vol-tmpChart.Volstart,
In der Delta-Regel bendet sich nun noch eine weitere Zuweisung, die aufgrund des
sliding Window
notwendig ist. Wie bereits oben angesprochen, müsste ein Fallun-
terscheidung durchgeführt werden. Da diese aber im SQL-Dialekt von Access nicht
möglich ist, muss sie mittels eines Tricks durchgeführt werden. Es ist zwar auch möglich, dass man die Fallunterscheidung in Visual Basic programmiert und dann jeweils
83
8. Änderungspropagierung zur Indikatorberechnung in TInTo
die passenden Regeln vom System auswählen lässt, was aber wieder zu einer Vermischung von Datenbanksprache und Programmiersprache führen würde. Daher sollte
ein Weg gefunden werden, auch die Fallunterscheidung in SQL ausdrücken zu können.
Der Trick besteht darin, dass sich das System merkt, ob eine Gruppenaktualisierung
oder eine Gruppeneinfügung stattgefunden hat. Dazu wurde in der Seed-Tabelle das
Attribut
Delete angelegt. Dieses wird später in einer Löschabfrage abgefragt. Da in
dieser Regel das Update kodiert wurde, ist das Attribut auf falsch zu setzen, somit
bendet sich in der Delta-Regel die Zuweisung
Tseed.Delete = False
Die andere Fallunterscheidung muss unterscheiden, ob überhaupt eine Aktualisierung oder doch eine Einfügung durchgeführt werden soll. Dieses kann durch eine
entsprechende
Where-Klausel
erreicht werden. Diese lautet
WHERE Round(tmpChart.[Date],5) = Tseed.[Date]
tmpChart aus, die nicht
Where-Bedingung falsch, dann ist
Gleichzeitig selektiert diese Bedingung auch alle Werte aus
die aktuellste Gruppe repräsentieren. Ist diese
das Kreuzprodukt aus
tmpChart und TSeed leer. Somit wird keine der ZuweisunTSeed.Delete nicht auf falsch
gen ausgeführt, folglich wird auch das Attribut
gesetzt. Die Anwendung der Round-Funktion rührt daher, dass in den ersten Tests
der zunächst unerklärliche Eekt auftrat, dass die
Where-Bedingung auch dann zu
falsch ausgewertet wurde, wenn der Datumswert augenscheinlich schon in der Tabelle vorhanden war. Es stellte sich heraus, dass oensichtlich durch verschiedene
Rundungen die beiden Datumswerte, die intern als Flieÿkommazahlen (vergangene
Tage seit dem Jahr 1900) gespeichert werden, in den Nachkommastellen Dierenzen aufwiesen. Leider führte auch eine Rundung während der Speichervorgänge nicht
immer zum Erfolg, so dass die Rundung in die Delta-Regeln übernommen werden
musste. Diese Rundung könnte sich eventuell negativ auf die Laufzeit auswirken. Eine
weitere Möglichkeit hätte eventuell noch darin bestanden, den Zeitwert als String abzuspeichern, wobei ein Stringvergleich, insbesondere bei gleichem Stringanfang, auch
laufzeitintensiv sein kann.
Es
folgt
die
Anweisung
für
eine
Gruppeneinfügung.
Diese
darf
erst
nach
der
Update-Anweisung ausgeführt werden, weil im umgekehrten Fall die schon erweiterte Tabelle aktualisiert würde, was gegebenenfalls zu falschen Ergebnissen, zumindest
aber zu Doppelberechnungen führen kann. Im Prinzip gestaltet sich die Berechnung
für den neuen Indikatorwert recht ähnlich, nur dass hier aus dem Mittelwert nicht der
neueste, veraltete Wert, sondern der erste Wert entfernt werden muss. Somit lautet
die Zuweisung für den neuen Indikatorwert
[T1].[Ind][tmpChart].[Close]/(SpGetPar("Periodenvorgabe=10")+1)+
[TSeed].[Close]/(SpGetPar("Periodenvorgabe=10")+1) AS Ind
wobei
T1
die Selektion der Charttabelle referenziert, die nur die letzte Gruppe re-
ferenziert, während
84
tmpChart
die Charttabelle mit der Gruppe, versetzt um die
8.5. Aufbau der Delta-Regeln
Periodenvorgabe, referenziert. Die Aktualisierung der Erönungs-, Schluss-, Tiefstund Höchstkurse gestaltet sich bei einer Einfügung einer neuen Gruppe sehr einfach,
da diese am Anfang alle gleich dem neuen Wert sind. Erst durch die nachfolgenden
Updates entfernen sich die Werte voneinander. Weiterhin muss noch die neue Kursnummer festgelegt werden, was mittels der in Abschnitt 8.1 vorgestellten Funktion
AutoIncrement
geschieht. Die Auswahl der passenden Tupel und die Fallunter-
scheidung erfolgen wiederum mittels der
Where-Bedingung:
FROM tmpChart, tmpChart AS T1, TSeed
WHERE Tseed.[Date]
NOT IN (SELECT Round([Date],5) FROM tmpChart)
AND
(((tmpChart.n)=(SELECT MAX(n) FROM tmpChart)SpGetPar("Periodenvorgabe=10"))
AND
((T1.n)=(SELECT MAX(n) FROM tmpChart)));
Die Fallunterscheidung erfolgt in diesem Fall durch die
Not In-Bedingung: nur wenn
in der Charttabelle der entsprechende Datumswert nicht vorhanden ist, wird die
Insert-Anweisung
durchgeführt, da anderenfalls die
Where-Bedingung
falsch ist.
Als letztes wird die Löschung der ersten Gruppe durchgeführt, falls erforderlich.
Die Löschanweisung lautet
DELETE *
FROM tmpChart
WHERE tmpChart.n =
(SELECT Min(n) FROM tmpChart)
AND
(SELECT Delete FROM TSeed) = TRUE
und wird folglich nur dann ausgeführt, wenn das Löschattribut in der Seedtabelle
noch gesetzt ist. Neben dem SMA gibt es noch andere Indikatoren mit einstuger
Aggregation. Im Wesentlichen unterscheiden sich die Delta-Regeln durch die inkrementelle Berechnung des Indikatorwertes, das restliche Verfahren bleibt gleich. Einige
Indikatoren benutzen Indikatorfunktionen, die aus mehreren Aggregationsfunktionen
zusammengesetzt sind. Hier wurden die Terme soweit zerlegt, bis die Teilterme wieder
inkrementell änderbar waren. Für Indikatoren, die die Minimums- und Maximumsfunktion verwenden, konnte der Indikatorwert bei Gruppeneinfügungen freilich nicht
berechnet werden, da nicht bekannt ist, ob der vorderste (zu entfernende) Wert der
Gruppe gerade das Minimum oder das Maximum darstellt. Auch ein Gleichheitstest
kann hier nicht weiterhelfen, da ein Extremwert in einer Gruppe durchaus mehrmals
auftreten kann. Statt der im Abschnitt 7.2.2 vorgestellten Technik zum Aunden
des zweithöchsten Wertes wurde in der Implementierung der Delta-Regeln die naive
Neuberechnung der Extremwerte gewählt, was vertretbar scheint, da die Periodendauer im Allgemeinen so gering ist, dass die vorgestellten Techniken mehr Overhead
erzeugen würden.
85
8. Änderungspropagierung zur Indikatorberechnung in TInTo
Auch für mehrstuge Aggregatfunktionen wurden Delta-Regeln erzeugt. Im Prinzip handelt es sich um die Mehrfachanwendung der eben vorgestellten Regel für die
einfache Aggregation. Neben der oben bereits verwendeten Zieltabelle
tmpChart
wurden Zwischentabellen angelegt, die die Aggregationsstufen widerspiegeln. Daneben wurden Seed-Tabellen für die einzelnen Zwischenrelationen angelegt. Es ist aber
auch möglich, die jeweils hinzugekommenen Werte in der Tabelle der nächstunteren Stufe zu suchen, was mit einem gewissen Laufzeitaufwand verbunden ist. Bei
geeigneter Indexwahl lässt sich eine solche Indexsuche allerdings in logarithmischer
Zeit durchführen, so dass der Suchaufwand kaum noch ins Gewicht fällt. Als Beispiel
für eine solche mehrstuge Aggregierung soll hier der Indikator CCI (Commodity
Channel Index) dienen. Wiederum sei an die Berechnungsvorschrift des Indikators
erinnert:
(t) − SMATPn (t)
0, 015 · MDn (t)
TP = High + Low + Close
P
i=0 n − 1 |TP(t − 1) − SMATPn (t − i)|
MDn (t) =
n
CCI
(t) =
TP
(8.2)
Die erste Aggregation ist also für den gleitenden Durchschnitt des typischen Preises
durchzuführen, dann für die mittlere Abweichung (MDn ), die dritte dann für den
CCI selbst.
Zuerst wird daher die Tabelle
tmpCCI0_Seed geleert. Diese nimmt den SMATP
auf:
DELETE * FROM tmpCCI0_Seed
Danach wird die Tabelle
tmpCCI_Seed
mit dem neuen SMATP-Wert gefüllt,
sofern der Fall einer Gruppenaktualisierung vorliegt:
INSERT INTO tmpCCI0_Seed(ID,n,[Date],[Open],High,Low,[Close],
Vol,Ind1)
SELECT TSeed.ID, TSeed.n, TSeed.[Date], tmpCCI0.Open,
myMax(Tseed.Last,tmpCCI0.High) AS High,
myMin(Tseed.Last,tmpCCI0.Low) AS Low,
TSeed.Last, TSeed.Vol, tmpCCI0.Ind1((tmpCCI0.High+tmpCCI0.Low+tmpCCI0.Close)/3)/
(SpGetPar("Periodenvorgabe=20"))
+((Tseed.Last+Tseed.Low+Tseed.High)/3)/
(SpGetPar("Periodenvorgabe=20")) AS Ind1
FROM tmpCCI0, TSeed
WHERE Round([tmpCCI0].[Date],5)=round([Tseed].[Date],5);
Die Berechnungsvorschrift ähnelt sehr der im vorigen Abschnitt beschriebenen, da es
sich hierbei ebenfalls um einen gleitenden Durchschnitt handelt. Höchst- und TiefstKurs werden bei dieser Implementierung ebenfalls über die Hilfsrelation weitergeleitet. Es ist aber prinzipiell auch möglich, diese aus der Tabelle
86
TSeed zu berechnen.
8.5. Aufbau der Delta-Regeln
In einem weiteren Schritt wird dann die erste Zwischentabelle
der Tabelle
tmpCCI0
anhand
tmpCCI0_Seed aktualisiert. Dies geschieht mittels eines einfachen Up-
date-Statements, das einfach alle Attribute übernimmt:
UPDATE tmpCCI0_Seed, tmpCCI0 SET
tmpCCI0.ID = [tmpCCI0_Seed].[ID],
tmpCCI0.High = [tmpCCI0_Seed].[High],...
tmpCCI0.Ind1 = [tmpCCI0_Seed].[Ind1]
WHERE
Round([tmpCCI0].[Date],5)=Round([tmpCCI0_Seed].[Date],5);
Alternativ dazu besteht auch hier die Möglichkeit, die Werte direkt mittels einer
Update-Anweisung zuzuweisen, ohne den Umweg über eine gesonderte Relation zu
nehmen. Für diesen Indikator wurde dies jedoch explizit verwendet, um die eventuelle
Funktionsweise eines automatischen Regelcompilers zu testen. In anderen mehrstugen Aggregationen wurde diese Stufe fortgelassen. Es folgt anschlieÿend wieder das
Setzen des Löschattributs in der Tabelle
TSeed
(s.o.).
Anschlieÿend wird die Aktualisierung der Zwischentabelle für den Fall einer Gruppeneinfügung vorgenommen:
INSERT INTO tmpCCI0(ID,n,[Date],High,Low,Open,Close,Vol,Ind1)
SELECT
Tseed.ID, AutoIncrement(0,False) AS n, TSeed.[Date],
TSeed.Last,...,TSeed.Vol,
[T1].[Ind1]([tmpCCI0].[Close]+[tmpCCI0].[High]+
[tmpCCI0].[Low])/3/(SpGetPar("Periodenvorgabe=20"))+
([TSeed].[Close])/(SpGetPar("Periodenvorgabe=20")) AS Ind1
FROM tmpCCI0, tmpCCI0 AS T1, TSeed
WHERE Tseed.[Date]
NOT IN (SELECT Round([Date],5) FROM tmpCCI0)
AND (((tmpCCI0.n)= (SELECT MAX(n) FROM tmpCCI0)spGetPar("Periodenvorgabe=20"))
AND ((T1.n)=(SELECT MAX(n) FROM tmpCCI0)));
Aus der nun bereits aktualisierten Zwischentabelle für den SMATP kann jetzt die
mittlere Abweichung berechnet werden. Dies erfolgt wiederum mit Hilfe einer Zwischentabelle namens
tmpCCI_MD,
die die mittlere Abweichung als einziges Attri-
but enthält. Diese wird zunächst geleert:
DELETE * FROM tmpCCI_MD
Anschlieÿend wird die mittlere Abweichung neu berechnet. Diese muss unter Verwendung des typischen Preises der vergangenen Perioden neu berechnet werden, deshalb
ndet hierfür erneut eine Aggregation statt:
87
8. Änderungspropagierung zur Indikatorberechnung in TInTo
INSERT INTO tmpCCI_MD ( MD )
SELECT Avg(Abs(tmpCCI0.Ind1((tmpCCI0.Close+tmpCCI0.High+tmpCCI0.Low)/3)))
FROM tmpCCI0
WHERE (((tmpCCI0.n)>
(SELECT Max(n) FROM tmpCCI0)SpGetPar("Periodenvorgabe=20")));
Nach diesem Schritt liegen alle Werte vor, die zur Aktualisierung des eigentlichen
Indikatorwertes benötigt werden: Der SMATP bendet sich in
mittlere Abweichung in
tmpCCI_MD.
tmpCCI0_Seed, die
Entsprechend wird nun zuerst das Update
für den Fall einer Gruppenaktualisierung ausgeführt:
UPDATE tmpChart, tmpCCI0_Seed, tmpCCI_MD
SET tmpChart.Ind =(((tmpCCI0_Seed.Close
+myMax(tmpChart.High,tmpCCI0_Seed.High)
+myMin(tmpChart.Low, tmpCCI0_Seed.Low))/3)
-(tmpChart.In3-(tmpChart.Close+tmpChart.High+tmpChart.Low)/3
/(spGetPar("Periodenvorgabe=20"))
+(tmpCCI0_Seed.Close+myMax(tmpChart.High,tmpCCI0_Seed.High)
+myMin(tmpChart.Low,
tmpCCI0_Seed.Low))/3/(spgetpar("Periodenvorgabe=20"))))/
(0.015*(tmpCCI_MD.MD)),
tmpChart.In2 = tmpCCI_MD.MD,
tmpChart.In3 = tmpCCI0_Seed.Ind1,
tmpChart.High=TmpCCI0_Seed.High,
tmpChart.Low=TmpCCI0_Seed.Low,
tmpChart.Close=TmpCCI0_Seed.Close,
tmpChart.Vol = TmpCCI0_Seed.Vol
WHERE Round(tmpChart.[Date],5) = Round(tmpCCI0_Seed.[Date],5)
Man erkennt im obigen Beispiel eine Besonderheit von SQL, die bereits im Grundlagenkapitel angesprochen wurde: Alle Zuweisungen in SQL verlaufen simultan. Deshalb ist es möglich, den im Hilfsattribut
In3 abgespeicherten alten Wert des SMATP
zu verwenden, obwohl dieser später mit dem neuen Wert überschrieben wird. Diese Besonderheit führt auch dazu, dass in Indikatorberechnungen, die den Höchstund den Tiefstkurs verwenden, die Attribute
High
und
Low
noch nicht zur Ak-
tualisierung verwendet werden können, da diese noch mit dem alten Wert ausgewertet werden. Stattdessen muss hier nochmals die Funktion
myMax
oder
myMin
verwendet werden, was den Code vergröÿert. Glücklicherweise kann Access mehrfache Funktionsaufrufe mit den selben Argumenten erkennen, so dass hierdurch kein
Performanceverlust auftritt. Eine andere mögliche Lösung hätte in der Verwendung
mehrerer Update-Anweisungen hintereinander bestanden.
Nach der Behandlung der Gruppenaktualisierung wird nun die
für den Fall einer Gruppeneinfügung durchgeführt:
88
Insert-Anweisung
8.5. Aufbau der Delta-Regeln
INSERT INTO tmpChart
(n,[Date],High,Low,[Open],[Close],Vol,Ind,In2,In3)
SELECT DISTINCT AutoIncrement(0,False), TSeed.Date,
TSeed.Last, TSeed.Last, TSeed.Last,
TSeed.Last, TSeed.Vol,
((TSeed.Last)-tmax.In3((TOld.Close+TOld.High+TOld.Low)/3)/
SpGetPar("Periodenvorgabe=20")+
(TSeed.Close/SpGetPar("Periodenvorgabe=20")))/
(0.015*(tmpCCI_MD.MD)) AS Ind,
0 AS In2,
tMax.In3+TSeed.Close/SpGetPar("Periodenvorgabe=20")(tMax.Low+tMax.High+tMax.Close)/3/
SpGetPar("Periodenvorgabe=20") AS In3
FROM TSeed, tmpChart AS TMax, tmpChart AS TOld, tmpCCI_MD
WHERE (((TSeed.Date)
NOT IN (SELECT Round([Date], 5) FROM tmpChart))
AND ((TOld.n)=(SELECT Max(n) FROM tmpChart)spGetPar("Periodenvorgabe=20"))
AND ((TMax.n)=(SELECT Max(n) FROM tmpChart)));
Wie im vorausgegangenen Abschnitt wird danach als letztes die Gruppenlöschung
durchgeführt, die hier nicht nochmals abgedruckt ist, da sie vollkommen identisch
ist.
Schlieÿlich werden in TInTo auch rekursive Indikatoren unterstützt, als Beispiel soll
hier wieder der
MACD dienen. Christian Hübel hat in seiner Diplomarbeit [Hüb07]
ein Verfahren zu dessen Berechnung vorgestellt, das mit
Update-Anweisungen
ar-
beitet. Hier noch einmal die Denition des MACD:
(t) = (Close(t) − EMA(t − 1)) · Ew(t) + EMA(t − 1)
2
Ew(t) =
n+1
MACD(t) = EMA12 (t) − EMA26 (t)
EMA
Die ursprüngliche Denition des MACD verwendete bereits Hilfsattribute in der
Kurstabelle, in der die Werte für EMA und MACD gespeichert wurden. Für die
Änderungspropagierung wurde dieser Ansatz fortgeführt. Die Delta-Regelmenge unterscheidet sich daher auch nicht wesentlich von den Anweisungen zur ursprünglichen
Indikatorberechnung. Zuerst wird in einer ersten Update-Anweisung das Löschattribut in
TSeed
zurückgesetzt, falls die Aggregierungsgruppe schon vorhanden sein
sollte. Danach wird zunächst die neue Gruppe in der Tabelle
tmpAggregation
angelegt, sollte dies erforderlich sein:
1
2
3
INSERT INTO tmpAggregation
(ID,[Date],n,Open,High,Low,Close,Vol,v1,v2)
SELECT Agg.Id, Tseed.Date, Agg.n+1, Tseed.Last,
89
8. Änderungspropagierung zur Indikatorberechnung in TInTo
4
5
6
7
8
Tseed.Last, Tseed.Last, Tseed.Last,Tseed.Vol,
Tseed.Last, Tseed.Last
FROM tmpAggregation AS Agg, Tseed
WHERE Agg.n=(SELECT MAX(n) FROM tmpAggregation)
AND TSeed.Date NOT IN (SELECT Date FROM tmpAggregation)
Dabei werden die Wertpapier-ID und die fortlaufende Kursnummer aus der bisherigen
Aggregationstabelle übernommen, alle anderen Werte werden direkt der Seed-Tabelle
entnommen. Das gleiche wird entsprechend auch für die Chart-Tabelle durchgeführt:
INSERT INTO tmpChart(n,[Date],High,Low,Open,Close, Vol)
SELECT tmpChart.n+1, Tseed.Date, Tseed.Last, Tseed.Last,
Tseed.Last, Tseed.Last, Tseed.Vol
FROM tmpChart, Tseed
WHERE tmpChart.n = (SELECT MAX(n) FROM
tmpChart) AND Tseed.Date NOT IN (SELECT Date FROM tmpChart)
Die Situation nach diesem Schritt stellt sich wie folgt dar: Entweder ist die Aggregationsgruppe schon vorhanden und die letzten beiden Anweisungen waren eektlos, so
dass die Tabellen nicht verändert wurden. In den Hilfsattributen
v1 , v2 , v3
benden
sich in diesem Fall noch die alten Werte. Anderenfalls wurden in den Tabellen neue
Tupel (Gruppen) eingefügt, die in diesen Hilfsattributen noch NULL-Werte enthalten. In den letzten Schritten werden nun die gleichen Schritte durchgeführt, die auch
zur Erstberechnung durchgeführt wurden. Man beachte, dass jetzt in jedem Fall nur
noch
Update-Anweisungen
benötigt werden, da nicht vorhandene Gruppen schon
im Bedarfsfall eingefügt wurden. Zuerst werden also in der aktuellen Gruppe die
Hilfswerte auf den neuen Schlusswert gesetzt:
UPDATE
tmpAggregation, TSeed SET v1=Tseed.Last, v2=Tseed.Last WHERE
tmpAggregation.Date=Tseed.Date
Anschlieÿend werden die Werte von
v1 , v2
und
v3
basierend auf den vorherigen
Schlusswerten neu berechnet:
UPDATE Tseed, tmpAggregation
INNER JOIN
tmpAggregation AS TK0
ON (tmpAggregation.ID=TK0.ID
AND (tmpAggregation.n-1)=TK0.n)
SET tmpAggregation.v1=
((tmpAggregation.v1-TK0.v1)*2/(26+1))+TK0.v1,
tmpAggregation.v2=
((tmpAggregation.v2-TK0.v2)*2/(12+1))+TK0.v2,
tmpAggregation.v3=
((((tmpAggregation.v2-TK0.v2)*2/(12+1))+TK0.v2)(((tmpAggregation.v1-TK0.v1)*2/(26+1))+TK0.v1))
WHERE tmpAggregation.Date=Tseed.Date
90
8.5. Aufbau der Delta-Regeln
Hier wird die Zuweisungssemantik von SQL ausgenutzt, dass die
rechten Zuweisungsseite noch die Werte im Zustand vor der
v -Werte
auf der
Update-Anweisung dar-
stellen. Anschlieÿend wird in einem weiteren Berechnungschritt der Indikator-Wert
in
v3
endgültig berechnet:
UPDATE Tseed,tmpAggregation
INNER JOIN
tmpAggregation AS TK0
ON (tmpAggregation.ID=TK0.ID
AND (tmpAggregation.n-1)=TK0.n)
SET tmpAggregation.v3=
((tmpAggregation.v3-TK0.v3)*2/(9+1))+TK0.v3
WHERE tmpAggregation.Date=Tseed.Date
Nach diesem Schritt liegt nun in der Aggregationstabelle im Attribut
v3
der aktuelle
Wert vor. Dieser muss nun noch in die Charttabelle kopiert werden (Zuweisungen für
High und Close nicht abgedruckt):
UPDATE tmpChart, tmpAggregation, TSeed SET
tmpChart.Low = myMin(tmpChart.Low,Tseed.Last),...
tmpChart.Ind = (v2-v1)-v3,
tmpChart.In3 = (v2-v1),
tmpChart.In2 = v3
WHERE tmpAggregation.Date=tmpChart.Date
AND
Tseed.Date=tmpChart.Date
Damit sind alle relevanten Tabellen aktualisiert. Schlieÿlich muss noch die erste Gruppe gelöscht werden, falls das Löschattribut nicht zurückgesetzt wurde. Hier folgt
wieder die schon besprochene
Delete-Anweisung.
Natürlich wurden auch Delta-Regeln für die Indikatoren erstellt, die ganz ohne
Aggregation auskommen. Hier beschränkt sich die Anweisungsfolge auf zwei Anweisungen, die entweder eine neue Gruppe einfügen und die berechneten Werte im Indikator-Attribut ablegen oder eine vorhandene Gruppe aktualisieren. Sie entsprechen
somit im Prinzip den Regeln für Indikatoren mit einfacher Aggregation, nur dass
die inkrementelle Berechnung des Indikatorattributs entfällt. Stattdessen werden in
jedem Fall die Indikatorwerte neu berechnet. Hierzu ein Ausschnitt aus den Regeln
für den ADO:
UPDATE tmpChart,TSeed SET
tmpChart.Ind =
(myMax(TSeed.Last,tmpChart.High)-tmpChart.Open)+
(Tseed.Last-myMin(Tseed.Last,tmpChart.Low))/
(2*(myMax(TSeed.Last,tmpChart.High)
-myMin(TSeed.Last,tmpChart.Low))),...
Tseed.Delete = False
WHERE Round(tmpChart.[Date],5) = TSeed.[Date]
91
8. Änderungspropagierung zur Indikatorberechnung in TInTo
Hier tritt das Problem auf, dass durch die Dierenz von
Close
und
High
dividiert
werden muss. Bei einer Gruppeneinfügung sind diese Werte aber zwangsläug gleich.
Dieser Fall der so auch in anderen Indikatordenitionen auftaucht wurde dadurch
gelöst, dass in diesem Fall der Indikatorwert auf 0 gesetzt wurde. Diese Festlegung
ist willkürlich, da die Division durch 0 nicht deniert ist. Andere Werte wären eventuell für andere Indikatoren passender. Gegebenenfalls könnte man den Wert auch
gesondert kennzeichnen und aus der Indikatordenition herausnehmen. Dieser Punkt
ist auch bei der Indikatordenition für die Neuberechnung zu berücksichtigen, da es
auch hier vorkommen kann, dass z. B. Schlusskurs und Höchstkurs identisch sind.
Access meldet in diesem Fall die irreführende Fehlermeldung Überlauf .
Im Rahmen dieser Diplomarbeit wurden für alle Indikatoren Delta-Regeln angelegt.
In der ursprünglichen Version waren auch für die Aggregierungszwischenstufen die Indikatordenition gesondert abgelegt, diese wurden aber nicht doppelt implementiert.
Stattdessen nden sich alle Delta-Regeln unter den jeweiligen Indikatordenitionen.
Alle Delta-Regeln wurden numerisch auf Korrektheit getestet, um Tippfehler auszuschlieÿen. Nach Bereinigung fanden sich keine Unterschiede mehr zwischen den naiv
und den inkrementell berechneten Indikatorwerten.
92
9. Perfomanceanalyse für verschiedene
Indikatorklassen
Wie man aus den Ausführungen im Kapitel 8 erkennt, ist der syntaktische Aufwand
für die Delta-Regeln im Vergleich zur ursprünglichen Indikatordenition sehr groÿ.
Es ist nun eine wichtige Frage, ob dieser Aufwand auch wie erhot zu Verbesserungen der Laufzeit führt, was ja die ursprüngliche Motivation der inkrementellen
Änderungspropagierung ist.
Zuerst lassen sich einige theoretische Überlegungen durchführen: Für einen Indikator mit einfacher Aggregation, wie den SMA, lässt sich erkennen, dass bei der Berech-
n Datensätzen bei einer Berechnungsperiode p aufgrund des durchgeführten
Theta-Joins n · p Tupel erzeugt werden, auf denen dann der Durchschnitt berechnet
nung auf
wird. Da bei der Mittelwertberechnung alle Werte des Mittelwertes betrachtet werden müssen, lässt sich die zu erwartende Laufzeit mit dieser Gröÿe abschätzen. Bei
der inkrementellen Berechnung nach der oben gegebenen Denition muss geprüft
werden, ob der entsprechende Datumswert bereits vorhanden ist, bzw. in welchem
Datensatz die Aktualisierung durchgeführt werden muss. Diese Schritte lassen sich
log n)
bei entsprechender Indizierung in logarithmischer Zeit (
durchführen.
Access bzw. die für die Abfrageauswertung zuständige Komponente, die sogenannte
JET-Engine,
ermöglicht es, den Auswertungsplan für Anfragen ausgeben zu lassen.
Diese Möglichkeit wird in [Zim05] näher beschrieben. Dazu ist es erforderlich, folgenden Key in der Windows-Registry anzulegen:
[HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Jet\4.0\Engines\Debug]
"JETSHOWPLAN"="ON"
Danach wird für jede Anfrage ein Eintrag in der Datei
showplan.out erzeugt. Diese
Datei wurde sowohl für die Neuberechnung als auch für die inkrementelle Änderungspropagierung für den Indikator CCI untersucht. Für die Neuberechnung ergibt sich
folgender Ablauf (systeminterne Anfragen fortgelassen):
1. Wertpapier aus
TKurs
selektieren (Rushmore)
2. Indikatordenition selektieren (Rushmore)
3. Aggregation löschen (Scan)
4. Aggregation füllen (Rushmore und Test)
5. Durchläufe für
6.
7.
8.
9.
ChartAddQuery
(Index o. Rushmore)
tmpCCI löschen (Scan)
tmpCCI0 füllen (Join mit temporärem Index u. Test)
tmpCCI0 einlesen (Join mit temporärem Index u. Test)
tmpCCI selektieren (Index-Suche)
93
9. Perfomanceanalyse für verschiedene Indikatorklassen
Besonders die letzten beiden Schritte sind sehr zeitintensiv, da der temporäre Index
nur auf die Wertpapier-ID wirkt, wie der Ausschnitt aus der Datei
showplan.out
zeigt:
--- CCI --- Inputs to Query Table ’tmpCCI0’
Table ’tmpCCI0’
- End inputs to Query 01) Sort table ’tmpCCI0’
02) Inner Join table ’tmpCCI0’ to result of ’01)’
using temporary index
join expression "CCI0.ID=CCI1.ID"
then test expression "CCI1.n>CCI0.n- And CCI1.n<=CCI0.n"
03) Group result of ’02)’
Grob gesagt handelt es sich dabei um nicht mehr als die Bildung eines Kreuzprodukts, aus dem dann die entsprechenden Tupel ausgewählt werden. Bei einer Tabelle
von 1269 Werten, wie sie in den weiter unten beschriebenen Tests verwendet werden,
bedeutet dies, dass eine Zwischenrelation mit
12692 = 1.610.361
Tupeln entsteht. Es
ist leicht einzusehen, dass die Verwendung einer solchen Zwischenrelation sehr laufzeitintensiv werden kann. Die restlichen Schritte verwenden meist Indizes oder den
Rushmore-Algorithmus, der auch eine Art Index-Suche ist (vgl. [Bla07]). Lediglich
die Datumseinschränkung für die Aggregationstabelle wird noch mit einem linearen
Scan durchgeführt. Diese Relation ist aber kleiner, da hier kein Join verwendet wird.
Für die inkrementelle Neuberechnung ergibt sich folgender Auswertungsplan:
1. Aktuelle Wertpapier-ID suchen (Index-Suche)
2. Abfragen, ob das Datum schon in der Intradaytabelle ist (Rushmore)
3.
TSeed
leeren und füllen (Scan-Suche)
4. Suchen in
tmpChart
(Rushmore)
5. Viewdenition suchen (Index-Suche)
6.
tmpCCI0_Seed
leeren (Scan-Suche)
7. Aktuelles Datum in
Join)
8. maximales
9. Aktuelles
tmpCCI0 mit dem in TSeed vergleichen (Kreuzprodukt-
tmpChart suchen (Index-Suche)
Datum in tmpCCI0 mit dem in tmpCCI0_Seed
n
in
(Kreuzprodukt-Join)
10. Update für
11.
tmpCCI0
12. maximales
13.
14.
15.
tmpChart
(Index-Join)
füllen (Rushmore und Kreuzprodukt)
n
in tmpChart suchen (Index-Suche)
tmpCCI_MD füllen (Rushmore)
tmpChart updaten (Kreuzprodukt-Join)
Einfügen in tmpChart (Rushmore und Kreuzprodukt)
16. Prüfen, ob Löschattribut gesetzt (Index-Suche und Test)
94
vergleichen
17.
tmpChart
neu einlesen (Index-Suche)
Es mag überraschen, dass hier sogar öfter der Kreuzprodukt-Join auftritt, als in
der vollständigen Neuberechnung. Dies ist der Tatsache geschuldet, dass als JoinKriterium hier gerundete Datumsangaben herangezogen werden, auf denen kein Index angelegt werden kann. Der Nachteil ist aber nicht gravierend, da in diesen Fällen
stets die Seed-Relation beteiligt ist, die nur ein Tupel enthält. Dadurch gleicht diese
Suche einer linearen Suche. Träte in Access nicht das Problem auf, dass Flieÿkommazahlvergleiche zu falschen Ergebnissen führen, könnte auch hier ein schnellerer
Algorithmus wie der Index-Join oder Rushmore zum Einsatz kommen. Insgesamt
fällt aber auf, dass kein groÿer Kreuzprodukt-Join mehr nötig wird. Alle Schritte
können aber bereits jetzt in linearer Zeit erledigt werden, bzw. bei Anwendungen, in
denen die Seed-Tabelle mehr als ein Tupel umfasst, in Zeit
Θ(m · n).
Obwohl die theoretischen Betrachtungen des Auswertungsplans schon eine deutliche Verbesserung erwarten lassen, sollte die Methode auch im praktischen Betrieb
auf ihre Laufzeit geprüft werden. Aus diesem Grund wurden Testläufe durchgeführt,
um die notwendige Zeit zur Berechnung zu messen.
Zum Testaufbau: Die Tests fanden unter Windows 2000 und Access XP auf einem
PC mit einem Intel Celeron 1000 Prozessor und 256 MB Arbeitsspeicher statt, die Anbindung an das Internet erfolgte über eine DSL-6000-Verbindung. Die Berechnungszeiten wurden mittels der Windows-API-Funktion
Systembibliothek
kernel32.dll
getTickCount
der Windows-
gemessen. Für die Neuberechnung lag der Beginn
der Messdauer an dem Punkt, ab dem die angelegten Abfragen der Indikatoren zum
ersten Mal geönet wurden, das Ende der Messung nach dem Festlegen der ChartParameter. Die Zeit für die Anlage der Aggregationstabelle und das Hinzufügen der
ChartDirector-internen Indikatoren wurde nicht in die Messung mit einbezogen. Für
die Messung der inkrementellen Änderungsberechnung lag der Beginn der Messungen
direkt am Anfang der Prozedur
addValue
und das Ende wiederum vor Anlage der
ChartDirector-internen Indikatoren. Die Messungen der Testläufe wurden mit einer
wechselnden Anzahl von Kurswerten durchgeführt, die Periodendauer wurde während der Versuche nicht geändert. Die Auösung wurde auf einen Tag gestellt. Für
die Werte wurden mehrere Testläufe durchgeführt, es wurde jeweils ein Mittelwert
verwendet, wobei extreme Ausreiÿer nicht mitgezählt wurden, die allerdings auch nur
selten auftraten. Diese können in einem Multitasking-System wie Windows auftreten,
wenn im Hintergrund andere Aktivitäten ausgeführt werden
Die Tabellen 9.1 bis 9.4 geben die Laufzeiten für die Indikatoren ADO, SMA, CCI
und MACD an, eine grasche Darstellung zeigt Abb. 9.1. Man erkennt deutlich, dass
alle vier Indikatoren ab einer gewissen Anzahl von Datensätzen von den Delta-Regeln
protieren. Für eine kleinere Anzahl von Datensätzen ist die inkrementelle Methode
jedoch etwas langsamer. Wie aufgrund der theoretischen Vorüberlegungen zu erwarten war, wirkt sich die Verbesserung besonders für die Indikatoren mit einfacher oder
mehrfacher Aggregierung aus. Für den SMA und einen Zeitraum von 5 Jahren, also
1269 Datensätzen, sinkt die Laufzeit auf
1
55
der Laufzeit der naiven Berechnung. Be-
sonders deutlich ist der überlineare Anstieg der Laufzeit für die Neuberechnung bei
Indikatoren mit Aggregation. Mit der inkrementellen Änderungspropagierung steigt
95
9. Perfomanceanalyse für verschiedene Indikatorklassen
MACD
600
500
500
Berechnungszeit [ms]
Berechnungszeit [ms]
ADO
600
400
300
200
100
0
400
300
200
100
0
0
200
400
600
800
1000
1200
1400
0
200
400
Anzahl Werte
Naiv
Inkrementell
Naiv
SMA
800
1000
1200
1400
1200
1400
Inkrementell
CCI
12000
12000
10000
10000
Berechnungszeit [ms]
Berechnungszeit [ms]
600
Anzahl Werte
8000
6000
4000
2000
0
8000
6000
4000
2000
0
0
200
400
600
800
1000
Anzahl Werte
Naiv
Inkrementell
1200
1400
0
200
400
600
800
1000
Anzahl Werte
Naiv
Inkrementell
Abbildung 9.1.: Grasche Darstellung der Laufzeiten für vier Indikatoren
auch hier die Laufzeit ungefähr linear an. Bei den beiden Indikatoren ohne Aggregation steigt die Laufzeit auch für die Neuberechnung nur linear an, jedoch steigt sie
für die inkrementelle Methode langsamer an, auch wenn man für eine geringe Anzahl von Datensätzen einen Overhead erkennt, so dass die Methode für eine kleinere
Anzahl von Werten eine längere Zeit benötigt. Dieses Problem lieÿe sich eventuell
dadurch beheben, dass man das System im Voraus in Abhängigkeit von der Anzahl
der Datensätze eine Auswahl treen lässt, welche Methode angewendet werden soll.
96
Berechnungs-
Indikator-
zeitraum
werte
Laufzeit
naiv
inkrementell
1 Monat
20
30 ms
50 ms
1 Quartal
61
50 ms
55 ms
250
130 ms
75 ms
1 Jahr
3 Jahre
753
340 ms
130 ms
5 Jahre
1269
561 ms
185 ms
Tabelle 9.1.: Die Laufzeiten für den Indikator ADO
Berechnungs-
Indikator-
zeitraum
werte
1 Monat
1 Quartal
20
Laufzeit
naiv
inkrementell
100 ms
55 ms
61
160 ms
60 ms
1 Jahr
250
700 ms
80 ms
3 Jahre
753
4300 ms
140 ms
5 Jahre
1269
11000 ms
200 ms
Tabelle 9.2.: Die Laufzeiten für den Indikator SMA
Berechnungs-
Indikator-
zeitraum
werte
Laufzeit
naiv
inkrementell
1 Monat
20
70 ms
90 ms
1 Quartal
61
140 ms
100 ms
1 Jahr
250
750 ms
125 ms
3 Jahre
753
4500 ms
200 ms
5 Jahre
1269
11400 ms
280 ms
Tabelle 9.3.: Die Laufzeiten für den Indikator CCI
Berechnungs-
Indikator-
zeitraum
werte
1 Monat
1 Quartal
1 Jahr
20
Laufzeit
naiv
inkrementell
41 ms
70 ms
61
50 ms
70 ms
250
120 ms
90 ms
3 Jahre
753
310 ms
140 ms
5 Jahre
1269
501 ms
190 ms
Tabelle 9.4.: Die Laufzeiten für den Indikator MACD
97
9. Perfomanceanalyse für verschiedene Indikatorklassen
98
10. Zusammenfassung und Ausblick
Aufgabe dieser Diplomarbeit war es, das System TInTo um eine inkrementelle Änderungspropagierung auf Finanzdatenströmen zu erweitern. Dieses Ziel konnte mittels der Implementierung einer Änderungspropagierungstrategie unter Visual Basic
for Applications und der Erstellung von Delta-Regeln unter SQL erreicht werden.
Grundidee für den Einsatz einer inkrementellen Änderungspropagierung war es, die
Ausführungsgeschwindigkeit von Abfragen zu steigern. Wie die beschriebenen Testergebnisse zeigen, trat durch die erfolgte Implementierung ein drastischer Geschwindigkeitszuwachs ein, wobei die Laufzeit für einige Indikatoren sogar von einem überlinearen Verhalten auf ein lineares Verhalten reduziert werden konnte. Somit liegt auch
eine Verbesserung der asymptotischen Laufzeit vor, die durch lineare Steigerung der
Rechnergeschwindigkeit nicht hätte erreicht werden können.
Ein groÿer Teil der Zeit bei der Erstellung dieser Arbeit wurde für die Erstellung
und Tests der Delta-Regeln verwendet. Die Grundtechniken für SQL-Delta-Regeln
von aggregierten Sichten wurde überhaupt erst entwickelt, da hierfür nur Ansätze,
aber keine Beispielimplementierungen in der Literatur existierten. Wie man bereits
an den im Kapitel 8 vorgestellten Beispielen sehen kann, werden diese Regeln schnell
kompliziert und sind bei noch gröÿeren Aufgaben nicht mehr überschaubar. Dies
macht die Korrektur von Fehlern recht mühsam und aufwendig.
Das nächste Forschungsziel sollte daher sein, einen automatischen Compiler für
Delta-Regeln zu entwickeln. Bei der manuellen Erstellung der Delta-Regeln el bisweilen auf, dass diese Arbeit sehr mechanisch werden kann. Es sollte daher möglich
sein, einen solchen Compiler zu erstellen. Solange entsprechende automatische Verfahren nicht vorhanden sind, wird sicherlich auch trotz beeindruckender Messergebnisse
die inkrementelle Änderungspropagierung keine breite Akzeptanz bei Datenbankentwicklern nden können.
Die implementierte Propagierungstechnik indes kommt zwar im Kern damit aus,
die Delta-Regeln aufzurufen, da die Reihenfolge der Delta-Regeln von Hand vorgegeben wurde. Allerdings wurde auch hier umfangreiche Änderungen an dem System
vorgenommen, angefangen beim automatischen Datenabruf, also der Einspeisung des
Datenstroms in das System, über die Erstellung von Hilfsrelationen bis hin zur automatischen Neuanzeige in grascher und textueller Form.
Ein weiterer Teil der Entwicklungszeit wurde für Änderungen aufgewendet, die nur
im mittelbaren Zusammenhang mit der Änderungspropagierung stehen.
So wurde das von Christian Hübel [Hüb07] entwickelte Verfahren zur Indikatorberechnung korrigiert, da die von TInTo berechneten Indikatorwerte nicht mit den
Ergebnissen des ChartDirectors übereinstimmten. Ohne die Erweiterung um Intraday-Daten wäre kaum ein Nutzen der inkrementellen Änderungspropagierung nach-
99
10. Zusammenfassung und Ausblick
weisbar gewesen. Andere Erweiterungen machten die Benutzung von TInTo einfacher oder fügten neue Funktionen hinzu. So wurde durch die Verwendung des neuen
Kürzelabrufs mittels XML und des Datenabrufs über die ActiveX-Schnittstelle die
Stabilität und die Geschwindigkeit erhöht. Die Oberäche wurde klarer strukturiert
und die Bindung zwischen Zeitraum und Frequenz exibel gestaltet. Beide Bereiche
sind zudem leicht erweiterbar.
Die jetzt vorliegende Version von TInTo enthält gewiss noch Verbesserungsmöglichkeiten. So muss bei Neuanlage eines Indikators nicht nur die Regelmenge von
Hand erstellt werden, auch die für die Materialisierung verwendeten Tabellen müssen
noch von Hand angelegt werden. Somit kann vom unversierten Benutzer die Änderungspropagierung nur für die bereits angelegten Indikatoren genutzt werden. Ferner
steht dem Laufzeitgewinn wie so oft in der Informatik ein erhöhter Speicherplatzverbrauch gegenüber. Während der Experimente konnte festgestellt werden, dass durch
die häugen Änderungen in den materialisierten Sichten der Speicherplatzverbrauch
der Datenbankdatei anwuchs, wobei durch die in Access integrierte Komprimierungsfunktion der Verbrauch wieder gesenkt werden konnte. Eventuell kann durch eine in
Access mögliche Auslagerung der temporären Tabellen eine Verbesserung des Speicherplatzverbrauchs hergestellt werden.
Auch eine Erweiterung von TInTo auf Mehrbenutzerumgebungen ist denkbar, jedoch sollte dann auch dafür Sorge getragen werden, dass die materialisierten Sichten
vor Verfälschungen absichtlicher oder unabsichtlicher Art geschützt sind. In TInTo
wird das Problem dadurch abgemildert, dass alle verwendeten Sichten bei Änderungen der Berechnugnsparameter vollständig neu materialisiert werden. Ferner müssen
in Mehrbenutzerumgebungen die Hilfstabellen für jeden einzelnen Benutzer vorliegen,
da sonst Zugriskonikte auftreten werden.
100
Literaturverzeichnis
[Ban05]
Basisinformationen über Vermögensanlagen in Wertpapieren Grundlagen, wirtschaftliche Zusammenhänge, Möglichkeiten und Risiken.
Köln,
2005.
[BD07]
Behrend, Andreas
und
Christian Dorau:
TInTo: A Tool for the
View-Based Analysis of Streams of Stock Market Data.
Advances in
In:
Databases: Concepts, Systems and Applications 12th International Conference on Database Systems for Advanced Applications, DASFAA 2007,
Seiten 11101114, Berlin, Heidelberg u.a., 2007. Springer.
[Beh04]
Behrend, Andreas:
Soft Stratication for Transformation-Based Ap-
proaches to Deductive Databases.
Doktorarbeit, Rheinische Friedrich-Wil-
helms-Universität Bonn, 2004.
[BFO04]
Bry, François, Tim Furche
und
Dan Olteanu:
Datenströme.
Tech-
nischer Bericht, Institut für Informatik, Universität München, 2004.
[Bla07]
Black, Neil:
Rushmore Query Optimization in Jet 2.0,
2007.
URL:
http://msdn.microsoft.com/archive/default.asp?url=
/archive/en-us/dnaraccessdev/html/rushmore.asp. MSDNArchive, [Online; Stand 15. September 2007].
[BLT86]
Blakeley, Jose A., Per-Ake Larson
ciently updating materialized views.
In:
und
Frank Wm Tompa:
E-
SIGMOD '86: Proceedings of the
1986 ACM SIGMOD international conference on Management of data,
Seiten 6171, New York, NY, USA, 1986. ACM Press.
[BM04]
Behrend, Andreas und Rainer Manthey: Update Propagation in Deductive Databases Using Soft Stratication. In: Gottlob, Georg, András A. Benczúr und János Demetrovics (Herausgeber): ADBIS,
Band 3255 der Reihe
Lecture Notes in Computer Science,
Seiten 2236.
Springer, 2004.
[CLS00]
Chan, Miranda, Hong Va Leong und Antonio Si: Incremental update
to aggregated information for data warehouses over Internet.
In:
DOLAP
'00: Proceedings of the 3rd ACM international workshop on Data warehousing and OLAP,
[Cod70]
Seiten 5764, New York, NY, USA, 2000. ACM Press.
Codd, Edgar F.: A
relational model of data for large shared data banks.
Communications of the ACM, 13(6):377387, 1970.
101
Literaturverzeichnis
[CW91]
Ceri, Stefano
und
Jennifer Widom:
Incremental View Maintenance.
In:
Deriving Production Rules for
VLDB '91: Proceedings of the 17th
International Conference on Very Large Data Bases,
Seiten 577589, San
Francisco, CA, USA, 1991. Morgan Kaufmann Publishers Inc.
[Gep05]
Geppert, Alexander:
Ein regelbasierter Ansatz zur Modellierung der
technischen Analyse von Wertpapierkursen.
Diplomarbeit,
Rheinische
Friedrich-Wilhelms-Universität Bonn, Institut für Informatik III, Dezember 2005.
[GMS93]
Gupta, Ashish, Inderpal Singh Mumick
Maintaining views incrementally.
In:
und
V. S. Subrahmanian:
SIGMOD '93: Proceedings of the 1993
ACM SIGMOD international conference on Management of data,
Seiten
157166, New York, NY, USA, 1993. ACM Press.
[Gri97]
Griefahn, Ulrike:
Reactive Model Computation: A Uniform Approach
to the Implementation of Deductive Databases.
Doktorarbeit, Rheinische
Friedrich-Wilhelms-Universität Bonn, 1997.
[Hüb07]
Hübel, Christian:
TInTo Ein datenbankgestütztes Werkzeug zur
regelbasierten Wertpapieranalyse.
Diplomarbeit,
Rheinische
Friedrich-
Wilhelms-Universität Bonn, Institut für Informatik III, Januar 2007.
[KE01]
Kemper, Alfons und André Eickler: Datenbanksysteme.
Oldenbourg
Wissenschaftsverlag, München, 4. überarbeitete und erweiterte Auflage,
2001.
[Kru05]
Krumme, Andreas: Objektorientierte und regelbasierte Modellierung von
Wertpapieren und Kursverläufen.
Diplomarbeit, Rheinische Friedrich-Wil-
helms-Universität Bonn, Institut für Informatik, Abteilung III, 2005.
[Man05]
Manthey, Rainer:
Folien zur Vorlesung Deduktive Datenbanken.
Rhei-
nische Friedrich-Wilhelms-Universität Bonn, Institut für Informatik III,
Sommersemester 2005.
[MB07]
Manthey, Rainer und Andreas Behrend: Folien zur Vorlesung Event
Monitoring Systems.
Rheinische Friedrich-Wilhelms-Universität Bonn, In-
stitut für Informatik III, Sommersemester 2007.
[Mur00]
Murphy, John J.:
Technische Analyse der Finanzmärkte.
FinanzBuch
Verlag, München, 2. Auflage, 2000.
[Pae06]
Paesler, Oliver: Technische
Indikatoren - simplied. Das ideale Instru-
ment für jeden erfolgsorientierten Anleger.
FinanzBuch Verlag, München,
2006.
[Pie01]
Pieper, Birgit:
rung in SQL.
Bonn, 2001.
102
Inkrementelle Integritätsprüfung und Sichtenaktualisie-
Doktorarbeit, Rheinische Friedrich-Wilhelms-Universität
Literaturverzeichnis
[QW91]
Qian, Xiaolei
und
Gio Wiederhold:
Active Relational Expressions.
Incremental Recomputation of
Knowledge and Data Engineering, 3(3):337
341, 1991.
[Sed03]
Sedgewick, Robert:
Algorithmen in Java. Grundlagen, Datenstruktu-
ren, Sortieren, Suchen. Teil 1-4.
[Sto]
StockCharts.com:
Charts.com.
Pearson Studium, München, 2003.
Commodity
Channel
Index
(CCI)
Stock-
http://stockcharts.com/school/doku.
php?id=chart_school:technical_indicators:commodity_
channel_index_cci. [Online; Stand 29. Juni 2007].
[Wik07a]
Wikipedia:
URL:
DAX Wikipedia, Die freie Enzyklopädie,
2007.
URL:
http://de.wikipedia.org/w/index.php?title=DAX&oldid=
33592247. [Online; Stand 29. Juni 2007].
[Wik07b]
Wikipedia:
Wertpapier
Wikipedia,
Die
freie
Enzyklopädie,
http://de.wikipedia.org/w/index.php?title=
Wertpapier&oldid=32639051. [Online; Stand 27. Juni 2007].
2007.
[Zim05]
URL:
Zimmermann, Michael:
cess.
In:
Datenbankperformance
mit
Skript zur 8. Access-Entwickler-Konferenz,
Microsoft
Oktober
Ac2005.
http://www.donkarl.com/AEK/AEKDownloads/AEK8_
Abfragen_Performance.zip [Online, Stand 17. September 2007].
URL:
103
Literaturverzeichnis
104
A. Anhang
A.1. Abkürzungsverzeichnis
ADO
Accumulation/Distribution Oscillator
AktG
Aktiengesetz
ANSI
American National Standards Institute
API
Application Programming Interface
AVG
Average
BGB
Bürgerliches Gesetzbuch
BMP
Balance of Market Power
CCI
Commodity Channel Index
COM
Component Object Model
DAO
Data Access Object
DAX
Deutscher Aktienindex
DBMS
Datenbankmanagementsystem
DDL
Data Denition Language
DepotG
Depotgesetz
DML
Data Manipulation Language
ECA
Event-Condition-Action
EOD
End-of-day
FPI
Fixpunktiteration
FSTOC
Fast Stochastic
HTML
Hypertext Markup Language
HTTP
Hypertext Transfer Protocol
ISIN
International Securities Identication Number
JPEG
Joint Photographic Experts Group (hier: Dateiformat)
MACD
Moving Average Convergence/Divergence
MB
Megabyte
MD
Mean Deviation
MS
Microsoft
OHLC-Chart
Open-High-Low-Close-Chart
PNG
Portable Network Graphics
RA
Relationale Algebra
RSI
Relative Strength Index
SFW
Select . . . From . . . Where
SMA
Simple Moving Average
SMATP
Simple Moving Average of Typical Price
105
A. Anhang
SQL/PL
SQL Programming Language
TInTo
Technical Indicator Tool
TP
Typical Price
URL
Uniform Ressource Locator
VBA
Visual Basic for Applications
XML
Extended Markup Language
A.2. Hinweis zu Markennamen
Die in dieser Diplomarbeit verwendeten Produkt-, Software-, Aktienindex- und Firmenbezeichnungen sowie Logos sind eingetragene Marken oder Warenzeichen. Alle
Rechte an den jeweiligen Marken oder Warenzeichen liegen beim jeweiligen Inhaber.
A.3. Hinweise zur beiliegenden CD-ROM
Auf der beiliegenden CD-ROM bendet sich das gesamte erweiterte TInTo-System
nebst den Delta-Regeln für alle Indikatoren. Es ist zu beachten, dass MS-Access
bereits installiert sein muss, um das System zu verwenden. Im Einzelnen sind folgende
Dateien auf der CD-ROM enthalten:
setup.exe
tinto.mdb
Setup-Datei, die das gesamte TInTo-System installiert
Die eigentliche Datenbank-Datei, lauähig unter MS-Access ab Version
2000
chartdir_com_win32.exe
msxmlger.msi
Die Installationsdatei für MS XML
diplomarbeit.pdf
dow.csv
Die Installations-Datei der ChartDirector-Komponente
Diese Diplomarbeit als PDF-Datei
Tagesdaten des Dow Jones als Testdaten
crontable
Cronjob-Einträge zum automatischen Datenabruf der Intraday-Daten
delta_CCI_plan.txt
naiv_CCI_plan.txt
Auswertungsplan zur Berechnung des CCI mit Delta-Regeln
Auswertungsplan zur Berechnung des CCI ohne Delta-Regeln
(Sollte die CD-ROM nicht verfügbar sein, so kann der Autor auch unter der EMail-Adresse [email protected] kontaktiert werden.)
106
Erklärung gemäÿ Ÿ 19 (7) der Prüfungsordnung
Hiermit erkläre ich, dass ich diese Diplomarbeit selbstständig durchgeführt, keine
anderen als die angegebenen Quellen und Hilfsmittel benutzt sowie die Zitate als
solche kenntlich gemacht habe.
Bonn, den
107