Ausarbeitung - Detlef Krömke - Goethe

Goethe-Universität Frankfurt
Diplomarbeit
Point Based Animation
eingereicht bei
Prof. Dr.-Ing. Detlef Krömker
Professur für Graphische Datenverarbeitung
von
Sven Pallus
Eingereicht am 21.03.2011
Eidesstattliche Erklärung
Ich erkläre hiermit an Eides Statt, dass ich die vorliegende Arbeit selbstständig und ohne Benutzung
anderer als der angegebenen Hilfsmittel angefertigt habe; die aus fremden Quellen direkt oder indirekt
übernommenen Gedanken sind als solche kenntlich gemacht.
Die Arbeit wurde bisher in gleicher oder ähnlicher Form keiner anderen Prüfungskommission vorgelegt und auch nicht veröffentlicht.
Frankfurt am Main, den 21. März 2011
—————————
(Sven Pallus)
i
ii
Danksagung
Ich danke allen, die mich während meines Studiums unterstützt und gefördert haben. Zuallererst bedanke ich mich bei meinen Eltern und meiner Familie, die mir dieses Studium ermöglicht haben.
Zudem bedanke ich mich bei allen Korrekturlesern, die diese Arbeit zu dem gemacht haben, was sie
jetzt ist: Nicole, Petra, Michael, Christian.
Mein weiterer Dank gilt meinem Betreuer Dipl. Inf. Daniel Schiffner für seine tatkräftige Unterstützung und zahlreichen Ratschläge, sowie Prof. Dr.-Ing. Detlef Krömker, der diese Arbeit erst ermöglicht hat.
Nicht zuletzt bedanke ich mich bei meiner Freundin Nicole, die mich während des gesamten Studiums
unterstützt hat und immer für mich da war.
Inhaltsverzeichnis
Zusammenfassung
1
Deutsch . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
Englisch . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
1
Einleitung
3
2
Grundlagen
5
2.1
Animation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.1.1
Animationspipeline . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.1.2
Prinzipien der Animation . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
Animationstechniken . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
2.2
2.3
3
4
2.2.1
Elementaranimation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
2.2.2
Simulative Animation . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
2.2.3
Kinematische Techniken . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
2.2.4
Animation durch Interpolation . . . . . . . . . . . . . . . . . . . . . . . . .
14
2.2.5
Bewegungserfassung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
2.2.6
Punktbasierte Animation . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
Grundlagen der Physik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
State of the Art
20
3.1
Partikelsysteme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
3.2
Smoothed Particle Hydrodynamics . . . . . . . . . . . . . . . . . . . . . . . . . . .
23
3.3
Anwendungen von punktbasierter Animation . . . . . . . . . . . . . . . . . . . . .
25
3.3.1
Animation von elastischen, plastischen und schmelzenden Objekten . . . . .
26
3.3.2
Punktbasierte Animation von elastoplastischen Festkörpern . . . . . . . . .
27
3.3.3
Punktbasierte Animation von inkompressiblen Strömungen . . . . . . . . . .
29
3.4
Physikengine . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
30
3.5
Bullet Grundlagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
Eigene Verfahren
38
4.1
38
Anforderungsanalyse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
iii
INHALTSVERZEICHNIS
5
iv
4.2
Punktmodell . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
39
4.3
Bullet Viewer . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
4.4
Verknüpfung Punktmodell mit Physikengine . . . . . . . . . . . . . . . . . . . . . .
45
4.5
Konzeption und Implementierung starrer Körperdynamik . . . . . . . . . . . . . . .
48
4.6
Konzeption und Implementierung elastischer Körperdynamik . . . . . . . . . . . . .
56
4.7
Benchmarks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
78
Aussichten und Diskussion
Literaturverzeichnis
80
83
Quellcode
3.1
Standard Bullet Welt für starre Körperdynamik . . . . . . . . . . . . . . . . . . . .
34
4.1
Bauminitialisierung der Punkte . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
4.2
Viewerkonstruktor zur Menübildung . . . . . . . . . . . . . . . . . . . . . . . . . .
43
4.3
Motion-State für das Punktmodell . . . . . . . . . . . . . . . . . . . . . . . . . . .
47
4.4
Punktmanipulation für elastische Körper . . . . . . . . . . . . . . . . . . . . . . . .
48
4.5
Bildung eines starren Körpers . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
4.6
Constraint zwischen starren Objekten . . . . . . . . . . . . . . . . . . . . . . . . .
54
4.7
Elastizität über starre Körperdynamik . . . . . . . . . . . . . . . . . . . . . . . . .
55
4.8
Node und dynamischer Link im Point Body . . . . . . . . . . . . . . . . . . . . . .
57
4.9
Initialisierung eines Point Body . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
57
4.10 Initialisierung eines Links . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
58
4.11 Strahlberechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
62
4.12 Herausschneiden von Punkten aus dem elastischen Objekt . . . . . . . . . . . . . .
66
4.13 Reparaturschritt des Point Body für Fall 5 . . . . . . . . . . . . . . . . . . . . . . .
72
4.14 Einfügen eines Nodes in den Point Body für Fall 1 . . . . . . . . . . . . . . . . . .
77
v
Abbildungsverzeichnis
2.1
Animationssequenz eines Daumenkinos [Dau] . . . . . . . . . . . . . . . . . . . . .
6
2.2
Animationspipeline nach [Bre07] . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.3
Masse-Feder-Dämpfer System [Mas] . . . . . . . . . . . . . . . . . . . . . . . . . .
11
2.4
Unterteilung in finite Elemente [Mü08] . . . . . . . . . . . . . . . . . . . . . . . .
12
2.5
Kinematische Kette eines Roboterarms [Bre07] . . . . . . . . . . . . . . . . . . . .
13
2.6
Hierarchischer Aufbau eines Menschen sowie die dazu gehörige Baumstruktur [Par02] 14
2.7
Interpolation zwischen zwei Bildern [Bre07] . . . . . . . . . . . . . . . . . . . . . .
15
2.8
Motion Capture [Mot] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
2.9
Meshbasierter [Mes] und punktbasierter [Poi] Standford Bunny . . . . . . . . . . . .
17
3.1
Animation eines Feuerwerks mit Hilfe eines Partikelsystems [Hei02] . . . . . . . . .
23
3.2
Flüssigkeitsdarstellung mit der SPH Methode [SPH] . . . . . . . . . . . . . . . . .
25
3.3
Das linke Bild zeigt Phyxel (gelb) und Surfels (blau), die übrigen Bilder zeigen elastische und plastische Verformungen nach [MKN+ 04] . . . . . . . . . . . . . . . . .
26
3.4
Elastoplastisches Objekt nach [GBB09] . . . . . . . . . . . . . . . . . . . . . . . .
29
3.5
Ablauf der punktbasierten Methode nach [SH09] . . . . . . . . . . . . . . . . . . .
30
3.6
Beliebteste Physikengines [Gam] . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
3.7
Organisation der Hauptkomponenten von Bullet [Bulb] . . . . . . . . . . . . . . . .
34
3.8
Drei am häufigsten verwendete Collision-Shapes zur Kollisionserkennung [Kle05] .
35
3.9
Drei verschiedene Gelenktypen [Bulb] . . . . . . . . . . . . . . . . . . . . . . . . .
36
3.10 Soft Body bestehend aus Nodes, Links und Faces . . . . . . . . . . . . . . . . . . .
37
4.1
Aufbau der Basisdaten des Punktmodell [SK10] . . . . . . . . . . . . . . . . . . . .
39
4.2
Punktinformationen werden aus dem Puffer gezogen . . . . . . . . . . . . . . . . .
40
4.3
Baumdarstellung für neun Punkte . . . . . . . . . . . . . . . . . . . . . . . . . . .
40
4.4
Aufbau eines beispielhaften Tree-Cut nach [SK10] . . . . . . . . . . . . . . . . . .
42
4.5
Aktualisierungsmethoden eines Tree-Cut [SK10] . . . . . . . . . . . . . . . . . . .
42
4.6
Bullet Viewer zur Anzeige der Animation . . . . . . . . . . . . . . . . . . . . . . .
44
4.7
Arbeitsablauf des Frameworks . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
45
4.8
Berechnung der Punktanzahl des Punktbaums . . . . . . . . . . . . . . . . . . . . .
46
vi
ABBILDUNGSVERZEICHNIS
4.9
vii
Aktualisierungsschritt bei der starren Körperdynamik . . . . . . . . . . . . . . . . .
50
4.10 Freier Fall eines starren Körpers . . . . . . . . . . . . . . . . . . . . . . . . . . . .
50
4.11 Kollisionen zwischen starren Objekten . . . . . . . . . . . . . . . . . . . . . . . . .
51
4.12 Auswirkung von Constraints auf Objektsabstände . . . . . . . . . . . . . . . . . . .
53
4.13 Animation einer elastischen Kette auf Grundlage der starren Körperdynamik . . . . .
55
4.14 Grundaufbau eines Point Body . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
59
4.15 Aktualisierungsschritt bei der elastischen Körperdynamik . . . . . . . . . . . . . . .
60
4.16 Kollision einer elastischen Ebene mit einem starren Körper . . . . . . . . . . . . . .
60
4.17 Werfen eines Strahls von der Mausposition in die Szene [Pic] . . . . . . . . . . . . .
62
4.18 Ziehen und Zurückschwingen eines Point Body . . . . . . . . . . . . . . . . . . . .
63
4.19 Herausschneiden eines Nodes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
4.20 Ausschneiden einzelner Nodes aus dem Point Body . . . . . . . . . . . . . . . . . .
65
4.21 Zerschnittener Point Body mit Gravitationswirkung . . . . . . . . . . . . . . . . . .
67
4.22 Kombiniertes Ziehen und Schneiden des Point Body . . . . . . . . . . . . . . . . .
68
4.23 Reparieren des Point Body für die Fälle 1 und 2 . . . . . . . . . . . . . . . . . . . .
69
4.24 Reparieren des Point Body für die Fälle 3 und 4 . . . . . . . . . . . . . . . . . . . .
71
4.25 Reparieren des Point Body für die Fälle 5 und 6 . . . . . . . . . . . . . . . . . . . .
72
4.26 Einfügen eines Punkts in den Point Body für die Fälle 1 und 2 . . . . . . . . . . . .
74
4.27 Einfügen eines Punkts in den Point Body für die Fälle 3 und 4 . . . . . . . . . . . .
75
4.28 Einfügen eines Punkts in den Point Body für die Fälle 5 und 6 . . . . . . . . . . . .
76
5.1
82
Krönchenbildung durch Auftreffen von Wassertropfen [Tro] . . . . . . . . . . . . .
Kurzfassung
Die punktbasierte Animation ist ein relativ neues Gebiet im Bereich der Animation. Der Unterschied
zu den weit verbreiteten polygonnetzbasierten Verfahren liegt darin, dass zwischen den einzelnen
Punkten, welche die Oberfläche des zu animierenden Objekts definieren, keine Topologieinformationen vorhanden sind. Mit polygonnetzbasierten Techniken ist keine Volumensimulation möglich, da
keine Volumeninformationen vorhanden sind. Die aktuellen Verfahren im punktbasierten Feld ermöglichen die Animation von Flüssigkeiten, Rauch oder Explosionseffekten. In dieser Arbeit wird eine
Animation auf Grundlage eines zur Verfügung gestellten Punktmodells ausgeführt. Um zu gewährleisten, dass die Animation korrekt nach den Gesetzen der Physik arbeitet, wird eine Physikengine
zu Hilfe genommen. Diese beiden Bereiche werden in dieser Arbeit miteinander verknüpft. Zunächst
werden einfache Simulationen im Sektor der starren Körperdynamik durchgeführt. Dabei werden einzelne Punkte unter Einfluss der Gravitation auf eine Ebene fallen gelassen. Vor allem die Berechnung
der Kollision mit der Ebene und der Punkte untereinander ist hierbei interessant. Um sehenswerte physikalische Effekte animieren zu können, muss die Elastizität mit berücksichtigt werden. Des Weiteren
wird in der Arbeit die Animation elastischer Körper verwirklicht. Hierbei wird eine an den Ecken
fixierte elastische Ebene animiert. Einzelne Punkte können aus diesem elastischen Objekt herausgezogen werden, in Folge dessen sich das Objekt selbst repariert. Ebenfalls kann ein herausgeschnittner
Punkt wieder in das Objekt eingefügt werden.
1
Zusammenfassung
2
Abstract
The point-based animation is a relatively new area in the field of animation. The difference to the well
known mesh-based methods is that there is no topology information between the single points which
define the surface of the animated object. With mesh-based methods no volume simulation is possible, because no volume information is available. The current techniques for point-based animation
allow the animation of liquids, smoke and explosion effects. In this diploma thesis, the animation is
performed on the basis of a provided point model. In order to ensure that the animation is physically
correct, a physics engine is used. The objective of this thesis is to combine these two fields. Initially
simple simulations are performed in the area of rigid body dynamics. In the process, single points are
dropped to the ground plane under the influence of gravity. Particularly interesting is the calculation
of the collision between the points and plane, and also between the points among themselves. To animate visual interesting physical effects, the influence of elasticity has to be included. Furthermore this
thesis shows how elastic objects can be animated. To achieve this, an elastic plane fixed at his corners
will be animated. Individual points can be extracted from this elastic object; in consequence the object
is able to repair the occurred hole by itself. Also a cut point can be integrated back to the object.
Kapitel 1
Einleitung
“Der Mensch ist ein Augentier” [Sei01]
Aus diesem Zitat lässt sich herauslesen, dass der wohl wichtigste Sinn der menschlichen Wahrnehmung der Sehsinn ist. In den meisten Fällen ist das, was zuerst wahrgenommen wird, die visuell
erfassbare Information. Aus den aufgenommenen visuellen Reizen zieht jeder Mensch die für ihn
persönlich relevanten Informationen heraus.
Auch aus diesem Grund ist es ein wichtiges Ziel der Computergraphik, Bilder möglichst realitätsnah darzustellen. In der fortlaufenden Entwicklung der Computergraphik ist es mittlerweile möglich,
fotorealistische Bilder zu erzeugen. Um der Szene, die durch das Bild angezeigt wird, Leben einzuhauchen, muss Bewegung in die Szene integriert werden. Solch “bewegte Bilder” sind unter dem
Namen Animation bekannt. Dabei handelt es sich um das zeitliche hintereinander Abspielen von einzelnen Bildern. Zu Beginn waren das einfache Strichmännchen, die sich durch die Szene bewegten.
Da im Laufe der Zeit die Leistungsstärke der Rechner stetig anstieg, ist die Erzeugung fotorealistischer Bilder mittlerweile auch für den normalen Anwender möglich. Doch mit der gewachsenen
Leistungsfähigkeit der Rechner stiegen auch die Ansprüche an die Animation. Aktuell sollen sich
Objekte in einer animierten Szene korrekt nach den physikalischen Gesetzmäßigkeiten verhalten. In
Computeranimationsfilmen wie “Findet Nemo” oder “Ratatouille” kann man beobachten, wie weit die
Animation inzwischen schon vorangeschritten ist und welche überzeugenden Ergebnisse sie liefert.
Diese Arbeit beschäftigt sich mit der punktbasierten Animation, die ein relativ neues Gebiet ist. Die
punktbasierten Methoden gewannen in den vergangenen Jahren zunehmend an Beliebtheit und sind
eine Alternative zu bekannten Animationsmethoden, die auf der Basis von Polygonnetzen arbeiten.
Dabei werden die Oberflächen der Objekte durch eine Vielzahl von Punkten abgetastet. Physikalisch
aufwendige Simulationen wie die von Gasen oder Flüssigkeiten werden aktuell mit der punktbasierten
Animation bearbeitet, da polygonnetzbasierte Verfahren keine Volumeninformationen besitzen. Dabei
enthält jeder definierte Punkt die Eigenschaften des Objekts an der jeweiligen Position in der Szene.
Die Animations- bzw. Physik-Simulation findet dann ausschließlich auf diesen Punkten statt. Somit
ist die Methode gut geeignet zur Modellierung eines großen Bereichs von verschiedenen Materialien.
Diese Vielseitigkeit macht sie speziell attraktiv für Computergraphik-Anwendungen.
3
KAPITEL 1. EINLEITUNG
4
Ziel der Arbeit ist es, diese beiden Bereiche miteinander zu verknüpfen. Es muss somit für jeden
einzelnen Punkt die Physik an der jeweiligen Stelle berechnet werden. Dadurch soll es ermöglicht
werden, auf einer gemeinsamen Datenstruktur die Geometrie, in diesem Fall die Punkte, als auch
die Physik auszuwerten. Es soll somit zu einem bestehenden Renderer und dem Punktmodell eine
Physiksimulation integriert werden. Zudem ist es wünschenswert zu untersuchen, inwiefern sich eine
vorhandene Datenhierarchie dafür eignet, die Anzahl der Simulationsknoten dynamisch festzulegen.
In Kapitel 2 werden die Grundlagen erklärt, wozu die Animation und verschiedene Animationstechniken gehören, sowie Felder der Physik, die für die Animation von Bedeutung sind. Eine Analyse
des aktuellen Stands der Technik im Gebiet der Animation auf Punkten, sowie ein Vergleich aktueller
Physikengines folgt in Kapitel 3. Kapitel 4 zeigt die Konzeption und Implementierung des eigenen
Verfahrens der Arbeit. Abschließend folgen in Kapitel 5 eine kritische Bewertung des entstandenen
Verfahrens und ein Ausblick auf mögliche Erweiterungen.
Kapitel 2
Grundlagen
Im Folgenden soll zunächst allgemein auf den Begriff der Animation eingegangen werden. Danach
werden verschiedene Animationstechniken näher gebracht. Abschließend wird auf die physikalischen
Grundlagen eingegangen, die zum Verständnis der Arbeit notwendig sind.
2.1
Animation
Der Begriff Animation bzw. etwas animieren stammt von dem lateinischer Wort “animare”, was so
viel wie “zum Leben erwecken” bedeutet.
In dieser Arbeit wird der Begriff der Animation ausschließlich im Sinne der Computergraphik verwendet. Daraus ergibt sich die Definition der Animation als “graphische Erzeugung von Lebendigkeit
mit Hilfe des Computers” [Bre07].
In [Par02] wird Animation als eine Abfolge von Standbildern definiert, die beim Betrachter den visuellen Eindruck von Bewegung hervorruft. Das ist möglich, da die visuelle Verarbeitung im Gehirn die
Abfolge von Standbildern aneinanderfügt und sie als fortlaufende Bewegung wahrnimmt. Diesen Effekt von Bewegung kennt man beispielsweise von einem Daumenkino, wie in Abbildung 2.1 zu sehen
ist. Um eine annähernd flüssige Bewegung zu erhalten, sind etwa 24 Bilder pro Sekunde notwendig.
Somit ist die Zeit ein wichtiger Bestandteil der Animation.
2.1.1
Animationspipeline
Eine Animationspipeline stellt die klassische Reihenfolge der Arbeitsschritte einer Animation dar. Es
handelt sich dabei um die Erstellung von Bewegtbildmedien. Die einzelnen Schritte der Animationspipeline werden in Abbildung 2.2 dargestellt und im Folgenden kurz verdeutlicht.
• Preproduction
Hierbei handelt es sich um die Vorarbeiten von der ersten Idee bis zum Konzept. Anhand des
Konzeptes wird die Handlung der Geschichte erzählt. Die Produktionsplanung, wie die Bildung
eines Teams, das Aufstellen eines Budgets und eines Ablaufplans, fallen ebenfalls in diesen
Bereich.
5
KAPITEL 2. GRUNDLAGEN
Abbildung 2.1: Animationssequenz eines Daumenkinos [Dau]
Abbildung 2.2: Animationspipeline nach [Bre07]
6
KAPITEL 2. GRUNDLAGEN
7
• Object Modelling
Unter einem Objekt versteht man in der Computergraphik einen darzustellenden Gegenstand
in einer Szene. Dafür können einfache Primitve wie Punkte, Linien oder Polygone verwendet
werden. Ein Objekt kann sowohl geometrisch, als auch prozedural modelliert werden, wie z.B.
bei Fraktalen. Parameter wie Farbe, Reflektion oder Textur können hierbei durch Oberflächenoder Volumenmodellierung bestimmt werden.
• Scene Modelling
Zur Modellierung der Szene gehören Bereiche wie die Positionierung der Objekte, die globale
Beleuchtung, das Festlegen des Hintergrunds, sowie Umgebungseigenschaften wie Nebel und
die Einstellung der Kamera. Das Scene Modelling ist häufig auch als Teil des Animationssystems implementiert.
• Animation
Hiermit ist im Zuge der Animationspipeline die “Belebung"der Szene gemeint. Da eine Animation aus einer bestimmten Anzahl von Bildern besteht, ist das Bild auch die wichtigste Zeiteinheit. Objekt-, Szene- und Renderingparameter spielen ebenfalls eine Rolle bei der Animation.
• Produktions-Rendering
Das Produktions-Rendering ist die Umsetzung der Geometrie- und Merkmalsrepräsentation in
Pixelrepräsentation. An das Produktions-Rendering werden sehr hohe Qualitätsanforderungen
bis hin zu einem guten Antialiasing1 gestellt. Da ein Produktionsrenderer ein System für interaktives Arbeiten ist, ist seine Flexibilität ein wichtiger Punkt.
• Postproduction
Bei der Postproduction wird die erstellte Arbeit auf klassische Bewegtbildmedien wie Video
aufgezeichnet, bzw. für moderne Medien in einem Computervideo. Zudem kann das Video
noch vertont und geschnitten werden.
2.1.2
Prinzipien der Animation
Um verschiedene Techniken und Algorithmen aus der Computergraphik genauer zu untersuchen, ist es
hilfreich, sich zunächst mit den Animationsprinzipien zu beschäftigen, die in handgezeichneten Animationen benutzt werden. [LJ87] beschreibt die Basisprinzipien der traditionellen, handgezeichneten
Animation und ihre Anwendung zur dreidimensionalen Computeranimation. Die Grundlage dafür
stammt aus [TJ81]. Hier werden die Erfahrungen führender Animatoren der Walt Disney Company
zusammengestellt, die seit 1930 entstanden sind, und es wird versucht, realistische Animation zu produzieren. Daraus leiten sich die zwölf Basisprinzipien der traditionellen Animation ab. Im Folgenden
wird auf diese Prinzipien eingegangen.
1 Antialiasing:
Methoden zur Reduzierung von unerwünschten Abtasteffekten
KAPITEL 2. GRUNDLAGEN
8
• Quetschen und Strecken
Ein Objekt kann zusammengedrückt oder in die Länge gezogen werden. Dabei ändert sich die
Form, aber das Objektvolumen bleibt erhalten. Das gibt ein Gefühl von Masse und Elastizität
eines Objekts.
• Bewegungsdauer
Beschreibt die Dauer, bzw. die Geschwindigkeit einer Bewegung. Wichtige Eigenschaften für
die Bewegungsdauer sind Masse und Größe eines Objekts, welche dazu beitragen, wie schnell
oder langsam es sich bewegen kann.
• Antizipation
Unter Antizipation versteht man die Vorbereitung einer Aktion. Dabei wird die Hauptaktion
durch eine Gegenbewegung vorbereitet, etwa wie bei einem Golfspieler, der vor einem Schlag
den Schläger nach hinten schwingt. So wird die eigentliche Bewegung für den Beobachter besser lesbar und wirkt natürlicher.
• Inszenierung der Posen
Es wird die Aufmerksamkeit des Publikums auf das Wichtigste der Szene gelenkt. Somit werden unnötige Details vermieden, und das Relevante der Szene steht im Fokus.
• Weiterführende und überlappende Bewegung
Hierbei handelt es sich um den Ablauf einer Aktion und das Etablieren seiner Beziehung zur
nächsten Aktion. Bei weiterführenden Bewegungen gehen Elemente in Folge der Hauptbewegung über deren Endpunkt zeitversetzt hinaus. Überlappende Bewegungen beschreiben, wie
Teile des Körpers sich mit verschiedenen Geschwindigkeiten bewegen. Die Definitionsgrenzen
zwischen weiterführenden und überlappenden Aktionen sind oft fließend.
• Straight Ahead und Pose-to-Pose
Dabei handelt es sich um zwei gegensätzliche Ansätze für die Bildung von Bewegung. Straight
Ahead ist dabei das Zeichnen einer Szene Bild für Bild vom Anfang bis zum Ende, wodurch eine
dynamische Illusion der Bewegung entsteht. Pose-to-Pose zeichnet zu Beginn wenige Schlüsselbilder, und füllt die Intervalle zu einem späteren Zeitpunkt. Es wird hauptsächlich für dramatische Szenen benutzt. Oft wird auch mit einer Kombination dieser beiden Techniken gearbeitet.
• Beschleunigung und Abbremsung
Bewegungen des menschlichen Körpers brauchen Zeit zur Beschleunigung und zum Abbremsen. Deshalb beginnt eine natürliche Bewegung meist langsam, beschleunigt dann, und bremst
zum Ende der Bewegung wieder ab. Zu Anfang und Ende einer Bewegung werden daher mehr
Einzelbilder verwendet als im Mittelteil.
• Bewegungsbögen
Die meisten menschlichen Aktionen treten entlang einer bogenförmigen Bewegungsbahn auf,
KAPITEL 2. GRUNDLAGEN
9
wie z.B. der Rotation von Gliedmaßen um ein Gelenk. Animation reproduziert diese Bewegung
für größeren Realismus.
• Übertreibung
Mit Übertreibung kann man das Wesentliche einer Idee hervorheben. Um Bewegungen deutlich zu machen, ist es eventuell nötig, diese zu übertreiben. Dabei muss allerdings kontrolliert
werden, dass die Übertreibung die Bewegung nicht zu ungenau macht.
• Zweitrangige Bewegung
Das Hinzufügen einer zweiten Aktion zur Hauptaktion hilft diese zu unterstützen, und gibt
der Szene mehr Leben. Beispielsweise kann eine laufende Person gleichzeitig mit den Armen
schwingen. Die Hauptaktion sollte dennoch im Fokus stehen.
• Anreiz
Sowohl das Aussehen einer Figur, als auch ihre Bewegungen sollen ihrem Charakter angemessen sein. Das Wichtigste ist, dass der Beobachter die Interessantheit und den Realismus des
Charakters wahrnimmt.
• Solides Zeichnen
Prinzip von solidem Zeichnen bedeutet, dass es Formen im dreidimensionalen Raum annimmt.
Dabei sollen die Objekte in der Szene richtig proportioniert und perspektivisch korrekt sein,
und diese Qualitäten auch in der Bewegung nicht verlieren.
Die Anwendungen dieser Prinzipien sind unabhängig vom Medium der Animation. Zweidimensionale, handgezeichnete Animation arbeitet mit einer Abfolge von Zeichnungen, welche Bewegung simulieren, wohingegen dreidimensionale Computeranimation ein dreidimensionales Modell im Computer
bildet. Bewegungsdauer, Antizipation, Inszenierung der Posen, weiterführende und überlappende Aktionen, Übertreibung und zweitrangige Bewegung wenden die gleichen Methoden für beide Arten der
Animation an. Während die Bedeutung von Quetschen und Strecken, Beschleunigung und Abbremsung, Bewegungsbögen, Anreiz und Straight-Ahead und Pose-to-Pose Aktionen gleich bleibt, ändert
sich ihre Anwendung, wenn die Animation in einem anderen Medium stattfindet.
2.2
Animationstechniken
Es gibt eine Vielzahl von Animationstechniken, die beim Beobachter den Eindruck von Bewegung
erwecken. Im Folgenden werden einige bekannte Animationstechniken vorgestellt. Den Abschluss
des Unterkapitels bildet die punktbasierte Animation, welche im Hauptteil dieser Arbeit genauer beschrieben wird.
KAPITEL 2. GRUNDLAGEN
2.2.1
10
Elementaranimation
Im Bereich der Elementaranimation, auch als klassische Animation bezeichnet, ist die wohl bekannteste Methode die Stop-Motion Technik. Diese Technik wird vor allem beim Film benutzt. Dabei können Objekte animiert werden, indem von ihnen mehrere aufeinanderfolgende Bilder gemacht werden,
wobei in den Aufnahmepausen die Position des Objekts geringfügig verändert wird. Dieses Schema
wird solange wiederholt, bis man alle für die zu animierende Szene notwendigen Bilder erstellt hat.
Danach werden die Bilder in der aufgenommen Reihenfolge hintereinander in einer Sequenz abgespielt, um so eine flüssige Bewegung zu erzeugen.
Der Pionier, der diese Technik im Film benutzte, war Willis O’Brien. Er verwendete die StopMotion Technik 1933 bei seinem Film King-Kong. Ray Harryhausen verfeinerte diese Technik in
den fünfziger Jahren und verwendete sie in seinen Filmen wie in Jason und die Argonauten. Weitere
Anwendungsgebiete von Stop-Motion sind Animation von Puppen oder Knetmännchen. Auch Zeichentrickfilme gehören zum Bereich der Elementaranimation. Hierbei verwendet man eine Vielzahl
von handgezeichneten Bildern, die zeitlich nacheinander dargestellt werden. Dabei entsteht ebenfalls
eine flüssige Bewegung. Die einfachste Form eines Zeichentrickfilms ist ein Daumenkino, was meist
ein Strichmännchen oder Objekt zeigt, das sich in einer Szene bewegt.
Obwohl Stop-Motion eine einfache und kostengünstige Technik ist, macht sie die Umpositionierung
der Szene für jedes neue Bild sehr zeitaufwendig. Für flüssige Bewegungen sind deshalb sehr viele
Bilder notwendig. Zudem wirken Bewegungsabläufe oft unrealistisch.
2.2.2
Simulative Animation
Aus dem Bereich der simulativen Animation sollen zwei Basisverfahren, die man zur Objektdeformation verwendet, näher erklärt werden. Bei beiden Verfahren muss die Objektverformung numerisch
berechnet werden. Dabei werden Objekte in eine endliche Anzahl von Unterelementen aufgeteilt, wovon jedes dann separat berechnet wird. Zur Berechnung werden die mechanischen Gesetze von Navier,
Stoke oder Hooke verwendet. Bei den beiden Methoden handelt es sich um das Masse-Feder-Dämpfer
System und um die Finite-Elemente-Methode [NC06].
Masse-Feder-Dämpfer Systeme sind wohl die einfachsten und intuitivsten aller deformierbaren Modelle. Hierbei muss die Deformation auf Grundlage der Polygonnetze von Objekten berechnet werden.
Das Modell besteht aus Punktmassen für jeden Eckpunkt des Polygonnetzes. Die Punktmassen sind
über ein Netzwerk von masselosen Federn miteinander verbunden.
Die physikalische Grundlage solcher Systeme basiert auf dem Hookschen-Gesetz. Es beschreibt ein
linear-elastisches Verhalten von Festkörpern. Dabei sind einwirkende Kraft und elastische Verformung
proportional zueinander.
Die Gesamtmasse des zu simulierenden Objekts verteilt sich gleichmäßig auf eine endliche Anzahl
verschiedener Massepunkte. Benachbarte Massepunkte sind über masselose elastische Federn miteinander verbunden, welche die Federkonstante k besitzen. Diese Konstante gibt die Starrheit der
jeweiligen Feder an. Durch Ändern der Federkonstante lässt sich die Elastizität des Objekts variieren.
KAPITEL 2. GRUNDLAGEN
11
Parallel zu den Federn befinden sich imaginäre masselose Dämpfungsglieder. Den Aufbau eines solchen Systems zeigt Abbildung 2.3. Dieses besitzt die Dämpfungskonstante cv . Das Dämpfungsglied
sorgt dafür, dass eine einmal in Schwingung versetzte Feder nach einer bestimmten Zeit langsam
ausschwingt und schließlich in die Ruhelage zurück kehrt. Je mehr dieser Federn in einem Objekt
vorhanden sind, desto genauer und realistischer kann die Deformation des Objekts dargestellt werden.
Die Gesamtkraft des Systems setzt sich aus drei Teilen zusammen: Dämpfer, Feder und Trägheit.
fGesamt = fDämpfer + fFeder + fTrägheit
(2.1)
Die einzelnen Elemente aus Gleichung (2.1) stellen sich folgendermaßen dar:
fDämpfer = v · cv
(2.2)
−
−
−
fFeder (→
x i ) = −k(→
x i −→
x rest )
(2.3)
fTrägheit = m · a
(2.4)
wobei k die Federkonstante, a die Beschleunigung, v die Geschwindigkeit, cv die Dämpfungskonstante, m die Masse und xrest die Ruheposition ist.
Die Gründe für die weite Verbreitung des Masse-Feder-Dämpfer Systems sind das leichtverständliche physikalische Konzept, die einfache Implementierung und die relativ niedrigen Rechenanforderungen. Allerdings ist es sehr ungenau. [TF88] liefert einen Ansatz der Masse-Feder-Dämpfer Systeme um Viskoelastizität, Plastizität und Fraktur erweitert.
Abbildung 2.3: Masse-Feder-Dämpfer System [Mas]
Die Finite-Elemente-Methode ist ein beliebtes Standardverfahren zur Festkörpersimulation. Bei diesem numerischen Verfahren werden partielle Differentialgleichungen auf irregulären Gittern gelöst.
Bei komplexen Zusammenhängen wird das Gesamtproblem in eine endliche Anzahl einfacher Teilprobleme zerlegt, wobei jedes Teilproblem, wie in Abbildung 2.4 dargestellt, ein finites Element be-
KAPITEL 2. GRUNDLAGEN
12
schreibt. Man überführt dadurch ein kontinuierliches Problem in ein diskretes und berechnet dabei
eine approximative Lösung. Je höher der Diskretisierungsgrad ist, desto genauer nähert sich die approximative Lösung der exakten Lösung an.
Die gebildeten finiten Elemente sind an ihren Eckpunkten mit den Nachbarelementen verbunden.
Innerhalb der finiten Elemente werden für die gesuchte Lösung Ansatzfunktionen definiert. Diese
Ansatzfunktionen werden dann in die zu lösenden Differentialgleichungen eingesetzt. Gemeinsam
mit den Randbedingungen erhält man ein Gleichungssystem von Gleichgewichts- und Bewegungsgleichungen. Dieses Gleichungssystem wird numerisch gelöst.
Wenn bei einem zu simulierenden Objekt bestimmte Gebiete von größerem Interesse sind, können
diese Bereiche mit kleineren Elementen beschrieben werden, um einen höheren Detaillierungsgrad zu
erhalten.
Im Bereich der numerischen Strömungsmechanik gibt es noch weitere Verfahren wie die FiniteDifferenzen-Methode oder die Finite-Volumen-Methode [NC06]. Diese Methoden liefern eine hohe
Genauigkeit bei der Simulation. Der Aufwand ist dafür größer, da ein vollständiges Polygonnetz zur
Simulation gespeichert werden muss.
Abbildung 2.4: Unterteilung in finite Elemente [Mü08]
2.2.3
Kinematische Techniken
Der Begriff Kinematik kommt aus dem Sektor der Robotik. Ein typischer Roboterarm besteht aus zwei
verschiedenen Elementtypen. Dies sind starre Elemente, welche auch als Hebel bekannt sind und als
Verbindungselemente Gelenke verwenden. Der Aufbau eines Roboterarms ist dabei ein hierarchisches
Modell, wobei Hebel an ihren Enden durch Gelenke miteinander verbunden werden. Die Abfolge von
Hebeln und Gelenken, die schließlich den Roboterarm bilden, bezeichnet man als kinematische Kette.
Den Fixpunkt des Roboterarms deklariert man als Basis, dass freie Ende der Kette heißt Endeffektor.
Dieser Aufbau wird in Abbildung 2.5 dargestellt.
KAPITEL 2. GRUNDLAGEN
13
Abbildung 2.5: Kinematische Kette eines Roboterarms [Bre07]
Wie bei [Bre05] beschrieben, kann man einen menschlichen Arm mittels Kinematik simulieren. Dabei ist der Rumpf die Basis mit der Schulter als Basisgelenk, an die in hierarchischer Weise Oberarm als erstes kinematisches Glied, Ellenbogen als Zweitgelenk, Unterarm als zweites kinematisches
Glied, Handbeuge als Drittgelenk und Hand als drittes kinematisches Glied angeheftet sind. Die Hand
fungiert gleichzeitig als Endeffektor. Das Ganze bildet eine offene kinematische Kette.
Um eine parametrische Beschreibung von kinematischen Ketten zu erreichen, verwendet man die
Regeln von Denavit und Hartenberg. Dabei wird jeder starre Hebel mit den Parametern Gelenkwinkel,
Hebelverschiebung, Hebellänge und Hebeldrehung beschrieben [Par02].
Zur Berechnung von offenen kinematischen Ketten gibt es in der Kinematik zwei Möglichkeiten.
Bei der Vorwärtskinematik wird die Position und Orientierung des Endeffektors als Funktion seiner
Gelenkwinkel berechnet. Bei gegebenen Gelenkwinkeln kann man ausgehend von der Basis entlang
der kinematischen Kette sukzessive die Positionen der kinematischen Glieder berechnen.
Als Eingangswerte der Berechnung dienen dabei die Koordinaten des jeweils vorherigen Kettengliedes, sowie die Winkelstellungen des vorherigen Gelenkes. Aus den gegebenen Gelenkstellungen wird
dann die finale Endeffektorstellung berechnet.
Bei der Inversen Kinematik ist die Berechnungsreihenfolge innerhalb der Hierarchie der kinematischen Kette genau entgegengesetzt zur Vorwärtskinematik. Hierbei hat der Nutzer die Position des
Endeffektors gegeben, und berechnet die Gelenkstellungen.
Die Vorwärtskinematik führt immer auf eine eindeutige analytische Lösung. Bei der Inversen Kinematik ist das Problem nicht immer analytisch lösbar, und enthält im Allgemeinen Mehrdeutigkeiten.
Eine Animationsart aus dem Feld der Kinematik ist die Boneanimation. Hierbei werden Bereiche
des Körpers durch gewisse Repräsentanten, auch Knochen genannt, dargestellt. Die Knochen bauen
den Menschen hierarchisch auf. Wie oben beschrieben besitzt die Darstellung Hebel und Gelenke.
Dieser Aufbau des menschlichen Skeletts kann somit in einer Baumdatenstruktur abgelegt werden
[Shi05, Par02].
Die Basis sitzt im Körperschwerpunkt, dem Rumpf. In der Baumdarstellung ist der Rumpf der Wurzelknoten. Da es sich um eine offene kinematische Kette handelt, besitzt das Modell Endeffektoren für
KAPITEL 2. GRUNDLAGEN
14
Füße, Hände und den Kopf. In der Baumdarstellung liegen die Endeffektoren an den Blattknoten. Die
Knoten werden über Kanten verbunden. Die Hebel werden als Knoten dargestellt, die Gelenke sind
die Baumkanten, wie in Abbildung 2.6 zu sehen ist. Die Knoten besitzen jeweils eine Transformationsmatrix. Ein Pfad enthält die Transformation des jeweiligen Hebels. Wenn man sich entlang des
Pfades zu einer Hand bewegt, entspricht das einer Hintereinanderausführung der einzelnen Transformationsmatrizen, um an die entsprechende Position zu gelangen. Das lässt sich beispielsweise durch
folgende Gleichung verdeutlichen.
Hand = Rumpf · Oberkörper · Schulter · Oberarm · Unterarm
Abbildung 2.6: Hierarchischer Aufbau eines Menschen sowie die dazu gehörige Baumstruktur [Par02]
2.2.4
Animation durch Interpolation
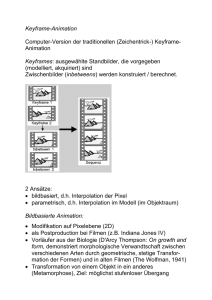
Bei der Animation durch Interpolation wird die Bewegung der Szene durch Schlüsselbilder, sogenannte Keyframes, dargestellt. Die Keyframes geben grob den Bewegungsablauf der Animation an.
Folglich findet zwischen den Keyframes eine Bildinterpolation statt, für welche die Zwischenbilder
berechnet werden müssen.
Eine der bekanntesten Keyframing-Techniken ist das Morphing. Dabei wird versucht, einen optisch
realistischen Übergang von einem Ursprungsbild zu einem Zielbild zu erzeugen. Dazu werden die
Positionen der korrespondierenden Pixel zwischen den beiden Keyframes interpoliert. Meist wird
parallel auch die Farbe der Pixel interpoliert, so dass ein weicher Übergang entsteht [Bre05]. Damit der
Übergang zwischen den Bildern möglichst realistisch wirkt, sollten sich Ursprungs- und Zielbild nicht
zu sehr voneinander unterscheiden. So ist es beispielsweise vorteilhafter, zwei Gesichter ineinander
umzuwandeln anstatt ein Gesicht in ein Objekt. Diese Technik wird vor allem in der Filmindustrie
angewandt.
KAPITEL 2. GRUNDLAGEN
15
Um die Technik etwas genauer zu erläutern, wird kurz der aus drei Arbeitsschritten bestehende Ablauf des Morphing erklärt.
Der erste Schritt ist das Verzerren. Hier wird das aktuelle Bild transformiert, um die Konturen der
beiden Bilder zur Übereinstimmung zu bringen. Das bedeutet, dass jeder Position eines Punktes im
Quellbild eine neue Position zugeordnet wird.
Der zweite Teil benutzt Zwischenbilder. Hierbei wird jeder Punkt im Quellbild in die durch die
Verzerrung berechnete Position überführt. Das geschieht durch eine lineare Interpolation.
Der finale Schritt ist die Überblendung, die parallel zur Berechnung der Zwischenbilder stattfindet.
Bei den ersten Interpolationsschritten ist der Anteil des Ursprungsbildes bestimmend. Im weiteren
Verlauf der Interpolation nimmt der Anteil des Zielbildes immer weiter zu, bis das Morphing schließlich beim Zielbild beendet ist.
Abbildung 2.7: Interpolation zwischen zwei Bildern [Bre07]
2.2.5
Bewegungserfassung
Eine weitere Technik um Bewegungen zu animieren ist das Motion Capture. Hierbei werden menschliche Bewegungen mit einer Kamera aufgezeichnet. Die dabei erfassten Informationen können ganz
allgemein sein, wie Positionen eines Körpers im Raum, oder komplex, wie die Deformation des Gesichts oder der Muskelmassen. Die Technik eignet sich zur Animation von Computercharakteren.
Dabei werden die aufgezeichneten menschlichen Bewegungen auf Bewegungen eines Computercharakters abgebildet [Stu94].
Zur Aufzeichnung der Bewegungen von realen Objekten gibt es im Motion Capture grundsätzlich
KAPITEL 2. GRUNDLAGEN
16
zwei verschiedene Verfahren [Shi05]. Bei optischen Methoden werden kleine Markierungen am jeweiligen Objekt angebracht. Diese Markierungen werden durch verschiedene Kameras aufgezeichnet,
die dabei Aufschluss über die Position des Objekts im Raum liefern. Allerdings müssen die Kameras
im Raum so angebracht sein, dass möglichst wenige Markierungen verdeckt werden.
Bei nicht-optischen Verfahren werden Ganzkörperanzüge benutzt, an denen elektromagnetische Sensoren angebracht sind. Die Sensoren geben Auskunft über die Position im Raum und dienen somit zur
Erfassung der Bewegung.
Nach der Aufnahme der Bewegung können die Daten weiter verarbeitet werden. Dabei werden die
Daten auf eine Art Strichmännchen abgebildet. Dieses Strichmännchen folgt den aufgenommenen
Bewegungen. Somit führt das virtuelle Objekt die aufgezeichneten Bewegungen des Menschen aus.
Ein Beispiel dafür ist die Figur des “Gollum” im Film “Der Herr der Ringe”, wie in Abbildung 2.8
gezeigt wird.
Abbildung 2.8: Motion Capture [Mot]
Mit der erwähnten Methode können komplexe Bewegungen wie Laufen mit geringerem Aufwand
als bei anderen Techniken dargestellt werden.
Allerdings können die mit Motion Capture erstellten Bewegungen einen unnatürlichen Eindruck
erwecken. Das kann passieren, wenn sich die menschliche Figur zu sehr von der neuen Figur unterscheidet, da hierbei zu wenige Daten zur Berechnung von Zwischenbildern zur Verfügung stehen.
Zudem müssen die Kosten für die verwendete Ausrüstung beachtet werden.
2.2.6
Punktbasierte Animation
Im bisherigen Verlauf wurden vor allem Methoden vorgestellt, die auf Netzen, sogenannten Meshes,
beruhen. Bei der Repräsentation eines menschlichen Skeletts werden die einzelnen Knochen über
Gelenke zusammengehalten, so dass immer ein Zusammenhang zwischen einzelnen Körperelementen
KAPITEL 2. GRUNDLAGEN
17
besteht.
Bei der punktbasierten Animation werden meshfreie Methoden verwendet. Diese Verfahren stellen
eine Alternative zu den bereits etablierten meshbasierten Techniken dar. Im Gegensatz zu meshbasierten Techniken, in welcher die einzelnen Dreiecke miteinander verbunden sind, besteht zwischen den
einzelnen Punkten dabei kein Zusammenhang. Die Punkte besitzen keine Topologieinformationen.
Die punktbasierten Techniken eignen sich zur Volumensimulation, da im Unterschied zu den meshbasierten Verfahren Volumeninformationen vorhanden sind. Jeder der Punkte hat in seiner Umgebung
lokale Eigenschaften, welche ihn beschreiben. Abbildung 2.9 vergleicht ein Objekt aus Meshes mit
einem auf Punkten basierenden Objekt.
Abbildung 2.9: Meshbasierter [Mes] und punktbasierter [Poi] Standford Bunny
Solche meshfreien Methoden, zu denen die punktbasierte Animation gehört, kommen in Partikelsystemen zum Einsatz. Hierdurch lassen sich Rauch und Flüssigkeiten besonders gut animieren, wobei
auf diesen Bereich in Kapitel 3 noch genauer eingegangen wird.
Punkte sind immer dann eine gute Wahl, wenn man dreidimensionale Objekte animieren möchte,
welche sich dynamisch ändern. Wenn bei der Simulation einzelne Punkte hinzugefügt oder gelöscht
werden, muss man sich keine Gedanken darüber machen, dass der Zusammenhang zerstört wird, da
Punkte nicht zusammenhängend sind. Bei meshbasierten Methoden würde eine solch dynamische
Änderung zu schlecht konditionierten Meshes führen. Zusammenhangs- und Nachbarschaftsinformationen würden teilweise nicht mehr stimmen, wodurch das Mesh neu berechnet werden müsste. Diese
Technik ist als Remeshing bekannt.
Aus diesem Grund eignen sich punktbasierte Techniken zur Animation von großen Deformationen.
Allerdings bringen diese Verfahren nicht nur Vorteile. Wenn neue Punkte in das Modell eingefügt
werden, muss in einem Schritt die Nachbarschaft neu berechnet werden, da man ohne Zusammenhangsinformationen kein Wissen darüber hat, welche Punkte nun in der Nachbarschaft liegen.
KAPITEL 2. GRUNDLAGEN
2.3
18
Grundlagen der Physik
Um eine Animation physikalisch korrekt ablaufen zu lassen, muss man feststellen, welche Bereiche
der Physik dafür wichtig und von Interesse sind.
Die Physik beschäftigt sich mit den Vorgängen der unbelebten Natur und ihrer mathematischen Beschreibung. Sie ist aus dem Wunsch der Menschen entstanden, die Naturerscheinungen zu verstehen,
auf allgemeine Gesetze zurückzuführen und sich die Natur durch diese Erkenntnisse zu Nutze zu machen. In der Experimentalphysik werden Naturgesetze durch Beobachtung und Erfahrung gewonnen,
in der Theoretischen Physik durch Mathematik und Logik. Dabei ergänzen sich Experimental- und
Theoretische Physik, indem die Experimentalphysik Hypothesen der Theoretischen Physik bestätigt
und die Theoretische Physik auf Ergebnisse der Experimentalphysik zurückgreift [Phya].
Der Überbegriff Physik besteht aus vielen Teilbereichen, wie z.B. Mechanik, Thermodynamik, Elektrodynamik, Optik oder Akustik.
Da die Animation physikalisch korrekt ablaufen soll, ist entscheidend, welche Gebiete der Physik
besonderen Einfluss darauf haben. Physikalische Korrektheit ist im Sektor der Computerspiele ein
wichtiger Faktor. Da hier einige Effekte aus verschiedenen physikalischen Bereichen keinen Einfluss
haben, lohnt sich der Blick auf dieses Feld.
Die Thermodynamik hat noch keinen Einzug erhalten, sonst würden Schüsse aus einer Laserwaffen
diese sofort verdampfen lassen [Kle05]. Die Optik und Akustik werden meist von speziellen Engines
berechnet. Zudem findet die Elektrodynamik im Computerspielebereich keinen direkten Einfluss auf
die physikalische Korrektheit. Unter den oben aufgezählten Teilgebieten hat die Mechanik somit den
größten und wichtigsten Einfluss auf das physikalisch korrekte Ablaufen der Animation.
Die Mechanik befasst sich mit der Bewegung von Körpern und der Einwirkung von Kräften auf diese
Körper. Dabei sind äußere Kräfte wie die Gravitation und Kräfte, welche Körper aufeinander ausüben,
zu beachten. Der einfachste Teil der Mechanik behandelt Fälle, in denen man von der Ausdehnung der
Körper absehen und sie als mit Masse behaftete Punkte, sogenannte Massenpunkte, betrachten kann
[Mes06].
Ein Bereich der Mechanik der Massepunkte ist die Kinematik, die den Ablauf der Bewegung untersucht, ohne nach dem Grund für diese zu Fragen. Wichtige Größen sind dabei der Ortsvektor, die
Geschwindigkeit und die Beschleunigung.
Das Gegenstück der Kinematik ist die Dynamik, die sich mit der Bewegung von Körpern unter Einwirkung von Kräften beschäftigt. Es wird also nach der Ursache der Bewegung, besser nach der Ursache einer Änderung des Bewegungszustandes gefragt. Kräfte und Impulse, sowie deren Erhaltung,
spielen also eine wichtige Rolle.
Aus der Punktmechanik kann man logisch einwandfrei die Mechanik des starren Körpers und die der
deformierbaren Körper entwickeln, indem man diese als Systeme unendlich vieler Massenpunkte mit
festen bzw. veränderlichen relativen Lagebeziehungen auffasst.
Bisher durften sich Dinge nur wie Massepunkte verhalten, d.h. translatorisch bewegen. In der Me-
KAPITEL 2. GRUNDLAGEN
19
chanik der starren Körper erhalten die Körper eine Ausdehnung und können sich daher auch drehen.
Eine Translation ist eine Bewegung, bei der alle Punkte des Körpers kongruente Bahnen beschreiben.
Diese Bahnen dürfen durchaus gekrümmt sein. Bei einer Rotation beschreiben alle Punkte konzentrische Kreise um eine bestimmte Gerade, die Drehachse [Mes06]. Weitere wichtige Begriffe aus diesem
Feld sind die Winkelgeschwindigkeit, das Drehmoment und der Drehimpuls.
Im täglichen Leben hat man es mit Systemen aus sehr vielen Teilchen zu tun, die alle aufeinander
Kräfte ausüben. Dazu kommen noch von außen wirkende Kräfte. Im Sektor der Mechanik deformierbarer Körper spielen zusätzlich noch die Kräfte eine Rolle, die innerhalb der Körper wirken. Insofern
können Körper bei Kollision oder Krafteinwirkung von außen ihre Form ändern, und sind deshalb
deformierbar.
Oben genannte physikalische Größen müssen nun für jedes Objekt gespeichert werden, um die
Grundlage für Simulationen zu erhalten. Das Problem besteht nun darin, die Bewegungsgleichung
der einzelnen Körper zu lösen. Die Bewegungsgleichung drückt aus, an welchem Ort sich ein Körper
zu einem bestimmten Zeitpunkt befindet.
Kapitel 3
State of the Art
Im vorigen Kapitel über die Grundlagen der Arbeit wurden einige Animationstechniken vorgestellt,
die auf der Basis von Polygonnetzen arbeiten. Im Zuge der punktbasierten Animation interessieren
Animationsmethoden, bei denen die einzelnen Punkte keine Topologieinformationen besitzen. In diesem Kapitel wird auf den aktuellen Stand der Technik im Bereich der meshfreien Techniken eingegangen. Hierzu werden Partikelsysteme, mit denen sich Feuer-, Rauch- oder Explosionseffekte animieren
lassen, und die Smoothed Particle Hydrodynamics Methode, mit der es möglich ist, Flüssigkeiten zu
animieren, näher betrachtet. Ebenfalls werden einige Anwendungsmethoden aufgezeigt, die mit der
punktbasierten Animation arbeiten. Da die physikalischen Berechnungen in dieser Arbeit mit Hilfe einer Physikengine durchgeführt werden, folgt eine Einführung dieser. Abschließend werden die
Grundlagen der in dieser Arbeit verwendeten Physikengine erläutert.
3.1
Partikelsysteme
Seit Beginn der Computergraphik werden dreidimensionale Objekte, die eine feste Oberfläche haben,
durch Netze und Kombinationen von Polygonen dargestellt. Die Darstellung von Objekten mit variabler Oberfläche war nicht möglich. Dabei handelt es sich um elastische Gegenstände oder auch die
Simulation von Feuer oder Nebel.
Eine Methode, um solche Phänomene zu simulieren, sind die Partikelsysteme. Ein Partikelsystem
ist eine Ansammlung von winzigen Partikeln, die zusammen das verschwommene Objekt bilden.
Es besitzt einen Kern, der alle Partikel steuert, deren Bewegungsabläufe bestimmt und ebenfalls die
physikalischen Gesetze definiert, durch welche die Partikel beeinflusst werden.
Diese Partikelsysteme wurden in [Ree83] eingeführt, um einen realitätsnahen Feuereffekt zu entwickeln. Die Objekte werden als verschwommen und somit als nicht starr bezeichnet. Die Darstellung
von Partikelsystemen unterscheidet sich in drei Arten von meshbasierten Techniken.
Als erstes wird ein Objekt nicht durch eine Menge von primitiven Oberflächenelementen wie Polygonen repräsentiert, sondern als Wolke von primitiven Partikeln, die das Volumen definieren. Ein
Partikel ist also ein Punkt im dreidimensionalen Raum, der das Volumen des Objekts darstellt [Kei06].
20
KAPITEL 3. STATE OF THE ART
21
Zum zweiten ist ein Partikelsystem kein statisches Objekt. Seine Partikel ändern ihre Form und
bewegen sich im Laufe der Zeit. Neue Partikel werden “geboren” und ältere Partikel “sterben”.
Als drittes ist ein Objekt, das durch ein Partikelsystem animiert wird, nicht deterministisch, da seine
Form nicht vollständig spezifiziert ist. Stattdessen benutzt man stochastische Prozesse, um die Objektform zu bilden und zu ändern.
Um jedes einzelne Bild in der Bewegungssequenz zu berechnen, werden fünf Phasen durchlaufen
[Ree83, Hei02].
In der ersten Phase werden neue Partikel im System erzeugt. In Phase zwei werden jedem neuen
Partikel individuelle Eigenschaften zugewiesen. Die dritte Phase untersucht die vorgeschriebene Lebensdauer der Partikel. Wenn ein Partikel innerhalb des Systems diese Lebensdauer überschritten hat,
wird er ausgelöscht. In Phase vier werden die noch vorhandenen Partikel gemäß ihrer definierten
Eigenschaften bewegt und verändert. In den ersten vier Phasen wurden alle benötigten Änderungen
an den Partikeln vorgenommen. Abschließend wird in Phase fünf ein Bild aus den noch “lebenden”
Partikeln in den Bildspeicher gerendert.
Im Ablauf von Partikelsystemen wurden schon die individuellen Eigenschaften jedes Partikels erwähnt. Für jedes in Phase eins neugebildeten Partikel muss das System die folgenden Eigenschaften
bestimmen:
• Position
Die Position beschreibt den Punkt im Raum, wo sich das entsprechende Partikel während der
Animation in der Szene befindet.
• Geschwindigkeit und Richtung
Die Bewegung eines Partikels in der Szene wird durch jeweils einen Geschwindigkeits- und
Richtungsvektor festgelegt. Sowohl die Geschwindigkeit, als auch die Richtung kann während
ihrer Lebensdauer noch durch äußere Einflüsse, wie die Gravitation, oder durch Interaktion mit
anderen Partikeln geändert werden.
• Größe
Im Normalfall werden Partikel als nulldimensionale Objekte wie Punkte im Raum definiert.
Tritt der Fall ein, dass ein- oder mehrdimensionale Strukturen benutzt werden, kann einem
Partikel ebenfalls eine Größe zugeordnet werden. Diese Größe kann sich im Laufe des Lebens
der Partikel durch Einflüsse des Systems ändern.
• Farbe
Die Partikelfarbe, die zu Beginn der Simulation festgelegt wurde, kann sich im Laufe der Zeit
auch ändern. Wenn beispielsweise ein Feuer animiert werden soll, kann die Anfangsfarbe ein
Weiß oder helles Gelb sein. Im Zuge der Simulation kann durch die Temperaturänderung dieser
Farbton ins Rötliche übergehen und schließlich einen immer dunkleren Farbton annehmen.
KAPITEL 3. STATE OF THE ART
22
• Transparenz
Aus vielen Computergraphik-Anwendungen kennt man den Begriff des Alpha-Kanals2 . Vergleichbar zu diesem Begriff ist die Transparenz, die ein Partikel durchsichtig macht. Auch die
Transparenz kann sich während der Lebensdauer ändern.
• Form
Neu erstellte Partikel haben eine bestimmte Form. Während der Simulation kann sich diese
Form durch äußere Einflüsse oder Interaktion mit benachbarten Partikeln ändern.
• Lebensdauer
Wie oben erwähnt, werden neue Partikel “geboren” und ältere Partikel “sterben”. Der Zeitraum
zwischen der “Geburt” und dem “Ableben” eines Partikels bezeichnet man als Lebensdauer.
Bei den aufgezählten Attributen handelt es sich um die Haupteigenschaften, die jeder Partikel eines
Partikelsystems besitzt. Natürlich können Partikel auch noch weitere Eigenschaften wie Masse oder
Alter besitzen.
Sobald die Positions- und Erscheinungsparameter aller Partikel berechnet wurden, erzeugt der Renderingalgorithmus daraus ein Bild. Klassische dreidimensionale Renderingverfahren wie das Raytracing sind für Partikelsysteme nicht geeignet. Da eine hohe Anzahl an Partikeln vorliegt, muss das
Verfahren sehr viele Schnittberechnungen für alle Partikel durchführen, was es extrem rechenaufwendig macht.
Für Partikelsysteme werden spezielle Renderingverfahren benötigt. Bei der Berechnung des Bildes
wird zwischen Methoden für selbstleuchtende und reflektierende Partikel unterschieden.
Partikelsysteme können zudem hierarchisch aufgebaut sein. Das bedeutet, dass ein Partikel, welcher
vom Partikelsystem erzeugt wurde, selbst ein Partikelsystem ist. Dieses neue Partikelsystem ist nun
auch in der Lage neue Partikel zu erschaffen und auszusenden, da es alle Regeln und Eigenschaften
des Elternsystems “erbt”. Somit gibt es nicht nur eine einzige Quelle zur Neubildung von Partikeln.
Die Datenstruktur, die sich für einen derartigen hierarchischen Aufbau eignet, ist ein Baum.
Ein Anwendungsbeispiel eines hierarchischen Aufbaus ist die Explosion von Feuerwerkskörpern,
wie in Abbildung 3.1 dargestellt. Zu Beginn wird die Explosion von einem zentralen Punkt gestartet.
Im weiteren Verlauf spaltet sich die Explosion in verschiedene Teilexplosionen auf, was sich sehr
schön mit einer Baumdatenstruktur verwirklichen lässt.
Beim Modellieren von verschwommenen Objekten haben Partikelsystem-Anwendungen einige wichtige Vorteile gegenüber klassischen, oberflächenorientierten Techniken [Ree83, Kei06]. Zunächst ist
ein Partikel ein einfacheres Primitiv als ein Polygon. Das ermöglicht die Animation einer großen
Anzahl von Partikeln für komplexe Szenen. Ein zweiter Vorteil ist die prozedurale Definition des Modells. Seine stochastische Kontrolle vereinfacht den Aufbau des Systems. Schließlich können durch
Partikelsysteme “lebende” Objekte modelliert werden, die ihre Form im Laufe der Zeit ändern. Es
2 Alpha-Kanal
gibt die Durchsichtigkeit eines Bildpunkts an
KAPITEL 3. STATE OF THE ART
23
ist schwierig, komplexe Dynamik solcher Form mit Hilfe von oberflächenbasierten Techniken zu repräsentieren. Somit lassen sich Animationen von physikalischen Phänomenen realitätsnah darstellen.
Partikelsysteme sind flexibel und lassen sich hierarchisch aufbauen. Mit diesen Partikelhierarchien
können verschwommene Objekte wie Wolken erzeugt und überwacht werden. Zudem nehmen Zufallskomponenten durch stochastische Prozesse Einfluss.
Da Partikelsysteme aus tausenden Partikeln bestehen, und für jedes Partikel individuell die Physik
berechnet werden muss, wird die Methode extrem rechenintensiv. Ein weiterer Nachteil ist der hohe
Implementierungsaufwand von Partikelsystemen.
Mit Partikelsystemen können eine Vielzahl von physikalischen Phänomenen animiert werden. Sie
werden gerne zur Animation von Feuer, Rauch oder Explosionen verwendet. Wie im Fall von Explosionen zuvor schon erwähnt, führt der hierarchische Aufbau von Partikelsystemen zu besseren
Ergebnissen bei der Animation. Ebenfalls können Wasserfontänen, Flüssigkeiten oder Wolken auf
diese Weise animiert werden. Andere Anwendungen von Partikelsystemen sind die Animation von
Gras bzw. Pflanzen oder Tierschwärmen. Gleichwohl finden sie Einzug in Computerspielen, sowie in
Kinofilmen, um Spezialeffekte darzustellen.
Abbildung 3.1: Animation eines Feuerwerks mit Hilfe eines Partikelsystems [Hei02]
3.2
Smoothed Particle Hydrodynamics
Ein zweites Verfahren im Bereich der meshfreien Anwendungen ist die sogenannte Smoothed Particle
Hydrodynamics3 (SPH). Es handelt sich um eine numerische Methode, mit welcher hydrodynamische
Gleichungen gelöst werden können.
Ursprünglich ist SPH eine Methode zur Simulation von astrophysikalischen Problemen, die von
[GM77] eingeführt wurde. Diese ist aber allgemein genug, um für jegliche Art von Flüssigkeitssimulation benutzt zu werden. Für vertiefende Informationen zur SPH Technik sei dem Leser [Mon92]
empfohlen.
3 SPH:
geglättete Teilchen-Hydrodynamik
KAPITEL 3. STATE OF THE ART
24
SPH ist eine Interpolationsmethode für Partikelsysteme. Bei der Methode werden diskrete, geglättete
Partikel benutzt, um approximierte Werte von den benötigten physikalischen Größen und ihren räumlichen Ableitungen zu berechnen. Mit Hilfe der Partikel wird eine Flüssigkeit abgetastet. Die Partikel
sind Punkte auf der Oberfläche der Flüssigkeit, welche zu Beginn zufällig, wie bei der Monte-CarloMethode, verteilt werden. Für jedes Partikel können physikalische Eigenschaften wie Masse, Position
oder Geschwindigkeit in Abhängigkeit seiner Nachbarn berechnet werden.
Die Zahl der Partikel in einem bestimmten Bereich des Fluids ist ein Maß für die Dichte. In SPH
wird die Dichte mit dem Wert 0 dadurch simuliert, dass sich in einem solchen Gebiet keine Partikel
befinden. Wird die Dichte in diesem Umfeld im Laufe der Zeit größer, wandern die Partikel in dieses
bisher leere Gebiet [Ott95]. Es folgt eine mathematische Beschreibung dieser Methode.
Eine Funktion A wird an einer Position x von seinen benachbarten Partikeln interpoliert und benutzt
eine Summation [NC06]:
A(x) = ∑ m j
j
Aj
W (r, h)
ρj
(3.1)
A j bezeichnet den Funktionswert des Partikel p j am Interpolationspunkt x j , m j und ρ j sind die Masse
und Dichte des Partikel p j , und entsprechend r = x − x j .
Die Dichte ρi kann mit Gleichung (3.1) berechnet werden und führt zu
ρi = ρ(xi ) = ∑ m jW (xi − x j , h).
(3.2)
j
W (r, h) ist ein sogenannter smoothing Kernel4 . h ist die Glattlänge und beschreibt den wichtigsten
Parameter der SPH Methode. Er stellt den mittleren Abstand der einzelnen Partikel dar. Die Glattlänge
bestimmt die Auflösung dieser Methode und hat somit einen großen Einfluss auf den Rechenaufwand
der Simulation. Je niedriger die Größe von h ist, desto genauer ist die Simulation.
In Bereichen mit einer höheren Dichte benutzt man eine große Glattlänge. Entsprechend wird in
Gebieten mit kleiner Dichte eine kleine Glattlänge zur Simulation verwendet. Somit lässt sich der Rechenaufwand bei gleich bleibender Genauigkeit verringern. Schließlich wird zwischen den Partikeln
der Flüssigkeit die Oberfläche mit Hilfe des Kernels geglättet.
R
Eigenschaften des Kernel sind W (r, h)dr = 1, W (r, h) = 0 für |r| > h und limh→0 W (x, h) = δ (x),
wobei h die zuvor beschrieben Glattlänge und δ die Dirac Funktion ist. Die Wahl des smoothing
Kernels ist eine wichtige Aufgabe der Methode, da hierdurch festgelegt wird, wie viele Nachbarn zur
Berechnung mit einbezogen werden. Somit lässt sich der Rechenaufwand eingrenzen. Ausführliche
Informationen über Kernels sind in [Mon92] nachzulesen.
Ganz allgemein lässt sich sagen, dass die Animationsqualität und die Genauigkeit mit größerer Anzahl an Partikeln wachsen.
Bei der Methode werden aus partiellen hydrodynamischen Differentialgleichungen gewöhnliche Differentialgleichungen. SPH Methoden haben gegenüber traditionellen gitterbasierten Verfahren einige
4 Glättungskern
KAPITEL 3. STATE OF THE ART
25
Vorteile. Da SPH eine Lagrange-Methode ist, ist die Kontinuitätsgleichung automatisch erfüllt. Die
Programmierungs- und Berechnungskomplexität wird im Gegensatz zu anderen Ansätzen reduziert,
was die Methode brauchbar für interaktive Anwendungen macht. Zudem ist der Code sehr robust.
Durch die zufällige Verteilung der Partikel zu Beginn der Anwendung werden zu erwartende Fehler
minimiert. Darüber hinaus wird für die Berechnung von Ableitungen kein Gitter benötigt.
Allerdings zeigt die Methode auch Nachteile gegenüber gitterbasierten Techniken. Manchmal ist der
Code zu robust, was zur Folge hat, dass SPH Ergebnisse zu einem falschen Modell liefert, die dann
aber nicht physikalisch korrekt sind. Im Übrigen ist es bisher nicht möglich, die Inkompressibilität
des Materials exakt aufrecht zu erhalten. Werden höhere Auflösungen gefordert, sind dazu sehr viele
Partikel notwendig, wodurch der Vorteil des geringeren Rechenaufwandes wieder aufgehoben oder
gar ins Gegenteil verkehrt wird.
Abschließend wird noch auf einige Anwendungen von SPH eingegangen. SPH wurde ursprünglich
von [GM77] eingeführt, um astrophysikalische Probleme wie die Teilung von Sternen zu simulieren.
Die Methode wird immer häufiger für die Animation von Flüssigkeitsbewegungen angewendet, wie in
Abbildung 3.2 gezeigt wird. Des Weiteren wird die Technik benutzt, um Feuer, gasartige Phänomene
und stark deformierbare Objekte zu animieren. Im Laufe der Zeit wurde die SPH Methode erweitert,
um Objekte wie kochendes Wasser, eingeschlossene Luft sowie die Dynamik einer Lavalampe zu
simulieren. Darauf wird in der Arbeit [MG05] genauer eingegangen.
Abbildung 3.2: Flüssigkeitsdarstellung mit der SPH Methode [SPH]
3.3
Anwendungen von punktbasierter Animation
Im Bereich der punktbasierten Animation werden nun verschiedene Arbeiten vorgestellt, die den Ansatz der punktbasierten Animation verwenden. Zunächst eine Methode, mit der sich elastische, plastische und schmelzende Objekte animieren lassen. Eine weitere Arbeit benutzt einen punktbasierten
Ansatz zur Animation von elastoplastischen Festkörpern. Abschließend wird eine punktbasierte Ani-
KAPITEL 3. STATE OF THE ART
26
mation von inkompressiblen Strömungen beschrieben.
3.3.1
Animation von elastischen, plastischen und schmelzenden Objekten
[MKN+ 04] beschreibt ein Verfahren zur Animation von volumetrischen Objekten mit Materialeigenschaften im Bereich starr-elastisch bis zu plastisch-fließend. Bei der meshfreien Methode wird sowohl
das Volumen, als auch die Oberfläche durch eine Punktwolke modelliert, wozu keine Zusammenhangsinformationen zwischen den Punkten benötigt werden. Das verwendete physikalische Modell
basiert auf der Kontinuumsmechanik.
Das Verfahren berechnet mit Hilfe der Methode der kleinsten Quadrate in jedem Zeitschritt die partiellen Ableitungen des Verformungsfeldes, welches für die Deformation benötigt wird. Aus den partiellen Ableitungen des Verformungsfeldes können dann Dehnungen, Spannungen und elastische Kräfte an jedem simulierten Punkt gewonnen werden. Basierend auf den ermittelten Kräften können anschließend die Bewegungsgleichungen gelöst werden. Zur Simulation von elastischen und plastischen
Verformungen wird sowohl ein Elastizitäts- wie auch ein Plastizitätsmodell benötigt.
Die Kontinuumselastizitätsgleichungen beschreiben, basierend auf einem gegebenen Verformungsfeld, wie elastische Spannungen innerhalb eines Volumenobjekts berechnet werden.
In meshfreien Methoden wird das Volumen an einer endlichen Anzahl von Punkten abgetastet, ohne
Zusammenhangsinformationen und ohne den Zwang ein Volumennetz zu generieren.
Abbildung 3.3: Das linke Bild zeigt Phyxel (gelb) und Surfels (blau), die übrigen Bilder zeigen elastische und plastische Verformungen nach [MKN+ 04]
Die Methode benutzt eine abgetrennte Datenrepräsentation. Ein Datensatz wird zur Simulation des
physikalischen Verhaltens benutzt. Diese physikalischen Simulationspunkte werden als phyxel5 bezeichnet. Sie führen alle Simulationsgrößen wie Position, Dichte, Deformation, Geschwindigkeit,
Dehnung, Spannung und Kraft mit. Die Phyxel befinden sich im Inneren des Elements, sind also
Volumenelemente, auf denen die Physik berechnet wird.
Der zweite Datensatz besteht aus Oberflächenelementen. In der Arbeit werden sie als surfels6 bezeichnet. Die Surfels befinden sich auf der Oberfläche des Objekts, bilden seine äußere Haut und
werden zum Rendering benutzt. Abbildung 3.3 zeigt diese Datenrepräsentation, sowie Ergebnisse der
Arbeit.
5 phyxel:
6 surfel:
physical element
surface element
KAPITEL 3. STATE OF THE ART
27
Beim Arbeitsablauf der vorgestellten Methode wird von einer high-level Sicht aus und für jeden
Zeitschritt ∆t die Simulationsschleife folgendermaßen beschrieben:
ut
|{z}
→
Verschiebungen
∇u
|{z}t
Ableitungen
→
εt
|{z}
→
Verformungen
σt
|{z}
Spannungen
→ ft → ut+∆t
|{z}
| {z }
Kräfte
Integration
Nach der Initialisierung startet die Simulationsschleife. Von den Verschiebungsvektoren ui werden
die partiellen Ableitungen approximiert, welche sowohl den Dehnungs- als auch den Spannungstensor definieren. Die Kräfte, die an den Punkten wirken, werden dann als negativer Gradient der Dehnungsenergie bezüglich ihrer Verschiebungen und Zeit berechnet, was neue Verschiebungen ut+∆t
zum Zeitpunkt t + ∆t ergibt.
Durch die Verwendung von Dehnungsstatusvariablen kann man auf elegante Art plastisches Verhalten simulieren [OH02]. Jedes Phyxel i speichert dabei einen plastischen Dehnungstensor εip . Die
Dehnung, welche die Elastizität ε̃i = εi − εip berücksichtigt, ist die Differenz zwischen gemessener
Dehnung εi und der plastischen Verformung. Ist die gemessene Dehnung gleich der plastischen Verformung, wirken keine Kräfte. Da εip innerhalb eines Zeitschritt konstant ist, werden die elastoplastsichen Kräfte durch Benutzen von σ̃i = Cε̃i , anstatt von σi berechnet. Die plastische Verformung wird
in jedem Zeitschritt gemäß [OH02] aktualisiert.
Mit der vorgestellten Methode lassen sich beliebig große Deformationen simulieren. Objekte mit den
Materialeigenschaften starr-elastisch bis plastisch-fließend sind mit diesem Verfahren gut realisierbar.
Eine Besonderheit der Anwendung ist, dass zwischen den verschiedenen Materialeigenschaften zur
Laufzeit gewechselt werden kann.
Allerdings ist die Methode nur zur Animation von dreidimensionalen Volumenobjekten geeignet,
da jedes Phyxel mindestens drei Nachbarn braucht. Daher ist die Animation von zweidimensionalen
Schichten nicht möglich. Zudem finden zwischen in der Nähe liegenden Phyxeln Wechselwirkungen
statt. Bruchsimulationen sind mit dieser Methode somit auch nicht zu verwirklichen.
3.3.2
Punktbasierte Animation von elastoplastischen Festkörpern
Die Animation von elastoplastischen Festkörpern steht im Fokus von [GBB09]. Elastoplastische Festkörper besitzen bei geringer Krafteinwirkung vorwiegend elastische Eigenschaften, d.h. ein Objekt
wird nach Krafteinwirkung wieder in seinen Anfangszustand zurückversetzt. Wenn die einwirkende
Kraft einen bestimmten Wert überschreitet, zeigt das Objekt plastische Eigenschaften und zerfließt,
anstatt in den Anfangszustand zurückzukehren. Stoffe die diese Eigenschaft besitzen, sind z.B. Kaugummi, Zahnpasta oder Knete.
Zur Animation von elastoplastischen Körpern stützt sich die Arbeit auf Modifikationen, die man zum
“Open-Source SPH-Simulator” aus [AG07] gemacht hat.
Ziel dieser Arbeit ist die Berechnung der Elastizität in einer punktbasierten Simulation. Dazu wird
zuerst die Deformation in der Umgebung von jedem Partikel pi berechnet; durch Finden einer affinen Abbildung, welche die Bewegung der benachbarten Partikel über einen einzelnen Zeitschritt am
KAPITEL 3. STATE OF THE ART
28
besten approximiert. Dabei sei xi die Position von pi am Anfang des Zeitschritts, und yi der Ort von
pi am Ende des Zeitschritts. p j sind dabei die Partikel in der Nachbarschaft von pi . Jetzt muss eine
Transformationsmatrix F gefunden werden, die jedes Partikel aus der jeweiligen Anfangsposition x in
die Endposition y transformiert. Dazu muss
n
∑ kF(x j − xi ) − (y j − yi )k
(3.3)
j=1
minimiert werden. Nach Gleichung (3.3) ist x j − xi der Anfangszustand von pi mit dem Nachbarn p j .
Die Transformationsmatrix F verschiebt diesen Anfangszustand nun möglichst nah an den Endzustand
y j − yi . Die Anfangszustände der Partikel werden in der Matrix X und die Endzustände in der Matrix
Y abgelegt. Mit diesen beiden Matrizen wird die Transformationsmatrix F gesucht, so dass
FX = Y.
(3.4)
Auf Gleichung (3.4) wird dann eine Methode der kleinsten Quadrate angewendet. Anschließend transponiert man die Matrizen, um nach der Matrix F aufzulösen, was genauer in[GBB09] beschrieben
ist. Hierdurch erhält man die beste lineare Transformation für die Nachbarschaft um pi , im Sinne
der kleinsten Quadrate. Allerdings muss noch beachtet werden, dass Partikel, die weiter vom Ausgangspartikel entfernt sind, weniger Einfluss haben, als Partikel, die näher an diesem sind. Dazu wird
auf die Spalten X und Y ein Gewichtungskernel multipliziert. Die Implementierung benutzt den poly6
Kernel, der in [MG03] als default smoothing kernel definiert wurde:

2
2 3
315 (h − r )
Wpoly6 (r, h) =
64πh9 0
0≤r≤h
(3.5)
andernfalls.
Der eben beschriebene Kernel multipliziert den konstanten Wert
315
64πh9
mit einem Abstandsterm auf
das jeweilige Nachbarpartikel, wenn das Partikel innerhalb des Abstandsradius liegt. Falls das Partikel
außerhalb des Abstandsradius liegt, wird es mit 0 multipliziert, wodurch das entsprechende Partikel
nicht mit einbezogen wird [Neu10].
Dieser Ansatz ergibt die Deformation über einen einzelnen Zeitschritt. Um die Matrix F zu erhalten,
welche die gesamte elastische Deformation für das jeweilige Partikel liefert, wird das Zeitintervall
in eine bestimmte Anzahl an Zeitschritten aufgetrennt. Für jeden Zeitschritt des Intervalls wird die
Deformation nun zur Gesamtdeformation aufmultipliziert.
Um nach der Elastizität nun noch die Plastizität einfließen zu lassen, wird die Matrix F mit einer
Singulärwertzerlegung diagonalisiert und anschließend mit dem Plastizitätsmodell nach [BT07] multipliziert.
Die vorgestellte Methode besitzt zwei wichtige Vorteile. Zunächst muss kein Anfangsruhezustand
gespeichert werden. Unter großen plastischen Deformationen würde die Abbildung vom Anfangsruhezustand zum aktuellen Zustand numerisch schlecht darzustellen sein. Dadurch, dass nur der elastische Teil der Deformation gespeichert wird, vermeidet man diese numerischen Probleme. Ein zweiter
KAPITEL 3. STATE OF THE ART
29
Vorteil ist, dass direkt mit dem Deformationsgradienten gearbeitet wird. Das Arbeiten mit einem Deformationsgradienten führt zu einer multiplikativen Formulierung der Deformation. Diese ist besser
zur Darstellung endlicher Deformationen geeignet als ein additives Modell von klassischer Plastizität, wie es oft in Graphikanwendungen benutzt wird [SH98]. Hinzu kommt, dass sich die Methode
relativ einfach implementieren lässt. Abbildung 3.4 zeigt ein Ergebnis dieser Arbeit. Wenn der Deformationsgradient abgeschätzt wird, tritt bei der Methode besonders dann ein Problem auf, wenn ein
Partikel zu wenige Nachbarn bei großen Deformationen hat. Das kann zu ungenauen Werten führen.
Aus diesem Grund wird der Deformationsgradient nicht mehr aktualisiert, wenn ein Partikel weniger
als sechs Nachbarn hat. Zudem eignet sich das Verfahren nicht für große elastische Deformationen.
Abbildung 3.4: Elastoplastisches Objekt nach [GBB09]
3.3.3
Punktbasierte Animation von inkompressiblen Strömungen
[SH09] beschäftigt sich mit inkompressiblen Strömungen. Bei der Methode werden die Abtastpunkte
durch die Strömung in einer Lagrangeschen Weise bewegt. Dafür müssen bei der Strömungssimulation die Navier-Stokes-Gleichungen gelöst werden. Es handelt sich dabei um die Grundgleichungen der
Strömungsmechanik. In strömenden Flüssigkeiten ist die Dichte im Allgemeinen überall gleich, denn
der Druck ist nirgendwo hoch genug, um sie wesentlich zu ändern. Strömungen mit konstanter Dichte
heißen inkompressibel [Mes06]. Wenn die Geschwindigkeit vernachlässigt werden kann, erhält man
die Euler-Gleichungen, welche einen Sonderfall der Navier-Stokes-Gleichungen darstellen.
∂u
= −(u · ∇)u − ∇p
∂t
(3.6)
∇ · u = 0,
(3.7)
wobei u die Geschwindigkeit, t die Zeit, p den Druck, und ∇ den Gradienten (∂ /∂ x, ∂ /∂ y, ∂ /∂ z)T
beschreibt.
Die in der Arbeit benutzte Methode kann in sechs Phasen aufgeteilt werden. Zuerst hat man eine
Menge von Abtastpunkten gegeben, welche die Werte des Geschwindigkeitsfelds aufbewahren. Im
zweiten Schritt wird aus den gegebenen Abtastwerten ein Voronoi-Diagramm gebildet. In Phase drei
werden freie Flächen als Vereinigung von Kugeln um die Abtastpunkte definiert. Danach wird das
Voronoi-Diagramm gegen die eben definierten Flächen geclippt. In Schritt fünf führt die Methode eine
Druckprojektion aus, mit deren Hilfe ein divergenzfreies Geschwindigkeitsfeld gebildet wird. Zum
KAPITEL 3. STATE OF THE ART
30
Abschluss werden die Abtastpunkte durch das Geschwindigkeitsfeld transportiert. Eine ausführliche
Beschreibung der einzelnen Schritte ist der Arbeit [SH09] zu entnehmen. Eine graphische Darstellung
der einzelnen Phasen wird in Abbildung 3.5 dargestellt.
Abbildung 3.5: Ablauf der punktbasierten Methode nach [SH09]
Mit dem vorgestellten Verfahren ist es möglich, inkompressible Strömungen und wirbelnden Rauch
zu modellieren. Im Gegensatz dazu kann die SPH Methode nur kompressible Strömungen darstellen. Bei SPH ist die Wahl des smoothing Kernel für die Lösung der Navier-Stokes-Gleichungen sehr
wichtig. Die hier vorgestellte Methode benutzt einen Kernel für alle Simulationen.
Im Vergleich zu gitterbasierten Techniken zeigt die Methode größere Flexibilität in der Repräsentation von Randbedingungen. Die Anwendung ist stabil, flexibel und kombiniert viele wünschenswerte
Eigenschaften von punkt- und gitterbasierten Techniken. Allerdings generiert SPH Bilder achtmal
schneller als der vorgestellte Ansatz.
3.4
Physikengine
Durch physikalische Berechnung kann man eine Szene realistischer erscheinen lassen. In den vorgestellten punktbasierten Methoden werden die simulierten physikalischen Eigenschaften durch eigene
Berechnungen per Hand gelöst. Im Zuge dieser Arbeit soll ein anderer Weg gegangen werden. Mit
Hilfe einer sogenannten Physikengine sollen die physikalischen Eigenschaften der Objekte korrekt
simuliert werden.
KAPITEL 3. STATE OF THE ART
31
Die Physikengine berechnet Kräfte und Gravitationskraft, die auf Objekte in der modellierten Szene
wirken. Dazu gehören auch Kräfte, welche Objekte gegenseitig aufeinander ausüben. Für jedes Objekt
werden Eigenschaften wie Masse, Geschwindigkeit und Reibung simuliert.
Ein weiterer wichtiger Einflussfaktor ist die Kollisionsberechnung. Sie simuliert, was passiert, wenn
Objekte sich berühren [Mil07]. Eine vollständige Physiksimulation ist sehr zeitaufwendig. Da der
Benutzer an einer echtzeitfähigen Simulation interessiert ist, werden die physikalischen Gesetze vereinfacht. Die Physik wird demzufolge approximativ berechnet, da bei Physikengines Effizienz vor
Exaktheit geht. Für jede Position eines Objekts wird eine Bewegungsgleichung für einen bestimmten
Zeitschritt gelöst. Sie drückt aus, an welchem Ort sich ein Objekt nach dem entsprechenden Zeitpunkt
befindet [Hei08].
Verschiedene Physikengines eignen sich zur Simulation von starren (rigid body) und elastischen Körpern (soft body). Sie werden in vielen unterschiedlichen Gebieten wie z.B. in der Wettersimulation,
der Fahrsimulation [Dik08], in Computerspielen und in Flugsimulatoren eingesetzt.
Die “rigid body dynamics” beschäftigt sich mit der Bewegung von starren Körpern, die nicht verformbar sind. Hierbei sind Bewegungen für alle sechs Freiheitsgrade möglich. Starre Körper werden
durch Kräfte, Masse, Reibung und Geschwindigkeit beeinflusst.
Die “soft body dynamics” behandelt die physikalisch realistische Simulation von volumetrisch deformierbaren Objekten. Im Gegensatz zu starren Körpern kann sich die Form eines Soft Body während
der Simulation ändern. Da sich die Simulation von Soft Bodies auf die Oberflächen von deformierbaren Körpern beschränkt, sind Flüssigkeitssimulationen mit diesen nicht möglich.
Physikengines haben zwei wichtige Vorteile, die ihre Verwendung begünstigen. Der erste Vorteil ist
die Zeitersparnis. Sollen physikalische Effekte in mehr als einer Anwendung benutzt werden, lohnt
sich der Einsatz einer Physikengine. Eine einmal entwickelte Engine ist relativ leicht in jedes neue
Projekt zu importieren.
Der zweite Vorteil von Physikengines ist deren Qualität. Werden mehrere physikalische Effekte in
die Simulation integriert, wird die Berechnung durch die Physikengine die Qualität der simulierten
Effekte verbessern.
Doch Physikengines sind kein Allheilmittel. Es gibt Schwachstellen, die Benutzer davon abhalten,
eine vollständige Physikengine in eine Anwendung zu integrieren. Der größte Nachteil ist der Geschwindigkeitsverlust. Da die Verwendung einer Engine zur Physiksimulation sehr prozessorintensiv ist, muss ihre Benutzung vorher gut überlegt sein. Zwischen dem zu erwartenden Ergebnis und
dem Geschwindigkeitsnachteil muss sorgfältig abgewogen werden. Ein weiterer Nachteil einer Physikengine ist deren Präzision. Um den Geschwindigkeitsnachteil zu kompensieren, wird die Physik
approximativ berechnet. Durch Rundungsfehler leidet die Präzision und die Ergebnisse werden ungenau. Ein weiterer Nachteil, der vor allem bei der Erstellung dieser Arbeit zu beachten war, ist dass
KAPITEL 3. STATE OF THE ART
32
Physikengines nicht punktbasiert arbeiten. Es muss somit eine Schnittstelle erstellt werden, damit die
Physikengine mit dem vorhandenen Punktmodell arbeiten kann.
Es gibt mittlerweile eine große Auswahl an Physikengines. In zwei Arbeiten wurden einige Physikengines durch verschiedene Simulationen getestet und bewertet. [SR06] evaluiert Physikengines, die
frei für eine nicht-kommerzielle Nutzung sind. Die Evaluation besteht aus theoretischem Vergleich
zwischen Physikengines und verschiedenen Laufzeittests. Wichtige Aspekte wie Reibung, Stabilität und Skalierbarkeit wurden getestet. Wenn die gleiche Szene mit verschiedenen Engines simuliert
wird, variieren die Ergebnisse. Sie zeigen, dass sich frei verfügbare Physikengines in vielen Situationen genauso gut verhalten wie kommerzielle. Allerdings wird beim Betrachten aller Tests klar, dass
kommerzielle Physikengines am besten abschneiden.
[BB07] evaluiert ebenfalls eine Anzahl von frei verfügbaren Physikengines für Simulationssysteme
und zusätzlich zur Spieletechnologie. Fünf verschiedene Tests bezüglich Materialeigenschaften und
Kollisionen wurden in dieser Evaluation durchgeführt. Keine der getesteten Engines erzielte für alle
Tests die besten Ergebnisse, und fast jeder Test wurde von einer anderen Engine als bestes absolviert.
Aus den Evaluationen kristallisiert sich heraus, dass die folgenden vier Physikengines am häufigsten
in der Praxis eingesetzt werden.
• Havok Physics
Havok Physics [Hav] ist eine kommerzielle Physikengine, die im September 2007 von der Intel
Corporation gekauft wurde. Sie wird in über 250 Video- und Computerspielen eingesetzt und
läuft auf den Plattformen Windows, Mac OS X, Sony Playstation, Nintendo Wii, sowie Microsoft Xbox. Havok eignet sich für Echtzeit-Kollisionserkennung und physikalische Simulation.
Starre Körperdynamik kann ebenso wie Charakteranimation oder die Simulation von Fahrzeugbewegungen verarbeitet werden.
• Nvidia PhysX
Nvidia PhysX [Phyb] ist ebenfalls eine kommerzielle Physikengine, die im Februar 2008 von
der Nvidia Corporation gekauft wurde. Zuvor war die Engine bekannt unter dem Namen NovodeX. Die leistungsfähige Physikengine ist für Echtzeit-Physikberechnungen in topaktuellen
PC- und Konsolenspielen geeignet und wird von Sony Playstation, Microsoft Xbox, Nintendo
Wii und PC unterstützt. Die Physikberechnungen können sowohl auf der CPU7 als auch von
der Grafikkarte durchgeführt werden. Mögliche zu simulierende Effekte sind Rauch und Nebel,
Charakteranimationen, und Stoffe.
• Bullet Physics Library
Bullet [Bula] ist eine Open-Source Physikengine, die in C++ implementiert ist. Sie ist auf den
Plattformen Sony Playstation, Microsoft Xbox, Nintendo Wii, Linux, Mac OS X, PC und iPhone verfügbar. Sie wird in Videospielen und für visuelle Effekte in Filmen verwendet. Ihre Hauptbestandteile sind eine dreidimensionale Kollisionserkennung, sowie eine starre Körperdynamik.
7 Central
Processing Unit
KAPITEL 3. STATE OF THE ART
33
Zudem können Stoffe über sogenannte elastische Körperdynamik simuliert werden.
• Open Dynamics Engine
ODE [ODE] ist eine Open-Source Physikengine, die für das Simulieren der Körperdynamik in
der virtuellen Realität eingesetzt wird. Ihre beiden Hauptbestandteile sind die Kollisionserkennung und die starre Körperdynamik. Sie ist robust, flexibel und plattformunabhängig mit einer
einfach zu nutzenden C/C++ API8 .
Die vier beschriebenen Physikengines werden ebenfalls in [CV07] verwendet. Wie in Abbildung 3.6
zu sehen ist, handelt es sich dabei um die vier am häufigsten verwendeten Physikengines in Videospielen [Gam]. In der Ausgabe August 2009 des Game Developers Magazine wurden über 100 Entwickler
zu verwendeten Physikengines befragt. Da die beiden Erstplazierten kommerzielle Closed-Source Engines sind, wird im Zuge dieser Arbeit die Open-Source Physikengine Bullet verwendet.
Abbildung 3.6: Beliebteste Physikengines [Gam]
3.5
Bullet Grundlagen
Die verwendete Open-Source Bullet Physics Library ist eine Physikengine, die frei zur kommerziellen
Nutzung ist. Die Hauptaufgabe der Physikengine besteht darin, Kollisionserkennung durchzuführen
und diese Kollisionen zu lösen. Zudem eignet sie sich zur Berechnung von starrer, wie auch von
elastischer Körperdynamik. Nach jedem Zeitschritt werden die aktuellen Positionen in der Umgebung
für jedes Objekt bestimmt. Der Aufbau der Hauptkomponenten der Physikengine wird in Abbildung
3.7 dargestellt.
Um Bullet in der eigenen dreidimensionalen Anwendung zu benutzen, werden die dafür wichtigsten
benötigten Komponenten vorgestellt [Bulb].
Jede Physiksimulation braucht zunächst eine Welt, in der gearbeitet wird. Je nachdem, ob nur starre Körper oder auch elastische Körper simuliert werden, erzeugt man eine entsprechende Welt. Zur
Erzeugung der Welt benötigt man die vier Komponenten broadphase, dispatcher, solver und collisionconfiguration. Sie braucht jede Welt, um zum einen die Objekte aufzunehmen, und eventuelle
8 Application
Programming Interface
KAPITEL 3. STATE OF THE ART
34
Abbildung 3.7: Organisation der Hauptkomponenten von Bullet [Bulb]
Berührungen oder Überlappungen mit einer entsprechenden Kollisionserkennung korrekt zu berechnen. Des Weiteren verursacht die Berechnung das richtige Interagieren von Objekten, sowie die Berücksichtigung der Schwerkraft und anderer wirkenden Kräften und Kollisionen. Codeabschnitt 3.1
ist Standard zur Erschaffung einer Bulletwelt für starre Körper.
1
2
3
void StandardWelt ()
{
b t B r o a d p h a s e I n t e r f a c e * bp = new btDbvtBroadphase ();
4
b t D e f a u l t C o l l i s i o n C o n f i g u r a t i o n * cC =
new b t D e f a u l t C o l l i s i o n C o n f i g u r a t i o n ();
5
6
7
b t C o l l i s i o n D i s p a t c h e r * dp =
new b t C o l l i s i o n D i s p a t c h e r ( cC );
8
9
10
b t S e q u e n t i a l I m p u l s e C o n s t r a i n t S o l v e r * sv =
new b t S e q u e n t i a l I m p u l s e C o n s t r a i n t S o l v e r ;
11
12
13
b t D i s c r e t e D y n a m i c s W o r l d * dynamicsWorld =
new b t D i s c r e t e D y n a m i c s W o r l d ( dp , bp , sv , cC );
14
15
16
}
Listing 3.1: Standard Bullet Welt für starre Körperdynamik
Nachdem die Welt erstellt wurde, können Kollisionsobjekte erzeugt und zur Welt hinzugefügt werden. Dazu müssen für das jeweilige Objekt zunächst einige Eigenschaften bestimmt werden. Die Masse jedes Objekts muss gesetzt werden. Für dynamische, sich bewegende Objekte ist die Masse positiv.
Danach wird für jedes Simulationsbild die Position des Körpers aktualisiert. Für statische Objekte
beträgt der Massewert 0. Diese Objekte bewegen sich nicht, aber sie können mit anderen Objekten
kollidieren. Zusätzlich gibt es kinematische Objekte, die ebenfalls die Masse Null haben. Diese können zwar vom Nutzer animiert werden, aber bei der Kollision mit dynamischen Objekten erhalten sie
keine Auswirkungen von diesen.
KAPITEL 3. STATE OF THE ART
35
Für jedes Objekt soll, wenn dieses Objekt ein anderes berührt, eine Kollisionsberechnung möglich
sein. Die Aufgabe der Kollisionserkennung ist es, genau diesen Berührungszeitpunkt festzustellen.
Die Form der verschiedenen Objekte kann sehr komplex sein. Um die Kollisionserkennung zwischen zwei komplexen Objekten zu erleichtern, bekommt jedes Objekt eine Hülle, ein sogenanntes
Collision-Shape. Bullet unterstützt eine große Auswahl von verschiedenen Collision-Shapes. Es besteht ebenfalls die Möglichkeit, eigene Collision-Shapes zu erstellen. Diese dienen ausschließlich der
einfacheren Berechnung der Kollision. Die meist verwendeten Hüllen, welche die Form des Objekts
nähern, sind eine Axis-Aligned Bounding Box (AABB), eine Kugel oder ein Dreiecksnetz.
Eine AABB ist ein Quader, dessen Seiten parallel zu den Achsen des Objekt-lokalen Koordinatensystems stehen.
Wenn eine Kugel um das Objekt gelegt wird, stimmt der Mittelpunkt des Objekts mit dem Mittelpunkt der Kugel überein. Diese Kugel ist durch den Mittelpunkt und ihren Radius festgelegt.
Ebenfalls kann ein Dreiecksnetz aus Polygonen die Form des Objekts annähern. Diese ist die präziseste der drei Methoden, aber auch die rechenaufwendigste. Abbildung 3.8 zeigt diese drei vorgestellten Collision-Shapes.
Abbildung 3.8: Drei am häufigsten verwendete Collision-Shapes zur Kollisionserkennung [Kle05]
Im Fall der starren Körperdynamik können Kräfte, Masse, Trägheit und Geschwindigkeit für jeden
starren Körper zur Simulation zugefügt werden. Des Weiteren hat jeder starre Körper einen MotionState. Die Motion-States übernehmen die mühsame Arbeit für den Benutzer, um die Weltposition der
simulierten Objekte nach jedem Aktualisierungsschritt zu ermitteln. Sie werden an zwei Stellen im
Programm verwendet.
Zum einen benutzt man den Motion-State, wenn der jeweilige starre Körper bei der Initialisierung
gebildet wird. Bullet erhält somit die Anfangsposition des Objekts vom Motion-State, wenn der Körper die Simulation betritt.
Nach jedem Aktualisierungsschritt ruft Bullet während der Simulation den Motion-State für ein Objekt ein weiteres Mal auf, um dieses Objekt zu bewegen. Mit den dabei erhaltenen neuen Positionsdaten wird die Position des Objekts aktualisiert.
Mit Hilfe der Masse, des Collision-Shapes und des Motion-States kann dann ein starrer Körper gebildet und anschließend in die Welt eingefügt werden.
Da die Objekte in jedem Simulationsschritt ihre Position ändern können, muss die Welt für jedes
KAPITEL 3. STATE OF THE ART
36
Animationsbild aktualisiert werden. Die Aktualisierung der Simulation für jedes Bild funktioniert
über die Step-Simulation Funktion. Dafür muss die Frequenz festgelegt werden, mit der aktualisiert
wird. Standardmäßig wird ein interner Zeitschritt von 60 Hertz verwendet. Nach T =
1
f
erhält man als
Zeiteinheit T = 0.0167s. Die Step-Simulation Funktion führt Kollisionserkennung und Physiksimulation aus. Daher muss die Funktion für die Welt in jedem Aktualisierungsschritt aufgerufen werden.
Es besteht die Möglichkeit, die Bewegung zwischen zwei Objekten zueinander einzuschränken. Um
das zu verwirklichen, bedient man sich sogenannter Constraints. Damit ein Constraint zwischen zwei
Objekten agieren kann, muss mindestens eines von ihnen dynamisch sein. Constraints lassen sich am
Besten erklären, wenn man sie als Gelenke interpretiert. Durch verschiedene Gelenkarten wie Kugelgelenk, Scharniergelenk oder Schiebegelenk ist es möglich, die Freiheitsgrade einzuschränken.
Bedingt durch seine Geometrie ist ein Kugelgelenk prinzipiell in alle Richtungen beweglich. Es sind
aber nur Rotationen und keine Translation möglich.
Ein Scharniergelenk beschränkt zwei Freiheitsgrade der Rotation, so dass der Körper nur um eine
Achse rotieren kann, die Schiebeachse. Dies ist hilfreich, wenn man Türen oder Reifen realisieren
möchte, die um eine Achse rotieren.
Ein Schiebegelenk erlaubt es, den Körper um eine Achse zu rotieren und ebenfalls entlang dieser
Achse zu verschieben. Abbildung 3.9 zeigt die verschiedenen Constrainttypen.
Abbildung 3.9: Drei verschiedene Gelenktypen [Bulb]
Bisher wurde sich ausschließlich mit der starren Körperdynamik beschäftigt. Um weitere sehenswerte physikalische Effekte animieren zu können, muss die Elastizität mit in die Simulation einfließen.
Bullet besitzt eine Möglichkeit, Elastizität mit einzubringen. Diese Datenstruktur benutzt den Soft Body Ansatz. Soft Bodies haben einen größeren Rechenaufwand als starre Körper, da zusätzlich zu den
vorher beschriebenen physikalischen Eigenschaften noch die elastische Verformung unter Einfluss
externer Kräfte berücksichtigt werden muss.
Mit Hilfe der elastischen Körperdynamik lassen sich zusätzlich zu der existierenden starren Körperdynamik Dinge wie Seile, Stoffe und volumetrische Objekte animieren. Solch ein elastisches Objekt leitet sich wie auch die starren Körper von allgemeinen Kollisionsobjekten ab. Im Gegensatz zu
starren Körpern haben elastische Objekte keine einzelne Position in der Welt. Beim Soft Body ist
jeder einzelne Eckpunkt in Weltkoordinaten spezifiziert.
In Codebeispiel 3.1 wurde gezeigt, wie man eine Standardwelt in Bullet für starre Körper implementiert. Diese ist aber nur für starre Körperdynamik geeignet. Wenn nun auch noch elastische Körper in
KAPITEL 3. STATE OF THE ART
37
die Simulation mit einfließen sollen, braucht man ein neues Weltkonstrukt. Dieses heißt btSoftRigidDynamicsWorld und kann elastische und starre Körper sowie Kollisionsobjekte simulieren.
Um bestimmte Soft Bodies zu erstellen, benutzt Bullet eine Hilfsklasse. Auf der Grundlage von
Dreiecksnetzen können so relativ leicht die Grundzüge eines elastischen Körpers erstellt werden.
Die drei grundlegenden Bestandteile eines Soft Body sind Eckpunkte (Nodes), Verbindungen zwischen den Eckpunkten (Links) und Flächen (Faces). Wenn man beispielsweise eine elastische Ebene,
also einen flachen Soft Body erstellen will, besteht das Grundgerüst zunächst aus den entsprechenden Nodes. Die Nodes sind über das Objekt gleichmäßig verteilt. Diese Punkte sind dann über Links
miteinander verbunden. Die Links halten die Nodes in einem bestimmten Abstand zusammen. Wenn
eine Kraft auf das Objekt wirkt, sind die Links die zusammenhaltende Kraft, wodurch der Soft Body
ins Schwingen gerät, also die Elastizität bekommt. Nachdem alle Links die Nodes verbinden, bilden
sie schließlich Dreiecke. Die Oberfläche eines jeden solchen Dreiecks bezeichnet man als Face. Nodes und vor allem Faces werden zur Kollisionserkennung verwendet, um festzustellen, ob ein anderes
Objekt auf die Oberfläche des Soft Body trifft. Abbildung 3.10 zeigt den Aufbau eines elastischen
Körpers. Zunächst besteht er aus 9 Nodes, die danach über Links verbunden werden. Im nächsten
Schritt stellen die Faces die Oberflächen zwischen den Links in grün dar.
Zudem ist es auch möglich, eine Kraft auf den elastischen Körper auszuüben. Entweder wirkt die
Kraft auf den gesamten Körper, oder die Kraft wirkt auf einen einzelnen Node des Soft Body. Über
die Links verteilt sich die Kraft auf den übrigen Körper.
Ebenfalls gibt es die Möglichkeit mit Hilfe von Constraints, die Bewegung verschiedener Körper
einzuschränken. Dabei ist es möglich, einen oder mehrere Nodes zu fixieren und sie dadurch unbeweglich zu machen. Dies wird erreicht, indem man den Massewert des jeweiligen Node auf 0 setzt.
Im späteren Teil der Implementierung wird noch genauer auf den Arbeitsablauf von elastischen Objekten und wie man diese mit dem Punktmodell verbinden kann, eingegangen.
Abbildung 3.10: Soft Body bestehend aus Nodes, Links und Faces
Kapitel 4
Eigene Verfahren
In diesem Kapitel werden die eigenen entwickelten Verfahren vorgestellt. Dazu wird zunächst eine
Anforderungsanalyse durchgeführt, sowie Mittel beschrieben, die zur Umsetzung der Arbeit benutzt
wurden. Es folgt die Beschreibung des gegebenen Punktmodells, sowie die für die Arbeit wichtige Verknüpfung mit der Physiksimulation. Um die Animation am Bildschirm anzuzeigen, wurde ein
Viewer erstellt. Zudem wurden einfache Punktanimationen für starre Körper sowie ein Implementierungsbeispiel zur Physiksimulation eines elastischen Körpers umgesetzt. Abschließend wurde die
Laufzeit der eigenen Implementierung mit der einer Demo der Physikengine verglichen.
4.1
Anforderungsanalyse
Die Aufgabenstellung dieser Diplomarbeit besteht darin, zu einem bestehenden Renderer und dem
Punktmodell eine Physiksimulation zu integrieren. Es soll untersucht werden, welche Anforderungen
an den Renderer und das Punktmodell gestellt werden müssen. Dies soll anhand eines Beispiels umgesetzt werden. Weiterhin soll festgestellt werden, inwiefern sich eine vorhandene Datenhierarchie
dafür eignet, die Anzahl der Simulationsknoten dynamisch festzulegen.
In dieser Arbeit findet die Animation auf der Grundlage von Punkten statt. Dabei handelt es sich um
die einfachste Form von Primitiven. Auf diesen Punktprimitiven soll die Physik berechnet werden. In
den bisherigen Arbeiten im Bereich der punktbasierten Animation, die in Kapitel 3 vorgestellt wurden,
erfolgte die Berechnung der Physik von Hand. In dieser Arbeit wird nun ein anderer Weg gegangen.
Dafür wird eine Physikengine benutzt, um die physikalische Simulation auf jedem einzelnen Punkt
zu berechnen. Es wird die Open-Source Physikengine Bullet verwendet.
Wichtiger Bestandteil ist dann die beiden Bereiche, das Punktmodell und die Physiksimulation, miteinander zu verknüpfen. Das entwickelte Programm soll zudem als Animationsplugin für das vorhandene Framework des Punktrenderes dienen.
Wünschenswert ist die Animation von sowohl starren, wie auch elastischen Objekten, die in der
jeweiligen Szene miteinander interargieren können. Dazu gehört vor allem die richtige Kollisionsberechnung, wenn Objekte aufeinander stoßen.
38
KAPITEL 4. EIGENE VERFAHREN
39
Das zur Verfügung stehende Framework wurde mit der objektorientierten Sprache C++ implementiert. Zudem ist sowohl die verwendete Physikengine Bullet, als auch die zur GUI9 -Verwirklichung benutzte Klassenbibliothek in dieser Hochsprache implementiert. Die benutzte Graphik-API ist OpenGL.
Aus diesem Grund wird das eigene Framework gleichfalls in dieser Sprache umgesetzt.
4.2
Punktmodell
Um eine punktbasierte Animation durchzuführen, braucht man eine entsprechende Datenstruktur. Diese Datenstruktur, die auf der Grundlage von Punkten arbeitet, wird für die Arbeit zur Verfügung gestellt. Das zu animierende Objekt besteht dabei aus einzelnen Punkten. Jeder dieser Punkte besitzt
dabei Eigenschaften wie Position, Normale, Punktgröße oder Farbe. Die einzelnen Punkte werden
dann gemeinsam in einer hierarchischen Datenstruktur abgelegt. Dafür eignet sich ein Baum. Um
die Baumdaten von den Renderingdaten abzugrenzen, werden ein Knotenpuffer und ein Punktpuffer
verwendet. Der Knotenpuffer bildet die Verbindung zwischen den Rohpunktdaten und der Baumrepräsentation. Dieser Puffer benutzt die Hauptoperationen der Datenstruktur. Der Punktpuffer beinhaltet
alle Rendering spezifischen Informationen wie Position, Normale und Farbwerte. Diese Trennung erlaubt es den Punktpuffer direkt zur GPU10 zu senden, während der Knotenpuffer im lokalen Speicher
bestehen bleibt. Dieser Aufbau ist in Abbildung 4.1 dargestellt.
Abbildung 4.1: Aufbau der Basisdaten des Punktmodell [SK10]
Ziel ist es nun, einzelne Punkte zu erzeugen, die dann animiert werden sollen. Je nachdem, wie viele
Punkte benötigt werden, wird ein Puffer mit der entsprechenden Größe erzeugt. Auf den Puffer wird
dann zur Erzeugung eines Punktes die createPoint Methode angewendet. Dieser Vorgang wird solange
wiederholt, bis alle benötigten Punkte erstellt wurden und im Puffer stehen. Beim Einfügen in den
9 Graphical
10 Graphics
User Interface
Processing Unit
KAPITEL 4. EIGENE VERFAHREN
40
Puffer erhält jeder Punkt einen entsprechenden Index, je nachdem, an welcher Stelle er in den Puffer
eingesetzt wurde. Mit Hilfe des Index kann der passende Punkt angesprochen werden. Gleichzeitig
ist es möglich, wie in Abbildung 4.2 zu sehen ist, Informationen des Punkts aus dem Puffer mit der
Funktion GetPoint(Index) wieder auszulesen.
Abbildung 4.2: Punktinformationen werden aus dem Puffer gezogen
Auf dem jeweiligen Punkt können dann mit separaten Get-Methoden die einzelnen Eigenschaften
ausgelesen werden. Sind nun alle für die zu animierenden Objekte benötigten Punkte im Punktpuffer mit den richtigen Eigenschaften vorhanden, so kann daraus eine hierarchische Datenstruktur, ein
Baum, gebaut werden. Dazu muss die Funktion generateTreeFromPoints auf den Punktpuffer anwendet werden. Als Beispiel für neun Punkte wird der gebildete Baum in Abbildung 4.3 dargestellt. Die
entsprechenden Indizes der Punkte sind in den Baumknoten zu sehen. Codebeispiel 4.1 beschreibt den
eben erläuterten Schritt, um die Punkte in eine hierarchische Datenstruktur zu bekommen.
0
1
5
6
2
7
3
4
8
Abbildung 4.3: Baumdarstellung für neun Punkte
Der Basisansatz für baumbasierte Objekte ist von der Wurzel absteigend bis zu den Blättern zu
traversieren oder solange, bis ein Abbruchkriterium erfüllt ist. Bei der erzeugten Baumdatenstruktur
hat, wie schon im Beispiel in Abbildung 4.3 gezeigt, jeder Knoten maximal vier Kinder. Die Tiefe des
resultierenden Baums beträgt dann dlog4 ne, wobei n die Anzahl der im Modell benutzten Blattknoten
ist.
KAPITEL 4. EIGENE VERFAHREN
1
2
3
4
5
6
7
8
9
10
41
void initPoints ( int pointsToCreate )
{
POINTS_NAMESPACE :: PointBuffer buf ( pointsToCreate );
POINTS_NAMESPACE :: Point * ptCurrent = NULL ;
for ( int i =0; i < pointsToCreate ; i ++)
{
buf . CreatePoint (& ptCurrent );
}
SetPointBuffer ( buf );
}
11
12
13
14
15
16
17
18
19
20
21
22
void resetPoints ( int pointsToReset )
{
POINTS_NAMESPACE :: PointBuffer & buf = GetPointBuffer ();
POINTS_NAMESPACE :: Point * ptCurrent = NULL ;
for ( int i =0; i < pointsToReset ; i ++)
{
ptCurrent = buf . GetPoint ( i );
ptCurrent - > SetPosition (0.0 ,0.0+ i ,0.0);
}
G e n e r a t e T r e e F r o m P o i n t s ( buf );
}
Listing 4.1: Bauminitialisierung der Punkte
In den vorhergehenden Kapiteln wurde erläutert, dass bei der punktbasierten Animation keine Zusammenhangsinformationen zwischen den einzelnen Punkten vorhanden sind. Für neueingefügte Punkte ist es dann schwierig festzustellen, welche anderen Punkte sich in seiner Nachbarschaft befinden.
Mit Hilfe der Baumdatenstruktur erhält man einen Zusammenhang zwischen den einzelnen Punkten,
denn jeder Punkt des Animationsobjekts entspricht einem Knoten im Baum. Die einzelnen Knoten
sind über Baumkanten miteinander verbunden. Jeder Knoten mit Ausnahme der Wurzel hat einen Vaterknoten, und alle Knoten, die keine Blattknoten sind, haben bis zu vier Kinder. Ein Punkt ist somit
mindestens mit einem und maximal mit fünf Knoten über eine Kante verbunden.
Das zur Verfügung gestellte Punktdatenmodell hat zusätzlich die Möglichkeit das Objekt dynamisch
zu unterteilen. Das eröffnet die Chance, die Anzahl der traversierenden Knoten zu reduzieren, wobei
der Worst Case gleich zur Basistraversierung bleibt. Diese erweiterte Datenstruktur heißt Tree-Cut,
benutzt eine bestehende Baumrepräsentation eines Objekts und wird nach [SK10] wie folgt definiert:
• Auf allen Pfaden P von der Wurzel zu den Blättern des Baums gibt es exakt einen Cut-Knoten
C auf jedem Pfad:
∀p ∈ P : |{Knoten ∈ p| Knoten liegt im Cut}| = 1
• Dann ist der Tree-Cut die Menge aller Cut-Knoten C.
Um eine erfolgreiche Oberflächenrekonstruktion zu erhalten, müssen folgende Bedingungen erfüllt
sein. Jeder Knoten im Baum muss den gesamten Bereich seiner Kinder überdecken. Wenn diese Bedingung erfüllt ist, können alle Kindknoten durch ihren gemeinsamen Elternknoten ersetzt werden.
KAPITEL 4. EIGENE VERFAHREN
42
Diese Operation resultiert in einer gröberen Darstellung. Umgekehrt können anstatt eines Elternknotens alle Kinder dargestellt werden, was zu einer detaillierteren Repräsentation führt. Abbildung 4.4
zeigt ein Beispiel für einen Tree-Cut, der Knoten von unterschiedlichen Leveln erben kann. Der grüne
Streifen zeigt den Schnitt durch den Baum, und damit genau welche Knoten im Tree-Cut liegen.
Abbildung 4.4: Aufbau eines beispielhaften Tree-Cut nach [SK10]
Die eingeführte Datenstruktur kann hilfreich sein, wenn man ein Objekt in verschiedenen Detaillierungsstufen animieren möchte. Dafür besitzt in der Datenstruktur jeder Punkt einen Prioritätswert.
Auf Grundlage dieser Prioritäten können dann Objekte in verschiedenen Detaillierungsstufen animiert
werden. Bereiche, in denen die Punkte eine sehr hohe Priorität besitzen, d.h. in denen viele wichtige
Informationen vorliegen, können fast in voller Stärke angezeigt werden. In Bereichen, in denen die
Punkte geringere Prioritätswerte besitzen, werden weniger Punkte dargestellt, was in einer gröberen
Darstellung resultiert. Die beiden dafür verantwortlichen Operationen heißen refine und coarse.
Abbildung 4.5: Aktualisierungsmethoden eines Tree-Cut [SK10]
Bei der refine-Operation wird zunächst der Knoten mit der höchsten Priorität ausgewählt. Danach
werden die Kinder des ausgewählten Knoten in der Baumdarstellung übernommen und in den TreeCut eingefügt. Nachdem sich alle Kinder des Knotens im Tree-Cut befinden, wird der anfangs eingefügte Knoten aus dem Tree-Cut entfernt.
Die coarse-Operation ist die Inversion der refine-Operation. Dafür wählt man den Knoten mit der
geringsten Priorität aus dem Tree-Cut. Nun bestimmt man den Vaterknoten des ausgewählten Knotens, entfernt alle seine Kinder aus dem Cut und fügt anschließend den Vaterknoten in den Cut ein.
Abbildung 4.5 zeigt diese beiden Aktualisierungsmethoden. Dabei ist p der Vaterknoten und die Kno-
KAPITEL 4. EIGENE VERFAHREN
43
ten 1-4 sind die Kinder von p. Wenn die Animation mit einem gültigen Tree-Cut gestartet wird, kann
ihn keine Operation ungültig machen, was am Bespiel der refine-Operation verdeutlicht wird. Das
Entfernen eines Vaterknotens macht den Cut ungültig, weil dabei ein Loch entsteht. Durch Zufügen
aller Kinder wird das eben gebildete Loch geschlossen und stellt den Cut wieder her. Somit ist das zu
Beginn beschriebene Cut-Kriterium wieder erfüllt.
4.3
Bullet Viewer
Um die punktbasierte Animation am Bildschirm betrachten zu können, muss zunächst ein Anzeigeprogramm (Viewer) dafür realisiert werden. Beim Viewer handelt es sich um eine GUI, womit die Interaktion des Benutzers mit der Maschine möglich ist. Dafür wird die Open-Source Klassenbibliothek wxWidgets [WxW] benutzt, um die Entwicklung graphischer Benutzeroberflächen zu ermöglichen. wxWidgets ist in C++ implementiert. Für eine Vielzahl anderer Programmiersprachen existiert ebenfalls
eine Anbindung. Die Programmierschnittstelle ermöglicht die Entwicklung von GUI-Programmen für
die Plattformen Windows, MAC, Linux und Unix. Des Weiteren besitzt das Framework einen großen
Compiler Support.
Für jede Anwendung muss eine neue Klasse geschrieben werden, die von der wxApp Klasse erbt.
Dabei handelt es sich um eine Applikationsklasse, welche unter anderem auch den Einstiegspunkt für
die Hauptfunktion liefert. In der neuen Klasse müssen die beiden Funktionen OnInit und OnExit überschrieben werden. Mit der ersten wird das Programm initialisiert und somit das Hauptfenster gebildet.
Dabei können Parameter wie der Text in der Titelzeile, die Position am Bildschirm sowie die Startgröße festgelegt werden. OnExit wird benutzt, um das Programm zu beenden, bzw. das Hauptfenster
zu schließen.
1
2
3
4
5
6
7
8
9
10
11
12
BulletViewer ( const wxString & title )
: wxFrame ( NULL , wxID_ANY , title ,
wxDefaultPosition , wxSize (800 , 600))
{
wxMenuBar * menubar = new wxMenuBar ;
wxMenu * file = new wxMenu ;
file - > Append ( wxID_EXIT , wxT ( " & Quit \ tCtrl + W " ));
file - > Append ( wxID_ABOUT , wxT ( " & Info \ tCtrl -? " ));
menubar - > Append ( file , wxT ( " & File " ));
SetMenuBar ( menubar );
wxStatusBar * pStatBar = this - > CreateStatusBar (2);
}
Listing 4.2: Viewerkonstruktor zur Menübildung
Das Hauptfenster wird in der zweiten wichtigen Klasse gebildet, die von der wxFrame Klasse hergeleitet wird. Dafür ist der Konstruktor, der in der OnInit Methode der Applikationsklasse gebildet
wird, wichtig. Im Konstruktor werden dann das für den Viewer wichtige Menü und die am unteren
Teil des Hauptfensters angezeigte Statusleiste gebildet. In Codebeispiel 4.2 wird gezeigt, wie im Kon-
KAPITEL 4. EIGENE VERFAHREN
44
struktor ein kleines Beispielmenü erzeugt wird. Dabei wird ein Menü mit zwei Menüitems erstellt, mit
denen zum einen das Fenster geschlossen und zum anderen ein Informationsfenster geöffnet werden
kann. Die Größe des Fensters kann nach dem Öffnen dynamisch angepasst oder in den Vollbildmodus
geschaltet werden.
Um auf ein Menükommando reagieren zu können, muss jedem Menüitem eine separate ID wie beispielsweise wxID_EXIT für das Schließen des Fensters gegeben werden. Da wxWidgets eventgesteuert ist, wird für jede Aktion eines Items ein entsprechendes Event definiert. Alle Aktionen werden in
einer Eventtabelle gebildet. Dort wird jeder ID eine Funktion zugewiesen, über die dann intern kommuniziert wird. Somit wird die Aktion an die entsprechende Funktion weitergeleitet. Beispielsweise
kann die Öffnung eines speziellen Eingabefensters ein Event sein.
Abbildung 4.6: Bullet Viewer zur Anzeige der Animation
Außer der Menüleiste besitzt der Viewer noch zwei weitere Teile. Der erste Teil davon ist ein Logfenster, das zur Textausgabe dient. Je nachdem, welche Aktion vom Benutzer durchgeführt wird, kann
eine entsprechende Benachrichtigung im Logfenster zusätzliche Informationen liefern. Nach Aufrufen der Logfunktion des Viewer erhält diese die auszugebende Textnachricht. Die Funktion verarbeitet
die Textnachricht und gibt sie über das Logfenster aus.
Der zweite wichtige Teil des Viewer ist das Renderfenster. Dieses wird von der Klasse wxPanel
abgeleitet und üblicherweise innerhalb des Hauptfensters platziert. Im Renderfenster wird später die
eigentliche Animation angezeigt. Dieses kann ebenfalls auf Events reagieren. Beispielsweise kann
für einen Tastendruck, den das Renderfenster erkennt, eine bestimmte Aktion, wie die Ausgabe der
Kameraposition über das Logfenster, ausgeführt werden. Zudem kann auf die Position der Maus,
deren Bewegung oder auf einen Mausklick reagiert werden. Man kann mit der Mausbewegung die
Kamera verschieben oder drehen.
KAPITEL 4. EIGENE VERFAHREN
45
Abbildung 4.6 zeigt exemplarisch den Bullet Viewer. Das weiße Fenster auf der linken Seite entspricht dem Logfenster zur Textausgabe. Der große schwarze Bereich, indem die Animation angezeigt
wird, ist das Renderfenster.
4.4
Verknüpfung Punktmodell mit Physikengine
Die beiden wichtigen Bestandteile der Arbeit, das Punktmodell und die Physikengine, wurden zuvor
grundlegend erläutert. Die Aufgabe ist es nun, diese beiden Bereiche miteinander zu verknüpfen. Die
Punktdaten werden in einer Baumhierarchie abgelegt, so dass sie über die jeweiligen Indizes angesprochen werden können. Diese Daten werden nun an die Verknüpfungsschnittstelle der Physikengine
geschickt. Die Physikengine simuliert die physikalischen Effekte und liefert die geänderten Daten an
die Schnittstelle zurück. Dieser verwendete Arbeitsablauf wird in Abbildung 4.7 dargestellt.
Abbildung 4.7: Arbeitsablauf des Frameworks
Ein Problem kann auftreten, wenn die Physikengine die Punktdaten weiter verarbeiten möchte. Um
zu verhindern, dass bei der Datenverarbeitung Kopien erstellt werden, muss Bullet direkten Zugriff auf
die Punktdaten haben. Die Verknüpfungsschnittstelle muss es dem Benutzer ermöglichen, die Daten
direkt zu verändern. Um die Gesamtperformance dabei so hoch wie möglich zu halten, dürfen keine
Kopien erstellt werden.
Der erstellte “Punktbaum” wird der Schnittstelle übergeben. Diese ermittelt auf Grundlage der Punktdatenstruktur die Anzahl der Punkte. Dieses Vorgehen wird für den Beispielbaum aus Abbildung 4.3,
einem Punktbaum mit 9 Knoten, erläutert. Um die Anzahl der Punkte aus dem Baum auszulesen und
entsprechend viele Körper zu erzeugen, benutzt man folgende zwei Baumoperationen. In der ersten
Operation gibt der Punktzähler die Anzahl aller Knoten in einem vollständigen Baum bis zum tiefsten
Level des Baums an. Jeder Knoten, der kein Blattknoten ist, hat vier Kinder. Für den Beispielbaum
KAPITEL 4. EIGENE VERFAHREN
46
mit 9 Einträgen besitzt der vollständige Baum 21 Knoten.
Die zweite Operation gibt die Baumgröße zurück. Darunter versteht man in der Datenstruktur die
Anzahl der Blattknoten, die im vollständigen Baum nicht besetzt sind. Im dargestellten Beispiel sind
dies 12 Knoten. Somit lässt sich mit folgender Formel die Anzahl der Punkte im Baum berechnen.
Punktanzahl = Punktzähler − Baumgröße = 21 − 12 = 9
Abbildung 4.8 zeigt den jeweiligen Baum für die beiden Baumoperationen, aus denen die Punktanzahl für die Schnittstelle berechnet wird.
Abbildung 4.8: Berechnung der Punktanzahl des Punktbaums
Den Zugriff von Bullet auf die Punktdaten ohne Erzeugung einer Kopie erklärt man am besten zunächst für starre Körper. Hierfür sind die in den Grundlagen von Bullet eingeführten Motion-States
wichtig. Anhand dieser wird nach jedem Aktualisierungsschritt die korrekte Objektposition in der
Welt bestimmt.
Der Standardmotion-State von Bullet kann nicht mit dem vorhandenen Punktmodell arbeiten. Bei Einsatz dieses Motion-State muss bei der Initialisierung zunächst die Position aus jedem Punkt in einen
Vektor kopiert werden, da eine Übergabe der Punktdatenstruktur nicht unterstützt wird. Ebenfalls
muss bei jeder Positionsänderung im Aktualisierungsschritt die neue Position jedes Punkts in einen
Vektor kopiert werden, und die Position für jedes Datenelement über SetPosition neu gesetzt werden.
Um diese Bildung von Kopien zu verhindern, wird ein eigener Motion-State, der PointDefaultMotionState, entwickelt, der alle Eigenschaften des DefaultMotionState erbt.
Diesem neuen Motion-State wird bei der Initialisierung ein Punkt aus dem Baum übergeben, um
die Anfangsposition aus dem Punkt auszulesen und danach für die Physiksimulation festzulegen. Außer bei der Initialisierung muss bei jedem Aktualisierungsschritt auf den Motion-State zugegriffen
werden. Dabei wird die Funktion setWorldTransform mit der Weltposition aufgerufen. Hierbei wird
KAPITEL 4. EIGENE VERFAHREN
47
die neue Position für den Punkt des aktuellen Motion-State gesetzt. Diese Funktionalitäten werden in
Codeteil 4.3 dargestellt.
1
2
3
4
5
6
7
8
9
10
11
12
13
class P o i n t D e f a u l t M o t i o n S t a t e : public b t D e f a u l t M o t i o n S t a t e
{
POINTS_NAMESPACE :: Point * p ;
public :
P o i n t D e f a u l t M o t i o n S t a t e ( POINTS_NAMESPACE :: Point * pNewPoint )
: p ( pNewPoint )
, b t D e f a u l t M o t i o n S t a t e ( btTransform ( btQuaternion (0 ,0 ,0 ,1) ,
btVector3 ( pNewPoint - > GetPosition (). GetX () ,
pNewPoint - > GetPosition (). GetY () ,
pNewPoint - > GetPosition (). GetZ ())) ,
btTransform :: getIdentity ())
{
}
14
virtual void set WorldT ransfo rm ( const btTransform & centerMassWT )
{
m_graphicsWT =
centerMassWT * m _ c e n t e r O f M a s s O f f s e t ;
p - > SetPosition ( m_graphicsWT . getOrigin (). getX () ,
m_graphicsWT . getOrigin (). getY () ,
m_graphicsWT . getOrigin (). getZ ());
}
15
16
17
18
19
20
21
22
23
}
Listing 4.3: Motion-State für das Punktmodell
Zusätzlich zur starren Körperdynamik kann man auch mit elastischen Körpern arbeiten. Dazu benutzt man die in den Grundlagen erwähnte dafür notwendige Datenstruktur Soft Body. Hierbei tritt
das Problem auf, dass die statische Soft Body Datenstruktur nicht in der Lage ist, mit dem verwendeten Punktmodell zu arbeiten. Um elastische Objekte auf Grundlage des Punktmodells erzeugen
zu können, muss eine eigene Datenstruktur Point Body entwickelt werden, die in den Grundzügen
äquivalent zu Soft Body arbeitet. Diese kommt dann mit der Punktdatenstruktur zurecht. Auf diese
Point Body Datenstruktur wird später noch im Detail eingegangen. Elastische Körperdynamik besitzt
im Gegensatz zu starren Körpern in Bullet keine Motion-States und somit keine einzelne Weltposition. Die für jeden Punkt benutzten Nodes sind direkt in Weltkoordinaten spezifiziert. Wie bei den
Motion-States wird in zwei Phasen auf die Position der Nodes zugegriffen. Bei der Initialisierung des
elastischen Körpers wird jeder Punkt aus dem Punktpuffer gezogen und in einen entsprechenden Node
geschrieben.
Der zweite Zugriff findet bei jedem Aktualisierungsschritt statt. Hier wird für jeden Punkt unter
Berücksichtigung der Kräfte und Geschwindigkeiten, die auf ihn wirken, die Position neu gesetzt.
Diese beiden Zugriffe auf die Punktdaten werden in Codebeispiel 4.4 exemplarisch aufgezeigt.
Nach der Aktualisierung der Punkte nach jedem Updateschritt sollen die Änderungen über den Viewer dargestellt werden, um die Bewegung aufzuzeigen. Dafür wird vom Renderer die Funktion Draw
aufgerufen und jeder Punkt aus dem Baum betrachtet. Da Punktpositionen eventuell im Updateschritt
KAPITEL 4. EIGENE VERFAHREN
48
“erneuert” wurden, werden nach jedem Schritt die Änderungen ins Renderfenster gezeichnet.
1
2
3
4
5
6
7
8
PointBodyInit ( POINTS_NAMESPACE :: PointBuffer buf )
{
for ( int i =0 , ni = node_count ;i < ni ;++ i )
{
Node &
n = m_nodes [ i ];
n . m_point = buf . GetPoint ( i );
}
}
9
10
11
12
13
14
15
16
17
18
19
PointBodyUpdate ( btScalar dt )
{
for ( i =0 , ni = m_nodes . size (); i < ni ;++ i )
{
Node &
n = m_nodes [ i ];
n . m_vel += n . m_force * n . invmass ;
n . m_point - >( n . m_point - > GetPosition ()+ n . m_vel );
n . m_force = btVector3 (0 ,0 ,0);
}
}
Listing 4.4: Punktmanipulation für elastische Körper
4.5
Konzeption und Implementierung starrer Körperdynamik
Die Physikengine hat jetzt direkten Zugriff über die definierte Schnittstelle auf die Punktdaten. Die
Verwendung kann nun an einigen einfachen Anwendungsbeispielen aus dem Bereich der starren Körperdynamik gezeigt werden. Zunächst wird bei der Initialisierung die Standardwelt für die physikalische Simulation gebildet. Ebenfalls wird zu Beginn die Bodenebene erstellt. Dafür wird als CollisionShape eine AABB als Hülle um die Ebene gelegt. Die Bodenebene wird um den Ursprung platziert
und bekommt dann die Hülle zugewiesen. Dabei ist entscheidend, die richtige Größe der Hülle zu
wählen. Wird beispielsweise der Y-Wert, der für die Höhe der Hülle steht, zu groß gewählt, entsteht in
der Darstellung der Eindruck, dass die Punkte nicht auf der Bodenebene liegen bleiben, sondern oberhalb von ihr in einem Schwebezustand verharren. Danach kann das neue Objekt zur Welt hinzugefügt
und von allen Beispielsimulationen benutzt werden.
Auf Grundlage dieses Standardaufbaus wird im Laufe der Implementierungsbeispiele für jeden einzelnen Punkt ein starrer Körper gebildet. Als Collision-Shape für nicht zur Bodenebene gehörige starre Objekte werden Kugeln oder Bounding-Boxen verwendet. Ebenfalls wird bei der Initialisierung
die sich auf die Simulation auswirkende Gravitationskraft festgelegt. Für eine realistische Simulation
wird die Schwerkraft auf

0




FGravitation = 
−10


0
gesetzt, was der Gravitationsbeschleunigung von ca. g = 9.81 sm2 des freien Falls im Schwerefeld der
KAPITEL 4. EIGENE VERFAHREN
49
Erde entspricht.
Um nun für jeden Punkt einen starren Körper zu bilden, wird die Funktion generateRigidBody mit
dem jeweiligen Punktindex sowie der Masse des Körpers aufgerufen. Bei der Körperinitialisierung
wird, wie bei der Schnittstellenberechnung erläutert, zunächst für den entsprechenden Punkt der
Motion-State gebildet, um der Physikengine die Position des aktuellen Punkts zu übergeben. Mit
Hilfe der Masse, dem Motion-State sowie dem Collision-Shape kann dann der starre Körper gebildet
und anschließend in die Welt eingefügt werden. Dieses Vorgehen zeigt Codebeispiel 4.5.
1
2
3
4
void gen erateR igidBo dy ( int i , float mass )
{
b t D e f a u l t M o t i o n S t a t e * pms = new
P o i n t D e f a u l t M o t i o n S t a t e ( pTree - > GetPointBuffer (). GetPoint ( i ));
5
btRigidBody :: b t R i g i d B o d y C o n s t r u c t i o n I n f o
FallRBCI ( mass , pms , pFallShape );
FallRB [ i ] = new btRigidBody ( FallRBCI );
dynamicsWorld - > addRigidBody ( FallRB [ i ]);
6
7
8
9
10
}
Listing 4.5: Bildung eines starren Körpers
Um bei der starren Körpersimulation während eines Zeitschritts die Szene zu aktualisieren, müssen
die folgenden Berechnungen abgewickelt werden. Zunächst wird unter Einbeziehung der festgesetzten
Gravitationskraft die auf den Körper wirkende Kraft berechnet. Mit
FNeu = FAlt + FGravitation
wird die neue Kraft aus der Gravitationskraft und der bisher auf den Körper wirkenden Kraft ermittelt.
Danach kann mit dieser neu berechneten Gesamtkraft die Geschwindigkeit des Körpers nach
v = FNeu ·
1
·t
m
bestimmt werden.
Nun muss überprüft werden, ob Kollisionen zwischen Objekten vorliegen. Hierbei wird getestet,
ob sich Collision-Shapes der starren Objekte untereinander oder mit der Bodenebene berühren. Wird
eine Berührung der Hüllen erkannt, so wird die Kollision berechnet und mit in die Simulation einbezogen. Falls verschiedene Objekte über Constraints verbunden sind, wird bestimmt, wie sich die
neuen Kräfte auf die Verbindungen zwischen den Objekten auswirken. Somit beeinflusst eine auf das
Objekt wirkende Kraft ebenfalls das über den Constraint verbundene benachbarte Objekt. Da nun alle
für die Objekte veränderlichen Operationen für den Aktualisierungsschritt berechnet wurden, werden
die Motion-States synchronisiert. Wie schon im vorigen Kapitel ausführlich erläutert, wird dabei für
jeden Punkt aus dem Punktbaum die Position aus der Weltposition aktualisiert. Am Ende des Updateschritts wird die Kraft wieder über eine clear-Funktion auf den Wert 0 gesetzt. Der Vorgang des
KAPITEL 4. EIGENE VERFAHREN
50
Arbeitsablaufs wird kompakt in Abbildung 4.9 zusammengefasst.
Abbildung 4.9: Aktualisierungsschritt bei der starren Körperdynamik
Abbildung 4.10: Freier Fall eines starren Körpers
Als erstes Implementierungsbeispiel im Bereich der starren Körperdynamik wird ein “Hallo Welt” Beispiel vorgestellt. Dabei wird ein einzelner Punkt als starrer Körper definiert und oberhalb der Bodenebene positioniert. Unter Einfluss der festgelegten Gravitationskraft nähert sich der Punkt für jeden
Zeitschritt sukzessiv der Bodenebene. Dieser freie Fall wird solange fortgeführt, bis es schließlich zur
Kollision zwischen Objekt und Bodenebene kommt. Wenn die Berührung der beiden Collision-Shapes
durch die Kollisionserkennung wahrgenommen wird, hat das Auswirkung auf die Geschwindigkeit
und auf die auf das Objekt wirkende Kraft. Der fallende Körper wird Aufgrund der abnehmenden
Kraft abgebremst und kommt, wenn die Kraft vollends aufgebraucht ist, nach kurzer Zeit auf der Bodenebene zum liegen. Damit der starre Körper exakt auf der Bodenebene liegen bleibt, und nicht den
Eindruck erweckt in der Luft zu schweben, müssen die Collision-Shapes des Körpers und der Boden-
KAPITEL 4. EIGENE VERFAHREN
51
ebene die richtige Größe besitzen. Die Simulation des freien Falls eines starren Körpers wird in der
Bildabfolge in Abbildung 4.10 dargestellt.
Abbildung 4.11: Kollisionen zwischen starren Objekten
Nach dem einfachen Einstiegsbeispiel soll die Animation von mehreren Punkten erläutert werden.
Hierbei ist nicht nur die Kollision der Punkte mit der Bodenebene interessant, sondern vielmehr die
Kollision der Punkte untereinander und die daraus entstehenden Folgen für die Simulation. Dabei
wird der gleiche Ablauf wie im “Hallo Welt” - Beispiel benutzt. Entscheidend sind die anfängliche
Positionierung der Punkte in der Welt und die Zuweisung der richtigen Collision-Shapes. Dabei werden die zu animierenden Punkte sowohl im linken als auch im rechten Bereich der Simulation so
angeordnet, dass sie eine Art Turm bilden. Da die Standardgravitationskraft die Objekte nur entlang
der Y-Achse beeinflusst, müssen die Punkte des jeweiligen Turms die gleichen Werten in den X- und
den Z-Koordinaten haben. Unterschiedliche Y-Werte der Punkte repräsentieren die verschiedenen Höhen, aus denen sie dann unter Einfluss der Gravitation zur Bodenebene herabfallen und auf dieser wie
auf einem Stapel zur Ruhe kommen. Damit diese “Turmpunkte” beim Aufprall aufeinander liegen
bleiben, muss ihnen als Collision-Shape eine Bounding-Box zugewiesen werden. Würde man statt
einer Bounding-Box eine Kugelhülle verwenden, dann würden die oberen Punkte von den unteren
herunterrollen und somit den Turm schon zu Beginn zerstören.
Zwischen den beiden Türmen werden ebenfalls Objekte positioniert. Ein Objekt befindet sich schon
zu Beginn auf der Ebene, und zwei weitere Objekte fallen in seine Richtung. Die X-Werte dieser
beiden Objekte variieren leicht zum X-Wert des auf der Ebene liegenden Punkts. Wenn diese drei
Punkte ebenfalls eine Rechteckhülle erhalten würden, könnte das Problem auftreten, dass sie sich nach
der Kollision nicht weit genug in Richtung der Türme weiterbewegen würden. Dafür ist die eckige
Form einer Bounding-Box nicht geeignet. Aus diesem Grund bekommen die zwischen den Türmen
positionierten Objekte als Hülle eine Kugel zugewiesen. Dadurch wird die seitliche Ablenkung nach
KAPITEL 4. EIGENE VERFAHREN
52
der Kollision gefördert und ein Weiterrollen begünstigt. Deshalb werden die Punkte beim Auftreffen
seitlich in Richtung der Türme abgelenkt und bringen diese beim Zusammentreffen zum Einsturz.
Diese Szenerie zeigt die Bilderserie in Abbildung 4.11.
Nachdem sich die beiden vorherigen Beispiele ausschließlich mit kollidierenden Objekten unter Einfluss der Gravitation beschäftigt haben, wird die Simulation nun mit Constraints erweitert. Damit kann
die Bewegung zweier Objekte zueinander eingeschränkt werden. Für ein weiteres Beispiel werden
vier starre Objekte erzeugt. Jeweils zwei davon werden übereinander positioniert, so dass sich zusammenhängende Objektpaare nur in der Y-Koordinate unterscheiden. Die übereinanderliegenden Körper
werden nun über einen Constraint miteinander verbunden. Dadurch soll die Bewegung der Objekte
zueinander entlang der Y-Achse eingeschränkt werden. Der Constraint des rechten Punktepaars wird
so eingestellt, dass der Abstand zwischen den Punkten konstant bleibt. Die beiden Objekte fallen mit
gleicher Distanz in Richtung der Bodenebene. Trifft der untere Körper auf diese auf, so bleibt der
obere Körper unter Beibehaltung des konstanten Abstands in der Luft stehen und schwebt.
Der Constraint des linken Punktpaars ist dynamisch einstellbar. Zwischen den beiden Punkten wirkt
eine Art Kraft, die für den Minimalabstand zwischen den Punkten verantwortlich ist. Diese Kraft für
das Objektpaar kann über einen Schieberegler eingestellt werden. Dabei muss das Problem beachtet werden, für jede Einstellungsstufe des Reglers den richtigen Abstand zwischen dem Objektspaar
zu berechnen. Es wird der Kraftwert für einen einzelnen Reglerschritt bestimmt und je nach Einstellungsstufe mit dieser multipliziert. Dadurch erhält man in der Simulation für jede Einstellung einen
entsprechenden Abstand, den die Punkte nicht unterschreiten können.
Wird der Regler auf seinen minimalen Wert ganz nach links geschoben, wirkt keine den Abstand
bestimmende Kraft zwischen den beiden Punkten. Sie fallen beide bis auf die Ebene, bzw. der obere
Punkt fällt, bis er auf dem unteren liegen bleibt. Wird der Regler hingegen ganz nach rechts auf seinen maximalen Kraftwert eingestellt, wird der anfängliche Abstand der Punkte beim Auftreffen auf
die Bodenebene beibehalten. Der übergebene Kraftwert hat dann den Wert 0, so dass die Bewegung
zueinander auf der Y-Achse komplett eingeschränkt wird. Somit sind in der Animation die beiden
Objektpaare gleich. Der Regler kann ebenfalls auf eine Zwischenposition eingestellt werden. Je nach
eingestellter Kraft wird sich der Abstand beim Auftreffen auf die Ebene zwischen den beiden Extremabständen einstellen. Abbildung 4.12 zeigt die beschriebene Beispielsimulation. Die am Regler
eingestellte Kraft wird der Initialisierungsfunktion als Parameter übergeben. Das Implementierungsbeispiel ist in Codebeispiel 4.6 zu sehen. Die Variable forceI enthält dabei den am Regler eingestellten
Kraftwert.
Nach den drei bisherigen Beispielen soll mit Hilfe der Elastizität mehr Leben in die Szene integriert werden. Deformationen können auch durch starre Körper erzeugt werden, indem die elastische
Bewegung durch ein Netzwerk von Constraints zwischen den Objekten simuliert wird. Dies soll am
Beispiel der Animation einer Welle gezeigt werden. Zu diesem Zweck werden zunächst sieben starre
Körper auf gleicher Höhe in einer Linie erzeugt. Dabei werden benachbarte Punkte jeweils über einen
Constraint miteinander verbunden, so dass eine Kette gebildet wird. Die beiden äußeren Punkte haben
KAPITEL 4. EIGENE VERFAHREN
Abbildung 4.12: Auswirkung von Constraints auf Objektsabstände
53
KAPITEL 4. EIGENE VERFAHREN
1
2
3
4
5
6
7
8
9
54
void C on s t r ai n t Ri g i dB o d y ( forceI )
{
for ( int i =0; i < FallRB_size ; i ++)
{
FallRB [ i ] - > se tA cti va ti on St at e ( D I S A B L E _ D E A C T I V A T I O N );
}
btTransform frameInA , frameInB ;
frameInA . setOrigin (0 , 1.5 , 0);
frameInB . setOrigin (0 , -1.5 , 0);
10
b t G e n e r i c 6 D o f C o n s t r a i n t * pGen6DOF = new
b t G e n e r i c 6 D o f C o n s t r a i n t ( FallRB [0] , FallRB [1] ,
frameInA , frameInB , true );
b t G e n e r i c 6 D o f C o n s t r a i n t * pGen6DOF1 = new
b t G e n e r i c 6 D o f C o n s t r a i n t ( FallRB [2] , FallRB [3] ,
frameInA , frameInB , true );
11
12
13
14
15
16
17
pGen6DOF - > s et L i ne a r Lo w e rL i m i t (0 , - forceI , 0);
pGen6DOF1 - > s et L i n ea r L ow e r Li m i t (0 , 0 , 0.);
pGen6DOF - > s et L i ne a r Up p e rL i m i t (0 , forceI , 0);
pGen6DOF1 - > s et L i n ea r U pp e r Li m i t (0 , 0 , 0);
18
19
20
21
22
dynamicsWorld - > addConstraint ( pGen6DOF , true );
dynamicsWorld - > addConstraint ( pGen6DOF1 , true );
23
24
25
}
Listing 4.6: Constraint zwischen starren Objekten
nur einen Constraint und sind am linken und rechten Rand fixiert. Sie bekommen den Massewert 0
zugewiesen und sind damit unbeweglich. In dieser Simulation wird ohne Gravitationskraft gearbeitet.
Da keine Kraft auf die Objekte wirkt, verharren alle Punkte in ihrer Anfangsposition.
Über dem mittleren Kettenelement wird ein separates Objekt definiert. Eine darauf wirkende nach
unten gerichtete Kraft bewegt es in Richtung der Kette. Beim Auftreffen auf die Kette wird auf diese
eine Kraft übertragen. Durch die Kraftübertragung wird das mittlere Kettenelement durch das fallende
Objekt mit in Richtung der Ebene gezogen. Über die Constraints wirkt sich diese Kraft ebenfalls auf
die Nachbarobjekte aus und streckt die Kette in Form einer Hängebrücke. Das einzelne Objekt fällt
weiter in Richtung Bodenebene, bis es auf dieser aufschlägt. Die auf die Hängebrücke wirkende Kraft
wird durch die am Rand fixierten Objekte immer kleiner, bis sie schließlich aufgebraucht ist. In Folge
dessen pendelt sich die Kette nach einiger Zeit wieder in ihrer Ruheposition ein. Die Simulation ist in
Abbildung 4.13 dargestellt und die Implementierung ist in Codebeispiel 4.7 aufgezeigt.
Die Simulation erweckt zwar den Eindruck einer elastischen Kette, doch ist man an komplexeren
elastischen Simulationen interessiert. Für umfangreichere Simulationen mit größeren Punktanzahlen
ist die Erstellung und Einstellung sehr vieler Constraints per Hand nötig, was die Initialisierung sehr
arbeitsintensiv macht. Zudem muss die gegenseitige Beeinflussung der Constraints vorher bedacht
werden. Für die Simulation umfangreicher elastischer Körper wird nun ein neues Modell entwickelt.
KAPITEL 4. EIGENE VERFAHREN
Abbildung 4.13: Animation einer elastischen Kette auf Grundlage der starren Körperdynamik
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void Wave ()
{
FallRB [0] - > setMassProps (0);
FallRB [6] - > setMassProps (0);
for ( int i =0; i <8; i ++)
{
FallRB [ i ] - > se tA cti va ti on St at e ( D I S A B L E _ D E A C T I V A T I O N );
}
for ( int i =0; i <6; i ++)
{
b t G e n e r i c 6 D o f C o n s t r a i n t * pDof = new
( FallRB [ i ] , FallRB [ i +1]);
setDOF ( pDof );
dynamicsWorld - > addConstraint ( pDof );
}
btVector3 relativeForce = btVector3 (0 , -6000 ,0);
btTransform boxTrans ;
boxTrans = btTransform :: getIdentity ();
19
FallRB [7] - > getMotionState () - > g etWorl dTrans form ( boxTrans );
btVector3 correctedForce =
( boxTrans * relativeForce ) - boxTrans . getOrigin ();
FallRB [7] - > ap plyCen tralF orce ( correctedForce );
20
21
22
23
24
}
Listing 4.7: Elastizität über starre Körperdynamik
55
KAPITEL 4. EIGENE VERFAHREN
4.6
56
Konzeption und Implementierung elastischer Körperdynamik
Die Erzeugung einer elastischen Simulation auf Grundlage der starren Körperdynamik liefert ein unbefriedigendes Ergebnis, da es für größere Punktanzahlen sehr aufwendig ist. Aus diesem Grund soll
ein elastischer Körper auf Basis einer neuen Datenstruktur erzeugt werden. Diese soll ebenfalls mit
dem zur Verfügung stehenden Punktmodell arbeiten. Mit dem Einführen der Elastizität in das Modell verspricht man sich eine lebendigere Szene und physikalisch ansprechendere Animationen von
einer größeren Anzahl an Punkten. Um elastische Objekte in einer Szene animieren zu können, stellt
Bullet die Klasse Soft Body zur Verfügung. Diese Klasse ist sehr umfangreich. Über eine Hilfsklasse
können verschiedene elastische Objekte wie ein Stofftuch, Seil, Dreiecksnetz oder Ellipsoid erstellt
werden. Für das in diesem Kapitel entwickelte Implementierungsbeispiel zur Simulation eines elastischen Körpers wurde sich an der Idee eines Bullet-Demobeispiels orientiert.
Nachdem ein erstes Beispiel eines elastischen Körpers auf Grundlage der statischen Soft Body Klasse entwickelt wurde, trat das Problem auf, dass diese nicht mit dem vorhandenen Punktmodell arbeiten
konnte. Aus diesem Grund musste eine eigene Klasse zur Erzeugung elastischer Körper auf Grundlage des Punktmodells erarbeitet werden. Diese neue Point Body Klasse orientiert sich an der Soft Body
Klasse von Bullet, benutzt aber nur die für das Implementierungsbeispiel notwendigen Konstrukte.
Um die benötigten Konstrukte ausfindig zu machen, wurde der Arbeitsablauf der Soft Body Beispielimplementierung ausführlich getestet und analysiert. Alle für den eigenen Ansatz nicht benötigten
Funktionalitäten der Soft Body Klasse wurden nicht in die Point Body Klasse übernommen. Für die
verbliebenen Konstrukte arbeitet der Ansatz äquivalent.
In der Simulation von starren Körpern konnte die dafür notwendige Welt verwendet werden. Wenn
nun elastische Objekte mit in die Szene einfließen, wird eine erweiterte Welt benötigt. Da Soft Bodies mit einer erweiterten SoftRigidDynamicsWorld arbeiten, wird eine dafür abgestimmte neue Welt
benötigt. Die PointBodyDynamicsWorld erbt alle Eigenschaften der Welt für starre Körperdynamik,
kann aber zusätzlich mit Point Bodies arbeiten. Wie schon oben erläutert und in Abbildung 3.10 aufgezeigt, wird ein Soft Body in Bullet aus Nodes, Links und Faces aufgebaut. Für einen Point Body
werden nun nur Nodes und Links übernommen, Faces aber nicht verwendet. Um die einzelnen Punkte
aus dem Punktbaum in den Point Body integrieren zu können, bekommt die Struktur Node zusätzlich
einen Punkt aus dem Punktmodell. Da dieser dann alle Eigenschaften der Datenstruktur besitzt, müssen Attribute wie Position oder Normale aus der Soft Body-Nodestruktur nicht übernommen werden.
Die Nodes entsprechen dann den Punkten der Simulation. Die Links werden in dynamische Links
umbenannt. Sie bekommen einen Distanzwert als zusätzliches Kennzeichen. Dieser gibt an, wie weit
die beiden durch den Link verbundenen Nodes voneinander entfernt sind. Links bilden somit den Zusammenhang zwischen benachbarten Punkten und übertragen ähnlich zu Constraints ebenfalls Kräfte.
Mit Hilfe der Links erhalten die Punkte Topologieinformationen, was sie vom “klassischen” punktbasierten Ansatz unterscheidet. Der Aufbau der wichtigsten Eigenschaften von Nodes und Links wird
in Codebeispiel 4.8 aufgezeigt.
KAPITEL 4. EIGENE VERFAHREN
1
2
3
4
5
6
7
struct Node : Feature
{
btVector3
btVector3
btScalar
POINTS_NAMESPACE :: Point *
};
57
m_vel
m_force ;
m_invmass ;
m_point ;
8
9
10
11
12
13
struct DynLink : Feature
{
Node *
m_n [2];
btVector3
m_distance ;
};
Listing 4.8: Node und dynamischer Link im Point Body
Ein Point Body besitzt genauso viele Nodes, wie Punkte im Punktbaum des elastischen Körpers
vorhanden sind. Auf Grundlage der Punkte im Punktpuffer kann nun ein Point Body erstellt werden.
Zur Initialisierung des Point Body wird der Konstruktor aufgerufen. Dieser erwartet als Eingabeparameter Weltinformationen wie Gravitation und Kollisionsinformationen. Zudem werden der Punktpuffer mit allen für den Point Body nötigen Punkten und die Masse übergeben. Zuerst erfolgt die
Festlegung der für die Simulation wichtigen Kräfte. Außerdem wird dem neuen Objekt als Hülle der
neue Point Body Collision-Shape zugewiesen. Er ist zur Erkennung und Berechnung der Kollision
notwendig. Aus dem Punktpuffer wird der Punktzähler ausgelesen, um die Anzahl der zu erstellenden
Nodes für den Point Body zu ermitteln. Schließlich werden die Nodes erzeugt. Jedem Node werden
Startwerte für den Punkt und für die inverse Masse zugewiesen. Die Initialisierung des Point Body ist
in Codebeispiel 4.9 aufgezeigt.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
PointBody ( PBWInfo * worldInfo , PointBuffer buf , const btScalar * mass )
{
m_collisionShape = new P o i n t B o d y C o l l i s i o n S h a p e ( this );
mPointBuffer = buf ;
int node_count = mPointBuffer . GetPointCount ();
for ( int i =0 , ni = node_count ;i < ni ;++ i )
{
Node &
n = m_nodes [ i ];
ZeroInitialize ( n );
n . m_point
=
mPointBuffer . GetPoint ( i );
n . m_invmass
=
mass ?* mass ++:1;
n . m_invmass
=
n . m_invmass >0?1/ n . m_invmass :0;
}
}
Listing 4.9: Initialisierung eines Point Body
Als elastischer Körper wird eine Art Stofftuch oder elastische Ebene implementiert. Zur Bildung
dieses elastischen Körpers orientiert man sich an der Hilfsklasse von Soft Body. Mit der Funktion
createPatch kann man ein solches Tuch erstellen. Der Funktion übergibt man die vier Eckpunkte des
KAPITEL 4. EIGENE VERFAHREN
58
Körpers, sowie die Anzahl der Punkte, aus denen das Objekt bestehen soll. Im Implementierungsbeispiel wird ein quadratisches Tuch gebildet. Bei der Initialisierung wird allen Punkten die gleiche
Y-Koordinate zugewiesen, so dass sie sich zu Beginn der Simulation auf gleicher Höhe in der Szene
befinden. Auf Grundlage dieser übermittelten Daten erzeugt die Funktion nun das Objekt.
Dabei sind nur die vier Eckpunkte exakt positioniert. Die übrigen Punktpositionen, die innerhalb
oder auf dem Rand des Tuchs liegen, werden durch lineare Interpolation bestimmt. Jedem Punkt wird
der Massewert 1 zugewiesen. Nach der Berechnung der interpolierten Positionen werden alle Punkte
einzeln aus dem Punktpuffer gelesen und mit der neu berechneten Position ausgestattet. Die Masse der
vier Eckpunkte wird zudem auf 0 gesetzt, um diese somit als starr festzulegen. Im bisherigen Aufbau
besitzen die Nodes keine Topologieinformationen. Da sich Punkte, die in der Nachbarschaft eines
anderen Punkts liegen, gegenseitig beeinflussen sollen, wird nun die Point Body Klasse benötigt.
Benachbarte Nodes werden über Links miteinander verbunden, so dass ein symmetrischer Aufbau
aus Nodes und Links entsteht. Links werden über die Funktion appendDynLink erstellt, wobei dafür
die beiden zu verbindenden Nodes übergeben werden. Die Funktionalität der Linkerstellung ist in
Codebeispiel 4.10 dargestellt.
1
2
3
4
5
6
7
8
9
10
void appendDynLink ( Node * node0 , Node * node1 )
{
DynLink &
l;
m_links . push_back ( l );
l . m_n [0]
=
node0 ;
l . m_n [1]
=
node1 ;
l . m_distance
=
(( l . m_n [0] - > m_point - > GetPosition ()) ( l . m_n [1] - > m_point - > GetPosition ()));
}
Listing 4.10: Initialisierung eines Links
Eine Kraft, die auf einen einzelnen Node wirkt, wird über die Links auf die benachbarten Nodes übertragen und kann so bei entsprechend starker Krafteinwirkung den gesamten Point Body beeinflussen.
Kräfte können durch die Gravitation erzeugt oder durch Kollision mit anderen Objekten auftreten.
Klingt die einwirkende Kraft ab, werden die Nodes über die Eigenkraft der Links wieder in Richtung
der Startposition gezogen, da die vier Eckpunkte des Objekts fixiert sind. Dadurch wird wieder ein
Gleichgewicht erzeugt. Die Links sind somit für die Elastizität des Point Body verantwortlich. Der
Aufbau eines Point Body aus 25 Punkten wird in Abbildung 4.14 dargestellt. Nach Erstellen des Point
Body kann dieser über die Funktion addPointBody zur Welt hinzugefügt werden.
Bei der Aktualisierung der Simulation mit einem Point Body müssen für jeden Zeitschritt folgende
Berechnungen sowohl für elastische Objekte, wie auch für starre Körper durchgeführt werden. Zunächst wird unter Berücksichtigung der Gravitationskraft und anderer in der Szene auf starre Körper
wirkende Kräfte die neue Gesamtkraft ermittelt. Anhand der Gesamtkraft und Masse wird die aktuelle Geschwindigkeit berechnet, mit der sich der starre Körper fortbewegt. Ebenfalls wird die neue
Geschwindigkeit für jeden Node des Point Body bestimmt. Dabei hat die Gravitation nur Einfluss auf
KAPITEL 4. EIGENE VERFAHREN
59
Abbildung 4.14: Grundaufbau eines Point Body
Nodes, die eine Masse ungleich 0 besitzen. Es folgt die Neuberechnung aller Nodepositionen mit Hilfe der zuvor ermittelten Geschwindigkeit. Die auf jeden Node wirkende Kraft wird nach Setzen der
neuen Position auf 0 gesetzt. Nachdem allen Objekten ihre neue Fortbewegungsgeschwindigkeit zugewiesen wurde, wird überprüft, ob es zur Kollision zwischen starren Objekten kommt. Für das Point
Body Objekt müssen nach den Nodes ebenfalls die Links aktualisiert werden. Da der jeweilige Link
auf die neuen Nodepositionen reagieren muss, wird daraus die neue Distanz des Link ermittelt, sowie
die zwischen den Nodes wirkenden Kräfte auf den neusten Stand gebracht. Nun wird getestet, ob es
zur Kollision zwischen dem elastischen Point Body und einem starren Körper kommt. Danach werden die Normalen aller Nodes aktualisiert. Nach den Kollisionsberechnungen werden wie im vorigen
Kapitel die Motion-States aller starren Körper synchronisiert, um die aktuellen Punktpositionen neu
zu setzen. Abschließend werden die Kräfte, die auf die starren Körper wirken, auf 0 gesetzt. Dieser
Ablauf eines Aktualisierungsschritts ist in Abbildung 4.15 zusammengefasst. Dabei steht PB für den
elastischen Körper (Point Body) und RB für einen starren Körper (Rigid Body).
Damit die Zeichenroutine nach einem Aktualisierungsschritt Zugriff auf alle zum Point Body gehörenden Punkte hat, wird dieser in einer Point Body Liste hinterlegt. Über die Variable m_point in jeder
Nodestruktur kann man die Punktinformationen auslesen und zeichnen.
Als erstes Anwendungsbeispiel im Bereich der elastischen Körperdynamik wird ein Stofftuch aus 25
Punkten als Point Body erstellt. Auf diesen Körper soll keine Gravitationskraft wirken. Ähnlich wie
im abschließenden Beispiel im Bereich der starren Körperdynamik wird zusätzlich ein starres Objekt
oberhalb der elastischen Ebene erstellt. Auf diesen Körper wird eine in Richtung Bodenebene wirkende Kraft ausgeübt. Während sich das starre Objekt in Richtung elastische Ebene bewegt, verharrt
diese unverändert in ihrer Startposition. Beim Auftreffen auf die elastische Ebene, genauer auf den im
Zentrum des Objekts liegenden Node des Point Body, beginnt die Kraftübertragung vom starren auf
den elastischen Körper. Diese Kraft wird auf den entsprechenden Node übertragen. Der Node bewegt
KAPITEL 4. EIGENE VERFAHREN
Abbildung 4.15: Aktualisierungsschritt bei der elastischen Körperdynamik
Abbildung 4.16: Kollision einer elastischen Ebene mit einem starren Körper
60
KAPITEL 4. EIGENE VERFAHREN
61
sich daraufhin in Folge der Kraftübertragung aus seiner Startposition in Richtung der Bodenebene.
Wie in Abbildung 4.14 dargestellt, ist der mittlere Node über vier Links mit seinen Nachbarn verbunden. Über diese Links wird nun die Kraft auf die Nachbarn übertragen. Sie folgen der Bewegung
des mittleren Nodes in Richtung der Bodenebene. Da die über die Links verbundenen Nachbarnodes
ebenfalls wieder über andere Links mit ihren eigenen Nachbarnodes verbunden sind, wird die Kraft
auf diese weiter übertragen. Dieses Szenario wird so lange fortgeführt, bis die Kraft an den vier fixierten Eckpunkten angekommen ist. Da diese Punkte unbeweglich sind und keine Kraft annehmen, wird
die von dem starren Körper übertragene Kraft hier aufgebraucht. Diese starren Eckpunkte sind nun
dafür verantwortlich, dass die anderen Nodes nicht unbegrenzt ihrer Bewegung in Richung Bodenebene fortsetzen. Über ihre Links wirkt nun eine Gegenkraft, welche die Nodes im Inneren des Objekts
wieder in Richtung ihrer Ruheposition zurückzieht. Diese entgegenwirkende Kraft wird wiederum
über die Links auf die Nachbarnodes und somit auf alle Nodes des elastischen Körpers übertragen.
Nach einiger Zeit schwingt der Körper somit aus und kehrt in die Ruhelage zurück. Die Szene ist mit
dem Hängebrücke-Beispiel, welches bei der starren Körperdynamik erläutert wurde, vergleichbar.
Die Beispielsimulation hierzu ist in Abbildung 4.16 dargestellt. Dabei ist der starre Körper in rot
gezeichnet. Das elastische Objekt mit seinen Nodes und Links ist in weiß gehalten.
Die erstellte elastische Ebene wird bisher nur durch die Gravitation oder durch Kollision mit einem
starren Körper beeinflusst. Um mehr Interaktivität in die Simulation mit einzubringen, soll es möglich
sein, einen beliebigen Node des elastischen Objekts mit der Maus auszuwählen und in eine beliebige
Richtung ziehen zu können. Die Verschiebung des Punkts soll sich dabei auf den gesamten Point
Body auswirken. Alle Punkte, die nicht starr sind, werden mit in die Richtung des ausgewählten
Punkts verschoben. Dabei ziehen sich die Links bis zu einem gewissen Maximalwert in die Länge.
Der Punkt, mit dem das ganze Objekt in eine Richtung gezogen wird, kann nach beliebiger Zeit los
gelassen werden. Daraufhin wird auf Grund der vier starren Eckpunkte des Point Body der ganze
Körper wieder in Richtung Ruhelage zurückgezogen, bis er nach einer gewissen Zeit ausschwingt.
Zunächst muss für diese Simulation beim Tastendruck der Maus die Position in der Szene berechnet und überprüft werden, ob ein Punkt des Objekts getroffen wurde. Dabei muss beachtet werden,
dass das Renderfenster die Position, an die mit der Maus geklickt wird, in Bildschirmkoordinaten
erkennt. Bevor diese weiter verarbeitet werden kann, muss sie in Weltkoordinaten der Szene umgerechnet werden. Beim Klicken in das Renderfenster wird ein Strahl von dieser Position aus in die
Szene projiziert. Über die Funktion gluUnProject werden die Schnittpunkte des Strahls mit der nearund far-clipping-Ebene berechnet. Dabei werden der Funktion die X- und Y-Koordinaten der Mausposition in Bildschirmkoordinaten übergeben. Für den Schnittpunkt p0 mit der near-clipping-Ebene gibt
man als z-Wert 0 an, für den Schnittpunkt p1 mit der dahinterliegenden far-clipping-Ebene 1. Diesen
Aufbau zeigt Abbildung 4.17. Der Strahl, der vom Schnittpunkt p0 zu p1 zeigt, berechnet sich nach
RayDirection = p1 − p0. Codeabschnitt 4.11 zeigt die Ermittlung des gesuchten Strahls.
Mit dem berechneten Strahl wird nun überprüft, ob ein Node des Point Body getroffen wurde. Auf
Grundlage dieses in die Szene geschickten Strahls wird von Bullet intern die getroffene Position in
KAPITEL 4. EIGENE VERFAHREN
62
Abbildung 4.17: Werfen eines Strahls von der Mausposition in die Szene [Pic]
1
2
3
4
btVector3 getRay ( int posX , int posY )
{
GLdouble xPos , yPos , zPos ;
GLfloat nearv [3] , farv [3] , dir [3];
5
gluUnProject ( posX , viewport [1] + viewport [3] - posY ,
0.0 , modelMatrix , projMatrix , viewport ,& xPos ,& yPos ,& zPos );
nearv [0]= xPos ; nearv [1]= yPos ; nearv [2]= zPos ;
6
7
8
9
gluUnProject ( posX , viewport [1] + viewport [3] - posY ,
1.0 , modelMatrix , projMatrix , viewport ,& xPos ,& yPos ,& zPos );
farv [0]= xPos ; farv [1]= yPos ; farv [2]= zPos ;
10
11
12
13
for ( int i =0; i <3; i ++)
{
dir [ i ] = farv [ i ] - nearv [ i ];
}
return btVector3 ( dir [0] , dir [1] , dir [2]);
14
15
16
17
18
19
}
Listing 4.11: Strahlberechnung
der Szene berechnet und über die Funktion RayTest folgendes überprüft. Wie beim Grundaufbau eines
Point Body gezeigt wurde, bilden benachbarte Nodes über ihre Links Dreiecke. Beim Klicken auf
die Oberfläche eines Point Body wird eines dieser Dreiecke identifiziert, so dass die drei zugehörigen
Nodes als Treffer in Frage kommen. Danach wird die Distanz der mit der Maus getroffenen Position zu
diesen drei Nodes berechnet. Der Node, der die geringste Entfernung zum Mauspunkt aufweist, wird
als getroffener Punkt ausgewählt und sein Index über das Logfenster ausgegeben. Dadurch wurden
KAPITEL 4. EIGENE VERFAHREN
63
Probleme durch nicht exaktes Treffen eines Nodes mit der Maus vermieden.
Abbildung 4.18: Ziehen und Zurückschwingen eines Point Body
Im nächsten Erweiterungsschritt wird ein ausgewählter Node und mit ihm das gesamte elastische
Objekt in eine beliebige Richtung gezogen. Beim Loslassen wird es durch die vier starren Eckpunkte
wieder in Richtung Ruhelage zurückgezogen. Dieser Vorgang läuft im Einzelnen folgendermaßen ab:
Mit der Maus wird ein Knoten durch Drücken der linken Maustaste ausgewählt. Jetzt muss das Renderfenster feststellen, ob eine Bewegung der Maus vorliegt. Dafür wird bei gedrückter Maustaste in
die Funktion MouseMove gesprungen. Bei ausreichender Mausbewegung wird die für die Simulation
wichtige Wahrheitsvariable m_drag auf true gesetzt. Um die Szene auf Aktualisierung zu überprüfen,
wird bei jedem Arbeitsschritt zur Überprüfung der Mausposition die Funktion pickingPreTickCallback aufgerufen. Hier wird die Simulation in der Funktion nur fortgesetzt, wenn die Wahrheitsvariable
m_drag den Wert true enthält. Ist dies der Fall, so wird die im letzten Updateschritt durch das Ziehen
der Maus zurückgelegte Strecke berechnet. Diese Distanz wird dann durch die Zeiteinheit geteilt und
auf die Geschwindigkeit des ausgewählten Nodes addiert. Dadurch wird bei der nächsten Nodeaktualisierung im Point Body der entsprechende Node mit der neuen Geschwindigkeit ausgestattet. Diese
Positionsveränderung überträgt sich über die Links auf die anderen Nodes des Körpers, die dadurch
ebenfalls eine Veränderung der Geschwindigkeit erfahren. Aus diesem Grund beeinflusst das Ziehen
eines einzelnen Punkts den gesamten Körper.
Wenn die Maustaste losgelassen wird, soll das Objekt wieder durch die starren Eckpunkte zurück-
KAPITEL 4. EIGENE VERFAHREN
64
gezogen werden. Dieses Loslassen der Maustaste wird vom Renderfenster erkannt. Daraufhin wird
der Wahrheitsvariablen m_drag der Wert false zugewiesen, um so das weitere Ziehen des Körpers zu
unterbinden. Die beschriebene Simulation wird in Abbildung 4.18 dargestellt.
Eine weitere wünschenswerte Eigenschaft des Point Body ist, einzelne ausgewählte Nodes aus dem
Objekt herauszuschneiden, so dass ein Loch im Stofftuch entsteht. Um dies zu verwirklichen, müssen alle Links, die mit dem ausgewählten Punkt verbunden sind, gelöscht werden. Bevor man jedoch
einfach die in Frage kommenden Links löscht, muss zuvor ein Blick auf die Datenstruktur geworfen
werden, mit der die Links verwaltet werden. Diese Links stehen in einer Stack-Datenstruktur. In einem Stack können eine nur durch den Speicherplatz beschränkte Anzahl von Elementen gespeichert
werden. Dabei kann allerdings nur mit dem zuletzt eingefügten Element operiert werden. Der Stack
arbeitet nach dem LIFO11 - Konzept. Die beiden Hauptoperationen, die auf einem Stack arbeiten, sind
die Push- und Pop-Operation. Push legt das einzufügende Element oben auf den Stapel. Pop löscht
das oberste Element. Eine weitere Funktion ist die Swap-Operation, mit der die Positionen von zwei
Elementen in der Datenstruktur getauscht werden können, um sie für einen Löschvorgang auf den
Stack zu platzieren.
Die Funktion cutDynLink entfernt die in Frage kommenden Links. Ihr wird der mit der Maus ausgewählte Node übergeben. Auf dem Stack m_links sind alle Links des Objekts abgelegt. In dieser Liste
wird nun abgefragt, ob ein Endpunkt des zu prüfenden Links mit dem ausgewählten Node übereinstimmt. Wird ein solcher Link gefunden, speichert man die Indexposition des Links auf dem separaten
Stapel LinksToCut. Auf dem zusätzlichen Stapel NodeNeighborIndex wird der Index des nicht ausgewählten Nodes hinterlegt, der ebenfalls mit dem Link verbunden ist.
Bevor nun die Links des ausgewählten Punkts gelöscht werden können, muss eventuell vorher der
Linkstapel noch aufgeräumt werden. Wie zuvor erwähnt, kann immer nur der oberste Stapeleintrag
gelöscht werden. Wenn ein zu löschender Link gefunden wurde, wird er über die Swap-Operation
oben auf dem Stapel platziert und anschließend gelöscht. Ein Problem tritt auf, wenn sich zum Zeitpunkt des Positionstauschs ein Link oben auf dem Stapel befindet, der zu einem späteren Zeitpunkt
noch gelöscht werden soll. Dadurch würde der in LinksToCut gespeicherte Index seine Gültigkeit
verlieren und ein nicht ausgewählter Link aus dem Point Body gelöscht werden.
Je nachdem, welche Anzahl von Links zu löschen sind, dürfen in der gleichen Anzahl obere Einträge des Stapels keine zu löschenden Links enthalten sein. Das zuvor erwähnte Problem wird in der
repairStruct Funktion überprüft. Beim Eintreffen eines solchen Falls wird der Link an die niedrigste
Position im Stapel geschoben, die durch keinen zu löschenden Link besetzt ist. Entsprechend wird
der Eintrag in LinksToCut aktualisiert. Dieses Vorgehen wird an einem aus 9 Nodes und 16 Links
bestehenden Point Body in Abbildung 4.19 erläutert.
Der im mittleren Bild markierte Punkt wird mit der Maus ausgewählt. In diesem Fall ist der Knoten
über 5 Links verbunden. Nach Überprüfen aller Links stehen die Indizes der zu löschenden Links in
der LinksToCut Liste.
11 Last
In - First Out
KAPITEL 4. EIGENE VERFAHREN
65
Abbildung 4.19: Herausschneiden eines Nodes
LinksToCut = {5, 6, 10, 12, 13}.
Bei einer Gesamtlinkanzahl von 16 und 5 zu löschenden Links betrifft das zuvor beschriebene Kriterium die Links Nr. 12 und 13. In der RepairStruct Funktion werden für diese beiden Links die
niedrigsten freien Positionen ausgewählt, die von keinem zu löschenden Link besetzt sind, so dass der
Stack nach dem Aufräumschritt die folgende Form hat.
LinksToCut = {5, 6, 10, 1, 0}.
Nachdem alle zu eliminierenden Links an zulässigen Positionen im Stapel platziert wurden, können
die den Indizes entsprechenden Links aus dem Point Body gelöscht werden. Den daraufhin entstehenden Point Body zeigt das rechte Bild.
Abbildung 4.20: Ausschneiden einzelner Nodes aus dem Point Body
KAPITEL 4. EIGENE VERFAHREN
66
Der in Abbildung 4.14 gezeigte Grundaufbau eines Point Body lässt erkennen, dass es fünf verschiedene Fälle von Nodes gibt. Die an den Ecken fixierten Punkte besitzen zwei Links. Ein Node, der
sich auf dem Rand des Tuchs befindet, ist entweder über drei oder fünf Links verbunden. Nodes im
Inneren des Objekts besitzen vier oder acht Links. Das Implementierungsbeispiel zeigt je nach Auswahl im Ausgangs-Point Body den neu entstandenen Körper mit entsprechendem Loch. Abbildung
4.20 stellt diese fünf möglichen Fälle dar. Den Implementierungsablauf der Schneideoperation zeigt
Codebeispiel 4.12.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void cutDynLink ( Node * node0 )
{
const Node * nbase1 = & m_nodes [0];
int targetX = int ( node0 - nbase1 );
int counter = 0;
for ( int i =0; i < m_links . size ();++ i )
{
DynLink & l = m_links [ i ];
int target1 = int ( l . m_n [0] - nbase1 );
int target2 = int ( l . m_n [1] - nbase1 );
if ( targetX == target1 || targetX == target2 )
{
DynLink & neuLink = m_links [ i ];
LinksToCut . push_back ( i );
if ( targetX != target1 )
Node Neigh borInd ex . push_back ( target1 );
else if ( targetX != target2 )
Node Neigh borInd ex . push_back ( target2 );
counter ++;
}
}
repairLinkStruct ( counter );
for ( int j =0; j < LinksToCut . size ();++ j )
{
btSwap ( m_links [ LinksToCut [ j ]] , m_links [ m_links . size () -1]);
m_links . pop_back ();
}
}
Listing 4.12: Herausschneiden von Punkten aus dem elastischen Objekt
Die Cutoperation im vorgestellten Beispiel wurde ohne Einwirkung einer Kraft durchgeführt. Deshalb schweben die heraus getrennten Nodes immer noch an ihrer Anfangsposition, sind aber nicht
mehr mit dem Point Body verbunden. Im folgenden Beispiel werden für einen Point Body mit einer größeren Anzahl an Nodes zunächst an einigen Stellen Löcher in das Tuch geschnitten. Diesmal
wird die Szene des zerschnittenen Körpers von vorne betrachtet. Um nun eindeutig zu sehen, dass die
herausgeschnittenen Punkte nicht mehr mit dem Point Body verbunden sind, lässt man die Gravitationskraft auf das Objekt wirken. Dabei kann man beobachten, dass sich das Tuch nach unten bewegt
und nach einer bestimmten zurückgelegten Strecke aber von den starren Eckpunkten zurückgezogen
wird. Die herausgeschnittenen Punkte, die nun nicht mehr mit dem Körper über Links verbunden
KAPITEL 4. EIGENE VERFAHREN
67
sind, erfahren keine zurückziehende Kraft der Eckpunkte mehr und fallen weiter nach unten bis zur
Bodenebene. Diese Simulation ist in Abbildung 4.21 zu sehen.
Abbildung 4.21: Zerschnittener Point Body mit Gravitationswirkung
Die beiden vorgestellten Features, das Ziehen des Point Body und das Herausschneiden einzelner
Nodes bringen mehr Leben in die Simulationsszene. Ein nächster Schritt ist es, diese beiden Funktionalitäten miteinander zu verbinden. Dafür kann über das Viewermenü die auszuführende Funktionalität ausgewählt werden. Ein Flag zeigt an, welche der drei Funktionalitäten Ziehen, Schneiden oder
beides kombiniert ausgewählt wurde. Bei der Kombination von Ziehen und Schneiden soll zunächst
in einem bestimmten Bereich der Körper gezogen werden und beim Loslassen der Maustaste wieder
zurück schwingen. Das Schneiden soll dann einsetzen, wenn der ausgewählte Punkt einen bestimmten Distanzwert von seinem Ausgangspunkt überschreitet. Dafür wird wieder in jedem Updateschritt
in die bei der Ziehsimulation erwähnte Funktion pickingPreTickCallback gesprungen. Wenn das entsprechende Flag gesetzt ist, wird das Ziehen simuliert. In der Routine wird nun bei jedem Schritt
überprüft, in wie weit sich der Körper aus seiner Ausgangsposition fortbewegt hat. Wird hier eine
festgelegte Distanz überschritten, wird wie im Fall des Herausschneidens von Punkten die Funktion
cutDynLink mit dem ausgewählten Node aufgerufen.
Ein Überschreiten des maximalen Distanzwertes hat somit eine vergleichbare Wirkung auf die Simulation wie das Loslassen der Maustaste in der Ziehsimulation. Allerdings wird nun der bis zu diesem
Zeitpunkt festgehaltene Punkt herausgeschnitten. Da er nach der Cutoperation über keine Links mehr
mit dem Point Body verbunden ist, wird dieser Node nicht von den fixierten Eckpunkten zurückgezogen. Nach einer gewissen Auspendelzeit beruhigt sich der Körper und weist wie in Abbildung 4.20
gezeigt ein Loch auf. Die kombinierte Simulation ist in Abbildung 4.22 dargestellt.
KAPITEL 4. EIGENE VERFAHREN
68
Abbildung 4.22: Kombiniertes Ziehen und Schneiden des Point Body
Nach Ausführen einer Cutoperation bleibt ein elastisches Objekt mit Löchern zurück. Man kann
einen starren Körper auf dieses fallen lassen. Wenn der starre Körper auf dem Tuch auftrifft und den
Bereich des entstandenen Lochs erreicht, fällt er durch dieses und setzt seinen Weg bis zum Auftreffen
auf die Bodenebene fort. Die Entwicklung einer weiteren Eigenschaft des Point Body besteht darin,
dass entstandene Loch mit der verbleibenden Anzahl an Nodes wieder zu schließen. Die neue RepairOperation ist an die Cut-Operation gekoppelt. Ein Reparieren des Objekts ist nur nach durchgeführtem
Cut möglich. Die Repair-Operation kann dann über ein Menüitem des Viewers ausgeführt werden.
Um das entstandene Loch wieder zu schließen, werden in der Repair-Operation neue Links in das
Objekt eingefügt. Doch dabei entsteht das Problem, dass durch bloße Neubildung von Links zwar
neue Punktverbindungen generiert werden, der Bereich zwischen den Punkten aber immer noch so
groß ist wie zuvor. Zudem würde die Linklänge entscheidend ansteigen. Um das Loch wirklich zu
verkleinern, müssen ebenfalls die Positionen der betroffenen Nodes verändert werden. Indem die in
Frage kommenden Nodes aufeinander zu geschoben werden, wird der Lochbereich verkleinert und
die Länge der Links steigt nicht wesentlich an.
Für den Repairschritt muss man wissen, welcher Node zuvor aus dem Point Body herausgeschnitten
wurde, bzw. mit wie vielen Links er verbunden war. Auf Grundlage dieser Linkanzahl kann man wie
bei der Cut-Operation zwischen sechs möglichen Fällen unterscheiden.
KAPITEL 4. EIGENE VERFAHREN
69
• Fall 1: Fixierter Eckpunkt mit zwei Links
• Fall 2: Fixierter Eckpunkt mit drei Links
• Fall 3: Randpunkt mit drei Links
• Fall 4: Randpunkt mit fünf Links
• Fall 5: Innerer Punkt mit vier Links
• Fall 6: Innerer Punkt mit acht Links
Abbildung 4.23: Reparieren des Point Body für die Fälle 1 und 2
Wenn es sich beim herausgeschnittenen Node um einen fixierten Eckpunkt des Objekts handelt, wird
zwischen Fall 1 und Fall 2 unterschieden.
Fall 1: Wenn die Wurzel aus der Nodeanzahl ungerade ist, ist jeder der vier Eckpunkte über zwei
Links mit Nachbarpunkten verbunden. In diesem Fall ist nach durchgeführter Cutoperation kein Reparieren des Objekts nötig, da das Objekt weiterhin eine geschlossene Außenhülle besitzt. Allerdings
ist der Point Body danach an einer Ecke nicht mehr fixiert. Daraus folgt, dass nach Einwirken der Gravitation nicht mehr das gewohnte Erscheinungsbild des durchhängenden Tuchs bleibt, sondern dass
der Bereich, in dem die Ecke nicht mehr fixiert ist, in Richtung Bodenebene fällt.
KAPITEL 4. EIGENE VERFAHREN
70
Fall 2: Ist die Wurzel der Nodeanzahl gerade, gibt es zwei Eckpunkte, die wie in Fall 1 über zwei
Links verbunden sind. Die beiden anderen Eckpunkte sind über drei Links mit dem Point Body verbunden. Nach Entfernen der drei Links wird ein neuer gebildet. Dafür werden die beiden auf dem
Rand des Point Body liegenden Nachbarpunkte verbunden, die zuvor mit einem fixierten Eckpunkt
verbunden waren. Dadurch ist der Umriss des Objekts wieder geschlossen und es entsteht das gleiche
Eckmuster wie in Fall 1.
Abbildung 4.23 zeigt den Reparaturschritt für die Fälle 1 und 2. Wie oben beschrieben, wird das
Erscheinungsbild für den Reparaturschritt in Fall 1 nicht verändert.
Wenn ein ausgeschnittener Punkt auf dem Rand des Körpers und nicht in einer Ecke liegt, wird
ebenfalls zwischen zwei Fällen unterschieden.
Fall 3: Der auf dem Rand liegende Punkt besitzt drei Links. Nach Abtrennen des Punkts wird ein
neuer Link eingefügt. Dieser neue Link verbindet die beiden ebenfalls auf dem Rand des Point Body
liegenden Nachbarpunkte des ausgewählten Punkts. Durch einfaches Verbinden wird das entstandene Loch nicht verkleinert. Aus diesem Grund müssen die beiden auf dem Rand liegenden Punkte
näher zusammen rücken. Für beide Nodes wird die Distanz zum vorher herausgeschnittenen Node
berechnet. Die jeweilige Nodeposition wird neu gesetzt, indem die Hälfte der Distanz in Richtung
des herausgeschnittenen Nodes zurückgelegt wird. Die Distanz des neu eingefügten Link entspricht
somit der Distanz der beiden zuvor entfernten Links zum herausgeschnittenen Node. Dadurch wird
das Loch verkleinert.
Fall 4: Ein auf dem Rand liegender Punkt kann auch über fünf Links mit dem Objekt verbunden
sein. Im Repairschritt müssen drei neue Links eingefügt werden. Einer davon ist äquivalent zum vorhergehenden Fall. Dabei werden die beiden angrenzenden auf dem Rand liegenden Nodes über einen
neuen Link miteinander verbunden. Zusätzlich wurden zwei diagonale Links aus dem Point Body gelöscht. Folgerichtig müssen nun auch wieder zwei neue diagonale Links an anderer Stelle eingefügt
werden. Dafür werden die beiden eben noch miteinander verbundenen Nodes ausgewählt. Diese werden jeweils mit dem Node verbunden, der zuvor mit dem heraus gelöschten Punkt verbunden war, und
noch mit keinem neuen Link verbunden wurde. Dafür werden ebenfalls die Positionen der betroffenen
Nodes neu gesetzt, um das Loch zu schließen, bzw. zu verkleinern. Die beiden letzten beschriebenen
Fälle sind in Abbildung 4.24 zu betrachten.
Übrig bleiben die beiden Fälle, in denen der herausgeschnittene Punkt innerhalb des Point Body
liegt.
Fall 5: Der innere herausgeschnittene Punkt besitzt vier Links. Im vorher dargestellten Grundaufbau
eines Point Body befindet sich der Node im Zentrum eines Kreuzes. Im Repairschritt müssen zwei
neue Links eingefügt werden. Wenn man von oben auf das Objekt schaut, sind die vorher durch Links
verbundenen Nachbarn oben, unten, links und rechts vom herausgeschnittenen Punkt positioniert.
Beim Repairschritt muss zum einen der obere mit dem unteren Punkt verbunden werden, und ebenso
der Rechte mit dem Linken. Dadurch entsteht wiederum ein Kreuz, in dessen Mitte sich jetzt aber kein
KAPITEL 4. EIGENE VERFAHREN
71
Abbildung 4.24: Reparieren des Point Body für die Fälle 3 und 4
Node mehr befindet. Um in der Repairfunktion die richtigen Nodes miteinander zu verbinden, bedient
man sich jetzt der Liste NodeNeighborIndex. In der vorher beschriebenen Cutfunktion, wurden die
Indizes der Nodes, die mit den abgetrennten Links verbunden waren, in diese Liste geschrieben. Die
Liste enthält also die Indizes der vier für den Repairschritt benötigten Nodes. Nun muss anhand der
vier zur Verfügung stehenden Nodes nur noch das richtige Paar miteinander verbunden werden. Hat
man die richtigen Paare zugeteilt, kann über insertNewLink mit den beiden Nodeindizes der neue Link
gebildet werden. Um nun das zuvor entstandene Loch zu verkleinern, müssen die Positionen der vier
betreffenden Punkte in Richtung des alten Mittelpunkts verschoben werden. Jeder der Punkte halbiert
seine Distanz zu diesem und verkleinert somit das Loch. Diese Positionsverschiebung funktioniert
über die Funktion setNewPosition für ein Punktpaar.
Fall 6: Im abschließenden Fall besitzt der innere Punkt acht Links. Im Grundaufbau des Point Body
befindet sich der Node im Zentrum eines Sterns. Beim Schließen des Lochs müssen vier neue Links
gebildet werden. Die erste Hälfte des Schritts läuft äquivalent zu Fall 5 ab. Dabei wurde der obere
mit dem unteren und der rechte mit dem linken Punkt verbunden. Es verbleiben noch die vier Nodes,
die über eine neue Diagonale verbunden werden müssen. Um diese vier Nodes zu finden, sucht man
nach den vier nächsten Nachbarn des alten Mittelpunkts und schließt die vier Nodes aus der Liste NodeNeighborIndex aus. Auf Grundlage dieser vier neuen Nodes muss noch überprüft werden, welche
Paare miteinander verbunden werden. Nachdem die neuen Links gesetzt wurden, werden identisch
zu Fall 5 die Positionen der acht Punkte neu gesetzt. Abschließend zeigt Abbildung 4.25 die beiden
KAPITEL 4. EIGENE VERFAHREN
72
Reparaturfälle für innere Punkte im Point Body. Codebeispiel 4.13 zeigt den Reparaturschritt im Fall
des inneren Nodes mit vier Links.
Abbildung 4.25: Reparieren des Point Body für die Fälle 5 und 6
1
2
3
4
5
6
7
8
9
10
void repair ( Node * node0 )
{
int counter = repairCounter ;
const Node * nbase1 = & m_nodes [0];
int targetX = int ( node0 - nbase1 );
int nodeSqrt = int ( sqrt ( float ( m_nodes . size ())));
if ( counter == 4)
{
// target1 - target4 bekommen durch Abfragen die
// entsprechenden Nodeindizes zugewiesen
11
insertNewLink ( target1 , target2 );
setNewPosition ( target1 , target2 );
insertNewLink ( target3 , target4 );
setNewPosition ( target3 , target4 );
12
13
14
15
}
for ( int k =0; k < counter ;++ k )
{
Node Neigh borInd ex . pop_back ();
}
16
17
18
19
20
21
}
Listing 4.13: Reparaturschritt des Point Body für Fall 5
KAPITEL 4. EIGENE VERFAHREN
73
Eine weitere Idee besteht darin, nachdem man einen Punkt durch Ziehen aus dem elastischen Objekt
herausgeschnitten hat, dieses direkt zu Reparieren. Nach einem Reparaturschritt werden die aktuellen
Linklängen als Ruhelängen gesetzt. Beim sofortigen Reparieren entsteht das Problem, dass die Links
im Moment der Cut-Operation in die Länge gezogen sind. Wird diese Länge nun als Ruhelänge des
Links fixiert, kann sich das elastische Objekt nicht zurückbilden. Um eine solche Funktionalität zu
verwirklichen, müsste man sich die gewünschte Linklänge vorher speichern und nach dem Reparaturschritt diese zuweisen. Dieses Feature wurde in der Arbeit nicht umgesetzt.
Mittlerweile kann man Punkte aus dem elastischen Körper herausschneiden und ebenfalls das entstehende Loch wieder schließen. Abschließend wurde eine Funktionalität entwickelt, um aus dem
Körper eliminierte Punkte wieder in das Objekt einzufügen. Es ist aber nicht nur möglich, den herausgeschnittenen Punkt wieder an seiner alten Stelle einzufügen, sondern man kann ihn an beliebiger
Stelle innerhalb des Point Body wieder einsetzen. Insgesamt wurden sechs verschiedene Fälle zum
Einfügen von Punkten implementiert.
• Fall 1: Entstandenes Loch für inneren Node mit vier Links
• Fall 2: Entstandenes Loch für inneren Node mit acht Links
• Fall 3: Reparierter Bereich, wo zuvor ein innerer Node mit vier Links war
• Fall 4: Reparierter Bereich, wo zuvor ein innerer Node mit acht Links war
• Fall 5: Bisher unveränderter Teilbereich
• Fall 6: In neuen Teilbereich nach Fall 5
Der herausgeschnittene Punkt, der über keine Links mehr mit dem Point Body verbunden ist, kann
mit der Maus ausgewählt werden. Dieser kann an eine beliebige Stelle des Körpers gezogen und
beim Loslassen der Maustaste in diesen Bereich eingefügt werden. Hierbei entsteht nun das Problem,
wie die verschiedenen Fälle unterschieden werden. Dafür wird an der eingefügten Stelle nach den
vier nächstliegenden Nachbarnodes gesucht. Diese vier Nodes bilden ein gedachtes Viereck um die
Einfügestelle. Danach werden alle Links, die jeweils zwei dieser Nachbarpunkte verbinden, in eine
Liste von für die Operation interessanten Links geschrieben. Anhand der Anzahl der interessanten
Links können die verschiedenen Fälle unterschieden werden. Aus den gefundenen Nodeindizes wird
der minimale und maximale Index ermittelt, die ebenfalls zur Fallunterscheidung benötigt werden.
Für die Fälle 1 und 2 wurde zunächst eine Cut-Operation an einem inneren Knoten vorgenommen.
Anschließend wurde allerdings kein Reparaturschritt durchgeführt, so dass das entstandene Loch noch
in seiner Originalgröße vorliegt.
Fall 1: Es wurde ein innerer Node aus dem Point Body herausgetrennt, der zuvor über vier Links
mit seinen Nachbarn verbunden war. In diesem Gebiet ist ein Loch zurückgeblieben. Wenn der Punkt
hier eingefügt wird, soll er sich im Zentrum des Lochs befinden und wie der zuvor herausgeschnittene
Punkt über vier Links mit den Nachbarpunkten verbunden werden. Zur Positionierung im Zentrum
KAPITEL 4. EIGENE VERFAHREN
74
des Lochs wird die Funktion setViereckMP mit den Indizes des einzufügenden Punkts sowie den vier
nächsten Nachbarn aufgerufen. Die vier Nachbarn befinden sich oben, unten, rechts und links vom
Zentrum. Die vier im Cutschritt entfernten Links sollen nun wieder eingefügt werden. Somit wird die
insertNewLink Funktion vier Mal aufgerufen. Der Index des einzufügenden Node wird dabei jeweils
mit einem der vier nächsten Nachbarn übergeben.
Fall 2: Ähnlich zu Fall 1 wurde zuvor mit der Cutoperation ein innerer Node herausgetrennt. Allerdings handelt es sich dabei um einen über acht Links mit den Nachbarn verbundenen Node. Dieser war
im Zentrum eines “Sterns” platziert. Dabei ist das größte mögliche Loch entstanden. Beim Einfügen
in diesen Teilbereich soll sich der Punkt danach ebenfalls wieder im Zentrum eines Sterns befinden
und über acht Links mit den Nachbarn verbunden werden. Wie in Fall 1 werden die vier nächsten
Nachbarnodes gefunden und über Links mit dem neuen Mittelpunktnode verbunden. Um aber wieder das vorherige Muster eines Sterns zu bekommen, müssen noch diagonale Links zu vier weiteren
Punkten des Point Body eingefügt werden. Dafür werden vier weitere nächste Nachbarsuchen durchgeführt, wobei die schon verbundenen Punkte ausgeschlossen werden. Auch diese werden mit dem
Mittelpunkt verbunden, was zum gewünschten Sternmuster führt. Abbildung 4.26 zeigt den Schritt
des Punkteeinfügens für die beiden eben beschriebenen Fälle. Der herausgeschnittene Punkt ist in der
jeweiligen linken Abbildung rechts vom Point Body platziert.
Abbildung 4.26: Einfügen eines Punkts in den Point Body für die Fälle 1 und 2
Für die Simulation von Fall 3 und 4 wurde zunächst mit einem Cutschritt ein innerer Node aus dem
KAPITEL 4. EIGENE VERFAHREN
75
Objekt gelöst. Im Gegensatz zu den beiden zuvor beschriebenen Fällen wurde danach ein Reparaturschritt durchgeführt, um neue Links einzufügen und das Loch zu verkleinern.
Fall 3: Nach erfolgreicher Cutoperation an einem inneren Punkt mit vier Links wurde zudem eine
Reparatur des Teilgebiets vorgenommen, was zum Einfügen von zwei neuen Links geführt hat. Wird
der Node nun in diesen reparierten Teilbereich eingefügt, soll sich der Sektor wieder in seine vorherige Form zurückbilden. Deshalb müssen die durch die Reparatur näher zusammen gerückten Punkte
auseinander gerückt werden, so dass wieder das Ursprungsmuster entsteht. Zunächst wird der einzufügende Punkt ins Zentrum der Zone gesetzt. Nun wird überprüft, wie viele Links innerhalb der vier
nächsten Nachbarnodes verlaufen. In Fall 3 sind das sechs Links. Vier davon bilden den Rahmen des
Vierecks, und jeweils einer verläuft zwischen den gegenüberliegenden Punkten. Diese beiden zuletzt
erwähnten Links müssen nun aus dem Point Body entfernt werden. Abschließend kann der neue Mittelpunkt mit allen vier nächsten Nachbarnodes verbunden werden. Allerdings muss vor diesem Einfügen die Position der nächsten Nachbarn verändert werden. Damit wieder das alte Muster entsteht,
wird der jeweilige Abstand zum Mittelpunkt berechnet und danach verdoppelt. Somit erreicht man
den Ausgangsabstand. Diese Positionsneusetzung kann mit der Funktion setOldPosition verwirklicht
werden.
Abbildung 4.27: Einfügen eines Punkts in den Point Body für die Fälle 3 und 4
Fall 4: Äquivalent zu Fall 3 wurde hier ein innerer Node aus dem Objekt herausgeschnitten und
danach über einen Reparaturschritt das entstandene Loch verkleinert. Allerdings handelt es sich in
KAPITEL 4. EIGENE VERFAHREN
76
diesem Fall um einen inneren Node, der über acht Links mit seinen Nachbarn verbunden war. Beim
Einfügen in diesen Bereich des Körpers soll wieder das vorangegangene Sternmuster entstehen. Die
bei der Reparatur vier neu eingefügten Links müssen nun wieder gelöscht werden. In diesem Fall
müssen zusätzlich zu den vier nächsten Nachbarnodes noch weitere vier nächste Nachbarn gefunden
werden, um neue diagonale Links einzufügen. Bevor der neue Mittelpunkt jetzt jeweils einen neuen
Link zu jedem der acht Nachbarn bilden kann, müssen die Positionen dieser Links neu gesetzt werden.
Hier wird wie in Fall 3 der Abstand zum Mittelpunkt berechnet und der Punkt mit doppeltem Abstand
neu gesetzt. Abbildung 4.27 zeigt das Einfügen in die beiden reparierten Gebiete.
Abbildung 4.28: Einfügen eines Punkts in den Point Body für die Fälle 5 und 6
In den vorangegangenen vier Fällen wurde der herausgeschnittene Node immer wieder in ein entstandenes Loch oder einen reparierten Teilbereich des Point Body eingefügt. Es besteht des Weiteren
die Möglichkeit einen Punkt in ein unverändertes Teilgebiet einzufügen.
Fall 5: Hierbei wird der herausgeschnittene Punkt an eine Stelle im Objekt eingefügt, die bisher
weder durch eine Cut- noch durch eine Repair-Operation verändert wurde. Das Muster dieses Teilbereichs besteht dabei aus einem Viereck mit einem diagonalen Link. Die ausgewählte Zone besteht
somit aus fünf Links. Der diagonale Link muss aus der Linkliste identifiziert und dann aus dem Point
Body gelöscht werden. Danach wird der einzufügende Node an den Mittelpunkt des Vierecks eingesetzt. Aus dieser Position wird der neu eingefügte Punkt mit insgesamt vier Links zu den vier Ecken
des Vierecks verbunden, die gleichzeitig die vier nächsten Nachbarn des Mittelpunkts sind. Dadurch
KAPITEL 4. EIGENE VERFAHREN
77
entsteht ein neues, bisher nicht vorhandenes Muster im Point Body.
Fall 6: Dieser Fall kann erst eintreten, wenn ein nach Fall 5 neu gebildeter Teilbereich entstanden ist.
Das neu entstandene Muster besteht dabei aus vier kleineren Dreiecken. Bei Auswahl des neuen Umfelds wird der Punkt in das jeweils ausgewählte kleine Dreieck eingefügt. Dafür wird die neue Position
des eingefügten Nodes auf den Mittelpunkt des Dreiecks gesetzt. Hier kommen im Gegensatz zu allen
fünf vorhergehenden Fällen zur neuen Linkbildung nur die drei nächsten Nachbarn in Frage. Dabei
handelt es sich um die drei Eckpunkte des neuen Dreiecks. Zu jedem dieser Eckpunkte wird dann ein
Link ausgehend vom Mittelpunkt gebildet. Das neue Muster zeigt drei noch kleinere Dreiecke als die
vorher im Fall 5 gebildeten Dreiecke. Abbildung 4.28 zeigt zunächst das neugebildete Teilgebiet nach
Fall 5 und den erst nach diesem Einfügen entstandenen Fall 6. Diese neu entstandenen Muster sind
rechts oben im Point Body zu sehen. Codebeispiel 4.14 zeigt das Einfügen eines Nodes nach Fall 1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
void insertPointNode ( Node * node )
{
int nodeIndex = 0;
const Node * nbase = & m_nodes [0];
int nodeSqrt = int ( sqrt ( float ( m_nodes . size ())));
for ( int i =0; i < m_nodes . size ();++ i )
{
if ( m_nodes [ i ]. m_point - > GetPosition () ==
node - > m_point - > GetPosition ())
{
nodeIndex = i ;
}
}
// Finden der vier nearest neighbornodes ( nn1 - nn4 )
// Aufteilen in minIndex , maxIndex , otherIndex1 und otherIndex2
int viereckInd = maxIndex - minIndex ;
if ( viereckInd == (( nodeSqrt )*2))
{
// Links die nearest neighbor Nodes verbinden werden
// in Liste interestingLinks geschoben
if ( interestingLinks . size () == 4)
{
setViereckMP ( nodeIndex , nn1 , nn2 , nn3 , nn4 );
insertNewLink ( nodeIndex , nn1 );
insertNewLink ( nodeIndex , nn2 );
insertNewLink ( nodeIndex , nn3 );
insertNewLink ( nodeIndex , nn4 );
}
}
}
Listing 4.14: Einfügen eines Nodes in den Point Body für Fall 1
KAPITEL 4. EIGENE VERFAHREN
4.7
78
Benchmarks
Die zuvor vorgestellte Implementierung eines elastischen Körpers orientiert sich an der Idee eines
Bullet-Demobeispiels. Aus diesem Grund werden nun für verschiedene Funktionalitäten die Laufzeiten für unterschiedliche Anzahl von Nodes verglichen. Die Tests für die in Tabelle 4.1 aufgezeigten
Benchmarks wurden auf folgendem System durchgeführt:
Intel(R) Core(TM) 2 Duo CPU E6750 at 2.66 GHZ 2.67 GHZ,
4.00 GB RAM, NVIDIA Quadro FX 4600.
Berechnungszeiten der verschiedenen Funktionen [ms]
Simulationsbeispiel Init Update Cut-Operation insertPoint-Operation
SB 5 × 5 Nodes
38
0.15
0.35
Nicht unterstützt
PB 5 × 5 Nodes
10
0.37
0.028
0.57
SB 12 × 12 Nodes
39
0.45
1.9
Nicht unterstützt
PB 12 × 12 Nodes
13
1.7
0.07
3.75
SB 32 × 32 Nodes
51
3.1
28
Nicht unterstützt
PB 32 × 32 Nodes
46
12
0.4
15
SB 64 × 64 Nodes 110
8.8
360
Nicht unterstützt
PB 64 × 64 Nodes 210
35
1
64
Tabelle 4.1: Vergleich zwischen Soft Body und Point Body Simulation
Die Init-Routine erstellt zu Beginn der Simulation das elastische Objekt. Für geringe Nodeanzahlen
ist sie im Falle des Point Body deutlich schneller als der Soft Body Ansatz. Das ist darauf zurück
zu führen, dass es sich bei einem Point Body um eine reduzierte Form eines Soft Body handelt. In
dem ausführlich beschriebenen Beispiel werden nur die für diesen Fall gebrauchten Funktionalitäten
aus dem Soft Body übernommen. Für wachsende Punktanzahlen wird der Laufzeitvorteil aber immer
geringer. Schließlich ist der Soft Body Ansatz für 4096 Nodes schneller als der Point Body Ansatz.
Dies ist damit zu begründen, dass die Init-Routine des Point Body nicht optimiert ist. In dieser werden
alle benötigten Punkte des Baums erst erzeugt und dann mit der entsprechenden Position ausgestattet.
Wenn die Punktbildung und Startpositionsberechnung vor die Init-Routine ausgelagert und dann nur
der Punktpuffer übergeben wird, sollte sich der Laufzeitvorteil auch für größere Mengen von Nodes
einstellen.
Die Funktionalität zum Ziehen des elastischen Körpers wurde nicht im Detail getestet. Die beiden
Implementierungen verwenden dafür nahezu die gleiche Funktion. Bei zwei Tests bestätigte sich die
Vermutung, dass sie die gleiche Laufzeit benötigen.
Für einen Updateschritt unter Einfluss der Standardgravitation ist die Bulletimplementierung für
alle getesteten Nodeanzahlen schneller als der Point Body Ansatz. Das kommt dadurch zu Stande,
dass beispielsweise für den Zugriff auf die Nodepositionen eine Funktion des zur Verfügung gestellten Punktmodells aufgerufen wird. Im Bulletbeispiel wird die Position direkt als Vektor gespeichert.
KAPITEL 4. EIGENE VERFAHREN
79
Zudem muss im vorgestellten Ansatz zwischen verschiedenen Vektordatenstrukturen umgerechnet
werden. Diese zusätzlichen Operationen lassen auf den Laufzeitnachteil schließen.
Für die Cut-Operation zum Herausschneiden von Nodes aus dem Körper liegt der Laufzeitvorteil
ganz klar auf Seiten des Point Body Ansatzes. Das ist dadurch zu erklären, dass hierbei lediglich die
Links, über die der ausgewählte Punkt mit dem elastischen Objekt verbunden ist, gelöscht werden.
Im Soft Body Ansatz werden beim Schneiden eines Lochs in das Objekt zusätzliche Operationen wie
Einfügen von neuen Nodes in das Objekt vollzogen.
Für die abschließende Funktionalität zum Wiedereinfügen von herausgeschnittenen Punkten in das
elastische Objekt sind keine vergleichenden Test möglich. Solch eine Funktionalität ist für den Soft
Body Ansatz nicht realisiert. Die Laufzeiten für dieses Feature sind für die Point Body Simulation
dennoch aufgeführt. Die beschriebenen Features mit entsprechenden Laufzeiten sind in Tabelle 4.1
dargestellt.
Kapitel 5
Aussichten und Diskussion
Innerhalb dieser Arbeit wurde eine Verknüpfung eines bestehenden Punktmodells mit der Physikengine Bullet Physics Library zur physikalisch korrekten Simulation entwickelt. Dabei wurden mehrere
kleine Beispiele im Bereich der starren Körperdynamik und ein umfangreicheres Beispiel zur Animation eines elastischen Objekts entwickelt.
Die Punktdaten werden über eine entwickelte Schnittstelle zur Physikengine gesendet. Diese führt
auf den Punktdaten eine Physiksimulation aus und liefert die geänderten Daten zurück. Über die
Schnittstelle hat die Physikengine direkten Zugriff auf die Punktdaten und kann diese unmittelbar
verändern. Dadurch müssen vor und nach der Simulation keine Kopien der Punktdaten erstellt werden,
was zu einer Reduzierung der Gesamtperformance führen würde.
Im Bereich der starren Körperdynamik wurden einfache Simulationsbeispiele dargestellt. Dabei wurde jeder Punkt als starrer Körper erzeugt und unter Einfluss der Gravitation animiert. Zudem wurden
starre Körper über Constraints miteinander verbunden, um so ihre Bewegung zueinander einzuschränken. Um interaktivere physikalische Simulationen zu erhalten, wurde die Elastizität mit in die Animation einbezogen. Deformationen können auch durch starre Körper erzeugt werden, indem die elastische Bewegung durch ein Netzwerk von Constraints zwischen den Objekten simuliert wird. Doch für
größere Anzahl von Punkten kann die Bildung eines solchen Constraintnetzwerks sehr umfangreich
werden. Da starre Körpersimulation lediglich für einzelne kleine Objekte durchgeführt wurde, ist die
Animation mehrerer starrer Körper, die aus einer größeren Anzahl an Punkten besteht, wünschenswert. Dadurch könnten für den Betrachter anschauliche und unterscheidbare Körper miteinander interagieren und beispielsweise Kettenreaktionen entstehen.
Um Elastizität nicht auf Grundlage der starren Körper zu benutzen, wurde sich an einer auf Soft
Bodies operierenden Beispielimplementierung von Bullet orientiert. Ein Problem eines Soft Body ist,
dass er auf Oberflächen beschränkt ist, und somit keine Flüssigkeiten darstellen kann. Dafür würde
man Volumeninformationen benötigen. Anhand dieser könnten unter der Oberfläche ablaufende Kompressionen dargestellt werden. Es würde sich dabei um eine elastische Verformung handeln, bei der
das Volumen abnimmt und gleichzeitig die Dichte steigt.
Nach der Implementierung des ersten Beispiels eines elastischen Körpers auf Grundlage der stati80
KAPITEL 5. AUSSICHTEN UND DISKUSSION
81
schen Soft Body Klasse trat das Problem auf, dass diese nicht mit dem vorhandenen Punktmodell
arbeiten konnte. Aus diesen beiden Gründen wurde eine mit dem Punktmodell arbeitende Point Body
Implementierung entwickelt.
Bei der allgemeinen punktbasierten Animation haben die Punkte keine Topologieinformationen und
sind somit nicht mit Punkten in der Nachbarschaft verbunden. Bei der Erstellung eines elastischen Objekts mit der Point Body Klasse wurden die nächstliegenden Nachbarpunkte über dynamische Links
miteinander verbunden, um sich gegenseitig zu beeinflussen und somit jedem Punkt Topologieinformationen zuteilen zu können. Insofern erhielten bei Krafteinwirkung auf einen Punkt des elastischen
Objekts über Links mit diesem Punkt verbundene Nachbarn ebenfalls Kräfte. Folglich konnte sich
die Kraft über das gesamte Objekt verteilen. Für die beschriebene Implementierung wurde erläutert,
dass es möglich ist, einzelne Punkte aus dem Objekt herauszuziehen und ebenfalls wieder in dieses einzufügen. Die Optimierung bei der Bildung eines elastischen Körpers, indem Punkte schon vor
der Init-Routine erstellt und dann nur noch aus dem Baum ausgelesen werden, würde auch für größere Punktanzahlen noch einen Geschwindigkeitsvorteil gegenüber der Soft Body Implementierung
bringen. Eine weitere erstrebenswerte Funktionalität wäre das sofortige Reparieren des in Folge des
Herausschneidens eines Punktes bei einer Zieh-Operation entstandenen Lochs im elastischen Körper.
Da bei der Reparatur die Ruhelängen aller Links auf die zu diesem Zeitpunkt aktuelle Länge gesetzt
wird, bleibt der Körper in dem gestreckten Zustand stehen. Es müsste eine alternative Vorhergehensweise zur Aktualisierung der Ruhelängen entwickelt werden. Zudem wäre es interessant, elastische
Objekte aus sehr viel größeren Punktanzahlen zu bilden. Reizvoll wären des Weiteren die Simulation
einer Szene mit mehreren verschiedenen elastischen Körpern und die Kollision von elastischen Objekten untereinander. Als weiteres Beispiel wäre es vorstellbar, Löcher in ein fixiertes elastisches Tuch
zu schneiden. Auf dieses zerschnittene Tuch könnte von oben ein Weiteres unbeschädigtes, an den
Ecken nicht fixiertes Tuch fallen. Im Laufe der Simulation sollten sich einzelne Teile des fallenden
Tuchs durch die im fixierten Tuch geschnittenen Löcher schlängeln.
Für eine Weiterführung der Arbeit wäre es interessant, auf dem bisher erstellten Modell ein Volumen
unter der Oberfläche zu animieren. Ein mögliches Ziel könnte die Darstellung einer Flüssigkeit sein.
Wenn dabei ein Wassertropfen auf die Wasseroberfläche trifft, kann in diesem Fall in der Natur der in
Abbildung 5.1 dargestellte Effekt entstehen.
Beim Auftreffen eines Wassertropfens auf die Wasseroberfläche wird ein Teil des Wassers mit Wellen nach außen getragen. Die zum Zentrum gerichtete Kraft des Wassers lässt hier eine kleine Fontäne
nach oben steigen. Überschreitet die Spitze der Fontäne einen bestimmten festgelegten Distanzwert,
können sich Teile der Wasseroberfläche von dieser lösen. Würde man diesen Effekt durch einfaches
Lösen des obersten Punkts und Verbinden der darunter liegenden Punkte durch Links darstellen, entstünde dabei ein komisches Bild. Sollte der obere Punkt seine Maximaldistanz zu den darunter liegenden Punkten überschreiten, so müsste man auch diese genauer betrachten, da sich möglicherweise mehrere Punkte von der Oberfläche lösen könnten. Beim Wiederauftreffen von gelösten Tropfen
auf die Wasseroberfläche würden sich diese erneut mit der Oberfläche verbinden und somit neue in-
KAPITEL 5. AUSSICHTEN UND DISKUSSION
82
teressante Effekte erzeugen. Durch Wechselwirkungen der Wassertropfen mit der Wasseroberfläche
kann dabei der Effekt einer Krönchenbildung oberhalb der Oberfläche beim Hochspringen von Wasser entstehen. Dieser Effekt ist nur bei der Betrachtung der Sequenz in Zeitlupe sichtbar. Beim Ablauf
in Echtzeit sieht man lediglich die Wellenbewegungen.
Abbildung 5.1: Krönchenbildung durch Auftreffen von Wassertropfen [Tro]
Eine dynamische Unterteilung des Objekts zur Reduzierung der Anzahl der zu traversierenden Punkte wurde nicht umgesetzt. Auch hier könnten weiterführende Arbeiten ansetzen. Mit Hilfe der vorgestellten Tree-Cut-Datenstruktur kann eine dynamische Unterteilung verwirklicht werden. Dafür kann
den Punkten ein Prioritäts- oder Relevantswert zugeordnet werden, der eine Aussage darüber macht,
wie viele interessante oder wichtige Informationen einzelne Punkte für die Szene enthalten. Bereiche,
die viele interessante Punkte enthalten, sollten in einer sehr detaillierten Darstellung angezeigt werden. Wenn sich dagegen in einem Umfeld Punkte mit wenig relevanten Informationen befinden, kann
dieser Sektor in einer gröberen Darstellung angezeigt werden. Im Falle der reduzierten Darstellung
können einzelne Punkte oder ganze Punktbereiche zusammengefasst werden. Dadurch müssen für die
Animation insgesamt weniger Punkte dargestellt werden. Solch eine Wiedergabe kann beim Beobachter den Eindruck erwecken, dass manche Bereiche durch das Auge sehr scharf und andere wiederum
unscharf wahrgenommen werden. Die dadurch entstehende Reduzierung der Punktanzahl lässt einen
Geschwindigkeitsvorteil für die Implementierung erwarten. Solch eine dynamische Unterteilung ist
erst für weitaus höhere Punktanzahlen sinnvoll.
Literaturverzeichnis
[AG07]
Pauly M. Keiser R. Adams, B. and L. J. Guibas. Adaptively sampled particle fluids. In
ACM Trans. Graph. 26, 3, 2007.
[BB07]
A. Boeing and T. Bräunl. Evaluation of real-time physics simulation systems. In GRAPHITE ’07: Proceedings of the 5th international conference on Computer graphics and
interactive techniques in Australia and Southeast Asia, (pp. 281–288), 2007.
[Bre05]
T. Breiner. Dreidimensionale virtuelle Organismen. Ph.D. thesis, Johann Wolfgang Goethe Universität, 2005.
[Bre07]
T. Breiner. Animation, 2007. Johann Wolfgang Goethe Universität.
[BT07]
Wojtan C. Hodgins J.K. Bargteil, A.W. and G. Turk. A Finite Element Method for Animating Large Viscoplastic Flow. In ACM Trans. Graph., vol. 26, #3, 2007.
[Bula]
Bullet Physics Library. URL http://bulletphysics.com/. Aufgerufen 01.09.2010.
[Bulb]
Bullet Physics Manual.
URL http://www.bulletphysics.com/ftp/pub/test/
physics/Bullet_User_Manual.pdf. Aufgerufen 01.09.2010.
[CV07]
E. Coumans and K. Victor. COLLADA Physics. In Proceedings of the twelfth international conference on 3D web technology, (pp. 104–105), 2007.
[Dau]
Animation eines Daumenkino. URL http://wiebo.files.wordpress.com/2007/
09/playera-128.png. Aufgerufen 10.01.2011.
[Dik08]
N. Dike. Physics simulation for an automotive simulator. Tech. rep., University of Western Australia, 2008.
[Gam]
Physikengines in Videospielen - Game Developers Magazine survey. URL http://
bulletphysics.org/wordpress/?p=88. Aufgerufen 06.09.2010.
[GBB09]
D. Gerszewski, H. Bhattacharya, and A. Bargteil. A point-based method for animating
elastoplastic solids. In Proc. of Symp. on Computer Animation, (pp. 133–138), 2009.
83
LITERATURVERZEICHNIS
[GM77]
84
R. A. Gingold and J. J. Monaghan. Smoothed particle hydrodynamics: theory and application to non-spherical stars. In Monthly Notices of the Royal Astronomical Society, vol.
181:pp. 375–389, 1977.
[Hav]
Havok. URL http://www.havok.com/. Aufgerufen 01.09.2010.
[Hei02]
J. Hein. Proseminar Computergraphik - Partikelsysteme, 2002. Universität Ulm.
[Hei08]
B. Heinecke. Simulation und Visualisierung von Fluiden und granularen Materialien mit
PhysX, 2008. Technische Universität Dresden.
[Kei06]
R. Keiser. Meshless Lagrangian Methods for Physics-Based Animations of Solids and
Fluids. Ph.D. thesis, ETH Zürich, 2006.
[Kle05]
F. Kleinert. Physik in Computerspielen, 2005. Universität Ulm.
[LJ87]
Rafael S. Lasseter J. Principles of Traditional Animation applied to 3D Computer Animation. In SIGGRAPH 87, Computer Graphics, Vol. 21, No. 4, (pp. 35–44), 1987.
[Mas]
Masse-Feder System. URL http://upload.wikimedia.org/wikipedia/en/7/79/
Mass_spring_damper.png. Aufgerufen 21.11.2010.
[Mes]
Mesh-based Stanford Bunny.
URL http://www.andrew.cmu.edu/user/sowen/
images/BUNNY.jpg. Aufgerufen 23.12.2010.
[Mes06]
D. Meschede. Gerthsen Physik. Springer Verlag, 2006.
[MG03]
Charypar D. Müller, M. and M. Gross. Particle-based fluid simulation for interactive
Applications. In The Proceedings of the Symposium on Computer Animation, (pp. 154–
159), 2003.
[MG05]
Solenthaler B. Keiser R. Müller, M. and M. Gross. Particle based fluid-fluid interaction.
In SCA 2005: Proceedings of the 2005 ACM SIGGRAPH/Eurographics Symposium on
Computer Animation, (pp. 237–244), 2005.
[Mil07]
I. Millington. Game Physics Engine Development: How to build a robust commercialgrade physics engine for your game. Morgan Kaufman, 2007.
[MKN+ 04] M. Müller, R. Keiser, A. Nealen, M. Pauly, M. Gross, and M. Alexa. Point-based Animation of Elastic, Plastic and Melting objects. In Proc. of Symp. on Computer Animation,
(pp. 141–151), 2004.
[Mon92]
J. J. Monaghan. Smoothed Particle Hydrodynamics. In Annual Review of Astrophysical
Physics, vol. 30:pp. 543–574, 1992.
[Mot]
Motion Capture. URL http://cache.kotaku.com/assets/resources/2007/08/
gollumserkis.jpg. Aufgerufen 10.01.2011.
LITERATURVERZEICHNIS
[Mü08]
85
Stam J. James D. Thürey N. Müller, M. Real Time Physics - Class Notes. In Proceedings
of SIGGRAPH 2008, 2008.
[NC06]
Müller M. Keiser R. Boxerman E. Nealen, A. and M. Carlson. Physically Based Deformable Models in Computer Graphics. In The Eurographics Association and Blackwell
Publishing Ltd., (pp. 809–836), 2006.
[Neu10]
K.O. Neumann. Punktbasierte Methode für die Animation von elastoplastischen Festköpern, 2010. Johann Wolfgang Goethe Universität.
[ODE]
Open Dynamics Engine. URL http://www.ode.org/. Aufgerufen 01.09.2010.
[OH02]
Bargteil A. W. O’Brien, J. and J. K. Hodgins. Graphical modeling and animation of
ductile fracture. In Proceedings of SIGGRAPH 2002, (pp. 291–294), 2002.
[Ott95]
F. Ott. Smoothed Particle Hydrodynamics: Grundlagen und Test eines speziellen Ansatzes für viskose Wechselwirkungen, 1995. Eberhard-Karls-Uni Tübingen.
[Par02]
R. Parent. Computer Animation: Algorithms and Techniques. Academic Press, 2002.
[Phya]
Definition
von
Physik.
URL
http://www.uni-muenster.de/Physik/
Studieninteressierte/Wissenswertes/definition.html.
Aufgerufen
22.12.2010.
[Phyb]
PhysX. URL http://www.ageia.com/. Aufgerufen 01.09.2010.
[Pic]
Strahlberechnung.
URL
http://www.codeproject.com/KB/openGL/
TranslationController.aspx. Aufgerufen 12.01.2011.
[Poi]
Point-based Stanford Bunny. URL http://www.ccs.neu.edu/home/gaob/images/
bunny_pc.png. Aufgerufen 23.12.2010.
[Ree83]
W.T. Reeves. Particle Systems - A Technique for Modelling a Class of Fuzzy Objects. In
from ACM Transactions on Graphics, Vol. 2, No. 2, (pp. 91–108), 1983.
[Sei01]
J.W. Seifert. Visualisieren, Präsentieren, Moderieren. GABAL Verlag, 2001.
[SH98]
J. Simo and T. Hughes. Computational Inelasticity. Springer Verlag, 1998.
[SH09]
Bargteil A.W. Sin, F. and J.K. Hodgins. A Point-based Method for Animating Incompressible Flow. In Proceedings of the ACM SIGGRAPH/Eurographics Symposium on
Computer Animation, (pp. 247–255). 2009.
[Shi05]
P. Shirley. Fundamentals of Computer Graphics. A K Peters, Ltd, 2005.
[SK10]
D. Schiffner and D. Krömker. Tree-Cut: Dynamic level of detail for point-based rendering. Tech. rep., Graphische Datenverarbeitung, Goethe Universität Frankfurt, 2010.
LITERATURVERZEICHNIS
[SPH]
86
Smoothed Particle Hydrodynamics.
URL http://bugman123.com/FluidMotion/
SPH.jpg. Aufgerufen 30.11.2010.
[SR06]
A. Seugling and M. Rölin. Evaluation of Physics Engines and Implementation of a Physics Module in a 3d-Authoring Tool, 2006. Umea University.
[Stu94]
D. J. Sturman. A brief history of motion capture for computer character animation. In
Proceedings of SIGGRAPH 1994, 1994.
[TF88]
D. Terzopoulos and K. Fleischer. Modeling Inelastic Deformation: Viscoelasticity, Plasticity, Fracture. In Proceedings of ACM SIGGRAPH, (pp. 269–278), 1988.
[TJ81]
F. Thomas and O. Johnston. Disney Animation- The Illusion of Life. Abbeville Press,
1981.
[Tro]
Wassertropfen.
URL http://en.wikipedia.org/wiki/File:Water_splashes_
001.jpg. Aufgerufen 02.09.2010.
[WxW]
WxWidgets. URL http://www.wxwidgets.org/. Aufgerufen 02.09.2010.