T_o1_Schulaufgabe_2_06-07_5c - Robert-Koch
Werbung

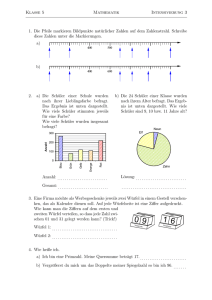
Klasse 5 c 2. Schulaufgabe aus der Mathematik Gruppe 15. 01. 2007 A 1. Berechne, gegebenenfalls mit allen notwendigen Zwischenschritten. a) 1476 − 489 b) 309 − 444 c) −79 − 254 d) −89 + 335 e) 456 − (234 − 567) f) 132 − (412 − 157) g) −45 + 87 − 23 − 78 + 198 + 58 − 125 + 27 2. Den fünften und sechsten Klassen des Robert-Koch-Gymnasiums soll am Vormittag in der Aula ein 90-minütiger Film gezeigt werden. Jede Vorführung kann von 80 Schülern besucht werden und kostet 110 e. Die Schülerzahlen sind wie folgt: Klasse 5A 5B 5C 5D 6A 6B 6C 6D Schüler 26 28 28 25 29 31 27 26 a) Erstelle einen sinnvollen und realistischen Zeitplan für die Filmvorführungen. b) Berechne einen gerechten Unkostenbeitrag für jeden Schüler. 3. Aus weißen und farbigen Fliesen wird ein Mosaik aufgebaut. Die unten gezeichnete Folge von Figuren beschreibt die ersten vier Schritte beim Aufbau des Mosaiks. Aus wie vielen Fliesen besteht die achte Figur, wenn das Muster entsprechend fortgeführt wird? 4. Steckbriefe a) Nenne alle ebenen geometrischen Figuren, auf die das Folgende immer zutrifft: Ich bin ein Viereck. Zwei gegenüberliegende Seiten sind zueinander parallel. Ich ” bin aber kein Parallelogramm“ b) Nenne einen räumlichen geometrischen Körper, für den gilt: Ich bin von ebenen Flächen begrenzt. Ich habe fünf Ecken.“ ” 5. Zeichne ein Koordinatensysten mit −6 ≤ x ≤ 6, −6 ≤ y ≤ 6 und 1 LE = 1 cm, ferner die Punkte M (0|2), S (1| − 5), A (4| − 1), B (−4| − 4). a) Zeichne einen Kreis k mit Radius 3, 5 cm um den Mittelpunkt M b) Markiere blau: Alle Gitterpunkte im Inneren des Kreises k, deren x- und yKoordinate zusammen 4 ergeben. c) Zeichne ein: [SA und [SB]. d) Bestimme mit dem Winkelmesser den Winkel α zwischen [SA und [SB]. Viel Erfolg ! Kink Klasse 5 c 2. Schulaufgabe aus der Mathematik 15. 01. 2007 B Gruppe 1. Berechne, gegebenenfalls mit allen notwendigen Zwischenschritten. a) 1477 − 589 b) 409 − 655 c) −89 − 466 d) −68 + 203 e) 156 − (534 − 267) f) 432 − (215 − 572) g) −55 + 97 − 33 − 98 + 198 + 78 − 135 + 36 2. Den fünften und sechsten Klassen des Robert-Koch-Gymnasiums soll am Vormittag in der Aula ein 90-minütiger Film gezeigt werden. Jede Vorführung kann von 80 Schülern besucht werden und kostet 110 e. Die Schülerzahlen sind wie folgt: Klasse 5A 5B 5C 5D 6A 6B 6C 6D Schüler 26 25 28 28 27 26 29 31 a) Erstelle einen sinnvollen und realistischen Zeitplan für die Filmvorführungen. b) Berechne einen gerechten Unkostenbeitrag für jeden Schüler. 3. Aus weißen und farbigen Fliesen wird ein Mosaik aufgebaut. Die unten gezeichnete Folge von Figuren beschreibt die ersten vier Schritte beim Aufbau des Mosaiks. Aus wie vielen Fliesen besteht die zehnte Figur, wenn das Muster entsprechend fortgeführt wird? 4. Steckbriefe a) Nenne alle ebenen geometrischen Figuren, auf die das Folgende immer zutrifft: Ich bin ein Viereck. Zwei gegenüberliegende Innenwinkel sind gleich groß. Ich ” bin kein Parallelogramm“ b) Nenne einen räumlichen geometrischen Körper, für den gilt: Ich bin von ebenen Flächen begrenzt. Ich habe sechs Ecken.“ ” 5. Zeichne ein Koordinatensysten mit −6 ≤ x ≤ 6, −6 ≤ y ≤ 6 und 1 LE = 1 cm, ferner die Punkte M (2|1), S (−1| − 5), A (5| − 3), B (−5| − 2). a) Zeichne einen Kreis k mit Radius 3, 5 cm um den Mittelpunkt M b) Markiere blau: Alle Gitterpunkte im Inneren des Kreises k, deren x- und yKoordinate zusammen 3 ergeben. c) Zeichne ein: [SA und [SB]. d) Bestimme mit dem Winkelmesser den Winkel α zwischen [SA und [SB]. Viel Erfolg ! Kink Klasse 5 c 2. Schulaufgabe aus der Mathematik Musterlösung Gruppe 1. 15. 01. 2007 A a) 1476 − 489 = 987 b) 309 − 444 = −135 c) −79 − 254 = −333 d) −89 + 335 = 246 e) 456 − (234 − 567) = 456 − (−333) = 456 + 333 = 789 f) 132 − (412 − 157) = 132 − 255 = −123 g) −45+87−23−78+198+58−125+27 = (87 + 198 + 58 + 27)−(45 + 23 + 78 + 125) = 370 − 271 = 99 2. a) Zeit 08.00 Uhr – 09.45 Uhr – 11.30 Uhr bis 09.30 Uhr: Pause – bis 11.15 Uhr: Pause – bis 13.00 Uhr: Klassen Schülerzahl 5 A, 5 B, 6 D 26 + 28 + 26 = 80 5 C, 5 D, 6 C 28 + 25 + 27 = 80 6 A, 6 B 29 + 31 = 60 b) Preisabrechnung: Gesamtpreis 110 e · 3 = 330 e Pro Schüler 330 e : 220 = 1, 50 e 3. 1 + 6 + 12 + 18 + 24 + 30 + 36 + 42 = 169 Die achte Figur besteht aus 169 Fliesen. 4. a) Nenne alle ebenen geometrischen Figuren, auf die das Folgende immer zutrifft: Ich bin ein Viereck. Zwei gegenüberliegende Seiten sind zueinander parallel. Ich ” bin aber kein Parallelogramm“ Quadrat, Rechteck, Raute, Trapez. b) Nenne einen räumlichen geometrischen Körper, für den gilt: Ich bin von ebenen Flächen begrenzt. Ich habe fünf Ecken.“ ” Pyramide (über einem Viereck) Klasse 5 c 2. Schulaufgabe aus der Mathematik Musterlösung Gruppe 5. a) y b) 5 4 3 2 M 1 c) -5 -4 -3 -2 -1 B d) α ≈ 116◦ 15. 01. 2007 A k 1 -1 -2 -3115,6° -4 -5 S 2 3 4 5 A x Klasse 5 c 2. Schulaufgabe aus der Mathematik Musterlösung Gruppe 1. 15. 01. 2007 B a) 1477 − 589 = 888 b) 409 − 655 = −246 c) −89 − 466 = −555 d) −68 + 203 = 135 e) 156 − (534 − 267) = 156 − 267 = −111 f) 432 − (215 − 572) = 432 − (−357) = 432 + 357 = 789 g) −55+97−33−98+198+78−135+36 = (97 + 198 + 78 + 36)−(55 + 33 + 98 + 135) = 409 − 321 = 88 2. a) Zeit 08.00 Uhr – 09.45 Uhr – 11.30 Uhr bis 09.30 Uhr: Pause – bis 11.15 Uhr: Pause – bis 13.00 Uhr: Klassen Schülerzahl 5 A, 5 C, 6 B 26 + 28 + 26 = 80 5 B, 5 D, 6 A 25 + 28 + 27 = 80 6 C, 6 D 29 + 31 = 60 b) Preisabrechnung: Gesamtpreis 110 e · 3 = 330 e Pro Schüler 330 e : 220 = 1, 50 e 3. 1 + 4 + 8 + 12 + 16 + 20 + 24 + 28 + 32 + 36 = 181 Die zehnte Figur besteht aus 181 Fliesen. 4. a) Nenne alle ebenen geometrischen Figuren, auf die das Folgende immer zutrifft: Ich bin ein Viereck. Zwei gegenüberliegende Innenwinkel sind gleich groß. Ich ” bin kein Parallelogramm“ Quadrat, Rechteck, Raute, Drachen. b) Nenne einen räumlichen geometrischen Körper, für den gilt: Ich bin von ebenen Flächen begrenzt. Ich habe sechs Ecken.“ ” Prisma (über einem Dreieck) Klasse 5 c 2. Schulaufgabe aus der Mathematik Musterlösung Gruppe 5. a) 15. 01. 2007 B y b) 5 c) 4 k 3 2 1 -5 B -4 -3 -2 -1 -1 1 2 3 4 5 -2 124,7° -3 -4 S -5 d) α ≈ 125◦ M A x