GW_Ph_10 - MWG Bayreuth

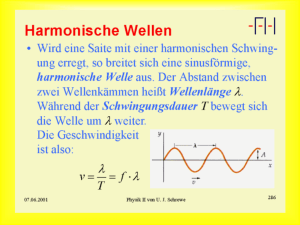
Markgräfin-Wilhelmine-Gymnasium Bayreuth
Thema
Grundwissen Physik Jahrgangsstufe 10 (G8)
Inhalt
Seite 1/8
Beispiele, Bemerkungen, Zusatzinfos
Astronomische
Weltbilder
Das geozentrische Weltbild Weltbild von Ptolemäus (um 100 n. Chr.) bis ins 15. Jh. vorherrschend (Erde
im Zentrum des Universums; Sonne ein Gestirn unter vielen)
Ptolemäus: ca. 85-160
Das heliozentrische
Weltbild
Durch die Arbeiten von Kopernikus (um 1500) wird die Vorstellung der Sonne Nikolaus Kopernikus: 1473-1543
als Zentralgestirn und der Erde als einem Planeten unter vielen langsam
allgemein akzeptiert (Kopernikanische Wende). Aus religiösen Gründen fällt
es den Menschen aber schwer zu glauben, dass die Erde einen weniger
ausgezeichneten Platz im Universum hat.
Das Weltbild der Neuzeit
Festigung des Heliozentrischen Weltbilds durch Galilei (um 1600) durch
Entdeckungen (Mondkrater, Jupitermonde) mit dem neu erfundenen Fernrohr.
Zuerst wurde Galileo jedoch durch die Inquisition zu Hausarrest bis zum
Lebensende verurteilt. Erst viel später allgemeine Akzeptanz.
Die Kepler'schen Gesetze
Bestätigung und Erweiterung des kopernikanischen Weltbilds durch Kepler
Veranschaulichungen:
(um 1600), der mit Hilfe genauer Himmelsbeobachtungen eines Astronomen
folgende Gesetze formulierte:
1. Kepler’sches Gesetz: Die Bahnen der Planeten sind Ellipsen. Die Sonne
steht in einem der beiden Brennpunkte.
2. Kepler’sches Gesetz: Die Verbindungsstrecke von der Sonne zum Planeten
1. Gesetz
2. Gesetz
überstreicht in gleichen Zeitabschnitten Flächen mit gleichem Flächeninhalt.
3. Kepler’sches Gesetz: Die Quadrate der Umlaufzeiten T1 und T2 zweier
Planeten verhalten sich wie die dritten Potenzen der großen Halbachsen a1 und
3
T12 a1
a2 der Planetenbahnen.
=
T22 a2 3
3. Gesetz: Halbachsen einer Ellipse
Gravitationstheorie
Erklärung der Keplerschen Gesetze durch Isaac Newtons Gravitationsgesetz;
unter Anderem besagt es, dass sich alle Körper aufgrund ihrer Masse
gegenseitig anziehen.
Urknalltheorie
Das Universum ist aus einem Punkt hervorgegangen. Über den Zustand am
Anfang lässt sich nichts Genaues aussagen. Nach dem Urknall vor knapp
14 Milliarden Jahren dehnte sich das Universum aus und kühlte ab.
Galileo Galilei: 1564-1642
Johannes Kepler: 1571-1630
siehe Gravitationsgesetz
Markgräfin-Wilhelmine-Gymnasium Bayreuth
Newton'sche Mechanik
Grundwissen Physik Jahrgangsstufe 10 (G8)
Newton'sche Gesetze
Seite 2/8
Sir Isaac Newton: 1643-1727
1. Trägheitssatz:
Wenn auf einen Körper keine Kraft wirkt oder alle auf ihn wirkenden Kräfte im
Gleichgewicht sind, so bleibt er in Ruhe oder bewegt sich geradlinig mit
gleichbleibender Geschwindigkeit weiter.
2. Grundgleichung der Mechanik:
Wirkt auf einen Körper der Masse m die Kraft F, so erfährt er eine
ρ
ρ
Beschleunigung a in Richtung von F. Es gilt: F = m ⋅ a , ( F = m ⋅ a )
ρ
ρ
3. Wechselwirkungsgesetz: „actio gegengleich reactio“, F12 = − F21
ρ
Übt Körper 1 auf Körper 2 eine Kraft F12 aus, so übt Körper 2 auf Körper 1 die
ρ
Gegenkraft F21 aus, die gleichen Betrag hat und entgegengesetzt gerichtet ist.
Methode der kleinen
Schritte
Methode der kleinen Schritte
Bewegungen mit nicht konstanter Beschleunigung lassen sich schrittweise mit
der „Methode der kleinen Schritte“ berechnen.
Anmerkung: Für die genauen
Iterationsformeln gibt es leicht
Man unterteilt die Bewegung in hinreichend kleine Zeitabschnitte ∆t und
verschiedene Möglichkeiten, die alle
nimmt als Näherung an, dass in jedem einzelnen Zeitabschnitt die
ähnliche Ergebnisse liefern. Alle orientieren
Geschwindigkeit v und die Beschleunigung a konstant sind.
sich aber an den Formeln für Bewegungen
Sind die Werte für xalt, valt und aalt zu einem Zeitpunkt talt bekannt, so berechnet mit konstanter Beschleunigung (siehe
man aus diesen Daten die neuen Werte dieser Größen nach Verstreichen der Zeit Klasse 9).
∆t z.B. mit folgenden Iterationsformeln:
1. t neu = t alt + ∆t
2. aneu aus xalt, valt und tneu berechnen
Mögliche Alternative:
1. t neu = t alt + ∆t
3. v = v + a ⋅ ∆t
4. x = x + v ⋅ ∆t
neu
alt
neu
neu
alt
neu
2. vneu = valt + aalt ⋅ ∆t
aneu lässt sich dabei jeweils über die verschiedenen Gesetze für die Kräfte F mit
3. xneu = x alt + vneu ⋅ ∆t
F
D
berechnen. (Z.B. für die harmonische Schwingung a = − ⋅ x .)
a=
4. aneu aus xneu, vneu und tneu berechnen
m
m
Nun ist wiederholt man das Verfahren immer wieder.
Markgräfin-Wilhelmine-Gymnasium Bayreuth
Kreisbewegungen
Grundwissen Physik Jahrgangsstufe 10 (G8)
Kreisbewegungen
Bewegt sich ein Körper auf einer kreisförmigen Bahn, so spricht man von einer
Kreisbewegung.
Die Zeit für einen Umlauf auf der Kreisbahn heißt Umlaufdauer T. Die (Dreh-)
Frequenz f gibt an, wie viele Umläufe ein Körper pro Zeiteinheit ausführt. Es
1
gilt: f = .
T
Die Winkelgeschwindigkeit ω gibt an, welchen Mittelpunktswinkel ∆ϕ der
∆ϕ 2π
Körper pro Zeiteinheit zurücklegt. Es gilt: ω =
=
= 2π f .
T
∆t
Die Bahngeschwindigkeit v gibt an, welche Kreisbogenlänge der Körper pro
2π r
=ω ⋅r .
Zeiteinheit zurücklegt. Es gilt: v =
T
ρ
Die Zentripetalkraft Fz ist stets zum Zentrum der Kreisbewegung, also
senkrecht zur Bahngeschwindigkeit gerichtet und ist notwendig, um den Körper
gegen seine Trägheit auf eine Kreisbahn zu zwingen. Es gilt:
mv 2
Fz = m ⋅ a z = mω 2 r =
mit Fz = m ⋅ a z gilt für die
r
Zentripetalbeschleunigung: a z = ω 2 r =
Gravitationsgesetz
v2
r
Das Gravitationsgesetz
Zwei Körper mit den Massen m1 bzw. m2 üben im Abstand r der Mittelpunkte
der Körper gleich große, anziehende Gravitationskräfte aufeinander aus. Es gilt:
FG = G ⋅
m1 ⋅ m2
1
, also FG ~ 2 .
2
r
r
mit der Gravitationskonstante G = 6,673 ⋅ 10−11
N ⋅ m2
m3
−11
=
6
,
673
⋅
10
.
kg 2
kg ⋅ s 2
Seite 3/8
Markgräfin-Wilhelmine-Gymnasium Bayreuth
Schwingungsbewegungen
Grundwissen Physik Jahrgangsstufe 10 (G8)
Seite 4/8
Schwingungsbewegungen
Bewegungen, bei denen sich die Richtung immer wieder umkehrt und sich nach
gleichen Zeiten immer wiederholen (=periodische Bewegungen), nennt man
Schwingungen. Schwingungsfähige Systeme heißen Oszillatoren.
1
Für Schwingungsdauer (=Periodendauer) T und Frequenz f gilt: f = .
T
1
Einheit von f : 1 Hz (Hertz) = .
s
Schwingungen mit abnehmender Amplitude nennt man gedämpfte
Aufzeichnung einer Federschwingung
Schwingungen.
Bsp.: f = 3 Hz bedeutet, dass pro Sekunde
Harmonische Schwingung
drei Schwingungsperioden ablaufen.
Ist die beschleunigende Kraft proportional zur Auslenkung s, so entsteht eine
harmonische Schwingung, bei der das t-s-Diagramm eine Sinuskurve ist.
Bsp.: Federpendel: F = − D ⋅ s ,
also F ~ s .
Impuls als
Erhaltungsgröße
Impuls
Der Impuls p eines Körpers ist das Produkt aus seiner Masse m und seiner
Geschwindigkeit v: p = m ⋅ v .
ρ
ρ
Impuls und Geschwindigkeit sind gleichgerichtete Vektoren: p = m ⋅ v .
Wirkt auf einen Körper die konstante Kraft F in der Zeitspanne ∆t (Kraftstoß),
so gilt für die Impulsänderung ∆p = F ⋅ ∆t .
m
Einheit: [ p ] = 1 kg ⋅ = 1 N ⋅ s
s
Mit der Größe Impuls können vor allem Stoßvorgänge berechnet werden.
Impulserhaltungssatz: Die Summe der Impulse aller Körper in einem
abgeschlossenen System ist konstant.
Für die Impulse aufeinander stoßender Körper gilt:
Summe der Impulse vor dem Stoß = Summe der Impulse nach dem Stoß
12
m
s
ruhend
1 kg 1 kg
1 kg
1 kg
9
1 kg 1 kg
1 kg
vor
dem
Stoß
m
s
1 kg
nach
dem
Stoß
Markgräfin-Wilhelmine-Gymnasium Bayreuth
Grundwissen Physik Jahrgangsstufe 10 (G8)
Seite 5/8
Grenzen klassischer Physik
Spezielle
Relativitätstheorie
Spezielle Relativitätstheorie
Bezugssysteme, in denen der Trägheitssatz gilt, heißen Inertialsysteme (lat.
inertia = Trägheit). Alle Inertialsysteme sind gleichberechtigt, d.h. in ihnen
gelten die bekannten physikalischen Gesetze der Mechanik und Dynamik.
Bezugssysteme, die sich mit konstanter Geschwindigkeit zueinander
bewegen, sind Inertialsysteme.
Ein beschleunigtes Bezugssystem ist kein
Inertialsystem. Z.B. setzt sich eine Kiste auf
der Ladefläche eines LKWs beim Bremsen
nach vorne in Bewegung, obwohl keine
beschleunigende Kraft auf die Kiste wirkt.
D.h. der Trägheitssatz gilt im Bezugssystem
„bremsender LKW“ nicht.
* Konstanz der Lichtgeschwindigkeit
Einstein postulierte: Die Lichtgeschwindigkeit c im Vakuum ist unabhängig von Bestätigung durch Experiment von
der Bewegung der Lichtquelle und vom Inertialsystem, in dem sie gemessen Michelson und Morley
m
wird. Ihr Wert ist ungefähr 3,00 ⋅10 8 .
s
Bei hohen Geschwindigkeiten (ab etwa v ≥ 0,1c ) treten folgende Phänomene
spürbar in Erscheinung:
Bestätigung z.B. durch Atomuhren in
Langstreckenflugzeugen (obwohl sogar
langsamer 0,1c) (Zeitdilatation)
* Zeitdilatation (=Zeitdehnung)
Bestätigung z.B. durch längere
Eine bewegte Uhr geht gegenüber ruhenden Uhren langsamer.
Halbwertszeit von Myonen bei hoher
* Längenkontraktion (=Längenverkürzung)
Geschwindigkeit (Zeitdilatation bzw.
Streckenlängen in Bewegungsrichtung erscheinen für den ruhenden Längenkontraktion; je nach Bezugssystem)
Beobachter verkürzt.
Kausalität und Chaos
Kausalität und Chaos
Man unterscheidet verschiedenes physikalisches Verhalten eines Systems:
Bsp. zu 1.: Die Fallzeit beim freien Fall
1. In der klassischen Physik geht man davon aus, dass kleine Änderungen der einer Kugel hängt von der Fallhöhe und der
Anfangsbedingungen auch nur kleine Auswirkungen auf die weitere zeitliche Fallbeschleunigung (an einem Ort konstant)
Entwicklung eines Systems haben, kurz:
ab. Der Luftwiderstand spielt keine
messbare Rolle.
Ähnliche Ursachen haben ähnliche Wirkung (starke Kausalität).
2. Bei manchen Versuchen ist nicht vorhersagbar, was genau passiert, obwohl
die Anfangsbedingungen sich nur geringfügig unterscheiden. Dann gilt:
Bsp. zu 2.: Die Fallzeit beim freien Fall
Markgräfin-Wilhelmine-Gymnasium Bayreuth
Grundwissen Physik Jahrgangsstufe 10 (G8)
Gleiche Ursachen haben gleiche Wirkung, aber kleinste Abweichungen
können zu völlig anderen Folgen führen (schwache Kausalität).
Auch Vorgänge mit schwacher Kausalität unterliegen genauen physikalischen
Gesetzen, d.h. sind „deterministisch“. Allerdings treten in ihnen oft
Entscheidungssituationen auf, die zu völlig unterschiedlichen Ergebnissen
führen können. Die zeitliche Entwicklung solcher Systeme lässt sich deshalb
nicht vorhersagen. Man spricht von deterministischem Chaos.
Seite 6/8
eines Blattes Papier ist dagegen nicht
berechenbar! Die genaue Fallzeit hängt
enorm vom Luftwiderstand, von der Lage
des Blattes und anderen Bedingungen ab.
Kleine, kaum wahrnehmbare
Veränderungen der Bedingungen führen zu
anderen Ergebnissen.
Wellen und Quanten
Wellen
Eine Welle ist die räumliche Ausbreitung einer Störung oder eines Zustandes in
einem Medium.
Mechanische Wellen benötigen ein schwingungsfähiges Medium. Dazu sind
elastisch gekoppelte Teilchen nötig.
Longitudinalwelle (Längswelle):
Schwingungsrichtung parallel zur Ausbreitungsrichtung
z.B. Schallwellen, Druckwellen (mechanisch)
Transversalwelle (Querwelle):
Schwingungsrichtung senkrecht zur Ausbreitungsrichtung
z.B. Seilwelle, Wasserwelle (mechanisch); Licht (elektromagnetisch)
Wellen transportieren Energie, im Normalfall aber keine Materie. Die
schwingenden Teilchen einer mechanischen, reinen Welle schwingen um einen
festen Ort hin und her.
Bei einer periodischen Welle kennzeichnet …
… die Frequenz f (Einheit: 1 Hertz = 1 Hz = 1 s-1) die zeitliche Wiederholung
gleichartiger Zustände,
… die Wellenlänge λ ihren kleinsten räumlichen Abstand (= Abstand zwischen
benachbarten Wellenbergen),
… die Schwingungsdauer T die Zeitspanne, bis sich der Zustand eines
bestimmten Teilchens wiederholt.
Schwingt der Erreger harmonisch, so wird eine harmonische Welle erzeugt.
Harmonische Transversalwellen sind sinusförmig.
Die Ausbreitungsgeschwindigkeit einer harmonischen Welle beträgt c = λ f .
m
m
Bsp.: Schallgeschwindigkeit ≈ 340 , Lichtgeschwindigkeit ≈ 3 ⋅ 10 8
s
s
Momentaufnahmen einer
Longitudinalwelle:
Momentaufnahmen einer sinusförmigen
Transversalwelle:
Markgräfin-Wilhelmine-Gymnasium Bayreuth
Grundwissen Physik Jahrgangsstufe 10 (G8)
Seite 7/8
Beugung
Die Abweichung jeder Wellenfortpflanzung von der geradlinigen Ausbreitung
wird als Beugung bezeichnet.
Wenn Wellen beispielsweise auf ein begrenztes Hindernis treffen, verlaufen
dahinter Wellenfronten auch in Bereiche, die eigentlich vom Hindernis verdeckt
sind.
Wellen mit niedriger Frequenz (d.h. großer Wellenlänge) werden stärker
gebeugt als Wellen mit hoher Frequenz.
Beugung an Hindernis bzw. Spalt 2
Interferenz
Verschiedene Wellen gleicher Art breiten sich aus, ohne sich gegenseitig zu
stören (Superpositionsprinzip). Sie überlagern sich (Interferenz).
Bei Interferenz addieren sich die Auslenkungen der einzelnen Wellen. Es
entstehen Orte, wo sich die Wellen verstärken (konstruktive Interferenz), und
andere, wo sie sich schwächen oder gar auslöschen (destruktive Interferenz).
Beugung und Interferenz sind charakteristisch für Wellen!
Interferenz zweier
Kreiswellen
Interferenz am
Doppelspalt 2
Wellencharakter des Lichts Fällt Laserlicht auf einen Einfachspalt oder einen Doppelspalt, so treten
ähnliche Beugungsbilder auf, wie sie z. B. bei Wasserwellen beobachtet werden.
Offensichtlich verhält sich Licht beim Durchgang durch die Spalte wellenartig.
Diese Erscheinungen könne nur dann beobachtet werden, wenn die Hindernisse
und Öffnungen von der Größenordnung des Lichtes sind.
2
Teilchencharakter des
Lichts
Die Erscheinung, dass Licht aus einer Oberfläche Elektronen herauslösen kann,
wird als (äußerer) Fotoeffekt bezeichnet.
Erklärung des Fotoeffekts (Einstein, Nobelpreis 1921):
– Licht besteht aus einzelnen Energieportionen, den Photonen. Die Frequenz des
Lichts im Wellenmodell entspricht der Energie der Photonen im Teilchenmodell.
– Die Beleuchtungsstärke ist durch die Anzahl der Photonen bestimmt.
– Beim Fotoeffekt überträgt ein Photon seine Energie vollständig auf ein
Elektron. Erhält das Elektron dadurch genügend Energie, um das Metall
verlassen zu können, fließt Strom.
h⋅c
Photonenenergie: E Ph = h ⋅ f =
λ
λ: Wellenlänge des Lichts, f: Frequenz des Lichts, c: Lichtgeschwindigkeit,
h Planck-Konstante ( h = 6,63 ⋅10 −34 Js ).
Modellvorstellung zum Fotoeffekt: 1
Markgräfin-Wilhelmine-Gymnasium Bayreuth
Grundwissen Physik Jahrgangsstufe 10 (G8)
Wellencharakter von
Elektronen
Auch Elektronen verhalten sich unter gewissen Umständen wie Wellen
(Elektronenbeugungsröhre: Elektronenstrahl auf Kristallfolie) und erzeugen
Interferenzmuster. Die Wellenlänge der Elektronen ist umso kleiner, je
h
h
energiereicher sie sind: λ =
= (de-Broglie-Wellenlänge)
m⋅v p
(m: Masse, v: Geschwindigkeit, p: Impuls des Elektrons)
Quanten
Bei Quantenobjekten treten physikalische Größen in bestimmten Portionen
(gequantelt) auf. Quantenobjekte (wie Elektronen oder Photonen) besitzen
Teilchen- und Welleneigenschaften (Welle-Teilchen-Dualismus). Welche
gerade beobachtet wird, hängt vom Experiment ab.
Seite 8/8
Stichwort: Elektronenbeugung
– Eigenschaften von Quantenobjekten werden durch eine Messung nicht
festgestellt, sondern erst hergestellt.
– Treffen die Quanten auf einen Schirm, treten sie als kleine Punkte in
Erscheinung. Auf jeden Bereich des Schirmes treffen die Quanten mit einer
bestimmten Wahrscheinlichkeit. Die Helligkeit am Schirm ist ein Maß für die
Wahrscheinlichkeit dafür, dass ein bestimmtes Photon auftrifft.
Beispiel: Gehen Quanten durch einen
Doppelspalt, und werden in der
Doppelspaltebene die Aufenthaltsorte nicht
bestimmt, so haben sie dort die Eigenschaft
„Ort“ nicht.
Macht man eine Ortsbestimmung direkt an
den Spalten, so registriert man immer nur
ein ganzes Quant, entweder rechts oder
links; solche „untersuchten“ Quanten
erzeugen kein Interferenzbild mehr.
Stand: 09/2011
(Bilder selbst erstellt außer:
1
Wikimedia Commons
2
ISB-Handreichung Atome, Wellen, Quanten)