Elektronik 2. Lehrjahr, Version 2015
Werbung

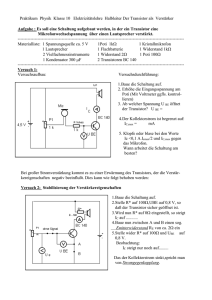
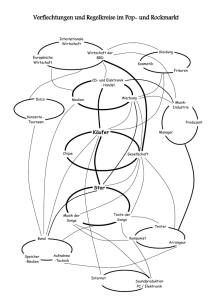
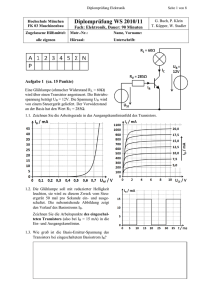
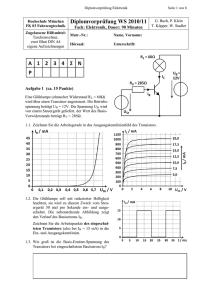
Elektronik für Elektroniker im 2. Lehrjahr von Alexander Wenk Quellen: Unterlagen von Urs-Peter Quitt Vogel Fachbücher Elektronik 1-3 Elektronik Unterlagen HTL Brugg-Windisch und weitere 2010, Alexander Wenk Inhaltsverzeichnis Der Bipolartransistor ______________________________________________________ 1 Laborübung NPN-Transistor __________________________________________________ 3 Erfassung von IB, UBE und IC _________________________________________________________ 4 Kennlinienfeld vom Transistor _________________________________________________ 5 Schlussfolgerung und Ersatzmodell _____________________________________________ 6 Der Transistor als Schalter ____________________________________________________ 8 Verlustleistung am Transistor__________________________________________________ 8 Feldeffekt-Transistoren ____________________________________________________ 9 Wo werden Feldeffekttransistoren eingesetzt _____________________________________ 9 Welche Eigenschaften haben Feldeffekttransistoren _______________________________ 9 Wie funktionieren Feldeffekttransistoren _______________________________________ 10 Messung der FET-Steuerkennlinien ____________________________________________ 11 Auswertung der FET-Kennlinien ____________________________________________________ 13 FET als Konstantstromquelle _________________________________________________ 14 Funktion der KO-Eingangsstufe _______________________________________________ 15 FET-Typen ________________________________________________________________ 16 Leistungsendstufen _______________________________________________________ 18 Darlington Schaltung ________________________________________________________ 18 Gegentaktverstärker ________________________________________________________ 18 Strom- und Spannungsquellen _____________________________________________ 19 Merkmale von Strom- und Spannungsquellen ___________________________________ 19 Versuche zur einfachen Strom- und Spannungquelle _____________________________ 20 Auswertung Strom- und Spannungsquellen _____________________________________ 21 Stromquelle _____________________________________________________________________ 21 Spannungsquelle _________________________________________________________________ 21 Lineare Spannungsregler und getaktete Schaltregler _____________________________ 22 Getakteter Schaltregler ____________________________________________________________ 23 Vergleich lineare und getaktete Spannungsquelle ________________________________________ 24 Kenndaten von Spannungsreglern _____________________________________________ 25 Bipolare Quellen ____________________________________________________________ 26 Bereichserweiterung von Festspannungsreglern__________________________________ 27 Interpretation von Anwendungsschaltungen_____________________________________ 28 Operationsverstärker _____________________________________________________ 31 Differenzverstärker _________________________________________________________ 32 Übung Differenzverstärker _________________________________________________________ 32 Messübung Operationsverstärker _____________________________________________ 33 Der ideale Operationsverstärker _____________________________________________________ 34 Der reale OP ____________________________________________________________________ 34 Der invertierende Verstärker _________________________________________________ 35 Der nichtinvertierende Verstärker _____________________________________________ 36 Leistungsendstufen mit OP als Vorverstärker ___________________________________ 38 Addierverstärker ___________________________________________________________ 39 Subtrahierverstärker ________________________________________________________ 40 Instrumentenverstärker _____________________________________________________ 41 Der Schmitt-Trigger_________________________________________________________ 42 Invertierender Schmitt-Trigger ______________________________________________________ Nicht invertierender Schmitt Trigger__________________________________________________ Nicht invertierender Schmitt-Trigger mit Offsetspannung _________________________________ Übung Schmitt-Trigger ____________________________________________________________ 42 43 44 45 Timer und Taktgeneratoren ________________________________________________ 46 Funktion vom Timerbaustein _________________________________________________ 46 Timerbaustein als Taktquelle _________________________________________________ 48 Der Bipolartransistor Wie können wir einen grossen Strom mit einem kleinen Strom steuern? 1948 entwickelten Forscher den ersten Transistor. Prinzipiell ist ein Transistor ein Dreischicht-Element: Zwei gleich dotierte Schichten werden durch eine sehr dünne, umgekehrt dotierte Schicht getrennt. Wir kennen entsprechend den Anfangsbuchstaben der Dotierungsart NPN- und PNP-Transistoren. Wie sind die Transistoren prinzipiell aufgebaut? Abbildung 1 erklärt die beiden Transistortypen: Abbildung 1: Transistoraufbau (Grundlagen der Elektronik S. 101) Wir sehen die drei Anschlüsse des Transistors: C = Kollektor B = Basis E = Emitter Die zwischen Emitter und Kollektor gezeichneten Dioden sind gegeneinander gerichtet. Wenn wir also nur diese Anschlüsse verwenden, kann nie ein Strom fliessen. Wenn ich die Basis-Emitter-Diode durch eine entsprechend gerichtete Spannung leitend mache, beginnt der Transistor zu leiten. Dass aber nicht nur ein Basis-Emitter Strom fliessen kann, sondern auch ein entsprechender Kollektor-Emitterstrom, vermag das Dioden-Ersatzschaltbild nicht zu veranschaulichen. Die Erklärung der Funktion finden wir nur, wenn wir die drei Schichten so zeichnen, wie sie in Tat und Wahrheit auch aussehen. Von der Diode her wissen wir, dass sich beim Kontakt zweier unterschiedlich dotierter Schichten Raumladungszonen aufbauen. Da die Basisschicht sehr dünn ist, erstreckt sich diese beim Transistor praktisch über die ganze Schicht. Um diesen Effekt besser zu verstehen, zeichnen wir den Aufbau einmal stark vergrössert: Elektronik Alexander Wenk Seite 1 Aufbau vom NPN-Transistor ohne angelegte Basis-Emitter-Spannung (Abbildung 2): C N B + + + + + - - - - - + + + + + P N Weil die freien Elektronen des N-Materials teilweise in das angrenzende P-Material diffundieren, wird das elektrische Gleichgewicht gestört, es bleiben etwas mehr (feste) positive Ladungen in der NSchicht als Elektronen vorhanden sind. Umgekehrt wird durch die eindiffundierten Elektronen die PSchicht negativ geladen. Das dadurch entstehende elektrische Feld verhindert, dass Elektronen direkt vom Emitter zum Kollektor gelangen können. Der Grund ist das elektrische Feld zwischen Emitter und Basis, das alle vom Emitter in die Raumladungszone eindringenden Elektronen zurückdrückt. E Abbildung 2: Transistor ohne Spannung In der Basiszone (P-Schicht) gibt es ausser den eindiffundierten Ladungen keine freien Elektronen, die zum Kollektor gelangen könnten. Es fliesst also kein Strom, selbst wenn wir eine Kollektor-Emitter-Spannung UCE anlegen würden. Nun legen wir eine Spannung UBE an. Dadurch wird die Raumladungszone zwischen Basis und Emitter aufgehoben wie Abbildung 3 zeigt: Nun fliesst zwischen Basis und C Emitter ein Strom, was die PZone mit Elektronen aus der NN Zone des Emitters überschwemmt. Diese Elektronen werden zum grossen Teil durch das elektrische Feld zwischen + + + + + Kollektor und Basis zum B - - - - - P Kollektor katapultiert. Voraussetzung dafür ist natürlich, dass auch eine KollektorEmitterspannung UCE vorhanden ist. N Es gelingt also mit einem relativ kleinen Strom direkt den grossen Kollektorstrom zu steuern. E Abbildung 3: Transistor mit angelegter Spannung Elektronik Alexander Wenk Seite 2 Nehmen wir den Basisstrom wieder weg, entsteht zwischen Basis und Emitter wieder die isolierende Raumladungszone. Der Stromfluss wird also wieder unterbrochen. Der PNP Transistor funktioniert ähnlich, nur ist alles umgekehrt polarisiert. Um Verwirrungen vorzubeugen, wollen wir darauf aber erst später wieder zu sprechen kommen. Vielleicht hilft uns zum prinzipiellen Verständnis vom Transistor noch eine weitere Grafik. Abbildung 4 zeigt uns den prinzipiellen Elektronenfluss am NPN-Transistor: Abbildung 4: Elektronenfluss im NPN Transistor (Grundlagen Elektronik S. 103) Wie werden die Ströme und Spannungen am Transistor bezeichnet? Abbildung 5 zeigt uns das Schaltzeichen und die dazu gehörenden genormten Bezeichnungen: Hierbei ist zu erwähnen, dass die gezeichnete Spannungsquelle mit UBE etwas irreführend ist. Da die BasisEmitter-Diode ja in Durchlassrichtung Abbildung 5: Bezeichnungen am Transistor ( Grundlagen Elektronik S.104) steht müssen wir den Basistrom mit einem Basiswiderstand begrenzen, damit der Transistor nicht zerstört wird. Laborübung NPN-Transistor Es ist nun an der Zeit, dass wir wichtige Kenngrössen am Transistor messtechnisch erfassen. Wir wollen die Kenndaten vom Transistor ausmessen, indem wir verschiedene Messungen durchführen und damit Kennlinien aufzeichnen. Am Schluss der Laborübung seid ihr im Besitz vom Kennlinienfeld Eures Transistors, den ihr selbst ausgemessen habt. Elektronik Alexander Wenk Seite 3 Erfassung von IB, UBE und IC Im Prinzip können wir den Transistor einfach ausmessen, indem wir eine Stromquelle an die Basis anhängen und damit einen definierten Eingangsstrom IB einspeisen Allerdings besitzen wir keine Stromquelle. Deshalb verwenden wir eine Spannungsquelle und einen genügend grossen Basiswiderstand (RB. = 10 k), so wie es Abbildung 6 zeigt. Wir verwenden die Schaltung aus Abbildung 6 für unsere Messung. A + Ic + Uein + + T1 IB RB + V A Uce UCE + V UBE Wir haben wahrscheinlich nicht 4 Messgeräte pro Arbeitsplatz zur Verfügung. Wir können deshalb auch Abbildung 6: Kennlinien-Messschaltung nur dort ein Multimeter einsetzen, wo wir gerade einen Effekt messen wollen. Mindestens 2 Geräte müsst ihr aber haben, um problemlos messen zu können. Anleitung: Baue die Schaltung auf mit RB = 10 k Fülle die Tabelle mit deinen Messergebnissen aus: UCE 10 V IB UBE IC 0 mA 10 V 1 mA 10 V 2 mA 10 V 5 mA 10 V 10 mA 10 V 20 mA 10 V 50 mA (nur kurz messen) Zeichne die Kennlinien grafisch auf: o Kennlinie 1: IC = f(IB) IB als X-Achse verwenden. o Kennlinie 2: IB = f(UBE) UBE als X-Achse verwenden. Wenn Du noch Zeit hast…: Lasse die Basisspannung konstant, und verändere die Spannung UCE. Beobachte dabei den Strom IC. Was stellst Du fest? Elektronik Alexander Wenk Seite 4 Kennlinienfeld vom Transistor In der Laborübung haben wir zwei Kennlinien vom Transistor ausgemessen. Aus diesen Kennlinien können wir uns ein vereinfachtes Modell für den Transistor entwickeln. Allerdings gibt es noch weitere Kennlinien, die wir für dieses Modell benötigen. Die wichtigsten sind IC = f(IB) und IC = f(UCE) und UB = f(IB) Weniger von Bedeutung ist die Rückwirkung vom Ausgang auf den Eingang (Abbildung 7). Lasst uns hier nochmals diese Kennlinien betrachten, diesmal in einer speziellen Darstellung: Abbildung 7: Kennlinienfeld vom Transistor (Bauelemente S. 173) Was könnten wir für Vereinfachungen aus unseren Kennlinienfeldern lesen? UBE ist konstant und beträgt etwa 0.7 V Der Verstärkungsfaktor ist konstant. Er beträgt = I C / IB IC ist fast unabhängig von UCE, sofern UCE > 1 V IC ist konstant (gesteuerte Stromquelle) Elektronik Alexander Wenk Seite 5 Wie gross ist der Stromverstärkungsfaktor bei deinem gemessenen Transistor? = IC / IB = 125; 145; 117; 120 … Wie gross ist RCE bei Deinem Transistor RCE = UCE/IC = … Schlussfolgerung und Ersatzmodell Der Transistor ist also ein Stromverstärker. Wenn wir ein erstes einfaches Modell für den Transistor entwickeln, berücksichtigen wir nur UBE und (Abbildung 8) C C + B B IC = IB UBE = 0.7 V E E Abbildung 8: Ersatzmodell für Transistor Interessant ist nun, dass wir mit dieser Ersatzschaltung einen Transistor relativ einfach mit uns bekannten Bauelementen beschreiben können! Übungen zu den Transistoren: Westermann S. 181 Nr. 1, 3, 4, 5. Elektronik Alexander Wenk Seite 6 Rc 1k Lasst uns die Transistor-Ersatzschaltung gerade einmal mit einer ersten Steuerschaltung testen. Erstelle unter Verwendung Deines ausgemessenen Transistors die dargestellte Schaltung, und messe sie aus. Zeichne dazu die Ein- Ausgangskennlinie Ua(Ue). Was für einen Faktor spielt hier eine sich ändernde Stromverstärkung? + RB 100k T1 BD 135 Ub 15 + + V Ua Ue 15 Ue 0V UCE = Ua 15 V 0.6 V 1V 2V 4V 6V 8V 10 V 12 V 0.14 V 14 V Wer noch Zeit hat: Simuliere die Schaltung und erstelle die EinAusgangskennlinie automatisch. Elektronik Alexander Wenk Seite 7 Der Transistor als Schalter Häufig werden Transistoren als Schalter eingesetzt. Wir können mit Transistoren LED's Relais oder sogar Motoren ansteuern. Ist der Transistor als Schalter eingesetzt, wollen wir möglichst kleine Verlustleistungen realisieren. Deshalb muss im ausgeschalteten Zustand der Strom 0 sein (logisch). Andererseits soll der Transistor im leitenden Zustand fast keinen Spannungsabfall bewirken, also in der Sättigung sein. Um dies zu erreichen, übersteuern wir den Transistor, wir geben ihm also einen höheren Basisstrom als eigentlich erforderlich wäre. Wir sprechen hier vom Übersteuerungsfaktor, der üblicherweise zwischen 2..10 liegt. Das Schema zum Schalten einer Ohmschen Last sieht folgendermassen aus: Übungen zum Thema: Westermann S. 241 Nr. 1-3, 7 Verlustleistung am Transistor Die Verlustleistung vom Transistor ist einfach zu berechnen. Die gesamte Verlustleistung ist die Leistung des Eingangskreises summiert mit der Leistung des Ausgangskreises: PV = PE + PA = UBEIB + UCEIC Die erzeugte Verlustleistung im Transistor bewirkt eine Erwärmung dieses Bauteils. Wenn wir nicht für genügend Kühlung sorgen, wird der Transistor durch zu starke Erwärmung zerstört! Übungen: Westermann S. 191 Nr. 2 Elektronik Alexander Wenk Seite 8 Feldeffekt-Transistoren In diesem Kapitel werden wir zunächst eine Anwendung vom Feldeffekttransistor betrachten. Dann werdet Ihr die theoretische Funktion vom FET kennen lernen. Schliesslich werdet Ihr die Kennlinie des neu eingeführten Bauteils Feldeffekttransistor aufnehmen. Wo werden Feldeffekttransistoren eingesetzt Das dargestellte Schema stellt die Eingangsstufe von einem KathodenstrahlOszilloskop (KO) dar. KO-Eingänge besitzen sehr hohe Innenwiderstände (1 M). Das muss also heissen, dass die eingesetzte Schaltung am Eingang sehr hochohmig ist. Welche Eigenschaften haben Feldeffekttransistoren Wir möchten unser neues Bauteil im Vergleich zu einer Transistorschaltung kennen lernen. Dazu nehmen wir eine LED-Ansteuerung, realisiert mit einem Bipolar- und mit einem Feldeffekt-Transistor: Feldeffekttransistor-Schaltung Bipolartransistor-Schaltung IB T2 BF245C + LED1 CQX35A + T1 BD135 Ub 5 + A Elektronik IG + A R1 220 + Ub 5 R1 220 R2 12k LED1 CQX35A SW1 SW2 Alexander Wenk UGS 5 Seite 9 Wie gross ist der Strom an den Eingängen der beiden LED-Ansteuerungen? Und was machen die LED's? Bipolartransistor-Schaltung SW1 offen: Feldeffekttransistor-Schaltung SW2 ist oben: LED ist dunkel IB = 0 LED leuchtet IG = 0 SW1 zu: SW2 ist unten: LED leuchtet IB ≠ 0 (302 A) LED ist dunkel IG = 0 Fazit: Mit einem Feldeffekttransistor können wir also einen Ausgang steuern, ohne dazu einen Eingangsstrom zu benötigen. Wie funktionieren Feldeffekttransistoren Im Gegensatz zum stromgesteuerten Bipolartransistor ist der Feldeffekttransistor, wie das Wort schon sagt, feldgesteuert. Dies gibt den grossen Vorteil, dass wir einen Strom leistungslos steuern können! Es muss also kein Steuerstrom durch den Eingang fliessen. Der einfachste Feldeffekttransistor ist der Sperrschicht-FET. Er wird auch JFET genannt (von Junction-FET). Schaltsymbol und Anschlüsse vom N-Kanal-JFET: D: Drain = (Elektronen)-Abfluss G: Gate = Tor (Steuereingang) S: Source = (Elektronen)-Quelle Funktionsbilder vom N-Kanal-JFET: D D N - + - + G P- + - + - + N G P N + - + - + - + - + N S S JFET ohne Spannungen Elektronik - JFET mit UDS Alexander Wenk Seite 10 D N - + - + G P- + - + - + N S JFET mit UGS (und UDS) Erkenntnisse aus den Funktionsbildern: Was isoliert den Gate-Eingang von der Drain-Source-Strecke? Die Sperrschicht vom PN-Übergang. Wie muss UGS gewählt werden, damit der N-Kanal-JFET sperrt? UGS muss genügend negativ sein. Was passiert, wenn UGS irrtümlich falsch polarisiert angelegt wird? Der PN-Übergang beginnt zu leiten. Vorsicht: Fehlfunktion, Zerstörung! Messung der FET-Steuerkennlinien Nachdem wir das Funktionsprinzip vom JFET verstehen, wollen wir einen realen JFET ausmessen. Die aus diesem Versuch ermittelten Daten werden wir für weitere Experimente benötigen. Es ist deshalb wichtig, dass die Nummer der verwendeten Platine notiert wird. Die wichtigste Kennlinie vom FET ist die Eingangskennlinie ID = f(UGS) Sie sagt aus wie gross der Drainstrom bei bestimmten Gate-SourceSpannungen ist. Ferner interessiert auch das Ausgangskennlinienfeld, weil ID auch von UDS abhängig ist. Elektronik Alexander Wenk Seite 11 Messanleitung: ID + A D + G T1 UD S + UGS + V UGS Rv 120 k UDS 10 V UGS 0 10 V -0.5 V 10 V -1.0 V 10 V -1.5 V 10 V -2.0 V 10 V -3.0 V 10 V -4.0 V 10 V S Notiere hier die Platinen-Nr:_______ (Damit Du für die nächsten Versuche denselben FET verwenden kannst) Baue nebenstehende Messschaltung auf. (Der Widerstand Rv dient hier nur zu Schutzzwecken). Bestimme bei verschiedenen Gatespannungen UGS den Drainstrom ID. Achtung: Beim N-Kanal-JFET muss UGS negativ sein. Führe Deine Messsungen gemäss der Tabelle aus und halte die Messergebnisse fest: ID 0 mA Zeichne die resultierende Kennlinie grafisch auf (ev. Excel-Darstellung): o ID = f(UGS) UGS als X-Achse verwenden. Wenn Du noch Zeit hast…: Nehme den Strom ID in Funktion von UDS auf für UGS = 0 V. Für grafische Aufzeichnung: UDS als X-Achse nehmen, ID als Y-Achse. Richte Dein Augenmerk vor allem auf kleine UDS. Achtung: UDS maximal 10 V wählen (wegen Verlustleistung des FET's) Nehme danach dieselbe Funktion für weitere UGS auf, die einen mittleren/kleinen Drainstrom ID bewirken. Eine gute Dokumentation erleichtert die Arbeit in den folgenden Versuchen Elektronik Alexander Wenk Seite 12 Auswertung der FET-Kennlinien Betrachten wir uns zuerst die Kennlinie ID = f(UGS): Sie zeigt quadratisches Verhalten. Es gilt ungefähr die Formel: Strom (A) 14.83m U I D I DSS 1 GS U p 7.42m 2 0.00 -3.00 -1.50 Eingangsspannung (V) 0.00 Bestimme zu dieser Formel die Parameter IDSS und UP für Deinen FET: Legende: ID: aktueller Drainstrom IDSS: Drain-SourceKurzschlussstrom (bei UGS = 0) UGS: aktuelle GateSourcespannung UP: Pinch-off-voltage; Abschnürspannung = UGS, wo ID = 0 wird. Die zweite FET-Kennlinie war ID = f(UDS): Strom (A) 14.83m An ihr sehen wir im Unterschied zum Bipolartransistor, dass bei UDS nahe von 0 V die Kennlinien verschiedene Steilheiten aufweisen, was darauf hindeutet, dass wir mit UGS tatsächlich den Widerstand der Drain-SourceStrecke verändern. 7.42m 0.00 0.00 5.00 Eingangsspannung (V) 10.00 Transistor Kennlinie IC = f(UCE): 150.00m Strom (A) 112.50m 75.00m 37.50m 0.00 0.00 2.50 Elektronik 5.00 7.50 Eingangsspannung (V) 10.00 Die Sättigungsspannung ist unabhängig von IC etwa gleich gross. Im Kleinsignalbereich sind die Kurven fast unabhängig der Ansteuerung deckungsgleich. Deshalb können wir beim Bipolartransistor nicht von einem veränderbaren (linearen) Widerstand sprechen. Alexander Wenk Seite 13 FET als Konstantstromquelle Wir haben in der Einleitung das Schema einer KO-Eingangsstufe betrachtet, wessen Funktion wir noch etwas näher betrachten wollen: Der untere FET im Schema hat zwischen Source und Gate nur ein Widerstand geschaltet. Der Strom im FET muss sich also so einstellen, dass die dem Strom zugehörige Gate-SourceSpannung sich einstellt. Dieser Teil der Schaltung ist also im Prinzip eine Konstantstromquelle. R1 150 RG 100k + Lasst uns die Vereinfachung dieses Schaltungsteils einmal realisieren: Berechne den Wert dieses Sourcewiderstandes R1, so dass ein mittlerer Drainstrom zu fliessen kommt. Verwende zur Lösung dieser Aufgabe die T1 BF245C VS2 15V Steuerkennlinie aus Deiner Messung. Baue die Schaltung auf derselben Laborplatine wie beim vorigen Versuch auf. Messe nach, ob Erwartungen und Messung übereinstimmen. Notizen: Elektronik Alexander Wenk Seite 14 Funktion der KO-Eingangsstufe Zur Einleitung hatten wir die Eingangsstufe eines KO's betrachtet. Zum Abschluss dieses Kapitels wollen wir nun die Frage lüften, was diese Stufe macht. Wir bedienen uns hier eines vereinfachten Modells der KOEingangsstufe. Aufgabe: Zeichne die Schaltung in Tina. C1 47u R1 7.13k Stelle UE auf 100 mV und 50 Hz + UE R2 332 + T1 BF245C VS1 12 UA + I Beobachte was der Ausgang UA sowie der Strom I in der Schaltung macht. R4 332 C2 47u R3 332 T1 BF245C VS2 12 Interpretiere die Funktion der Schaltung. Was macht der obere Teil, was der untere? Notizen: Elektronik Alexander Wenk Seite 15 FET-Typen Wir haben bis jetzt nur den JFET betrachtet. Bei diesem Typ wurde die Isolationsschicht vom Gate durch die Sperrschicht selber realisiert. Es gibt aber noch die grosse Gruppe der MOSFET's. Bei ihnen wird mit einem Oxyd das Gate vom Drain-Source-Kanal isoliert. Solange diese Isolationsschicht nicht zerstört wird, kann bei diesen Typen nie ein Gatestrom fliessen. Dies gilt allerdings nur bei Gleichspanung… Während die JFET's nur Verarmungstypen sind (Sperrschicht wächst mit zunehmender Sperrspannung) können wir mit MOS-Technik sowohl Verarmungs- und Anreicherungstypen realisieren. Folgende Übersicht zeigt die verschiedenen Feldeffekttransistoren: Elektronik Alexander Wenk Seite 16 Der kleine Sperrschicht FET, auch JFET genannt ist häufig als Hochfrequenzverstärker im Einsatz. Power MOSFETS dienen zum Schalten hoher Ströme und Spannungen. Mit ihnen können auch leistungsfähige Motoren angesteuert werden, oder wir können verlustarme Wechselrichter damit bauen. Während wir die prinzipielle Funktion vom JFET schon kennen, sind uns die MOSFET's neu. Die Schaubilder zeigen die Funktion: Beim Verarmungstyp kann durch positive Spannung der N-Kanal noch verbreitert werden, indem Elektronen in die N-Schicht hineingezogen werden. Durch negative Spannung können wir die Sperrschicht soweit verbreitern dass wie beim JFET irgendwann keine freien Elektronen mehr im Kanal vorhanden sind. Beim Anreicherungstyp sieht die Sache ähnlich aus. Nur haben wir bei UGS = 0 V gar keine freien Ladungsträger zwischen Drain und Source, respektive einer der PN-Übergänge sperrt wie eine Diode. Wenn wir nun ans Gate eine positive Spannung legen, verziehen wir quasi die Sperrzone soweit, dass sich Elektronen auf der ganzen Länge zwischen den beiden N-Schichten ansammeln und so ein leitender Kanal zwischen Source und Drain entsteht. Da wir umso mehr Ladungsträger in den Kanal ziehen, je höher die Spannung UGS ist, wird der FET immer besser leitend! Elektronik Alexander Wenk Seite 17 Leistungsendstufen In diesem Kapitel wollen wir einige Leistungsendstufen-Schaltungen betrachten. Darlington Schaltung Gerade Leistungstransistoren haben den Nachteil, dass sie nicht unwesentliche Eingangsströme benötigen, um durchgesteuert zu werden. Durch eine Serieschaltung von 2 Transistoren können wir diese entscheidend verkleinern Wie gross ist die Stromverstärkung dieser Stufe, wenn wir annehmen, beide Transistoren hätten das gleiche ? T1 BD135 T2 BD135 Gegentaktverstärker Elektronik-Schaltungen dienen eigentlich immer der Ansteuerung von irgendwelchen Aktoren (Motoren, Anzeigen, Antennen etc.) Für diese Anwendungen benötigen wir natürlich eine gewisse Leistung, die wir mit Leistungsendstufen erzeugen können. Eine sehr gute Endstufe ist die AB-Leistungsendstufe: Was für Aufgaben haben die beiden Transistoren? R2 1k IEnd U3 UA T7 !PNP R1 1k VG1 D1 1N1183 D2 1N1183 + T5 !NPN Der obere Transistor steuert die positive Halbwelle, der untere die negative. U4 Elektronik Wozu dienen die Dioden? Die Dioden kompensieren die BasisEmitter Spannungen der beiden Transistoren. Alexander Wenk Seite 18 Strom- und Spannungsquellen In diesem Kapitel behandeln wir die Spannungsversorgungen. Da ohne Quellen nichts geht, ist das ein ziemlich wichtiger Aspekt der Elektronik. Wir kennen beispielsweise schon den FET als Konstantstromquelle oder die Z-Diode als Spannungsstabilisator. Zunächst werden wir diese Erkenntnisse verknüpfen mit den grundsätzlichen Modellen der Strom- und Spannungsquellen. Wir werden auf lineare Spannungsregler wie auf getaktete Schaltnetzteile eingehen und einfache Schaltungen berechnen. Merkmale von Strom- und Spannungsquellen Prinzipiell können wir sagen, dass eine Spannungsquelle bei unterschiedlicher Belastung die Spannung möglichst konstant hält. Bei der Stromquelle wird die Stromstärke aufrechterhalten. Diese Ideale kommen in der Praxis natürlich nicht vor. In der Elektrotechnik habt Ihr die Ersatzschaltungen von Strom- und Spannungsquellen kennen gelernt: Reale Spannungsquelle: Reale Stromquelle: Elektronik Alexander Wenk Seite 19 Versuche zur einfachen Strom- und Spannungsquelle Messe zu folgenden Schaltungen das Spannungs- Stromdiagramm UL = f(IL)aus und bestimme daraus: Den Innenwiderstand der Quelle Die Leerlaufspannung Den Kurzschlussstrom Achtung: Bitte vor allem bei grösseren Strömen IL und UL jeweils nur kurz messen und den Stromkreis danach wieder unterbrechen, da sich sonst der Transistor erhitzt und sich die Messdaten dadurch verfälschen. R1 = 3.3k IL RL = z.B 100 UL + T1 BD135 RE = 47 R2 = 1k UB 15 Rv = 330 + SW1 Ue = 9V RL = 1k Z1 BZX79F5V6 Erstelle zu diesem Versuch einen Laborbericht! Elektronik Alexander Wenk Seite 20 Auswertung Strom- und Spannungsquellen Die Versuche haben gezeigt, dass die Schaltungen einen normalen, vorgesehenen Arbeitsbereich haben. Werden die Quellen überlastet, ergibt sich ein anderes Verhalten. Generell interessiert uns aber der vorgesehene Arbeitsbereich besonders. Auf diesen Bereich beziehen wir dann auch unsere Kennwerte. Interessant wäre insbesondere der Kurzschlussstrom resp. die Leerlaufspannung, wenn der Arbeitsbereich durch keine Überlastsymptome beschränkt würde. Stromquelle Die ausgemessene Stromquelle hat einen Kurzschlussstrom von ca. 50 mA gehabt. Dieser bleibt eigentlich fast konstant bis UL zu stark angestiegen ist. Dann beginnt der Strom rasch zu sinken. Im Konstantstrombereich ist Ri mehrere k gross. Theoretisch, also ohne Zusammenbruch, wäre die Leerlaufspannung: Spannungsquelle Die ausgemessene Spannungsquelle war nur mit einer Zenerdiode aufgebaut. Deshalb können wir von ihr auch keine allzu grosse Dynamik erwarten. Die Leerlaufspannung beträgt ca. 5.6 V. Die Spannung bleibt solange fast konstant, bis durch die Zenerdiode kein Strom mehr fliessen kann. Von diesem Zeitpunkt an wirkt die Schaltung wie ein Spannungsteiler, und die Spannung sinkt entsprechend. Der Kurzschlussstrom beträgt ca. 27 mA Im normalen Regelbereich hat die Spannungsquelle einen Innenwiderstand von 10 bis 30 . Theoretisch wäre der Kurzschlussstrom: Elektronik Alexander Wenk Seite 21 Lineare Spannungsregler und getaktete Schaltregler In diesem Kapitel widmen wir uns den zwei prinzipiellen Reglerarten. Beide haben Vor- und Nachteile, die wir hier kennen lernen wollen. Beginnen wir mit den linearen Spannungsreglern, wozu wir die Messschaltung von vorletzter Seite etwas ausbauen: Iglein Uc RL 1k Rvz 1k Z1 BZX55C5V6 C1 100u + GR 1 1N1183 Ue = 8V SW1 T1 BD 135 UL Vorgehen: Baue die Schaltung auf. Anstelle von Brückengleichrichter und Stützkondensator darf auch ein Netzteil mit 10 V DC verwendet werden. Messe nun in einem Bereich von IL = 0 bis 100 mA: o Den Eingangsstrom Iglein und die Eingangsspannung o Den Ausgangstrom IL und die Ausgangsspannung UL Wie gross ist der Innenwiderstand dieser Stabilisierungsschaltung? Bestimme aus diesen Daten den Wirkungsgrad des Spannungsreglers. (Wirkungsgrad in Funktion der Belastung) Beschreibe in Worten die Stabilisierungsfunktion der Schaltung. Wenn Du Zeit hast: Simuliere die Schaltung und versuche mit Tina/Multisim eine Wirkungsgradskurve aufzunehmen. Halte die Ergebnisse in einem Laborbericht fest! Elektronik Alexander Wenk Seite 22 Getakteter Schaltregler Nachdem wir einen linearen Spannungsregler ausgemessen haben, wollen wir nun einen Schaltregler untersuchen. Simuliere folgende Schaltung in Tina/Multisim: C1 100u R1 200 Ia D1 1N1183 Ie Ua + L1 50m Ue 10 T1 BD135 U1 UBE Stelle die Pulsquelle folgendermassen ein: Beobachte den zeitlichen Verlauf von Ie, Ia und Ua Bilde den zeitlichen Mittelwert dieser Strom- und Spannungswerte. Berechne aus den gemittelten Werten die Ein- und Ausgangsleistung des Schaltreglers und bestimme den Wirkungsgrad der Schaltung. Vergleiche die Schaltungseigenschaften mit dem linearen Spannungsregler von voriger Seite und nenne daraus einige Vor- und Nachteile des getakteten Schaltreglers. Elektronik Alexander Wenk Seite 23 Vergleich lineare und getaktete Spannungsquelle Der lineare Spannungsregler hat ungefähr denselben Eingangs- und Ausgangsstrom. Vom Prinzip her wird der Längstransistor wie ein regelbarer Widerstand eingesetzt um den Ausgang zu stabilisieren. Das bedeutet entsprechende Wärmeverluste, die einen schlechten Wirkungsgrad bedeuten, wie das Ausmessen vom linearen Spannungsregler bestätigt: Wirkungsgrad 50% 45% 40% Wirkungsgrad 35% 30% 25% 20% 15% 10% 5% 0% 0 100 200 300 400 500 600 I [mA] Beim Schaltregler ist das anders: Der Transistor sperrt entweder oder wird voll 24.69m durchgesteuert. Von dem her Ia sind hier geringe Verluste zu 24.37m erwarten. Wenn wir die Ein51.56m und Ausgangswerte vom Ie Schaltregler betrachten, können -7.45m 974.15m wir die Ein- und UBE Ausgangsleistung und damit 0.00 den Wirkungsgrad bestimmen. 4.94 Ua 4.87 0.100 0.101 Zeit (s) 0.102 Mittelwerte Ua 4.90594365 Pa = 0.12035357 W Pe = Wirkungsgrad Ia 0.024532196 Ie Ue 0.01479105 10 0.14791052 W 81% Schaltregler haben bessere Wirkungsgrade als lineare Spannungsregler, dafür haben sie aber auch geringe hochfrequente Wechselspannungsanteile überlagert. Elektronik Alexander Wenk Seite 24 Kenndaten von Spannungsreglern Im Datenblatt vom LM7812 sind folgende Kenndaten zu finden: Es sind hier Begriffe zu finden, die vielleicht nicht auf den ersten Blick verständlich sind. Eine Hilfe bei der Interpretation bieten die Einheiten der Werte, aber auch die Bedingungen (Conditions) Hier sind die wichtigsten Daten umschrieben (in Englisch): Line regulation is the capability to maintain a constant output voltage level on the output channel of a power supply despite changes to the input voltage level. Line regulation is expressed as percent of change in the output voltage relative to the change in the input line voltage Uaus=f(Uein) resp. Stromquelle Iaus=f(Uein) Load regulation is the capability to maintain a constant voltage (or current) level on the output channel of a power supply despite changes in load Uaus=f(Iaus) dropout voltage (minimaler Spannungsabfall) of a voltage regulator is the smallest possible difference between the input voltage and output voltage to remain inside the regulator's intended operating range. Ud = Uein - Uaus Elektronik Alexander Wenk Seite 25 Bipolare Quellen Für elektronische Schaltungen werden häufig bipolare Spannungsversorgungen benötigt, so z.B. 15 V. Um solche Spannungen gegenüber 0 V zu realisieren benötigen wir positive und negative Spannungsregler: U1 LM7815C IN OUT + VS1 20 VS1 20 GND IN RL- 1k + RL+ 1k GND OUT U2 LM7915C Leider funktioniert die Sache mit dem negativen Regler im Tina 6 nicht, weshalb wir zur bipolaren Stromversorgung auch keine Simulation machen können… Aber ev. geht das im Multisim??? Deshalb simulieren wir zur Übung nur den oberen Teil der Schaltung: Realisiere die Schaltung mit dem LM7815C (Tab Spice Makro) und mache Kennlinien für: Line Regulation Load Regulation Wie hoch ist die Dropout Voltage? Wie gross ist der Innenwiderstand dieses Reglers Wie hoch ist der Kurzschlussstrom? Elektronik Alexander Wenk Seite 26 Bereichserweiterung von Festspannungsreglern Durch einen Trick kann ich beispielsweise einen 5 V Festspannungsregler auch verwenden um eine andere (höhere) Ausgangsspannung zu realisieren: Ich hänge den Groundanschluss nicht an Ground sondern an einen Spannungsteiler. Wie hoch ist die Ausgangsspannung der gezeigten Schaltung? U1 LM7805C IN OUT Ue 20 Ireg R1 1k + GND UR 1 + UL R2 1k V Unter der Voraussetzung Ireg = 0 A können wir diese Ausgangsspannung einfach berechnen: Elektronik Alexander Wenk Seite 27 Interpretation von Anwendungsschaltungen Gegeben ist folgende Stabilisierungsschaltung: Fragen: Welcher Transistor arbeitet als Stellglied und welcher als Regler? Wie wird die Ausgangsspannung UA bei Laständerungen konstant gehalten? T1 = Regler, T2 = Stellglied Bei Belastung der Quelle sinkt die Ausgangsspannung. Damit sinkt auch UR3, wobei IB1 sinkt. Deshalb sinkt der Strom IC1, IB2 steigt deshalb und T2 leitet etwas besser, womit die Ausgangsspannung wieder auf den Sollwert ansteigt. Elektronik Alexander Wenk Seite 28 Elektronik Alexander Wenk Seite 29 Elektronik Alexander Wenk Seite 30 Operationsverstärker Wir haben Transistoren für Verstärkungsschaltungen gebraucht. Wir haben dort bereits gesehen, dass wir mit einer Stabilisierung des Arbeitspunktes, d.h. einer Rückkopplung ein lineareres Verhalten vom Verstärker hinkriegen. Allerdings war die Verstärkung unserer Schaltungen doch eher gering. Wie wäre es, wenn wir einen Baustein mit fast unendlich hoher Verstärkung haben, den wir dann auf den gewünschten Verstärkungsfaktor zähmen? Diese Bausteine heissen Operationsverstärker: Operationsverstärker haben eine invertierenden und einen nicht invertierenden Eingang. Sie bilden die Differenz dieser Eingangssignale und verstärken anschliessend diese Differenz. Die Ausgangsspannung rechnet sich mit folgender Formel: Bevor wir Operationsverstärker als Bauteile einsetzen, wollen wir betrachten wie die Eingangsstufe eines Operationsverstärkers aussieht. Elektronik Alexander Wenk Seite 31 Differenzverstärker Eine weitere wichtige Grundschaltung ist der Differenzverstärker. Er verstärkt die Differenz zweier Spannungen, wie schon das Wort verrät. Doch wie genau funktioniert diese Schaltung? Am besten analysieren wir die Schaltung in 2 Schritten: Indem wir U2 = U1 setzen, untersuchen wir die sogenannte Gleichtaktverstärkung. Ua1 Rc2 10k Rc1 10k Ub Ua2 T2 !NPN + + T1 !NPN U1 Re 10k U2 -Ub Wenn wir U2 = -U1 setzen, beobachten wir die Differenzverstärkung. Übung Differenzverstärker Baue einen Differenzverstärker gemäss obigem Schema und messe für diesen die Gleichtaktverstärkung mit U1 = U2 = 100 mV die Gegentaktverstärkung mit U1 = -U2 = 10 mV (Sinus mit 180° Phasenverschiebung) VGleichtakt = Ua2 / U2 = klein (0.5) VGegentakt = Ua2 / U2 = gross (261) Elektronik Alexander Wenk Seite 32 Messübung Operationsverstärker Wir wollen nun einen Operationsverstärker gemäss Schema ausmessen: Stelle einige Spannungen U1 ein und messe am Ausgang. Welche Werte messe ich? Und wann ändern sie? Wie gross ist der Eingangsstrom in den OP? Theoretisch 0, praktisch 70 nA (gemessen) Wie erreiche ich, dass der OP bei U1 = 5 V schaltet? Wie gross ist der Ausgangswiderstand vom OP? Im Bereich von 100 Elektronik Alexander Wenk Seite 33 Der ideale Operationsverstärker Ausgehend von unserem Experiment können wir den idealen OP definieren: Die Verstärkung vom OP ist unendlich gross: Folgerung: Sobald wir eine Eingangsspannungsdifferenz haben, geht der Verstärker in die positive oder negative Sättigung. Der Eingangswiderstand vom OP ist unendlich gross: Er nimmt durch die Eingänge keinen Strom auf. Der OP verstärkt nur die Differenz der Eingangssignale. Setze ich U1 = U2 = Ue und variiere diese Spannung, so hat das keinen Einfluss auf den Ausgang Ua: Der Ausgangswiderstand vom OP ist 0: Er kann jede Last treiben. Der reale OP Selbstverständlich gib es solch ideale Bedingungen gar nicht. Jeder OP hat Fehler, es kommt eigentlich nur auf die Betriebsart an, ob diese einen Einfluss haben oder nicht. Betrachten wir einmal, was beim OP alles schief gehen kann: Die Verstärkung vom OP ist endlich, typischerweise 100'000. Die Verstärkung nimmt zudem mit steigender Frequenz ab. Der OP verstärkt nicht nur die Differenz der Eingangssignale. Er ist also nicht nur ein Differenzverstärker. Wenn wir U1 = U2 = Ue setzen und diese Spannung variieren so stellen wir am Ausgang eine Veränderung fest. Wir sprechen von der Gleichtaktverstärkung. Allerdings ist die Gleichtaktverstärkung bei einem OP klein, typischerweise viel kleiner als 1. Wir konnten diesen Effekt beim Differenzverstärker mit Transistoren beobachten. Der Eingangswiderstand ist nicht ganz unendlich. Der Ausgangswiderstand vom OP ist nicht 0: Er liefert in der Regel nur einige mA. Zudem ist er kurzschlussgeschützt, d.h. er besitzt meist eine Strombegrenzung. Die Ausgangskennlinie ist also gekrümmt: Elektronik Alexander Wenk Seite 34 Der invertierende Verstärker Um den OP auch anwenden zu können, wollen wir damit eine erste Verstärkerschaltung aufbauen. Die einfachste Schaltung ist der invertierende Verstärker. Bei ihm wird der Minuseingang vom Eingangssignal beeinflusst, der Pluseingang an Masse gelegt. Es muss uns nun gelingen, die unendlich hohe Verstärkung durch eine Widerstandsbeschaltung zu bändigen. Wir müssen also eine Rückkopplung erstellen. Zeichne dazu eine mögliche Schaltung und analysiere sie: Wie gross wird die Verstärkung dieser Schaltung? Wie gross ist der Eingangswiderstand? Und wie gross der Ausgangswiderstand? Versuch: Dimensioniere einen invertierenden Verstärker mit v = 100. Baue die Schaltung auf. Gebe eine Wechselspannung ein und messe die Ausgangsspannung. Variiere die Frequenz zwischen 100 Hz und 100 kHz. Wo beginnt sich die Ausgangskurve zu verformen(Notiere jeweils die Frequenz)? Messe die Verstärkung v=Uaus/Uein und schreibe v=f(fsignal) in tabellarischer Form auf. Lasse in Excel eine Grafik ausgeben, am Besten in doppelt logarithmischer Darstellungsart. Zusatz: Baue den Verstärker um auf v = 10. Variiere die Frequenz auch wieder im selben Bereich und notiere wie oben das Frequenzverhalten. Übungen: Westermann S. 220 Nr. 1 – 6 Elektronik Alexander Wenk Seite 35 Ergebnisse Laborversuch invertierender Verstärker Der Frequenzgang vom nicht invertierenden Verstärker zeigt frequenzabhängigkeit der Verstärkung. Die Schaltung hat Tiefpasscharakter. Je höher der Verstärkungsfaktor gewählt wird, desto niedriger ist die Frequenz, wo die Verstärkung einzubrechen beginnt. Bei sehr hohen Frequenzen treffen die Linien zusammen (besonders gut in der doppelt logarithmischen Darstellung ersichtlich). 60.00 Verstärkung (dB) 50.00 Die Verstärkung beginnt einzubrechen bei v = 1000 40.00 Verstärkung 1000 100 10 v = 100 30.00 20.00 Frequenz 400 Hz 4 kHz 40 kHz v = 10 10.00 Wir erkennen: 0.00 vf=GBWP =const v= 1 -10.00 10 100 1k 10k Frequenz (Hz) 100k 1M (Gain bandwidth product) Auf dem Oszilloskop sehen die Ein- und Ausgangsspannung bei einem Verstärkungsfaktor v=100 wie folgt aus: 50.00m 50.00m Ue VG1 -50.00m 5.00 -50.00m 5.00 Ua VM1 -5.00 -5.00 0.00 0.00 10.00m Zeit (s) Bei 100 Hz stimmt der Verstärkungsfaktor mit der Erwartung überein. Elektronik 20.00m 100.00u Zeit (s) 200.00u Bei 10 kHz hat die Ausgangsspannung gegenüber der Erwartung bereits deutlich abgenommen. Der Verstärkungsfaktor ist kleiner geworden Alexander Wenk Seite 36 Der nichtinvertierende Verstärker Beim invertierenden Verstärker legten wir den Pluseingang an Masse und steuerten nur den Minuseingang an. Deshalb wurde das Eingangssignal invertiert: Eine Erhöhung der Eingangsspannung bewirkt eine Absenkung des Ausgangspegels. Beim nichtinvertierenden Verstärker steuern wir den Pluseingang an, weshalb das Signal nicht invertiert wird. Allerdings müssen wir auch hier die sehr grosse Verstärkung vom Op auf einen vernünftigen Wert dämpfen, was mit folgender Schaltung geschieht: Eingangswiderstand: Laborversuch: Baue einen nicht-invertierenden Verstärker mit der Verstärkung v = 1 und v = 10 und v = 100. Teste diese Verstärker ebenfalls in einem Frequenzbereich von 100 Hz bis 100 kHz aus (wie beim Versuch vom invertierenden Verstärker!) Abgeben: Versuchsergebnisse vom Inv- oder nicht Inv Verstärker Übungen: Westermann S. 221 Nr. 1 – 3, 6 Elektronik Alexander Wenk Seite 37 Leistungsendstufen mit OP als Vorverstärker Unser OP-IC kann nur einen Ausgangsstrom von maximal 25 mA liefern. Wie können wir einen stärkeren Strom erzeugen? Wir wollen eine solche Endstufe einmal selber entwickeln. Versucht eine Leistungsendstufe so mit einem OP zu koppeln, dass die Verstärkung trotzdem linear ist, aber die Stromstärke am Ausgang mindestens 100 mA betragen kann. Nach einer Kontrolle können wir die Schaltung in Tina austesten und allenfalls korrigieren. Elektronik Alexander Wenk Seite 38 Addierverstärker Der Operationsverstärker hat seinen Namen nicht zuletzt wegen der Tatsache, dass er auch Rechenoperationen ausführen kann. Er kann einerseits verschiedene Eingangsspannungen addieren, aber auch subtrahieren, wie wir später sehen werden. Der Addier- resp. Summierverstärker ist wie folgt aufgebaut: Wie wir bereits wissen, ist beim invertierenden Verstärker der invertierende Eingang stets auf Massepotenzial, solange der Verstärker nicht in Sättigung ist. Deshalb können wir die einzelnen Eingangsströme einfach berechnen. Der Strom im Rückkopplungswiderstand muss nun all diese Eingangsströme abführen können, womit wir eine Formel für die Ausgangsspannung aufstellen können: Zur Übung: Westermann S 222 Nr. 1, 2, 6 Elektronik Alexander Wenk Seite 39 Subtrahierverstärker Etwas schwieriger wird es, wenn wir die Differenz von zwei Spannungssignalen bestimmen wollen. Dazu wird folgende Schaltung eingesetzt: Berechnung der Ausgangsspannung: Zur Übung: Westermann S 223 Nr. 1 - 4 Elektronik Alexander Wenk Seite 40 Instrumentenverstärker Der Subtrahierverstärker hat den Nachteil von nicht sehr hohen Eingangswiderständen. Wenn wir aber ohne Verfälschungen vom Messignal eine Spannungsdifferenz ermitteln wollen, benötigen wir einen Instrumentenverstärker. Prinzipiell könnten wir den hohen Eingangswidertand auch mit nichtinvertierenden Verstärkern am Eingang realisieren. Es wurde aber eine ausgeklügelte Schaltung entwickelt, die wir nun analysieren wollen. Dieser Instrumentenverstärker zeichnet sich also nicht nur durch den sehr hohen Eingangswiderstand aus. Schön ist auch, dass sich die Verstärkung der Schaltung durch einen einzigen Widerstand variieren lässt. Einsatzgebiet: 4 Leiter Widerstandsmessung, Messignalverstärker etc. Elektronik Alexander Wenk Seite 41 Der Schmitt-Trigger Im Gegensatz zu den bisherigen Schaltungen, wo wir auf Linearität achteten, geht der OP-Ausgang bei Trigger-Anwendungen immer in die positive oder negative Sättigung. Trigger können also nur ein- und ausschalten. Der Komparator wäre eigentlich auch ein Trigger. Was für ein Problem bereitet aber der normale Komparator? Wenn der Komparator-Eingang gleich der Schwellspannung ist, reicht ein sehr kleines Störsignal, dass der Komparator dauernd hin- und herschaltet. Dieses Problem können wir mit dem Schmitt-Trigger lösen. Der Trick dabei ist, dass wir den Operationsverstärker so beschalten, dass eine Mitkopplung entsteht. Wenn wir mit der Eingangsspannung die Schaltspannung überschreiten, wechselt der OP seinen Ausgangszustand. Durch die Mitkopplung wird die Spannungsdifferenz an den OP-Eingängen vergrössert, der neue Ausgangszustand wird so stabilisiert. Um den Trigger wieder auszuschalten, muss die Eingangsspannung wesentlich unter die Einschaltspannung sinken. UA Die Differenz zwischen der Ein- und Ausschaltspannung nennen wir auch Hysteresespannung. UH. UE Wenn wir Eingangs- und Ausganspannung vom Trigger grafisch darstellen, sieht das in etwa so aus: Wir werden nun einige Trigger Schaltungen kennen lernen und miteinander die Berechnungsgrundlagen erarbeiten. Invertierender Schmitt-Trigger Die Invertierung erhalten wir, indem wir das Eingangssignal dem Minuseingang zuführen. Wir müssen nun noch eine Mitkopplung realisieren anstelle der Gegenkopplung beim Verstärker, und der erste Trigger wäre erfunden. 15.00 12.50 OSC1 10.00 7.50 + OP1 !OPAMP Ue + + R2 4.7k + - R1 1k Ub+ + + Ch1 - + Ch2 - Spannung (V) Ub- 5.00 2.50 0.00 -2.50 -5.00 -7.50 -10.00 -12.50 -15.00 0.00 Elektronik Alexander Wenk 25.00m Zeit (s) 50.00m Seite 42 Bei dieser Schaltung können wir nicht mehr davon ausgehen, dass der Plusund Minuseingang jederzeit dieselbe Spannung haben, denn der Operationsverstärker wird ja dauernd in der Sättigung betrieben. Zur Berechnung der Schaltspannung können wir aber aussagen, dass die kritische Spannung dann erreicht wird, wenn beide OP-Eingänge dieselbe Spannung haben, womit wir die Schaltspannungen berechnen können: Nicht invertierender Schmitt Trigger Der Nicht-invertierende Schmittrigger kann mit folgender Schaltung realisiert werden: 15.00 12.50 OSC1 10.00 + 7.50 + Ch1 - R1 1k + + + Ue OP1 !OPAMP Ub+ + + Ch2 - Spannung (V) UbR2 4.7k 5.00 2.50 0.00 -2.50 -5.00 -7.50 -10.00 -12.50 -15.00 0.00 25.00m Zeit (s) 50.00m Die Berechnung der Schaltung geht wieder über die Bestimmung der Schaltspannungen, wobei dazu der positive und negative Eingang dieselbe Spannung haben müssen: Elektronik Alexander Wenk Seite 43 Nicht invertierender Schmitt-Trigger mit Offsetspannung Bis jetzt hatten wir die Schaltspannung symmetrisch um den Nullpunkt angeordnet. In der Praxis möchten wir aber vielleicht einen Trigger, der bei frei definierbaren Eingangsspannungen schaltet, also z.B. bei +5V ein und bei -1V wieder aus. Eine solche Schaltung erhalten wir durch eine kleine Modifikation des Nicht-Invertierenden Triggers von oben: OSC1 15.00 U + b- 12.50 10.00 R2 4.7k R1 1k + + Ue + + OP1 !OPAMP + Ub+ Uofs 1.5V + Ch2 - 7.50 Spannung (V) + Ch1 - 5.00 2.50 0.00 -2.50 -5.00 -7.50 -10.00 -12.50 -15.00 0.00 25.00m Zeit (s) 50.00m Die Berechnung dieses Triggers gestaltet sich schon echt spannend. Versucht einmal, die Gleichung für die Schwellspannungen herzuleiten. Wir werden die Formel anschliessend noch etwas genauer analysieren, um herauszufinden, wie wir uns die Schaltung den Bedürfnissen entsprechend skalieren können. Interessant ist die Tatsache, dass die Hysteresespannung genau gleich gross ist wie beim normalen nichtinvertierenden Schmitt-Trigger. Daraus gelingt es uns, die Werte für R1, R2 und Uofs aus den vorgegebenen Schwellspannungen zu ermitteln: Elektronik Alexander Wenk Seite 44 Übung Schmitt-Trigger 1. Löse folgende Aufgaben aus dem Westermann-Rechenbuch: S. 224 Nr. 1 - 4 2. Ein Operationsverstärker hat eine Sättigungsspannung von 13.5 V. Wir möchten eine Ladezustandskontrolle für einen 6 V Akku mit diesem OP realisieren. Konstruiere einen nichtinvertierenden Trigger, der bei 7.2 V ein und bei 6.4 V wieder ausschaltet. (Tip: Berechne Verhältnis R1/R2 und Uofs 3. Entwickle vom invertierenden Trigger ausgehend eine Schaltung eines invertierenden Schmitt-Triggers mit skalierbarer Offsetspannung, bestehend aus nur einem OP, und suche die Formeln zur Berechnung der Schwellspannungen. Elektronik Alexander Wenk Seite 45 Timer und Taktgeneratoren In elektronischen Schaltungen werden häufig Timer oder Taktgeneratoren irgendwelcher Art gebraucht Für die Realisation von sequentieller Logik wird meist irgendein Clock benötigt. Und konventionelle Elektronik braucht beispielsweise für Schaltnetzteile ein Takt- oder PWM-signal, um verlustarm Spannungen zu konvertieren. In diesem Kapitel wollen wir den Timer 555 genauer kennenlernen und damit verschiedene Timer- und Taktanwendungen ausprobieren. Funktion vom Timerbaustein Der Timer 555 gibt es heute sowohl in bipolarer wie auch in low power CMOS Bauweise. Das Blockdiagramm zeigt die prinzipielle Funktion dieses Bausteins. Der Timer besteht aus zwei Komparatoren und einem nachgeschalteten Flipflop. Die beiden Komparatoren haben folgende Funktion Der obere Komparator setzt das Flipflop zurück (Out = 0), sobald der Threshold Eingang höher als die Control-Voltage wird. Ohne Beschaltung der Control-Voltage ist das der Fall bei 2/3 VCC. Der untere Komparator setzt das Flipflop (Out = 1), sobald der Trigger Eingang kleiner als 1/3 VCC wird. Zusätzlich hat der Baustein noch ein Reset-Eingang, um einen geordneten Timerstart durchführen zu können. Als Ausgang haben wir nebst dem regulären Out noch den Discharge-Pin, um typischerweise den Elektronik Alexander Wenk Seite 46 Ladekondensator wieder zu entladen, der in den Anwendungsschaltungen benötigt wird. Aufgabe zur Funktionsanalyse des Timerbausteins: Baue eine Schaltung in Tina auf um auszutesten, wann der Timer Ein- und ausschaltet. Die Anwendungsschaltungen werden üblicherweise mit RC-Schaltungen aufgebaut. Finde eine Formel um herauszufinden, wie lange es dauert bis der Kondensator von einer Ausgangsspannung UC0 = 1/3 U0 auf 2/3 U0 aufgeladen wird. t = 0.693RC Suche ein Datenblatt zum Timer 555 auf dem Internet, das möglichst informativ ist. www.Alldatasheet.com ist eine gute Suchmöglichkeit, um Datenblätter verschiedener Hersteller zu vergleichen. Elektronik Alexander Wenk Seite 47 Timerbaustein als Taktquelle Wenn wir einen Taktgenerator benötigen, hilft uns folgende Anwendungsschaltung: Die Berechnung der Taktfrequenz leitet sich aus der Berechnung von voriger Seite ab: f = 1.44/[(RA + 2 RB)C] (Die Formel auf dem abgedruckten Schema ist falsch…) Übung Simuliere obige Schaltung in Tina mit sinnvoll gewählten Komponenten, so dass sie eine Frequenz f = 1 kHz generiert. Simuliere nach Lust und Laune eine weitere Anwendungsschaltung aus Deinem Datenblatt zum Timer. Elektronik Alexander Wenk Seite 48