PDF_4

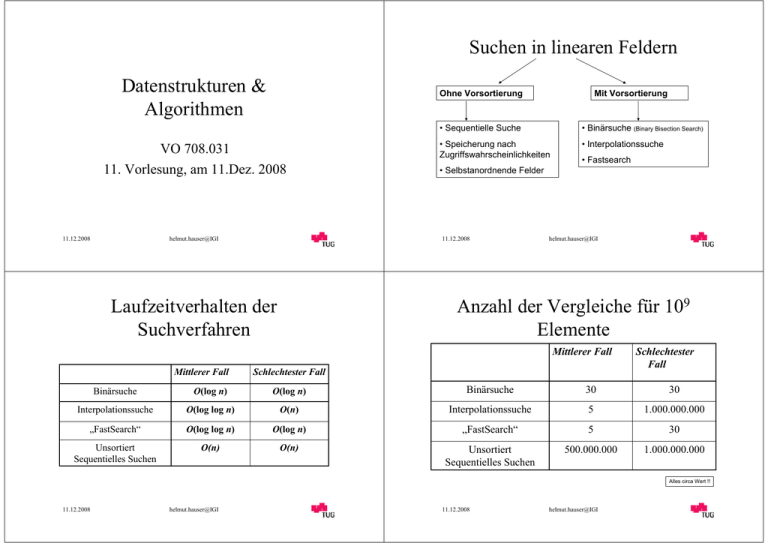
Suchen in linearen Feldern
Datenstrukturen &
Algorithmen
Ohne Vorsortierung
VO 708.031
11. Vorlesung, am 11.Dez. 2008
11.12.2008
helmut.hauser@IGI
• Sequentielle Suche
• Binärsuche (Binary Bisection Search)
• Speicherung nach
Zugriffswahrscheinlichkeiten
• Interpolationssuche
• Fastsearch
• Selbstanordnende Felder
11.12.2008
Laufzeitverhalten der
Suchverfahren
Mit Vorsortierung
helmut.hauser@IGI
Anzahl der Vergleiche für 109
Elemente
Mittlerer Fall
Mittlerer Fall
Schlechtester Fall
Schlechtester
Fall
Binärsuche
O(log n)
O(log n)
Binärsuche
30
30
Interpolationssuche
O(log log n)
O(n)
Interpolationssuche
5
1.000.000.000
„FastSearch“
O(log log n)
O(log n)
„FastSearch“
5
30
Unsortiert
Sequentielles Suchen
O(n)
O(n)
Unsortiert
Sequentielles Suchen
500.000.000
1.000.000.000
Alles circa Wert !!
11.12.2008
helmut.hauser@IGI
11.12.2008
helmut.hauser@IGI
Bäume - Grundlagen
Definition:
Anwendungsstrukturen
Ein Baum ist eine Menge, die durch eine sog.
Nachfolgerrelation strukturiert ist.
Elemente: Knoten
Chef
Gruppenleiter 1
Hierarchische Strukturen
GL 2
GL 3
In einem Baum gilt:
Mitarbeiter 1
M2
M3
Inklusionsstrukturen
1
∃ Knoten w ohne Vater(w) Æ (w=Wurzel)
k
Buch
Vater(x)
Lebewesen
1
∀ Knoten k≠w ∃ Knotenfolge k0, k1, …, kt
mit k0=k, kt=w und ki=Vater(ki-1) für
i=1, 2, …, t.
(Ast zwischen k und w, Länge t)
11.12.2008
x
Sohn(k)
Kap. 1
Abschn. 1.1
11.12.2008
helmut.hauser@IGI
Jeder Knoten hat maximal zwei Nachfolger
QUICK(1,n)
QUICK(1,k)
helmut.hauser@IGI
QUICK(k+1,n)
/
*
+
2
11.12.2008
1.4
Binärbäume
Anwendungsstrukturen
Beispiel:
Arithmetische Ausdrücke
Blätter (= Knoten ohne Söhne) enthalten
Zahlen, innere Knoten speichern
Operatoren (+, -, *, /).
Insekten
Tiere
Käfer
helmut.hauser@IGI
– Rekursionsbäume
– Entscheidungsbäume
– Suchbäume
– Haldenbäume
– Codebäume u.v.a.
Kap. 5
+
3
4
3
5
11.12.2008
helmut.hauser@IGI
Reihenfolge der Knoten
(1) Symmetrische Reihenfolge (SR):
Reihenfolge der Knoten
(2) Hauptreihenfolge (HR):
Linker Teilbaum in SR, Wurzel, rechter Teilbaum in SR.
Wurzel, linker Teilbaum in HR, rechter Teilbaum in HR.
/*+253+43
SR(k)
1: IF k≠nil THEN
2:
SR(LINKS(k))
3:
WRITE k
4:
SR(RECHTS(k))
Leicht rekursiv zu
programmieren.
(Def. übersetzen!)
Aufruf: SR(w)
((2+5)*3)/(4+3)
Infix-Notation
(3) Nebenreihenfolge (NR):
Linker Teilbaum in NR, rechter Teilbaum in NR, Wurzel.
Postfix-Notation
(leichte Auswertung, mit
Stapel)
25+3*43+/
7 21 7 3
11.12.2008
helmut.hauser@IGI
11.12.2008
Sortierte Binärbäume
helmut.hauser@IGI
Sortierte Binärbäume
Sortiert nach SR
Binäre Suche
15
6
3
2
18
7
17
5
20
13
O(Höhe)
Weitere Operationen möglich:
9
……………….....
11.12.2008
1: SUCHE(w,k)
2: IF k=nil OR w=WERT(k) THEN
3:
WRITE k
4: ELSE IF w<WERT(k) THEN
5:
SUCHE(w , LINKS(k))
6: ELSE SUCHE(w , RECHTS (k))
helmut.hauser@IGI
Einfügen (Erstellen), Löschen,
Minimum, Maximum, Vorgänger, Nachfolger
„Fädelung“ der Knoten
11.12.2008
helmut.hauser@IGI
Binärbäume - online
Binärbäume - Zusammenfassung
Durch Update-Operation
(Löschen, Einfügen)
Binärbäume sind spezielle Bäume, welcher maximal 2 Söhne haben.
1
9
Höhe ≠ log(n)
Knotenreihenfolgen (Symmetrische, Haupt- und Nebenreihenfolge)
Æ geordneter Binärbaum möglich (Nachfolgerrelation)
8
Entartet!
3
Implementierbare Funktionen:
Alle Funktionen:
O(„Baumhöhe“)
• Minimum
• Maximum
• Vorgänger
• Nachfolger
11.12.2008
helmut.hauser@IGI
Zur Erhaltung von: Höhe=log(n)
Techniken zur Erhaltung einer logarithmischen Baumhöhe
Höhenbalanciert
Gewichtsbalanciert
h(B)=Höhe des Baums
g(B) = Anzahl der Blätter
Für jeden Knoten k gilt:
Für jeden Knoten k gilt:
|h(Blinks)-h(Brechts)|≤k
1/α ≤ g(Blinks)/g(Brechts)| ≤ α
Bsp: AVL-Bäume (k=1)
BB-Bäume (bounded
balance)
Mehrwegbäume
11.12.2008
Umstrukturieren
O(n)
• Einfügen (Aufbau)
• Löschen
• Suchen
Wörterbuchproblem
helmut.hauser@IGI
Höhe = O(n)
teuer!
(fast) ausgeglichen
= gut, da minimale
Höhe = O( log n)
11.12.2008
Definition:
7
4
5
helmut.hauser@IGI
(2-4)-Bäume
Ein (2-4)-Baum ist ein Baum mit folgenden Eigenschaften:
(1) Alle Äste sind gleich lang.
(2) Die max. Anzahl der Söhne eines Knotens ist gleich 4.
(3) Innere Knoten haben ≥ 2 Söhne.
(4) Die Blätter enthalten v.l.n.r. die Werte aufsteigend sortiert.
(5) Jeder innere Knoten mit t Söhnen (2 ≤ t ≤ 4) speichert t-1
Hilfsinformationen x1, …, xt-1, wobei xi = größter Wert im Teilbaum
des i-ten Sohnes von links.
11.12.2008
helmut.hauser@IGI
(2-4)-Bäume
Höhe=O(log n)
Enthalten nur
Hilfsinformationen.
4,6
1,2
1
2
10,11
5
4
(2-4)-Bäume
5
6
10
11
Wir wollen damit das Wörterbuchproblem lösen:
SUCHEN, EINFÜGEN, ENTFERNEN
Achtung:
Nach den Update-Funktionen (Einfügen, Entfernen)
muss wieder ein korrekter 2-4-Baum vorliegen !
24
Daten werden in den Blättern gespeichert.
Æ Zeitlicher Mehraufwand, der sich aber rentiert Æ Amortisierte Kosten
siehe später
11.12.2008
helmut.hauser@IGI
11.12.2008
(2,4)-Bäume - Suchen
8
helmut.hauser@IGI
(2,4)-Bäume - Einfügen
Definition:
11
α(k) ist die Ordnung des k-ten Knoten (=Anzahl der Söhne)
2
4
5
10
12
24
Zwei Fälle (nach! dem Einfügen):
1.) Falls α(k) ≤ 4 Æ fertig !!
2
4
5
8
10
11
12
24
31
2.) Falls α(k) > 4 Æ Bedingung verletzt Æ SPALTEN
v
Pro Knoten maximal 3 Vergleich Æ O(1)
Æ Höhe garantiert Θ(log n) Æ T(n)=Θ(log n)
11.12.2008
helmut.hauser@IGI
v
k
k
11.12.2008
v’
helmut.hauser@IGI
k’
(2,4)-Bäume - Entfernen
Analyse der Operationen
Zwei Fälle (nach dem Entfernen):
Wörterbuchproblem
1.) Falls α(k) ≥ 2 Æ fertig !!
2.) Falls α(k) < 2 Æ Bedingung verletzt (underflow) Æ
STEHLEN (wenn α(k‘) ≥ 3)
k’
k
oder VERSCHMELZEN (α(k‘) = 2)
STEHLEN
k’
v
k’
O(log n)
O(log n)
O(log n)
Speicher:
O(n)
k
v
k
11.12.2008
Suchen:
Einfügen:
Entfernen:
VERSCHMELZEN
k
helmut.hauser@IGI
11.12.2008
helmut.hauser@IGI
Mischbare Warteschlangen
Mischbare Warteschlangen
9
-Unsortierter (2,4)-Baum
Definition:
•
•
•
•
EINFÜGEN (S,x)
MAXIMUM (S)
ENTFERNE_MAX (S)
MISCHE (S,S‘)
3
3
9
1
9
- innere Knoten speichert
Maximum in seinen Teilbaum
und Zeiger darauf
8
5
Maximum trivial Æ
in Wurzel O(1)
2
6
8
Entferne Maximum Æ Update der
Information O(log n)
8
Halde Æ 3 Operationen in O(log n)
Mischen aber teuer !! Æ O(n)
Mit Baum alle Operation Æ O(log n)
Einfügen ist
Spezialfall von
Mischen!
5
3
11.12.2008
helmut.hauser@IGI
11.12.2008
helmut.hauser@IGI
8
1
5
2
6
8
Amortisierte Kosten
Mischbare Warteschlangen
Mische (S, S‘): Æ Beides 2-4-Bäume mit der Höhe h und h‘
1.Fall: h = h‘
2.Fall: h > h‘
Neue Wurzel = O(1)
Check α(v) Æ O(log n)!!
2-4-Bäume benötigen zusätzliche Operation, damit sie 2-4-Bäume
bleiben und damit garantiert h=O(log n) besitzen.
Potentielle Laufzeit:
O(m*log(n))
v
k
w’
Beobachtung: z.B. nach Spalt-Operation ist der Baum „ausgeglichener“.
h’
T
T’
Æ Investierte Zeit rentiert sich später Æ Amortisierungsanalyse.
Durchschnittliche Zeit über alle Operation
(in unserem Fall: Einfügen, Löschen) im schlimmsten Fall.
11.12.2008
helmut.hauser@IGI
11.12.2008
helmut.hauser@IGI