Die Bestimmung der Masse visueller Doppelsterne

1
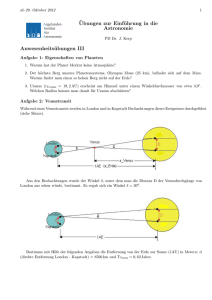
2 M⊙
Die Bestimmung der Masse
visueller Doppelsterne
Stefan Völker1
1
2 M⊙
1
AG Fachdidaktik Physik und Astronomie der Friedrich-Schiller-Universität Jena
1
1M⊙
1M⊙
1
2 M⊙
Inhaltsverzeichnis
1 Grundlagen
1.1 Stellare Zustandsgrößen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2 Visuelle Doppelsterne . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3 Die Methode der kleinsten Quadrate . . . . . . . . . . . . . . . . . . . . . . . . .
3
3
3
10
2 Aufgaben
2.1 Vorbereitung . . . . . . . . . . . . . . . . . . . . .
2.2 Die scheinbare Bahn des Doppelsterns 70 Ophiuchi
2.3 Die wahre Bahn des Doppelsterns 70 Ophiuchi . . .
2.4 Die Massen von 70 Ophiuchi . . . . . . . . . . . . .
.
.
.
.
14
14
14
15
15
3 Hinweise zur Durchführung
3.1 Berechnung der Koeffizienten mit Excel . . . . . . . . . . . . . . . . . . . . . . .
3.2 Lösen den Gleichungssystems mit einem CAS-Rechner . . . . . . . . . . . . . . .
3.3 Anpassen der scheinbaren Bahn . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
16
16
17
A Anhang - Die Summenschreibweise
20
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1M⊙
1
2 M⊙
1 Grundlagen
1.1 Stellare Zustandsgrößen
Ein Stern ist eine Gaskugel, deren Masse deutlich über derjenigen von Planeten, d.h. jenseits
von 1028 kg liegt. Im Sterninneren finden Kernfusionsprozesse statt, sodass zwischen den inneren
Druckkräften und der Eigengravitation des Gases ein stabiles Gleichgewicht herrscht.
Dabei wird ein Stern in allen seinen globalen Erscheinung durch die stellaren Zustandsgrößen
(Masse, Leuchtkraft, effektive Temperatur, Spektraltyp, Radius, mittlere Dichte, schwere Beschleunigung an der Oberfläche, Winkelgeschwindigkeit der Rotation und Stärke des Magnetfeldes) beschrieben (nach [1]).
Der Masse kommt dabei eine besondere Rolle zu. Denn diese entscheidet letztlich auch über
Temperatur, Leuchtkraft und Radius sowie über die Art und den zeitlichen Verlauf der Sternentwicklung.
Abgesehen von wenigen Ausnahmen gelingt die Massenbestimmung von Himmelsobjekten nur
über deren gegenseitige gravitative Wechselwirkung, wie beispielsweise in Doppel- oder Mehrfachsystemen. Einen besonders günstigen Fall stellen dabei die visuellen Doppelsterne dar, denn
diese ermöglichen eine zuverlässige Bestimmung der Masse beider Komponenten.
1.2 Visuelle Doppelsterne
Visuelle Doppelsterne bestehen aus zwei Sternen in einem gravitativ gebundenen System. Dabei
können die beide Komponenten mit einem Teleskop einzeln aufgelöst werden, so dass die Beobachtung der Positionen und Positionsänderungen beider Sterne getrennt voneinander möglich
ist. Die hellere Komponente (Stern A) bezeichnet man als Hauptstern und die dunklere Komponente als Begleiter (Stern B). Beide Sterne umkreisen ihren gemeinsamen Massenschwerpunkt
(Sp ) auf Kepler-Ellipsen (vgl. Abbildung 1).
y
t3
t2
t4
t1
t5
Stern B
rB
t6
SP
rA
x
t6
Stern A
t5
t1
t2
t3
t4
Abbildung 1: Bewegung der Sterne um den gemeinsamen Schwerpunkt, dargestellt für sechs
Zeitpunkt t1 bis t6 .
3
1M⊙
1
2 M⊙
Der Drehsinn, die Umlaufperiode und die Exzentrizität der Bahnen sind dabei für beide Sterne
gleich. Die große Halbachse der Bahnen unterscheiden sich in der Regel, da in einem Doppelsternsystem der Schwerpunktsatz
mA · rA = mB · rB
(1)
zu jedem Zeitpunkt gelten muss. Anders ausgedrückt ist das Verhältnis der Sternmassen invers
zum Verhältnis der Abstände der Sterne zum Schwerpunkt
mA
rB
=
.
mB
rA
(2)
Selbstverständlich gilt der Schwerpunktsatz auch für den Spezialfall, dass die Abstände der
Komponenten vom Schwerpunkt gerade den großen Halbachsen der Umlaufbahnen
mA · aA = mB · aB
(3)
entsprechen. Sind die Bahnen beider Sterne und damit die großen Halbachsen aA und aB bekannt,
können die Einzelmassen nach dem in Abbildung 2 dargestellten Schema bestimmt werden. Das
dritte Keplersche Gesetz und der Schwerpunktsatz bilden dabei ein Gleichungssystem aus zwei
Gleichungen für die beiden unbekannten Massen.
T /s
3. Keplersches
Gesetz
(aA+aB)
/''
(mA + mB)
(aA+aB) /m
d
mA & m B
aA /''
Schwerpunktsatz
mA / m B
aB /''
Abbildung 2: Schema zur Bestimmung der Einzelmassen; Messgrößen sind blau hinterlegt; d ist
die Entfernung des Doppelsternsystems
Allerdings liegt auch hier, wie so oft, die eigentliche Schwierigkeit im Detail, denn die Bewegungen der Komponenten auf ihren Bahnen sind überlagert von der Eigenbewegung µ des Systems
und der Positionsverschiebung aufgrund der jährlichen Parallaxe.
Zu diesen störenden Einflüssen kommt hinzu, dass nicht die dreidimensionale Bewegung der
Sterne (wahre Bahn) erfasst werden kann, sondern nur ihre Projektion in die Himmelsebene
(scheinbare Bahn). Berücksichtigt man alle diese Effekte bei der Auswertung der Beobachtungsdaten lässt sich das in Abbildung 2 dargestellte Schema anwenden.
1.2.1 Die absolute und die relative Bahn
Setzt man die Hauptkomponente (Stern A) eines Doppelsterns in den Ursprung des (relativen)
Koordinatensystems und beschreibt die Position des Begleiters (Stern B) durch den Positionswinkel θ und den Abstand ρ vom Hauptstern, erhält man wie in Abbildung 3 grün eingezeichnet
die scheinbare relative Bahn. Die eingezeichneten Himmelsrichtungen gehören zum äquatorialen
Koordinatensystem.
4
1M⊙
1
2 M⊙
S (180°)
scheinbare,
relative Bahn
Stern A
W (270°)
ρ
O (90°)
θ
Stern B
N (0°)
Abbildung 3: Scheinbare, relative Bahn und deren Koordinaten ρ und θ
Tatsächlich bewegen sich aber beide Sterne um ihren gemeinsamen Schwerpunkt. Setzt man
deshalb den Schwerpunkt in den Ursprung des (absoluten) Koordinatensystems (vgl. Abbildung
1), erhält man die scheinbaren absoluten Bahnen1 .
Die Form der Bahnellipsen ist in beiden Fällen ähnlich, d.h. die relative und die absoluten
Bahnellipsen haben die gleiche Exzentrizität. Auch der Umlaufsinn ist identisch. Unterschiedlich
sind die großen Halbachsen. Während die absoluten Bahnen die Halbachsen aA und aB haben,
ist die große Halbachse der relativen Bahn die Summe der beiden a = aA + aB .
1.2.2 Die wahre und die scheinbare Bahn
Bei der Beobachtung visueller Doppelsterne werden deren Positionen in der Himmelsebene gemessen. Entweder, die absoluten Positionen beider Sterne oder die Position der dunkleren Komponente im Bezug zur helleren Komponenten (relative Bahn).
Im Allgemeinen ist die Bahnebene eines Doppelsterns nicht mit der Himmelsebene identisch. Ist
die Bahnebene um einen Winkel i, der sogenannten Inklination gegenüber der Himmelsebene
geneigt, bewegen sich die Sterne auch in radialer Richtung, d.h. von der Erde weg oder auf sie
zu. Diese Bewegung ist der visuellen Beobachtung aber nicht zugänglich. Beobachtet wird die
Projektion der wahren Bewegung in die Himmelsebene.
Zwei gegeneinander geneigte Ebenen schneiden sich in einer Schnittgeraden. Diese heißt im
astronomischen Kontexten Knotenlinie. Auf dieser Linien liegen der aufsteigende und der
absteigende Knoten . Im aufsteigenden Knoten durchstößt der Stern auf seiner Bahn von Innen
die Himmelsebene, bewegt sich somit von der Erde weg. Im absteigenden Knoten durchstößt er
die Himmelsebene von Außen und bewegt sich damit auf die Erde zu (vgl. Abbildung 4).
1
Siehe hierzu die Simulation Die Bahnform visueller Doppelsterne“ [3]
”
5
1M⊙
1
2 M⊙
Stern B
Periastron
i
θ
Stern A
ω
Ω
E
Bahnebene Apastron
Himmels
ebene
N
Abbildung 4: Die scheinbare Bahn ist die Projektion der wahren Bahn an die Himmelsebene.
Die Form und die Lage der wahren Bahn wird durch die Bahnelemente a, e, i, Ω,
ω beschrieben. Hier ist die wahre relative Bahn gezeigt.
Die Lage der Bahnebene im Raum wird neben der Inklination durch die Angabe eines zweiten
Winkels der Länge des aufsteigenden Knotens Ω angegeben. Dieser wird in der Himmelsebene
ausgehend von der Nordrichtung bis zur Knotenlinien bzw. dem aufsteigenden Knoten gemessen.
Die beiden Bahnelemente i und Ω bestimmen die Projektion der wahren auf die scheinbare Bahn
in der Himmelsebene maßgeblich.
Drei weitere Bahnelemente, der Winkel ω die Länge des Periastrons, die große Halbachse a und
die Exzentrizität e der Bahn legen die Form und die Orientierung der wahren Bahn innerhalb der
Bahnebene fest. Der Winkel ω wird in der Bahnebene ausgehenden vom aufsteigenden Knoten
in Bewegungsrichtung des Planeten bis zum Periastron der Bahn gemessen. Im Periastron haben
die beiden Sterne den geringsten Abstand voneinander.
Die zur Massenbestimmung benötigte Größe (aA + aB ) lässt sich nicht direkt aus der scheinbaren
Bahn ablesen. Allerdings lässt sich aus der scheinbaren Bahn die wahre Bahn durch geometrische
Konstruktion oder analytische Verfahren gewinnen. Aus der absoluten oder relativen wahren
Bahn lässt sich (aA + aB ) einfach bestimmen.
1.2.3 Jährliche Parallaxe
Als jährliche Parallaxe oder trigonometrische Parallaxe eines Sterns bezeichnet man dessen
scheinbare Positionsänderung vor dem festen Fixsternhintergrund2 in Folge der Bewegung der
Erde um die Sonne. Abbildung 5 zeigt diese Positionsänderung für drei Sterne. Befindet sich
der Stern genau oberhalb der Erdbahn, ist die Projektion der Erdbewegung eine kreisförmige
Parallaxenbewegung. Befindet sich der Stern in der Bahnebene der Erde um die Sonne ändert
er seine Position nur auf einer Linie, er wackelt hin und her. Alle Sterne zwischen diesen beiden
Extremen zeigen eine elliptische Fixsternparallaxe.
2
Gemeint sind Sterne, die soweit von der Erde entfernt sind, dass ihr jährliche Parallaxe nicht mehr beobachtet
werden kann.
6
1M⊙
1
2 M⊙
Kreis
1
2
Kreis
3
4
1
Ellipse
2
3
Linie
1
4
3
2
2
3
1
Sonne
Erdbahn
4
4
Abbildung 5: Links: Form der jährliche Parallaxenbewegung; Rechts: Entfernungsbestimmung
mit Hilfe der Parallaxe.
Je geringer der Abstand zwischen Erde und Stern ist, desto größer ist die scheinbare Positionsänderung p des Sterns (vgl. Abbildung 5 rechts). Die Beobachtung der trigonometrischen
Parallaxe ermöglicht einen direkten und geometrischen Zugang zur Entfernung d eines Sterns.
Aus Abbildung 5 entnimmt man den Zusammenhang
tan p =
1 AE
≈ p,
d
(4)
wobei die Näherung nur für kleine Winkel p gilt. Die jährlichen Parallaxen von Sternen sind
jedoch alle kleiner als eine Bogensekunde (p < 100 ), dem 3600-Teil eines Grades. Daraus ergibt
sich für den Abstand
1
d/pc = 00 .
(5)
p/
Es ist unbedingt darauf zu achten, dass man in Gleichung (5) den Winkel p in Bogensekunden
einsetzen muss und die Entfernung dann in der Einheit parsec (pc) angeben wird (1 pc = 3, 09 ·
1016 m).
Beide Komponenten eines Doppelsterns führen eine scheinbare Bewegung aufgrund der jährlichen
Parallaxe aus, deren Form (Strich, Ellipse oder Kreis) von den äquatorialen Koordinaten α und δ
des Doppelsterns und deren Größe von dessen Entfernung abhängt. Die Koordinatenänderungen
in Richtung der Rektaszension ∆αp und in Richtung der Deklination ∆δp zu einem bestimmten
Zeitpunkt t lassen sich als
∆αp (t) = Pα (t) · p
(6)
∆δp (t) = Pδ (t) · p
(7)
schreiben. Die Entfernung und damit der Winkel p beschreibt die Größe der Verschiebung. Die
Koeffizienten Pα und Pδ können Werte im Bereich von 0 ≤ Pα , Pδ ≤ 1 annehmen. Sie hängen
von der Position des Sterns und der Position der Erde auf ihrer Bahn und damit von der Zeit
ab.
7
1M⊙
1
2 M⊙
1.2.4 Eigenbewegung µ
Sterne stehen im Allgemeinen nicht ruhig im Raum, z.B. wandert unsere Sonne um das galaktische Zentrum der Milchstraße mit einer Rotationsgeschwindigkeit von ca. 220 km/s. Auch
Doppel- und Mehrfachsternsysteme als Ganzes bewegen sich durch den Raum. Dabei führen
alle Komponenten eines Systems und der Schwerpunkt die gleiche Bewegung durch den Raum
aus. Der 3-dimensionale Geschwindigkeitsvektor kann in eine Komponente senkrecht zur Himmelsebene der Radialgeschwindigkeit vr und in zwei Komponenten in der Himmelsebene vα und
vδ zerlegt werden. vα zeigt in Richtung der Rektaszension und vδ in Richtung der Deklination
(vgl. Abbildung 6).
δ
r
v
vδ
vr
Stern
α
vα
Abbildung 6: Zerlegung des 3-dimensionalen Geschwindigkeitsvektors ~v
Der Betrag der beiden Geschwindigkeiten in der Himmelsebene ist jedoch nur messbar, wenn
auch der Abstand zum Stern bekannt ist. Ansonsten kann die Bewegung in der Himmelsebene nur
als zurückgelegter Winkel pro Zeit angegeben werden. Die Geschwindigkeit in der Himmelsebene
wird dann als Eigenbewegung µ bezeichnet bzw. zerlegt in Richtung der Rektaszension µα und
in Richtung der Deklination µδ .
Für die Massebestimmung von visuellen Doppelsternen ist die Eigenbewegung interessant, denn
diese überlagert die Bewegung der Sterne auf ihren Umlaufbahnen (vgl. Abbildung 7).
Da der Abstand eines Sterns a priori nicht bekannt ist, wird die Eigenbewegung in der Einheit
Winkel pro Zeit“ meist in 00/Jahr angegeben. Das Verhältnis der Eigenbewegung zur scheinbaren
”
Größe der Doppelsternbahn entscheidet letztlich über das Erscheinungsbild der überlagerten
Bewegung3 (vgl. Abbildung 8).
Die Koordinatenverschiebungen des Systems in Richtung der Rektaszension ∆αµ und in Richtung der Deklination ∆δµ nach einer Zeit ∆t lassen sich als
∆αµ (t) = µα · ∆t
(8)
∆δµ (t) = µδ · ∆t
(9)
schreiben.
3
Siehe hierzu die Simulation Die Bahnform visueller Doppelsterne mit Eigenbewegung“ [4]
”
8
1M⊙
1
2 M⊙
y
Eigenbewegung
Stern A
Stern B
Drehsinn des
Doppelsterns
x
Abbildung 7: Überlagerung der Doppelstern- mit der Eigenbewegung
Eigenbewegung
Abbildung 8: Überlagerung der Umlaufbahnen mit der Eigenbewegung µ. Die rote Linie beschreibt die Bewegung des Schwerpunktes, die durchgezogene gelbe Linie jene von
Stern A und die gestrichelte Linie jene von Stern B. In der Abbildung haben beide
Sterne gleiche große Halbachsen und kreisförmigen Bahnen. Die Größe der Umlaufbahn (in 00 ) nimmt im Vergleich zur Eigenbewegung (in 00 /Jahr) von oben nach
unten hin zu. Die Umlaufperiode des Doppelsterns bleibt dabei konstant.
9
1M⊙
1
2 M⊙
1.3 Die Methode der kleinsten Quadrate
Die Methode der kleinsten Quadrate geht auf den deutschen Mathematiker Carl Friedrich Gauß
zurück. Sie ist das gängige Verfahren um Ausgleichsfunktionen an gegebene Messwerte anzupassen. Sie beruht auf der Idee, dass die Summe der Abweichungen der einzelnen Messwerte
bzw. genauer die Summe der Quadrate der Abweichungen von der Ausgleichsfunktion möglichst
gering sein soll. Diese Annahme führt zu einer Extremwertaufgabe, der Suche nach der minimalen Abweichung. Nachfolgend wird zunächst die lineare Ausgleichsfunktion von einer Variablen
betrachtet, bevor das Verfahren auf das Problem der visuellen Doppelsterne angewandt wird.
1.3.1 Beispiel einer linearen Ausgleichsfunktion
Das Hookesche Gesetz beschreibt den linearen Zusammenhang zwischen der Kraft F und der
Auslenkung x einer Feder
F = D · x.
Im Experiment wurden die in Tabelle 1 dargestellten Werte gemessen. Im Nachhinein soll nun mit
Hilfe der Methode der kleinsten Quadrate die Ausgleichsgerade und damit die Federkonstante
D bestimmt werden.
x/cm
1
2
3
4
F/N
0,20
0,36
0,67
0,77
Tabelle 1: Messwerte Federexperiment
F /N
F /N
1,0
1,0
0,8
0,8
0,6
0,6
N
D = 0,2 cm
0,4
0,4
N
D = 0,16 cm
0,2
0,2
1
2
3
4
5 x /cm
1
2
3
4
5 x /cm
Abbildung 9: Ausgleichsrechnung Federexperiment; links: minimale Summe der Fehlerquadrate,
rechts: Summe der Fehlerquadrate nicht minimal
Für jedes Messwertepaare (xi, Fi ) kann eine Gleichung der Art
Ai = D · xi − Fi
(10)
aufgeschrieben werden. Darin steht Ai für die Abweichung und i ist ein Index der von 1 bis
n, der Anzahl der Messwerte läuft (i = 1, 2, 3, ... , n). In Abbildung 9 sind die Messwerte rot
dargestellt, die Abweichung Ai zwischen Messwert und Ausgleichsfunktion ist als blauer Strich
eingezeichnet.
10
1M⊙
1
2 M⊙
Die Methode der kleinsten Quadrate verlangt nun, dass die Summe S der Quadrate der Abweichungen
n
X
S=
A2i = A21 + A22 + ... + A2n
(11)
i=1
wird4 .
minimal
Dies erreicht man durch eine geeignete Wahl des Parameters D. Abbildung 9
zeigt links die Ausgleichsgerade, als Ergebnis der Methode der kleinsten Quadrate. Die Summe
der Quadrate der Abweichungen ist minimal. Rechts ist der Wert der Federkonstanten D zu
klein und die Abweichungen auch augenscheinlich nicht minimal.
Zur Berechnung der optimalen Federkonstante D setzt man Gleichung (10) in Gleichung (11) ein
und bildet die Ableitung nach dem anzupassenden Parameter D. Da nach einem Extremwert,
dem Minimum gefragt ist, setzt man die Ableitung S 0 gleich null
!0
!0
n
n
n
X
X
X
2
0
2
S (D) =
Ai =
(D · xi − Fi )
=2·
(D · xi − Fi ) · xi = 0 .
(12)
i=1
i=1
i=1
Gleichung (12) stellt die eine Gleichung dar, die man zur Bestimmung der einen unbekannten
D benötigt. Stellt man diese um, bleibt
Pn
(F · x )
Pn i 2 i .
(13)
D = i=1
i=1 xi
Am konkreten Beispiel der Feder heißt das
D =
=
0, 2 N · 1 cm + 0, 36 N · 12 cm + 0, 67 N · 3 cm + 0, 77 N · 4 cm
(1 cm)2 + (2 cm)2 + (3 cm)2 + (4 cm)2
6, 01 N · cm
N
= 0, 20
.
2
30 cm
cm
1.3.2 Bahnbestimmung visueller Doppelsterne
Die Position einer Komponente eines visuellen Doppelsterns im Raum bzw. deren Projektion
in die Himmelsebene hängt, wie im Abschnitt 1.2 beschrieben, von mehreren Parametern ab
(der Anfangsposition, der Eigenbewegung, der jährlichen Parallaxe und der Bewegung auf der
Doppelsternbahn). Bildet man die visuellen Beobachtungen mit einem Teleskop auf eine Fotoplatte ab, findet man alle Größen auf dieser wieder. Die Fotoplatte soll so orientiert sein, dass
die x-Achse in Richtung der Rektaszension und die y-Achse in Richtung der Deklination zeigt.
Verfügt man über mehrere Fotoplatten die zu verschiedenen Zeiten aufgenommen wurden,
können aus der Verschiebung der Doppelsternkomponenten gegenüber den feststehenden Hintergrundsternen die Bahnen der beiden Sterne abgeleitet werden. Allerdings nur die Überlagerung
mit der Eigenbewegung und der Parallaxe. Für die x-Position XA der Komponente A eines
Doppelsterns auf einer Fotoplatte gilt
XA = x0,A + µx · ∆t + p · Px −B
| {z· ∆x}
(14)
YA = y0,A + µy · ∆t + p · Py −B · ∆y .
| {z }
(15)
+xA (t)
und für die y-Position YA
+yA (t)
xA (t) und yA (t) ist die eigentliche Bahnbewegung des Doppelsterns. In den Gleichungen (14)
und (15) sind die Parameter x0,A , µx , p und das Massenverhältnis B
B=
4
mB
mA + mB
Informationen zur Summenschreibweise finden Sie im Anhang A
11
(16)
1M⊙
1
2 M⊙
zunächst noch unbekannt. Gesucht ist die Bahnkurve, welche die Messwerte optimal wiedergibt.
Auch dieses Problem kann mit der Methode der kleinsten Quadrate gelöst werden. Im Gegensatz
zum Beispiel des Hookeschen Gesetzes muss hier jedoch nicht nur ein Parameter gewählt werden,
sondern es muss die minimale Abweichung der Fehlerquadrate gefunden werden durch Variation
der Parameter x0 , µ, p und B. Dies führt auf ein Gleichungssystem aus vier Gleichungen für die
vier unbekannten Parameter. Nachfolgend betrachten wir nur die x-Position. Die Lösung für die
y-Position erfolgt analog.
Bei n Fotoplatten erhält man n Messwertgruppen (∆ti , Px,i , ∆xi , XA,i ) und man berechnet
analog zu Gleichung (11) zunächst die Summe der Abweichungsquadrate
n
X
S(x0,A , µx , p, B) =
(Ai )2 =
i=1
n
X
(x0,A + µx · ∆ti + p · Px,i − B · ∆xi − XA,i )2 .
i=1
Die Summe der Abweichungsquadrate S hängt von vier Parametern ab. Diese gibt man in der
Klammer nach S an. Zur Minimierung der Summe bildet man nacheinander die Ableitung nach
x0,A , µx , p und B, setzt diese gleich null und erhält die vier Gleichungen zur Bestimmung der
vier Unbekannten
0
!
n
X
!
i=1
n
X
!
i=1
n
X
!
i=1
n
X
S (x0,A ) = 0 = 2 ·
S 0 (µx ) = 0 = 2 ·
S 0 (p) = 0 = 2 ·
(x0,A + µx · ∆ti + p · Px,i − B · ∆xi − XA,i )
(17)
(x0,A + µx · ∆ti + p · Px,i − B · ∆xi − XA,i ) · ∆ti
(18)
(x0,A + µx · ∆ti + p · Px,i − B · ∆xi − XA,i ) · Px,i
(19)
S 0 (B) = 0 = −2 ·
(x0,A + µx · ∆ti + p · Px,i − B · ∆xi − XA,i ) · ∆xi .
(20)
i=1
Leitet man die Summe S z.B. nach x0,A ab, stellt man sich vor alle anderen Parameter wären
Konstanten. Analog geht man bei den Ableitungen nach den anderen Parametern vor. Bringt
man zum Schluss alle Terme mit der gemessenen Position XA,i auf die andere Seite entsteht das
Gleichungssystem
n · x0,A + µx ·
n
X
n
X
!
∆ti
+p·
i=1
n
X
!
∆ti
· x0,A + µx ·
i=1
n
X
n
X
Px,i
· x0,A + µx ·
i=1
n
X
i=1
n
X
n
X
· x0,A + µx ·
n
X
−B·
Px,i · ∆ti
−B·
i=1
n
X
!
∆ti · Pi
+p·
−B·
i=1
!
∆ti · ∆xi
!
2
Px,i
+p·
i=1
n
X
i=1
oder in einer anderen, gängigen Schreibweise:
12
!
∆xi
=
i=1
!
i=1
!
∆xi
+p·
i=1
!
Px,i
i=1
!
∆t2i
n
X
!
n
X
∆xi · ∆ti
i=1
n
X
=
!
∆xi · Pi
=
i=1
!
Px,i · ∆xi
!
−B·
n
X
i=1
n
X
i=1
n
X
XA,i
XA,i · ∆ti
XA,i · Px,i
i=1
n
X
i=1
!
∆x2i
=
n
X
i=1
XA,i · ∆xi
1M⊙
1
2 M⊙
xA,0
µx
p
B
n
P
( ni=1 ∆ti )
Pn
2
i=1 ∆ti
P
( ni=1 ∆ti · Pi )
P
( ni=1 ti · ∆xi )
P
( ni=1 Px,i )
P
( ni=1 Px,i · ∆ti )
P
n
2
i=1 Px,i
P
( ni=1 Px,i · ∆xi )
P
− ( ni=1 ∆xi )
P
− ( ni=1 ∆xi · ∆ti )
P
− ( ni=1 ∆xi · Pi )
Pn
2
−
i=1 ∆xi
P
( ni=1 ∆ti )
P
( ni=1 Px,i )
P
( ni=1 ∆xi )
Pn
i=1 XA,i
Pn
· ∆ti .
Pn
· Px,i
Pn
· ∆xi
i=1 XA,i
i=1 XA,i
i=1 XA,i
Aus den Messwerten XA,i , ∆ti , Px,i , ∆xi und der Anzahl der Werte n werden nun die einzelnen
Koeffizienten des Gleichungssystems ausgerechnet. Dies kann z.B. mit Hilfe der Software Excel
von Microsoft geschehen. Dort gibt es die Befehle Summe“ und Summenprodukt“ mit denen
”
”
sich die Größen schnell und einfach berechnen lassen. Näheres hierzu im Abschnitt 3.1.
Sind alle Koeffizienten berechnet wird das Gleichungssystem gelöst und man erhält nur aus der
X-Position des Sterns A bereits die gesuchten Parameter cx , p, µx und das Massenverhältnis B.
13
1M⊙
1
2 M⊙
2 Aufgaben
2.1 Vorbereitung
A1
Lösen Sie das Gleichungssystem bestehend aus dem Schwerpunktsatz (I) und dem
dritten Keplerschen Gesetz (II)
I:
II :
mA · aA
(aA + aB )3
T2
= mB · aB
G · (mA + mB )
=
4π 2
nach den beiden Massen mA und mB auf!
A2
Zeigen Sie, dass aus dem Schwerpunktsatz in seiner allgemeinen Form
mA · rA = mB · rB
der Zusammenhang
rA = B · r
folgt. Dabei bedeutet r = rA + rB !
A3
Begründen Sie, dass für die Zerlegung des Abstandes rA in eine x- und y-Komponente
die Zusammenhänge xA = B · ∆x und yA = B · ∆y mit ∆x = xA + xB sowie
∆y = yA + yB gelten (vgl. Abbildung 10)!
y
Stern B
rB
yA
xA
yB
xB
rA
Δy
x
Stern A
Δx
Abbildung 10: Zerlegung des Abstands rA in eine x- und y-Komponente
2.2 Die scheinbare Bahn des Doppelsterns 70 Ophiuchi
Der Doppelstern 70 Ophiuchi aus dem Sternbild Schlagenträger besteht aus zwei Hauptreihensternen. Der hellere der beiden Sterne ist vom Spektraltyp K0 V (Stern A), der andere ist ein
K5 V Stern (Stern B). Man findet das Doppelsternsystem bei den äquatorialen Koordinaten
α = 18h 2, 9m und δ = 2◦ 310 am Himmel. 70 Ophiuchi wurde zwischen den Jahren 1910 bis
1951 in 48 Nächten am Yerkes-Observatorium beobachtet [2], d.h. es wurden Aufnahmen auf
14
1M⊙
1
2 M⊙
Fotoplatten angefertigt. Die dunklere der beiden Komponenten konnte nur in 42 Nächten beobachtet werden. Als Teleskop wurde das 40-inch (102 cm) Linsenteleskop, das größte jemals
gebaute Linsenteleskop, verwendet.
Aus der zugehörigen Veröffentlichung von Kaj Strand stammt der in der Excel-Datei Beobach”
tungsdaten 70 Ophiuchi - Schüler“ enthaltene Datensatz. Dort sind die Beobachtungszeit, die
X- und Y - Koordinaten beider Doppelsternkomponenten auf der Fotoplatte und die ParallaxenKoeffizienten für jedes Beobachtungsdatum angegeben. Die Fotoplatten waren so ausgerichtet,
dass die x-Achse in Richtung der Rektaszension α und die y-Achse in Richtung der Deklination
δ zeigt. 1 mm auf der Fotoplatte entspricht einem Winkel von 10, 65500 am Himmel.
A4
Lösen Sie das in Abschnitt 1.3.2 beschriebene Gleichungssystem für die X-Position
der Hauptkomponente des Doppelsterns 70 Ophiuchi mit einem CAS-Rechner und
bestimmen Sie so die unbekannten Parameter x0 , µx , p und B!
Berechnen Sie hierfür zunächst alle Koeffizienten des Gleichungssystems mit Excel!
A5
Berechnen Sie die Entfernung des Doppelsterns aus der von Ihnen bestimmen Parallaxe p! Beachten Sie, dass 1 mm auf der Fotoplatte einem Winkel von 10, 65500 am
Himmel entspricht.
2.3 Die wahre Bahn des Doppelsterns 70 Ophiuchi
Die Beobachtungsdaten von Kaj Strand [2] umfassen nur etwa die Hälfte der Umlaufperiode
des Doppelsterns. Dementsprechend schwierig ist es, die wahre Bahn aus der scheinbaren zu
konstruieren. Deshalb greifen wir hier auf einen zweiten, vollständigeren Datensatz zurück.
Im WDS-Katalog (Washington Double Star Catalog) sind die scheinbaren relativen Bahnen von
über 100000 Doppelsternen enthalten; so auch von 70 Ophiuchi.
Der Doppelstern wurde bereits im Jahre 1779 zum ersten Mal von William Herschel beobachtet
und seit dem über 1700 mal. Im WDS-Katalog sind neben den Beobachtungszeiten, der relative
Abstand und der Positionswinkel der dunkleren Komponente enthalten.
Interessant ist hierbei auf welch unterschiedliche Weisen diese Daten im Lauf der Jahre gewonnen
wurden. Während William Herschel noch mit bloßem Auge am Teleskop beobachtete, wurden
Doppelsterne im Laufe der zweiten Hälfte des 19. Jahrhunderts auf Photoplatten abgebildet. In
der heutigen astronomischen Forschung haben CCD-Kameras die Photoplatten wiederum längst
abgelöst. CCD-Kameras findet man in kleinerer Form z.B. in allen modernen Digitalkameras.
A6
Bestimmen Sie die Bahnelemente der wahren Bahn aus der scheinbaren Bahn mit Hilfe der GeoGebra-Datei Konstruktion der wahren Bahn von 70 Ophiuchi - Schüler“!
”
Variieren Sie die Bahnelemente a, e, i, Ω, ω der wahren relativen Bahnellipse so, dass
die zugehörige scheinbare Bahn die Messwerte optimal überlagert! Lesen Sie dann
am Schieberegler a den Wert der großen Halbachse in Bogensekunden ab!
2.4 Die Massen von 70 Ophiuchi
A7
Berechnen Sie mit der von Ihnen bestimmten Entfernung des Doppelsterns die tatsächliche
Größe der großen Halbachse der relativen Bahn (a = aA + aB ) in Metern!
A8
Berechnen Sie die Massen der beiden Komponenten! Geben Sie Ihre Ergebnisse in kg
und in Sonnenmassen M an! Die Umlaufperiode des Doppelsternsystems beträgt
87, 85 Jahre.
15
1M⊙
1
2 M⊙
3 Hinweise zur Durchführung
3.1 Berechnung der Koeffizienten mit Excel
Die Datei Beobachtungsdaten 70 Ophiuchi - Schüler“ enthält im Tabellenblatt Beobachtungs”
”
daten“ die Beobachtungszeit, die X- und Y -Positionen der beiden Doppelsternkomponenten auf
der Fotoplatte, die relativen Abstände ∆X und ∆Y , sowie die Parallaxen-Koeffizienten Pα und
Pδ für die Beobachtungszeiten.
Zeit t
(t − t0 )/a
XA /mm
YA /mm
XB /mm
YB /mm
Pα
Pδ
∆X/mm
∆Y /mm
1911,309
0
-18,2949
-1,0664
-18,1339
-1,3519
0,854
0,234
0,1610
-0,2855
1913,589
2,280
-18,2928
-1,2769
-18,0601
-1,5993
-0,652
0,340
0,2327
-0,3224
...
...
...
...
...
...
...
...
...
...
Tabelle 2: Tabellenkopf und Beispiel des Datensatz aus [2]
Zudem sind die Positionen der Doppelsternkomponenten auf den Fotoplatten im Diagramm
Positionen der Doppelsternkomponenten auf der Fotoplatte“ eingezeichnet. Das Diagramm
”
Relative Positionen der Doppelsternkomponenten “ zeigt die relative Bahn mit Stern A im
”
Koordinatenursprung.
Im Tabellenblatt Position X A“ sind nochmal alle Angaben für die X-Position des Sternes
”
A enthalten. In diesem Tabellenblatt wird die Berechnung der Koeffizienten des linearen Gleichungssystem durchgeführt.
Berechnung der Koeffizienten des Gleichungssystems
Mit Hilfe der beiden Befehle SUMME“ und SUMMENPRODUKT“ können alle Koeffizienten
”
”
des linearen Gleichungssystems berechnet werden:
P
• Summen bei denen nur über eine Variable summiert wird (z.B. ni=1 ∆ti ) können in Excel
mit dem Befehl SUMME(Zelle 1:Zelle n)“ berechnet werden. Beispielsweise addiert Excel
”
beim Befehl Summe(A1:A43)“ alle Werte der Zellen A1, A2, A3 usw. bis A43.
”
P
• Summen bei denen über das Produkt zweier Variablen summiert wird (z.B. ni=1 ∆ti · Pi )
können in Excel mit dem Befehl SUMMENPRODUKT(A1:An;B1:Bn)“ berechnet wer”
den. Beispielsweise berechnet Excel beim Befehl SUMMENPRODUKT(A1:A43;B1:B43)“
”
mit den Werten der einzelnen Zellen A1 · B1 + A2 · B2 + A3 · B3 + ... + A43 · B43 .
Tragen Sie die berechneten Koeffizienten im Tabellenblatt Position X A“ ein.
”
3.2 Lösen den Gleichungssystems mit einem CAS-Rechner
Das Lösen des linearen Gleichungssystems wird hier exemplarisch am Casio Classpad 300 PLUS
vorgestellt. Die wesentlichen Schritte sind in Abbildung 11 dargestellt. Die Lösung ist aber mit
jedem CAS-Rechner möglich.
16
1M⊙
1
2 M⊙
Symbol Gleichungssystem
Abbildung 11: Lösung des Gleichungssystems mit dem CAS
• Lassen Sie sich zunächst die Software-Tastatur anzeigen und wählen Sie die 2D-Tastatur
aus.
• Klicken Sie auf das Symbol Gleichungssystem. Das angezeigte Gleichungssystem hat bisher
zwei Zeilen. Klicken Sie zwei weitere Male auf das Symbol um zwei zusätzliche Zeilen zu
erhalten.
• Schreiben Sie die vier Gleichungen ihres Gleichungssystems in die vier Zeilen. Verwenden
Sie die Variablen x, y, z, t des CAS-Rechner stellvertretenden für die Größen cx , µx , p, B.
• Geben Sie rechts unten neben dem Gleichungssystem die Variablen an, nach denen das
System aufgelöst werden soll. Hier x, y, z und t. Die Variablen sind durch Kommata zu
trennen.
• Lösen Sie das Gleichungssystem durch Klicken auf EXE.
3.3 Anpassen der scheinbaren Bahn
Öffnen Sie die GeoGebra-Datei Konstruktion der wahren Bahn von 70 Ophiuchi - Schüler.ggb“.
”
Diese enthält alle Positionsdaten von 70 Ophiuchi aus dem WDS Katalog. Zudem enthält die
Simulation Schieberegler für die Größen a, e, ω, Ω, i (vgl. Abbildung 12).
Mit den Reglern für a und e wird die Form und Größe der wahren Bahn (grün) in der Bahnebene
eingestellt. Der Regler ω bestimmt die Lage des Periastrons der Bahn innerhalb der Bahnebene.
Mit dem Schieberegler Ω kann die Lage der Knotenlinie (blau) und damit der Bahnebene variiert
werden. Dies ist besonders wichtig, da die Projektion in die Himmelsebene von der Lage dieser
Linie abhängt. Die Inklination i bestimmt wie sehr die Bahn bei der Projektion verformt wird.
Für i = 0◦ ∨ 180◦ sind scheinbare (rot hinterlegt) und wahre Bahn identisch, für i = 90◦ ist die
Verformung maximal, die scheinbare Bahn entartet zu einer Linie.
Fünf der über 1700 Beobachtungen aus dem WDS-Katalog sind mit der zugehörigen Jahreszahl
versehen, so dass sich die Umlaufrichtung ableiten lässt. Bewegen sich die Doppelsternkomponenten auf ihren Bahnen bzw. Stern B um Stern A auf der relativen Bahn entgegen dem
Uhrzeigersinn, spricht man von einer prograden (rechtläufigen) Bewegung. Ist die Bewegung
entgegengesetzt und somit im Uhrzeigersinn nennt man dies retrograd (rückläufig). Den prograden Bewegungen ordnet man Bahninklinationen zwischen 0◦ ≤ i < 90◦ zu und den retrograden
90◦ < i ≤ 180◦ .
17
1M⊙
1
2 M⊙
Aus den eingestellten Werten berechnet GeoGebra automatisch die Lage und Form der scheinbaren Bahn in der Himmelsebene. Die Parameter sind so zu wählen, dass die scheinbare Bahn
die Messwerte optimal überlagert. Der Wert der relativen großen Halbachse a = aA + aB in
Bogensekunden wird zur Massenbestimmung benötigt.
a = 3.6 ''
Ω = 28°
e = 0.39
ω = 92°
i = 42°
wahre Bahn
scheinbare
Bahn
Periastron der
wahre Bahn
O
aufsteigender Knoten
lini
ten
Kno
e
N
Abbildung 12: Ausschnitt aus der GeoGebra-Datei Konstruktion der wahren Bahn von 70
”
Ophiuchi - Schüler.ggb“
18
1M⊙
1
2 M⊙
Literaturverzeichnis
[1] W. Kuhn (Hrsg.); Handbuch der experimentellen Physik, Sekundarbereich II, Band 11: Astronomie - Astrophysik Kosmologie; AULIS
VERLAG; 2011; S.217
[2] Strand K., Spong R.: The parallax and mass-ratio of 70 Ophiuchi ; The
Astronomical Journal; Volume 57 (1952); S. 102-104
[3] S. Völker: Die Bahnform visueller Doppelsterne; Download unter:
http://www.physik.uni-jena.de/didaktik download geogebra.html
[4] S. Völker: Die Bahnform visueller
genbewegung;
Download
unter:
jena.de/didaktik download geogebra.
19
Doppelsterne mit Eihttp://www.physik.uni-
1M⊙
1
2 M⊙
A Anhang - Die Summenschreibweise
Die Summenschreibweise ist eine Kurzschreibweise für Summen die aus vielen Summanden bestehen. Beispielsweise lässt sich die Summe S aller Zahlen von 1 bis 10 als
S = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55
oder kurz als
S=
10
X
i = 55
i=1
schreiben. Das Summenzeichen ist ein griechisches großes Sigma. Unterhalb des Summenzeichens
wird die Laufvariable und ihr Startwert (untere Summationsgrenze) angegeben. Darüber findet
man den letzten Wert den die Laufvariable einnehmen kann (obere Summationsgrenze). Nach
dem Summenzeichen steht die Summationsvariable (vgl. Abbildung 13). Die Summationsvariable
muss nicht zwangsläufig wie im obigen
Beispiel der Laufindex selbst sein. Möglich sind alle
√
denkbaren Rechenvorschriften (i2 , 3i + 5, etc.).
Obere Summationsgrenze
Summationsvariable
Laufindex
Untere Summationsgrenze
Abbildung 13: Erklärung Summenschreibweise; Summenzeichen in rot
Eine weitere Möglichkeit ist der Verweis auf die in einer Tabelle gelisteten Werte. In diesem
Projekt bedeutet die Summe
42
X
XA,i
i=1
beispielsweise, dass alle 42 Positionsmessung des Doppelsterns auf der Fotoplatte summiert
werden. Die Positionsmessungen sind einer Tabelle in der Excel Datei Beobachtungsdaten 70
”
Ophiuchi - Schüler“ gegeben.
Rechenregeln mit Summen
(1)
Auch für die Summenschreibweise gilt das Kommutativgesetz
n
X
(ai + bi ) =
i=1
n
X
ai +
i=1
n
X
bi ,
i=1
d.h. es ist egal ob man zuerst die Summe a1 +b1 bildet und dazu dann a2 +b2 addiert,
oder ob man a1 + a2 zu b1 + b2 addiert.
(2)
Es gilt das Distributivgesetz
n
X
k · ai = k ·
i=1
n
X
i=1
20
ai ,
1M⊙
1
2 M⊙
d.h. es ist egal ob man jeden Summanden zuerst mit der Konstanten k multipliziert
und anschließend addiert, oder ob man zum Schluss die komplette Summe mit k
multipliziert.
(3)
Es gilt Punkt vor Strich“
”
n
X
ai · bi 6=
i=1
n
X
i=1
ai ·
n
X
bi ,
i=1
steht innerhalb des Summenzeichens ein Produkt zweier vom Laufindex abhängiger
Summationsvariablen muss die Multiplikation vor der Summation ausgeführt werden.
21
1M⊙