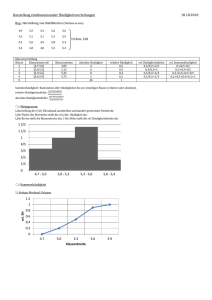
i/n

7. Konzentrations- und Disparitätsmessung
Betrachte:
• Merkmal X, bei dem alle Daten xi ≥ 0 sind und die MerkPn
malssumme i=1
xi eine sinnvolle Interpretation besitzt
(extensives Merkmal)
314
Beispiel:
• X: Haushaltseinkommen
=⇒
Alle xi sind größer oder gleich Null
Pn
i=1 xi ist Gesamteinkommen der Population
Fragestellung:
Pn
• Wie ist die Merkmalssumme i=1 xi auf die einzelnen Merk-
malsträger verteilt?
(Konzentration, Ungleichheit)
315
7.1 Disparität und Konzentration
Jetzt:
• Klärung der Begriffe
Ungleichheit (= Disparität)
Konzentration
316
Messung von Disparität:
• Welcher Anteil der Merkmalssumme fällt auf einen bestimmten
Anteil der Merkmalsträger?
• Beispiel:
Welchen Anteil am Gesamteinkommen einer Bevölkerung vereinigen die 10% Reichsten auf sich?
(Anteil des Gesamt-EK ←→ Anteil der Bevölkerung)
317
Messung von Konzentration:
• Welcher Anteil der Merkmalssumme fällt auf eine bestimmte
Anzahl von Merkmalsträgern?
• Beispiel:
Welchen Anteil am Gesamtumsatz eines Industriesektors haben
die 5 größten Unternehmen?
(Anteil des Gesamtumsatzes ←→ Anzahl von Unternehmen)
318
7.2 Konzentrationsmessung
Wichtige Grundvoraussetzung:
• Die Daten x1, . . . , xn sind absteigend geordnet:
x1 ≥ x2 ≥ . . . ≥ xn ≥ 0
Bemerkungen und Bezeichnungen: [I]
• An dieser Stelle verzichten wir auf die Schreibweise der geordneten Urliste x(n) ≥ x(n−1) ≥ . . . ≥ x(1) ≥ 0
319
Bemerkungen und Bezeichnungen: [II]
• Stattdessen ordnen wir (nötigenfalls) unsere Urliste einfach
so um, dass gilt
x1 ≥ x2 ≥ . . . ≥ xn ≥ 0
• Es bezeichne
xr
xr
hr = n
,
=
X
n·x
xi
r = 1, . . . , n
i=1
den Merkmalsanteil des r-ten Merkmalsträgers an der Merkmalssumme
• Wegen x1 ≥ x2 ≥ . . . ≥ xn ≥ 0 gilt für die Merkmalsanteile:
h1 ≥ h2 ≥ . . . ≥ hn ≥ 0
320
7.2.1 Konzentrationsraten und Konzentrationskurve
Definition 7.1: (Konzentrationsrate i-ter Ordnung)
Die Summe der i größten Merkmalsanteile,
CR(i) =
i
X
r=1
i
X
hr = r=1
n
X
xr
xr
r=1
heißt Konzentrationsrate der Ordnung i. CR(i) ist der Merkmalsanteil, der auf die i größten Merkmalsträger entfällt. Für i = 0
wird CR(0) = 0 gesetzt.
321
Definition 7.2: (Konzentrationskurve)
Zeichnet man für i = 0, . . . , n die Punkte (i, CR(i)) in ein Koordinatensystem und verbindet man die Punkte durch einen linearen
Streckenzug, so erhält man die Konzentrationskurve.
Bemerkung:
• Per Definition beginnt die Konzentrationskurve im Punkt
(0, CR(0)) = (0, 0) und endet im Punkt (n, CR(n)) = (n, 1).
322
Beispiel: [I]
• Fünf Unternehmen eines Marktes weisen die folgenden Umsätze
auf (in Mill. Euro)
x1 = 330,
x2 = 120,
x3 = 90,
x4 = 30,
x5 = 30
Man beachte:
Die Daten sind bereits absteigend geordnet
323
Beispiel: [II]
• Arbeitstabelle:
i
0
1
2
3
4
5
P
xi
hi
330
120
90
30
30
600
0.55
0.20
0.15
0.05
0.05
1.00
CR(i)
0
0.55
0.75
0.90
0.95
1.00
324
Beispiel: [III]
• Verbinden der Punkte (i, CR(i)) ergibt die Konzentrationskurve:
1
CR(i)
0,8
0,6
0,4
0,2
0
0
1
2
3
4
5
i
325
Eigenschaften der Konzentrationskurve: [I]
• Die Konzentrationskurve ist der Graph einer Funktion, die
das Intervall [0, n] auf das Intervall [0, 1] abbildet. Die Funktion ist stückweise linear und streng monoton wachsend vom
Anfangspunkt (0, 0) bis zum Endpunkt (n, 1)
• Die Steigung des r-ten Segmentes (r = 1, . . . , n) beträgt
CR(r) − CR(r − 1)
= hr .
1
Die Steigungen hr nehmen mit wachsendem r ab. Somit ist
die Konzentrationskurve konkav
326
Eigenschaften der Konzentrationskurve: [II]
• Der Fall maximaler Konzentration:
Ein Merkmalsträger vereinigt die gesamte Merkmalssumme
auf sich:
h1 = 1,
h2 = h3 = . . . = hn = 0
Es folgt:
CR(0) = 0,
CR(1) = CR(2) = . . . = CR(n) = 1
327
Eigenschaften der Konzentrationskurve: [III]
• Der Fall minimaler Konzentration (egalitäre Verteilung):
Jeder Merkmalsträger hat denselben Anteil 1/n an der Merkmalssumme. Es gilt:
h1 = h2 = . . . = hn =
1
n
Es folgt:
i
CR(i) = ,
n
i = 0, . . . , n
328
Offensichtlich gilt:
• Jede Konzentrationskurve liegt zwischen den Extremen der
maximalen Konzentration und der minimalen Konzentration
1
CR(i)
0,8
0,6
0,4
0,2
0
0
1
2
3
4
5
i
329
Naheliegende Vorgehensweise:
• Benutze die Konzentrationskurven zweier Grundgesamtheiten
(Märkte) zum Vergleich des Ausmaßes der Konzentration in
beiden Grundgesamtheiten (Märkten), z.B. zum Vergleich
der Konzentration eines Merkmals auf ein und demselben
Markt zu verschiedenen Zeitpunkten
(zeitlicher Vergleich der Konzentration)
der Konzentration eines Merkmals auf zwei unterschiedlichen Märkten zum gleichen Zeitpunkt
(räumlicher Vergleich der Konzentration)
330
Beispiel: [I]
• Umsätze auf 2 Märkten:
Markt I:
38, 12, 106, 34, 10
Markt II:
25, 20, 39, 7, 9
• Man beachte:
Daten müssen zunächst geordnet werden
331
Beispiel: [II]
• Arbeitstabelle:
i
0
1
2
3
4
5
P
xi
hi
106
38
34
12
10
200
0.53
0.19
0.17
0.06
0.05
1.00
CRI (i)
0
0.53
0.72
0.89
0.95
1.00
xi
hi
39
25
20
9
7
100
0.39
0.25
0.20
0.09
0.07
1.00
CRII (i)
0
0.39
0.64
0.84
0.93
1.00
332
Beispiel: [III]
• Konzentrationskurven CRI und CRII :
1
CR(i)
0,8
0,6
0,4
0,2
0
0
1
2
3
4
5
i
333
Offensichtlich:
• Markt I weist gleichmäßig höhere Konzentration als Markt II
auf
Häufiges praktisches Problem:
• Konzentrationskurven CRI und CRII schneiden sich
−→ Kein eindeutiger Konzentrationsvergleich möglich
334
Ausweg:
• Beschreibe Konzentrationsausmaß in einer Grundgesamtheit
durch geeignete Zahlen (Indizes)
−→ Eindeutiger Konzentrationsvergleich durch Vergleich von
Zahlen ist immer möglich
335
7.2.2 Konzentrationsindizes
Hier nur zwei Indizes:
• Herfindahl- und Rosenbluth-Index
Definition 7.3: (Herfindahl-Index)
Die Summe der quadrierten Merkmalsanteile
KH =
n
X
h2
i
i=1
bezeichnet man als Herfindahl-Index.
336
Bemerkungen:
• Der Herfindahl-Index ist normiert. Es gilt
1
≤ KH ≤ 1
n
• Es gilt KH = 1/n genau dann, wenn minimale Konzentration
vorliegt
• Es gilt KH = 1 genau dann, wenn maximale Konzentration
vorliegt
337
Jetzt:
• Index, der die ’Biegung’ der Konzentrationskurve ausnutzt
Erinnerung:
• Bei maximaler Konzentration ist die Konzentrationskurve ’maximal gebogen’
• Bei egalitärer Verteilung ist die Konzentrationskurve gar nicht
gebogen (sondern eine Gerade)
338
Dehalb:
• Fläche A innerhalb des Rechtecks [0, n] × [0, 1], die oberhalb
der Konzentrationskurve liegt, ist sinnvolle Maßzahl für die
Konzentration des Merkmals
’Kleines’ A −→ ’hohe Konzentration’
’Großes’ A −→ ’geringe Konzentration’
Jetzt:
• Formale Berechnung des Flächeninhaltes A
339
Zur Berechnung des Rosenbluth-Index
1
CR(i)
0,8
0,6
0,4
0,2
0
0
1
2
3
4
5
i
340
Zunächst:
• Berechnung der Flächeninhalte A1, . . . , A5
A1 =
2·1−1
h1
= h1 ·
2
2
1
3
2·2−1
A2 = h2 · 2 − · h2 = · h2 = h2 ·
2
2
2
A3 = h3 · 3 −
1
5
2·3−1
· h3 = · h3 = h3 ·
2
2
2
7
2·4−1
1
A4 = h4 · 4 − · h4 = · h4 = h4 ·
2
2
2
A5 = h5 · 5 −
2·5−1
1
9
· h5 = · h5 = h5 ·
2
2
2
341
Allgemein gilt für alle i = 1, . . . , n:
2i − 1
Ai = hi ·
2
Somit folgt für den gesuchten Flächeninhalt A:
n
X
n
X
2i − 1
1
hi ·
A =
=
Ai =
hi · (i − )
2
2
i=1
i=1
i=1
n
X
n
1 X
hi · i −
hi
=
2 i=1
i=1
n
X
=
n
X
i=1
hi · i −
1
2
342
Jetzt:
• Definition eines Konzentrationsindexes basierend auf dem
Flächeninhalt A
Definition 7.4: (Rosenbluth-Index)
Der Rosenbluth-Index ist definiert als
1
1

KR =
.
=
n
2A
X
2
i · hi − 1
i=1
343
Bemerkungen:
• Der Rosenbluth-Index ist normiert. Es gilt
1
≤ KR ≤ 1
n
• Es gilt KR = 1/n genau dann, wenn minimale Konzentration
vorliegt
• Es gilt KR = 1 genau dann, wenn maximale Konzentration
vorliegt
344
7.3 Disparitätsmessung
Wichtige Grundvoraussetzung:
• Die Daten x1, . . . , xn sind aufsteigend geordnet:
0 ≤ x1 ≤ x2 ≤ . . . ≤ xn
(vgl. Folie 319)
345
Weitere Bezeichnungen:
• Wie bei der Konzentrationsmessung bezeichne
xr
hr = n
X
xi
i=1
den Anteil des r-ten Merkmalsträgers an der Merkmalssumme
• Wegen 0 ≤ x1 ≤ . . . ≤ xn gilt für die Merkmalsanteile:
0 ≤ h1 ≤ h2 ≤ . . . ≤ hn
Frage:
• Welchen Anteil an der Merkmalssumme vereinigen bestimmte
Anteile der Population auf sich?
346
7.3.1 Lorenzkurve
Definition 7.5: (Lorenzkurve)
Für i = 1, . . . , n bezeichne
’ “
i
X
i
X
xr
i
hr = r=1
L
=
n
X
n
r=1
xr
r=1
den Anteil der i kleinsten Merkmalsträger an der Merkmalssumme.
Zeichnet man nun die Punkte
’
’ ““ ’
’ ““
’
““
’
2
n−1
1
1
2
n−1
,L
,
,L
,...,
,L
, (1, 1)
(0, 0),
n
n
n
n
n
n
in ein Koordinatensystem und verbindet man diese durch einen
linearen Streckenzug, so erhält man die Lorenzkurve der Daten
x1 , . . . , x n .
347
Bemerkung:
• Die Lorenzkurve ordnet dem Anteil i/n der i kleinsten Merkmalsträger der Population den dazugehörigen Merkmalsanteil
L(i/n) an der Grundgesamtheit zu. Die Lorenzkurve trägt
somit zwei Anteile gegeneinander ab
Beispiel: [I] (vgl. Folie 323)
• Fünf Unternehmen eines Marktes weisen die folgenden Umsätze
auf (in Mill. Euro)
x1 = 330,
x2 = 120,
x3 = 90,
x4 = 30,
x5 = 30
348
Beispiel: [II]
• Umordnung (vom kleinsten zum größten) ergibt folgende Arbeitstabelle:
i
1
2
3
4
5
P
xi
30
30
90
120
330
600
hi
0.05
0.05
0.15
0.20
0.55
1.00
P
L( 5i ) = ir=1 hr
0.05
0.10
0.25
0.45
1.00
349
Lorenzkurve:
1
L(i/n)
0,8
0,6
0,4
0,2
0
0
0,2
0,4
0,6
0,8
1
i/n
350
Eigenschaften der Lorenzkurve: [I]
• Der Graph der Lorenzkurve befindet sich im Einheitsquadrat.
Es gilt L(0) = 0 und L(1) = 1. Die Lorenzkurve ist stückweise
linear, streng monoton wachsend und konvex.
• Der Fall minimaler Disparität (absolute Gleichheit):
Gilt x1 = x2 = . . . = xn, so folgt
h1 = h2 = . . . = hn
Dies impliziert
L(i/n) = i/n,
i = 0, . . . , n
(Lorenzkurve ist die Diagonale im Einheitsquadrat)
351
Eigenschaften der Lorenzkurve: [II]
• Der Fall maximaler Disparität (absolute Ungleichheit):
Die gesamte Merkmalssumme entfällt auf einen (den größten)
Merkmalsträger:
x1 = x2 = . . . = xn−1 = 0,
xn =
n
X
xi
i=1
Es folgt
h1 = h2 = . . . = hn−1 = 0,
hn = 1
Dies impliziert
’ “
’ “
’
“
2
n−1
1
=L
= ... = L
= 0,
L
n
n
n
(Lorenzkurve ist ’maximal’ gebogen)
L(1) = 1
352
Lorenzkurven minimaler und maximaler Disparität:
L(i/n)
1
0
0
1
i/n
353
Es gilt:
• Jede Lorenzkurve liegt zwischen den Extremen der minimalen Disparität (absolute Gleichheit) und der maximalen
Disparität (absolute Ungleichheit)
• Wenn sich zwei Lorenzkurven nicht schneiden, weist die höhere
Lorenzkurve eindeutig weniger Disparität auf als die niedrigere
Lorenzkurve
354
Praktisches Problem:
• Lorenzkurven schneiden sich in vielen Fällen
−→ Kein eindeutiger Disparitätsvergleich möglich
Ausweg:
• Beschreibe Ausmaß der Disparität durch einen Index
−→ Disparitätsvergleich anhand von Zahlen
355
7.3.2 Der Gini-Koeffizient
Bekanntester Disparitätsindex:
• Der Gini-Koeffizient
Intuition:
• Gini-Koeffizient nutzt ’Biegung’ der Lorenzkurve aus
356
Definition 7.6: (Gini-Koeffizient)
Der Gini-Koeffizient (in Zeichen: DG) ist definiert als das Zweifache
der Fläche zwischen der Lorenzkurve und der Diagonalen im Einheitsquadrat.
Formale Darstellung: [I]
• Es bezeichne B die Fläche unterhalb der Lorenzkurve im Einheitsquadrat.
Dann gilt:
’
“
1
− B = 1 − 2B
DG = 2 ·
2
357
Zur Berechnung des Gini-Koeffizienten
L(i/n)
1
0
0
1
i/n
358
Formale Darstellung: [II]
• Man kann zeigen, dass gilt:
B=
n
X
Bi =
i=1
• Damit folgt
DG = 1 − 2B = 1 −
n
X
n
X
i=1
n
X
i=1
hi ·
hi ·
2n − 2i + 1
2n
2n − 2i + 1
n
’
n
X
2n − 2i + 1
2n − 2i + 1
=
=
hi · 1 −
hi −
hi ·
n
n
i=1
i=1
i=1
=
n
X
i=1
n
X
hi ·
2i − n − 1
n
359
“
Bemerkungen:
• Der Gini-Koeffizient ist normiert. Es gilt
0 ≤ DG ≤ 1 −
1
n
• Es gilt DG = 0 genau dann, wenn minimale Disparität (absolute Gleichheit) vorliegt
• Es gilt DG = 1 − 1/n genau dann, wenn maximale Disparität
(absolute Ungleichheit) vorliegt
360
Beispiel: (vgl. Folie 348)
• Gini-Koeffizient für die 5 Unternehmen eines Marktes
Arbeitstabelle:
i
xi
hi
1
2
3
4
5
30
30
90
120
330
600
0.05
0.05
0.15
0.20
0.55
1.00
P
L( 5i ) =
Pi
r=1 hr
0.05
0.10
0.25
0.45
1.00
2i−5−1
5
2i−5−1 h
i
5
−0.8
−0.4
0.00
0.4
0.8
0
−0.04
−0.02
0.00
0.08
0.44
0.46 = DG
361