Titel des Vortrags - Otto Hahn

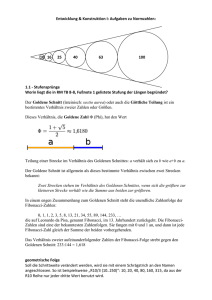
1
Titel des Vortrags:
Der Goldene Schnitt und die Fibonacci – Folge
oder
Der Einfluss der Vermehrungsquote idealer Kaninchen auf
ästhetische Prinzipien der abendländischen Kunst
oder
Wie es fast einmal gelang, den Teufel in einer mathematischen Falle
für immer einzukerkern
Inhalt:
1. Definition und Eigenschaften des
Goldenen Schnittes
2. Konstruktionsverfahren zur
Teilung einer Strecke im
Goldenen Schnitt
3. Auftreten des Goldenen Schnittes
in klassischen geometrischen
Objekten
4. Definition der Fibonacci–Folge und
ihre Bedeutung für den Goldenen
Schnitt
5. Die Bedeutung des Goldenen
Schnittes in der
abendländischen Kunst
6. Auftreten des Goldenen Schnittes
in den Bauplänen der
Natur
2
Verehrte Gäste, liebe Kolleginnen und Kollegen, sehr geehrte Damen
und Herren,
es ist mir eine Ehre, Sie anlässlich der Feiern zum 150-jährigen Bestehen des Otto-Hahn-Gymnasiums Saarbrücken zu diesem Festvortrag begrüßen zu dürfen. Ganz besonders freut es mich, in unserer
Mitte auch ehemalige Schüler unserer Schule, gegenwärtige Schüler
und deren Eltern zu sehen, von denen erstere und letztere wohl in
der Mehrzahl in ihrem nachschulischen Leben von der Mathematik
Abschied nehmen mussten oder durften.
Ich habe mich bemüht, das von mir gewählte Thema „Der Goldene
Schnitt und die Fibonacci-Folge“ so anschaulich und unterhaltsam
darzustellen, dass auch der mathematische Laie an hinreichend
vielen Stellen auf seine Kosten kommt.
Die im heutigen Vortrag behandelten mathematischen Objekte
waren vor einigen Jahren schon einmal Thema einer von mir am
OHG durchgeführten Mathematik-AG und fanden auf Seiten der teilnehmenden Schüler ein bemerkenswertes Interesse. Dies soll auch
den hier anwesenden Eltern zeigen, dass die von außerhalb der
Schule so oft an uns gerichtete Forderung, mit über den Lehrplan
hinaus gehenden Angeboten die Schüler zu fördern, von uns aus
stets bereitwillig erfüllt wird, sofern man uns nur einen hinreichenden zeitlichen und organisatorischen Spielraum hierfür lässt. Dies ist
in den letzten Jahren leider zunehmend nicht mehr der Fall.
Der „Goldene Schnitt“ ist die Lösung des folgenden
elementargeometrischen Problems:
Gegeben ist eine Strecke AB der Länge AB : g und ein
beliebiger Punkt P  AB.
Wir bezeichnen dann die größereTei lstreckenlänge
(oben AP ) mit M (Major ) und die kleinere mit m (min or ).
Es ist dann M  m  g
Bei beliebiger Lage von P sin d dann die beiden Längen 
verhältnisse
AP
PB

AB
M
g
und

verschieden.
gM
M
AP
Im gezeichneten Beispiel ist z.B.
AB
AP

AP
PB
3
Ist aber etwa P der Mittelpunkt von AB, so ist
AB
AP
2
AP
PB
1
Die Aufgabe " Teile die Strecke AB im " Goldenen Schnitt" besagt nun :
Lege den Punkt P so auf AB, dass
AB
AP

AP
PB
ist.
Es soll somit, wenn wir voraussetzen, dass AP das längere Teilstück ist,
gelten :
Gesamtlänge
größere Teilstücklänge

AB
AP

AP
PB

AP
2

größere Teilstücklänge
kleinere Teilstücklänge
*
 AB  PB
 Das Quadrat über dem Major ist inhaltsgleich dem Re chteck
aus der Gesamtstrecke und dem Minor.
Die letztere Formulierung wurde von Euklid(365–300 v.Chr.)
als Definition des Goldenen Schnittes angegeben.
Wir formen nun die Gleichung (*) noch etwas um :
M  M  m  m
2

Setzt man nun  :
Lösung :  2    1
M2
m2

Mm
m

M
 
m
2

M
1
m
M
, so lautet die zu lösende Gleichung :
m
2    1
 2  2 
 
1
  1
2
2

1
5

   
2
4

1
5
1
5

  
2
2
2
2
Da   IR  sein muss, fo lg t
1 5
 1,618033988749894848204586834
2
 ist somit die einzige positive reelle Zahl, die eine der fo lg enden

äquivalenten Eigenschaften besitzt :

   


  

 



 1
  







4
AB mit Länge g wird genau dann im Goldenen Schnitt geteilt,
wenn für Major M bzw. Minor m gilt :

M   g    1  g

bzw.
2

m     g  2     g

Im folgenden Bild ist die Teilung im Goldenen Schnitt realisiert:
------------------------------------------------------------Fasst man das Problem der Teilung einer Strecke im Goldenen
Schnitt als elementargeometrisches Problem auf (Konstruktion
mit Zirkel und Lineal), so gibt es zahlreiche Lösungen, von denen
wir hier zwei präsentieren.
1.Konstruktion:
1. Zeichne die gegebene Strecke AB mit AB  g
2. Konstruiere C auf der Senkrechten zu AB in B mit BC 
g
3. Konstruiere D  CA und D  k C ; 
2


4. Konstruiere P  AB und P  k A ; AD
g
2

Behauptung: P teilt AB im Goldenen Schnitt
Beweis : Es gilt nach dem Satz von Pythagoras :
g 2 5g 2
5

und somit AC 
g
4
4
2
5
1
5 1
 AP  AD  AC  CD 
g 
g

g 
2
2
2
Dies bedeutet aber : P teilt AB im Goldenen Schnitt q.e.d.
AC
2
 AB
2
 BC
2
n.K .
 g2 
-------------------------------
1
g

5
2. Konstruktion (von George Odom, 1982):
Gegeben sei hier nicht AB , sondern AP mit AP  x und die Aufgabe
lautet: Konstruiere
B  AP so, dass P die Strecke AB im Goldenen Schnitt teilt !
Wir verlängern AP zur Geraden g und konstruieren das gleichseitige
Dreieck mit Grundseite AP und Spitze Z. Dann verdoppeln wir
ZA und ZP über A und P hinaus bis zu X bzw. Y und erhalten das
gleichseitige Dreieck XYZ mit der Seitenlänge 2x und konstruieren
dessen Umkreis. Dieser schneidet die Gerade g in C und B, wobei B
so liegt, dass P AB ist.
Behauptung: P teilt AB im Goldenen Schnitt
Beweis : XYZ ist gleichseitig mit Seitenlänge 2x, denn es ist
n.K .
ZX  ZY  2x und somit YXZ  ZYX 
1
2
 180  YZX 

1
2
 180  60  60
Da MZ die Mittelsenkrechte sowohl von CB als auch von
AP ist,
gilt: CA  CR  AR  BR  PR  BP  y
Wir betrachten nun den Punkt P als Punkt im Inneren des Umkreises
von XYZ. Durch ihn führen die beiden Sehnen ZY und CB.
Dann gilt nach dem Sehnensatz:
6
ZP  PY  PB  PC , wobei ZP  PY  x
und PB  y und PC  x  y ist. Somit ist x 2  y  x  y .
Hieraus fo lg t aber nach Division beider Seiten durch y 2 :
x
 
y
2

x
1
y
2
 AP 
  AP  1
Es ist also 
 PB 
PB


Dies bedeutet aber  wie vorne gezeigt  : P teilt AB im Goldenen Schnitt.
---------------------------------------------------------Wir gehen nun auf einige bemerkenswerte Beziehungen zwischen
dem Goldenen Schnitt und dem regelmäßigen (regulären) Fünfeck
ein (Ein n-Eck heißt regulär genau dann, wenn alle seine Seiten
maßgleich und zugleich alle seine Innenwinkel maßgleich sind).
Man beweist nun leicht den folgenden Satz:
7
Satz: Sei F  P1P2P3P4P5 ein reguläres Fünfeck. Dann gilt:
a) Jeder Innenwinkel hat das Maß108°
b) Alle Diagonalen sind maßgleich
c) Jede Seite ist parallel zu derjenigen Diagonalen, die nicht
in einem der Endpunkte dieser Seite beginnt
(Wir nennen diese die gegenüberliegende Diagonale)
d) Die beiden von einer Ecke ausgehenden Diagonalen teilen
den Innenwinkel an dieser Ecke in drei maßgleiche Teil winkel vom Maß 36°
e) Je zwei Diagonalen, die keinen gemeinsamen Anfangspunkt
haben, teilen sich gegenseitig im Goldenen Schnitt
f) Das Verhältnis der Diagonalenlänge d zur Seitenlänge a ist der
Goldene Schnitt
g) Die „inneren“ Diagonalenschnittpunkte bilden selbst ein reguläres Fünfeck, dessen Seiten parallel zur jeweils gegenüber
liegenden Seite von F sind, und dieses innere Fünfeck hat die
2
 1
a1     a  2     a

h) In diesem inneren Fünfeck lassen sich nun wiederum die Diagonalen zeichnen und diese erzeugen ein inneres Fünfeck
„zweiter Ordnung“ mit der Seitenlänge
Seitenlänge
2
4
 1
 1
a 2     a1     a  2   2  a  5  3   a


Setzt man dieses Verfahren fort, so erhält man eine unendliche
Folge ineinander geschachtelter regulärer Fünfecke mit
„Diagonalensternen“, deren Seitenlänge
2n
 1
an     a für n  

auf den Grenzwert Null hin schrumpft
i) Das ursprüngliche Fünfeck F lässt sich aber auch nach außen hin
„aufblasen“ zu einem „umgebenden“ Fünfeck, welches das gegebene Fünfeck F als inneres Diagonalenfünfeck besitzt; verlängert
man nämlich je zwei nicht benachbarte Seiten von F bis zu ihrem
Schnittpunkt, so bilden die so entstehenden Schnittpunkte ein
reguläres Fünfeck und dieses hat die Seitenlänge
a1   2  a
Auch diese Konstruktion lässt sich zu einer unendlichen Serie
regulärer Fünfecke mit den Seitenlängen
an   2n  a , wobei an   für n   gilt.
8
Diese Eigenschaften machten das aus den Diagonalen gebildete
„Sternfünfeck“ zu einer magischen Figur; es ist das bekannte
„Hexenpentagramm“ und wird auch als „Drudenfuß“ bezeichnet
(Schutzamulett gegen die Druden = Geister des Alpdruckes).
Die labyrinthische Schachtelung in der oben zu sehenden
Konstruktion ließen das Pentagramm als „Teufelsfalle“ in Goethes
„Faust“ Eingang finden, aus der Mephisto in der StudierzimmerSzene nur zu entkommen vermag, indem er eine Ratte zu Hilfe ruft,
welche eine Ecke des Pentagrammes aufnagt:
Mephisto:
Gesteh ich’s nur!
dass ich hinausspaziere
verbietet mir ein kleines Hindernis,
der Drudenfuß auf Eurer Schwelle ...
Faust:
Das Pentagramma macht dir Pein?
Anmerkung: Der Goldene Schnitt tritt auch in vielfältiger Weise bei
den fünf Platonischen Körpern und deren Beziehungen untereinander
und zu Goldenen Rechtecken und regelmäßigen Fünfecken auf.
9
Das Ikosaeder besitzt eine Oberfläche aus 20 zueinander kongruenten gleichseitigen Dreiecken, von denen jeweils 5 in einer der 12
Ecken zusammenstoßen.
Die 12 Ecken des Ikosaeders bilden die Ecken von drei gleich
großen, senkrecht aufeinander stehenden Rechtecken mit gemeinsamem Mittelpunkt und mit den Seitenverhältnissen des Goldenen
Schnittes.
Die Anordnung der drei Rechtecke heißt auch
Goldener-Schnitt-Stuhl.
------------------------------------------------------------Die Fibonacci-Folge und ihre Beziehung zum Goldenen Schnitt
(1) Anmerkung: Im Jahre 1202 veröffentlichte Leonardo von Pisa
(1175 – 1250), der den Beinamen Fibonacci (= filius Bonacci –
Sohn des Bonacci) hatte,das Buch „Liber abaci “(Buch des
Abakus; Abakus = Handrechenmaschine).
Ein Hauptziel dieses Buches war es, die Überlegenheit des
arabischen Zahlensystems gegenüber dem römischen zu
demonstrieren.
Berühmt wurde dieses Buch nicht zuletzt durch die folgende,
scheinbar belanglose Aufgabe.
(2) Das Kaninchenproblem:
Zur Zeit 0 lebt ein Kaninchenpaar vom Alter 0 Monate, das sich
nach dem folgenden Gesetz vermehrt:
(i) Jedes Kaninchenpaar (Männchen und Weibchen) gebiert im Alter
von 2 Monaten erstmals und von da an nach jedem weiteren
Monat genau ein Paar (Männchen und Weibchen)
(ii) Alle Kaninchen leben ewig
Frage: Wie groß ist die Anzahl fn der Kaninchenpaare zu Beginn des
n-ten Monats?
Wir erweitern diese Fragestellung um die folgende
10
Frage:
Wie entwickelt sich die monatliche Zuwachsrate
fn 1
der
fn
Kaninchenpaare im Laufe der Zeit?
(3) Die Antwort auf die erste Frage liefert der folgende Satz, den wir
leicht beweisen können:
Satz: Es gilt für alle n  IN: fn 2  fn 1  fn
Beweis:
fn  2 = Anzahl der Paare, die zu Beginn des (n+2)-ten Monats leben
= Anzahl der Paare, die schon zu Beginn des (n+1)-ten Monats
lebten
+
Anzahl der soeben neugeborenen Paare
= fn  1 + Anzahl der Paare, die jetzt mindestens zwei Monate alt
= fn  1
sind
 fn
q. e . d.
---------------------------------(3) Folgerung : Aus f1  1 und f2  1 fo lg t nun :
f3  2 , f4  3 , f5  5 , f6  8 , f7  13 , f8  21 , f9  34 , f10  55 ...
f20  6765 ,... f30  832 040 , ... f40  102 334 155 , ...
f50  12 586 269 025 ...
Man kann so jede beliebige Fibonacci-Zahl fn berechnen. Ein Nachteil des Ergebnisses aus dem obigen Satz ist allerdings, dass zur
Berechnung von fn  2 alle vorhergehenden Werte f1 , f2 , ... fn  1
berechnet werden müssen. Diesen Nachteil werden wir später durch
eine bessere Formel beseitigen können.
------------------f
(4) Für die interessierende Zuwachsrate n 1 der Kaninchenpaare
fn
erhält man zunächst durch simples „Probieren“:
f8
f3
f2
 1,6154 ,
1
,
2,
f7
f1
f2
f10
f4
f5
 1,5
,
 1, 6 ,
 1,6176 ,
f3
f4
f9
f6
 1,6 ,
f5
f7
 1,625
f6
f12
 1,61798 ,
f11
f9
 1,61190 ,
f8
f11
 1,6182 ,
f10
f13
 1,61806
f12
11
Zur Erinnerung: Der Goldene Schnitt ist
1 5

 1,61803398874989484820...
2
Beobachtung:
Die Zahl  liegt in jedem der obigen Intervalle der Form
 f2n f2n  1 

 und diese Intervalle werden mit wachsender Nummer n
 f2n 1 f2n 
stetig kürzer.
Man kann nun in der Tat mit etwas algebraischem Aufwand den
folgenden Satz beweisen:
Satz: Die Folge der Intervalle
 f2n f2n  1 


 f2n 1 f2n 
ist eine Intervallschachtelung; d.h.:
das nachfolgende Intervall liegt ganz im jeweils vorhergehenden und
die Länge der Intervalle wird mit wachsendem n beliebig klein.
Der Goldene Schnitt  liegt in jedem dieser Intervalle und somit ist
f2n  1
f
  lim 2n  lim
n f
n
f2n
2n  1
------------------(5) Die oben erwähnte verbesserte Berechnungsformel für die
Fibonacci-Zahlen fn stammt nach Coxeter von dem französischen
Mathematiker Jacques Philippe Marie Binet(1786-1856). Es gibt
aber auch Autoren, die sie De Moivre(1718) und ihren Beweis
Nicolas Bernoulli (1728) zuschreiben. Diese Formel lautet:
n
 1
   
n
n
1 5  1 5


fn 

5
2n  5
Für große n ergibt dies für fn die gute Näherungsformel
n

fn 



n
5
und es gilt sogar für alle nIN:
fn
Beispiel f20
n 1
 größte ganze Zahl, die 

ist
5 2
 20 1
 größte Zahl  IN, die 
  6765,50003 ist  6765
5 2
------------------------------
12
Die Kettenbruchentwicklung von 
und ihre Beziehung zur Fibonacci-Folge
Aus der Beziehung   1 
1
ergibt

sich die folgende Kettenbruchentwicklung für den Goldenen Schnitt:
Bricht man diese Entwicklung nach dem n-ten Schritt ab, so erhält
man die folgenden Näherungswerte für :
f
f
1  1  2
2  2  3
f1
f2
3 
3 f4

2
f3
und al lgemein  n 
4 
f
5
 5
3 f4
fn  1
fn
------------------------------Die Bedeutung des Goldenen Schnittes in der abendländischen
Kunst
In der Kunst und Architektur wird der Goldene Schnitt oft als ideale
Proportion verschiedener Längen zueinander angesehen. Er gilt als
Inbegriff von Ästhetik und Harmonie. Darüber hinaus tritt das
Verhältnis des Goldenen Schnittes auch in der Natur in Erscheinung
und zeichnet sich durch eine Reihe interessanter mathematischer
Eigenschaften aus. Weitere verwendete Bezeichnungen sind stetige
Teilung und göttliche Teilung (lat. proportio divina).
13
Beispiele:
a) die Vorderfront des 447–432 v. Chr.
unter Perikles erbauten
Parthenon-Tempels auf der
Athener Akropolis
b) die Kathedrale von Chartres (1194 – 1220)
14
c) das Freiburger Münster (1200 – 1513)
Turmhöhe = g; Turmhelm = m
g–m=M
g : M = M : m =  und
Säulenabstand Nord-Süd :
Säulenabstand Ost-West = 
15
d) das Rathaus von Leipzig
(1556/57, Hieronymus Lotter)
Die Turmachse teilt die Vorderfront im Goldenen Schnitt
e) Säulenkapitell im Hadriansbogen (Athen, 2.Jh.n.Chr.)
16
f) Aphrodite von Melos (150 - 100 v. Chr.)
g) Leonardo da Vinci (1452 – 1519)
Proportionsstudie nach Vitruv (1492)
Körpergröße : Nabelhöhe = 
17
h) Leonardo da Vinci (1452 – 1519)
Mona Lisa
„Goldenes“ gleichschenkliges Dreieck
Schenkellänge : Basislänge = 
i) Raffael (1483 – 1520)
Triumph der Galatea (um 1511)
18
j) Salvador Dali (1904 – 1989)
Riesige Mokkatasse, fliegend, mit unerklärlicher Fortsetzung von
5 Metern Länge
Bildformat: Goldenes Rechteck, zerlegt in ein Quadrat und ein
weiteres Goldenes Rechteck, das wiederum durch die rechte
vertikale Würfelkante in ein Quadrat und ein drittes Goldenes
Rechteck zerlegt wird. Dieses wird durch die obere horizontale
Würfelkante der Vorderfläche in ein weiteres Quadrat und ein viertes
Goldenes Rechteck zerlegt. Der linke vertikale Rand der Tasse
schließlich zerlegt das vierte Goldene Rechteck in ein Quadrat und
ein fünftes Goldenes Rechteck. Der untere horizontale Rand der
Tasse endlich zerlegt das 5. Goldene Rechteck in ein Quadrat und
ein 6.Goldenes Rechteck. (  Goldene Spirale)
19
k) Salvador Dali – Halocigenous Bullfighter
l) Goldener Schnitt bei Gebrauchsgegenständen
-------------------------------------------------------------
20
Der Goldene Schnitt und
die Fibonacci-Zahlen in der Natur
(1): Bei vielen Pflanzen trifft man auf das folgende Phänomen:
Ihre Samen sind, von einem Zentrum ausgehend, in rechtsdrehenden und linksdrehenden Spiralen angeordnet.
Dabei sind seltsamerweise die Anzahlen der rechts- und der linksdrehenden Spiralen stets zwei aufeinander folgende Fibonacci
Zahlen.
Der Grund hierfür liegt darin, dass auf kleiner Fläche die Anzahl der
Samen maximiert wird, wenn das Keimzentrum den jeweils nächsten
Samen stets um den „Goldenen Winkel“
= 360° : 
222,5°
bzw. * = 360° 137,5° versetzt entstehen lässt.
Dieser Winkel wiederum kann am besten dann näherungsweise
erreicht werden, wenn die Anzahlen der rechts- und linksdrehenden
Spiralen zwei benachbarte Fibonacci-Zahlen sind, denn deren Verhältnis ergibt mit größer werdenden Zahlen immer bessere
Näherungswerte für .
(2): Die Blattansätze am Stängel einer Pflanze verschieben sich in
der Höhe und von einem Blatt zum nächsten um einen bestimmten
Drehwinkel . Dieser ist bei vielen höheren Pflanzenarten der
Goldene Winkel
= 360° :  222,5° bzw.
* = 360° - 222.5° = 137,5°.
Weil hierbei zwei Blätter in unterschiedlicher Höhe nie senkrecht
übereinander stehen, kann das einfallende Sonnenlicht optimal
genutzt werden und die Belüftung wird ebenfalls optimiert.
21
Seitliche Ansicht
Draufsicht
===============================
Ich bedanke mich für Ihre Aufmerksamkeit und wünsche Ihnen einen
guten Nachhauseweg.