Schulcurriculum Mathematik, Jahrgang 7, gemäß Kerncurriculum

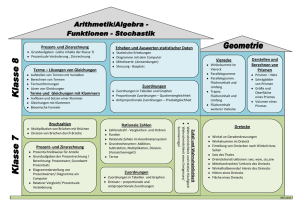
Schulcurriculum Mathematik, Jahrgang 7, gemäß Kerncurriculum Mathematik 2015, Stand 19.01.2016
zum eingeführten Lehrwerk: Elemente der Mathematik 7, Schroedel, ISBN 978-3-507-88594-3
Reihenfolge der Themen:
Der Themenbereich „Geometrie“ ist ab dem Schuljahr 2016/2017 verbindlich für alle 7. Klassen als erstes zu unterrichtendes Thema festgelegt
Der Themenbereich „Wahrscheinlichkeiten“ ist ab dem Schuljahr 2016/2017 verbindlich für alle 7. Klassen als letztes zu unterrichtendes Thema festgelegt.
Thema: Geometrie (8 Wochen)
Themenbereich
Inhaltsbezogene Kompetenzen lt. KC
und weitere Anmerkungen zu inhaltlichen Vereinbarungen
Prozessbez. Kompetenzen
und methodische Hinweise
Kongruente Figuren
(Kap. 4.1, 4.2, 4.3)
Die Schülerinnen und Schüler...

erkennen und begründen Kongruenz

formulieren Aussagen zur Lösbarkeit und Lösungsvielfalt bei Konstruktionen

ermitteln Längen durch Konstruktion maßstäblicher Figuren

konstruieren mit Zirkel, Geodreieck und DGS, um ebene Figuren zu erstellen und reproduzieren.
M1: Einführung der
Kongruenzsätze
M2: Festigung der
Kongruenzsätze
Inhaltliche Vereinbarungen:
Begriff Kongruenz
Zusammenhang zu den Kongruenzabbildungen (Klasse 6) herstellen
vier Dreieckskonstruktionen, Kongruenzsätze
Anwendungen
Winkel, besondere
Linien und Punkte bei
ebenen Figuren
(Kap. 4.4, 4.5)
Kreis und Gerade:
Besondere Punkte
und Linien
(Kap. 4.6)
Die Schülerinnen und Schüler...

konstruieren mit Zirkel, Geodreieck und DGS, um ebene Figuren zu erstellen/zu reproduzieren.

wenden Eigenschaften von Ortslinien zur Lösung von Sachproblemen an.

beschreiben und erzeugen Parallele, Mittelsenkrechte und Winkelhalbierende als Ortslinien.

kennen Höhen, Mittelsenkrechte, Seitenhalbierende und Winkelhalbierende als besondere Linien
deren Schnittpunkte als besondere Punkte im Dreieck.und

Optional: Konstruktion besonderer Vierecke
Inhaltliche Vereinbarungen:
Mittelsenkrechte, Winkelhalbierende, Mittelparallele als Ortslinien
Inkreis und Umkreis
Seitenhalbierende, Schwerpunkt, Höhen
Bearbeitung von Sachproblemen
Optional: Parallelogramm, Trapez
Die Schülerinnen und Schüler...

begründen den Zusammenhang zwischen Umfangs- und Mittelpunktswinkel im Kreis

begründen damit den Satz des Thales

wenden den Satz des Thales für besondere Tangentenkonstruktionen an
Inhaltliche Vereinbarungen:
Umfangs- und Mittelpunktswinkel (nicht im Buch)
Satz des Thales
Tangentenkonstruktion mit Zirkel und Lineal (nicht im Buch)
M3: Cabri Junios mit dem TI-84
M4: Seitenhalbierende im
Dreick
Thema: Zuordnungen, proportionale und antiproportionale Zusammenhänge (5 Wochen)
Themenbereich
Inhaltsbezogene Kompetenzen lt. KC
und weitere Anmerkungen zu inhaltlichen Vereinbarungen
Prozessbez. Kompetenzen
und methodische Hinweise
Graphen (lesen und
darstellen) und
Tabellen (Kap.1.1 bis
1.2)
Die Schülerinnen und Schüler…
 erkennen Zuordnungen zwischen Zahlen und zwischen Größen in Tabellen, Graphen,
Diagrammen und Sachtexten
Mathematische
Darstellungen verwenden:
- Darstellungsformen wie
Tabellen, Skizzen oder
Graphen zur Problemlösung
nutzen
Inhaltliche Vereinbarungen
 Graphen lesen, beschreiben und interpretieren
 Graphen anhand von Tabellen erstellen und umgekehrt
 Graphen Anwendungsbezügen zuordnen und Graphen anhand von Sachsituationen erstellen
 Einführung des Begriffs Zuordnung
 verschiedene Darstellungen von Zuordnungen nutzen und zwischen ihnen wechseln (Tabelle,
Graph (kartesisches Koordinatensystem), Zuordnungsvorschrift)
Proportionale
Die Schülerinnen und Schüler…
Zuordnungen und
 identifizieren und klassifizieren proportionale und antiproportionale Zuordnungen in Tabellen,
antiproportionale
Graphen und Rechenvorschriften (Quotientengleichheit).
Zuordnungen (Kap.1.3
 nutzen proportionale und antiproportionale Zuordnungen als Mittel zur Beschreibung
bis 1.8)
quantitativer Zusammenhänge.
 wechseln proportionale und antiproportionale Zuordnungen in Tabellen, als Graphen und durch
Rechenvorschriften darstellen und zwischen diesen Darstellungen.
 modellieren Sachsituationen durch proportionale bzw. antiproportionale Zuordnungen.
 wenden den Dreisatz an.
 wenden die Eigenschaften der proportionalen und antiproportionalen Zuordnungen zur Lösung
von Problemen an und bewerten die Lösungen.
Inhaltliche Vereinbarungen
 Eigenschaften der proportionalen und der antiproportionalen Zuordnungen erkennen und diese
anhand von Tabelle und Graph verdeutlichen und überprüfen
 Nachweis der Proportionalität bzw. der Antiproportionalität durch die Quotientengleichheit
(Proportionalitätsfaktor) bzw. durch die Produktgleichheit
 Zuordnungsvorschrift bestimmen und mit dieser rechnen
 Rechen mit dem Dreisatz
 Anwendungen der Zuordnungen
Mathematische
Darstellungen verwenden:
- einfache, auch nicht durch
Terme zu beschreibende
Zuordnungen durch Tabellen
oder Graphen darstellen,
solche Darstellungen
interpretieren und nutzen
Mit symbolischen, formalen
und technischen Elementen
der Mathematik umgehen
- nutzen Taschnerechner zum
Erstellen von Tabellen und
Zeichnen von Graphen
Mathematisch modellieren:
- Modellannahmen in
Sachaufgaben finden,
beschreiben und nutzen
- einem mathematischen
Modell eine passende
Realsituation zuordnen
Mathematisch argumentieren
- die im Modell gewonnenen
Ergebnisse im Hinblick auf die
Realsituation überprüfen
Thema: Prozent- und Zinsrechnung (2 Wochen)
Themenbereich
Inhaltsbezogene Kompetenzen lt. KC
und weitere Anmerkungen zu inhaltlichen Vereinbarungen
Relativer Vergleich,
Grundwert –
Prozentsatz –
Prozentwert (Kap.2.12.4)
Die Schülerinnen und Schüler…
 deuten Prozentangaben als Darstellungsform für Brüche und führen Umwandlungen durch (auch
über 100%).
 lösen Grundaufgaben der Prozent- und Zinsrechnung mit dem Dreisatz.
Geld und Prozente,
Prozente im Alltag
(Kap. 2.5 und 2.7)
Prozessbez. Kompetenzen
und methodische Hinweise
Mathematisch modellieren
- Verwenden geometrischer
Objekte, Diagramme, Tabellen,
relative Häufigkeiten zur
Ermittlung von Lösungen im
Inhaltliche Vereinbarungen
mathematischen Modell
Mit symbolischen, formalen
 Wiederholung des Umgangs mit Anteilen, Prozentangaben, Kreisdiagrammen
und technischen Elementen
 Einführung der Begriffe Grundwert, Prozentsatz und Prozentwert und deren Berechnung
der Mathematik umgehen
Die Schülerinnen und Schüler …
- Erstellen von Diagrammen
 deuten Prozentangaben als Darstellungsform für Brüche und führen Umwandlungen durch (auch
und Daten ablesen
über 100%) und nutzen dies zur Lösung von Anwendungsproblemen.
Inhaltliche Vereinbarungen:
 Einführung der Begriffe Kapital, Darlehen, Zinssatz, Jahreszinsen, Tageszinsen und deren
Berechnung
 Prozent- und Zinsrechnung in der Anwendung
Thema: Rationale Zahlen (6 Wochen)
Themenbereich
Inhaltsbezogene Kompetenzen lt. KC
und weitere Anmerkungen zu inhaltlichen Vereinbarungen
Prozessbez. Kompetenzen
und methodische Hinweise
Negative Zahlen
Die Schülerinnen und Schüler…
beschreiben
 begründen die Notwendigkeit der Zahlbereichserweiterungen von natürlichen zu ganzen und
Situationen und
rationalen Zahlen an Beispielen.
Vorgänge, Anordnung
 rechnen mit Zahlen in Sachsituationen (Zustandsänderungen).
und Betrag an der
 tragen Zahlenwerte an die Zahlengerade.
Zahlengeraden
 ordnen und vergleichen rationale Zahlen.
(Kap.3.1 – 3.4)
 erweitern das Koordinatensystems
Inhaltliche Vereinbarungen
 negative Zahlen in der Anwendung als Beschreibung von Zuständen und Veränderungen
 Ausweitung des Zahlenstrahls zur Zahlengeraden

Ablesen und Markieren von rationalen Zahlen auf der Zahlengeraden
 Einführung der Begriffe Betrag und Gegenzahl (Spiegelzahl)
 Ordnen von rationalen Zahlen
 Menge der rationalen Zahlen
Probleme mathematisch
lösen:
- deuten ihre Ergebnisse in
Bezug auf die urspüngliche
Problemstellung und beurteilen
sie durch
Plausibilitätsüberlegungen
Mathematisch argumentieren
- einfache mathematische
Sachverhalte, Begriffe, und
Zusammenhänge mit eigenen
Worten und geeigneten
Fachbegriffen erläutern
Grundrechenarten
(Kap. 3.5 bis 3.9)
Mathematisch argumentieren
- einfache mathematische
Regeln und Verfahren und mit
eigenen Worten und
geeigneten Fachbegriffen
erläutern
Die Schülerinnen und Schüler…
 lösen einfache Rechenaufgaben im Kopf.
 addieren, subtrahieren, multiplizieren und dividieren schriftlich und potenzieren mit einfachen
natürlichen Exponenten.
 nutzen Rechengesetze zum vorteilhaften Rechnen.
 lösen Klammern auf (Vorzeichen / Rechenzeichen).
 nutzen das Runden sowie Überschlagsrechnungen in Sachzusammenhängen.
Inhaltliche Vereinbarungen
 Einführung der Grundrechenarten mit rationalen Zahlen
 Hinweis: Einführung mit Hilfe der Zahlengeraden
 Terme mit rationalen Zahlen berechnen
 Potenzen mit rationalen Zahlen
Thema: Gleichungen (8 Wochen)
Themenbereich
Inhaltsbezogene Kompetenzen lt. KC
und weitere Anmerkungen zu inhaltlichen Vereinbarungen
Lösen von
Gleichungen und
Ungleichungen
(Kap. 6.1-6.4)
Die Schülerinnen und Schüler...

beschreiben Sachverhalte durch Gleichungen und Ungleichungen.

nutzen Gleichungen zur mathematischen Argumentation.

modellieren inner- und außermathematische Problemsituationen mit Hilfe von (Un-)Gleichungen.

lösen lineare (Un-)Gleichungen

lösen Gleichungen in Sachzusammenhängen durch Probieren und unter Verwendung des TRs.

untersuchen Fragen der Lösbarkeit von (Un-)Gleichungen und formulieren diesbezüglich Aussagen.

nutzen die Probe zur Kontrolle und beurteilen die Ergebnisse.
Inhaltliche Vereinbarungen:
Aufstellen von Gleichungen
Begriffe Lösung, Lösungsmenge
Sonderfälle: leere Menge und unendlich viele Lösungen
Begriff äquivalent
Strategieentwicklung zur algebraischen Lösung einer (Un-)Gleichung
Anwendungen, Modellieren von Sachsituationen
Prozessbez. Kompetenzen
und methodische Hinweise
Thema: Wahrscheinlichkeiten (3-4 Wochen)
Themenbereich
Inhaltsbezogene Kompetenzen lt. KC
und weitere Anmerkungen zu inhaltlichen Vereinbarungen
Voraussagen mit
Die Schülerinnen und Schüler...
relativen Häufigkeiten
 identifizieren einstufige Zufallsexperimente und führen eigene durch.
(Kap. 5.1)
 ordnen Ergebnisse von Zufallsexperimenten Wahrscheinlichkeiten zu, einerseits durch
Symmetriebetrachtungen und andererseits durch Schätzen von relativen Häufigkeiten für lange
Versuchsserien.
Inhaltliche Vereinbarungen:
 Einführung der Begriffe Zufallsexperiment, Wahrscheinlichkeit, Gesetz der großen Zahlen
 Wiederholung der Grundbegriffe, absolute und relative Häufigkeit
 Unterschied zwischen der relativen Häufigkeit und Wahrscheinlichkeit
Theoretische
Wahrscheinlichkeiten
(Kap. 5.2, 5.3, 5.4)
Die Schülerinnen und Schüler...
 geben Wahrscheinlichkeiten an.
 begründen und wenden die Additions- und Komplementärregel zur Ermittlung von
Wahrscheinlichkeiten an.
 nutzen Wahrscheinlichkeiten als Prognosen für absolute Häufigkeiten von Ereignissen.
 bestimmen Wahrscheinlichkeiten bei komplexen Zufallsexperimenten durch Simulationen,
gestützt durch digitale Mathematikwerkzeuge
Inhaltliche Vereinbarungen:
 Einführung und Anwendung der Begriffe Ergebnis, Ergebnismenge, Ereignis, Gegenereignis
 Laplace-Experimente erkennen und benennen
 Wahrscheinlichkeiten berechnen inklusive der Summen- und Komplementärregel
Prozessbez. Kompetenzen
und methodische Hinweise
Mathematisch
argumentieren:
- beschreiben, begründen und
beurteilen Zuordnungen von
Wahrscheinlichkeiten zu
Zufallsexperimenten
(Vermutungen im Vorfeld
aufstellen)
Kommunizieren:
- dokumentieren ihre Arbeit
und aus dem Unterricht
erwachsene Merksätze und
Ergebnisse unter Verwendung
geeigneter Medien
Achtung: Der Taschenrechner wird in diesem Jahrgang eingeführt!
Taschenrechnerfähigkeiten, die die Schüler am Ende der Jahrgangsstufe 7 können müssen:
HOME-Fenster
MATH-Fenster
Y-Menü
TABLE-SET-Menü
TABLE-Menü
WINDOW-Menü
GRAPH-Menü
TRACE
Übliche Rechnungen
Prioritäten der Rechenoperationen
Frac-Operator (zur Bruchrechnung)
Beispielsaufgabe:
Im Supermarkt ist Sportlersalami im Angebot. 100g kosten 1,29€.
Erstelle mithilfe des Taschenrechners eine Tabelle, aus der man ablesen kann, was 50g,
150g, und 250g Salami kosten.
Schüler-Musterlösung:
Eingabe im „y=“-Menü: y1=0,0129x.
Angabe der Werte im TableSetup Menü, z.B.:
TblStart=50
ΔTbl=100
Angabe der Werte aus dem Table-Menü
Y
Y1
50
0,645
250
3,225
150
1,935
Das bedeutet, dass 50g Salami 0,65€, 150g Salami 1,94€ und 250g Salami 3,23€ kosten.
Verbindliche Dokumentation für in Klasse 7 eingeführte Funktionen:
Die angegebene Form der Dokumentation ist bei schriftlichen Arbeiten Teil der Lösung und muss mit angegeben werden. Grundsätzlich sollte der Einsatz des
Taschenrechners nach folgendem Muster notiert werden:
1. Wenn nötig (insbesondere bei Anwendungsaufgaben): mathematische Beschreibung des Problems
2. Nennung der Taschenrechnereingaben (nur Befehle, keine Tastenkombinationen)
3. Aufschreiben der Taschenrechnerausgabe
4. „Rückübersetzung“ der Ausgabe auf das untersuchte Problem