Kachelungen, die mit Nachbar

Kachelungen,
die mit Nachbar-Bewegungen erzeugt werden
Edzard Salow
1. Beispiel
Unter einer Kachel verstehen wir in diesem Text ein Polygon (n-Eck), bei dem zwei
verschiedene Seiten höchstens einen Punkt gemeinsam haben. Einen gemeinsamen Punkt
verschiedener Seiten bezeichnen wir als 'Eckpunkt'. Das Innere einer Kachel ist nicht leer (wie
z. B. bei einem Zweieck). Die Seiten jeder Kachel seien gegen den Uhrzeigersinn von 1 bis zur
Seitenanzahl n ∈ N nummeriert oder im Uhrzeigersinn von −1 bis − n . Zwei Kacheln, die sich
nur in dieser Nummerierung unterscheiden, werden als verschieden angesehen. Die Seite mit
der Nummer 1 oder −1 markieren wir in allen Zeichnungen durch einen Halbpfeil, der auch
den Durchlaufsinn des Randes bei der Nummerierung festlegt. Im Folgenden denken wir uns
auch den anderen Seiten Halbpfeile zugeordnete, die zu diesem Durchlaufsinn passen.
Abb. 1
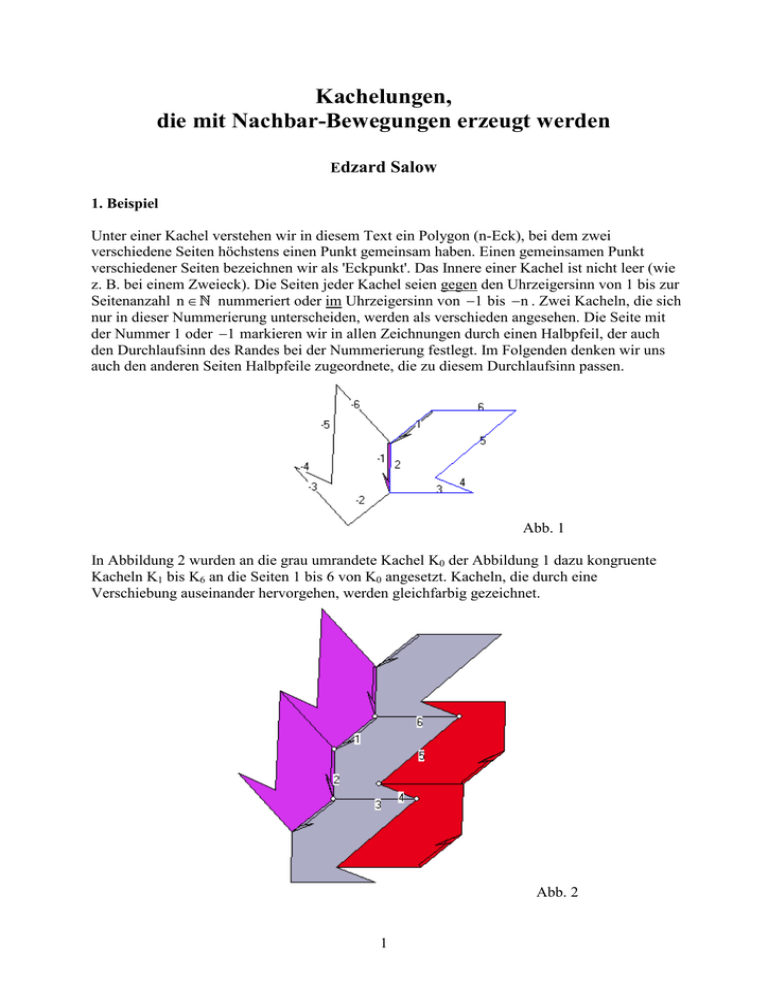
In Abbildung 2 wurden an die grau umrandete Kachel K0 der Abbildung 1 dazu kongruente
Kacheln K1 bis K6 an die Seiten 1 bis 6 von K0 angesetzt. Kacheln, die durch eine
Verschiebung auseinander hervorgehen, werden gleichfarbig gezeichnet.
Abb. 2
1
Bei K2 hat sich der Umlaufsinn gegenüber K0 verändert, so dass die Seiten von -1 bis -6
nummeriert werden. Die Bewegung, die K0 in K2 abbildet, ist ungerade. Da die Seite -1 von K2
mit der Seite 2 von K0 zusammenfällt, ist diese Bewegung die Gleitspiegelung, die die Seite 1
von K0 auf die Seite 2 von K0 abbildet. Das ist nur deshalb möglich, weil diese beiden Seiten
gleich lang sind. Die Kachel K1 entsteht aus K0 durch Anwendung der inversen
Gleitspiegelung, die die Seite 2 von K0 in die Seite 1 von K0 überführt. K3 ist das Bild der
Verschiebung, die die Seite 6 von K0 auf die Seite 3 von K0 abbildet. K4 und K5 entstehen aus
K0 durch Spiegelung an den Mittelpunkten der Seiten 4 und 5 von K0. K6 ergibt sich durch
Verschiebung der Seite 3 in die Seite 6 von K0. Bei den Kacheln K3 bis K6 hat sich der
Umlaufsinn gegenüber K0 nicht verändert, die zugehörigen Bewegungen sind also gerade. Das
Verfahren des Ansetzens kann man kurz so beschreiben:
2 in 1 ungerade
1 in 2 ungerade
6 in 3 gerade
4 in 4 gerade
5 in 5 gerade
3 in 6 gerade
Abb. 3
2
oder noch kürzer durch die Zahlenfolge -2-16453. Diese Zahlenfolge bezeichnen wir als
'Signatur' des Ansetzungsverfahrens. Sie stellt einen Zusammenhang zwischen den
Seitennummern von K0 und den Nummern der anschließenden Seiten der benachbarten
Kacheln her. Denn z.B. schließt an die Seite 2 von K0 die Seite -1 von K2 an, wobei -1 die
zweite Zahl der Signatur ist.
Die Kacheln K1 bis K6 haben die Seitennummerierung, die sich aus den Abbildungen ergibt
und die durch die Lage des ersten Halbpfeils festgelegt ist. Man kann darum entsprechend der
Signatur an diese Kacheln weitere Kacheln ansetzen, wobei man bei Kacheln mit negativen
Seitennummern das Vorzeichen aller Zahlen der Signatur ändern muss. Im Fall der Abbildung
3 erhält man dann eine lückenlose Überdeckung der ganzen Ebene, bei der die Schnittmenge
zweier verschiedener Kacheln leer ist oder nur aus einem Eckpunkt besteht oder die
Punktmenge einer gemeinsamen Seite ist. Die rot-weißen Markierungen geben in Abbildung 3
eine Gleitspiegelungs-Achse und Zentren von Punktspiegelungen an.
Abb. 4
3
Wenn man die geradlinige Begrenzung der Kacheln durch andere Kurven ersetzt, wird die
Zuordnung der Seiten zu Nachbar-Bewegungen deutlicher. In Abbildung 4 markiert eine
S-Kurve Seiten, deren Nachbar-Bewegungen 180°-Drehungen sind. Paarweise gleichgeformte
Kurven signalisieren Zuordnungen durch eine Verschiebung oder eine Gleitspiegelung. Das
Ergebnis nennen wir 'Kachelungs-Variante' der Kachelung aus Abbildung 3. Je nachdem,
welche Nachbar-Bewegungen den Seiten zugeordnet sind, müssen die Kurven, die die SeitenStrecken ersetzen, gewissen Einschränkungen genügen. Wenn die Nachbarbewegung eine
180°-Drehung ist, muss die Kurve punktsymmetrisch sein, und bei einer Achsen-Spiegelung ist
nur eine Strecke möglich. Wenn zwei Seiten durch eine Drehung, eine Translation oder eine
Gleitspiegelung als Nachbar-Bewegung auseinander hervorgehen, müssen die ersetzenden
Kurven nur kongruent sein. Bei allen Kurven ist darauf zu achten, dass es zu keinen
Überschneidungen kommt.
Abbildung 5 zeigt eine Variante, bei der die Seiten der Kacheln in Abbildung 3 durch PolygonZüge ersetzt sind. Wir nennen derartige Kacheln 'P-Kacheln' und die daraus entstandene
Kachelung 'P-Kachelung'. Diese Kacheln spielen beim Nachweis eine Rolle, dass es zu jeder
der in Tabelle 1 auf Seite 20 genannten Signaturen eine Kachel gibt, die eine Kachelung
erzeugt.
Abb. 5
4
Damit eine Kachelung entsteht, muss die Signatur aus einer beschränkten Menge von
Zahlenfolgen gewählt werden und das Basis-Polygon muss einschränkenden geometrischen
Bedingungen genügen. Das soll im Folgenden untersucht werden.
2. Definitionen
Definition : K0 sei ein Polygon mit Seitennummern 1 bis n ∈ N . Eine Folge von ganzen Zahlen
s1s2...sn heißt Signatur von K0, wenn gilt:
1. Die Folge der Beträge s1 s 2 ... s n ist eine Permutation der ganzen Zahlen von 1 bis n.
2. Für Indizes i und k in {1, 2,..., n} gilt: Wenn s k = i ist, dann ist si = k, und si und sk
haben das gleiche Vorzeichen.
Unter den Nachbar-Bewegungen von K0 zu der Signatur s1s2...sn verstehen wir die
Bewegungen B1, B2, ..,Bn mit folgenden Eigenschaften:
1. Bi ist gerade oder ungerade je nachdem ob si positiv oder negativ ist.
2. Bi bildet die Seite von K0 mit der Nummer si in die Seite mit der Nummer i ab.
Um den Bezug auf das Polygon deutlich zu machen benutzen wir auch die Bezeichnung BiK 0 .
Das Bild K0 bei Bi sei mit K0Bi bezeichnet, und wir nennen dies die 'Kachel, die durch Anlegen
an die i-te Seite von K0 entsteht'. (Wir hängen das Abbildungszeichen rechts an das Urbild an,
damit bei Hintereinanderschaltungen die Reihenfolge der Leserichtung entspricht.). Wenn Bi
eine gerade Bewegung ist, hat das Bild der Seite von K0 mit der Nummer j in K0Bi ebenfalls
die Nummer j; wenn Bi ungerade ist, hat das Bild die Nummer − j .
Die Seite von K0 mit der Nummer i schließt dann an die Seite von K0Bi mit der Nummer si an.
Aus der Definition folgt, dass die Menge {B1 , B2 , .., Bn } der Nachbar-Bewegungen mit jeder
Bewegung Bi auch die dazu inverse Bewegung Bi−1 enthält, denn diese ist für si = i eine
Punkt- oder Achsen-Spiegelung, also zu sich selbst invers, und für si = k ≠ i ist Bk = Bi−1 .
Wenn die Seiten einer anderen Kachel K1 mit positiven Zahlen nummeriert werden, verstehen
wir unter BiK1 für i ∈ {1,..., n} die Nachbar-Bewegung von K1 , deren Definition aus der von
BiK 0 dadurch entsteht, dass man K0 durch K1 ersetzt.
Um Kacheln zu erfassen, die mit negativen Zahlen nummeriert werden, erweitern wir die
Definition der Zahlen si.
Definition : Für i ∈ {−1,..., −n} sei
si := −s i .
Dann ist k = si äquivalent mit i = s k .
Wenn die Seiten von K1 mit negativen Zahlen nummeriert werden, verstehen wir unter BiK1 mit
i ∈ {−1,..., −n} die Bewegung, die folgende Eigenschaften hat:
1. BiK1 ist gerade oder ungerade je nachdem ob si negativ oder positiv ist.
2. BiK1 bildet die Seite von K1 mit der Nummer − si in die Seite mit der Nummer i ab.
Die Seite von K1 mit der Nummer i schließt dann an die Seite von K1BiK1 mit der Nummer si
an.
5
Für positive Zahlen t ∈ {1..., n} benutzen wir im Folgenden die Bezeichnung BK± t für eine
Nachbar-Bewegung der Kachel K. Dabei ist das Plus-Zeichen vor t zu wählen, wenn die Seiten
von K positiv nummeriert werden und sonst das Minus-Zeichen.
Definition : Wir sagen 'K0 mit der Signatur s1s2...sn erzeugt eine Kachelung', wenn für alle
Kacheln K1 und K2, die sich durch fortgesetztes Anlegen von Kacheln entsprechend dieser
Signatur ergeben, die Schnittmenge leer ist oder nur aus einem gemeinsamen Eckpunkt besteht
oder die Punktmenge einer gemeinsamen Seite ist oder K1 = K2 ( bei gleicher Nummerierung)
gilt. Diese Kachelung wird dann auch von irgendeiner anderen Kachel K1 dieser Kachelung
erzeugt.
Nach dieser Definition ist es möglich, dass der Winkel zwischen zwei aufeinanderfolgenden
Seiten 180° beträgt und die zugehörigen Nachbar-Bewegungen 180°-Drehungen um den
Scheitelpunkt A des Winkels sind. Wenn K0 dann eine Kachelung erzeugt, treffen bei A nur
zwei Kacheln zusammen. Würde man den Punkt A weglassen und die zwei Schenkel zu einer
Seite zusammenfassen, der eine 180°-Drehung zugeordnet ist, so würde die Kachelung sich
nicht wesentlich verändern. Genauso könnte man verfahren, wenn den beiden Schenkeln des
gestreckten Winkels Achsenspiegelungen zugeordnet sind. Wir setzen darum im Folgenden
stets voraus, dass bei der von K0 erzeugten Kachelung an jedem Eckpunkt mindestens drei
Kacheln zusammentreffen.
Definition : Bei einer positiv nummerierten Kachel sei der Eckpunkt E1 mit der Nummer 1 der
gemeinsame Punkt der 1. und 2. Seite. Die in Richtung des Halbpfeils folgenden Eckpunkte
werden von 2 bis zur Eckenanzahl n nummeriert. Bei einer negativ nummerierten Kachel sei
der Eckpunkt mit der Nummer -1 der gemeinsame Punkt der Seiten -1 und -2. Die in Richtung
des Halbpfeils folgenden Eckpunkte werden von -2 bis zur Eckenanzahl -n nummeriert.
Wenn man sich die Seiten den Kacheln durch Halbpfeile repräsentiert vorstellt, die den
Umlaufsinn entsprechend der Nummerierung 1,..., n,1 bzw. −1,..., − n, −1 angeben, dann
ordnen wir also jedem Eckpunkt die Nummer i der Seite zu, für die der Eckpunkt die
Pfeilspitze bildet und bezeichnen den Eckpunkt mit Ei.
Wir benutzen im Folgenden orientierte Winkel, die durch ein (geordnetes) Paar ( g + , h + ) von
Halbgeraden (Strahlen) mit gemeinsamen Anfangspunkt D zugeordnet sind. Die zugehörige
Winkelgröße ist dann der Drehwinkel mit Werten in [0°, 360°) , um den man g + gegen den
Uhrzeigersinn um D drehen muss, um zu h + zu gelangen. Für z < 0 soll z° die Winkelgröße
(360+z)° bedeuten.
Definition : Für i ∈ {1,..., n − 1} bzw. i = n sei αi die Größe des Drehwinkels, mit dem eine
Seite mit der Nummer i+1 bzw. 1 gegen den Uhrzeigersinn in die Seite i gedreht wird.
Für i ∈ {−1,..., − n + 1} bzw. i = − n sei α i die Größe des Drehwinkels mit dem eine Seite mit
der Nummer i gegen den Uhrzeigersinn in die Seite i − 1 bzw. −1 gedreht wird.
α i gibt dann also die Größe des Innenwinkels der Kachel am Eckpunkt Ei an. Diese
Innenwinkelgrößen sind bei allen Kacheln gleich, egal welchen Umlaufsinn sie haben: αi = α-i.
6
Definition : Es sei t1t2...tm eine endliche Folge mit t i ∈ {1,..., n} und K0 eine Kachel. Dann
t3
t1
t2
tm
nennen wir die Kachelfolge K 0 
→ K1 
→ K 2 
→ ... 
→ K m die 'von t1t2...tm
bestimmte Kette mit der Startkachel K0', wenn K i +1 = K i B± tii .
K
Hierbei entsteht also Ki+1 durch Anlegen an die Kachel Ki an deren Seite mit der Nummer ± t i .
Derartige Ketten mit der Zusatzeigenschaft, dass alle ihre Kacheln einen gemeinsamen
Eckpunkt haben, werden im Folgenden benutzt, um Signaturen auszusondern, die keine
Kachelungen erzeugen. Es wird sich herausstellen, dass nur die Signaturen der Tabelle 1 auf
Seite 20 Kachelungen ermöglichen.
3. Automorphismengruppe
Satz 1 : K0 sei eine positiv nummerierte Kachel, die die Signatur s1s2...sn und die
Nachbarbewegungen B1, ..., Bn hat und eine Kachelung erzeugt. Dann gilt:
1. Wenn K 0 K1K 2 ...K m die von t1t2...tm bestimmte Kette mit der Startkachel K0 ist, dann
folgt
K m = K 0 B t m B t m−1 ...B t1 und
B±Kim = B−t11B−t 21...B−t m1 Bi Bt m Bt m−1 ...Bt1 für alle i mit 1 ≤ i ≤ n .
2.
3.
4.
5.
(In dem Term für Km werden also nicht die Nachbar-Bewegungen der Ki für i > 0
benutzt, sondern die von K0, und zwar in umgekehrter Reihenfolge.)
Die Nachbarbewegungen B1, ..., Bn von K0 bilden die Kachelung auf sich ab.
Die Automorphismengruppe der Kachelung ist das Erzeugnis der Nachbarbewegungen
B1, ..., Bn von K0.
Die von K0 erzeugte Kachelung ist periodisch, d.h. es gibt in der
Automorphismengruppe zwei Verschiebungen mit linear unabhängigen
Translationsvektoren.
In der Menge der Translationsvektoren ungleich dem Nullvektor gibt es einen Vektor
mit minimaler Länge.
Beweis : 1. Die Nachbarbewegung
BK± t12 von K1 ist die Hintereinanderschaltung B−t11Bt 2 Bt1 .
K1B−t11Bt 2 = K 0 Bt 2 ist eine Kachel, die an die Seite t2 der Kachel K0 angelegt wird;
und da B t1 eine Bewegung ist, die die Seite t2 von K0 in die Seite ± t 2 von K1 abbildet, wird
Denn
auch die daran anhängende Kachel K 0 Bt 2 mitbewegt, so dass
die Seite ± t 2 von K1 anschließt. Darum ist
K1B−t11Bt 2 Bt1 = K 0 Bt 2 Bt1 an
K 2 = K 0 Bt 2 Bt1 .
Wenn man K3 an die Stelle von K2 setzt und
B t 2 B t1 an die Stelle von B t1 , dann erschließt
man analog K 3 = K 0 B t 3 B t 2 B t1 , und diese Argumentation kann bis
K m = K 0 B t m B t m−1 ...B t1 entsprechend fortgesetzt werden. Für ϕ = Bt m Bt m−1 ...B t1 ist also
−1
−1
−1
−1
K m = K 0 ϕ . Wie oben für B± t12 folgt daraus B± im = ϕ Bi ϕ = Bt1 Bt 2 ...Bt m Bi Bt m Bt m−1 ...Bt1 .
K
K
2. Nach 1. lässt sich jede Kachel der Kachelung in der Form K 0 B t m B t m−1 ...B t1 darstellen.
Das Bild bei einer Nachbar-Bewegung Bi von K0 ist dann K 0 B t m B t m−1 ...B t1 Bi , also nach 1.
7
ebenfalls eine Kachel der Kachelung. Bi bildet aneinander anschließende Kacheln wieder in
derartige Kacheln ab, da Bi eine Bewegung ist.
3. Nach 2. sind die Nachbarbewegungen B1, ..., Bn von K0 in der Automorphismengruppe der
Kachelung enthalten.
Ein Automorphismus ϕ der Kachelung ist eine Bewegung, die K0 auf eine Kachel Km abbildet,
die man nach 1. in der Form K m = K 0 Bt m Bt m−1 ...Bt1 darstellen kann. Dann ist ϕ = Bt m Bt m−1 ...Bt1 ,
denn es gibt nur eine Bewegung, die K0 auf Km abbildet. ( Hierbei wird benutzt, dass Kacheln
mit der gleichen Form und Größe aber unterschiedlicher Seitennummerierung als verschieden
betrachtet werden.)
4.
1.Fall : Eine der Nachbarbewegungen von K0 ist eine Drehung ϑ0 mit einem Drehwinkel
α ≠ 0 . Der Drehpunkt sei D0. Da für alle anderen positiv nummerierten Kacheln die i-te
Nachbar-Bewegung ebenfalls eine Drehung mit den gleichen Drehwinkel α ist, gibt es für sie
einen entsprechenden Drehpunkt. Es seien zwei dieser Drehpunkte D1 und D2 zu Drehungen
ϑ1 und ϑ2 gewählt, so dass D0D1D2 ein nicht ausgeartetes Dreieck bildet. ϑ0−1ϑ1 ist eine
Verschiebung, da ϑ0−1 jeden Vektor um den Winkel −α dreht und die anschließende Drehung
ϑ1 dann wieder um α zurückdreht. Ein zugehöriger Verschiebungspfeil verbindet D0 mit
D 0 ϑ0−1ϑ1 = D 0 ϑ1 . Analog ergibt sich eine Verschiebung zum Verbindungsvektor von D0 mit
D 0 ϑ0−1ϑ2 = D 0 ϑ2 , der nicht auf der Geraden durch D0 und D 0 ϑ1 liegt. Beide Translationen
liegen in der Automorphismengruppe der Kachelung, da sie sich als Hintereinanderschaltung
von Nachbarbewegungen ergeben.
2. Fall: Keine der Nachbarbewegungen von K0 ist eine Drehung, d. h. alle Nachbarbewegungen
sind Verschiebungen oder Gleitspiegelungen. Wenn Bi eine Gleitspiegelung ist, dann ist
Bi2 = Bi Bi eine Translation in Richtung der Gleitspiegelungsachse. Es gibt also in diesem Fall
mindestens eine Translation, (die nicht die identische Abbildung id ist). Es muss auch noch
eine dazu linear unabhängige Translation geben, da andernfalls alle Translationspfeile und
Gleitspiegelungsachsen sonst in die gleiche Richtung zeigen würden. Das steht aber im
Widerspruch dazu, dass durch Anlegen von Kacheln jeder Punkt der Ebene erreicht werden
kann.
5. Da das Innere von K0 nicht leer ist, gibt es einen Kreis mit dem Radius r > 0, der ganz im
Innern von K0 liegt. Jede Verschiebung τ, deren Verschiebungsvektor eine Länge kleiner als r
hat, verschiebt K0 so, dass K0 und K0τ innere Punkte gemeinsam haben. Nach der Definition
der Kachelung ist dann K0 = K0τ und folglich τ die idenische Abbildung id (zu einem
Verschiebungsvektor der Länge Null). Wenn man also alle Translationsvektoren ≠ 0 von
einem Punkt O aus abträgt und die Spitzen dieser Vektoren betrachtet, hat einer dieser Punkte
einen minimalen Abstand ≠ 0 zu O; denn diese Punkte können nicht beliebig dicht liegen, weil
die Differenz zweier Translationsvektoren wieder ein Translationsvektor ist.
□
Satz 2 : K0 sei eine positiv nummerierte Kachel, die die Signatur s1s2...sn und die
Nachbarbewegungen B1, ..., Bn hat, und die eine Kachelung erzeugt. ϑ sei ein Drehung in der
Automorphismengruppe der Kachelung mit dem Drehpunkt D und dem Drehwinkel α ≠ 0 .
Dann ist D entweder Seitenmitte einer Kachel und α = 180°, oder D ist Eckpunkt und
α ∈ {60°,90°,120°,180°, 240°, 270°,300°} . Ist D Eckpunkt und ϑ Nachbar-Bewegung, dann
ist α ≠ 180° .
Beweis : Wenn D im Innern einer Kachel K liegen würde, dann wäre Kϑ = K und α = 0, da
Kϑ und K beide den Punkt D enthalten und sie dann übereinstimmen müssen.
8
Wenn D kein Eckpunkt ist, liegt dieser Punkt folglich im Innern einer Kachelseite. Wenn diese
Seite bei der Drehung ϑ nicht auf sich abgebildet würde, dann würden Kϑ und K innere
Punkte gemeinsam haben und müssten zusammenfallen im Widerspruch zu α ≠ 0 . Die Seite
wird also auf sich abgebildet, was nur möglich sein kann, wenn D der Seitenmittelpunkt und α
= 180° ist.
Sei D nun ein Eckpunkt und τmin eine Verschiebung ≠ id mit einem Verschiebungsvektor
1
minimaler Länge. Dann sind τ−min
, ϑ−1τmin ϑ und ϑ−2 τmin ϑ2 Verschiebungen mit Vektoren
gleicher Länge, die aber gegenüber dem Vektor von τmin um 180° bzw. α bzw. 2α gedreht sind.
1
Sei E = Dτmin , F = Dτ−min
, G = Dϑ−1τmin ϑ und H = Dϑ−2 τmin ϑ2 . Dann liegen E, F , G und H
auf einem Kreis um D und die Verbindungsvektoren EG , FG und FH sind Vektoren von
Translationen der Automorphismengruppe der Kachelung, denn z. B. EG gehört zur
1
ϑ−1τmin ϑ . Wenn nun α eine Winkelgröße zwischen 0° und 60° wäre, dann wäre
Translation τ−min
die Länge EG kleiner als DE , im Widerspruch dazu, dass τmin einen minimalen
Verschiebungsvektor hat. Im Fall 60° < α < 90° oder 90° < α < 120° wäre FH kleiner als
DE , und im Fall 120° < α < 180° wäre FG kleiner als DE . Darum sind im Intervall
[ 0°;180°]
nur die Winkelgrößen 60°, 90° , 120° und 180° möglich. Da mit jeder Drehung
auch die dazu inverse Drehung in der Automorphismengruppe liegt, sind im Intervall
( −180°; 0°] nur die Winkelgrößen -60° = 300°, -90° = 270°, und -120° = 240° möglich. Wenn
D Eckpunkt und ϑ Nachbar-Bewegung ist, dann folgt α ≠ 180° , weil sonst bei D nur zwei
□
Kacheln zusammentreffen würden.
4. Ketten
Abb. 6
Abbildung 6 zeigt zu der blau umrandeten Startkachel K0 die von der Zahlenfolge 13
bestimmte Kette bei der Signatur -2 -1 6 4 5 3. Der rot markierte Punkt A hat in K0 die
Nummer 1, in K1 = K 0 B1 die Nummer -2 und in K 2 = K 0 B3 B1 die Nummer -6. In A laufen
drei Seiten zusammen, nämlich die gemeinsamen Seiten von K0 und K1 mit der Nummer 1
bzw. -2, die von K1 und K2 mit der Nummer -3 bzw. -6 und die von K2 und K0 mit der
Nummer -1 bzw. 2.
(1 − 2 ) → ( −3 − 6 ) → ( −1 2 ) → (1 − 2 )
α6
α2
9
α1
Dieses Schema gibt die Paarungen der Seitennummern wieder und die Innenwinkel-Größe
zwischen aufeinanderfolgenden Seiten gegen den Uhrzeigersinn. Dabei ist die Winkelnummer
der Betrag der Nummer, den der Punkt A in der zugehörigen Kachel hat. Jedes Paar von
Seitennummern hat die Form ( i s i ) entsprechend der Signatur s1s 2s3s 4s5s 6 = −2 − 1 6 4 5 3 .
Bei aufeinanderfolgenden Paaren ist die erste Zahl des folgenden Paars um 1 kleiner als die
zweiten Zahl im vorangehenden Paar, wobei man −7 = −6 − 1 durch −1 ersetzen muss. Das ist
der Grund für folgende Definition, die zu einer Seitennummer i einer Kachel K eine Zahl i ←
definiert, die die Nummer der Seite angibt, die sich an die Seite i in der Kachel K im
Uhrzeigersinn anschließt.
Definition : Für i ∈ {1,..., n, −1,..., − n} sei
 i − 1 für 2 ≤ i ≤ n

n für i = 1

←
i := 
i − 1 für − 1 ≥ i ≥ − n+1

−1 für i = − n
und
 i + 1 für 1 ≤ i ≤ n − 1

1 für i = n

→
i := 
i + 1 für − 2 ≥ i ≥ − n
 − n für i = − 1
Das oben angegebene Schema kann hiermit in folgender Weise verallgemeinert werden:
(t
0
(
)
)
(
)
(
s t 0 
→ t1 = s ←
→ t 2 = s←
→ t m = s←
t s t1 
t1 s t 2 ... 
t m −1 s t m
0
)
Satz 3 : K0 sei eine positiv nummerierte Kachel, die die Signatur s1s2...sn und die
Nachbarbewegungen B1, ..., Bn hat, und die eine Kachelung erzeugt.
t 0 t1t 2 ...t m −1t m sei eine Folge von Zahlen, für die gilt:
• t0 ist eine Nummer einer Seite von K0; ihre Spitze sei der Punkt A.
• t i +1 = s ←
t i für 0 ≤ i ≤ m − 1 ,
0
1
2
m −1
K 0 
→ K1 
→ K 2 
→ ... 
→ K m sei die von t 0 t1 ... t m-1 bestimmte Kette mit der
Startkachel K0. Dann gilt:
1. Der Eckpunkt A von K0 ist Eckpunkt auch aller Kacheln Ki mit 1 ≤ i ≤ m . Die Nummer
t
t
ei von A in Ki ist
t
t
t i→ oder t i , je nachdem ob t i negativ oder positiv ist.
2. Wenn t m = t 0 und t i ≠ t 0 für 1 ≤ i ≤ m − 1 , dann ist ϑ = B t m−1 B t m−2 ...B t0 eine Drehung
mit A als Fixpunkt. Die Summe αP der Winkel α j mit j = ei für 0 ≤ i ≤ m − 1 ist der
zugehörige Drehwinkel. Es gibt ein µ ∈ {1, 2,3, 4,6} mit α P =
(
auch B t0 B t m−1 B t m−2 ...B t1
)
µ
360°
, so das ϑµ und
µ
die identische Abbildung ist.
Beweis : Die Strecke, die in K0 die Seite mit der Nummer t0 ist, hat in der Nachbar-Kachel die
Nummer s t 0 . Die zugehörige Nachbar-Bewegung Bt0 ist gerade oder ungerade, je nachdem s t 0
positiv oder negativ ist.
Wenn s t 0 negativ ist, dann sind die Halbpfeile der Seite zur Markierung der Durchlaufrichtung
in beiden Kacheln K0 und K1 gleichgerichtet. Da die Nummer eines Eckpunktes einer Kachel
stets mit der Nummer der Seite übereinstimmt, für die der Punkt die Halbpfeil-Spitze bildet,
hat A in K1 dann die Nummer e1 = s t 0 = t1→ . Dann ist A auch Eckpunkt der Seite mit der
10
Nummer s ←
t 0 = t1 , die in K1 der Seite mit der Nummer s t 0 im Uhrzeigersinn folgt. Für j = e1
ist α j = α − j der Winkel, um den man gegen den Uhrzeigersinn um A drehen muss, damit man
von der Seite mit der Nummer s t 0 in die mit der Nummer s ←
t 0 gelangt.
Wenn s t 0 positiv ist, dann sind die Halbpfeile der Seite zur Markierung der Durchlaufrichtung
in den Kacheln K0 und K1 entgegengesetzt gerichtet. A ist dann in K1 die Spitze des Halbpfeils,
der dem Pfeil mit der Nummer s t 0 vorangeht, also die Nummer s ←
t 0 hat, so dass e1 = t1 ist. Hier
ist für j = e1 = e1 der Winkel α j der Drehwinkel einer Drehung gegen den Uhrzeigersinn um
A , welche die Seite mit der Nummer s t 0 in die mit der Nummer s ←
t 0 dreht.
Die Aussage 1. ergibt sich, indem man die vorangegangene Argumentation analog für K1 bis
Km-1 an Stelle von K0 fortsetzt. Die Seiten, die in den Kacheln Ki die Nummer ti haben, sind
dann gegen den Uhrzeigersinn aufeinander folgende Seiten mit dem Endpunkt A.
2. Sei nun t m = t 0 und t i ≠ t 0 für 1 ≤ i ≤ m − 1 . Dann ist tm positiv und A hat in Km die gleiche
Nummer wie in K0. Nach Satz 1 ist darum K m = K 0 ϑ und ϑ eine gerade Bewegung, die den
Punkt A festlässt, also eine Drehung um A ist. Aus der vorangegangenen Überlegung folgt,
dass der Drehwinkel die Summe der Winkel α j mit j = ei ist. Da die Drehung nach Satz 1
ein Automorphismus der Kachelung ist, muss der Drehwinkel nach Satz 2 ein ganzzahliges
Vielfaches von 60° oder 90° sein. Wenn ϑ keine Drehung um 360° ist, dann muss der
Drehwinkel ≤ 180° sein, da man dann die Zahlenfolge t 0 t1 ... t m-1 mindestens zweimal
durchlaufen muss, um den Winkelbereich von 360° auszufüllen. Darum hat der Drehwinkel αP
360°
eine der Größen 60°, 90°, 120°, 180° oder 360° . Für µ :=
gilt dann ϑµ = id und
αP
(B
t0
B t m−1 B t m−2 ...B t1
)
µ
= B t0 ϑB−t01 = id .
□
Eine Zahl m mit tm = t0 wie in Satz 3 muss es für eine Kachel K0, die eine Kachelung erzeugt,
zu jedem Eckpunkt geben, da man durch Anlegen von Kacheln gegen den Uhrzeigersinn um A
stets wieder zur Ausgangsseite gelangt.
Definition : t 0 t 2 ...t m mit t m = t 0 und t i ≠ t 0 für 1 ≤ i ≤ m − 1 sei eine Folge von Zahlen wie in
Satz 3 zu einer Kachel K0, die eine Kachelung erzeugt. Dann nennen wir die Folge t 0 t 2 ...t m −1
'Periode zu t0', die Zahl m nennen wir 'Periodenlänge zu t0' und αP 'Periodenwinkel zu t0'. Die
(
)(
) (
)
periodische Fortsetzung der Folge t 0 s t 0 , t1 s t1 ,..., t m −1 s t m−1 soll 'Folge der Seiten zu t0'
heißen. Die periodische Fortsetzung der Folge der Nummern ei in Satz 3 sei 'Folge der
Ecknummern zu t0' genannt, die Menge dieser Folgenglieder 'Menge der Ecknummern zu t0'
und die periodische Fortsetzung der Folge der Winkelgrößen α ei 'Folge der Winkelgrößen zu
t0'.
11
Abb. 7
Die Folgen der Seiten und der Ecknummern zu t0 haben innerhalb einer Periode keine gleichen
(
Folgenglieder, da in dem Paar t i s ti
) schon eine der beiden Komponenten die ganze Folge
eindeutig bestimmt. Dagegen kann es in der Folge der Winkelgrößen zu t0 innerhalb einer
Periode gleiche Winkelgrößen geben, auch wenn alle Innenwinkel von K0 unterschiedlich groß
sind. Wir betrachten dazu das Beispiel einer Kachel mit der Signatur
−1 − 2 4 3 (siehe Abb. 7):
to = 1 :
to = 2 :
to = 3 :
to = 4 :
(1 −1) → ( −2 2 ) → (1 −1)
( 2 −2 ) → ( −3 −4 ) → ( −1 1) → ( 4 3) → ( 2 −2 )
( 3 4 ) → ( 3 4 )
( 4 3) → ( 2 −2 ) → ( −3 −4 ) → ( −1 1) → ( 4 3)
α1
α1
α2
α4
α4
α2
α3
α2
α2
α4
12
α4
In der Folge der Winkel zu t0 = 1 kommt α1 innerhalb einer Periode der Seitenfolge zweimal
vor, weil die Gerade, auf der die Seite 1 liegt, Spiegelachse der Kachelung ist und darum der
Punkt A, der in K0 die Nummer 1 hat, in K1 mit -1 nummeriert ist. Auch bei den Folgen zu
t0 = 2 und t0 = 4 tritt diese Verdopplung durch Spiegelung auf. Diese nach links und rechts
unendlich fortgesetzten Seiten-Folgen stimmen überein. Die Periodenwinkel zu t0 = 1, 2, 3 und
4 betragen 120°, 360°, 60° und 360°.
In dem folgenden Beispiel ist K0 ein Viereck mit der einzigen Einschränkung, dass zwei
aufeinanderfolgende Seiten gleich lang sind. Die Signatur ist −2 − 1 3 4 (siehe Abb. 8).
to = 1 :
to = 2 :
to = 3 :
to = 4 :
(1 −2 ) → ( −3 −3) → ( −4 −4 ) → ( −1 2 ) → (1 −2 )
( 2 −1) → ( −2 1) → ( 4 4 ) → ( 3 3) → ( 2 −1)
( 3 3) → ( 2 −1) → ( −2 1) → ( 4 4 ) → ( 3 3)
( 4 4 ) → ( 3 3) → ( 2 −1) → ( −2 1) → ( 4 4 )
α3
α2
α1
α2
α3
α4
α4
α1
α2
α3
α2
α4
α3
α1
Abb. 8
13
α1
α4
In diesem Beispiel stimmen die unendlich fortgesetzten Seiten-Folgen zu t0 = 2, 3 und 4
überein. Die Folge zu t0 = 1 ist dagegen die 'Reversion' dieser Folge, die dadurch entsteht, dass
bei allen Seitennummern das Vorzeichen geändert und die Pfeilrichtung umgedreht wird, so
dass die Folge von rechts nach links fortschreitet. Wenn man die entstehende Folge dann
wieder von links nach rechts schreibt, statt von rechts nach links, hat man die Zahlen in den
Paaren zu vertauschen. Die Folge ...1 − 2 − 3 − 4 1... der Ecknummern zu t0 = 1 wird bei der
Reversion zu der Folge ... − 1 4 3 2 − 1... der Ecknummern zu t0 = 2, 3 und 4.
Defintion : K0 sei positiv nummerierte Kachel zur Signatur s1s2...sn, die eine Kachelung
erzeugt. Die Zahlen i und j in {1, 2,..., n} heißen äquivalent, wenn es einen Automorphismus ϕ
der Kachelung gibt mit der Eigenschaft, dass für die Eckpunkte Ei und Ej von K0 gilt: Ei = Ejϕ.
Eckpunkte P1 und P2, die in Kacheln K1 bzw. K2 Nummern haben, deren Betrag i bzw. j ist,
werden äquivalent genannt, wenn i und j äquivalent sind.
Statt 'i äquivalent j' schreiben wir auch i ~ j.
Es ist i ~ i . Denn Ei = Ejid.
Aus i ~ j folgt j ~ i. Denn aus Ei = Ejϕ folgt Eiϕ-1 = Ej.
Aus i ~ j und j ~ k folgt i ~ k. Denn aus Ei = Ejϕ und Ej = Ekη folgt Ei = Ekηϕ.
Es handelt sich also bei '~' um eine Äquivalenzrelation. Die Menge {1, 2,..., n} zerfällt darum
in paarweise disjunkte Teilmengen, den Äquivalenzklassen, mit der Eigenschaft, dass zwei
Zahlen genau dann äquivalent sind, wenn sie zur gleichen Teilmenge gehören. In den
Zeichnungen markieren wir äquivalente Eckpunkte mit der gleichen Farbe.
Wenn si positiv ist, wird durch die Nachbar-Bewegung Bi ein Punkt an der Spitze des zur Seite
mit der Nummer si gehörigen Halbpfeils in den Startpunkt des Halbpfeils zur Nummer i
abgebildet. Das heißt, dass der Punkt von K0 mit der Nummer si durch die Nachbar-Bewegung
Bi in den mit der Nummer i ← abgebildet wird, und entsprechend der Punkt mit der Nummer
si← in den mit der Nummer i. Dann ist also si äquivalent mit i ← und si← äquivalent mit i. Wenn
si negativ ist, wird der Punkt von K0 mit der Nummer si in den mit der Nummer i abgebildet
und der mit der Nummer si
und si
←
←
in den mit der Nummer i ← ; dann ist also si äquivalent mit i
äquivalent mit i ← .
Im Fall si = i > 0 bedeutet dies, dass i äquivalent mit i ← ist. Denn der Eckpunkt von K0 mit der
Nummer i wird durch Punktspiegelung in den mit der Nummer i ← abgebildet.
Im Fall si = i → > 0 ist die i-te Nachbarbewegung von K0 die Drehung um den Eckpunkt Ei
von K0, die den Eckpunkt mit der Nummer i → in den mit der Nummer i ← abbildet . Dann ist
also i → äquivalent mit i ← .
Definition : Unter dem Klassenwinkel αÄ einer Äquivalenzklasse Ä verstehen wir die Summe
der Innenwinkelgrößen an den Eckpunkten von K0, deren Nummer in Ä vorkommt.
Falls k > 1 ist und Ä = {t1 , t 2 ,..., t k } schreiben wir statt α{t1 ,t 2 ,...,t k } auch α t1t 2 ...t k . Diese
Schreibweise benutzen wir nur bei Äquivalenzklassen. Die Klasse {1, 2,5} hat also z. B. den
Klassenwinkel α125 = α1 + α 2 + α 5 .
14
Definition : Unter der Eckenordnung eines Eckpunktes A in einer Kachelung verstehen wir die
Anzahl der Seiten, die ihren Endpunkt in A haben. Diese Anzahl stimmt mit der Anzahl der
Kacheln überein, die A als Eckpunkt haben.
Satz 4 : K0 sei positiv nummerierte Kachel zur Signatur s1s2...sn, die eine Kachelung erzeugt.
t0 sei eine Seitennummer und A der Eckpunkt mit der Nummer t0. Die Periode zu t0 sei
t 0 t 2 ...t m −1 . Der Periodenwinkel von t0 sei αP, der Klassenwinkel der Äquivalenzklasse Ä zu t0
sei αÄ. Die Anzahl der Zahlen in Ä sei Ä . Dann gilt:
1. Die Periodenlänge m zu t0 ist ein Teiler der Eckenordnung von A.
2. Der Periodenwinkel αP zu t0 beträgt 60°, 90°, 120°, 180° oder 360°.
3. Eine Ecknummer k ist genau dann äquivalent mit t0, wenn k oder -k in der Folge der
Ecknummern zu t0 vorkommt. Die Menge der Ecknummern zu t0 stimmt entweder mit
der Menge der Ecknummern zu k überein oder mit der Menge, die daraus entsteht, dass
alle Elemente darin ihr Vorzeichen ändern.
4. Die Folge der Ecknummern zu t0 enthält die Zahl − t 0 genau dann, wenn es eine
Spiegelung an einer Geraden durch A gibt, die Automorphismus der Kachelung ist. In
diesem Fall enthält die Menge der Ecknummern zu t0 mit jeder Nummer k auch die
Nummer -k.
5. Ä ist die Menge der Beträge der Ecknummern zu t0. Ä = m und αP = αÄ, falls es
keine Spiegelung an einer Geraden durch den Eckpunkt mit der Nummer t0 gibt, die
Automorphismus der Kachelung ist, andernfalls ist Ä = 0,5 ⋅ m und αÄ = 0,5 ⋅ α P .
6. Die Summe aller Klassenwinkel ist 180° ⋅ (n − 2) .
7. Aus Ä = 1 folgt αÄ = αP ∈ {60°,90°,120°} oder αÄ = 0,5 ⋅ α P ∈ {30°, 45°, 60°,90°} ..
8. Aus Ä = 2 folgt α Ä ≤ 180° .
9. Sei Ä = 3. Dann gilt:
•
•
Im Fall n = 3 ist α Ä = 180° .
Ä = 3 kommt bei n = 4 nicht vor.
Im Fall von n ∈ {5, 6} ist α Ä = α P = 360° . Bei n = 6 gibt es neben der
Äquivalenzklasse Ä mit drei Elementen keine mit zwei Zahlen.
10. α Ä ≤ 120°⋅ Ä
•
11. Die Eckenzahl n ist stets kleinergleich 6 und Ä ≤ 4.
Beweis: 1. Da man nach einer Drehung um 360° um den Punkt A wieder zu Ausgangsseite
gelangt, folgt 1. aus der Periodizität der Folge der Seiten zu t0.
360°
2. Nach Satz 3 gibt es ein µ ∈ {1, 2,3, 4,6} mit α P =
.
µ
3. Wenn k oder -k in der Folge der Ecknummern zu t0 vorkommt, dann ist k bzw. -k die
Nummer von A in einer Kachel, die mit K0 den Punkt A gemeinsam hat und aus K0 durch eine
Folge von Nachbar-Bewegungen entsteht. Darum ist dann k äquivalent mit t0.
Sei umgekehrt k äquivalent mit t0. Dann gibt es einen Automorphismus ϕ , der den Eckpunkt B
von K0 in A abbildet. Folglich ist K 0 ϕ eine Kachel, die mit K0 den Punkt A gemeinsam hat.
Darum muss k bzw. -k in der Folge der Ecknummern zu t0 vorkommen, je nachdem ϕ gerade
oder ungerade ist.
15
Wenn k in der Folge der Ecknummern zu A vorkommt, stimmt die Folge der Seiten zu t0 mit
der zu k überein. Wenn -k in der Folge der Ecknummern vorkommt, dann ergibt die Reversion
dieser Folge die Folge der Ecknummern zu k.
4. Wenn die Folge der Ecknummern zu t0 die Zahl − t 0 enthält, dann hat in einer Kachel K der
Punkt A die Nummer -t0. Die Bewegung σ , die K0 in K abbildet , ist dann ungerade und hat A
als Fixpunkt. Sie ist folglich eine Spiegelung an einer Geraden durch A, die nach Satz 1 ein
Automorphismus der Kachelung ist.
Wenn es umgekehrt eine derartige Spiegelung gibt, muss sie Spiegelung an einer Seitengerade
sein, da sie sonst eine Kachel fix lassen müsste, im Widerspruch zur Voraussetzung, nach der
nur die identische Abbildung eine Kachel festlässt. Die Spiegelung kommt deshalb unter den
Nachbar-Bewegungen der periodisch fortgesetzten Kette zu t0 vor. In der Folge der
Ecknummern folgt darum irgendwann auf eine Nummer k die Nummer -k. In der Reversion
der Ecknummern-Folge zu k kommt k darum ebenfalls vor, und sie stimmt folglich mit dieser
Folge überein. Darum enthält die Menge der Ecknummern zu k mit jeder Nummer auch die
Nummer mit geändertem Vorzeichen, also mit t0 auch die Nummer − t 0 .
5. ist eine unmittelbare Folgerung aus 2., 3. und 4..
6. Die Summe aller Klassenwinkel ist die Summe aller Innenwinkel von K0, folglich gleich
180° ⋅ (n − 2) .
7. Sei Ä = 1. Im Fall αP = αÄ ist Bt0 eine Drehung. Der Drehwinkel ist nach Satz 3
αÄ ∈ {60°,90°,120°} . Im Fall αP = 2αÄ ist Bt0 eine Achsenspiegelung. αP kann nicht 360°
sein, da dann die Eckenordnung von A gleich 2 wäre. Darum ist αP ∈ {60°,90°,120°,180°} und
αÄ ∈ {30°, 45°, 60°,90°} .
8. Sei Ä = 2. Wenn es eine Spiegelung an einer Geraden durch A gibt, die Automorphismus
der Kachelung ist, dann ist α Ä = 0, 5 ⋅ α P ≤ 180° , da α P ≤ 360° gilt. Wenn es keine derartige
Spiegelung gibt, dann ist α Ä = α P ≤ 180° , da α P = 360° dadurch ausgeschlossen wird, dass
die Ordnung von A mindestens 3 ist.
9. Sei nun Ä = 3 vorausgesetzt. η sei die Summe der Innenwinkelgrößen der Kachel K0, die
nicht in der Summe von αÄ vorkommen.
Falls n = 3 : {1 , 2 , 3} ist dann eine Äquivalenzklasse und αÄ die Summe aller Innenwinkel,
also 180°.
Falls n = 4: α Ä + η = 360° und η ist die Größe eines Innenwinkels zu einer Ecknummer k, die
einziges Element ihrer Äquivalenzklasse ist. Nach 7. folgt 0 < η <180° und 180° < αÄ <360°.
Das ist aber ein Widerspruch dazu, dass nach 2. 180° < α P < 360° und αP >360° unmöglich ist.
Falls n = 5 : α Ä + η = 540° und η ist die Summe der Größe zweier Innenwinkel zu Ecknummer
k1 und k2. Wenn k1 und k2 äquivalent sind, folgt aus 8. η ≤ 180° . Dann ist αÄ ≥ 360°, folglich
α Ä = α P = 360°
Wenn k1 und k2 nicht äquivalent sind, bilden {k1} und {k 2 } einelementige
Äquivalenzklassen. Nach 7. sind die Innenwinkel α k1 und α k 2 beide kleiner als 180°. Dann ist
16
αÄ > 180°, folglich auch αP > 180°. Da 180° < α P < 360° und αP >360° unmöglich ist, muss
α Ä = α P = 360° gelten.
Falls n = 6 : α Ä + η = 720° und η ist die Summe der Größe dreier Innenwinkel zu Ecknummer
k1, k2 und k3.
Wenn {k1 , k 2 , k 3 } eine Äquivalenzklasse ist, dann ist der zugehörige Periodenwinkel
kleinergleich 360°, folglich auch η ≤ 360° . Wegen α Ä + η = 720° müssen dann α Ä und η
beide die Größe 360° haben.
Bei einer Aufteilung von k1, k2 und k3 in eine Äquivalenzklasse {k1 , k 2 } mit zwei Elementen
und eine mit einem Element folgt aus 8. und 7. α k1 + α k 2 ≤ 180° und α k3 < 180° . Dann ist
α k1 + α k 2 + α k 3 < 360° . Wegen α Ä ≤ 360° und α k1 + α k 2 + α k 3 + α Ä = 720° kann dieser Fall
nicht vorkommen.
Wenn {k1} , {k 2 } und {k 3 } einelementige Äquivalenzklassen sind, folgt
α k1 < 180° , α k 2 < 180° und α k3 < 180° , also α k1 + α k 2 + α k 3 < 540° und α Ä > 180° . Auch
dann ist α Ä = α P = 360°.
10. Aus 7., 8. und 9. folgt α Ä ≤ 120°⋅ Ä für Ä gleich 1, 2 oder 3. Wegen αÄ ≤ αP ≤360° gilt
α Ä ≤ 120°⋅ Ä auch für Ä >3.
11. Nach 10. und 6. gilt für die Summe aller Innenwinkel von K0 180° ⋅ (n − 2) ≤ 120° ⋅ n ,
woraus n ≤ 6 folgt. Ä gleich 5 oder 6 ist nicht möglich, weil αÄ ≤ 360° gilt, die
Winkelsumme bei n = 5 bzw. n = 6 aber 540° bzw 720° beträgt.
□
Hilfssatz 1 : m sei die Periode zur Nummer k.
1. m = 1 genau dann, wenn s k = k → .
2. m = 2 genau dann, wenn s ←
k = sk→ .
→
bedeutet.
Beweis : 1. m = 1 gilt genau dann, wenn s ←
k = k gilt, was s k = k
2. m = 2 gilt genau dann, wenn sich folgendes Schema ergibt
→ (s
( k s ) 
k
←
k
)
k → 
→ ( k sk )
Dies gilt genau dann, wenn s ←
k = sk→ .
□
Hilfssatz 2 : Die Äquivalenzklasse zur Ecknummer k ist einelementig genau dann, Bk eine
Drehung ist oder sowohl Bk als auch Bk → Achsenspiegelungen sind.
Beweis : Wenn Bk gerade Bewegung ist, dann ist die Äquivalenzklasse zur Ecknummer k
genau dann einelementig, wenn die Periode m zu k gleich 1 ist, d. h. s k = k → und Bk eine
Drehung ist.
Wenn Bk eine ungerade Bewegung ist, dann ist die Äquivalenzklasse zur Ecknummer k genau
dann einelementig, wenn in der Menge der Ecknummern nur k und -k vorkommen, also die
Periode m gleich 2 ist und s k = − k . Das bedeutet wegen (− k)← = − k → nach Hilfssatz 1, dass
sowohl Bk als auch Bk → Achsenspiegelungen sind.
□
Satz 5 : K0 sei positiv nummerierte Kachel zur Signatur s1s2...sn mit n ∈ {5, 6} , die eine
Kachelung erzeugt. Dann gibt es eine Äquivalenklasse mit drei Ecknummer. Die möglichen
Kombinationen von Äquivalenzklassen-Anzahlen sind
17
• für n = 5 :
3, 2 und 3, 1, 1
• für n = 6 :
3, 3 und 3, 1, 1, 1.
Für n = 5 gibt es höchstens eine Nachbar-Bewegung, die Achsenspiegelung ist, bei n = 6 gibt
es keine.
Beweis : Falls eine Nachbar-Bewegung Bk Drehung ist, gilt k → ∼ k ← , so dass es dann
mindestens eine Äquivalenzklasse mit mehr als einem Element gibt.
Falls n = 5 : Es können nicht alle Äquivalenzklassen einelementig sein. Denn wäre das der
Fall, könnte keine Nachbar-Bewegung eine Drehung sein, folglich wären alle NachbarBewegungen Achsenspiegelungen und nach Satz 4 (7.) alle Innenwinkel kleinergleich 90°. Das
widerspricht aber der Innenwinkelsumme 540°.
Es kann auch nicht sein, dass eine Äquivalenzklasse Ä zweielementig und die andern
einelementig sind. Denn nach Satz 4 (8.) wäre dann αÄ ≤ 180° und die anderen drei
Klassenwinkel müssten 120° betragen; aber drei Nachbar-Drehungen sind bei fünf Seiten nicht
möglich, da sie immer Seiten-Paaren zugeordnet sind.
Auch zwei zweielementige Äquivalenzklassen und eine einelementige sind wegen
2 ⋅180° + 120° < 540° nicht möglich. Darum bleiben nur die Äquivalenzklassen-Anzahlen der
Behauptung übrig.
Falls n = 6 : Wie für n = 5 zeigt man, dass nicht alle Äquivalenzklassen einelementig sind.
Wegen 180° + 4 ⋅120° < 720° und 2 ⋅180° + 2 ⋅120° < 720° sind auch eine oder zwei
Äquivalenzklassen mit zwei Elementen und die andern mit einem Element nicht möglich. Es
gibt also mindestens eine dreielementige Äquivalenzklasse, und nach Satz 4 (9.) kann es dann
keine zweielementige geben.
□
6. Aussonderung möglicher Signaturen
i → für i > 0
Definition : Es sei i :=  ←
. Wir sagen, dass die Signatur r1r2...rn durch einfache
i für i < 0
Rotation aus der Signatur s1s2...sn entsteht, wenn riρ = sρi ist für alle i ∈ {1, 2,..., n} . Sie entsteht
durch Rotation, wenn sie sich durch Hintereinanderschaltung mehrerer einfacher Rotationen
ergibt.
Aus der Signatur -132 erhält man z. B. durch einfache Rotation die Signatur 3-21. Diese
Signaturen beschreiben im Wesentlichen den gleichen Kachelungstyp mit dem einzigen
Unterschied, dass die Seitennummerierung 1 2 3 durch 2 3 1 ersetzt wird.
ρ
Die Bestimmung unmöglicher Signaturen filtert Signaturen heraus, so dass nur noch die in
Tabelle 1 auf Seite 20 übrigbleiben. Wir gehen dabei von einer Liste mit denkbaren Signaturen
aus, die nacheinander für n = 3, 4, 5 und 6 folgendermaßen in mehreren Stufen entsteht:
In Stufe 0 sei die erste Signatur 1 2 ... n. Anschließend wird die Signatur angefügt, die durch
Änderung des Vorzeichens an der ersten Stelle entsteht. Dann wird bei allen bisher
geschriebenen Signaturen das Vorzeichen der 2. Stelle geändert und die geänderten Fassungen
an die Liste angehängt, die dann aus vier Signaturen besteht. Dieses Verfahren wird bei den
folgenden Stellen fortgesetzt, wobei sich die Liste jeweils verdoppelt.
In Stufe 1 werden an die bisherigen Liste die Signaturen angehängt, die durch Vertauschung
von zwei Folgengliedern si = ±i und s j = ± j mit gleichem Vorzeichen entstehen, wobei
zunächst i = 1 ist und j die folgenden Stellen durchläuft und i dann schrittweise erhöht wird.
In Stufe 2 wird das Verfahren von Stufe 1 für ein weiteres Stellenpaar durchgeführt, falls n > 3
ist, und analog in Stufe 3 für ein drittes Stellenpaar, wenn n > 5 ist.
18
Anschließend werden die Signaturen gelöscht, die durch Rotation aus einem vorangehenden
Listeneintrag entstehen. Es entsteht folgende (rechner-generierte) Liste:
123
-1 3 2
-1 2 3
-2 -1 3
-1 -2 3
-2 -1 -3
-1 -2 -3
213
1234
-1 -2 -3 -4
-1 2 4 3
-2 -1 -3 4
2143
-3 -4 -1 -2
-1 2 3 4
2134
-2 -1 3 4
-3 -2 -1 4
3412
-1 -2 3 4
3214
-1 -2 4 3
-1 -3 -2 4
-2 -1 4 3
-1 2 -3 4
-1 3 2 4
-3 2 -1 4
-2 -1 -3 -4
-3 4 -1 2
-1 -2 -3 4
-1 4 3 2
-1 4 -3 2
-3 -2 -1 -4
-2 -1 -4 -3
12345
-1 -2 3 -4 5
-1 3 2 4 5
-1 2 3 5 4
-3 2 -1 4 5
-3 -2 -1 4 5
-1 -4 3 -2 5
-1 -3 -2 -4 5
21435
-1 5 4 3 2
-3 5 -1 4 2
-2 -1 5 -4 3
-4 -3 -2 -1 5
-1 2 3 4 5
-1 -2 -3 -4 5
-1 4 3 2 5
-2 -1 3 4 5
-1 4 -3 2 5
-1 -3 -2 4 5
-1 -2 5 -4 3
-1 -4 -3 -2 5
21543
-2 -1 4 3 5
-3 2 -1 5 4
-4 -2 5 -1 3
-2 -1 -4 -3 -5
-1 -2 3 4 5
-1 -2 -3 -4 -5
-1 5 3 4 2
-1 -2 4 3 5
-1 5 -3 4 2
-1 -2 -3 5 4
-2 -1 -3 -4 5
-1 -2 -4 -3 5
34125
-2 -1 5 4 3
-2 -1 -3 5 4
-1 -4 5 -2 3
-2 -1 -5 -4 -3
-1 2 -3 4 5
21345
-1 2 4 3 5
-1 -2 5 4 3
-1 2 -3 5 4
-2 -1 3 -4 5
-3 -2 -1 -4 5
-2 -1 -3 -4 -5
-1 3 2 5 4
-2 -1 3 5 4
-3 -2 -1 5 4
-2 -1 -4 -3 5
-3 -4 -1 -2 -5
-1 -2 -3 4 5
32145
-1 2 5 4 3
-1 -2 3 5 4
-2 -1 -3 4 5
-4 -2 3 -1 5
-4 -2 -3 -1 5
-3 -2 -1 -4 -5
-1 4 5 2 3
-3 4 -1 2 5
-1 -3 -2 5 4
-3 -4 -1 -2 5
123456
-1 2 3 -4 5 6
-1 -2 -3 4 -5 6
321456
-1 6 3 4 5 2
-1 2 3 6 5 4
-1 -2 6 4 5 3
-1 4 -3 2 5 6
-1 2 -3 4 6 5
-1 -2 -3 6 5 4
-1 6 3 -4 5 2
-1 -2 5 -4 3 6
-1 5 -3 -4 2 6
-3 -2 -1 -4 5 6
-1 -2 -3 -4 6 5
-5 -2 -3 4 -1 6
-2 -1 3 -4 -5 6
-2 -1 -3 -4 -5 6
-1 -4 -3 -2 -5 6
-2 -1 -3 -4 -5 -6
216453
321654
-1 4 5 2 3 6
-1 5 3 6 2 4
-1 2 3 4 5 6
-1 -2 3 -4 5 6
-1 -2 3 -4 -5 6
423156
-1 2 4 3 5 6
-1 2 3 4 6 5
-1 -2 3 5 4 6
-1 5 -3 4 2 6
-2 -1 -3 4 5 6
-1 -2 -3 4 6 5
-1 2 6 -4 5 3
-1 -2 6 -4 5 3
-1 6 -3 -4 5 2
-4 -2 -3 -1 5 6
-3 2 -1 4 -5 6
-1 -3 -2 4 -5 6
-4 -2 3 -1 -5 6
-3 -2 -1 -4 -5 6
-1 -5 -3 -4 -2 6
-3 -2 -1 -4 -5 -6
213546
453126
-1 4 6 2 5 3
-1 6 4 3 5 2
-1 -2 3 4 5 6
-1 2 -3 -4 5 6
-1 -2 -3 -4 -5 6
-1 3 2 4 5 6
-1 2 5 4 3 6
-2 -1 3 4 5 6
-1 -2 3 6 5 4
-1 6 -3 4 5 2
-3 -2 -1 4 5 6
-4 2 3 -1 5 6
-2 -1 3 -4 5 6
-1 -2 3 -4 6 5
-1 2 -4 -3 5 6
-1 -3 -2 -4 5 6
-1 4 -3 2 -5 6
-1 -5 -3 4 -2 6
-5 -2 3 -4 -1 6
-4 -2 -3 -1 -5 6
-1 -2 -4 -3 -5 6
-4 -2 -3 -1 -5 -6
213654
-1 3 2 5 4 6
-1 4 3 2 6 5
-1 6 5 4 3 2
-1 2 -3 4 5 6
-1 -2 -3 -4 5 6
-1 -2 -3 -4 -5 -6
-1 4 3 2 5 6
-1 2 6 4 5 3
-1 -2 4 3 5 6
-1 -2 3 4 6 5
-1 2 -3 5 4 6
-1 -3 -2 4 5 6
-1 3 2 -4 5 6
-4 -2 3 -1 5 6
-3 2 -1 -4 5 6
-1 2 -3 -4 6 5
-1 -4 -3 -2 5 6
-2 -1 -3 4 -5 6
-1 -2 -5 4 -3 6
-1 -5 3 -4 -2 6
-5 -2 -3 -4 -1 6
-1 -2 -5 -4 -3 6
214356
341256
-1 3 2 6 5 4
-1 5 4 3 2 6
-1 6 3 5 4 2
19
-1 -2 -3 4 5 6
-1 2 -3 4 -5 6
213456
-1 5 3 4 2 6
-1 2 3 5 4 6
-1 -2 5 4 3 6
-3 2 -1 4 5 6
-1 2 -3 6 5 4
-1 -2 -3 5 4 6
-1 5 3 -4 2 6
-1 -4 3 -2 5 6
-4 2 -3 -1 5 6
-2 -1 -3 -4 5 6
-1 -2 -4 -3 5 6
-3 -2 -1 4 -5 6
-1 -2 -3 6 -5 4
-1 -2 6 -4 -5 3
-1 -3 -2 -4 -5 6
-1 -2 -3 -5 -4 6
215436
351426
-1 3 2 4 6 5
-1 5 6 4 2 3
-1 2 4 3 6 5
-1 2 5 6 3 4
-2 -1 3 5 4 6
-1 2 6 5 4 3
-2 -1 3 6 5 4
-2 -1 4 3 5 6
-2 -1 3 4 6 5
-2 -1 5 4 3 6
-1 -2 4 3 6 5
-2 -1 6 4 5 3
-1 -2 5 6 3 4
In Tabelle 1 bleiben für n = 3 alle acht Signaturen übrig, bei n = 4 sechsehn von 26, bei n = 5
sechs von 64 und bei n = 6 sieben von 130. Zur Aussonderung zeigen wir für n = 4 mit Hilfe
von Perioden die Unmöglichkeit von 10 Signaturen, für n = 5 und n = 6 suchen wir mit Hilfe
der Äquivalenzklassen die möglichen Signaturen heraus. Dass sich für die übrig gebliebenen
Signaturen wirklich Kachelungen ergeben, muss dann in einem folgenden Schritt gezeigt
werden.
Satz 6 : K0 sei positiv nummerierte Kachel zur Signatur s1s2...sn. Wenn K0 eine Kachelung
erzeugt, dann ist s1s2...sn eine der Signaturen in der Tabelle 1 oder eine Rotation davon.
Zeilennummer
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
n=3
123
-1 2 3
-1 -2 3
-1 -2 -3
213
-1 3 2
-2 -1 3
-2 -1 -3
n=4
1234
-1 2 -3 4
-1 -2 -3 4
-1 -2 -3 -4
3214
-1 4 3 2
-2 -1 3 4
-1 -2 4 3
-3 2 -1 4
-1 4 -3 2
-3 -2 -1 -4
2143
3412
-3 4 -1 2
-2 -1 -4 -3
-3 -4 -1 -2
n=5
32145
-1 5 3 4 2
21435
-2 -1 5 4 3
-2 -1 5 -4 3
-3 -4 -1 -2 5
n=6
423156
-2 -1 6 4 5 3
-3 -5 -1 4 -2 6
214365
456123
-2 -1 6 -5 -4 3
-5 -4 6 -2 -1 3
Tab. 1
Beweis:
n = 4 : In der folgenden Tabelle 2 geben wir zu den Signaturen, die ausgesondert werden
sollen, eine Periode t 0 t 2 ...t m −1 an, aus der sich entweder ein Periodenwinkel 720° ergibt oder
eine Anzahl 3 der zugehörigen Äquivalenzklasse Ä. Beides ist nach Satz 4 unmöglich, so dass
nur die rot markierten Signaturen übrig bleiben. Wir stellen die Periode in der Form
< t 0 t 2 ...t m −1t 0 > dar, um die Periodizität deutlicher zu machen.
Signatur
1234
-1 2 3 4
-1 -2 3 4
-1 2 -3 4
-1 -2 -3 4
-1 -2 -3 -4
2134
3214
-1 3 2 4
Periode
Periodenwinkel
<1 -2 -3 -4 -1 4 3 2 1 >
<4 3 2 -3 -4 -1 4 >
720°
Ä
3
<4 3 2 4 >
3
<1 -2 -4 -1 4 3 1 >
3
20
-1 4 3 2
-1 2 4 3
-2 -1 3 4
-1 -2 4 3
-3 2 -1 4
-1 4 -3 2
-2 -1 -3 4
-3 -2 -1 4
-1 -3 -2 4
-2 -1 -3 -4
-3 -2 -1 -4
2143
3412
-2 -1 4 3
-3 4 -1 2
-2 -1 -4 -3
-3 -4 -1 -2
<1 -2 -3 -1 4 2 1 >
<1 -3 2 -2 4 3 -4 -1 1 >
<1 -4 -1 2 -3 4 3 -2 1 >
<1 -2 2 -4 -1 4 3 -3 1 >
<1 -3 2 -2 4 -1 1 >
3
720°
720°
720°
3
<1 -3 -1 1 >
3
Tab. 2
Wenn wir im Folgenden schreiben 'k1 und k2 folgen aufeinander', bzw. 'k1, k2 und k3 folgen
aufeinander ' dann ist damit gemeint, dass dass die Eckpunkte mit den Nummern k1 und k2
bzw. k1, k2 und k3 bei einem Umlauf um den Kachelrand aufeinanderfolgen.
n = 5:
1. Fall (Abb. 9): Es gibt zwei einelementige Äquivalenzklassen
{k1} und {k 3 } und eine dreielementige Ä = {k 2 , k 4 , k 5 } . Nach
Satz 4 (9.) ist dann α Ä = α P = 360° , wobei αP Periodenwinkel
ist. Wegen αÄ = αP liegt kein Eckpunkt mit der Nummer k2, k4
oder k5 auf einer Seite, deren Nachbarbewegung eine
Achsenspiegelung ist. Wegen n = 5 liegen auch die andern
Eckpunkte nicht auf Geraden, die Achsen von Spiegelungen in
der Automorphismengruppe sind. Darum sind die NachbarBewegungen
und
Abb. 9
Bk1 und Bk 3 Drehungen (um 120°). Dann ist s k1 = k1→ , s k → = k1 , s k2 = k →
2
1
→
s k → = k 2 . Wegen k1← ∼ k1→ und k ←
2 ∼ k 2 folgen zwei der Zahlen in Ä aufeinander,
2
z. B k4 und k5, nicht aber alle drei. Da folglich die Seite k5 durch eine Nachbarbewegung auf
sich abgebildet wird, ist Bk 5 eine 180°-Drehung. Die Signatur ist 2 1 4 3 5 oder entsteht
daraus durch Rotation (Tab. 1, Zeile 3).
2. Fall : Es gibt eine zweielementige Äquivalenzklasse und eine
dreielementige.
Fall 2.1 (Abb. 10): Die Zahlen beider Klassen folgen
aufeinander.
Nach eventueller Rotation ergeben sich die Klassen {5,1} und
{2,3, 4} . Die Seite 1 wird dann durch ihre Nachbar-Bewegung auf
21
Abb. 10
sich abgebildet, die eine Achsenspiegelung oder eine 180°-Drehung sein kann. Die Seite 5
wird durch eine gerade Nachbar-Bewegung in die Seite 2 abgebildet, da die Endpunkte von
Seite 5 in dazu äquivalente Eckpunkte abgebildet werden. Die Seiten 3 und 4 gehen durch
zueinander inverse Nachbar-Gleitspiegelungen auseinander hervor oder ihre NachbarBewegungen sind 180°-Drehungen.
Die Signaturen sind darum 1 5 3 4 2, -1 5 3 4 2 , 1 5 -4 -3 2 oder -1 5 -4 -3 2.
Durch Rotation entstehen die folgenden Signaturen in Tabelle 1 :
3 2 1 4 5 (Zeile 1), -1 5 3 4 2 (Zeile 2), -2 -1 5 4 3 (Zeile 4) und -2 -1 5 -4 3 (Zeile 5)
Fall 2.2 (Abb. 11): Nur zwei der Zahlen in der dreielelementigen
Klasse folgen aufeinander. Wenn dies die Zahlen 4 und 5 sind,
dann sind {1,3} und {2, 4,5} die beiden Klassen. Die Seite 5 bleibt
bei B5 fest, da sie die einzige Seite mit zwei äquivalenten
Eckpunkten ist. B5 ist keine Achsenspiegelung, da nach Satz 4 (9.)
α245 Periodenwinkel ist. Also ist B5 180°-Drehung. B1 kann die
Seite 2 nicht in die Seite 1 abbilden, da sonst {1} eine
Äquivalenzklasse wäre. Aus analogem Grund ist es unmöglich,
dass B2 die Seite 3 in die Seite 2 abbildet. B1 bewegt darum
Abb. 11
notwendig die Seite 3 in die Seite 1 und muss eine Gleitspiegelung
sein, weil dabei E3 auf den äquivalenten Punkt E1 abgebildet wird. Entsprechend wird die
Seite 4 durch eine Gleitspiegelung in die Seite 2 bewegt. Die Signatur ist darum
-3 -4 -1 -2 5 (Tab. 1 Zeile 6).
n=6:
1. Fall (Abb. 12): Es gibt drei einelementige
Äquivalenzklassen und eine dreielementige. Die
einelementigen gehören zu Drehungen, da es nach
Satz 4 (9.) für n = 6 keine Nachbar-Bewegungen gibt, die
Achsenspiegelungen sind. Bei geeigneter Rotation erhält
man darum die Signatur 2 1 4 3 6 5 (Tab. 1 Zeile 4).
Abb. 12
2.Fall : Es gibt zwei dreielementige Äquivalenzklassen.
Fall 2. 1 (Abb. 13): In beiden Klassen folgen die Zahlen
aufeinander. Nach eventueller Rotation hat man also die
Klassen {1, 2,3} und {4,5, 6} . Die Seite 4 muss dann
durch eine gerade Bewegung in die Seite 1 abgebildet
werden, da nur diese Seiten nicht-äquivalente Eckpunkte
Abb. 13
haben. Seite 2 kann nur auf sich selbst mit einer 180°Drehung oder auf die Seite 3 mit einer Gleitspiegelung bewegt werden. Im ersten Fall ist auch
B3 eine 180°-Drehung. Entsprechend kann man die Seite 5 nur auf sich oder auf die Seite 6
abbilden. Die möglichen Signaturen sind darum 4 2 3 1 5 6, 4 -3 -2 1 5 6, 4 2 3 1 -6 -5 und
4 -3 -2 1 -6 -5, wobei die beiden mittleren Signaturen durch Rotation auseinander
hervorgehen.
Durch Rotation entstehen die folgenden Signaturen in Tabelle 1 :
4 2 3 1 5 6 (Zeile 1), -2 -1 6 4 5 3 (Zeile 2) und -2 -1 6 -5 -4 3 (Zeile 6).
Fall 2.2 (Abb. 14): Je zwei der Zahlen in den dreielelementigen Klasse folgen aufeinander.
Durch eventuelle Rotation erhält man die Klassen {1,3, 4} und {2,5, 6} . Die Seiten 4 und 6
müssen dann durch 180°-Drehungen auf sich abgebildet werden, da nur sie äquivalente
22
Endpunkte haben. B2 kann nicht die Seite 3 in die Seite 2
bewegen, denn dann wäre B3 eine Drehung und {2} eine
einelementige Klasse. B2 bildet aus entsprechendem Grund
auch nicht die Seite 1 in die Seite 2 ab. Folglich muss die
Seite 5 in Seite 2 bewegt werden, und zwar durch eine
Gleitspiegelung, da E5 und E2 äquivalent sind. Die übrig
gebliebenen Seiten 1 und 3 werden schließlich durch
zueinander inverse Gleitspiegelungen ineinander
abgebildet. Die Signatur ist folglich
-3 -5 -1 4 -2 6 (Tab. 1 Zeile 3).
Abb. 14
Fall 2.3 (Abb. 15): Keine zwei aufeinanderfolgende Zahlen
sind äquivalent. Durch eventuelle Rotation erhält man die Klassen {1,3,5} und {2, 4, 6} . Nach
Satz 3 ist eine Hintereinanderschaltung von drei NachbarBewegungen die identische Abbildung; nicht alle drei können darum
ungerade sein. Sei ohne Beschränkung der Allgemeinheit B3 gerade
Bewegung. B3 bildet weder die Seite 4 noch die Seite 2 auf die Seite
3 ab, da sonst {3} und {2} einelementige Äquivalenzklassen wären.
Die Seiten 5 und 1 können durch B3 nicht in Seite 3 bewegt werden,
da dann B3 ungerade wäre. Also bildet B3 die Seite 6 in Seite 3 ab,
folglich die inverse Abbildung B6 die Seite 3 in Seite 6. B1 kann
keine Drehung sei, also die Seite 2 nicht in Seite 1 bewegen. B1 kann
auch Seite 1 nicht auf sich abbilden, da E1 und E6 nicht äquivalent
Abb. 15
sind.
Fall 2.3.1 : B1 bewegt Seite 4 in Seite 1. Dann ist B1 gerade, weil E3 in E1 abgebildet wird und
E4 in E6. Auch B5 ist dann gerade, da eine Hintereinanderschaltung der Bewegungen zur
Klasse {1,3,5} die identische Abbildung ergibt. Folglich ist die Signatur 4 5 6 1 2 3 (Tab. 1
Zeile 5).
Fall 2.3.1 : B1 bewegt Seite 5 in Seite 1. Dann ist B1 ungerade, weil E5 in E1 abgebildet wird
und E4 in E6. B5 muss dann auch ungerade sein. Es ergibt sich die Signatur -5 -4 6 -2 -1 3
(Tab. 1 Zeile 7).
□
7. Kachel-Eigenschaften :
Für jede in Satz 6 herausgefilterte Signatur sollen nun für Seitenlängen und Innenwinkel
notwendige Bedingungen dafür bestimmt werden, dass eine Kachel mit dieser Signatur eine
Kachelung erzeugt. Dabei wird angestrebt, so viele Bedingungen zu finden, dass damit in
einem folgenden Abschnitt 8 gezeigt werden kann, dass sie für eine Kachelung auch
hinreichen. Dabei treten einige Signaturen mehrfach auf, wenn nämlich bei einelementigen
Klassen die Klassenwinkel mehrere verschiedene Winkelgrößen haben können. In den
folgenden Tabellen 4, 6, 8 und 10 beschreibt jede Zeile einen Kacheltyp, der durch eine
Signatur und derartige Winkelgrößen bestimmt ist.
Die Bedingungen für Seitenlängen ergeben sich unmittelbar aus der Signatur, wenn si ≠ i ist.
Denn dann wird die Seite von K0 mit der Nummer si in die mit der Nummer i bewegt, so
dass die Seitenlängen ℓ si und ℓ i übereinstimmen müssen. Die Bedingungen für die
Innenwinkel folgen aus den Periodenwinkeln.
Wir geben in den folgenden Tabellen zu jeder Äquivalenzklasse die Periode einer
Eckennummer i von K0 und den zugehörigen Periodenwinkel δi an, zunächst für
23
n=3:
Signatur
123
-1 2 3
-1 -2 3
-1 -2 -3
213
-1 3 2
-2 -1 3
-2 -1 -3
Perioden
<1 3 2 1 >
<1 -2 -3 -1 3 2 1 >
<1 -2 1 >, <2 -3 -1 3 2 >
<1 -2 1 >, <2 -3 2 >, <3 -1 3 >
<1 1 >, <2 3 2 >
<1 -2 -1 3 1 >, <2 2 >
<1 -3 -1 1 >
<1 -3 2 -2 3 -1 1 >
Periodenwinkel
δ1 = δ2 = δ3 = α1+α2+α3
δ1 = δ2 = δ3 = 2α1+2α2+2α3
δ1 = 2α1, δ2 = δ3 = 2α2+2α3
δ1 = 2α1, δ2 = 2α2, δ3 = 2α3
δ1 = α1, δ2 = δ3 = α2+α3
δ1 = δ3 = 2α1+2α3, δ2 = α2
δ1 = δ2 = δ3 = α1+α2+α3
δ1 = δ2 = δ3 = 2α1+2α2+2α3
Tab. 3
Bei den Signaturen 1 2 3 ergeben die Periodenwinkel keine Einschränkungen, da α1+α2+α3
im Dreieck stets 180° beträgt, was nach Satz 4 ein möglicher Periodenwinkel ist. Da {1,2,3}
eine Äquivalenzklasse ist, gibt es nur den Klassenwinkel 180°. Nach Satz 3 ist (B1B2B3)2
wegen 2δ1 = 360° die identische Abbildung.
Signatur -1 2 3 : Es gibt auch hier nur eine Äquivalenzklasse. Der einzige Periodenwinkel ist
δ1 = δ2 = δ3 = 360° , der einzige Klassenwinkel α123 = α1+α2+α3 =180°. Wegen der Periode
<1 -2 -3 -1 3 2 1 > ist nach Satz 3 B1B2B3B1B3B2 die identische Abbildung.
Signatur -1 -2 3 : Die Summe der beiden Periodenwinkel δ1 und δ2 beträgt 360°. Einer von
beiden muss also größergleich 180° sein; folglich sind beide gleich 180°, da es zwischen 180°
und 360° keine möglichen Werte gibt. Also ist α1 = α23 = 90°. Nach Satz 4 ist (B1B2)2 = id
und (B2B3B1B3)2 = id.
Signatur -1 -2 -3 : δ1 + δ2 + δ3 = 360°. Da für Periodenwinkel nach Satz 4 nur die Werte 60°,
90°, 120°, 180° und 360° in Frage kommen, gibt es bis auf Rotationen nur drei
Kombinationsmöglichkeiten:
δ1 = δ2 = δ3 = 120°, also α1 = α2 = α3 = 60° und (B1B2)3 = (B2B3)3 = (B3B1)3 = id.
δ1 = 180°, δ2 = 120°, δ3 = 60°, also α1 = 90°, α2 = 60°, α3 =30° und (B1B2)2 = (B2B3)3 =
(B3B1)6 = id.
δ1 = 90°, δ2 = 180°, δ3 = 90°, also α1 = 45°, α2 = 90°, α3 = 45° und (B1B2)4 = (B2B3)2 =
(B3B1)4 = id.
Signatur 2 1 3 : δ1 + δ2 = 180°. Also gibt es nur die Möglichkeiten
δ1 = 60°, δ2 = 120° und δ1 = 90°, δ2 = 90° , was wegen ℓ1 = ℓ 2 bis auf Rotationen auf
α1 = α2 = α3 = 60° oder α1 = 90°, α2 = 45°, α3 = 45° oder α1 = 120°, α2 = 30°, α3 = 30°
führt. Dann ist B16 = (B2B3)3 = id bzw. B14 = (B2B3)4 = id bzw. B13 = (B2B3)6 = id.
Signatur -1 3 2 : Da die Seitenlängen ℓ 2 und ℓ 3 gleich sind, gilt α1 = α3 . Daraus folgt δ1 =
4α1. Wegen δ1 < 360° gibt es dann nur die Möglichkeiten α1 = α3 = 45°, α2 = 90° und α1 =
α3 = 30°, α2 = 120°. Im ersten Fall ist δ1 =180°, δ2 = 90°, also (B1B3B1B2)2 = B42 = id. Im
zweiten Fall ist δ1 = δ2 = 120°, also (B1B3B1B2)3 = B32 = id.
24
Signatur -2 -1 3 : Aus folgt ℓ1 = ℓ 2 und daraus α2 = α3. Die Periodenwinkel ergeben keine
weitere Einschränkung. Wegen δ1 = α1+α2+α3 = 180° ist (B1B1B3)2 = id .
Signatur -2 -1 -3 : Auch hier folgt α2 = α3 aus ℓ1 = ℓ 2 . Wegen δ1 = 2α1+2α2+2α3 = 360° und
der Periode <1 -3 2 -2 3 -1 1 > ist B1B1B3 B2B2B3 = id .
Wir fassen für n = 3 die Längen-, Winkel- und Bewegungs-Relationen in einer Tabelle
zusammen.
Nr.
Signatur
1
2
3
123
-1 2 3
-1 -2 3
4
-1 -2 -3
Längen=
relationen
ℓ1 = ℓ 2 = ℓ 3
5
-1 -2 -3
6
-1 -2 -3
7
213
ℓ1 = ℓ 2 = ℓ 3
8
213
ℓ1 = ℓ 2
9
213
ℓ1 = ℓ 2
10
-1 3 2
ℓ 2 = ℓ3
ℓ 2 = ℓ3
Winkelrelationen
Bewegungs=
relationen
2
(B
α123 =180°
1B2B3) =id
B1B2B3B1B3B2=id
α123 =180°
(B1B2)2 =
α1 = α23 =90°
(B2B3B1B3)2 = id.
3
3
α1 = α2 = α3 = 60° (B1B2) = (B2B3)
3
= (B3B1) = id
2
3
α1 = 90°, α2 = 60°, (B1B2) = (B2B3)
6
= (B3B1) = id
α3 =30°
4
2
α1 = 45°, α2 = 90°, (B1B2) = (B2B3)
= (B3B1)4 = id
α3 = 45°
α1 = α2 = α3 = 60° B16 = (B2B3)3 = id
α1 = 90°,
α2 = α3 = 45°
α1 = 120°,
α2 = α3 = 30°
α1 = α3 = 45°,
α2 = 90°
11
-1 3 2
ℓ 2 = ℓ3
α1 = α3 = 30°,
α2 = 120°.
12
-2 -1 3
ℓ1 = ℓ 2
13
-2 -1 -3
ℓ1 = ℓ 2
α123 =180°,
α2 = α3
α123 =180°,
α2 = α3
Beschreibung
beliebiges Dreieck
beliebiges Dreieck
90°-Dreieck
60°-60°- Dreieck
30°-60°- Dreieck
45°-45°- Dreieck
60°-60°- Dreieck
B14 = (B2B3)4 = id
45°-45°- Dreieck
B13 = (B2B3)6 = id
30°-30°- Dreieck
(B1B3B1B2)2 = B42
= id
(B1B3B1B2)3 = B32
= id
(B1B1B3)2 = id
45°-45°- Dreieck
30°-30°- Dreieck
gleichschenkliges
Dreieck
B1B1B3B2B2B3= id gleichschenkliges
Dreieck
Tab. 4
Die Längen - und Winkel-Relationen ermöglichen es im nächsten Abschnitt zu zeigen, dass
diese Dreiecke als Start-Kacheln von Kachelungen geeignet sind. Zunächst aber wiederholen
wir das für n = 3 durchgeführte Verfahren für die Eckenzahlen 4, 5 und 6.
25
n=4:
Signatur
1234
-1 2 -3 4
-1 -2 -3 4
-1 -2 -3 -4
3214
-1 4 3 2
-2 -1 3 4
-1 -2 4 3
-3 2 -1 4
-1 4 -3 2
-3 -2 -1 -4
2143
3412
-3 4 -1 2
-2 -1 -4 -3
-3 -4 -1 -2
Perioden
<1 4 3 2 1 >
<1 -2 -3 2 1 >,
<3 -4 -1 4 3 >
<1 -2 1 >, <2 -3 2 >,
<3 -4 -1 4 3 >
<1 -2 1 >, <2 -3 2 >,
<3 -4 3 > , <4 -1 4 >
<1 2 1 > ,
<3 4 3 >
<1 -2 -1 4 1 >,
<2 3 2 >
<1 -3 -4 -1 1 >
<1 -2 1 >, <2 -3 -1 4 2 >,
<3 3 >
<1 -4 -1 2 1 >
<1 -2 -1 4 1 >,
<2 3 -4 -3 2 >
<1 -4 3 -2 1 >,
<2 -3 4 -1 2 >
<1 1 >, <2 4 2 >,
<3 3 >
<1 2 3 4 1 >
<1 -4 -3 4 1 >
<1 -3 3 -1 1 >
<1 -4 1 >, <2 -1 2 >
Periodenwinkel
δ1 = δ2 = δ3 = δ4 = α1+α2+α3+α4
δ1 = δ2 = 2α1+2α2,
δ3 = δ4 = 2α3+2α4
δ1 = 2α1, δ2 = 2α2,
δ3 = δ4 = 2α3+2α4
δ1 = 2α1, δ2 = 2α2,
δ3 = 2α3, δ4 = 2α4
δ1 = δ2 = α1+α2,
δ3 = δ4 = α3+α4
δ1 = δ4 = 2α1+2α4,
δ2 = δ3 = α2+α3
δ1 = δ2 = δ3 = δ4 = α1+α2+α3+α4
δ1 = 2α1, δ2 = δ4 = 2α2+2α4,
δ3 = α3
δ1 = δ2 = δ3 = δ4 = α1+α2+α3+α4
δ1 = δ4 = 2α1+2α4,
δ2 = δ3 = 2α2+2α3
δ1 = δ3 = 2α1+2α3,
δ2 = δ4 = 2α2+2α4
δ1 = α1, δ2 = δ4 = α2+α4,
δ3 = α3
δ1 = δ2 = δ3 = δ4 = α1+α2+α3+α4
δ1 = δ2 = δ3 = δ4 = α1+α2+α3+α4
δ1 = δ2 = δ3 = δ4 = α1+α2+α3+α4
δ1 = δ3 = α1+α3, δ2 = δ4 = α2+α4
Tab. 5
Bei der Signatur 1 2 3 4 ergeben die Periodenwinkel keine Einschränkungen, da
α1+α2+α3+α4 im Viereck stets 360° beträgt, was nach Satz 4 ein möglicher Periodenwinkel
ist. α1234 = 360° ist der einzige Klassenwinkel. Wegen δ1 = 360° ist nach Satz 3 B1B2B3B4 =
id.
Signatur -1 2 -3 4 : Wegen δ1 + δ3 = 2α1+2α2+2α3+2α4 = 720° können δ1 und δ3 nicht beide
kleiner als 360° sein, folglich sind sie beide nach Satz 4 gleich 360°. Darum ist α1+α2 =
α3+α4 = 180° . Das Viereck ist also ein Trapez.
Wegen δ1 = δ3 = 360° ist B1B2B3B2 = id = B3B4B1B4.
Signatur -1 -2 -3 4: δ1 = 2α1 und δ2 = 2α2 betragen höchstens 180°, da sonst nur 360° in
Frage kommt, und δ3 = 2α3+2α4 höchstens 360°. Wegen δ1 + δ2 + δ3 = 720° gilt darum δ3 =
δ1 + δ2 = 360°. Darum ist δ1 = δ2 = 180° und α1 = α2 = 90°.
Aus δ3 = 360° und δ1 = δ2 = 180° folgt B3B4B1B4 = id und (B1B2)2 = (B2B3)2 = id.
26
Signatur -1 -2 -3 -4 : Da δ1, δ2, δ3 und δ4 kleinergleich 180° ist, die Summe aber 720°, folgt
δ1 = δ2 = δ3 = δ4 = 180°, also α1 = α2 = α3 = α4 = 90°, und (B1B2)2 = (B2B3)2 = (B3B4)2
=(B4B1)2 = id.
Signatur 3 2 1 4 : Wegen ℓ1 = ℓ 3 und ℓ 2 = ℓ 4 muss das Viereck ein Parallelogramm sein.
Dann ist α1 = α3, α2 = α4 und α12 = α34 =180° = δ1 = δ3. Daraus folgt (B1B2)2 = (B3B4)2 = id.
Signatur -1 4 3 2 : Wegen δ2 = α2+α3 <360° gilt δ2 ≤ 180°. Wegen δ1 = 2α1+2α4 ≤ 360° und
δ1 + 2δ2 = 720°, muss δ2 = 180° und δ1 = 360° sein. Es folgt α2+α3 = α1+α4 = 180°, so dass
das Viereck ein Parallelogramm ist. Wegen δ1 = 2δ2 = 360° ist B1B4 B1B2 = (B2B3)2 = id.
Signatur -2 -1 3 4 : Wegen δ1 = α1234 = 360° gibt es durch Winkelrelationen keine
Einschränkung. Das Viereck muss nur die Bedingung ℓ1 = ℓ 2 erfüllen.
Aus δ1 = 360° folgt B1B1B4B3 = id.
Signatur -1 -2 4 3 : Es ist δ1 = 2α1 ≤ 180° und δ2 = 2α2+2α4 ≤ 360°. Wegen δ1 + δ2 +2δ3 =
720° muss darum 2δ3 ≥ 180° sein, also δ3 = α3 ≥ 90°, d. h. dass α3 gleich 90° oder 120° groß
ist.
Im Fall α3 = 90° folgt δ1 = 2α1 = 180°, also α1 = 90°, und δ2 = 360°. Das Viereck ist dann also
ein Kreis-Viereck mit einer Diagonalen durch den Kreismittelpunkt, über der wegen ℓ 3 = ℓ 4
eines der beiden rechtwinkligen Teildreiecke gleichschenklig ist. Es ist (B1B2)2 = B2B4B1B3 =
B34 = id.
Im Fall α3 = 120° folgt δ1 = 2α1 = 120°, also α1 = 60°, und δ2 = 360°. Das Viereck ist dann ein
Kreis-Viereck mit gegenüberliegenden Winkeln der Größe 120° und 60°, wobei die Schenkel
des 120°-Winkels wegen ℓ 3 = ℓ 4 gleich lang sind. Hier ist (B1B2)3 = B2B4B1B3 = B33 = id.
Signatur -3 2 -1 4 : Wegen α1234 = 360° gibt es durch Winkelrelationen keine Einschränkung.
Das Viereck muss nur die Bedingung ℓ1 = ℓ 3 erfüllen.
Aus δ1 = 360° folgt B1B2B1B4 = id.
Signatur -1 4 -3 2 : Aus δ1 + δ3 = 2α1+2α2+2α3+2α4 = 720° folgt δ1 = δ3 = 360°. Darum ist
α14 = α23 = 180° . Da außerdem ℓ 2 = ℓ 4 gilt, ist das Viereck ein Parallelogramm.
Aus δ1 = δ3 = 360° folgt B1B4B1B2 = id = B2B3B4B3.
Signatur -3 -2 -1 -4 : Aus δ1 + δ2 = 2α1+2α2+2α3+2α4 = 720° folgt δ1 = δ2 = 360° und
α13 = α24 = 180°. Wegen ℓ1 = ℓ 3 ist das Viereck darum ein symmetrisches Trapez mit α1 = α2
und α3 = α4.
Aus δ1 = δ2 = 360° folgt B1B2B3B4 = id = B2B1B4B3.
Signatur 2 1 4 3 : Aus ℓ1 = ℓ 2 und ℓ 3 = ℓ 4 folgt α4 = α2 . Da δ1 = α1 und δ3 = α3 beide nur
die Werte 60°, 90° und 120° annehmen können, ist δ2 = α24 ≥ 120°, kann also nur die Werte
120° und 180° haben.
Im Fall δ2 = 180° ist (α1 = 60° und α3 = 120°) oder α1 = α3 = 90° oder (α1 = 120° und α3 =
60°). Folglich ist das Viereck dann 60°-120°-Drachen oder ein Quadrat. Dann ist B16 = (B2B4)2
= B33 = id bzw. B14 = (B2B4)2 = B34 = id bzw. B13 = (B2B4)2 = B36 = id.
27
Im Fall δ2 = 120° folgt α1 = α3 = 120°. Dann ist das Viereck eine 120°-Raute und
B13 = (B2B4)3 = B33 = id
Signatur 3 4 1 2 : Wegen ℓ1 = ℓ 3 und ℓ 2 = ℓ 4 ist das Viereck ein Parallelogramm. Es gibt nur
eine Äquivalenzklasse. Aus δ1 = 360° folgt B1B4B3B2 = id.
Signatur -3 4 -1 2 : Auch dies Viereck ist wegen ℓ1 = ℓ 3 und ℓ 2 = ℓ 4 ein Parallelogramm. Es
gibt nur eine Äquivalenzklasse. Wegen δ1 = 360° ist B1B4B3B4 = id.
Signatur -2 -1 -4 -3 : Wegen ℓ1 = ℓ 2 und ℓ 3 = ℓ 4 ist das Viereck ein Drachen mit α4 = α2. Es
gibt nur eine Äquivalenzklasse.Die Winkelrelationen ergeben keine Einschränkungen.
Aus δ1 = 360° folgt B1B1B3B3 = id.
Signatur -3 -4 -1 -2 : Aus δ1 + δ2 = α1 + α3 + α2 + α4 =360° folgt δ1 = δ2 = 180°. Das Viereck
ist folglich ein Kreis-Viereck. Da es wegen ℓ1 = ℓ 3 und ℓ 2 = ℓ 4 außerdem ein Parallelogramm
ist, muss es ein Rechteck sein. Aus δ1 = δ2 = 180° folgt (B1B4)2 = (B2B1)2 = id.
Zusammenfassung für n = 4:
Nr
.
14
15
Signatur
1234
-1 2 -3 4
α1234 = 360°
α12 = α34 = 180°
16
-1 -2 -3 4
α1 = α2 = 90°,
α34 = 180°
17 -1 -2 -3 -4
Längen=
relationen
α1 = α3, α2 = α4
α12= α34 = 180°
Bewegungs=
relationen
B1B2B3B4 = id
B1B2B3B2 = id
B3B4B1B4= id
(B1B2)2 = id
(B2B3)2 = id
B3B4B1B4 = id
(B1B2)2 = id
(B2B3)2 = id
(B3B4)2 = id
(B4B1)2 = id
(B1B2)2 = id
(B3B4)2 = id
B1B4 B1B2 = id
(B2B3)2 = id
Parallelogramm
ℓ2 = ℓ4
α1 = α3, α2 = α4
α14 = α23 = 180°
ℓ1 = ℓ 2
α1234 = 360°
B1B1B4B3 = id
Viereck mit ℓ1 = ℓ 2
Kreis-Viereck mit
ℓ3 = ℓ 4
und α3 = 90°
Kreis-Viereck mit
ℓ3 = ℓ 4
und α3 = 120°
Viereck mit ℓ1 = ℓ 3
Parallelogramm
ℓ1 = ℓ 3 ,
Winkelrelationen
α1 = α2 = α3 = α4=90°
ℓ2 = ℓ4
18
3214
ℓ1 = ℓ 3 ,
ℓ2 = ℓ4
19
20
-1 4 3 2
-2 -1 3 4
ℓ1 = ℓ 3 ,
21
-1 -2 4 3
ℓ3 = ℓ 4
α1 = α3 = 90°,
α14 = 180°
22
-1 -2 4 3
ℓ3 = ℓ 4
α1 = 60°, α3 = 120°,
α14 = 180°
23
-3 2 -1 4
ℓ1 = ℓ 3
α1234 = 360°
24
-1 4 -3 2
ℓ1 = ℓ 3 ,
α14 = α23 = 180°
ℓ2 = ℓ4
28
2
(B1B2) = id
B2B4B1B3 = id
B34 = id.
(B1B2)3 = id
B2B4B1B3 = id
B33 = id.
B1B2B1B4 = id
B1B4B1B2 = id
B2B3B4B3 = id
Beschreibung
beliebiges Viereck
Trapez
90°-90°-Viereck
Rechteck
Parallelogramm
25 -3 -2 -1 -4
26
2143
α1 = α2 , α3 = α4,
α13 = α24 = 180°
ℓ1 = ℓ 2 = ℓ 3 =αℓ14 = α2 = α3 = α4=90°
ℓ1 = ℓ 3
B1B2B3B4 = id
B2B1B4B3 = id
B14 = (B2B4)2 =
symmetrisches
Trapez
Quadrat
B34 = id
27
2143
28
2143
ℓ1 = ℓ 2 = ℓ 3 = ℓ 4 α1 = α3 = 120°,
α2 = α4 = 60°
ℓ1 = ℓ 2 ,
3412
-3 4 -1 2
B36 = id
B1B4B3B2 = id
Parallelogramm
α1 = α3, α2 = α4
α1234 = 360°
B1B4B3B4 = id
Parallelogramm
B1B1B3B3 = id
Drachen
ℓ3 = ℓ 4
α2 = α4,
α1234 = 360°
ℓ1 = ℓ 3 ,
α1 = α2 = α3 = α4=90°
(B1B4)2 = id
(B2B1)2 = id
Rechteck
ℓ1 = ℓ 3 ,
ℓ1 = ℓ 3 ,
ℓ2 = ℓ4
31 -2 -1 -4 -3
32 -3 -4 -1 -2
B33 = id
120°-60°-Drachen
ℓ2 = ℓ4
30
120°-Raute
B13 = (B2B4)2 =
ℓ3 = ℓ 4
29
α1 = 120°, α3 = 60°,
α2 = α4 = 90°
B13 = (B2B4)3 =
ℓ1 = ℓ 2 ,
α1 = α3, α2 = α4
α1234 = 360°
ℓ2 = ℓ4
Tab. 6
n=5:
Signatur
32145
-1 5 3 4 2
21435
-2 -1 5 4 3
-2 -1 5 -4 3
-3 -4 -1 -2 5
Perioden
<1 2 1 >,
<3 5 4 3>
<1 -2 -1 5 1 >,
<2 4 3 2>
<1 1 >, <2 5 4 2 >,
<3 3>
<1 -3 -1 1 >,
<3 4 3 >
<1 -3 -1 1 >,
<2 -2 5 2 >
<1 -4 1 >,
<2 -5 1 2 >
Periodenwinkel
δ1 = δ2 = α1+α2,
δ3 = δ4 = δ5 = α3+α4+α5
δ1 = δ5 = 2α1+2α5,
δ2 = δ3 = δ4 = α2+α3+α4
δ1 = α1, δ2 = δ4 = δ5 = α2+α4 +α5,
δ3 = α3
δ1 = δ3 = δ5 = α1+α3+α5,
δ3 = δ4 = α3+α4
δ1 = δ2 = δ5 = α1+α2+α5,
δ3 = δ4 = 2α3+2α4
δ1 = δ3 = α1+α3,
δ2 = δ4 = δ5 = α2+α4+α5
Tab. 7
Bei jeder dieser Signaturen gibt es eine Periode mit der Länge 3.
Nach Satz 4 ist der zugehörige Periodenwinkel dann 360° und
nach Satz 3 das Produkt dreier Nachbarbewegungen die identische
Abbildung.
Signatur 3 2 1 4 5 (Abb.16): δ3 = α345 = 360°, also α12 = α1+α2 =
180°, da die Summe aller Innenwinkel 540° beträgt. Darum sind
die Seiten Nummer 1 und 3 parallel. Da außerdem ℓ1 = ℓ 3 gilt,
29
Abb. 16
bilden die Eckpunkte mit den Nummern 5, 1, 2 und 3 ein
Parallelogramm. E4 muss dazu so gelegt werden, dass es zu
keinen Überschneidungen der Seiten kommt. Aus δ3 =2δ1 = 360°
folgt B3B4B5 = (B1B2)2 = id.
Signatur -1 5 3 4 2 (Abb. 17): δ2 = α234 = 360°, also α15 = 180°.
Darum sind die Seiten Nummer 2 und 5 parallel. Wegen ℓ 2 = ℓ 5
bilden dann die Eckpunkte 4, 5, 1 und 2 ein Parallelogramm. E3
unterliegt nur der Beschränkung wie E4 bei der vorigen Signatur.
Aus δ1 = δ2 = 360° folgt B1B5B1B2 = B2B3B4 = id.
Abb. 17
Signatur 2 1 4 3 5 (Abb. 18) : Dann ist ℓ1 = ℓ 2 und ℓ 3 = ℓ 4 .
δ2 = 360° , also α1+α3 = 180°. Dafür bleibt nur die
Möglichkeiten α1 = α3 = 90° oder {α1 , α3 } = {60°,120°} . Im
ersten Fall ergibt sich das Fünfeck, indem man zwei
gleichschenklige Rechtwinkel-Haken aneinandersetzt, so
dass keine Überschneidungen entstehen, und die Endpunkte
verbindet. Im zweiten Fall nimmt man statt zweier
Rechtwinkel-Haken einen gleichschenkligen 60°-Haken und
einen gleichschenkligen 120°-Haken. Aus δ2 = 360° folgt
B2B4B5 = id.
Abb. 18
Signatur -2 -1 5 4 3 (Abb. 19) : Hier ist ℓ1 = ℓ 2 und ℓ 3 = ℓ 5 . δ1 =
360°, also α34 = 180°. Darum sind die Seiten Nummer 3 und 5
parallel und gleich lang. Die Eckpunkte mit den Nummern 2, 3, 4
und 5 bilden ein Parallelogramm. Wegen ℓ1 = ℓ 2 sind die
Eckpunkte Nummer 1 und 2 durch einen gleichschenkligen Haken
verbunden. Darum ist der Winkel
α3 − α5 = ∠E 2 E5 E 4 − ∠E 2 E 5 E1 = ∠E3 E 2 E5 − ∠E 3 E 2 E1 = α 4 − α 2 .
Abb. 19
Aus δ1 = 2δ3 = 360° folgt B1B1B3 = (B3B4) = id.
2
Signatur -2 -1 5 -4 3 (Abb. 19): Auch hier ist
ℓ1 = ℓ 2 und ℓ 3 = ℓ 5 . δ1 = 360°, also α34 = 180°.
Auch dieses Fünfeck ist darum ein Parallelogramm
mit angesetztem gleichschenkligen Haken, so dass
α3 − α5 = α 4 − α 2 . Wegen δ1 = 360° ist auch hier
B1B1B3 = id, wegen δ3 = 360° aber B3B4B5B4 = id.
Signatur -3 -4 -1 -2 5 (Abb. 20) : Es ist ℓ1 = ℓ 3 und
ℓ 2 = ℓ 4 . δ2 = 360°, also α13 = 180°. Daraus folgt
B2B1B5 = (B1B4)2 = id. Da B5 eine Punktspiegelung
ist, folgt B2B1 = B5. Die Anwendung dieser
Abbildung auf die Achse g der Gleitspiegelung B2
ergibt gB1 = gB2B1 = gB5. Da g parallel zu gB5 ist
und folglich B1 die Gerade g auf eine dazu parallele
abbildet, muss g senkrecht zur Achse von B2
stehen, denn diese kann nicht g selbst sein, weil
B2B1 sonst eine Verschiebung wäre.
30
180°−α1
α1
Abb. 20
Zusammenfassung für n = 5:
Wenn dabei von einem gleichschenkligen Dreieck ABC die Rede ist, dann sollen die Winkel
bei A und bei C gleich groß sein.
Nr
Signatur
Winkelrelationen
32145
Längen=
relationen
ℓ1 = ℓ 3
α12= 180° ,
α345 = 360°
Bewegungs=
relationen
(B1B2)2 = id,
B3B4B2 = id
33
34
-1 5 3 4 2
ℓ1 = ℓ 3 ,
α15 = 180°,
α234 = 360°
B1B5B1B2 =
B2B3B4 = id
α1 = α3 = 90°,
α245 = 360°
B14 = B34 = id
B2B4B5 = id
ℓ 2 = ℓ5
35
21435
ℓ1 = ℓ 2 ,
ℓ3 = ℓ 4
36
21435
ℓ1 = ℓ 2 ,
ℓ3 = ℓ 4
37
-2 -1 5 4 3
ℓ1 = ℓ 2 ,
ℓ3 = ℓ5
38
-2 -1 5 -4 3
ℓ1 = ℓ 2 ,
ℓ3 = ℓ5
39 -3 -4 -1 -2 5
ℓ1 = ℓ 3 ,
ℓ2 = ℓ4
α1 = 120°,
α3 = 60°.
α245 = 360°
α34 = 180°,
α125 = 360°
α3 ̶ α5 = α4 ̶ α2
α34= 180°,
α125= 360°
α3 ̶ α5=α4 ̶ α2
α13= 180°
α245 = 360°
Beschreibung
E1E2E3E5
Parallelogramm,
E4 beliebig
E1E2E4E5
Parallelogramm,
E3 beliebig
E5E1E2 und E2E3E4
45°-45°-Dreieck
B13 = B36 = id E5E1E2 30°-30°-Dreieck
B2B4B5 = id E2E3E4 60°-60°-Dreieck
(B3B4)2 = id
B1B1B3 = id
E2 E3 E4 E5
Parallelogramm,
E5E1E2 gleichschenklig
B3B4B5B4=id
E2 E3 E4 E5
B1B1B3 = id
Parallelogramm,
E5E1E2 gleichschenklig
2
(B1B4) = id E1E2E3 und α1 beliebig,
B2B1B5 = id
E5 mit ℓ1 = ℓ 3 ,
E4 mit α3 =180°- α1
und ℓ 2 = ℓ 4
Tab. 8
n=6:
Signatur
423156
-2 -1 6 4 5 3
-3 -5 -1 4 -2 6
214365
456123
-2 -1 6 -5 -4 3
-5 -4 6 -2 -1 3
Perioden
<1 2 3 1 >,
<4 6 5 4>
<1 -3 -1 1 >,
<2 -2 6 2>
<1 -4 -5 1 >,
<2 -6 -1 2>
<1 1 >, <2 6 4 2>
<3 3 >, <5 5 >
<1 3 5 1 >,
<2 4 6 2 >
<1 -3 -1 1 >,
<2 -2 6 2 >
<1 -6 -4 1 >,
<2 -5 6 2 >
Periodenwinkel
δ1 = δ2 = δ3 = α1+α2+α3,
δ4 = δ5 = δ6 = α4+α5+α6
δ1 = δ2 = δ6 = α1+α2+α6,
δ3 = δ4 = δ5 = α3+α4+α5
δ1 = δ3 = δ4 = α1+α3+α4,
δ2 = δ5 = δ6 = α2+α5+α6
δ1 = α1, δ2 = δ4 = δ6 = α2+α4+α6,
δ3 = α3, δ5 = α5
δ1 = δ3 = δ5 = α1+α3+α5,
δ2 = δ4 = δ6 = α2+α4+α6
δ1 = δ2 = δ6 = α1+α2+α6,
δ3 = δ4 = δ5 = α3+α4+α5
δ1 = δ3 = δ5 = α1+α3+α5,
δ2 = δ4 = δ6 = α2+α4+α6
31
Tab. 9
Auch für n = 6 gibt es zu allen Signaturen mindestens eine Periode mit der Länge 3. Darum ist
auch hier die 9. Behauptung von Satz 4 anwendbar.
Signatur 4 2 3 1 5 6 : Dann ist ℓ1 = ℓ 4 und δ1 = δ4 = 360°. Daraus
folgt B4B5B6 = B1B2B3 = id, also B1 = B3B2, weil B2 und B3
Punktspiegelungen sind. Da die Hintereinanderschaltung zweier
Punktspiegelungen eine Verschiebung ist, sind die Seiten Nummer
1 und 4 parallel und gleich lang. Die Eckpunkte Nummer 6, 1, 3
und 4 bilden darum ein Parallelogramm. Die Eckpunkte Nummer 2
Abb. 21
und 5 können beliebig so gewählt werden, dass es zu keinen
Überschneidungen kommt. Denn auf Grund der Parallelität der Seiten Nummer 1 und 4 ist die
Bedingung δ1 = δ4 = 360° keine weitere Einschränkung.
Signatur -2 -1 6 4 5 3 : Es ist ℓ1 = ℓ 2 , ℓ 3 = ℓ 6 und δ1 = δ3 = 360°.
Daraus folgt B1B1B3 = B3B4B5 = id. Da B4 und B5
Punktspiegelungen sind, ist B3 eine Verschiebung. Darum sind die
Seiten Nummer 3 und 6 parallel und gleich lang. Die Eckpunkte
Nummer 2, 3, 5 und 6 bilden darum ein Parallelogramm. Der
Punkt Nummer 1 ist von den Punkten Nummer 2 und 6 gleich weit
entfernt. Der Punkt 4 ist beliebig, sofern es zu keinen
Überschneidungen kommt.
Signatur -3 -5 -1 4 -2 6 : Es ist ℓ1 = ℓ 3 ,
ℓ 2 = ℓ 5 und δ1 = δ2 = 360°. Aus δ1 = 360°
folgt α1 =180° - α3 + 180° - α4 . α1 ist
also gleich der Summe der Nebenwinkel bei
E3 und E4. Aus δ1 = δ2 = 360° folgt
außerdem B2B1B6 =B1B5B4 = id, also B1B5
= B4 , da B4 eine Punktspiegelung ist. Sei j
die Gleitspiegelungs-Achse von B1. Dann ist
jB5 = jB1B5 =jB4 zu j parallel. Darum steht j
senkrecht zur Gleitspiegelungs-Achse von
B5, denn j kann nicht parallel dazu sein, weil
B1B5 sonst eine Verschiebung wäre.
Abb. 22
E3
S
E2
α3
180°−α1
α1
E6
E4
α4
E1
Zur Konstruktion eines Sechsecks zu dieser
Signatur geht man von weitgehend
Abb. 23
E5
beliebigen Eckpunkten E1, E2, E3 und E4 aus
und trägt in E1 an die Seite E1E2 einen
ebenfalls weitgehend beliebigen Winkel α1 an. Auf dem neuen Schenkel trägt man die Länge
ℓ 3 = E 2 E3 ab und erhält so den Punkt E6. Zur Konstruktion von E5 setzt man den Winkel α4 =
360° - α1 - α3 in E4 an E3E4 an und trägt auf dem neuen Schenkel ℓ 2 = E1E 2 ab. Abbildung 23
zeigt eine andere Möglichkeit mit Hilfe des Schnittpunktes S der Seitengeraden 3 und 5.
Bei ungünstiger Wahl von E1, E2, E3, E4 und α1 kann es beim Sechseck zu Überschneidungen
kommen; dann muss man die Ausgangswerte variieren.
32
Signatur 2 1 4 3 6 5 : Es ist ℓ1 = ℓ 2 , ℓ 3 = ℓ 4 und ℓ 5 = ℓ 6 .
Aus δ2 = α2 + α4 + α6 = 360° und δ2 + α2 + α4 + α6 =
720° folgt α1 + α3+ α5 = 360°. Da B1, B2 und B3
Nachbar-Drehungen sind, sind die Drehwinkel
kleinergleich 120°. Daraus ergibt sich α1 = α3 = α5 =
Abb. 24
120°. Diese Bedingungen werden dadurch erfüllt, dass
man an ein beliebiges Dreieck so gleichschenklige Dreiecke mit dem Winkel 120° ansetzt, dass
es zu keinen Überschneidungen kommt und die 120°-Winkel auch Innenwinkel des Sechsecks
werden. Aus δ2 = 360° folgt, dass B2B4B6 die identische Abbildung ist.
Signatur 4 5 6 1 2 3 : Es ist ℓ1 = ℓ 4 , ℓ 2 = ℓ 5 , ℓ 3 = ℓ 6 und δ1 = α1 + α3 + α5 = 360°. B1 ist eine
gerade Bewegung. Angenommen, B1 wäre eine Drehung um einen
Punkt D. D müsste dann auf dem Rand einer Kachel liegen, da
andernfalls eine Kachel fix bleiben würde, im Widerspruch zu
unserer Voraussetzung. Da B1 Seiten wieder auf Seiten abbildet,
müsste D eine Seitenmitte oder ein Eckpunkt sein. Im ersten Fall
wäre B1 eine 180°-Drehung, also eine Nachbar- Bewegung. Auch
im zweiten Fall wäre B1 eine Nachbar-Drehung, da an jedem
Abb. 25
Eckpunkt nur drei Kacheln zusammentreffen. Das widerspricht
aber der Signatur, bei der keine Seite sich selbst oder einer anschließenden Seite zugeordnet
ist. Darum ist B1 eine Verschiebung und dies gilt entsprechend auch für die anderen NachbarBewegungen. Folglich sind die Seiten Nummer 1 und 4 parallel und gleich lang, und ebenso
die Seiten 2 und 5 sowie 3 und 6. Bei den Winkeln ist α1 = α4, α2 = α5 und α3 = α6 . Wir
bezeichnen ein derartiges Sechseck als 6-Parallelogramm. Ebenso wie das normale 4Parallelogramm spielt es eine wichtige Rolle beim Nachweis im nächsten Abschnitt, dass
nämlich die als mögliche Kacheln ausgesonderten Polygone eine periodische Kachelung
erzeugen. Aus δ1 = δ2 = 360° folgt B1B5B3 = B2B6B4 = id, wobei alle Nachbar-Bewegungen
als Verschiebungen miteinander vertauschbar sind.
E6
E5
Signatur -2 -1 6 -5 -4 3 : Es ist ℓ1 = ℓ 2 ,
ℓ 4 = ℓ 5 , ℓ 3 = ℓ 6 und δ1 = δ3 = α1 + α2 + α6 =
E4
E1
360°. Daraus folgt B1B1B3 = B3B5B5 = id . Da
die Summe der drei aufeinanderfolgenden
M
Innenwinkel α6, α1 und α2 gleich 360° ist,
beträgt die Summe der zugehörigen
Nebenwinkel 3 ⋅180° − α 6 − α1 − α 2 = 180° , so
dass ein Richtungspfeil auf der Seite 6 beim
Fortschreiten über die Seiten 1 und 2 zur Seite
E3
E2
3 um 180° gedreht wird. Darum ist die Seite 6
Abb. 26
parallel und gleich lang wir die Seite 3. Die
Eckpunkte mit den Nummern 2, 3, 5 und 6 bilden darum ein Parallelogramm. Das Sechseck
entsteht dadurch, dass die Eckpunkte 6 und 2 sowie die Eckpunkte 3 und 5 durch
gleichschenklige Haken miteinander verbunden werden. Es sei M der Schnittpunkt der
Parallelen zu E1E2 durch E3 und zu E1E6 durch E5. Dann bildet ME5E4E3 einen Drachen mit
gleich großen Innenwinkeln bei E3 und E5. Darum ist
180° − α3 − α 2 = ∠ME3 E 4 = ∠E 4 E5 M = 180° − α5 − α 6 , folglich α3 + α 2 = α5 + α 6 .
33
Signatur -5 -4 6 -2 -1 3 : : Es ist ℓ1 = ℓ 5 ,
E5
E6
ℓ 2 = ℓ 4 , ℓ 3 = ℓ 6 und δ2 = δ1 = α2 + α4 + α6 =
360°. Folglich ist B1B4B6 = B2B6B5 = id.
Wie oben zeigt man auch hier, dass B3 eine
Verschiebung ist. Darum ist E2E3E5E6 ein
Parallelogramm. Das Dreiecke E3E5E4 ist
E4
umgekehrt orientiert und kongruent zum
Dreieck E2E6E1, denn die Seitenlängen
stimmen überein. Es sei wieder M der
E1
Schnittpunkt der Parallelen zu E1E2 durch E3
E3
E2
M
und zu E1E6 durch E5. Dann bildet ME5E4E3
wie bei der vorigen Signatur einen Drachen,
Abb.27
aber hier mit gleich großen Innenwinkeln
bei M und E4. Darum ist 360° − α 4 == ∠E3 E 4 E5 = ∠E5 ME3 = 360° − α1 , folglich α 4 = α1 .
Zusammenfassung für n = 6:
Nr
Signatur
Längen=
Winkelrelationen Bewegungs=
Beschreibung
.
relationen
relationen
40
423156
B1B2B3 = id,
E6E1E3E4
α123=360°,
ℓ1 = ℓ 4
B
B
B
=
id
Parallelogramm,
4 5 6
α456=360°
E2 und E5 beliebig
41 -2 -1 6 4 5 3
B
B
B
=
id,
E2E3E5E6
α126=360°,
ℓ1 = ℓ 2 ,
3 4 5
B1B1B3 = id
Parallelogramm,
α345=360°
ℓ3 = ℓ6
E4 beliebig
E1 mit ℓ1 = ℓ 2
42 -3 -5 -1 4 -2 6
B1B5B4 = id,
E1E2E3E4 beliebig,
α134=360°,
ℓ1 = ℓ 3 ,
B2B1B6 = id
E6 mit ℓ1 = ℓ 3 und
α256=360°,
ℓ 2 = ℓ5
beliebigem α1,
E5 mit ℓ 2 = ℓ 5 und
α4 =360°-α1-α3
3
3
beliebiges
Dreieck
43
214365
α1 = α3 = α5 =
ℓ1 = ℓ 2 ,
B1 = B3 =
E2E4E6,
120°,
ℓ3 = ℓ 4
B35 = id
E
E
E
,
2 3 4 E4 E5 E6 , E6 E1 E2
α246= 360°
ℓ5 = ℓ6
B2B4B6=id
30°-30°-Dreiecke
44
456123
B
B
B
=
id,
6-Parallelogramm
α246=360°,
ℓ1 = ℓ 4 ,
1 5 3
B
2B6B4 = id
α
=360°
135
ℓ =ℓ ,
2
5
ℓ3 = ℓ6
45 -2 -1 6 -5 -4 3
ℓ1 = ℓ 2 ,
ℓ3 = ℓ6
ℓ 4 = ℓ5
46 -5 -4 6 -2 -1 3
ℓ1 = ℓ 5 ,
ℓ2 = ℓ4
ℓ3 = ℓ6
α126 = 360°.
α345 = 360°
α3 + α 2 = α5 + α 6
B1B1B3 = id,
B3B5B5 = id
α2+α4+α6=360°,
α1+α3+α5=360°
α 4 = α1
B1B4B6 = id,
B2B6B5 = id
Tab. 10
34
Parallelogramm
E2 E3 E5 E6 ,
E6 E1 E2 , E3 E4 E5
gleichschenklig
Parallelogramm
E2 E3 E5 E6 ,
E6 E1 E2 , E5 E4 E3
kongruent und
entgegengesetzt
orientiert
8. Translations-Kacheln :
Definition : Unter einer Translations-Kachel verstehen wir eine P-Kachel-Variante zu einem
orientierten 4- oder 6-Parallelogramm K0. Sie entsteht dadurch, dass jedes parallele Seitenpaar
von K0 durch ein Paar zweier Polygonzüge ersetzt wird, die durch eine Verschiebung
auseinander hervorgehen. Dabei darf es bei den Seitenpolygonen zu keinen Überschneidungen
kommen. Den Polygonzug, der dabei an die Stelle der i-ten Seite von K0 tritt, bezeichnen wir
als i-ten Polygonzug.
Die Translations-Kacheln sind also die P-Kachel-Varianten der Kacheln mit den Signaturen
3 4 1 2 und 4 5 6 1 2 3. Wir benutzen die Translation-Kacheln für den Nachweis, dass die
Kacheln mit den Signaturen in Tabelle 1 eine Kachelung erzeugen.
Satz 7 : K0 sei positiv nummerierte Kachel zur Signatur 3 4 1 2 oder 4 5 6 1 2 3. Dann erzeugt
K0 eine Kachelung. Die Automorphismen-Gruppe wird von je zwei der Nachbar-Bewegungen
erzeugt.
Beweis : Signatur 3 4 1 2 : Die Nachbar-Bewegung B2 verschiebt die Seite 4 des
Parallelogramms in die Seite 2. Dabei bleiben die Geraden E4E1 und E2E3 fest. Die Kacheln
K 0 Bi2 für ganze Zahlen i füllen den Bereich zwischen diesen Geraden vollständig aus, wobei
die Schnittmengen leer oder Seiten sind. Die Nachbarbewegungen Bi3 mit ganzzahligen i
verschieben diesen Bereich so, dass durch die Vereinigung der Bildmengen die ganze Ebene
ausgefüllt wird.
E3
E4
E4B3
E2
E6
E1
Abb.28
Signatur 4 5 6 1 2 3 (siehe Abb. 28) : Die Nachbar-Bewegung B3 verschiebt die Seite 6 des 6Parallelogramms in die Seite 3. Dabei bleiben die Geraden E6E2 und die durch E4 und E4B3
fest. Der Polygonzug P mit den Eckpunkten E6, E1 und E2 ist kongruent zum Polygonzug P'
mit den Eckpunkten E4, E3 und E4B3. Wenn man die Polygonzüge P Bi3 bzw. P' Bi3 für
ganzzahlige i aneinandersetzt, dann entstehen zwei kongruente Polygonzüge, welche die
Ränder der Vereinigungsmenge der Kacheln K 0 Bi3 bilden. Dabei sind die Schnittmengen leer
oder Seitengeraden. Die Nachbarbewegungen Bi4 mit ganzzahligen i verschieben den Bereich
zwischen den beiden Polygonzügen so, dass durch die Vereinigung der Bildmengen die ganze
□
Ebene ausgefüllt wird.
35
Aus Satz 7 folgt, dass auch jede P-Kachel-Variante eines 4- oder 6-Parallelogramms eine
Kachelung erzeugt. Im Folgenden soll gezeigt werden, dass es zu jeder Kachel mit einer
Signatur in Tabelle 1 eine Kette von Kacheln gibt, deren Vereinigungsmenge P-KachelVariante eines 4- oder 6-Parallelogramms ist. Dazu muss z. B. beim 6-Parallelogramm gezeigt
werden, dass die Rand-Polygone P1, P2 und P3, welche die Rolle der Seiten 1, 2 und 3
übernehmen, kongruent zu den Rand-Polygonen P4, P5 und P6 sind. Das bedeutet, dass die
Längen und Richtungen gewisser Teilstrecken der Polygone übereinstimmen. Dabei werden
die Längen- und Winkel-Relationen der Tabellen 4, 6, 8 und 10 benutzt. Der Zusammenhang
zwischen der Gleichheit von Richtungen und den Winkel-Relationen wird mit Hilfe von
'Richtungswinkeln' hergestellt, die zunächst definiert werden sollen.
Definition : In der Zeichen-Ebene sei eine Halbgerade (Strahl) g 0+ (z. B. der nicht-negative Teil
einer x-Achse) als Null-Halbgerade ausgezeichnet. Unter dem Richtungswinkel w( h + )
irgendeiner Halbgeraden h + verstehen wir den kleinsten Drehwinkel, um den man g 0+ gegen
den Uhrzeigersinn drehen muss, bis das Drehungsbild gleich gerichtet (also insbesondere
parallel) mit h + ist. Für die Definition des Richtungswinkels w(h) einer Geraden h
identifizieren jede Drehwinkelgröße α mit α + 180° und mit α - 180°, da Geraden in zwei
entgegengesetzten Richtungen ins Unendlich führe. Der Richtungswinkel der Geraden h ist
dann der Richtungswinkel α einer Halbgeraden h + auf h, wobei α mit α + 180° und mit
α - 180° identifiziert wird.
Nach dieser Definition ist die von einem Halbgeraden-Paar (g+,h+) bestimmte Winkelgröße
gleich w(h+) − w(g+) und entsprechend die von einem Geraden-Paar (g,h) bestimmte
Winkelgröße gleich w(h) −w(g).
g und h seien parallele Geraden, für die also w(g) = w(h) gilt. Für jede Bewegung B ist dann
auch gB parallel zu hB, also w(gB) = w(hB). Darum induziert B eine Abbildung auf der Menge
aller Richtungswinkel von Geraden.
Definition : Es sei B eine Bewegung und ω ein Richtungswinkel einer Geraden g. Dann sei
Bw(ω) der Richtungswinkel von gB.
Definition : Zu einer positiv nummerierten Kachel K0 bezeichnen wir den Richtungwinkel der
Geraden, auf der die i-te Seite liegt mit ωi.
Nach dieser Definition ist α i = ωi − ωi→ für alle i ∈ {1, 2,..., n} .
Satz 8 : K0 sei positiv nummerierte Kachel zur Signatur s1s2...sn. Bi sei die i-te
Nachbarbewegung und k der Bertrag von si. Für die durch Bi auf der Menge aller
Richtungswinkel ω von Geraden induzierte Abbildung Biw gilt dann:
•
Biw (ω) = ω + ωi − ωk , falls Bi gerade Bewegung ist,
•
Biw (ω) = −ω + ωi + ωk , falls Bi ungerade Bewegung ist.
Beweis : Bi sei zunächst gerade, also eine Drehung oder eine Verschiebung. Im Fall der
Drehung sei γ der Drehwinkel und im Fall der Verschiebung sei γ gleich 0°. Dann ist
Biw (ω) = ω + γ . Aus ωi = Biw (ωk ) = ωk + γ folgt γ = ωi − ωk und Biw (ω) = ω + ωi − ωk .
36
Sei nun Bi ungerade. Dann ist Bi eine Spiegelung an einer Geraden g oder eine
Gleitspiegelung mit einer Achse g. γ sei jetzt der Richtungswinkel von g. Dann ist
Biw (ω) = 2 γ − ω . Aus ωi = Biw (ωk ) = 2 γ − ωk folgt 2γ = ωi + ωk und Biw (ω) = −ω + ωi + ωk . □
Wenn die Nachbar-Bewegung Bi insbesondere eine 180°-Drehung ist, dann gilt
Biw (ω) = ω + ωi − ωi = ω . Hierbei geht die Identifikation von ω mit ω + 180° ein.
Wir wenden die Abbildungen Biw nur auf Winkel an, die sich als Linearkombinationen der
Richtungswinkel ω1, ω2, ..., ωn mit ganzzahligen Vorzahlen ergeben, denn nach Satz 8 können
nur diese Größen als Richtungwinkel von Kacheln vorkommen, die aus K0 durch Anwendung
einer Hintereinanderschaltung von Nachbar-Bewegungen ergeben. Darum ist es sinnvoll, diese
Winkel mit Hilfe eines n-Tupels aus ganzen Zahlen anzugeben. K0 sei z.B. eine Kachel mit der
Signatur -3 -5 -1 4 -2 6. Dann wird der Winkel B1w (ω4 ) = −ω4 + ω1 + ω3 durch (1, 0, 1, -1, 0, 0)
bezeichnet und wir schreiben B1w ((0, 0, 0,1, 0, 0)) = (1, 0,1, −1, 0, 0) . Diese Schreibweise
erleichtert insbesondere den Einsatz von Rechnern bei der Winkelberechnung.
Wenn K0 eine Kachelung erzeugt, gibt es nur endlich viele Richtungswinkel von KachelSeiten.
Wir erklären jetzt den Nachweis, dass es zu K0 eine Translationskachel gibt, ausführlich an
Hand der Signaturen 1 2 3 und -3 -5 -1 4 -2 6, danach in verkürzter Form für anderen
Signaturen der Tabelle 1. Bei der Zusammensetzung von Kacheln zu einer Translationskachel
gibt es verschiedene Möglichkeiten. Wir haben jeweils eine Möglichkeit auf Grund der
Anschauung ausgewählt. Zum Nachweis, dass es sich wirklich um eine Translationskachel
handelt, werden die Strecken-Längen und -Richtungen in den Polygonzügen verglichen, die
den Rand der Translationskachel bilden. Wenn die Translationskachel eine P-Kachel-Variante
eines 4-Parallelogramms ist, muss nachgewiesen werden, dass der 1. (bzw. 2.) Polygonzug und
der 3. (bzw. 4.) Polygonzug die gleichen Strecken-Längen und -Richtungen in umgedrehter
Reihenfolge hat. Wenn die Translationskachel eine P-Kachel-Variante eines 6Parallelogramms ist, müssen der 1. (bzw. 2. bzw. 3.) Polygonzug und der 4. (bzw. 5. bzw. 6)
Polygonzug verglichen werden. Für den Nachweis der Gleichheit der Strecken-Länge reicht es,
den Betrag der Nummer zu vergleichen, welche die Strecke als Kachel-Seite hat. Der
Nachweis der Gleichheit der Richtungen verlangt zum Teil einen Rückgriff auf die WinkelRelationen in den Tabellen 4, 6, 8 und 10.
Nr. 1 : Signatur 123
Translationskachel : 01#23#01#23
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0)
2.Polygonzug : Seite 3: (0,0,0)
3.Polygonzug : Seite 1: (1,0,0)
4.Polygonzug : Seite 3: (0,0,0)
Es gibt keine einschränkenden Richtungsrelationen.
Abb. 29
Die Kachel K0 ist in Abbildung 21 grau gezeichnet. Die Translationskachel entsteht durch
Vereinigung der Kacheln K0 und K0B2. Man erkennt ohne Rechnung, dass es ein
Parallelogramm ist. Das Rand-Polygon wird durch
01#23#01#23 beschreiben. Die
Trennungszeichen '#' trennen die vier Seiten des Parallelogramms. Das Ziffernpaar 01 vor dem
37
ersten Trennungszeichen gibt an, dass der erste Polygonzug nur aus der Seite 1 von K0 besteht.
Das Paar 23 besagt, dass der zweite Polygonzug nur die Seite 3 der Kachel K0B2 ist. Die '0' im
nächsten Paar 01 drückt aus, dass die Kachel K0B2 nicht gewechselt wir. Der 3. Polygonzug
besteht darum aus der Seite 1 von K0B2. Um zum vierten Polygonzug zu gelangen, wird wieder
B2 angewandt. Er besteht also aus der Seite 3 von K0B2B2 = K0.
Da nur 180°-Drehungen als Nachbar-Bewegungen vorkommen, haben alle Seiten mit der
gleichen Nummer auch den gleichen Richtungswinkel. Eine formale Berechnung ergibt z. B.
für den 2. Polygonzug B2((0,0,1)) = B2(ω3) = ω3 + ω2 - ω2 = ω3 = (0, 0, 1).
Da sowohl der 1. und 3. als auch der 2. und 4. Polygonzug dieselben Längen und Richtungen
hat, ist die Zusammensetzung von K0 und K0B2 tatsächlich eine Translationskachel. Folglich
erzeugt K0 eine Kachelung.
Abb. 30
In Abbildung 30 zur Signatur -3-5-14-2 6 und in den folgenden Abbildungen geben die Zahlen
an den Seiten die Beträge der Seitennummern in der zugehörigen Kachel an.
Nr. 42 : Signatur -3-5-1 4-2 6
Translationskachel : 06+01+24#03#02+01+65#04+03+26#01#02+03+45 (Abb. 30)
Richtungen der Seiten im
1.Polygonzug : Seite 6: (0,0,0,0,0,1)
2.Polygonzug : Seite 3: (0,1,-1,0,1,0)
3.Polygonzug : Seite 2: (0,0,0,0,1,0)
4.Polygonzug : Seite 4: (0,1,0,-1,1,0)
5.Polygonzug : Seite 1: (1,0,0,0,0,0)
6.Polygonzug : Seite 2: (0,1,0,0,0,0)
Seite 1: (1,0,0,0,0,0)
Seite 4: (0,1,0,-1,1,0)
Seite 1: (-1,1,0,0,1,0)
Seite 3: (0,1,-1,0,1,0)
Seite 5: (0,1,0,0,0,0)
Seite 6: (0,0,0,0,0,1)
Seite 3: (0,0,1,0,0,0)
Seite 5: (0,0,0,0,1,0)
Richtungsrelationen :
ω1 - ω2 + ω3 - ω5 = 0
Startpunkt für die Beschreibung der Translationskachel ist der mit zwei Kreisen markierte
Punkt in den grauen Kachel K0. Der 1. Polygonzug setzt sich aus der 6. und 1. Seite von K0
und der Seite mit dem Nummernbetrag 4 von K0B2 zusammen. Die Richtung der 4. Seite ist
38
B2w (ω4 ) = −ω4 + ω2 + ω5 = (0,1, 0, −1,1, 0) . Der 2. Polygonzug besteht nur aus der Strecke, deren
Seitennummer-Betrag in K0B2 gleich 3 ist. B2w (ω3 ) = −ω3 + ω2 + ω5 = (0,1, −1, 0,1, 0) . Der 3.
Polygonzug setzt sich aus den Seiten mit den Seitennummer-Beträgen 2 in K0B2, 1 in K0B2 und
5 in K0B6B2 zusammen. Die Richtungswinkel sind
B2w (ω2 ) = −ω2 + ω2 + ω5 = (0, 0, 0, 0,1, 0) , B2w (ω1 ) = −ω1 + ω2 + ω5 = (−1,1, 0, 0,1, 0) und
B2w B6w (ω5 ) = B2w (ω5 ) = −ω5 + ω2 + ω5 = (0,1, 0, 0, 0, 0) . (Auch hier ist die umgedrehte
Reihenfolge der Nachbar-Bewegunggen entsprechend Satz 1 zu beachten.)
Der 4., 5. und 6. Polygonzug ergibt sich analog.
Zum Nachweis, dass wirklich eine Translationskachel entsteht, werden zunächst beim 1. und 4.
Polygonzug die Strecken-Längen und -Richtungen überprüft. Die erstgenannte Seite im 1.
Polygonzug und die letztgenannte im 4. Polygonzug stimmen in der Länge überein, weil der
Nummern-Betrag beidesmal 6 ist. Die beiden mittleren Seiten stimmen in der Länge überein,
weil ℓ1 = ℓ 3 ist. Die letztgenannte Seite im 1. Polygonzug und die erstgenannte im 4.
Polygonzug stimmen in der Länge überein, weil der Nummern-Betrag beidesmal 4 ist. Die
entsprechende Überprüfung der Richtungen zeigt bei den Seiten mit dem Nummern-Betrag 6
bzw. 4 die Übereinstimmung der Tupel (0,0,0,0,0,1) bzw. (0,1,0,-1,1,0). Bei der mittleren
Seite 1 bzw. 3 muss der Richtungswinkel zu (1,0,0,0,0,0) mit dem zu (0,1,-1,0,1,0)
übereinstimmen, also ω1 = ω2 - ω3 + ω5 sein. Das heißt, dass die unter 'Richtungsrelationen'
genannte Gleichung ω1 - ω2 + ω3 - ω5 = 0 erfüllt sein muss. Dies ist aber der Fall, da nach
Tabelle 10 gilt : α1 + α 3 + α 4 = 360° , folglich
ω1 − ω2 + ω3 − ω5 = (ω1 − ω2 ) + (ω3 − ω4 ) + (ω4 − ω5 ) = 0° .
Aus der Tatsache, dass sich eine Translationskachel ergibt, folgt insbesondere, dass die von
2624 bestimmte Kette mit der Startkachel K0 wieder zu K0 zurückführt. Darum ist B4B2B6B2
die identische Abbildung.
In verkürzter Form führen wir jetzt den Nachweis für die übrigen Signaturen durch. Falls es
einschränkende Richtungsrelationen gibt, greifen wir auf die Winkelrelationen aus den
Tabellen 4, 6, 8 und 10 zurück.
Nr. 2 : Signatur -123 (Abb. 31)
Translationskachel : 01#23+13#21#03+20+10+23
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0)
2.Polygonzug : Seite 3: (0,0,1)
Seite 3: (2,0,-1)
3.Polygonzug : Seite 1: (1,0,0)
4.Polygonzug : Seite 3: (2,0,-1)
Seite 3: (0,0,1)
Es gibt keine einschränkenden Richtungsrelationen.
39
Abb. 31
Nr. 3 : Signatur -1-23
Translationskachel : 13#23#13#23
Richtungen der Seiten im
1.Polygonzug : Seite 3: (2,0,-1)
2.Polygonzug : Seite 3: (2,-2,1)
3.Polygonzug : Seite 3: (4,-2,-1)
4.Polygonzug : Seite 3: (4,-4,1)
Richtungsrelationen :
- 2ω1 + 2ω2 = 0
Aus α1 = 90° folgt −2ω1 + 2ω2 = −2 ⋅ (ω1 − ω2 ) = −180° = 0 .
Abb. 32
Nr. 4 : Signatur -1-2-3
Translationskachel : 01#21#31#21#31#21
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0)
2.Polygonzug : Seite 1: (-1,2,0)
3.Polygonzug : Seite 1: (1,2,-2)
4.Polygonzug : Seite 1: (-1,4,-2)
5.Polygonzug : Seite 1: (1,4,-4)
6.Polygonzug : Seite 1: (-1,6,-4)
Richtungsrelationen :
2ω1 - 4ω2 + 2ω3 = 0
- 2ω1 - 2ω2 + 4ω3 = 0
Abb. 33
Aus α1 = α2 = α3 = 60° folgt 2ω1 − 4ω2 + 2ω3 = 2 ⋅ (ω1 − ω2 ) − 2 ⋅ (ω2 − ω3 ) = 0 und
−2ω1 − 2ω2 + 4ω3 = 2 ⋅ (ω3 − ω1 ) − 2 ⋅ (ω2 − ω3 ) = 0
Nr. 5 : Signatur -1-2-3 (Abb. 34)
Translationskachel :
01+21#30+10+31+21#31+21#30+10+31+21
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0) Seite 1: (-1,2,0)
2.Polygonzug : Seite 1: (3,2,-4) Seite 1: (1,4,-4)
3.Polygonzug : Seite 1: (3,4,-6) Seite 1: (1,6,-6)
4.Polygonzug : Seite 1: (5,6,-10) Seite 1: (3,8,-10)
Richtungsrelationen :
- 4ω1 - 2ω2 + 6ω3 = 0
- 6ω2 + 6ω3 = 0
40
Abb. 34
Aus α1 = 90°, α2 = 60° und α3 = 30° folgt −6ω2 + 6ω3 = −6 ⋅ (ω2 − ω3 ) = −6 ⋅ 60° = 0 und
−4ω1 − 2ω2 + 6ω3 = 4 ⋅ (ω3 − ω1 ) − 2 ⋅ (ω2 − ω3 ) = 4 ⋅ 30° − 2 ⋅ 60° = 0
Nr. 6 : Signatur -1-2-3
Translationskachel : 02+32#12+32#12+32#12+32
Richtungen der Seiten im
1.Polygonzug : Seite 2: (0,1,0)
2.Polygonzug : Seite 2: (-2,1,2)
3.Polygonzug : Seite 2: (-4,1,4)
4.Polygonzug : Seite 2: (-6,1,6)
Seite 2: (0,-1,2)
Seite 2: (-2,-1,4)
Seite 2: (-4,-1,6)
Seite 2: (-6,-1,8)
Richtungsrelationen :
4ω1 + 2ω2 - 6ω3 = 0
4 ω1 - 2 ω2 - 2 ω3 = 0
Aus α1 = 45°, α2 = 90° und α3 = 45° folgt
4ω1 + 2ω2 − 6ω3 = −4 ⋅ (ω3 − ω1 ) + 2 ⋅ (ω2 − ω3 ) = −4 ⋅ 45° + 2 ⋅ 90° = 0 und
4ω1 − 2ω2 − 2ω3 = 2 ⋅ (ω1 − ω2 ) − 2 ⋅ (ω3 − ω1 ) = 2 ⋅ 45° − 2 ⋅ 45° = 0 .
Abb. 35
Nr. 7 : Signatur 213 : ℓ1 = ℓ 2
Translationskachel : 03#13#13#13#13#13
Richtungen der Seiten im
1.Polygonzug : Seite 3: (0,0,1)
2.Polygonzug : Seite 3: (1,-1,1)
3.Polygonzug : Seite 3: (2,-2,1)
4.Polygonzug : Seite 3: (3,-3,1)
5.Polygonzug : Seite 3: (4,-4,1)
6.Polygonzug : Seite 3: (5,-5,1)
Richtungsrelationen :
- 3 ω1 + 3 ω2 = 0
Aus α1 = 60° folgt −3ω1 + 3ω2 = −3 ⋅ (ω1 − ω2 ) = −3 ⋅ 60° = 0
Abb. 36
Nr. 8 : Signatur 213 : ℓ1 = ℓ 2
Translationskachel : 13#13#13#13
Richtungen der Seiten im
1.Polygonzug : Seite 3: (1,-1,1)
2.Polygonzug : Seite 3: (2,-2,1)
3.Polygonzug : Seite 3: (3,-3,1)
4.Polygonzug : Seite 3: (4,-4,1)
Richtungsrelationen :
- 2 ω1 + 2 ω2 = 0
Abb. 37
Aus α1 = 90° folgt −2ω1 + 2ω2 = −2 ⋅ (ω1 − ω2 ) = −2 ⋅ 90° = 0
41
Nr. 9 : Signatur 213 : ℓ1 = ℓ 2
Translationskachel : 03#10+30+13#13#10+30+13
Richtungen der Seiten im
1.Polygonzug : Seite 3: (0,0,1)
2.Polygonzug : Seite 3: (2,-2,1)
3.Polygonzug : Seite 3: (3,-3,1)
4.Polygonzug : Seite 3: (5,-5,1)
Richtungsrelationen :
- 3ω1 + 3ω2 = 0
Abb. 38
Aus α1 = 120° folgt
−3ω1 + 3ω2 = −3 ⋅ (ω1 − ω2 ) = −3 ⋅120° = 0 .
Nr. 10 : Signatur -132 : ℓ 2 = ℓ 3
Translationskachel : 02+33#13+22#12+33#13+22
Richtungen der Seiten im
1.Polygonzug : Seite 2: (0,1,0)
Seite 3: (0,-1,2)
2.Polygonzug : Seite 3: (2,-1,0)
Seite 2: (2,-3,2)
3.Polygonzug : Seite 2: (0,-1,2)
Seite 3: (0,-3,4)
4.Polygonzug : Seite 3: (2,-3,2)
Seite 2: (2,-5,4)
Abb. 39
Richtungsrelationen :
4ω2 - 4ω3 = 0
Aus α2 = 90° folgt 4ω2 − 4ω3 = 4 ⋅ (ω2 − ω3 ) = 4 ⋅ 90° = 0 .
Nr. 11 : Signatur -132 : ℓ1 = ℓ 2 (Abb. 40)
Translationskachel : 01#20+10+31#31#30+10+21
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0)
2.Polygonzug : Seite 1: (1,2,-2)
3.Polygonzug : Seite 1: (1,3,-3)
4.Polygonzug : Seite 1: (1,5,-5)
Abb. 40
Richtungsrelationen :
- 3ω2 + 3ω3 = 0
Aus α2 = 120° folgt 3ω2 − 3ω3 = 3 ⋅ (ω2 − ω3 ) = 3 ⋅120° = 0 .
Nr. 12 : Signatur -2-13 : ℓ1 = ℓ 2
Translationskachel : 03#11+32#13#01+20+30+22
Richtungen der Seiten im
1.Polygonzug : Seite 3: (0,0,1)
42
2.Polygonzug : Seite 1: (0,1,0)
Seite 2: (1,0,0)
3.Polygonzug : Seite 3: (0,0,1)
4.Polygonzug : Seite 1: (1,0,0)
Seite 2: (0,1,0)
Es gibt keine einschränkenden Richtungsrelationen.
Abb. 41
Nr. 13 : Signatur -2-1-3 : ℓ1 = ℓ 2
Translationskachel : 03#11#03#22
Richtungen der Seiten im
1.Polygonzug : Seite 3: (0,0,1)
2.Polygonzug : Seite 1: (0,1,0)
3.Polygonzug : Seite 3: (1,1,-1)
4.Polygonzug : Seite 2: (0,1,0)
Abb. 42
Richtungsrelationen :
- ω1 - ω2 + 2ω3 = 0
Aus α2 = α3 folgt −ω1 − ω2 + 2ω3 = (ω3 − ω1 ) − (ω2 − ω3 ) = 0 .
Abb. 43
Nr. 14 (Abb. 43): Signatur 1234
Translationskachel : 01#23#04#01#23#04
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0)
2.Polygonzug : Seite 3: (0,0,1,0)
3.Polygonzug : Seite 4: (0,0,0,1)
4.Polygonzug : Seite 1: (1,0,0,0)
5.Polygonzug : Seite 3: (0,0,1,0)
6.Polygonzug : Seite 4: (0,0,0,1)
Es gibt keine einschränkenden Richtungsrelationen.
43
Nr. 15 : Signatur -12-34
Translationskachel : 01+23#04+14#03+21#04+34
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0)
2.Polygonzug : Seite 4: (0,0,0,1)
3.Polygonzug : Seite 3: (2,0,-1,0)
4.Polygonzug : Seite 4: (2,0,0,-1)
Seite 3: (0,0,1,0)
Seite 4: (2,0,0,-1)
Seite 1: (1,0,0,0)
Seite 4: (2,0,-2,1)
Abb.44
Richtungsrelationen :
- 2ω1 + 2ω3 = 0
Aus α1+α2 = 180° folgt −2ω1 + 2ω3 = −2 ⋅ ((ω1 − ω2 ) − (ω2 − ω3 )) = −2 ⋅180° = 0 .
Nr. 16 : Signatur -1-2-34
Translationskachel : 02+32#01+40+34+01#02+32#01+40+34+01
Richtungen der Seiten im
1.Polygonzug : Seite 2: (0,1,0,0)
Seite 2: (0,-1,2,0)
2.Polygonzug : Seite 1: (-1,0,2,0)
Seite 4: (0,0,0,1)
Seite 1: (1,0,0,0)
3.Polygonzug : Seite 2: (0,1,0,0)
Seite 2: (0,-1,2,0)
4.Polygonzug : Seite 1: (-1,0,2,0)
Seite 4: (0,0,0,1)
Seite 1: (1,0,0,0)
Abb. 45
Richtungsrelationen :
- 2ω1 + 2ω3 = 0
Aus α1 = α2 = 90° folgt
2ω2 - 2ω3 = 0
2ω2 − 2ω3 = 2 ⋅ (ω2 − ω3 ) = 2 ⋅ 90° = 0 und −2ω1 + 2ω3 = −2 ⋅ ((ω1 − ω2 ) − (ω2 − ω3 )) = .
−2 ⋅ (90° − 90°) = 0
Nr. 17 : Signatur -1-2-3-4
Translationskachel : 01+21#04+34#01+21#04+34
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0)
2.Polygonzug : Seite 4: (0,2,0,-1)
3.Polygonzug : Seite 1: (1,2,-2,0)
4.Polygonzug : Seite 4: (0,4,-2,-1)
Seite 1: (-1,2,0,0)
Seite 4: (0,2,-2,1)
Seite 1: (-1,4,-2,0)
Seite 4: (0,4,-4,1)
Richtungsrelationen :
- 2ω 1 + 2ω 3 = 0
2ω1 - 4ω2 + 2ω3 = 0
- 2ω 2 + 4ω 3 - 2ω 4 = 0
- 2ω 2 + 2ω 4 = 0
Aus α1 = α2 = α3 = α4 = 90° folgt
2ω1 − 4ω2 + 2ω3 = 2 ⋅ ((ω1 − ω2 ) − (ω2 − ω3 )) = 2 ⋅ (90° − 90°) = 0 ,
−2ω1 + 2ω3 = −2 ⋅ ((ω1 − ω2 ) + (ω2 − ω3 )) = −2 ⋅ (90° + 90°) = 0 ,
44
Abb. 46
−2ω2 + 4ω3 − 2ω4 = −2 ⋅ ((ω2 − ω3 ) − (ω3 − ω4 )) = −2 ⋅ (90° − 90°) = 0 und
−2ω2 + 2ω4 = −2 ⋅ ((ω2 − ω3 ) + (ω3 − ω4 )) = −2 ⋅ (90° + 90°) = 0 .
Nr. 18 : Signatur 3214 : ℓ1 = ℓ 3
Translationskachel : 01#23#04#01#23#04
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0)
2.Polygonzug : Seite 3: (0,0,1,0)
3.Polygonzug : Seite 4: (0,0,0,1)
4.Polygonzug : Seite 1: (1,0,0,0)
5.Polygonzug : Seite 3: (0,0,1,0)
6.Polygonzug : Seite 4: (0,0,0,1)
Abb. 47
Es gibt keine einschränkenden Richtungsrelationen.
Nr. 19 : Signatur -1432 : ℓ 2 = ℓ 4
Translationskachel :
02+34+14+32#01#04+32+12+34#01
Richtungen der Seiten im
1.Polygonzug :
Seite 2: (0,1,0,0)
Seite 4: (0,0,0,1)
Seite 4: (2,0,0,-1)
Seite 2: (2,-1,0,0)
2.Polygonzug : Seite 1: (1,0,0,0)
3.Polygonzug :
Seite 4: (2,0,0,-1)
Seite 2: (2,-1,0,0)
Seite 2: (0,1,0,0)
Seite 4: (0,0,0,1)
4.Polygonzug : Seite 1: (1,0,0,0)
Abb. 48
Richtungsrelationen :
ω2 - ω4 = 0
Aus α2 = α4 folgt ω2 − ω4 = (ω2 − ω3 ) − (ω4 − ω3 ) = 0 .
Nr. 20 : Signatur -2-134 : ℓ1 = ℓ 2
Translationskachel :
03#04#01+20+43+02#13#04#01+20+
43+02
Richtungen der Seiten im
1.Polygonzug : Seite 3: (0,0,1,0)
2.Polygonzug : Seite 4: (0,0,0,1)
3.Polygonzug : Seite 1: (1,0,0,0)
Seite 3: (1,1,-1,0)
Seite 2: (1,0,0,0)
4.Polygonzug : Seite 3: (0,0,1,0)
5.Polygonzug : Seite 4: (0,0,0,1)
6.Polygonzug : Seite 1: (1,0,0,0)
Seite 3: (1,1,-1,0)
Seite 2: (1,0,0,0)
Es gibt keine einschränkenden Richtungsrelationen.
45
Abb. 49
Nr. 21 : Signatur -1-243 : ℓ 3 = ℓ 4
Translationskachel :
02+31#02+31+21+42#01+42#01+42+12+
31
Richtungen der Seiten im
1.Polygonzug :
Seite 2: (0,1,0,0)
Seite 1: (1,0,1,-1)
2.Polygonzug :
Seite 2: (0,1,1,-1)
Seite 1: (1,0,2,-2)
Seite 1: (-1,2,2,-2) Seite 2: (0,1,3,-3)
3.Polygonzug :
Seite 1: (-1,2,3,-3) Seite 2: (0,1,4,-4)
4.Polygonzug :
Seite 1: (-1,2,4,-4) Seite 2: (0,1,5,-5)
Seite 2: (-2,3,5,-5) Seite 1: (-1,2,6,-6)
Abb. 50
Richtungsrelationen :
2ω1 - 2ω2 - 2ω3 + 2ω4 = 0
- 4ω3 + 4ω4 = 0
ω1 - ω2 - 5ω3 + 5ω4 = 0
- ω1 + ω2 - 3ω3 + 3ω4 = 0
Aus α1 = α3 = 90° folgt −4ω3 + 4ω4 = −4 ⋅ (ω3 − ω4 ) = −4 ⋅ 90° = 0 ,
2ω1 − 2ω2 − 2ω3 + 2ω4 = 2 ⋅ ((ω1 − ω2 ) − (ω3 − ω4 )) = 2 ⋅ (90° − 90°) = 0 ,
ω1 − ω2 − 5ω3 + 5ω4 = (ω1 − ω2 ) − 5 ⋅ (ω3 − ω4 ) = 90° − 5 ⋅ 90° = 0 und
−ω1 + ω2 − 3ω3 + 3ω4 = −(ω1 − ω2 ) − 3 ⋅ (ω3 − ω4 ) = −90° − 3 ⋅ 90° = 0 .
Nr. 22 : Signatur -1-243 : ℓ 3 = ℓ 4
Translationskachel :
02+31#02+31#21+42#01+42
Richtungen der Seiten im
1.Polygonzug : Seite 2: (0,1,0,0)
Seite 1: (1,0,1,-1)
2.Polygonzug : Seite 2: (0,1,1,-1)
Seite 1: (1,0,2,-2)
3.Polygonzug : Seite 1: (-1,2,2,-2)
Seite 2: (0,1,3,-3)
4.Polygonzug : Seite 1: (-1,2,3,-3)
Seite 2: (0,1,4,-4)
Abb. 51
Richtungsrelationen : - 3ω3 + 3ω4 = 0 ,
2 ω1 - 2 ω2 - ω3 + ω4 = 0
Aus α1 = 60°, α3 = 120° folgt −3ω3 + 3ω4 = −3 ⋅ (ω3 − ω4 ) = −3 ⋅120° = 0 und
2ω1 − 2ω2 − ω3 + ω4 = 2 ⋅ (ω1 − ω2 ) − (ω3 − ω4 ) = 2 ⋅ 60° − 120° = 0 .
46
Nr. 23 : Signatur -32-14 : ℓ1 = ℓ 3 (Abb. 52)
Translationskachel : 01+23#04+12#01+43#02+14
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0)
Seite 3: (0,0,1,0)
2.Polygonzug : Seite 4: (0,0,0,1)
Seite 2: (1,-1,1,0)
3.Polygonzug : Seite 1: (0,0,1,0)
Seite 3: (1,0,0,0)
4.Polygonzug : Seite 2: (1,-1,1,0)
Seite 4: (0,0,0,1)
Abb. 52
Es gibt keine einschränkenden Richtungsrelationen.
Nr. 24 : Signatur -14-32 : ℓ 2 = ℓ 4
Translationskachel : 01#02+32#01#04+34
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0)
2.Polygonzug : Seite 2: (0,1,0,0)
Seite 2: (0,-1,2,0)
3.Polygonzug : Seite 1: (-1,0,2,0)
4.Polygonzug : Seite 4: (0,0,2,-1)
Seite 4: (0,0,0,1)
Abb. 53
Richtungsrelationen :
2ω1 - 2ω3 = 0
ω2 - ω4 = 0
Aus α1 + α3 = α2 + α4 = 180° folgt 2ω1 − 2ω3 = 2 ⋅ ((ω1 − ω2 ) + (ω2 − ω3 )) = 2 ⋅180° = 0 und
ω2 − ω4 = (ω2 − ω3 ) + (ω3 − ω4 ) = 180° = 0 .
Nr. 25 : Signatur -3-2-1-4 : ℓ1 = ℓ 3
Translationskachel : 02#34#03#02#14#01
Richtungen der Seiten im
1.Polygonzug : Seite 2: (0,1,0,0)
2.Polygonzug : Seite 4: (1,0,1,-1)
3.Polygonzug : Seite 3: (1,0,0,0)
4.Polygonzug : Seite 2: (1,-1,1,0)
5.Polygonzug : Seite 4: (0,0,0,1)
6.Polygonzug : Seite 1: (1,0,0,0)
Richtungsrelationen :
- ω1 + 2ω2 - ω3 = 0 ,
ω1 + ω3 - 2ω4 = 0
Abb. 54
Aus α1= α2 und α3= α4 folgt −ω1 + 2ω2 − ω3 = −(ω1 − ω2 ) + (ω2 − ω3 ) = 0 und
ω1 + ω3 − 2ω4 = −(ω4 − ω1 ) + (ω3 − ω4 ) = 0 .
47
Nr. 26 : Signatur 2143 : ℓ1 = ℓ 2 und ℓ 3 = ℓ 4
Translationskachel : 01+22#03+44#01+22#03+44
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0)
2.Polygonzug : Seite 3: (-1,1,1,0)
3.Polygonzug : Seite 1: (0,1,-1,1)
4.Polygonzug : Seite 3: (-2,2,0,1)
Seite 2: (-1,2,0,0)
Seite 4: (-1,1,-1,2)
Seite 2: (-2,3,-1,1)
Seite 4: (-2,2,-2,3)
Richtungsrelationen :
3ω1 - 3ω2 + ω3 - ω4 = 0
Abb. 55
- ω1 + ω2 + ω3 - ω4 = 0
ω1 - ω2 + 3ω3 - 3ω4 = 0
Aus α1= α2 = α3= α4=90° folgt 3ω1 − 3ω2 + ω3 − ω4 = 3(ω1 − ω2 ) + (ω3 − ω4 ) = 3 ⋅ 90° + 90° = 0 ,
−ω1 + ω2 + ω3 − ω4 = −(ω1 − ω2 ) + (ω3 − ω4 ) = −90° + 90° = 0 und
ω1 − ω2 + 3ω3 − 3ω4 = (ω1 − ω2 ) + 3 ⋅ (ω3 − ω4 ) = 90° + 3 ⋅ 90° = 0 .
Nr. 27 : Signatur 2143 : ℓ1 = ℓ 2 und ℓ 3 = ℓ 4
Translationskachel : 01#02#31#02#31#02
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0)
2.Polygonzug : Seite 2: (0,1,0,0)
3.Polygonzug : Seite 1: (1,0,1,-1)
4.Polygonzug : Seite 2: (0,1,1,-1)
5.Polygonzug : Seite 1: (1,0,2,-2)
6.Polygonzug : Seite 2: (0,1,2,-2)
Richtungsrelationen :
Abb.56
ω1 - ω2 - ω3 + ω4 = 0
- ω1 + ω2 - 2ω3 + 2ω4 = 0
Aus α1= α3 = 120° folgt ω1 − ω2 − ω3 + ω4 = (ω1 − ω2 ) − (ω3 − ω4 ) = 120° − 120° = 0 und
−ω1 + ω2 − 2ω3 + 2ω4 = −(ω1 − ω2 ) − 2 ⋅ (ω3 − ω4 ) = −120° − 2 ⋅120° = 0 .
Nr. 28 : Signatur 2143 : ℓ1 = ℓ 2 und ℓ 3 = ℓ 4
Translationskachel :
02+31#02+31#02+31#02+31#02+31#02+31
Richtungen der Seiten im
1.Polygonzug : Seite 2: (0,1,0,0)
2.Polygonzug : Seite 2: (0,1,1,-1)
3.Polygonzug : Seite 2: (0,1,2,-2)
4.Polygonzug : Seite 2: (0,1,3,-3)
5.Polygonzug : Seite 2: (0,1,4,-4)
6.Polygonzug : Seite 2: (0,1,5,-5)
Richtungsrelationen :
- ω1 + ω2 - 4ω3 + 4ω4 = 0
Seite 1: (1,0,1,-1)
Seite 1: (1,0,2,-2)
Seite 1: (1,0,3,-3)
Seite 1: (1,0,4,-4)
Seite 1: (1,0,5,-5)
Seite 1: (1,0,6,-6)
ω1 - ω2 - 2ω3 + 2ω4 = 0
48
Abb. 57
Aus α1= 120° und α3 = 60° folgt
−ω1 + ω2 − 4ω3 + 4ω4 = −(ω1 − ω2 ) − 4(ω3 − ω4 ) = −120° − 4 ⋅ 60° = 0 und
ω1 − ω2 − 2ω3 + 2ω4 = (ω1 − ω2 ) − 2 ⋅ (ω3 − ω4 ) = 120° − 2 ⋅120° = 0 .
Nr. 29 : Signatur 3412 : ℓ1 = ℓ 3 und ℓ 2 = ℓ 4
Translationskachel : 01#02#03#04
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0)
2.Polygonzug : Seite 2: (0,1,0,0)
3.Polygonzug : Seite 3: (0,0,1,0)
4.Polygonzug : Seite 4: (0,0,0,1)
Abb. 58
Richtungsrelationen :
ω1 - ω3 = 0
ω2 - ω4 = 0
Aus α1 + α2 = 180° und α3 + α4 =180° folgt ω1 − ω3 = (ω1 − ω2 ) + (ω2 − ω3 ) = 0 und
ω2 − ω4 = (ω2 − ω3 ) + (ω3 − ω4 ) = 0 .
Nr. 30 : Signatur -34-12 : ℓ1 = ℓ 3 und ℓ 2 = ℓ 4
Translationskachel : 04+12#01#04+32#03
Richtungen der Seiten im
1.Polygonzug : Seite 4: (0,0,0,1)
2.Polygonzug : Seite 1: (0,0,1,0)
3.Polygonzug : Seite 4: (1,0,1,-1)
4.Polygonzug : Seite 3: (0,0,1,0)
Seite 2: (1,-1,1,0)
Seite 2: (0,1,0,0)
Richtungsrelationen :
- ω2 + ω4 = 0
Aus α2 + α3 =180° folgt −ω2 + ω4 = −(ω2 − ω3 ) − (ω3 − ω4 ) = −180° = 0 .
Abb. 59
Nr. 31 : Signatur -2-1-4-3 : ℓ1 = ℓ 2 und ℓ 3 = ℓ 4
Translationskachel : 01#02#03#42#01#04
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0)
2.Polygonzug : Seite 2: (0,1,0,0)
3.Polygonzug : Seite 3: (0,0,1,0)
4.Polygonzug : Seite 2: (0,-1,1,1)
5.Polygonzug : Seite 1: (-1,0,1,1)
6.Polygonzug : Seite 4: (0,0,1,0)
Abb. 60
Richtungsrelationen :
ω1 + ω2 - ω3 - ω4 = 0
Aus α2 = α4 folgt ω1 + ω2 − ω3 − ω4 = (ω2 − ω3 ) − (ω4 − ω1 ) = 0 .
49
Nr. 32 : Signatur -3-4-1-2 : ℓ1 = ℓ 3 und ℓ 2 = ℓ 4
Translationskachel : 01+23#02+14#01+23#02+14
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0)
Seite 3: (0,1,-1,1)
2.Polygonzug : Seite 2: (0,0,0,1)
Seite 4: (-1,1,-1,2)
3.Polygonzug : Seite 1: (0,1,-1,1)
Seite 3: (-1,2,-2,2)
4.Polygonzug : Seite 2: (-1,1,-1,2)
Seite 4: (-2,2,-2,3)
Abb. 61
Richtungsrelationen :
2ω1 - 2ω2 + 2ω3 - 2ω4 = 0
Aus α1 = α3 = 90° folgt 2ω1 − 2ω2 + 2ω3 − 2ω4 = 2 ⋅ (ω1 − ω2 ) + 2 ⋅ (ω3 − ω4 ) = 2 ⋅ 90° + 2 ⋅ 90° = 0 .
Nr. 33 : Signatur 32145 : ℓ1 = ℓ 3
Translationskachel : 03+04+51#02#03+04+51#02
Richtungen der Seiten im
1.Polygonzug : Seite 3: (0,0,1,0,0)
Seite 4: (0,0,0,1,0) Seite 1: (1,0,0,0,0)
2.Polygonzug : Seite 2: (0,1,0,0,0)
3.Polygonzug : Seite 3: (0,0,1,0,0)
Seite 4: (0,0,0,1,0) Seite 1: (1,0,0,0,0)
4.Polygonzug : Seite 2: (0,1,0,0,0)
Abb. 62
Richtungsrelationen :
- ω1 + ω3 = 0
Aus α1 + α2 = 180° folgt
−ω1 + ω3 = −((ω1 − ω2 ) + (ω2 − ω3 )) = −180° = 0 .
Nr. 34 : Signatur -15342 : ℓ 5 = ℓ 2
Translationskachel :
02+03+45+15+43+02#01#05+43+02+12+03+45#
01
Richtungen der Seiten im
1.Polygonzug :
Seite 2: (0,1,0,0,0) Seite 3: (0,0,1,0,0)
Seite 5: (0,0,0,0,1) Seite 5: (2,0,0,0,-1)
Seite 3: (2,0,-1,0,0) Seite 2: (2,-1,0,0,0)
2.Polygonzug : Seite 1: (1,0,0,0,0)
3.Polygonzug :
Seite 5: (2,0,0,0,-1) Seite 3: (2,0,-1,0,0)
Seite 2: (2,-1,0,0,0) Seite 2: (0,1,0,0,0)
Abb. 63
50
Seite 3: (0,0,1,0,0) Seite 5: (0,0,0,0,1)
4.Polygonzug : Seite 1: (1,0,0,0,0)
Richtungsrelationen :
ω2 - ω5 = 0
Aus α1 + α5 = 180° folgt ω2 − ω5 = −((ω1 − ω2 ) + (ω5 − ω1 )) = −180° = 0 .
Nr. 35 : Signatur 21435 : ℓ1 = ℓ 2 und ℓ 3 = ℓ 4
Translationskachel :
04+05+13#04+05+13#04+05+13#04+05+13
Richtungen der Seiten im
1.Polygonzug : Seite 4: (0,0,0,1,0)
Seite 5: (0,0,0,0,1) Seite 3: (1,-1,1,0,0)
2.Polygonzug : Seite 4: (1,-1,0,1,0)
Seite 5: (1,-1,0,0,1) Seite 3: (2,-2,1,0,0)
3.Polygonzug : Seite 4: (2,-2,0,1,0)
Seite 5: (2,-2,0,0,1) Seite 3: (3,-3,1,0,0)
4.Polygonzug : Seite 4: (3,-3,0,1,0)
Seite 5: (3,-3,0,0,1) Seite 3: (4,-4,1,0,0)
Richtungsrelationen :
- 3ω1 + 3ω2 - ω3 + ω4 = 0
Abb. 64
- 2ω1 + 2ω2 = 0
- ω1 + ω2 + ω3 - ω4 = 0
Aus α1 = α3 = 90° folgt −3ω1 + 3ω2 − ω3 + ω4 = −3 ⋅ (ω1 − ω2 ) − (ω3 − ω4 ) = −3 ⋅ 90° − 90° = 0 ,
−2ω1 + 2ω2 = −2 ⋅ (ω1 − ω2 ) = −2 ⋅ 90° = 0 und
−ω1 + ω2 + ω3 − ω4 = −(ω1 − ω2 ) + (ω3 − ω4 ) = −90° + 90° = 0 .
Nr. 36 : Signatur 21435 : ℓ1 = ℓ 2 und ℓ 3 = ℓ 4
Translationskachel :
04+05+13#44+05+13#04+05+13#44+05+13
Richtungen der Seiten im
1.Polygonzug : Seite 4: (0,0,0,1,0)
Seite 5: (0,0,0,0,1) Seite 3: (1,-1,1,0,0)
2.Polygonzug : Seite 4: (1,-1,-1,2,0)
Seite 5: (1,-1,-1,1,1) Seite 3: (2,-2,0,1,0)
3.Polygonzug : Seite 4: (2,-2,-1,2,0)
Seite 5: (2,-2,-1,1,1) Seite 3: (3,-3,0,1,0)
4.Polygonzug : Seite 4: (3,-3,-2,3,0)
Seite 5: (3,-3,-2,2,1) Seite 3: (4,-4,-1,2,0)
Richtungsrelationen :
Abb. 65
- 3ω1 + 3ω2 = 0
- 2ω1 + 2ω2 + ω3 - ω4 = 0
ω1 + ω2 + 2ω3 - 2ω4 = 0
Aus α1 = 120° und α3 = 60° folgt −3ω1 + 3ω2 = −3 ⋅ (ω1 − ω2 ) = −3 ⋅120° = 0 ,
−2ω1 + 2ω2 + ω3 − ω4 = −2 ⋅ (ω1 − ω2 ) + (ω3 − ω4 ) = −2 ⋅120° + 60° = 0 und
−ω1 + ω2 + 2ω3 − 2ω4 = −(ω1 − ω2 ) + 2(ω3 − ω4 ) = −60° + 2 ⋅120° = 0 .
51
-
Nr. 37 : Signatur -2-1543 : ℓ1 = ℓ 2 und ℓ 3 = ℓ 4
Translationskachel :
01#02#03+45+01+25+43#02#01#
05+43+02+13+45
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0,0)
2.Polygonzug : Seite 2: (0,1,0,0,0)
3.Polygonzug : Seite 3: (0,0,1,0,0)
Seite 5: (0,0,0,0,1) Seite 1: (1,0,0,0,0)
Seite 5: (1,1,0,0,-1) Seite 3: (1,1,-1,0,0)
4.Polygonzug : Seite 2: (1,0,0,0,0)
5.Polygonzug : Seite 1: (0,1,0,0,0)
6.Polygonzug : Seite 5: (1,1,0,0,-1)
Seite 3: (1,1,-1,0,0) Seite 2: (1,0,0,0,0)
Seite 3: (0,0,1,0,0) Seite 5: (0,0,0,0,1)
Abb. 66
Richtungsrelationen :
ω3 - ω5 = 0
Aus α3+α4 = 180° folgt ω3 − ω5 = (ω3 − ω4 ) + (ω4 − ω5 ) = 180° = 0
Nr. 38 : Signatur -2-15-43 : ℓ1 = ℓ 2 und ℓ 3 = ℓ 5
Translationskachel : 01#02#03+43#02#01#05+45
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0,0)
2.Polygonzug : Seite 2: (0,1,0,0,0)
3.Polygonzug : Seite 3: (0,0,1,0,0)
Seite 3: (0,0,-1,2,0)
4.Polygonzug : Seite 2: (0,-1,0,2,0)
5.Polygonzug : Seite 1: (-1,0,0,2,0)
6.Polygonzug : Seite 5: (0,0,0,2,-1)
Seite 5: (0,0,0,0,1)
Abb. 67
Richtungsrelationen :
ω1 + ω2 - 2ω4 = 0
ω3 - ω5 = 0
Aus α3 ̶ α5=α4 ̶ α2 folgt ω1 + ω2 − 2ω4 = (ω3 − ω4 ) − (ω5 − ω1 ) − ((ω4 − ω5 ) − (ω2 − ω3 )) = 0 .
Aus α3+α4 = 180° folgt ω3 − ω5 = (ω3 − ω4 ) + (ω4 − ω5 ) = 180° = 0 .
Nr. 39 : Signatur -3-4-1-25 : ℓ1 = ℓ 3 und ℓ 2 = ℓ 4 (Abb. 68)
Translationskachel : 01+23#02+14#05#01+23#02+14#05
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0,0)
Seite 3: (0,1,-1,1,0)
2.Polygonzug : Seite 2: (0,0,0,1,0)
Seite 4: (-1,1,-1,2,0)
52
3.Polygonzug : Seite 5: (-1,1,-1,1,1)
4.Polygonzug : Seite 1: (0,1,-1,1,0)
Seite 3: (-1,2,-2,2,0)
5.Polygonzug : Seite 2: (-1,1,-1,2,0)
Seite 4: (-2,2,-2,3,0)
6.Polygonzug : Seite 5: (-2,2,-2,2,1)
Richtungsrelationen :
2ω1 - 2ω2 + 2ω3 - 2ω4 = 0
Aus α1+α3 = 180° folgt
2 ⋅ ((ω1 − ω2 ) + (ω3 − ω4 )) = 2 ⋅180° = 0 .
Abb. 68
Nr. 40 : Signatur 423156 : ℓ1 = ℓ 4
Translationskachel : 01+02+34#05#06#01+02+34#05#06
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0,0,0)
Seite 2: (0,1,0,0,0,0) Seite 4: (0,0,0,1,0,0)
2.Polygonzug : Seite 5: (0,0,0,0,1,0)
3.Polygonzug : Seite 6: (0,0,0,0,0,1)
4.Polygonzug : Seite 1: (1,0,0,0,0,0)
Seite 2: (0,1,0,0,0,0) Seite 4: (0,0,0,1,0,0)
5.Polygonzug : Seite 5: (0,0,0,0,1,0)
6.Polygonzug : Seite 6: (0,0,0,0,0,1)
Richtungsrelationen :
ω1 - ω4 = 0
Da die Seiten Nummer 1 und 4
parallel sind, ist ω1 = ω4.
Abb. 69
Nr. 41 : Signatur -2-16453 : ℓ1 = ℓ 3 und ℓ 2 = ℓ 4 (Abb. 70)
Translationskachel : 03+45+06+01+26+54+03#02#01# 06+54+03+02+13+45+06#01#02
Richtungen der Seiten im
1.Polygonzug : Seite 3: (0,0,1,0,0,0)
Seite 5: (0,0,0,0,1,0) Seite 6: (0,0,0,0,0,1)
Seite 1: (1,0,0,0,0,0) Seite 6: (1,1,0,0,0,-1)
Seite 4: (1,1,0,-1,0,0) Seite 3: (1,1,-1,0,0,0)
2.Polygonzug : Seite 2: (1,0,0,0,0,0)
3.Polygonzug : Seite 1: (0,1,0,0,0,0)
4.Polygonzug : Seite 6: (1,1,0,0,0,-1)
53
Seite 4: (1,1,0,-1,0,0) Seite 3: (1,1,-1,0,0,0)
Seite 2: (1,0,0,0,0,0) Seite 3: (0,0,1,0,0,0)
Seite 5: (0,0,0,0,1,0) Seite 6: (0,0,0,0,0,1)
5.Polygonzug : Seite 1: (1,0,0,0,0,0)
6.Polygonzug : Seite 2: (0,1,0,0,0,0)
Richtungsrelationen :
ω3 - ω6 = 0
Da die Seiten Nummer 3 und 6 parallel
sind, ist ω3 = ω6.
Nr. 42 : Signatur -3-5-14-26 siehe oben
Abb.70
Nr. 43: Signatur 214365 : ℓ1 = ℓ 2 , ℓ 4 = ℓ 3 und ℓ 5 = ℓ 6 (Abb. 71)
Translationskachel : 02+03#04+51#02+03#04+51#02+03#04+51
Richtungen der Seiten im
1.Polygonzug : Seite 2: (0,1,0,0,0,0)
2.Polygonzug : Seite 4: (0,0,0,1,0,0)
3.Polygonzug : Seite 2: (0,1,0,0,1,-1)
4.Polygonzug : Seite 4: (0,0,0,1,1,-1)
5.Polygonzug : Seite 2: (0,1,0,0,2,-2)
6.Polygonzug : Seite 4: (0,0,0,1,2,-2)
Seite 3: (0,0,1,0,0,0)
Seite 1: (1,0,0,0,1,-1)
Seite 3: (0,0,1,0,1,-1)
Seite 1: (1,0,0,0,2,-2)
Seite 3: (0,0,1,0,2,-2)
Seite 1: (1,0,0,0,3,-3)
Abb. 71
54
Richtungsrelationen :
- ω1 + ω2 - 2ω5 + 2ω6 = 0
ω3 - ω4 - ω5 + ω6 = 0
- ω3 + ω4 - 2ω5 + 2ω6 = 0
ω1 - ω2 - ω5 + ω6 = 0
Aus α1 = α3 = α5 = 120° folgt
−ω1 + ω2 − 2ω5 + 2ω6 = −(ω1 − ω2 ) − 2(ω5 − ω6 ) = −120° − 2 ⋅120° = 0 ,
ω3 − ω4 − ω5 + ω6 = (ω3 − ω4 ) − (ω5 − ω6 ) = 120° − 120° = 0 ,
−ω3 + ω4 − 2ω5 + 2ω6 = −(ω3 − ω4 ) − 2(ω5 − ω6 ) = −120° − 2 ⋅120° = 0 und
ω1 − ω2 − ω5 + ω6 = (ω1 − ω2 ) − (ω5 − ω6 ) = 120° − 120° = 0
Nr. 44 : Signatur 456123 : ℓ1 = ℓ 4 , ℓ 2 = ℓ 5 und ℓ 3 = ℓ 6
Translationskachel : 01#02#03#04#05#06
Richtungen der Seiten im
1.Polygonzug : Seite 1: (1,0,0,0,0,0)
2.Polygonzug : Seite 2: (0,1,0,0,0,0)
3.Polygonzug : Seite 3: (0,0,1,0,0,0)
4.Polygonzug : Seite 4: (0,0,0,1,0,0)
5.Polygonzug : Seite 5: (0,0,0,0,1,0)
6.Polygonzug : Seite 6: (0,0,0,0,0,1)
Richtungsrelationen :
Abb.72
ω1 - ω4 = 0
ω2 - ω5 = 0
ω3 - ω6 = 0
Da die Seiten Nummer 1 und 4 parallel sind, ist ω1 = ω4. Entsprechendes gilt für die
Seitenpaare 2, 5 und 3, 6.
Nr. 45 : Signatur -2-16-5-43 :
ℓ1 = ℓ 2 , ℓ 3 = ℓ 6 und ℓ 4 = ℓ 5
Translationskachel : 03+04+53#02#01#06+05+46#01#02
Richtungen der Seiten im
1.Polygonzug : Seite 3: (0,0,1,0,0,0)
Seite 4: (0,0,0,1,0,0) Seite 3: (0,0,-1,1,1,0)
2.Polygonzug : Seite 2: (0,-1,0,1,1,0)
3.Polygonzug : Seite 1: (-1,0,0,1,1,0)
4.Polygonzug : Seite 6: (0,0,0,1,1,-1)
Seite 5: (0,0,0,1,0,0) Seite 6: (0,0,0,0,0,1)
5.Polygonzug : Seite 1: (1,0,0,0,0,0)
6.Polygonzug : Seite 2: (0,1,0,0,0,0)
Richtungsrelationen :
ω3 - ω6 = 0
- ω1 - ω2 + ω4 + ω5 = 0
Da die Seiten Nummer 3 und 6 parallel sind,
Abb. 73
ist ω3 = ω6.
Aus α3 + α 2 = α5 + α 6 folgt
−ω1 − ω2 + ω4 + ω5 = (ω6 − ω1 ) − (ω2 − ω3 ) − (ω3 − ω4 ) + (ω5 − ω6 ) = α 6 − α 2 − α3 + α5 = 0 .
55
Nr. 46 : Signatur -5-46-2-13 : ℓ1 = ℓ 5 , ℓ 2 = ℓ 4
und ℓ 3 = ℓ 6
Translationskachel :
03+41+06#05#04#03+25+06#01#02
Richtungen der Seiten im
1.Polygonzug : Seite 3: (0,0,1,0,0,0)
Seite 1: (-1,1,0,1,0,0) Seite 6: (0,1,0,1,0,-1)
2.Polygonzug : Seite 5: (0,1,0,1,-1,0)
3.Polygonzug : Seite 4: (0,1,0,0,0,0)
4.Polygonzug : Seite 3: (0,1,-1,1,0,0)
Seite 5: (0,0,0,0,1,0) Seite 6: (0,0,0,0,0,1)
5.Polygonzug : Seite 1: (1,0,0,0,0,0)
6.Polygonzug : Seite 2: (0,1,0,0,0,0)
Richtungsrelationen :
ω3 - ω6 = 0
- ω1 + ω2 + ω4 - ω5 = 0
Da die Seiten Nummer 3 und 6 parallel sind,
ist ω3 = ω6.
Aus α 4 = α1 folgt
−ω1 + ω2 + ω4 − ω5 = −(ω1 − ω2 ) + (ω4 − ω5 ) =
−α1 + α 4 = 0 .
Abb. 74
Damit ist bewiesen der
Satz 9 : K0 sei positiv nummerierte Kachel zur Signatur s1s2...sn. Dann erzeugt K0 genau dann
eine Kachelung, wenn s1s2...sn eine der Signaturen in Tabelle 1 ist und K0 die geometrischen
Eigenschaften hat, die zu s1s2...sn in den Tabellen 4, 6, 8 oder 10 genannt werden, oder wenn
K0 und s1s2...sn aus einer derartigen Kachel durch Rotation entsteht.
Ein ähnlicher Satz wird mit anderen Methoden in [1] bewiesen. Die von uns betrachteten
Kachelungen entsprechen dort weitgehend den 'Parketts mit Markierungen'.
Anhang: Die Laves-Charakteristik
Zur Aussonderung der unmöglichen Signaturen wird üblicherweise (z. B. auch in [1]) statt der
hier verwandten Klassenwinkel-Methode ein anderes Verfahren benutzt, das wesentlich auf
dem eulerschen Polygonsatz beruht. Es soll in diesem Anhang dargestellt werden.
Die Abbildung 75 zeigt vier farbige Kacheln der Kachelung aus Abbildung 3, welche die
Translationskachel K bilden. Die Translationspfeile zweier Translationen τ1 und τ2, die die
zugehörige Translationsgruppe erzeugen, sind im Hintergrund gezeichnet. Die Bilder Kτ2 ,
Kτ1 und Kτ1τ2−1 von K schließen oben und rechts an K an. K hat mit der Vereinigung von Kτ2 ,
56
Kτ1 und Kτ1τ2−1 den Streckenzug S mit den Endpunkten P1 und P2 gemeinsam, der durch kleine
farbige Punkte markiert ist.
Die Menge F der Punkte der Translationskachel mit Ausnahme des Streckenzugs S (auch ohne
P1 und P2) wird 'Fundamentalbereich der Translationsgruppe ' oder 'Translationszelle' genannt.
Der Sinn dieser Reduzierung der Punktmenge der Translationskachel besteht darin, dass die
Schnittmenge von F und Fτ leer ist für alle Translationen τ ≠ id in der Automorphismengruppe
der Kachelung.
P2
P1
Abb. 75
Bei der Anwendung der eulerschen Polyederformel beschränkt man sich auf die KachelEckpunkte und Teilmengen von Kachel-Seiten und -Flächen, die sich innerhalb von F
befinden. Durch diese Beschränkung kann es vorkommen, dass bei einer Kachel-Seite ein
Endpunkt P fehlt, weil er auf dem Streckenzug S liegt. Zu P gibt es genau einen Punkt P' in F
und genau eine Verschiebung τ im Erzeugnis von τ1 und τ2 mit P'τ = P . Diesen Punkt P'
betrachtet man als Endpunkt der Kachel-Seite. Man identifiziert also P mit P'. Entsprechend
verfährt man, wenn durch die Beschränkung auf F bei einer Kachel-Fläche eine Seite wegfällt,
weil sie zum Streckenzug S gehört. In Abbildung 75 werden die Punkte mit der gleichen
57
Farbe, egal ob groß oder klein, als gleich angesehen. Dann stimmen die Eckenordnungen in der
Translationszelle mit denen in der Kachelung überein.
In Abbildung 75 gibt es innerhalb von F e = 8 Kachel-Eckpunkte, k = 12 Kachel-Seiten und f =
4 Kachel-Flächen, so dass also e − k + f = 0 ist. Dies ist die eulersche Polyederformel für den
Torus, die auch für jede Translationszelle gilt. Die Grundidee beim Beweis dieser Formel
beruht darauf, dass bei der Unterteilung einer Seite durch einen zusätzlichen Punkt sich sowohl
die Eckenzahl e, als auch die Seitenzahl k um 1 erhöhen. Bei der Unterteilung einer Fläche
durch eine zusätzliche Seite gilt: Wenn sich dabei e um eine Zahl ∆e ∈ {0,1, 2} erhöht, dann
erhöht sich k um ∆e − 1 und f um 1, so dass e − k + f unverändert bleibt.
Definition : K0 sei eine positiv nummerierte Kachel, die die Signatur s1s2...sn und die
Nachbarbewegungen B1, ..., Bn hat und eine Kachelung erzeugt. Die Eckenordnung des
Eckpunkts Ei, d. h. die Anzahl der Seiten, die in Ei enden, sei mit oi benannt. Die Folge der
Eckenordnungen o1o2...on bezeichnen wir als Laves-Charakteristik (nach dem Kristallographen
Fritz Laves, der die folgenden Rechnungen zuerst durchgeführt hat).
.
Die in der Behauptung des folgenden Satzes zu den Laves-Charakteristiken angegebenen
Kachelungsbeispiele haben die Besonderheit, dass an jedem Eckpunkt alle dort
zusammentreffenden Kacheln einen gleich großen Innenwinkel haben. Jede der in den
Tabellen 4, 6, 8 und 10 angegebenen Kachelungs-Typen ergibt eine dieser Kachelungen mit
spezifischen Halbpfeil-Markierungen, wenn αi = αj für alle Innenwinkel αi und αj mit i ∼ j
gilt. Die Nummern der Kachelungstypen sind unter den Abbildungen in Klammern angegeben.
Satz : K0 sei eine Kachel, die mit Nachbarbewegungen eine Kachelung erzeugt. Dann ist die
Eckenzahl n gleich 3, 4, 5 oder 6. Die einzig möglichen Laves-Charakteristiken sind
666
(Nr. 1, 2, 4, 7, 12, 13)
884
(Nr. 3, 6, 8, 10)
12 6 4
(Nr. 5)
12 12 3
(Nr. 9, 11)
4444
(Nr. 14-21, 23-26, 29-32)
6434
(Nr. 22, 28)
58
6363
(Nr. 27)
63333
(Nr. 36)
44333
(Nr. 33, 34, 37, 38)
43433
(Nr. 35, 39)
333333
(Nr. 40-46)
oder zyklische Permutationen oder Inversionen davon.
Beweis : Wir wenden die eulersche Polyederformel e − k + f = 0 auf die Kachel-Eckpumkte,
-Seiten und -Flächen an, die sich in einer Translationszelle befinden, wobei Randpunkte
identifiziert werden.
Jede Kachel-Seite gehört je zur Hälfte zu den beiden daran anschließenden Kachel-Flächen.
1
Darum ist in der eulerschen Polygonformel k = f ⋅ ⋅ n . Wenn in einer Ecke oi Seiten
2
zusammenstoßen, dann treffen dort auch oi Kacheln aufeinander. Darum gehört zu jeder dieser
1
Kacheln dort der Anteil
von diesem Eckpunkt. Also ist die Gesamtzahl e aller Eckpunkte
oi
n
n
1
1
1
. Es folgt 0 = e − k + f = f ⋅ ∑ − f ⋅ ⋅ n + f , also
oi
2
i =1 o i
n
n
− 1 . Da die
2
i =1
i =1 i
n
1 n
Eckenordnung nach der Voraussetzung in Abschnitt 2 mindestens 3 ist, gilt ∑ ≤ , also
3
i =1 o i
n
n
− 1 ≤ und n ≤ 6 .
2
3
e = f ⋅∑
1
∑o
=
Vorüberlegung zum Nachweis der Laves-Charakteristiken: Die vom Eckpunkt Ei
verschiedenen Endpunkte der Seiten, die von Ei ausgehen, bilden ein Polygon Pi mit der
Eckenzahl oi. Die periodische Folge der Ordnungen der Eckpunkte dieses Polygons bezeichnen
wir als O-Folge von Ei. Wir sagen 'die Zahl k alterniert in der O-Folge von Ei', wenn jede
zweite Zahl dieser Folge gleich k ist, die Folge aber nicht konstant ist. Wenn alle
Eckordnungen verschieden sind, wechseln sich in der O-Folge von Ei die Ordnungen oi→ und
oi← ab, so dass dann oi→ und oi← beide alternieren.
59
Wenn oi ungerade ist, kann es kein in der O-Folge von Ei alternierendes k geben. Mit diesem
Sachverhalt können wir Eckordnungs-Kombinationen ausschließen.
1.Fall : n = 3
3
1 1
Wegen ∑ = ist mindesten eine der Zahlen ≤ 6 , z. B. o1 .
2
i =1 o i
1 1 1
+ = , also mindestens eine der beiden Zahlen o2 oder o3 kleinergleich
Im Fall o1 = 3 ist
o 2 o3 6
12. Es bleiben für {o 2 , o3 } nur die Kombinationen {7, 42} , {8, 24} , {9,18} , {10,15} und
{12,12}
übrig, von denen die Vorüberlegung alle bis auf {12,12} auschließt.
Im Fall o1 = 4 ist
1 1 1
+ = , also mindestens eine der beiden Zahlen o2 oder o3 ≤ 8 . Für
o 2 o3 4
{o2 , o3} ergibt das die Kombinationen {5, 20} , {6,12} und {8,8} , daraus entfällt {5, 20} nach
der Vorüberlegung.
1 1
3
Im Fall o1 = 5 ist
+ = , also mindestens eine der beiden Zahlen o2 oder o3 ≤ 6 . Für
o 2 o3 10
{o2 , o3} gibt es nur die Kombination {5,10} . Sie ist nach der Vorüberlegung unmöglich, da 5 in
der O-Folge von E1 alterniert.
1 1 1
Im Fall o1 = 6 ist
+ = , also mindestens eine der beiden Zahlen o2 oder o3 ≤ 6 . Für
o 2 o3 3
{o2 , o3} ergibt das die Kombinationen {4,12} und {6, 6} .
Insgesamt bleiben im Fall n = 3 für {o1 , o 2 , o3 } nur die Kombinationen {3,12,12} , {4,6,12} ,
{4,8,8} und {6, 6, 6} übrig.
2.Fall : n = 4
4
1
Wegen ∑ = 1 ist mindesten eine der Zahlen ≤ 4 , z. B. o1 .
i =1 o i
1 1 1 2
Im Fall o1 = 3 ist
+ + = , also mindestens eine der drei Zahlen o2 , o3 oder o4 kleiner
o 2 o3 o 4 3
3⋅3 9
1 1 1
als
= . Sei z.B. o2 = 3. Dann ist
+ = , was für {o3 , o 4 } die Kombinationen
2
2
o3 o 4 3
{4,12} und {6, 6} ergibt. Wäre die Laves-Charakteristik 3 3 4 12, dann wäre 3 in der O-Folge
von E1 alternierend; wäre sie 3 4 3 12, dann wäre 4 in der O-Folge von E1 alternierend.
Deshalb ist die Eckordnungs-Kombination {3,3, 4,12} unmöglich.
Wenn o2 = 4, dann ist
{3,12}
1 1
5
+ =
mit den Kombinationen {4, 6} und {3,12} , wobei hier
o3 o 4 12
aus dem gleichen Grund entfällt.
60
1 1 1 3
+ + = , also mindestens eine der drei Zahlen o2 , o3 oder o4
o 2 o3 o 4 4
3⋅ 4
1 1
5
kleinergleich
= 4 . Sei z.B. o2 = 3. Dann ist
+ = , was wie oben für {o3 , o 4 } nur
3
o3 o 4 12
Im Fall o1 = 4 ist
die Kombinationen {4, 6} ergibt.
Wenn o2 = 4 ist, dann ist
1 1 1
+ = mit den Kombinationen {4, 4} und {3, 6} ,
o3 o 4 2
Insgesamt ergeben im Fall n = 4 für {o1 , o 2 ,o3 , o 4 } nur die Kombinationen {3,3, 6, 6} ,
{3, 4, 4, 6} und {4, 4, 4, 4} .
Bei der Kombination {3,3, 6, 6} ist die Reihenfolge 3 3 6 6 unmöglich, da 3 in der O-Folge von
E1 alterniert. Bei der Kombination {3, 4, 4, 6} ist die Reihenfolge 3 4 4 6 unmöglich, da 6 in der
O-Folge von E1 alterniert.
Für n = 4 bleiben also bis auf zyklische Permutationen nur die Laves-Charakteristiken 6 3 6 3,
6 4 3 4 und 4 4 4 4 übrig.
3.Fall : n = 5
5
Dann ist
1
∑o
i =1
i
=
3
1 1 1 1 1 3
1 1 1 1 1 3
. Wegen + + + + = und + + + + =
und oi ≥ 3 gibt es
2
3 3 3 3 6 2
3 3 3 4 4 2
in diesem Fall für {o1 , o 2 ,o3 , o 4 , o5 } nur die Kombinationen {3,3,3,3, 6} und {3,3,3, 4, 4} . Für
{3,3,3,3, 6} ergibt sich daraus die Reihenfolge 6 3 3 3 3 oder eine zyklische Permutation
davon. Bei der Eckenordnungs-Menge {3,3,3, 4, 4} kann zwischen den beiden Vieren die
Anzahl der Dreien 0, 1 oder 2 sein. Diese Möglichkeiten werden durch die LavesCharakteristiken 4 4 3 3 3 und 4 3 4 3 3 oder zyklische Permutationen davon erfasst.
4.Fall : n = 6
6
Dann ist
1
∑o
i =1
i
1
= 2 . Wegen 6 ⋅ = 2 gibt es in diesem Fall für {o1 , o 2 ,o3 , o 4 , o5 , o 6 } nur die
3
Kombinationen {3,3,3,3,3,3} .
[1] Bigalke, Hans-Günther/ Wippermann, Heinrich, Reguläre Parkettierungen,
BI Wissenschaftsverlag, Mannheim 1994
Bremen, 29.9.2013
61