4. Funktionen und Relationen

4. Funktionen und Relationen
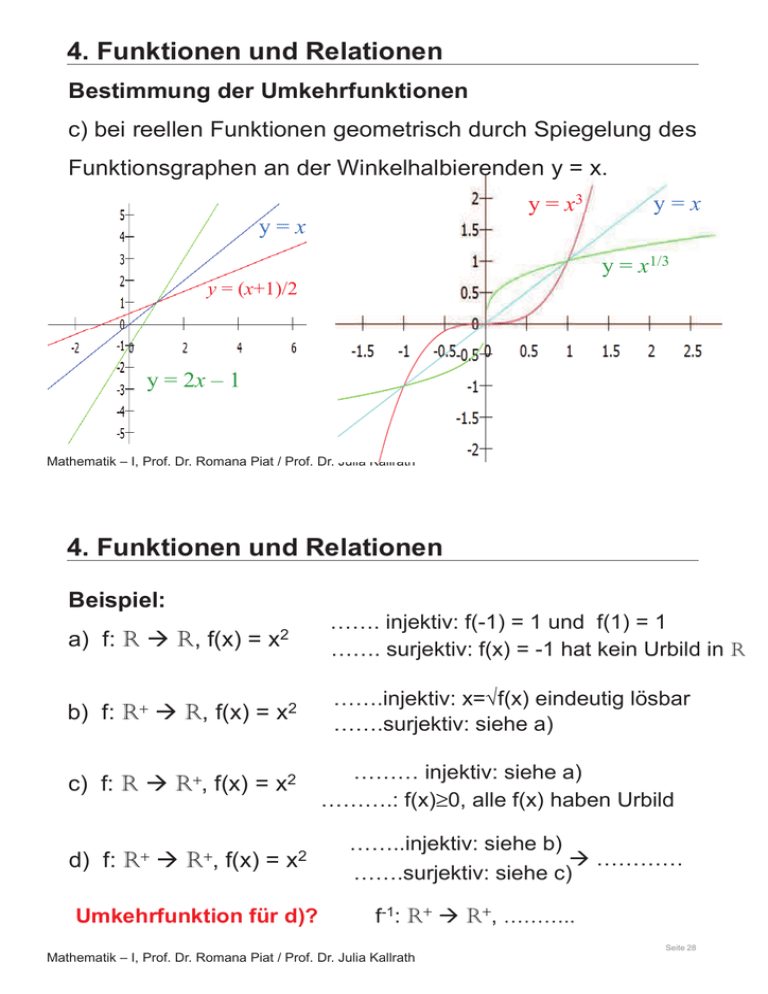
Bestimmung der Umkehrfunktionen
c) bei reellen Funktionen geometrisch durch Spiegelung des
Funktionsgraphen an der Winkelhalbierenden y = x.
y = x3
y=x
y=x
y = x1/3
Archivierungsangaben
y = (x+1)/2
y = 2x – 1
Seite 27
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Beispiel:
a) f: R R, f(x) = x2
……. injektiv: f(-1) = 1 und f(1) = 1
……. surjektiv: f(x) = -1 hat kein Urbild in R
b) f: R+ R, f(x) = x2
…….injektiv: x=√f(x) eindeutig lösbar
…….surjektiv: siehe a)
Archivierungsangaben
c) f: R R+, f(x) = x2
d) f: R+ R+, f(x) = x2
Umkehrfunktion für d)?
……… injektiv: siehe a)
……….: f(x)≥0, alle f(x) haben Urbild
……..injektiv: siehe b)
…………
…….surjektiv: siehe c)
f-1: R+ R+, ………..
Seite 28
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Wiederholung!
Spezielle reelle Funktionen:
Bekannt aus der Schule!
• Lineare Funktionen f(x) = ax + b
Beispiel: f(x) = 4x – 1
• Polynome oder ganzrationale Funktionen
f(x) = anxn + an-1xn-1 + … + a1x + a0
Archivierungsangaben
Beispiel: f(x) = 2x3 – x2 + x – 2
• Gebrochen-rationale Funktionen, z.B. f(x) = 2x3 / (x2 – 3x)
• Trigonometrische Funktionen: sin x, cos x …
• Weitere Funktionen f(x) = √x etc
Seite 29
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Exponentialfunktionen zur Basis a: f(x) = ax mit einer
Konstanten a > 0 (Basis) sind definiert für x ∈ R.
Die Umkehrfunktion von f(x) = ax ist Logarithmus zur
Basis a: loga x, D = (0, ∞).
Spezialfall:
Archivierungsangaben
f(x) = ex – Exponentialfunktion zur Basis e ≈ 2,71
Die Umkehrfunktion von f(x) = ex ist der natürliche
Logarithmus ln x, definiert für x ∈ (0, ∞).
Seite 30
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Rechenregeln:
an = a·a·a·…·a; a0 = a; a1 = a
a1/n
, n∈N
n∈
am/n
ax+y
, n,m∈N
=
ax ·
ay,
Wiederholung!
Bekannt aus der Schule!
x,y∈R
Archivierungsangaben
(ax)y = ax·y, x,y∈R
ax · bx = (a·b)x, x∈R
a-x = 1/ax = (1/a)x, x∈R
ax = ex·ln a , x∈R
Seite 31
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Polynome:
p(x) = anxn + an-1xn-1 + … + a1x + a0
Sind reelle Funktionen, die sich ausschließlich mit den
Rechenoperationen Addition, Subtraktion und Multiplikation
berechnen lassen.
n
Allgemein: p(x) = Ʃ akxk, mit a0, a1, …, an ∈ R
Archivierungsangaben
k=0
Ist an ≠ 0, so ist n = deg p ∈ N der Grad des Polynoms p
Beispiel: p1(x) = x2 + x + 2, p2(x) = – x3,
p3(x) = 2x7 – 4x4 + 3x2 – 1 sind
Polynome vom Grad ……,
. bzw. …………
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
Seite 32
4. Funktionen und Relationen
Definition 4.6
Eine zweistellige Relation R auf Menge M ist eine
Abbildung, die jedem Paar (x,y) ∈ M x M einen
Wahrheitswert
Archivierungsangaben
{wahr, falsch}
zuordnet.
Schreibweise: x R y, (x,y) ∈ R
Seite 33
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Beispiel:
Bezeichnet M die Menge der Prozeduren in einer
Programmiersprache (z.B. in C++) und
N die Menge der (Programmier-)Klassen,
Archivierungsangaben
so wird durch
p R c :⇔ (p wird exportiert von c)
für eine Prozedur p∈M und eine Klasse c∈N eine
Relation zwischen M und N erklärt.
Seite 34
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Darstellung der Relationen:
1. als Paare: R = {(x,y) ∈ M x M: x < y}
Beispiel: Sei Relation R ist „<„ und M = {0,1,2,3}, dann
Archivierungsangaben
R = {(0,1), (0,2), (0,3), (1,2), (1,3), (2,3)}
(0,0), (3,1) ∉ R, weil nicht gilt 0 < 0, 3 < 1
Seite 35
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Darstellung der Relationen:
Archivierungsangaben
2. als Schema: R = {(x,y) ∈ N0xxN0: x + y = 4}
0
1
2
3
0
1
2
3
4
5
…
4
5
…
Seite 36
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Darstellung der Relationen:
Archivierungsangaben
3. Als Graphen: Sei M = {A, B, C, D}
R = {(A,B), (B,C), (B,D), (C, A), (C,B), (C,C), (C,D), (D,A)}
A
B
C
D
Seite 37
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Definition 4.7
Eine Relation R auf M heißt
• reflexiv, wenn jedes Element in Relation zu sich selbst
steht , d.h. ∀x ∈ M: x R x, z.B.:
Archivierungsangaben
„<„ ist ………. reflexiv, da 3 < 3 falsch ist
„≤„ ist ………. reflexiv, da 3 ≤ 3 wahr ist
Seite 38
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Archivierungsangaben
Beispiel
A
B
C
D
nur (C,C) ∈ R
………..reflexiv, da (A,A), (B,B), (D,D) ∉R
Wird reflexiv, wenn alle Schleifen existieren!
Seite 39
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Definition 4.7 (Fortsetzung)
• symmetrisch, wenn ∀x,y ∈ M: aus x R y ⇒ y R x, z.B:
Archivierungsangaben
„≠„ ist ………symmetrisch, da aus „3 ≠ 5“ folgt „5 ≠ 3“
„≤„ ist ………symmetrisch, da aus „3 ≤ 5“ nicht folgt „5 ≤ 3“
Seite 40
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Archivierungsangaben
Beispiel
A
B
C
D
(B,C) ∈ R und (C,B) ∈ R
…….. symmetrisch: (A,C), (A,D), (B,A), (D,B), (D,C) ∉R
Seite 41
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Archivierungsangaben
Beispiel
0
1
2
3
0
1
2
3
4
5
…
4
5
…
Es gilt Kommutativgesetz in N0 : a + b = b + a, deshalb
symmetrisch: wenn 0 R 4, dann auch 4 R 0 etc.
Seite 42
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Archivierungsangaben
Beispiel
A
B
C
D
……………………………..
Seite 43
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Definition 4.7 (Fortsetzung)
• transitiv, wenn ∀x,y,z ∈ M: aus
(x R y) und (y R z) ⇒ x R z, z.B.:
Archivierungsangaben
„≤„ ist ………transitiv, da aus „3 ≤ 5 und 5 ≤ 7“ folgt: „3 ≤ 7“
„≠„ ist …….. transitiv, da aus „3 ≠ 5 und 5 ≠ 3“ nicht folgt „3 ≠ 3“
Seite 44
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Beispiel
A
B
C
D
Transitivitätsbedingung für z.B. B, C, D:
Archivierungsangaben
(B,C)∈R, (C,D)∈R folgt ……………
nicht transitiv: für z.B. A, B und D:
(B,C)∈R und (C,A)∈R, aber ………………
Seite 45
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Archivierungsangaben
Beispiel
0
1
2
3
0
1
2
3
4
5
…
4
5
…
Aus 1 R 3 und 3 R 1, folgt nicht 1 R 1
1 + 3 = 4 und 3 + 1 = 4, aber 1 + 1 ≠ 4
…… transitiv
Seite 46
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Archivierungsangaben
Beispiel
……reflexiv ,
A
B
C
D
symmetrisch und
transitiv.
(A,B)∈R und (B,D)∈R, aber (A,D) ∉R
Seite 47
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Einige wichtige Relationen in der Informatik sind:
Äquivalenzrelationen, Ordnungen, Verbände…
Anwendungsgebiete: Objektorientierte Programmierung,
Archivierungsangaben
relationalen Datenbanken, Prozessplanung etc…
Seite 48
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Definition 4.8
Eine Äquivalenzrelation auf einer Menge M ist eine
reflexive, symmetrische und transitive Relation auf M.
Archivierungsangaben
Beispiel 4.6
Auf der Menge M aller Studierenden im Hörsaal wird
durch
x R y ⇔ x und y haben denselben Geburtsmonat
eine Äquivalenzrelation erklärt, deren Äquivalenzklassen
gerade die verschiedenen Geburtsmonate sind.
Seite 49
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Beispiel 4.7
Auf der Menge Z eine Relation R definiert durch
x R y ⇔ haben gleichen Rest bei Division durch 3, d.h.
x R y ⇔ (x – y) = 3k, k∈ M.
Überprüfe, ob diese Relation eine Äquivalenzrelation ist.
Archivierungsangaben
• reflexiv: (x – x) = 0 = 3k; also ist durch 3 teilbar
• symmetrisch:
wenn (x – y) = 3k, dann y – x=
• transitiv: sei (x – y) = 3k1 und (y – z) = 3k2, dann
(x – z) =
d.h.
Seite 50
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Beispiel 4.7 (Fortsetzung)
Somit x R y („ x – y teilbar durch 3“) ist eine
Äquivalenzrelation.
Archivierungsangaben
Diese Äquivalenzrelation teilt die Menge Z in 3
Äquivalenzklassen: Z = [0] ∪ [1] ∪ [2]
1) alle ganzzahligen Vielfachen der 3 (Rest 0): [0]
2) alle ganzen Zahlen, die sich mit Rest 1 durch 3 teilen
lassen: [1]
3) alle ganzen Zahlen, die sich mit Rest 2 durch 3 teilen
lassen: [2]
Seite 51
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Übung:
Überprüfen, ob die Relation x R y := x⋅y = 0 eine reflexive,
symmetrische und transitive Relation auf Menge N0.
1) Reflexivität: ………..Z.B. 1 R 1, da 1⋅1 ≠ 0
Archivierungsangaben
2) Symmetrie: ……….Wenn x R y, dann y R x.
3) Transitivität: ……..Z.B: 1 R 0, 0 R 2, aber 1 R 2.
Somit ist R keine Äquivalenzrelation !
Seite 52
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Eine Relation R auf einer Menge M heißt
• antisymmetrisch, wenn ∀x,y ∈ M:
aus x R y und y R x ⇒ x = y, z.B:
„≤“, „|“ oder „ ⊆“ ist antisymmetrisch
a | b :⇔
⇔ „a teilt b“ auf M=N
„Zahlenbeispiele“ Tafel
Archivierungsangaben
„≠“ ist nicht antisymmetrisch, da aus „3≠5“ und „5≠3“
folgt nicht, dass 3 und 5 identisch sind.
Hinweis: aus „R ist nicht symmetrisch“ folgt nicht „R ist antisymmetrisch“
aus „R ist antisymmetrisch“ folgt nicht „R ist symmetrisch“
Beispiel : „=„ sowohl symmetrisch, als auch antisymmetrisch
Fazit: für verschiedene x und y sind beide Relationen: x R y
und y R x nicht möglich. Wenn, dann nur eine Relation!!!
Seite 53
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Definition 4.9
Die Relation R heißt eine partielle Ordnung auf einer
Menge M, falls R reflexiv, antisymmetrisch und transitiv
ist.
Archivierungsangaben
Beispiel: „≤“ eine partielle Ordnung auf einer Menge M
a) reflexiv: ja, da für alle x gilt: x ≤ x
b) antisymmetrisch: ja, da gilt: wenn x ≤ y und y ≤ x
dann und nur dann, wenn x = y.
c) transitiv: ja, da gilt: wenn x ≤ y und y ≤ z, dann ist
auch x ≤ z.
Seite 54
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Beispiel: Überprüfe, ob R ist eine Äquivalenz- oder eine
partielle Ordnungsrelation auf M.
M = {1, 2, 3}, R = {(1,1), (2,2), (3,3), (1,2), (1,3)}
Archivierungsangaben
a) reflexiv: …., da für alle x gilt: x R x (1,1), (2,2), (3,3)
(1,2) ∈ R, aber (2,1) ∉ R
b) symmetrisch: ……..
c) antisymmetrisch: ……, da gilt: wenn x R y und y R x
dann und nur dann, wenn x = y.
Es gibt keine Paare (y,x) mit y ≠ x, (2,1), (3,1) ∉ R
a) transitiv: ….., da gilt: wenn x R y und y R z, dann ist
auch x R z. (1,2) ∈ R, (2,2) ∈ R (1,2) ∈ R
(1,1) ∈ R, (1,3) ∈ R (1,3) ∈ R
etc.
!!! partielle Ordnungsrelation
Seite 55
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Definition 4.10
Es sei „≤“ eine partielle Ordnung auf einer Menge M.
Dann heißt „≤“
„ “ eine totale Ordnung, wenn für alle
(x,y)∈M x M gilt: x ≤ y oder y ≤ x. Das bedeutet, dass je
Archivierungsangaben
zwei Elemente hinsichtlich „≤“ vergleichbar sind.
„≤“ ist totale Ordnung auf R
• reflexiv
• antisymmetrisch
• transitiv
Seite 56
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Beispiel:
Archivierungsangaben
1.
•
•
•
„⊆“ auf P (M) ist nicht total, wenn |M| ≥ 2 ist.
reflexiv
antisymmetrisch
partielle Ordnungsrelation
transitiv
Total? entweder x ⊆ y oder y ⊆ x (x≠y)
Sei M = {a,b,c}, dann
P (M) = {∅, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}}.
nicht total
z.B. für {b} und {c} gilt: weder {b} ⊆ {c}, noch {c} ⊆ {b}.
2. M = {1,2,3}, R = {(1,1),(2,2),(3,3),(1,2),(1,3)}: totale
Ordnung?
Nein! Per Definition: (x,y)∈R oder (y,x)∈R, aber z.B. (2,3)∉R und (3,2)∉R
Seite 57
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Darstellung partieller Ordnungen (auf endlichen Mengen)
wird durch Hasse-Diagramme veranschaulicht.
Archivierungsangaben
a) Sei (M, |) eine partiell geordnete Menge mit M= {1,2,3,4,6}
Seite 58
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Bemerkung: Hasse-Diagramm einer totalen Ordnung ist
eine Linie.
Archivierungsangaben
Sei (A, ≤ ) eine total geordnete Menge mit A = {1,2,3,4}.
Seite 59
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
b) Sei (P (M), ⊆) eine partiell geordnete Menge mit M = {1,2,3}.
Archivierungsangaben
P (M) = {∅, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}.
Seite 60
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
c) Tafel
Sei (M, |) eine partiell geordnete Menge mit M = T(12) =
...................
....................
Archivierungsangaben
= {1, 2, 3, 4, 6, 12}
Seite 61
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Hinweise zu Erstellung eines Hasse-Diagramms für Teil(er)menge T(a):
Primfaktorzerlegung von a durchführen:
z.B. a = 12 = 22·31 hat zwei Primfaktoren.
Bei einem Primfaktor (z.B. 16 = 24 oder 35 oder 1135) ist
Archivierungsangaben
das Hasse-Diagramm eindimensional (eine Linie).
Bei zwei Primfaktoren (z.B. 15 = 3·5, 500 = 22·53 etc.) ist
das Hasse-Diagramm zweidimensional (Quadrat bzw.
Gitter, das aus mehreren Quadraten besteht).
Seite 62
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Bei drei Primfaktoren ist das Hasse-Diagramm
dreidimensional (Quader).
Quader
Für a = p1·q1·r1 siehe das Beispiel für T(30) in der Mitschrift.
Allgemein das Hasse-Diagramm für T(a), vorbei a die
Archivierungsangaben
Form von p1·q1·r1 hat, hat das gleiche Hasse-Diagramm
wie T(30) (einstöckiger Quader).
Seite 63
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Wenn einer der drei Primfaktoren eine zweite Potenz
enthält, z.B. a = p1·q2·r1, dann wird der Quader
zweistöckig (siehe Übung 6.5 b)).
Hasse-Diagramme für T(a), wobei in der Primfaktorzerle-
Archivierungsangaben
gung von 4 Primfaktoren oder zwei der drei Primfaktoren
eine höhere Potenz als die zweite haben, sind nicht
mehr überschaubar.
Seite 64
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Beispiel (Tafel):
Erstellen Sie die Hasse-Diagramm für T(a):= (M, |), wobei:
• T(250),
• T(70)
Archivierungsangaben
T(250) = ........... zwei Primaktoren Gitter
T(70) = ................. drei Primfaktoren Quader
Seite 65
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
In geordneten Mengen wird durch die Ordnungsrelation
eine Anordnung ihrer Elemente vorgenommen .
Archivierungsangaben
Definition 4.11
Sei M eine Menge und R Relation auf M. Dann heißt kϵ M
kleinstes Element (bzw. größtes Element) von M, wenn für
alle xϵ M gilt, dass kRx (bzw. xRk) ist.
Beispiel
a) (M, ≤), M={2, 3, 4, 5}; 2 - kleinstes El.; 5- größtes El.
b) (N0, ≤), hat 0 als kleinstes Element und klein größtes.
Seite 66
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
In partiell geordneten Mengen existieren es nicht immer
bzw. ein kleinstes/größtes Element.
• Sei (M, |) = ({1, 2, 3, 4, 6}, |).
Archivierungsangaben
kleinstes Element: 1, weil 1 teilt alle Zahlen aus M
größtes Element: kein, da es keine Zahl Z gibt, die durch alle
x∈M teilbar ist.
Wie kann man die Menge M erweitern, so dass es ein
größtes Element bzgl. „|“ gibt?
Seite 67
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Beispiel:
Ist (M, ⊆) eine partiell geordnete Menge, dann x∈M ein
kleinstes Element, falls ∀y∈M gilt x ⊆ y. Entsprechend ist z∈M
Archivierungsangaben
ein größtes Element, falls ∀y∈M gilt y ⊆ z.
Z.B. bzgl. P (M) = {∅ ,{a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}}
…….. das kleinste und …………. das größte Element.
Seite 68
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Betrachten wir jetzt die Teilmengen der geordneten Menge
(R, ≤ ):
• Sei A = [a, +∞) = {x∈R : x ≥ a}, dann ….. - kleinstes
Element und es existiert ……. größtes Element.
• Sei B = (a, +∞) = {x∈R : x > a}, dann hat B ……..
Archivierungsangaben
kleinstes …………….. größtes Element.
Dennoch ist die Zahl …... in gewisser Weise optimal als untere
Schranke für B, da es keine andere Zahl x gibt: x > a und x∉B.
Für a gibt es spezieller Begriff!
Seite 69
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Definition 4.12
Es sei (M, R) eine geordnete Menge mit Relation R und
A ⊂ M eine Teilmenge, dann:
1. Ein Element b ∈ M heißt obere Schranke von A, falls für
∀x ∈ A die Relation x R b gilt.
2. Ein Element u ∈ M heißt untere Schranke von A, falls
für ∀x ∈ A die Relation u R x gilt.
Archivierungsangaben
Beispiel 4.8: Sei A = (a,b) eine Teilmenge von (R, ≤ ),
dann ist a die untere Schranke für A und b die obere Schranke
für A.
a
b
Es gilt auch: ∀x ∈ A: (a-1) ≤ x, daraus folgt, dass auch (a-1)
eine untere Schranke für A ist. Es könnte mehrere untere/obere
Schranken geben.
Seite 70
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Definition 4.13
Es sei (M, R) eine geordnete Menge mit Relation R und
A ⊂ M eine Teilmenge, dann:
1. Eine obere Schranke b ∈ M heißt Supremum von A, kurz
b = sup A, wenn b die kleinste obere Schranke von A ist.
Archivierungsangaben
a
b
2. Eine untere Schranke u ∈ M heißt Infimum von A, kurz
u = inf A, wenn u die größte untere Schranke von A ist.
Im Beispiel 4.8: a = inf A; (a-1) dagegen ist nur untere
Schranke.
3. Ist b ∈ A (bzw. u ∈ A), so nennen wir b = max A das
Maximum (bzw. das Minimum) von A.
Seite 71
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Beispiel 4.9
Sei R eine geordnete Menge: (R, ≤ ). Falls:
1. A = (a,b), dann ….. = inf A; …. = sup A, aber es gibt kein
min A und kein max A.
Archivierungsangaben
2. A = (a,b], dann …. = inf A; ………………= sup A, es gib
kein min A.
3. A = [a,b], dann ……………. inf A; ………………..= sup A.
Seite 72
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Archivierungsangaben
Beispiel 4.10
Sei N eine partiell geordnete Menge: (N, | ). Wir betrachten die
folgenden Teilmengen von (N, | ):
1. A1 = ({3,6,9}, |), dann:
a) 1 und 3 sind untere Schranken von A1.
b) inf A1 = 3 = min A1;
Infimum: ggt
c) obere Schranken: Zahlen, die von 3,6 und 9 geteilt
werden, z.B: 36, 54, 162 oder 18, ….
d) sup A1 = 18.
Supremum: kleinste gemeinsame Vielfache
2. A2 = ({12,18}, |), dann:
a) untere Schranken: 1,2,3,6
b) inf A2 = 6;
c) obere Schranken: 36, 72, 144 … d) sup A2= 36.
min A2; max A2 - kein
Seite 73
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Beispiel: Suprema und Infima lassen sich aus dem HasseDiagramm leicht ablesen: so sind z.B. ∅, {2} untere Schranken
der Teilmenge A = {{1,2}, {2,3}} ⊂ P (M).
Archivierungsangaben
Da ∅ ⊂ {2}, gilt: inf A = inf {{1,2}, {2,3}} = {2}.
Infimum - Schnittmenge
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
Das minimale Element
von P(M) steht am
weitesten unten und ist
kleiner als jedes andere
Element in der
gegebenem
Ordnungsrelation. Seite 74
4. Funktionen und Relationen
Obere Schranken der Teilmenge A ={{1}, {3}} sind {1,3} und
Archivierungsangaben
{1,2,3}. Wegen {1,3} ⊂ {1,2,3} gilt: sup A = sup {{1}, {3}} = {1,3}.
Supremum - Vereinigungsmenge
Das maximale
Element von P(M)
steht am weitesten
oben und ist größer
als jedes andere
Element von P(M) ist.
Seite 75
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Definition:
Eine geordnete Menge V ist ein Verband, in der das
Supremum und das Infimum jeder beliebigen
zweielementigen Teilmenge stets existieren und sind
Elemente V.
Teilerverband
kein Verband
Archivierungsangaben
Beispiel:
z.B. für {6,10}:
Infimum ist 2
Supremum ist 30.
für {b,c} existieren untere Schranken:
d,e und f, aber kein Infimum, da
f nicht das größte Element; und keines von
d und e – „größte“ untere Schranke Seite 76
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Übung:
Sei A = {pq, q2, qr, wobei p,q,r ∈ N - Primzahlen , p≠q≠r}
und (A, |). Geben Sie, falls existieren: das kleinste
Element/das größte Element; untere/obere Schranken;
Infimum/Supremum an.
max A – kein; min A - kein
untere Schranken: 1, q;
Archivierungsangaben
obere: p⋅q2⋅r;
inf A = q;
sup A = p⋅q2⋅r
Seite 77
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
4. Funktionen und Relationen
Übung:
Zeichnen Sie das Hasse-Diagramm für (M, |), mit
M = {t ∈ N : t teilt 30}. Geben Sie min M, max M, Infimum und
Supremum an.
Sei A = {2, 5, 10} ⊂ M. Bestimmen
Archivierungsangaben
Sie min A, max A, untere Schranken,
Infimum, obere Schranken und
Supremum.
min A – kein; max A = 10;
untere Schranke: 1; obere Schranken 10,30
Seite 78
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
inf A = 1, sup A = max A = 10
Die Begriffsbildung des Verbandes geht auf
Richard Dedekind zurück.
Anwendungen:
Archivierungsangaben
-
Semantik der Programmiersprachen,
- logische Schaltungen
Richard Dedekind
(1831 - 1916)
- der Programmanalyse
- Algorithmik.
Seite 79
Mathematik – I, Prof. Dr. Romana Piat / Prof. Dr. Julia Kallrath
Bildquelle: http://en.wikipedia.org/wiki/Richard_De
http://en.wikipedia.org/wiki/Richard_Dedekind#mediaviewer/File:Dedekind.jpeg
dekind#mediaviewer/File:Dedekind.jpeg
4. Funktionen und Relationen