PDF_4

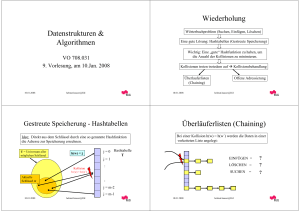
Datenstrukturen &
Algorithmen
Achtung: VO am 8.Jan 2008
entfällt!
VO 708.031
10. Vorlesung, am 12.Dez. 2008
12.04.2008
helmut.hauser@IGI
Wörterbuchproblem
Definition der Wörterbuchproblems durch 3 Funktionen:
1.
2.
3.
EINFÜGEN
SUCHEN
LÖSCHEN
12.04.2008
helmut.hauser@IGI
Gestreute Speicherung - Hashtabellen
Idee: Direkt aus dem Schlüssel durch eine so genannte Hashfunktion
die Adresse zur Speicherung errechnen.
U = Universum aller
möglichen Schlüssel
h(w) = j
Kollision
j = 0 Hashtabelle
T
j=1
:
h (w) = h (w´)
Anwendungsbeispiele: Telefonbuch, Wörterbuch,
Symboltabelle beim Kompilieren, …
Aktuelle
Schlüssel w
:
j = m-2
j = m-1
12.04.2008
helmut.hauser@IGI
12.04.2008
helmut.hauser@IGI
Behandlung von Kollisionen
Überläuferlisten (Chaining)
Bei einer Kollision h(w) = h(w´) werden die Daten in einer
verketteten Liste angelegt:
Kollision: h(w) = h(w´)
Achtung: Kollisionen können immer auftreten.
zu erwartende Laufzeit:
1.) Linderung des Problems:
• Durch geschickte Wahl der Hashfunktion
EINFÜGEN =
O(1)
LÖSCHEN =
O(1+α)
SUCHEN =
O(1+α)
2.) Behandlung von Kollisionen
a) Überläuferlisten (Chaining)
b) Offene Adressierung
12.04.2008
helmut.hauser@IGI
12.04.2008
Offene Adressierung
Bei einer Kollision wird erneut eine Adresse berechnet, indem die
Versuchzahl i um eins erhöht wird, und zwar so lange bis ein freier
Platz gefunden wird, oder i=m ist.
i…0,1,2,…m-1 Versuchzahl (Probing)
i=1
Θ( 1/(1+α) )
Ohne Vorsortierung
Mit Vorsortierung
• Sequentielle Suche
• Binärsuche (Binary Bisection Search)
• Speicherung nach
Zugriffswahrscheinlichkeiten
• Interpolationssuche
• Fastsearch
• Selbstanordnende Felder
noch frei
besetzt
12.04.2008
Suchen in linearen Feldern
α≤1 Æ T kann voll werden.
h(w,i) = j
i=2
helmut.hauser@IGI
helmut.hauser@IGI
Θ( 1/α[ln(1/(1+α))+1] )
12.04.2008
helmut.hauser@IGI
Ungeordnet - Speicher nach
Wahrscheinlichkeiten
Ungeordnet - Sequentielle Suche
Idee: Einfach von Anfang bis Ende alle Werte durchgehen.
Idee: Die Elemente nach ihren Zugriffswahrscheinlichkeiten ordnen.
worst case:
O(n)
best case:
O(1)
average case: O(n)
Æ O(n)
Gleichverteilung:
pi = 1/(n+1)
Exponentielle Verteilung:
pi = 1/(2i) für 1≤i≤n Æ O(1)
Nachteil: Zugriffswahrscheinlichkeit muss bekannt sein.
12.04.2008
helmut.hauser@IGI
12.04.2008
Ungeordnet - Selbstanordnende Felder
Idee: Die Elemente, welche gesucht und gefunden wurden, werden
nach vorne verschoben.
helmut.hauser@IGI
Suchen in linearen Feldern
Ohne Vorsortierung
Mit Vorsortierung
Verschieben
um eine Position
Verschieben
an die Position 1
• Sequentielle Suche
• Binärsuche (Binary Bisection Search)
• Speicherung nach
Zugriffswahrscheinlichkeiten
• Interpolationssuche
• Fastsearch
• Selbstanordnende Felder
Annahmen:
• aufsteigend sortiert
• falls nicht gefunden return (-1)
Im Mittel beide Methoden halb so gut wie bei bekannten pi‘s.
12.04.2008
helmut.hauser@IGI
12.04.2008
helmut.hauser@IGI
Binärsuche
Binärsuche
(Binary Bisection Search)
(Binary Bisection Search)
Idee: Teile das Feld in zwei gleich große Hälften. Vergleiche den
gesuchten Wert mit dem mittleren Element. Falls sie gleich sind, dann
ist man fertig. Wenn der gesuchte Wert kleiner ist, dann suche in der
unteren Hälfte, sonst in der oberen Hälfte.
rekursive Version
T(n) = T(n/2) + O(1)
T(n) =O(log n)
12.04.2008
helmut.hauser@IGI
12.04.2008
Binärsuche
helmut.hauser@IGI
Interpolationssuche
(Binary Bisection Search)
Idee: Man sucht nicht jeweils in der Mitte, sondern dort, wo das
Element sein sollte, mit der Annahme, dass die Werte linear ansteigen.
iterative Version
A[bis]
x
A[von]
von
12.04.2008
helmut.hauser@IGI
12.04.2008
t
helmut.hauser@IGI
bis
Interpolationssuche
FastSearch
rekursive Version
Idee:
Kombination von Binärsuche und Interpolationssuche. Das
Ergebnis ist O(log log n) im mittleren Fall und O(log n) im
schlechtesten Fall.
A
von
T(n) =O( log log(n) )
12.04.2008
helmut.hauser@IGI
12.04.2008
bis
Interpolationssuche
helmut.hauser@IGI
rekursive Version
helmut.hauser@IGI
mI
Laufzeitverhalten der
Suchverfahren
FastSearch
12.04.2008
C
mB
Binärsuche
Zu erwartende
Laufzeit
B
Mittlerer Fall
Schlechtester Fall
Binärsuche
O(log n)
O(log n)
Interpolationssuche
O(log log n)
O(n)
„FastSearch“
O(log log n)
O(log n)
Unsortiert
Sequentielles Suchen
O(n)
O(n)
12.04.2008
helmut.hauser@IGI
Anzahl der Vergleiche für 109
Elemente
Mittlerer Fall
Laufzeitverhalten der
Suchverfahren
Schlechtester
Fall
Mittlerer Fall
Schlechtester Fall
Binärsuche
30
30
Binärsuche
O(log n)
O(log n)
Interpolationssuche
5
1.000.000.000
Interpolationssuche
O(log log n)
O(n)
„FastSearch“
5
30
O(n)
O(n)
Unsortiert
Sequentielles Suchen
500.000.000
1.000.000.000
Unsortiert
Sequentielles Suchen
Alles circa Wert !!
12.04.2008
helmut.hauser@IGI
12.04.2008
FastSearch
Idee:
FastSearch
rekursive Version
Kombination von Binärsuche und Interpolationssuche. Das
Ergebnis ist O(log log n) im mittleren Fall und O(log n) im
schlechtesten Fall.
Binärsuche
12.04.2008
helmut.hauser@IGI
*
Interpolationssuche
helmut.hauser@IGI
12.04.2008
helmut.hauser@IGI
Laufzeitverhalten der
Suchverfahren
Anzahl der Vergleiche für 109
Elemente
Mittlerer Fall
Mittlerer Fall
Schlechtester Fall
Schlechtester
Fall
Binärsuche
O(log n)
O(log n)
Binärsuche
30
30
Interpolationssuche
O(log log n)
O(n)
Interpolationssuche
5
1.000.000.000
„FastSearch“
O(log log n)
O(log n)
„FastSearch“
5
30
Unsortiert
Sequentielles Suchen
O(n)
O(n)
Unsortiert
Sequentielles Suchen
500.000.000
1.000.000.000
Alles circa Wert !!
12.04.2008
helmut.hauser@IGI
12.04.2008
helmut.hauser@IGI