Vier Folien pro Seite

Funktionale Programmierung
10.5.2005
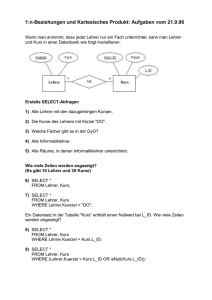
Das Funktionale Quiz
In C sind Pointer auf Funktionen Werte. Sind Funktionen also in C
higher-oder?
Nein, es gibt nur Funktionsdefinitionen auf oberster Ebene.
Das Funktionale Quiz
Das Funktionale Quiz
Woran ist das x in add3 im Rumpf von g gebunden und warum?
Was weiß man über den Rumpf von f?
add x = (\y -> x + y)
add3 = add 3
g x = add3 4
data Foo = Bar Int
f :: Int -> Foo
Ergebnis wird mit Bar berechnet
3, wegen statischer Bindung
1-7
Themen heute
Theoreme helfen dem Compiler: Deforestation
Beob: Oft werden Listen erzeugt und sofort wieder konsumiert
Idee: Wende Konsument anstelle der Listenkonstruktoren an
• Deforestation
• Kombination von Typklassen
• Konstruktorklassen
• Das Modulsystem von Haskell
Kombination
sumToZero :: Int -> Int
sumToZero = sum . toZero
Ohne Zwischenliste:
sumToZero 0 = 0
sumToZero n = n + sumToZero (n - 1)
toZero :: Int -> [Int]
toZero 0 = []
toZero n = n:(toZero (n - 1)
sum []
=0
sum (x:xs) = x + (sum xs)
Deforestation
f :: a -> [b]
f pat1 = []
f pat2 = e1:(f e2)
g :: [b] -> c
g []
= eNil
g (x:xs) = ... x ... (g xs)
gDotf :: a -> c
gDotf pat1 = eNil
gDotf pat2 = ... e1 ... (g (f e2))
8-11
Mit Abstraktion
• Abstraktion über primitive Rekursion: foldr
• Abstraktion über Erzeugen der Listen:
build g = g (:) []
mit g :: (a -> b -> b) -> b -> b
• Beispiel:
replicate i x = build (repl i x)
where
repl 0 x c n = n
repl i x c n = c x (repl (i - 1) x c n)
Typklassen kombinieren
Deforestation mit foldr/build
• Es gilt: foldr f c (build g) = g f c
• Also Deforestation: Zwischenliste wird nicht erzeugt
• build zu verwenden ist umständlich, aber
Eingebaute Funktionen damit definieren
List-Comprehension dahin Übersetzen
Compiler versucht, nach build umzuformen
2D-Punkte und Figuren
data Point = Point Float Float
deriving Show
Typklasse für bewegliche 2D-Objekte:
data Vector = Vec Float Float
class Movable a where
move
:: Vector -> a -> a
instance Movable Point where
move (Vec v1 v2) (Point x y) = Point (x+v1) (y+v2)
data Figure = Line Point Point
| Circle Point Float
deriving Show
instance Movable Figure where
move v (Line p1 p2) = Line (move v p1) (move v p2)
move v (Circle p r) = Circle (move v p) r
12-15
Typklasse für Objekte mit Namen
class Named a where
lookName :: a -> String
giveName :: String -> a -> a
Namen für Movables
Container für Objekte mit Namen
data Name a = Pair a String
deriving Show
instance Named (Name a) where
lookName (Pair obj nm) = nm
giveName new (Pair obj nm) = (Pair obj new)
Kombination der Typklassen
• Erweitern ("Liften") beliebiger Operationen auf Objekte inName:
mapName :: (a -> b) -> Name a -> Name b
mapName f (Pair obj nm) = Pair (f obj) nm
• Damit Objekte mit Namen zu Movable hinzufügen:
instance Movable a => Movable (Name a) where
move v = mapName (move v)
• Jetzt funktionieren move und ...Name:
a = Pair (Point 0 0) "Punkt A"
move a
--> Pair (Point 1.0 2.0) "Punkt A"
lookName a
--> "Punkt A"
• Typklasse für 2D-Objekte mit Namen
class (Movable b, Named b) => NamedMovable b
• Movable eingewickelt in Name sind Mitglieder von NamedMovable:
instance Movable a => NamedMovable (Name a)
16-19
map auf verschiedenen Typen
map überladen
mapList :: (a -> b) -> [a] -> [b]
mapList f []
= []
mapList f (x:xs) = f x : map f xs
mapTree :: (a -> b) -> Tree a -> Tree b
mapTree f Leaf = Leaf
mapTree f (Node a t1 t2) =
Node (f a) (mapTree t1) (mapTree t2)
mapMaybe :: (a -> b) -> Maybe a -> Maybe b
mapMaybe f Nothing = Nothing
mapMaybe f (Just a) = Just (f a)
Konstruktorklasse
Klasse von Typkonstuktoren
class Functor f where
map :: (a -> b) -> f a -> f b
Instanzen:
instance Functor [] where
map f []
= []
map f (x:xs) = f x : map f xs
instance Functor Tree where
map = mapTree
instance Functor Maybe where
map = mapMaybe
mapList :: (a -> b) -> [a] -> [b]
mapTree :: (a -> b) -> Tree a -> Tree b
mapMaybe :: (a -> b) -> Maybe a -> Maybe b
Abstraktion über Typkonstruktor
map :: (a -> b) -> c a -> c b
c ist [], Tree oder Opt
Kind: Stelligkeit von Typkonstruktoren
In map :: (a -> b) -> f a -> f b ist f ein einstelliger Typkonstuktor
Int oder Bool können nicht Instanzen von Funktor sein, sie
akzeptieren keine Parameter
(,) auch nicht, er akzeptiert 2 Parameter
Stelligkeit wird repräsentiert durch "Kind":
• Int, Bool :: *
• [],Tree,Maybe :: * -> *
• (,) (->) :: * -> * -> *
Faustregel: Anzahl Typvariablen = Anzahl Pfeile
Für Funktor also * -> *
20-23
Beispiel: Konstruktorklasse für Folgen
class Seq s where
empty :: s a
cons :: a -> s a -> s a
isEmpty :: s a -> Bool
hd :: s a -> a
tl :: s a -> s a
foldRight :: (a -> b -> b) -> b -> s a -> b
foldRight c n s
| isEmpty s = n
| otherwise = c (hd s) (foldRight c n (tl s))
Bäume als Folgen (Preorder)
instance Seq Tree where
empty
= Leaf
cons a Leaf
= Node a Leaf Leaf
cons a (Node b t1 t2) = Node b (cons a t1) t2
isEmpty Leaf
= True
isEmpty _
= False
hd (Node b Leaf _) = b
hd (Node _ t1 _)
= hd t1
tl (Node b Leaf t2) = t2
tl (Node b t1 t2)
= Node b (tl t1) t2
Listen als Folgen
instance Seq [] where
empty
= []
cons
= (:)
isEmpty [] = True
isEmpty _ = False
hd
= head
tl
= tail
foldRight = foldr
Funktionen auf Folgen
seqMap :: Seq s => (a -> b) -> s a -> s b
seqMap g =
foldRight (\el rest -> cons (g el) rest) empty
seqLength :: Seq s => s a -> Int
seqLength = foldRight (\ _ rest -> rest + 1) 0
seqToList :: Seq s => s a -> [a]
seqToList = foldRight (:) []
24-27
Mehr Operationen
Zusammenfassung
Besser: seqMap, seqLength, seqElem auch als Operationen der
Konstruktorklasse definieren
Zusammenfassung Seq:
Vorteil: Instanzen könnten sie überschreiben
• Sinnvolle Ergänzung: Abstraktion über generelle Rekursion
class Seq s where
...
seqToList :: s a - a
seqToList = foldRight (:) []
• Dann wären mehr Defaultdeklarationen möglich
instance Seq [] where
...
seqToList l = l
• Ermöglicht Abstraktion über Typrepräsentation
Zusammenfassung Konstruktorklassen:
• Erweiterung von Typklassen
• Später noch wichtige Konstruktorklasse Monad
Das Haskell-Modulsystem
Moduldefinition
• Nur auf oberster Ebene
Ein Modul ist eine austauschbare Codeeinheit, die eine komplexe
Leistung erbringt und eine eindeutige Rolle im System hat.
Syntax:
module → module modid [exports] where body
Komponenten:
• Definitionen
• Schnittstelle
• Importe
|
body
body
→ { impdecls ; topdecls }
• module modid definiert Modul mit Namen modid
• Sollte in Datei mit Namen modid .hs stehen
• Fehlt Angabe der Exporte, werden alle Definitionen exportiert
28-31
Importe
impdecl → import [qualified] modid [as modid] [impspec]
impspec → ( import1, ... ,importn)
|
hiding ( import1, ... ,importn)
• Importiert Bezeichner aus Modul modid
Einträge der Import-Spezifikationen
import → var
|
tycon [ (..)| ( cname1, ... , cnamen)]
|
tycls [ (..)| ( var1 , ... , varn)]
cname → var | con
• Suchpfad ist Installation und momentanes Verzeichnis (Vorsicht im
XEmacs!)
• Namen aus Definitionen
• Mit qualified nur als Module.name ("qualifiziert")
• Typdefinitionen mit
• as vergibt neuen Modulnamen für qualifizierte Namen
(..) allen Konstruktoren
• Ist Importspezifikation vorhanden, so legt sie fest, welche der
exportierten Namen importiert werden
(cname1, ... , cnamen) ausgewählten Konstruktoren
• Analog für Typklassen
• Andernfalls alle
Exporte
Das Modul Prelude
exports → ( export1, ... , exportn)
export
→ qvar
|
qtycon [(..)| ( cname1, ... , cnamen)]
• Wird immer implizit importiert
|
qtycls [(..)| ( var1 , ... , varn)]
• Außer, wenn es explizit importiert wird
|
module modid
• import Prelude (...) importiert also selektiv aus der Prelude
• Analog zu Importen
• module modid re-exportiert Exporte eines Imports
32-35
Beispiele
Beispiele
module Bar (Stack (..),stackIsEmpty)
import Prelude hiding (head)
module Foo (a)
import List
a = nub [1,2,1,2]
b = 23
• Exportiert a
• Importiert List
data Stack a = Stk [a]
stackIsEmpty (Stk []) = True
stackIsEmpty _
= False
head (Stack (x:xs)) = x
• Importiert alles aus der Prelude außer head
• Exportiert alg. Datentyp mit Konstruktor Stk
Abstrakte Datentypen in Haskell
Beispiel-ADT: Speicher
module Store (Store, initial, value, update) where
import qualified List
data Store = Sto [(Int, String)]
• ATD = Datentyp bei dem die Repräsentation nicht nach außen
gegeben wird
• Sinn: Implementierung kann ausgetauscht werden
• In Haskell: Modul mit algebraischem Datentyp dessen
Konstruktoren nicht exportiert werden
initial = Sto []
value (Sto l) addr = x
where
Just x = lookup l addr
update (Sto l) addr val = Sto (addr,val):l
• Außerhalb kein Matching möglich, da Sto nicht exportiert
36-39
newtype
Algebraischer Datentyp mit nur einen Konstruktor = neuer Typ mit
bekannter Repräsentation
Bsp. siehe Store
Effizienter mit newtype
Syntax: Wie data aber nur ein Konstruktor
40