Frequenzkamm -- Nobelpreis 2005

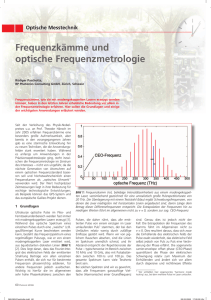
Frequenzkamm -- Nobelpreis 2005
Vortrag von Andreas Jöckel
im Rahmen des Seminars über moderne Experimente der
Quantenoptik und Atomphysik
Inhalt
●
Motivation
●
Eigenschaften
●
Technische Umsetzung
●
Anwendungen
●
Der Nobelpreis
Motivation: Genaue Messung von
Frequenzen
Es sollen Frequenzen mit größtmöglicher Genauigkeit
gemessen werden (10-15 -10-17)
●
Wie misst man: Messung von Anzahl der Perioden und
Zeitspanne
●
Umgekehrt: je höher eine bekannte Frequenz, desto genauer
kann eine Zeitspanne berechnet werden
●
Es ist daher das Ziel Frequenzen im optischen Bereich zu
messen
●
Problem: Frequenzen zu groß für Zählelektronik
●
Lösung: Schwebung zwischen bekannter und zu
untersuchender Frequenz messen
●
Zur Schwebung
●
●
●
Schwebungsfrequenz:
fs=(f1-f2)/2
Optische Frequenzen
sind im 100THz-Bereich
(400 bis 800 THz)
Maximal messbare
Frequenz ist ca 100GHz
Früher: Frequenzkette
●
●
Erzeugung von
Oberschwingungen einer
bekannten Frequenz, die
der Cäsiumuhr.
Nachteile:
–
sehr aufwendig
–
teuer
–
Unflexibel (muss für
eine zu messende
Frequenz gebaut
werden)
Besser: Die Frequenzdifferenz
verkleinern
●
●
●
●
n Teiler bedeuten eine
Intervallverkleinerung um 2n
Prinzip: Durch Rückkopplung
Frequenz auf 2 f3=f1+f2
fixieren. Damit ist f3 genau in
der Mitte von f1 und f2, Abstand
f3 – f2 ist genau die Hälfte des
vorherigen Abstandes
Vorteile: Flexibler und
einfacher als Frequenzkette
Nachteil: Frequenz eines
Lasers muss bekannt sein.
Der Frequenzkamm
●
●
Ein Frequenzkamm besteht
aus einer großen Anzahl
möglichst äquidistanter
Moden, mit denen man große
Frequenzlücken überbrücken
kann
Bei Kenntnis von b1,b2
sowie r und n kann man den
Frequenzabstand  daraus
bestimmen bestimmen
Eigenschaften des
Frequenzkamms
●
Zusammenhang zwischen
Frequenz- und
Zeitdarstellung des
Frequenzkammes ist durch
die Fouriertransformation
gegeben:
Wichtige Größen:
CE und r
n=CE+ nr
Eigenschaften der
Fouriertransformation
●
●
●
Reihenentwicklung der Einhüllenden:
●
-Funktion nur Näherung für
Mode
Für unendlich viele Moden
ergeben sich die Pulse als
-Funktionen mit Abstand
T=2/r
Modenabstand ist die
Pulsfrequenz
Ein Wellenpaket, bestehend
aus Trägerfrequenz und
Einhüllender kann mit einer
Fourierreihe mit dem
entsprechenden
Modenabstand entwickelt
werden.
Pulslänge und Modenanzahl
●
Je mehr Moden, desto schmaler der Puls. Für Gaußsches Wellenpaket
gilt =1/t
●
Die -Funktion ergibt sich für unendlich viel Moden als Grenzfall
●
Ein 10fs-Puls mit 300MHz Pulsrate enthält ca 106 Moden
●
Dies funktioniert aber nur, wenn die Phasen der Moden aneinander
gekoppelt sind
20 Moden
40 Moden
Der Frequenzoffset f0
●
Er entsteht, da sich die Trägerwelle fc
mit ihrer Phasengeschwindigkeit
ausbreitet, die Einhüllende aber mit
der Gruppengeschwindigkeit. Falls
diese Geschwindigkeiten nicht gleich
sind, entsteht eine
Phasenverschiebung von Puls zu Puls
um .
Erzeugung von fs-Pulsen:
Titan:Saphir-Laser
•
•
Wellenlängenbereich des Ti:Sa: 670nm-1070nm -> viele Moden möglich
Es bildet sich eine stehende Welle von sehr vielen Moden aus, die einem
umlaufenden Puls entspricht
Umlauffrequenz:
r =2/T
T=L/vg
Übergang zum Pulsbetrieb: KerrLens Mode-locking
●
●
●
●
Bei hohen Laserintensitäten
sind viele Materialien nicht
mehr linear:
n(t)=n0+n2 I(t)
Phasenflächen krümmen sich
beim Durchlaufen des
Mediums
Ab einer Mindestintensität Ist
die Fokussierung größer als
die Dispersion
Ausnutzen der Selbstfokussierung
●
●
●
Die Selbstfokussierung bei hohen
Intensitäten im Pulsbetrieb kann
man ausnutzen: ein Puls hat ca.
4MW/cm² , während ein CWStrahl nur 4W/cm² hat.
Der gepulste Strahl kann die
Blende ohne Verlusste passieren,
der cw-Strahl erleidet Verluste.
Ein kleines Inversionsvolumen in
der Mitte des Kristalls begünstigt
dies auch.
Bei jedem Umlauf entstehen
weitere Seitenbänder und der
Puls wird kürzer
Das Problem mit der Dispersion
●
●
●
Dispersion entsteht in
sämtlichen optischen
Materialien.
Der Term k' ist für f0
verantwortlich.
k'' sorgt dafür, das sich
die rote Flanke des
Kamms schneller bewegt
als die Blaue → das
Wellenpaket driftet
auseinander.
Reihenentwicklung von k():
Lösung:Weg für rotes Lich
verlängern
Links: Kompensation mit 2 Prismen
Rechts: mit dispersivem Spiegel
Verbreiterung des
Frequenzkammes
●
Wird mit spezieller Glasfaser erreicht.
●
Ziel ist es den Frequenzkamm auf eine ganze Oktave zu erweitern
Spektrum vor und nach der Faser
Messen mit dem Frequenzkamm
●
Jeder Frequenzkamm hat zunächst zwei Freiheitsgrade:
–
r – kann einfach mit Photodiode gemessen
werden
–
0 – muss über Umwege berechnet werden:
Wenn der
Frequenzkamm mehr als
eine Oktave umspannt,
kann eine Mode fn
verdoppelt und mit der
Mode f2n überlagert
werden. Die
Schwebungsfrequenz ist
der Offset
Stabilisierung von r und 0
●
●
Stabilisierung von r durch
Variation der
Resonatorlänge mit PiezoKristall.
0 kann durch
Einschieben eines
Kristalls, der die
durchschnittliche
Gruppengeschwindigkeit
ändert, variiert werden.
Messapparatur
Beispiel: Einlaser-Frequenzkette
Anwendungen:
●
Genaue bestimmung von Naturkonstanten
–
●
Mit dem Frequenzkamm können Übergänge im
Atom viel genauer als bisher bestimmt werden
und daraus z.b.  und R∞
Optische Atomuhren
–
Atomuhren auf Basis optischer Frequenzen
können die Synchronisation von Netwerken
verbessern und eignen sich zum Test der
Relativitätstheorie
Messung des 1S-2S Übergangs im
Wasserstoffatom
Dieser Übergang ist besonders interessant, da er Metastabil ist und daher eine sehr
geringe natürliche Linienbreite hat.
●
●
Ein Diodenlaser erzeugt
variable Frequenzen um
486nm
Aufspaltung des Strahls:
–
Ein Teil wird als
Frequenzkamm
benutzt
–
Mit dem anderen
Teil, der
Frequenzverdoppelt
wird, kann die
Messung
durchgeführt werden
Die optische Atomuhr
●
●
●
Ausschlaggebend für die
Genauigkeit einer Uhr ist die
Frequenz des Pendels, da die
Periode die minimal messbare
Zeitdifferenz darstellt
Höhere Frequenzen, also
optische, erhöhen die
theoretische Genauigkeit enorm.
Mit einem Frequenzkamm kann
eine optische Frequenz in dafür
ausreichender Genauigkeit
gemessen werden.
Prinzip
●
●
●
Ein CW-Laser, der auf den 2S½↔ 2D5/2 Übergang im 199Hg+ Ion
eingestellt ist wird mit Hilfe eines Frequenzkammes vermessen.
Die Phase der Einhüllenden des Pulslasers wird dabei an die des
CW-Lasers gekoppelt.
Daher ist die Repetitionsrate ein Bruchteil der Übergangsfrequenz
Frequenzkamm im UV-Bereich
●
●
●
=m (n r+0)
Um höhere Frequenzen
als die im normalen
Frequenzkamm zu
erreichen, muss eine
Frequenzverfielfachung
benutzt werden
Der Frequenzkamm wird
dabei in einen Resonator
eingeleitet und an einer
Stelle mit Xenon in
Kontakt gebracht.
Erzeugt Harmonische bis
zur 13.Ordnung, die
ebenfalls noch kohärent
sind.
Der Nobelpreis 2005
●
Vergeben für:
–
Entwicklung von
laserbasierter
PräzisionsSpektroskopie
–
Beiträge zur
Quantentheorie der
optischen Kohärenz
Die Preisträger
Theodor W. Hänsch
John L. Hall
Jeweils ¼ für die Entwicklungen in
der Spektroskopie
Roy J.Glauber:
½ des Preises für
theoretische Arbeiten
Literaturangabe
●
Kasper, A. Erzeugung und Charakterisierung ultrakurzer Lichtpulse aus Titan:Saphir LaserOszillatoren
–
●
●
●
●
Gohle,C., Udem, T., Herrmann, M., Rauschenberger, J., Holzwarth, R., Schuessler, H.,
Krausz, F. & Hänsch, T. W. A frequency comb in the extreme ultraviolet, Nature 436, 234237 (2005)
Diddams, S. A., Udem,Th. et al. An optical clock based on a single trapped 199Hg+ ion,
Science 293, 825-828 (2001)
Udem, Th., Holzwarth, R. & Hänsch, T.W. Uhrenvergleich auf der Femtosekundenskala,
Physik Journal 2/2002, 39-45 (2002)
Hänsch, T.W., Holzwarth, R., Reichert, J. & Udem, Th. Measuring the frequency of light with
a femtosecond laser frequency comb (2002)
–
●
http://www.mpq.mpg.de/~haensch/grafik/fermi_1.pdf
Advanced information on the Nobel Prize in Physics 2005
–
●
http://www.laser.physik.uni-muenchen.de/lsw/axelKasperDiss.pdf
http://nobelprize.org/physics/laureates/2005/phyadv05.pdf
Cundiff, S. T. & Ye, Jun Colloquium: Femtosecond optical frequency combs