Statische CMOS-Schaltungen - Fakultät für Mathematik und Informatik

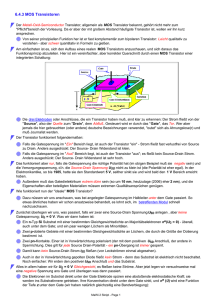
Schumann, Arne
Mat.Nr.: 73900
Informatik Diplom
[email protected]
Statische CMOS-Schaltungen
Aufbau und Funktionsweise von MOS Transistoren
Prof. Dr. Eberhard Zehendner
Institut für Informatik
Fakultät für Mathematik und Informatik
Friedrich Schiller Universität Jena
Sommersemester 2005
28.07.05 – 01.08.05
Inhaltsverzeichnis
1.
1.1
1.1.1
1.1.2
1.1.3
1.2
1.2.1
1.2.2
1.2.3
1.2.4
1.3
1.3.1
1.3.2
1.3.3
2.
2.1
2.2
2.2.1
2.2.2
2.2.3
2.2.4
2.3
2.4
2.4.1
2.4.2
2.4.3
2.5
2.6
Die CMOS Technologie
Chemische und physikalische Grundlagen
Das Bändermodell
Energieniveaus und -bänder
Valenz- und Leitungsband
Generation, Rekombination und Eigenleitfähigkeit
Dotierung
Störstellenleitfähigkeit
n-Dotierung
p-Dotierung
Majoritäts- und Minoritätsladungsträger
pn-Übergang
Aufbau eines pn-Übergangs
Diffusion und Feldwirkung
Spannungsgesteuerter pn-Übergang
Aufbau und Funktionsweise von MOS Transistoren
Aufbau eines nMOS Transistors
MOS Struktur und Feldeffekt
Kapazität der MOS Struktur
Oberflächenpotential und Feldeffekt
Verarmung, Inversion und Ladung bei der MOS Struktur
Rechnerische Bestimmung der Schwellspannung
Der Body Bias Effekt
Strom-Spannung-Charakteristiken
Verarmung und Inversion im nMOS Transistor
Ermittlung der Stromstärke
Gesättigter und ungesättigter Stromfluss
Aufbau und Funktionsweise eines pMOS Transistors
Schaltsymbole der Transistoren
Quellenverzeichnis
3
4
4
4
5
5
6
6
6
7
7
8
8
8
9
10
10
11
11
11
12
13
14
15
15
16
16
18
19
20
Die CMOS Technologie
Der folgende Text soll ein Verständnis für die Grundlagen der CMOS-Technologie, die
Funktionsweise der verwendeten Transistoren und deren Hintergründe vermitteln. CMOS
bedeutet „Complementary Metal Oxide Semiconductor“ (koplementäre Metall Oxid
Halbleiter). Der Name ergibt sich – wie weiter unten erklärt – aus dem Aufbau der
Technologie und den verwendeten Transistoren.
Seit ihrer Entdeckung in den 60er Jahren gewann die CMOS-Technologie viel an
Bedeutung und wird heute in nahezu allen Bereichen der Elektrotechnik verwendet. Das
Grundprinzip ist das Zusammenschalten von zwei gegenteiligen (complementary)
Transistoren (einem n- und einem p-MOSFET). Aufgrund dieser Konstruktion, der
Beschaffenheit der Transistoren und nicht zuletzt der weit vorangeschrittenen
Herstellungsverfahren (z.B. Aufdampfungs-, Maskenverfahren) zeichnen sich CMOSSchaltungen durch Vorteile wie eine nahezu leistungslose Steuerung (geringe
Verlustleistung), hohe Integrierbarkeit und billige Herstellung aus, haben aber auch
Nachteile, wie zum Beispiel Anfälligkeit gegenüber statischen Aufladungen und
Überspannungen, die im Allgemeinen entsprechende Schutzschaltungen notwendig
machen.
1. Chemische und physikalische Grundlagen
1.1 Das Bändermodell
1.1.1 Energieniveaus und -bänder
Die Grundlage für die Funktionsweise von Halbleitern ist der chemische Aufbau von
sogenannten Halbleiterkristallen, wie z.B. Germanium oder Silizium. Auf diesen Aufbau
und seine Besonderheiten wird im Folgenden eingegangen.
Atome bestehen aus Elektronen und Protonen. Die Protonen bilden den Kern, während sich
die Elektronen auf Orbitalen um ihn herumbewegen. Für ein spezielles Atom gibt es
bestimmte Energieniveaus auf denen sich die Elektronen aufhalten können. In der
nachstehenden Grafik ist eine beispielhafte Verteilung dieser Energieniveaus für ein Atom
gezeigt.
Wie viele Elektronen sich auf welchem Energieniveau aufhalten, hängt vom Zustand des
Atoms ab. So kann ein Elektron durch Energiezufuhr in höhere Energieniveaus gehoben,
oder sogar komplett vom Atom getrennt werden. Außerdem beeinflussen benachbarte
Atome ihre Energieniveaus wechselseitig, sodass diese leicht voneinander abweichen.
Wenn nun viele Atome des gleichen Typs dicht aneinander liegen, wie es z.B. in (Ein-)
Kristallstrukturen der Fall ist, entstehen so viele leicht abweichende Energieniveaus, dass
man diese vereinfachend als Energiebänder zusammenfassen kann (Abb1.1). Elektronen
können sich in einer solchen Struktur also ausschließlich innerhalb dieser Bänder
aufhalten1.
W/eV
Atom
2er Molekül
Kristall
Abb. 1.1: Energieniveaus bei Einzelatomen und Kristallen
1 Im Weiteren wird stets von Aufenthalt in einem Band gesprochen, obwohl ein solches Band in einem
Kristall nicht existiert. Es handelt sich tatsächlich um eine Zuordnung der Elektronen nach ihrem
energetischen Zustand, wie sie im Bohrschen Atommodell beschrieben ist
1.1.2 Valenz- und Leitungsband
Die Halbleiter bei denen sich eine solche Bänderform der Energieniveaus ausbildet, sind
hochgradig reine Silizium- oder Germanium-Einkristallstrukturen. Wichtig für die
Halbleitertechnik (und somit die CMOS Technologie) ist dabei das beim
Temperaturnullpunkt höchste noch von Elektronen besetzte Band. Die Elektronen, die sich
in diesem Band befinden, stellen die Bindungen zu anderen Atomen her und heißen
entsprechend Valenzelektronen2. Das Band mit den Valenzelektronen wird Valenzband
genannt.
Über dem Valenzband liegt das sogenannte Leitungsband. Die Elektronen im Leitungsband
bestimmen die elektrische Leitfähigkeit des Stoffes. Bei Halbleitern ist dieses Band am
Temperaturnullpunkt unbesetzt, was dazu führt, dass der Halbleiter in diesem Zustand
nicht leitfähig ist.
1.1.3 Generation, Rekombination und Eigenleitfähigkeit
Valenz- und Leitungsband liegen jedoch so dicht beieinander, dass mit bereits wenig
Energiezufuhr (z.B. Zimmertemperatur) Elektronen aus dem Valenzband ins Leitungsband
gehoben werden und der Halbleiter somit leitfähig wird. Wenn ein Elektron das
Valenzband verlässt, bleibt dort ein positives Defektelektron, oft „Loch“ genannt zurück.
Dieses Loch ist eine positive Ladung, die ortsfest ist, da sie in der Kristallstruktur fest
eingebunden ist. Ihr gegenüber steht das frei bewegliche Elektron im Leitungsband.
Den Vorgang des Bildens eines solchen Paars aus ortsfestem Loch und frei beweglichem
Elektron nennt man Generation. Der gegenteilige Prozess, bei dem ein Elektron aus dem
Leitungsband zurück ins Valenzband fällt und sich dort mit einem Loch neutralisiert nennt
man Rekombination. Bei einer bestimmten Temperatur stellt sich ein Gleichgewicht
zwischen beiden Prozessen ein, was zu einer festen Anzahl an Elektronen im Leitungsband
für eben diese Temperatur führt. Aus dieser festen Anzahl resultiert eine feste
Leitfähigkeit, die Eigenleitfähigkeit genannt wird.
2 Valenz (Chemie): Wertigkeit, offene Bindungsmöglichkeit eines Atoms oder Moleküls
1.2 Dotierung
1.2.1 Störstellenleitfähigkeit
Die Eigenleitfähigkeit eines reinen Halbleiterkristalls ist jedoch nicht hoch genug, um in
elektrotechnischen Schaltungen Anwendung zu finden. Deshalb wurden sogenannte
Dotierungsverfahren entwickelt, um die Leitfähigkeit eines Halbleiterkristalls zu erhöhen.
Bei der Dotierung werden absichtlich Fremdatome in die Kristallstruktur eingebracht.
Genutzt wird dabei die Tatsache, dass sowohl Germanium, als auch Silizium je vier
Valenzelektronen besitzen, sich also Kristallstrukturen bilden in denen jedes Atom vier
Bindungen zu Nachbaratomen aufbaut. Eine durch solche Fremdatome erhöhte
Leitfähigkeit nennt sich Störstellenleitfähigkeit.
Man unterscheidet als Dotierungsmöglichkeiten die p- und die n-Dotierung.
1.2.2 n-Dotierung
W
Si
Si
Si
Si
Si
Si
Si
P
Si
Si
Si
Si
Si
Si
Si
L
WD
DN
V
x
Abb. 1.2: n-Dotierung von Siliziumkristallen mit Phosphoratomen
Bei der n-Dotierung werden Atome mit 5 Valenzelektronen in den Kristall eingebracht.
Vier dieser Elektronen bilden Bindungen zu Nachbaratomen aus. Das fünfte hat keine
Möglichkeit mehr eine Bindung einzugehen, da die Kristallatome nut vier Bindungen
zulassen. Es wird also nur durch die Kern-Anziehungskraft des Fremdatoms an seinem
Platz gehalten. Entsprechend leicht ist es möglich dieses Elektron vom Kern zu trennen, es
also mit nur wenig Energieaufwand ins Leitungsband zu heben. Das Energieniveau dieses
Elektrons liegt aufgrund der geringen Energiezufuhr ΔWD, die für ein Anheben ins
Leitungsband benötigt wird dicht unterhalb des Leitungsbandes. Zurück bleibt das positiv
geladene, ortsfest eingebundene Fremdatom. Das Fremdatom funktioniert also als ein
Elektronendonator (lat. donare: geben) und wird entsprechend Donatoratom genannt. Der
mit Donatoratomen dotierte Halbleiter heißt n-dotiert.
1.2.3 p-Dotierung
W
Si
Si
Si
Si
Si
Si
Si
B
Si
Si
L
AN
WA
Si
Si
Si
Si
Si
V
x
Abb. 1.3: p-Dotierung von Siliziumkristallen mit Boratomen
Bei der p-Dotierung verwendet man 3-wertige Fremdatome. Alle drei Valenzelektronen
werden für Bindungen benötigt. Zur vollständigen Einbindung ins Kristallgitter fehlt
jedoch noch eine weitere Bindung. Das entsprechende Elektron für diese Bindung wird von
einem benachbarten Kristallatom „geklaut“, was dazu führt, dass das 3-wertige Fremdatom
eine ortsfest eingebundene negative Ladung ergibt, da es ein negatives Elektron mehr als
im neutralen Zustand besitzt. Das Kristallatom, welches sein Elektron hergeben musste ist
entsprechend positiv geladen, also ein Loch. Dieses Loch ist bestrebt wieder alle
Kristallbindungen herzustellen und benötigt dazu ein Elektron, welches es sich von einem
anderen Kristallatom holt. Durch diesen Vorgang wandert das Loch durch den Kristall. Es
stehen also negative ortsfeste Ladungen in Form der Fremdatome beweglichen Löchern
(positiven Ladungen) gegenüber. Das Fremdatom nimmt in diesem Fall also Elektronen
auf und heißt entsprechend Akzeptoratom (lat. accipere: annehmen). Der mit
Akzeptoratomen dotierte Halbleiter heißt p-dotiert.
1.2.4 Majoritäts- und Minoritätsladungsträger
Für beide Dotierungsarten gilt: diejenigen Ladungsträger (Elektronen oder Löcher), die in
der Lage sind sich frei zu bewegen tragen den wesentlichen Teil zur Leitfähigkeit bei und
heißen entsprechend Majoritätsladungsträger. Die ortsfesten Ladungsträger heißen
Minoritätsladungsträger. So sind bei n-dotierten Halbleitern also die (frei beweglichen)
Elektronen die Majoritätsladungsträger und die (ortsfesten) Löcher die
Minoritätsladungsträger.
1.3 pn - Übergang
1.3.1 Aufbau eines pn-Übergangs
Damit ein Transistor auf die gewünschte Weise funktioniert, werden stets beide
Dotierungsarten benötigt. Interessant und ausschlaggebend sind dabei vor allem die Zonen,
an denen p-dotierter Halbleiter auf n-dotierten Halbleiter trifft, die sogenannten pnÜbergänge. Die an diesen Übergängen ablaufenden Prozesse werden im Folgenden
zunächst für einen pn-Übergang ohne das Umfeld eines Transistors betrachtet:
p-Zone
n-Zone
Abb. 1.4: pn-Übergang
1.3.2 Diffusion und Feldwirkung
In der n-Zone des Übergangs befinden sich als Majoritätsladungsträger freie Elektronen
und in der p-Zone entsprechend freie Löcher. An der Grenze zwischen beiden Zonen
kommt es dazu, dass die frei beweglichen Elektronen aus der n-Zone in die p-Zone
diffundieren und dort mit den beweglichen Löchern rekombinieren. Die Grenzschicht wird
also frei von beweglichen Ladungsträgern. Zurück bleiben die Unbeweglichen, wie in der
folgenden Grafik dargestellt.
Diffusion
p
n
Feldwirkung
Abb. 1.5: Grenzschicht am pn-Übergang
Zwischen diesen festen Ladungen in beiden Zonen bildet sich ein elektrisches Feld aus,
was in seiner Wirkung auf die Elektronen der Diffusion entgegen steht3. Eine ansteigende
Diffusion führt also zu einer ansteigenden Feldstärke, die entsprechend stärker der
Diffusion entgegenwirkt. Wird das Feld schwächer, so steigt die Diffusion, was das Feld
wieder verstärkt. Es stellt sich also stets ein Gleichgewicht ein, bei dem beide Effekte
gleich groß sind. Die Spannung, die bei diesem Gleichgewicht zwischen beiden Zonen
anliegt heißt Diffusionsspannung UD.
3 Genau in die andere Richtung – also ebenfalls entgegengesetzt - verlaufen Diffusion und Feldwirkung in
Bezug auf die positiven freien Ladungsträger aus der p-Zone
1.3.3 Spannungsgesteuerter pn-Übergang
Für den bisher betrachteten pn-Übergang galt stets, dass dieser frei von äußeren
Einwirkungen war. In Transistoren wird jedoch kein passiver Übergang, bei dem sich stets
das beschriebene Gleichgewicht einstellt benötigt, sonder eine Art steuerbarer Übergang.
Diese Steuerbarkeit ergibt sich durch das Anlegen einer Spannung an den pn-Übergang.
UD+UA
-
p
n
+
Abb. 1.6: pn-Übergang mit Spannung in Sperrrichtung
Zunächst sei der Pluspol an der n-Zone und der Minuspol an der p-Zone angelegt. Die
äußere Spannung UA verstärkt also die Diffusionsspannung auf UD+UA. Entsprechend
erhöht sich die Feldwirkung und die Raumladungszonen, in denen sich nur die ortsfesten
Ladungsträger aufhalten werden größer. Durch größere Raumladungszonen wird die
Leitfähigkeit des Halbleiters in diesem Gebiet stark verringert, was dazu führt, dass die
Raumladungszonen eine sogenannte Sperrschicht ausbilden. Der pn-Übergang ist in
diesem Fall also nicht mehr leitend. Man spricht hier auch von einer „Spannung in
Sperrrichtung“, die an den Übergang angelegt ist.
UD-UA
+
p
I
n
-
Abb. 1.7: pn-Übergang mit Spannung in Durchlassrichtung
Bei umgekehrt angelegter Spannung verringert sich die Diffusionsspannung auf UD-UA.
Die Feldstärke und die Raumladungszonen werden entsprechend kleiner. Kleinere
Raumladungszonen begünstigen den Diffusionsstrom – also den Fluß von Elektronen aus
der n-Zone in die p-Zone. Da dieser Diffusionsstrom aus Majoritätsladungsträgern besteht,
wird der pn-Übergang leitend. Eine Spannung, die den Übergang leitend macht nennt sich
„Spannung in Durchlassrichtung“.
2. Aufbau und Funktionsweise von MOSTransistoren
2.1 Aufbau eines nMOS Transistors
Source
Drain
Metal
Metal
Plug
Gate [M]
n+, Nd
Plug
Oxide [O]
L
p+ Substrat, Na
n+, Nd
Semiconductor [S]
Bulk
Abb. 2.1: Aufbau eines nMOS Transistors
Ein MOSFET4 hat vier Anschlüsse, um in einem Stromkreis eingebunden zu werden: Gate,
Source, Bulk und Drain. Im Bild ist hier ein n-(Kanal-)MOSFET dargestellt. Die Source
und Drain Anschlüsse bestehen aus Metall und liegen direkt an den beiden pn-Übergängen
des Transistors an. Im Fall des nMOS besteht der Hauptanteil des Transistors aus pdotiertem Halbleiter mit kleinen n-dotierten Zonen an den Drain und Source Anschlüssen.
Über der Lücke zwischen beiden pn-Übergängen liegt der Gate-Anschluss, der durch eine
dünne Isolationsschicht vom Halbleiter getrennt ist. Diese Trennung verhindert, dass ein
Strom am Gate fließen kann und ermöglicht somit die leistungslose Steuerung des
Transistors. Das Gate selbst besteht aus einer Polysiliziumschicht über der eine dünne
Metallschicht liegt. Polysilizium deshalb, weil es gegenüber der Isolationsschicht bessere
Abdeck- und Hafteigenschaften besitzt. Andererseits ist der elektrische Widerstand von
Polysilizium so hoch, dass eine besser leitende Metallschicht darübergelegt werden muss.
Als vierter Anschluss ist unten am Transistor ebenfalls in Form einer Metallschicht der
Bulk-Anschluss angebracht. Wichtige Größen, die in der Grafik bereits eingeführt werden
sind der Abstand zwischen beiden pn-Übergängen (die sogenannte Kanalbreite) L, die
Gatebreite L' und die Dotierungsdichten Na und Nd der akzeptor- bzw. donatordotierten
Halbleiter. Eine weitere wichtige Größe ist die Kanallänge W und das Seitenverhältnis
W/L.
Zum Verständnis des Aufbaus sei hier bereits erwähnt, dass es sich um einen nMOS des
Anreicherungstyps handelt, einen Transistor also, der bei keiner Spannung am Gate einen
möglichen Stromfluß von Drain zu Source sperrt. Sollte die Spannung am Gate jedoch
einen bestimmten Schwellwert überschreiten, so wird der Transistor leitend und es fließt
ein Strom vom Drain zur Source.
4 MOSFET: Metal Oxide Semiconductor Field Effect Transistor
2.2 MOS Struktur und Feldeffekt
2.2.1 Kapazität der MOS Struktur
+VG
Metall
Gate
Polysilizium
M
O xox
Gate Oxid
S
x
p-Typ, Na
Abb. 2.2: Aufbau der MOS Struktur
Grundlegend für die Funktionalität des Transistors ist zunächst einmal die MOS Struktur
in der Mitte zwischen beiden pn-Übergängen. Deshalb wird sie vorerst isoliert betrachtet.
Wie in der Grafik zu erkennen ist, bildet das Gate, mit der isolierenden Oxidschicht und
dem p-dotierten Halbleiter eine Kondensatorstruktur. Entsprechend lässt sich für diesen
Kondensator eine Kapazität nach der allgemeinen Formel ermitteln:
 F
∗A
C=
=C ox = ox
,
d
x ox cm2
wobei εox die Permittivität des Oxids ist, und d = xox der Abstand der Kondensatorplatten,
also die Dicke der Oxidschicht. Für Siliziumdioxid als Isolator ergibt sich εox zu ca.
3,9*ε0 F/cm2 mit ε0 als der konstanten Permittivität des Vakuums (ε0 = 8.854...*10-12Fm-1),
xox liegt bei heutigen Transistoren bei 0.01μm oder weniger. Folglich liegt Cox
normalerweise in der Gegend von 10-7 F/cm2 oder mehr.
2.2.2 Oberflächenpotential und Feldeffekt
Legt man nun eine positive Spannung VGn am Gate an, so entsteht ein elektrisches Feld,
welches das Oxid durchdringt und Einfluss auf den darunter liegenden Halbleiter hat. Der
Spannungsabfall über die MOS Struktur lässt sich wie folgt darstellen:
M
O
S
VG
Vox
S
x
Abb. 2.3: Spannungsabfall über die MOS Struktur
Aus der Grafik ist zu erkennen, dass für das Potential an der Oberfläche des Halbleiters
folgende Beziehung gilt:
VGn = Vox + ΦS
Da der Spannungsabfall über das Oxid bei konstanter Oxiddicke ebenfalls konstant ist,
ergibt sich aus einer Erhöhung der Gatespannung VGn ebenfalls eine Erhöhung des
Oberflächenpotentials ΦS. Der Vorgang in dem das entstandene elektrische Feld die
Isolatorschicht durchdringt und im darunter liegenden Halbleiter eine Wirkung auf die dort
vorhandenen Ladungsträger entfaltet wird Feldeffekt genannt.
2.2.3 Verarmung, Inversion und Ladung bei der MOS Struktur
Im Falle des betrachteten nMOS ist der Halbleiter unter der Isolierschicht p-dotiert. Durch
die positive Spannung am Gate und das erzeugte Feld werden also die ebenfalls positiv
geladenen frei beweglichen Teilchen (Majoritätsladungsträger) aus dem Halbleiter direkt
unterhalb des Gates verdrängt. Zurück bleiben – wie schon beim pn-Übergang – die
ortsfesten negativen, Akzeptoratome. Gleichzeitig werden frei bewegliche Elektronen5 aus
dem Halbleiter in die Region unter dem Gate gezogen, wo sie mit einem Teil der
Majoritätsladungsträger rekombinieren. Diesen Vorgang, bei dem das Gebiet unter dem
Gate von den Majoritätsladungsträgern befreit wird, nennt man Verarmung.
+VG<VTn
Metall
Gate
Polysilizium
M
O
QB
S
x
Verarmungs-Region
p-Typ, Na
Abb. 2.4: Verarmung in der MOS Struktur
Wie in der Grafik zu sehen ist, hat die Verarmung die Ausbildung einer bestimmten
Ladung unterhalb des Gates – der sogenannten Bulk-Ladung QB - zur Folge. Die
Bulkladung
Q B =− 2 q Si N a S
berechnet sich aus den Größen der Elementarladung q = 1.6*10-19 C, der Permittivität von
Silizium εSi = 11.8*ε0, der Akzeptordotierungsdichte Na (meist ca. 1015 cm-3) und des
Oberflächenpotentials ΦS.
Die gesamte Ladung an der Oberfläche des Halbleiters QS stimmt während der Verarmung
mit der Bulk-Ladung überein
QS ≈ QB
Wenn man die Gatespannung solange erhöht, bis unter dem Gate keine freien
Majoritätsladungsträger mehr vorhanden sind, ist die Schwellspannung VTn erreicht. Jede
weitere Erhöhung der Gatespannung über VTn führt dazu, dass sich unter dem Gate freie
Elektronen, die aus dem Halbleiter angezogen werden ansammeln.
+VG<VTn
Metall
Gate
Polysilizium
M
O
QB
S
x
Inversions-Schicht
p-Typ, Na
Abb. 2.5: Inversion in der MOS Struktur
5 Diese sind aufgrund der Eigenleitfähigkeit im Halbleiter enthalten
Die Elektronen bilden eine Schicht unter dem Gate und tragen somit zu einer Erhöhung der
negativen Gesamtladung an der Oberfläche des Halbleiters auf
QS = QB + Qn
bei, wobei Qn die Ladungsträgerdichte der Elektronen unter dem Gate ist und sich zu
Q = C*V = Qn = -Cox (VGn - VTn) ergibt. Das Oberflächenpotential, welches bei erreichen
der Schwellspannung (bzw. Einsetzen der Inversion) vorhanden ist entspricht einem Wert
ΦS ≈ 2|ΦF| . Dabei beschreibt ΦF das sogenannte Fermi-Potential, es hat bei normalen
nMOS Transistoren und Raumtemperatur einen Wert von ca. 0.58V.
2.2.4 Rechnerische Bestimmung der Schwellspannung
Um nun die Schwellspannung VTn rechnerisch zu ermitteln, ist die Beobachtung hilfreich,
dass die Inversion bei Überschreiten von VTn gerade erst beginnt. Man kann also in einer
Näherung Qn ≈ 0 (da VG-VTn ≈ 0) setzen. Somit gilt QS ≈ QB und über die Beziehung
V = Q/C ergibt sich:
∣Q ∣  2 q Si N a 2∣ F∣
V ox = B =
C ox
C ox
für den Spannungsabfall über das Oxid. Der gesamte Spannungsabfall ergibt sich nach dem
Kirchhoffschen Spannungssatz aus der Addition aller Spannungswerte und da die
Spannung über den Halbleiter gegen Masse gemessen wird, entspricht sie dem
Oberflächenpotential bei Einsetzen der Inversion, also 2|ΦF |:
1
V ideal
 2 q Si N a 2∣ F∣
Tn =2∣ F∣
C ox
Diese Formel für die Schwellspannung lässt jedoch diverse in der Praxis auftretende
Effekte unberücksichtigt. So sind gewisse Unreinheiten in der Oxidschicht nicht zu
vermeiden. Diese Verunreinigungen und die Materialunterschiede zwischen Gate und
Halbleiter können die Schwellspannung beeinflussen. Um ihnen Rechnung zu tragen,
addiert man zur Schwellspannung eine sogenannte Flachbandspannung VFB hinzu. Leider
ist es jedoch oft der Fall, dass diese Effekte die Schwellspannung in den negativen Bereich
verschieben, betrieben werden soll ein nMOS jedoch mit einer positiven Gatespannung.
Um nun die Schwellspannung wieder in den positiven Bereich zu verschieben, implantiert
man eine Menge von DI Donator- oder Akzeptorionen pro Quadratzentimeter im Halbleiter
unter dem Gate. Im Fall des nMOS mit negativer Schwellspannung werden Akzeptorionen
implantiert6. Unter Berücksichtigung dieser beiden Modifikationen stellt sich die Formel
für die Schwellspannung wie folgt dar:
qD
1
V Tn=V FB 2∣ F∣
2 q Si N a 2∣ F∣± I

C ox
C ox
Für ein Akzeptorimplantat ist das positive Vorzeichen und für ein Donatorimplantat das
Negative zu wählen.
6 Dies ist hier äquivalent zu einer Erhöhung der Bulk Ladung, da diese ebenfalls aus Akzeptorionen besteht
2.3 Der Body Bias Effekt
VGSn-VTn
VS = 0
+VGSn
n+, Nd
QB
n+, Nd
p-Typ, Na
Abb. 2.6: nMOS Transistor mit Bulk-Ladung
Die Formel der Schwellspannung für die MOS Struktur lässt sich nicht eins zu eins auf den
Transistor übertragen, da sich im Transistor ein sogenannter Body Bias Effekt einstellt, der
den Wert der Schwellspannung verändert. Der Effekt besteht darin, dass die Spannung
zwischen Source und Bulk VSBn eine Spannung in Sperrrichtung für den entsprechenden
pn-Übergang darstellt. Dadurch bildet sich eine Sperrschicht um den Übergang, was die
Bulk Ladung QB erhöht. Mit dieser erhöhten Bulkladung, die von der Source Bulk
Spannung abhängt ergibt sich die Schwellspannung des Transistors zu
qD
1
V T ' n=V FB 2∣ F∣
2 q Si N a 2∣ F∣V SBn ± I

C ox
C ox
oder in anderer Schreibweise
1
V Tn=V T0n  2∣ F∣V SBn−  2∣ F∣ , =
 2 q Si N a
C ox
γ ist dabei der sogenannte Body Bias Koeffizient. Er beinhaltet alle wichtigen Größen über
die bei der Herstellung des Transistors die Schwellspannung beeinflusst werden kann: Cox
ist beeinflussbar durch Variation der Dicke und des Materials des Isolators und Na ist als
Dotierungsdichte ebenfalls variabel. VT0n ist die Schwellspannung der MOS Struktur (bzw.
die Schwellspannung des Kondensators bei einer Source Bulk Spannung von 0V).
Für normale nMOS-Anreicherungs-Transistoren liegt die Schwellspannung zwischen 0.5V
und 0.9V. Die folgende Grafik verdeutlicht den Body Bias Effekt, indem die
Schwellspannung gegen das Potentialgefälle zwischen Source und Bulk aufgetragen ist.
VTn
VT0n
VSBn
0
Abb. 2.7: Schwellspannung in Abhängigkeit der Source Bulk Spannung
2.4 Strom-Spannung-Charakteristiken
2.4.1 Verarmung und Inversion im nMOS Transistor
Nachdem geklärt wurde, dass der Transistor über die Gatespannung gesteuert wird und hier
die Schwellspannung eine wichtige Rolle spielt, wird nun der eigentliche Stromfluß durch
den Transistor in Abhängigkeit der Gatespannung thematisiert.
Solange die Gate-Source-Spannung unterhalb der Schwellspannung liegt, besteht die
Ladungsschicht unter dem Gate nur aus ortsfesten Akzeptorionen und einer der beiden pnÜbergänge ist immer gesperrt, was einen Stromfluß durch den Transistor unmöglich
macht: IDn ≈ 0.
VGSn-VTn
VS = 0
+VGSn
n+, Nd
q-
E
Qn
IDn
n+, Nd
QB
p-Typ, Na
Abb. 2.8: nMOS mit Verarmungs- und Inversionsschicht
Sobald die Schwellspannung überschritten wird, kann ein Strom durch den Transistor
fließen. Unter dem Gate entsteht eine Elektronen-Inversionsschicht. Wenn nun noch eine
Spannung zwischen Drain und Source anliegt, wird der Transistor leitend und es kann ein
sogenannter Drainstrom IDn von Drain zu Source fließen. Dieser Strom wird deshalb
möglich, da die Inversionsschicht – auch Kanal genannt - aus Elektronen besteht und diese
genau die Majoritätsladungsträger der angrenzenden n-dotierten Zonen sind.
Die Ladung dieser Schicht lässt sich – ähnlich wie bei der MOS Struktur - über die
folgende Formel ermitteln:
Q n =−C ox [V GSn −V Tn −V  y]
V(y) ist dabei die Spannung an einer Stelle y des Kanals. y nimmt Werte von 0 bis L an. Es
gilt: V(0) = VS = 0V, V(L) = VDSn.
Wie in der Grafik zu erkennbar, ist die Inversionssicht am Source-Anschluss dicker, als am
Drain-Anschluss. Diese Kanalschräge ergibt sich, aufgrund der Potentialunterschiede GateSource bzw. Gate-Drain. So wird der Potentialunterschied von Drain und Source mit
steigender Spannung VGSn geringer, was zu einer Abschwächung des elektrischen Feldes
beim Drain führt. Durch ein schwächeres Feld, fällt auch der Feldeffekt schwächer aus und
die Inversionsschicht verliert an Dicke.
2.4.2 Ermittlung der Stromstärke
0
dy
y
L
Source
Drain
V(0)
W
n+, Nd
V(L)
n+, Nd
p-Typ, Na
Abb. 2.9: 3-dimensionale Sicht des Kanals im nMOS
Um nun einen Wert für die Stromstärke IDn des durch den Transistor fließenden Strom zu
ermitteln, macht man den Ansatz zuerst einen Teil des Kanals gesondert zu betrachten.
Über den Widerstand kommt man zu folgender Formel für den Stromfluß durch das
entsprechende Kanalstück:
I Dn dy=n C ox W [V GSn −V Tn −V  y] dV
Für den gesamten Kanal – und somit den Transistor – ergibt sich der Strom IDn also, indem
man über die Kanallänge integriert:
V DSn
W
I Dn =k ' n   ∫ [V GSn−V Tn−V  y] dV
L V =0
Hier ergeben sich zwei neue wichtige Werte. Der Leitwertparameter k'n = μnCox beinhaltet
alle die Größen, die die Leitfähigkeit bestimmen: μn bestimmt als Beweglichkeit der
Elektronen maßgeblich die Leitfähigkeit, εox und 1/xox haben Einfluss auf den Feldeffekt
und somit die Elektronenkonzentration im Kanal.
Der Verstärkungsfaktor βn = k'n(W/L) fasst alle wichtigen Größen zusammen, die man bei
der Produktion beeinflussen kann, um den Strom durch den Transistor zu erhöhen.
2.4.3 Gesättigter und ungesättigter Stromfluss
Der Stromfluß, der direkt nach Überschreiten der Schwellspannung einsetzt, wird
Ungesättigter Stromfluss genannt. Wenn man das Integral aus der vorigen Gleichung
ausrechnet, ergibt sich folgende Formel für den ungesättigten Stromfluß durch einen
nMOS Transistor:

W
1
I Dn =k ' n  [V GSn−V Tn V DSn− V 2DSn ]= n [2V GSn−V Tn V DSn −V 2DSn ]
L
2
2
Mit einem Anstieg der Drain-Source Spannung VDSn ist hier also stets ein Anstieg des
Stroms IDn verbunden. Bildet man die partielle Ableitung des Stroms nach der DrainSource Spannung und setzt diese gleich Null, so erhält man die folgende Beziehung:
n
[V GSn−V Tn −V DSn ]=0
2
Wenn nun also VDSn = VGSn – VTn ist, hat die Drain Source Spannung einen Wert erreicht,
bei dem ein weiterer Spannungszuwachs keinen Zuwachs des Drainstroms mehr
verursacht. Physikalisch zu erklären ist dieses Phänomen dadurch, dass zwischen Gate und
Drain kein Potentialunterschied mehr vorhanden ist und das Feld an dieser Stelle
vollständig verschwindet. Entsprechend halten sich auch keine Elektronen mehr am Drain
auf, der Kanal ist vollkommen abgeschürt.
VGSn-VTn
VS = 0
+VGSn
n+, Nd
q-
pinch off
IDn
n+, Nd
QB
p-Typ, Na
Abb. 2.10: Kanalabschnürung beim nMOS Transistor
Ab diesem Spannungswert VDSn = Vsat = VGSn – VTn spricht man von einem gesättigten
Stromfluß. Die Formel für diesen ergibt sich, indem man die Beziehung VDSn = Vsat in die
Formel für den ungesättigten Stromfluß einsetzt:


2
2
I Dn= n [2V GSn−V Tn V sat −V sat ]= n V GSn −V Tn 
2
2
Da eine weitere Erhöhung der Spannung VDSn eine weitere Verkürzung des Kanals mit sich
bringt und diese dem Widerstand des Kanals verringert, ist in der Praxis ein leichtes
Ansteigen des Drainstroms bei weiter steigender Spannung zu beobachten:

I Dn = n V GSn−V Tn 2 [1V DSn−V sat ]
2
λ ist der Kanallängenparameter und dient dazu den Drainstrom entsprechend eines
kürzeren Kanals in der Formel zu erhöhen.
In folgender Grafik ist der Wert des Drainstorms im gesättigten und ungesättigten Bereich
aufgetragen.
IDn
VGSn
0
VDSn
Abb. 2.11: Drainstrom in Abhängigkeit von der Gate Source Spannung
Wie zu erkennen ist, fällt die Erhöhung der Stromstärke im gesättigten Bereich nur sehr
gering aus, weshalb es durchaus vertretbar ist in einer Näherung den Drainstrom im
gesättigten Bereich als konstant anzusehen (also λ = 0).
2.5 Aufbau und Funktionsweise eines pMOS Transistors
Der pMOS ähnelt vom Aufbau her dem nMOS, es gibt jedoch einige Unterschiede. Erstens
sind die Drain und Source Anschlüsse nun p-dotiert und zweitens ist eine n-Wanne in das
Substrat eingedampft, um die benötigten pn-Übergänge zu ermöglichen. Aus dem
Abschnitt über pn-Übergänge ist herzuleiten, dass die Wanne für eine korrekte Funktion
der Übergänge an die größte positive Spannung des Schaltkreises angeschlossen sein sollte.
Um eine Leitfähigkeit des Transistors herzustellen muss auch hier ein Kanal aus
Majoritätsladungsträgern der diesmal p-dotierten Anschlussbereiche erzeugt werden (also
aus Löchern). Die dazu benötigte Gatespannung muss also negativ sein. Ein weiterer
Unterschied ist, dass der Strom durch den Transistor von Source zu Drain fließt.
Da die Herleitung der Formeln für Schwellspannung und Stromfluß analog zum nMOS
durchgeführt werden kann, sind diese hier nur in Form einer Übersicht gegeben:
Schwellspannung ohne Bias Effekt:
V T0p=V FB , p 2∣ F , p∣
Schwellspannung:
Ungesättigter Strom:
1
 2 q Si N d 2∣ F , p∣0
C ox
V Tp =V T0p  p   2∣ F , p∣V SBp−  2∣ F , p∣
I Dp=
p
2
[2V SGp −∣V Tp∣V SDp −V SDp ]
2
Gesättigter Strom:
I Dp =
p
V SGp −∣V Tp∣[1V SDp −V sat ]
2
Da der Kanal aus Löchern besteht und diese eine geringe Beweglichkeit als Elektronen
aufweisen, fällt der Leitwertparameter hier entsprechend kleiner aus. Tatsächlich gilt
k'p ≈ 2.5 k'n. Will man also diese verminderte Leitfähigkeit ausgleichen, so kann man dies
über eine Variation des Seitenverhältnisses (W/L) erreichen. Dies ist der Grund dafür, dass
pMOS Transistoren oft ein wenig größer sind als nMOS Transistoren.
2.6 Schaltsymbole der Transistoren
Zuletzt sei noch eine Übersicht über die in Schaltkreisen verwendeten Transistorsymbole
und deren Bedeutung gegeben. Für CMOS Schaltungen werden die p- und n-MOSFETs als
Anreicherungstypen (selbstsperrend) benötigt:
E-Mode nMOS:
G
VGSn
-
+
IDn
+ VSBn
S
-
D
B
- VDSn +
E-Mode pMOS:
G
VSGp
-
+
IDp
D
+
B
VBSp -
- VSDp +
S
Quellenverzeichnis:
Viele der Grafiken dieses Textes orientieren sich an Grafiken aus den hier genannten
Quellen, sind jedoch selbst neu erstellt worden und beinhalten einige Abänderungen.
John P. Uyemura
CMOS Logic Circuit Design
Kluwer 1999
B. Van Zeghbroeck
Principles of Semiconductor Devices
http://ece-www.colorado.edu/~bart/book/
University of Colorado 2004
Vishwa Shanth, R. Kasula Sirnivas
Modelling Semiconductor Devices using the VHDL-AMS Language
http://www.ececs.uc.edu/~dpl/vishwa_thesis/
Tutorium – Funktionsweise des MOS Transistors
Transistortutorium an der Universität Oldenburg
http://olli.informatik.uni-oldenburg.de/weTEiS/weteis/tutorium.htm
Holger Göbel
Einführung in die Halbleiter-Schaltungstechnik
http://smile.unibw-hamburg.de/smile/toc.htm
Springer Verlag, Berlin, 2005
Nachschlagewerk / Enzyklopädie Wikipedia
http://www.wikipedia.org