Potenzfunktionenn

Potenzfunktionen
Theorie
Eine Funktion der Gestalt
f : y = xk
mit k ∈ Z
heisst Potenzfunktion mit ganzzahligem Exponenten.
k<0
k>0
y
y=
y
x4
y=x
y = x2
y = x−2
y = x−4
x
y = x−3
y = x3
x
y = x−1
Falls k ungerade:
Falls k ungerade:
• D=R
• D = R \ {0}
• W=R
• W = R \ {0}
• Graph symmetrisch zum Ursprung
• Graph symmetrisch zum Ursprung
• Punkte: (−1|−1), (0|0), (1|1)
• Punkte: (−1|−1), (1|1)
Falls k gerade:
Falls k gerade:
• D=R
• D=R
• W = R+
0 = [0, ∞[
• W = R+ = ]0, ∞[
• Graph symmetrisch zur y-Achse
• Graph symmetrisch zur y-Achse
• Punkte: (−1|1), (0|0), (1|1)
• Punkte: (−1|1) (1|1)
Eine Funktion der Gestalt
f : y = an xn + an−1 xn−1 + · · · + a2 x2 + a1 x + a0
wird ganzrationale Funktion oder Polynomfunktion genannt. Die reellen Zahlen a0 , a1 ,
. . . , an sind die Koeffizienten des Polynoms. Der grösste Exponent n ∈ N heisst Grad des
Polynoms. Ein einzelner Summmand ai xi (i ∈ {0, 1, . . . , n}) ist ein Monom.
Eine Polynomfunktion vom Grad n kann nicht mehr als n reelle Nullstellen besitzen.
Ist der Grad einer Polynomfunktion ungerade, so besitzt die Polynomfunktion mindestens
eine relle Nullstelle.
Ist der Grad einer Polynomfunktion gerade, braucht es keine rellen Nullstellen zu geben.
Ganzrationale Funktionen
Übungsaufgaben
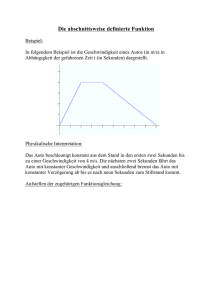
1. Bestimme die Gleichung der Potenzfunktion, die zum Graphen gehört
y
y
y
1
2 8
x
−2 41
2 41
x
x
− 12 −8
2. Bestimme den Grad der Polynomfunkion
√
(a) f : y = x5 − 3x7 + 3x2 + 3
(b) g : y = (x − 3)6
(c) p : y = (x + 4)(x − 2) x2 + 1
3. Bestimme die reellen Nullstellen und den Ordinatenabschnitt der Polynomfunktionen – falls nötig verwende den Taschenrechner
(a) f : x 7→ x4 − 3x3 − 3x2 + 7x + 6
(b) g : x 7→ x6 + 7x4 + 14x2 + 8
(c) h : x 7→ 2(x − 3)(x − 1)(x − 4)
4. Bestimme die minimal und maximal mögliche Anzahl der Nullstellen
(a) f (x) = x7 − 3x2 + 2x − 1
(b) g(x) = x4 + 1
(c) h(x) = (x3 + x − 5) · (x5 + 3x4 − 5x2 )
Ganzrationale Funktionen
1.
• y = x3
Lösungen zu den Übungsaufgaben
• y = x−2 =
1
x2
• y = x−3 =
1
x3
2. (a) f hat den Grad 7
(b) g hat den Grad 6
(c) p hat den Grad 4
3. (a) Nullstellen: x1 = x2 = −1, x3 = 2, x4 = 3; Ordinatenabschnitt: y0 = 6
(b) keine reellen Nullstellen; Ordinatenabschnitt: y0 = 8
(c) Nullstellen: x1 = 3, x2 = 1, x3 = 4; Ordinatenabschnitt: y0 = −24
4. (a) maximal 7 Nullstellen; minimal 1 Nullstelle
(b) maximal 4 Nullstellen; minimal 0 Nullstelle
(c) maximal 8 Nullstellen; minimal 0 Nullstelle