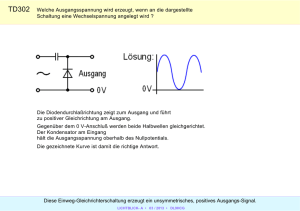
Formelsammlung Leistungselektronik - Flo
Werbung
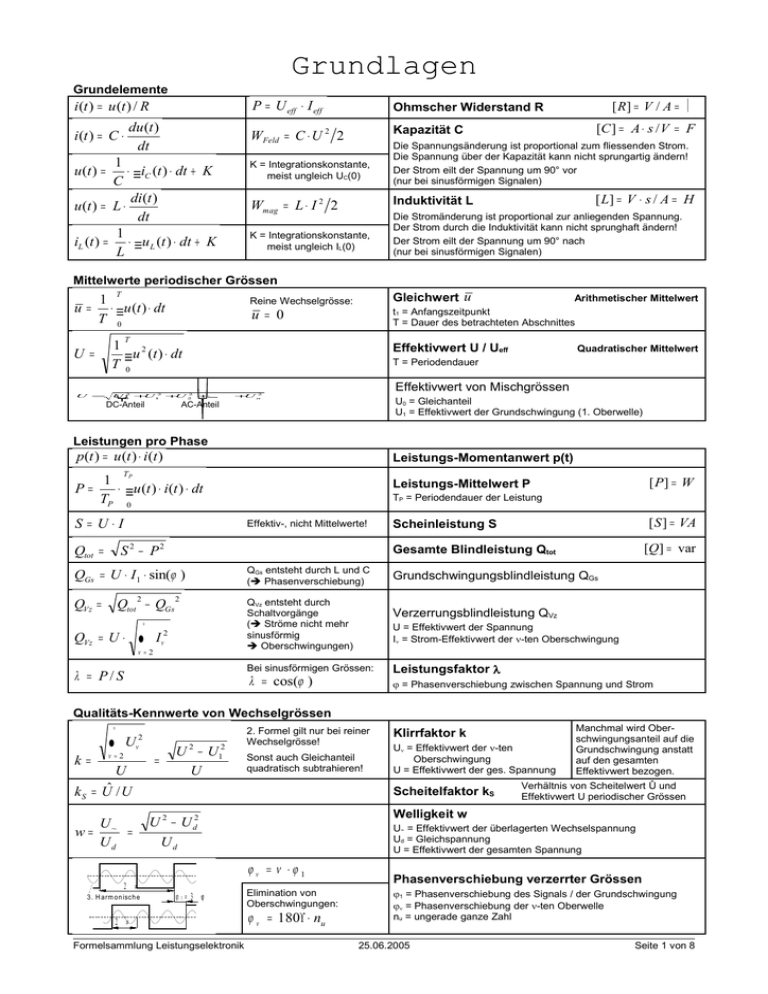
Grundlagen Grundelemente i (t ) = u (t ) / R du (t ) dt i (t ) = C ⋅ 1 ⋅ iC (t ) ⋅ dt + K C ∫ di (t ) u (t ) = L ⋅ dt 1 iL (t ) = ⋅ ∫ u L (t ) ⋅ dt + K L P = U eff ⋅ I eff Ohmscher Widerstand R WFeld = C ⋅ U 2 2 Kapazität C K = Integrationskonstante, meist ungleich UC(0) u (t ) = [C ] = A ⋅ s / V = F Die Spannungsänderung ist proportional zum fliessenden Strom. Die Spannung über der Kapazität kann nicht sprungartig ändern! Der Strom eilt der Spannung um 90° vor (nur bei sinusförmigen Signalen) [ L] = V ⋅ s / A = H Induktivität L Wmag = L ⋅ I 2 2 K = Integrationskonstante, meist ungleich IL(0) [ R] = V / A = Ω Die Stromänderung ist proportional zur anliegenden Spannung. Der Strom durch die Induktivität kann nicht sprunghaft ändern! Der Strom eilt der Spannung um 90° nach (nur bei sinusförmigen Signalen) Mittelwerte periodischer Grössen T 1 u = ⋅ ∫ u (t ) ⋅ dt T 0 Gleichwert u Arithmetischer Mittelwert t1 = Anfangszeitpunkt T = Dauer des betrachteten Abschnittes Reine Wechselgrösse: u= 0 T 1 2 u (t ) ⋅ dt T ∫0 U= U = 2 2 U0 + U12 + U2 + ....... DC-Anteil Effektivwert U / Ueff Quadratischer Mittelwert T = Periodendauer Effektivwert von Mischgrössen 2 + Un U0 = Gleichanteil U1 = Effektivwert der Grundschwingung (1. Oberwelle) AC-Anteil Leistungen pro Phase p (t ) = u (t ) ⋅ i (t ) P= Leistungs-Momentanwert p(t) TP 1 ⋅ u (t ) ⋅ i(t ) ⋅ dt TP ∫0 S= U⋅I Qtot = TP = Periodendauer der Leistung Effektiv-, nicht Mittelwerte! S 2 − P2 2 Qtot − QGs ∞ ∑ QVz = U ⋅ ν =2 [ S ] = VA Scheinleistung S [Q] = var Gesamte Blindleistung Qtot QGs = U ⋅ I1 ⋅ sin(ϕ ) QVz = [ P] = W Leistungs-Mittelwert P 2 Iν2 QGs entsteht durch L und C ( Phasenverschiebung) QVz entsteht durch Schaltvorgänge ( Ströme nicht mehr sinusförmig Oberschwingungen) Verzerrungsblindleistung QVz U = Effektivwert der Spannung Iν = Strom-Effektivwert der ν-ten Oberschwingung Bei sinusförmigen Grössen: λ = P/S Grundschwingungsblindleistung QGs λ = cos(ϕ ) Leistungsfaktor λ ϕ = Phasenverschiebung zwischen Spannung und Strom Qualitäts-Kennwerte von Wechselgrössen ∞ k= ∑ 2 ν U ν =2 U ˆ kS = U / U U w= ~ = Ud 2 π 3. H arm onisch e = U 2 − U12 U 2. Formel gilt nur bei reiner Wechselgrösse! Sonst auch Gleichanteil quadratisch subtrahieren! Klirrfaktor k Uν = Effektivwert der ν-ten Oberschwingung U = Effektivwert der ges. Spannung Scheitelfaktor kS U~ = Effektivwert der überlagerten Wechselspannung Ud = Gleichspannung U = Effektivwert der gesamten Spannung ϕν = ν ⋅ϕ1 2 π Formelsammlung Leistungselektronik Verhältnis von Scheitelwert Û und Effektivwert U periodischer Grössen Welligkeit w U 2 − U d2 Ud ϕ3= 3 ϕ Manchmal wird Oberschwingungsanteil auf die Grundschwingung anstatt auf den gesamten Effektivwert bezogen. Elimination von Oberschwingungen: ϕ ν = 180° ⋅ nu Phasenverschiebung verzerrter Grössen ϕ1 = Phasenverschiebung des Signals / der Grundschwingung ϕν = Phasenverschiebung der ν-ten Oberwelle nu = ungerade ganze Zahl 25.06.2005 Seite 1 von 8 Fourierreihe a0 + 2 x(t ) = ∞ ∑ n= 1 an ⋅ cos(n ⋅ ω T ⋅ t ) + ∞ ∑ n= 1 bn ⋅ sin( n ⋅ ω T ⋅ t ) T /2 an = 2 ⋅ x(t ) ⋅ cos( n ⋅ ω T ⋅ t ) ⋅ dt T − T∫ / 2 T /2 2 ⋅ x (t ) ⋅ sin( n ⋅ ω T ⋅ t ) ⋅ dt T − T∫ / 2 bn = Winkel und Zeit nicht verwechseln! x = ω ⋅t ω T = 2⋅ π T Fourierreihen-Darstellung Fourier-Koeffizienten • gerade Funktionen ( x(-t) = x(t); symmetrisch zur y-Achse): nur an-Glieder (Kosinus), alle bn = 0 ungerade Funktionen ( x(-t) = -x(t); symm. zum Ursprung): Nur bn-Glieder, (Sinus), alle an = 0 • Transformator Ersatzschaltbild (einphasig) U2' = umgerechnete Sekundärspannung R1 = primärer Wicklungswiderstand (Kupferverluste) Xσ1 = primäre Streuinduktivität RFe = Ersatzwiderstand für Eisenverluste (Ummagnetisierung) X1m = Hauptreaktanz Ui = induzierte Spannung (Sekundär-Leerlaufspannung) I10 = Leerlaufstrom umgerechnete Sekundärseite Primärseite σ σ Übersetzung ü ü= RFe und X1m werden häufig vernachlässigt. Vereinfachtes Ersatzschaltbild (dreiphasig, Y) Primärseite umgerechnete Sekundärseite σ dreiphasig σ εK = RFe und X1m vernachlässigt, R1 und R2' zu R1c sowie Xσ1 und Xσ2' zu Xσ1c zusammengefasst. σ U Ph ( Ks ) ⋅ 100% U Ph Nenn εR U R1c = ⋅ 100% = ε K ⋅ cos(ϕ K ) U Ph Nenn ε = X U Xσ 1c ⋅ 100% = ε K ⋅ sin(ϕ K ) U Ph Nenn Kurzschluss-Sp.: Nötige PhasenSpannung, damit am kurzgeschlossenen Ausgang Nennstrom fliesst. Primär- und sekundärseitig tritt gleichzeitig Nennstrom auf. U1 I 2 = U 2 I1 U2 '= U2 ⋅ ü I2 '= I2 / ü Xσ 2 '= Xσ 2 ⋅ ü2 S Ph I Nenn = U Ph Nenn Z1 c = U Ph ( Ks ) I Nenn U1 = Primärspannung = U2' (im Leerlauf) I2 = Sekundärstrom = I1'(im Leerlauf) Ströme / Spannungen werden mit ü, Impedanzen mit ü2 auf die andere Trafoseite umgerechnet. Umrechnungen gelten nur im Leerlauf. SPh = Scheinleistung pro Phase UPh Nenn = Nenn-Phasenspannung UPh (Ks) = Phasenspannung bei Nennstrom im Kurzschlussbetrieb Z1c = Kombinierte Impedanz des Trafos U1 verk = verkettete Primärspannung = √3UPh Kurzschlussspannung UPh (KS) εK = relative Kurzschlussspannung in % εR = ohmscher Anteil der Kurschlussspannung εX = induktiver Anteil der Kurschlussspannung ϕK = Verschiebung zwischen Phasenspannung und Leiterstrom der entsprechenden Phase im Kurschluss Die Absolutwerte der Kurzschlussspannungen sind für Primär- und Sekundärseite verschieden, die relativen Werte jedoch identisch. Diode rd = ∆ u AK ∆ i AK = 1 Kurvensteigung u f = U T0 + rd ⋅ id p = u f ⋅ id P= U T0 T T 0 iA K Durchgangsspannung uf (t) = U T0 ⋅ id + rd ⋅ id ⋅ ∫ id ⋅ dt + Differentieller Widerstand rd T P = U T0 ⋅ I d mittel + rd ⋅ I d2eff Verlustleistung p(t) / P UT0 = Schleusenspannung (konstant) Id mittel = Mittelwert des Diodenstromes Id eff = Effektivwert des Diodenstromes Thyristor • • K ∆ id uA K 2 rd ⋅ id2 ⋅ dt T ∫0 A Sperrt solange in Vorwärtsrichtung, bis er durch einen Steuerimpuls am Gate gezündet wird Lässt sich nicht über das Gate ausschalten, sondern leitet solange, bis ein minimaler Haltestrom unterschritten wird id ∆ D u rc h b ru c h spannun g D u rc h b ruch uf iA K uA K uA K UT ( S c h l e u s e n s p a n n u n g ) 0 S p e r r -D u r c h l a s s b e r e i c h Abschaltbare Elemente • • • Lassen sich über die Steueranschlüsse ein- und ausschalten. Ventilwirkung gleich wie bei Diode Beispiele: GTO, Leistungstransistoren, MOSFET, JGBT, JGCT Verluste am Schalter Gesamtverluste = Schaltverluste + Durchlassverluste + Sperr- und Blockierverluste + Steuerleistung Formelsammlung Leistungselektronik 25.06.2005 Seite 2 von 8 Netzgeführte Stromrichter Grundlagen Gleichrichter-Betrieb 0° < α < 90° Wechselrichter-Betrieb 90° < α < 180° abgegebene GleichstromLeistung bei idealer Glättung: Energie: ~ Netz → = Netz Ud negativ; id positiv Energie: = Netz → ~ Netz Bei rein ohmscher Belastung: P = I d eff ⋅ U d eff P = I d ⋅ U diα Bei rein ohmscher Belastung: S = m ⋅ U Netzeff ⋅ I Netzeff U d eff S = m ⋅ U Netz eff ⋅ Die Scheinleistung wird vor dem Stromrichter gemessen! U diα = U dio ⋅ cos( α Mittelwert der Gleichspannung: Pd = U diα ⋅ I d Bei idealer Glättung: T 1 P P= ⋅ ud ⋅ id ⋅ dt TP ∫0 Ud und id positiv R ) Betriebsarten Wirkleistung P Id eff = Effektivwert des Stromes auf der Gleichspannungsseite Id = Mittelwert des Stromes auf der Gleichspannungsseite Ud eff = Effektivwert der Spannung auf der Gleichspannungsseite Udiα = Mittelwert der Spannung auf der Gleichspannungsseite Scheinleistung S m = Phasenzahl (meist 1 oder 3) INetz eff = Effektivwert des Stromes in einer Netzphase UNetz eff = Effektivwert der Netz-Phasenspannung (meist 230V) Einphasen – Brückenschaltung B2 v1 + v4 leitend 180° v2 + v3 leitend ud(t) induktive Last α α α -Nullpunkt α-Nullpunkt bei Nulldurchgang der Netzspannung U⋅ √ 2 rein ohmsche Last Udio= Idealer Gleichspannungs-Mittelwert (Spannungsabfälle vernachlässigt) bei Steuerwinkel α = 0 Udiα = dito, beim aktuellen Steuerwinkel α Id = zeitlich konstanter Gleichstrom iN(t) = zeitlicher Verlauf des Netzstromes V1 iN U1 V2 V3 id ud / Ud αi V4 ud1 V1 V3 V5 id V2 V4 V6 iL 2 U ud2 Ud αi / ud = ud1 - ud2 Die Ausgangsspannung ist 2-pulsig! 2⋅ 2 ⋅ cos( α ) π 2 U diα = U ⋅ ⋅ (1 + cos( α π Û ⋅ sin ( α ) ≥ U dio ⋅ cos( α = U dio ⋅ cos( α U diα = U ⋅ Mittelwert Udiα der Gleichspannung ) bei nicht-lückendem Betrieb (z.B. Induktivität in der Last) U dio ⋅ (1 + cos( α ) ) 2 → α min = 32.48° )) Verhältnisse bei rein ohmscher Last = ) Lückbetrieb Einschalt-Minimalwinkel bei geglättetem Laststrom Dreiphasen – Brückenschaltung B6 ud1 V1 V3 V5 U ud2 V2 V4 ud = zeitlicher Verlauf der Ausgangsspannung ud1 = positive Spannung, gebildet von v1, v3, v5 ud2 = negative Spannung, gebildet von v2, v4, v6 Die Ausgangsspannung ist 6-pulsig! Udiα / ud = ud1 - ud2 iL2 Zusammensetzung der Gleichspannung u d = u d 1 − ud 2 id 3⋅ 6 ⋅ U ⋅ cos( α π = 3⋅ 6 ⋅ U / π U diα = V6 U di 0 Phasenspannungen ) = U di 0 ⋅ cos( α Verkettete Spannungen beiα =0° V erlauf der Ausgangsspannung d bei uα =20° uL 1 uL1 Ud iα uL 2 uL3 U⋅ √6 V erkettete Spannung Ud iα ud 1 ud 2 60° U⋅ √2 60° 30° α Mittelwert Udiα der Gleich-Spannung bei nicht-lückendem Betrieb V erlauf der A usgangsspannung d u bei α =0° Verlauf der A usgangsspannung d u ) U⋅ √6 Udiα uL3 ud2 30° α α 60° α -N ullpunkt uL2 Verlauf der Ausgangsspannung d beiα u=20° U⋅ √6 Verkettete S pannung U⋅ √2 60° 60° Udiα U⋅ √6 α 60° α -Nullpunkt Phasenspannung α -Nullpunkt Phasenspannung α -N ullpunkt α-Nullpunkt 30° nach dem Nulldurchgang der Phasenspannung oder 60° nach dem Nulldurchgang der verketteten Spannung Û ⋅ sin ( α ) ≥ U dio ⋅ cos( α + 60° ) Formelsammlung Leistungselektronik → α min = 10.08° Einschalt-Minimalwinkel 25.06.2005 bei geglättetem Laststrom Seite 3 von 8 Eigenschaften der netzgeführten Schaltungen Einphasen – Brückenschaltung bei nicht-lückendem Betrieb Ausgangsspannung Udiα U diα = U dio ⋅ cos( α 2⋅ 2 ⋅U π U dio = ) Einschalt-Minimalwinkel αmin α bei geglättetem Laststrom Spannungsabfälle • An zwei in Serie geschalteten Halbleiterelementen: • An ohmscher Komponente der Quellenimpedanz: • An Quellenreaktanz (bedingt durch Kommutierung) Kommutierungsreaktanz U iN RN XK min DX min = 10.08° DR = I d ⋅ RN DR = I d ⋅ 2 ⋅ R N 2 ⋅ X K ⋅ Id π 3⋅ X K ⋅ Id π DX = An Klemmen gemessene Gleichspannung Udiα U diα = U dio ⋅ cos( α ) − 2 ⋅ U F − DR − DX Udi α DR α = 32.48° = 2.339 ⋅ U 2 ⋅ U F ≈ 2 − 3V id uf 3⋅ 6 ⋅U π U dio = = 0.9003 ⋅ U 2 ⋅ U F ≈ 2 − 3V DX = X k = ω ⋅ LK Dreiphasen – Brückenschaltung UF = Spannungsabfall an der Diode Dx = Spannungsabfall an der induktiven Quellenreaktanz DR = Spannungsabfall am ohmschen Quellenwiderstand uf Lückbetrieb Gründe für Lückbetrieb Änderungen bei Lückbetrieb • • • • • • rein ohmsche Last zu kleine Induktivität im Gleichstromkreis Gegenspannung im Gleichstromkreis Verlauf der Steuerkennlinie Zeitlicher Verlauf der Klemmenspannung auf DC-Seite Beanspruchung der Halbleiterelemente Rückwirkungen auf das Netz Einphasen – Brückenschaltung Dreiphasen – Brückenschaltung Strombelastung der Netzleiter π bei idealer Glättung von id 180 ° α Id = Gleichstrom-Mittelwert auf der Gleichspannungsseite Die Grundschwingung des Stromes eilt der Netzspannung um α nach Τ = 2 π Ι eff = √ ( 2 / 3 ⋅) Ι d π 180° Τ = 2 π = ω ⋅t α I eff = 2 π /3 π /3 120° 60° Ι eff = √ ( 2 / 3 )⋅ Ι d x α Τ = 2π = ω ⋅t 2 3 ⋅ Id 6 ⋅ Id π ν = ( k ⋅ p ± 1) I L (1) = ν = 5, 7, 11, 13... I L1 ν Zν = ∆ U1+Σ Uν I L (ν ) = I L1 ν RN2 + (ω ν ⋅ LN ) 2 ≈ ω ν ⋅ LN ων = Kreisfrequenz der Oberschwingung ∆ U1-Σ Uν OberschwingungsGenerator Formelsammlung Leistungselektronik Ιd = ω ⋅t Impedanz Zν der Oberschwingung ν I1+Σ Iν andere Verbraucher Ι eff = Ι d Τ = 2π ν = 1, 3, 5, 7, 9... I L (ν ) = Ιd x 2 ⋅ 2 ⋅ Id π ν = ( k ⋅ p ± 1) Effektivwert einer Oberschwingung nur Grundschwingung! 2 π /3 π /3 12 0° 6 0° x α I L (1) = Ordnungszahlen (für Spektrum) u(t) = Û ⋅ sin( ω ⋅ t) Ιd = ω ⋅t I eff = I d Grundschwingungseffektivwerte LN Ι eff = Ι d x Gesamter Effektivwert RN Ιd Oberschwingungsspannung Uν bei idealer Glättung des Gleichstromes (RN vernachlässigt) Uν ( Z ) = Iν ⋅ Zν 25.06.2005 ≈ Iν ⋅ ω ν ⋅ LN (pro Phase) Seite 4 von 8 Gleichstromsteller (Chopper) Nichtlückender Betrieb Chopper Q uelle iq RQ U1 iq U d1 LQ S tr o m d urch S Str o m d u r c h DF TEin TAus DF ic iF RL U d2 Mittelwert Ud2 der Ausgangsspannung UG u d2(t) T Aus T Ud 2 U d1 DF + S DF le ite n d g e s p e rr t S le i te n d U d2 Tastverhältnis β LL T Ein U d1 TEin = β ⋅ T Las t i2 S CP ∆ uc UG i d2=0 T U ⋅T = d 1 Ein T = U d1 ⋅ β T = Periodendauer TEin = Zeit, während der S eingeschaltet ist TAus = Zeit, während der S ausgeschaltet ist Lückbetrieb Chopper Quelle iq RQ iq U1 Ud1 LQ Str o m d u rc h S S tr o m d u rc h DF TEin TAu s Last i2 S CP ∆ uc DF ic iF Ud1 Ud2 RL Ud2 Zeitlicher Verlauf der Ausgangsspannung ist lastabhängig! Mittelwert der Ausgangsspannung steigt bei Lückbetrieb LL UG TEin ud2 (t) TAus S le ite n d DF le ite n d T DF + S g esp errt Ud1 Chopper-Ausgangsspannung u2(t) (Bezeichnungen siehe folgende Skizze) UG id2 =0 T Abwärtssteller • Ausgangsspannung ist tiefer als Quellenspannung • Pufferkondensator Cp, um Eingangsspannung zu stützen • Kein Rückwärtsbetrieb möglich U1 = Quellenspannung RQ = Ohmscher Innenwiderstand der Quelle ∆uc = Welligkeit der Eingangsspannung ud1(t) S = Leistungsschalter, z.B. GTO Cp = Pufferkondensator DF = Freilaufdiode LG = Glättungsinduktivität im Lastkreis UG = Gegenspannung im Lastkreis Chopper Rq i1 iF i2 DF S ∆ uc Lq U1 (< Ud2) ic i1 iF LG UG Leistungsbilanz T ud2 : PQuelle = PLast I2 k o n s t a n t G, w→ e i l L βT ⋅ F r e i la u f s t r o m ∞ R e a l itä t U1 ⋅ I q = I 2 ⋅ U d 2 ∆ i2 Iq = β ⋅ I2 U d 2 = β ⋅ U1 ( 1β -)⋅ T I2 iF : Q u e lle n s tr o m Ud2 ic LQ S c h a lte r s t r o m RG DF ∆ uc Ud1 L a s ts p a n n u n g Last i2 S CP U1 i1 : U2 Chopper iq RQ i2 : L2 Ud2 is Quelle L a s t s tr o m R2 CP K o n d e n s a to rs tro m | I2- Iq| ic : S p a n n u n g s w e l lig k e i t ∆ uc : Ohmscher Quellenwiderstand RQ wird vernachlässigt U1 = Quellenspannung Ud1 = Mittelwert der Chopper-Eingangsspannung Ud2 = Mittelwert der Chopper-Ausgangsspannung β = Tastverhältnis Iq = Quellenstrom I2 = Laststrom ∆i2 = Welligkeit des Laststromes I2 Iq M it t e lw e r t d e s S c h2a lt e r s t ro m e s I iq : • Cp = I 2 nenn 4 ⋅ f ⋅ ∆ uc max LG = U1 4 ⋅ f ⋅ ∆ i2 max Pufferkondensator Cp [C ] = F uc max = maximale Spannungsschwankung am Kondensator (tritt bei β = 0.5 auf) f = 1/T = Schaltfrequenz von S | Iq| ∆ uc M a x im a le K o n d e n s a to r B e l a s tu nβ g = b 0e.i5 Glättungsinduktivität LG [ L] = H Aufwärtssteller Quelle Rq i1 Chopper iF U1 (< Ud2) i2 DF S CP ∆ uc Lq is Last Ud2 ic Formelsammlung Leistungselektronik • R2 L2 U2 • • Für Energieübertragung aus einer Gleichspannungsquelle mit tiefer Spannung in ein Gleichspannungsnetz mit höherer Spannung Anwendung z.B. Rückgewinnung Bremsenergie von Gleichstrommaschinen Abhängen der Last im Betrieb hat fatale Folgen: Strom steigt und steigt… Ud2 = U1 1− β 25.06.2005 Chopper-Ausgangsspannung Ud2 bei primärseitig nicht-lückendem Betrieb Seite 5 von 8 Selbstgeführte Wechselrichter Erzeugung der Ausgangsspannung Gleichspannung Ud wird in zwei gleiche Hälften unterteilt (ergibt Rechteckspannung am Ausgang) Die Umschaltzeitpunkte werden nicht durch eine vorgegebene Wechselspannung bestimmt (im Unterschied zum netzgeführten Wechselrichter) Dies erfordert abschaltbare Elemente Frequenz und Spannung sind variabel Dient als Bindeglied zwischen Gleichspannungsebene und Wechselspannungsebene Sowohl bei positiver als auch bei negativer Spannung sind beide Stromrichtungen möglich • • • • • Ud /2 S1 D1 i S1 iD1 S2 D2 iS2 iD2 u S1 Funktionsprinzip Ud /2 ILast u S2 Last • Grundschwingung Û1 Erzeugte Ausgangsspannung Ûd /2 AusgangsSpannung viertelperiodensymmetrisch T 4 U U1 = ⋅ d π 2 • Ud = von der Quelle gelieferte Gleichspannung Ud /2 = Amplitude des Ausgangs (Rechteck) Û1 = Amplitude der Grundschwingung Grundfrequenztaktung Grundschwingung U1 = 0.637 ⋅ U d Alle geraden Oberschwingungen sind null, da sie nichts zur viertelperiode-symmetrischen Spannungsform beitragen Dreiphasenwechselrichter, sterngeschaltete Last: Alle 3fachen (gleichphasigen) Oberscwingungen sind null, da sie in alle 3 Phasen den gleichen zeitlichen Verlauf haben Sternpunkt verhindert alles ausser Null • Oberschwingungen Grundsätzlich treten alle ungeraden Vielfachen der Grundschwingung auf. Bei 3Phasen-WR können zusätzlich alle 3fachen Oberschwingungen fehlen. Verbesserung des Ausgangssignals G ru n d sch w in g un g π /2 Û1 Elimination einzelner Oberschwingungen durch Zwischentaktung Ûd /2 3π / 2 • α1 α2 viertelperiodensymmetrisch, alle cos-Glieder der Fourierreihe sind 0 T /2 A u sg a n gsS p a nn u n g 2. H a lb p e rio d e Unterschwingung Puls-Modulationsverfahren Sinusbewertete Pulsmodulation x Ûd /2 Û1 π /2 0 π T(-) Ûd /2 Û1⋅ sin(x) TT viertelperiodensymmetrisch x T( + ) Ûd /2 Û1⋅ sin(x) TT T(+ ) TT • • • TT T(+ ) Erzeugte Spannung T(-) • • TT = • Idee: Momentanwerte der Ausgangsspannung durch positive und negative Spannungsimpulse nachbilden Ausgangsspannung ist die Unterschwingung der Pulse Uˆ 1 ⋅ sin( x) 1 + Ud 2 Uˆ1 1 ≤ Ud 2 Synthese der Ausgangsspannung Modulation des Spannungs-Raumzeigers bei DreiphasenWechselrichtern Formelsammlung Leistungselektronik Pro Zwischentaktung lassen sich 2 beliebige (ungerade) Oberschwingungen eliminieren Dabei sinkt aber auch die Amplitude der Grundschwingung Grundschwingungsmaximum bei Grundfrequenztaktung Grundschwingungsmaxim um ist die Hällfte der Gleichspannung T(+) = Zeitdauer des positiven Pulses T(-) = Zeitdauer des negativen Pulses TT = Summe der beiden Pulse Ud /2 = Pulsamplitude Û1 = Amplitude des Unterschwingung (des Ausgangs) x = ωt = betrachteter Winkel Weitere Möglichkeiten zur Qualitätsverbesserung der Ausgangswechselspannung 25.06.2005 Seite 6 von 8 Einphasenwechselrichter Phasenschwenkverfahren • • Mittelpunkt MP der Gleichspannungsquelle wird nicht benötigt Ausgangswechselspannung uWR lässt sich mit α zwischen Wert 0 (bei α = π) und Maximum (bei α = 0) steuern Nachteil: Last nicht an Masse Phasenschwenkung und Zwischentaktverfahren lassen sich kombinieren: In einem Umschaltpol eliminierte Oberschwingungen sind auch in uWR nicht enthalten • • uA - M P Ud / 2 π 4 α Uˆ 1 = ⋅ U d ⋅ cos π 2 2π x =ω t α ⋅ uB - M P R AusgangsSpannung π β = π -α Ud Û1 Grundfrequenztaktung Û1 = Amplitude der Grundschwingung MP = gedachter (aber nicht benötigter) Mittelpunkt der Gleichspannungsquelle 4 β = ⋅ U d ⋅ sin π 2 Ud / 2 uW oder Uˆ 1 max = 4 ⋅ U d π 2π G ru n d s c h w in g u n g UWf=1−απ⋅de = 1.273 ⋅ U d Dreiphasenwechselrichter • • Phasenschwenkverfahren nicht anwendbar, weil nur 1 Schaltpol pro Phase Regulierung der Ausgangsspannung durch Zwischentaktung Pufferkondensator Cp Cp = 1 2 ⋅ ∆ ucmax t ∫ i (t ) ⋅ dt c 0 ∆uc = maximale Spannungswelligkeit uL 1 - M P 2π / 3 Ud / 2 π 2π x =ω t ⋅ uL 2 - M P uL 3 - M P 4 U Uˆ 1 = ⋅ d π 2 2π / 3 4 U Uˆ verk = ⋅ d ⋅ 3 π 2 uL 1 - L 2 Ud 2π / 3 π = 0.637 ⋅ U d Grundfrequenztaktung Û1 = Amplitude der Grundschwingung pro Phase Ûverk = Amplitude der verketteten Spannung = 1.103 ⋅ U d Ûv e r k 2π Anspeisung von Dreiphasen-Asynchronmotoren • • • • • Eine im gewünschten Bereich variable Frequenz Spannungsänderung proportional zur Frequenzänderung für konstanten magnetischen Fluss Drei Phasen für Wechselrichterausgang 23 = 8 verschiedene Schaltzustände An der Wicklung liegt eine andere Spannung als am Wechselrichter- Ausgang u0 ≠ 0, weil nicht-harmonische Anregung u1 + u 2 + u3 3 2 ⋅ u1 − u 2 − u3 uU − X = 3 u0 = Formelsammlung Leistungselektronik 25.06.2005 = u1 − u0 Seite 7 von 8 Raumzeiger Durchflutungs-Raumzeiger a Θ = Im Θb e j⋅ 2⋅ π 3 =ˆ Θa • • Θ a = Re( Θ Für sterngeschaltete Last: ) Θ b = Re Θ ⋅ e − j⋅ 2⋅π ( Re( Θ ⋅ e j ⋅ 2⋅ π 3 + Θ c⋅e 3 − j⋅ 4⋅ π 3 u = Uˆ ⋅ e j⋅ω ⋅ t + e j⋅ϕ ) ) j ⋅ 4⋅ π 3 ] Analog zu Durchflutungsraumzeiger: Strom-, Spannungs-, Flussraumzeiger ( b e lie b ig e L ä n g e ) Die drei einzelnen Durchflutungsraumzeiger werden addiert ( a) und im komplexen Koordinatensystem dargestellt Θc= + Θ b⋅e Re 120° Θc j⋅ 0 Θa = Momentanwert der Durchflutung in der Wicklung a Zeigerdrehung in der komplexen Ebene um 120° 120° [ 2 ⋅ Θ a⋅e 3 Θ = Θa+ j ⋅ (Θ b − Θ 3 c ) Komplexe Wicklung Gilt nur für sterngeschaltete Last! Rückrechnung Bedingungen: • System symmetrisch • Spannungen sinusförmig Spannungsraumzeiger des Dreiphasensystems Formelsammlung Leistungselektronik Θa = Momentanwert der Durchflutung in der Wicklung a • • 25.06.2005 Konstante Länge Û (Amplitude der Phasenspannung) Konstante Umlaufgeschwindigkeit ω mit Anfangswert ϕ Seite 8 von 8