druck und zusammensetzung

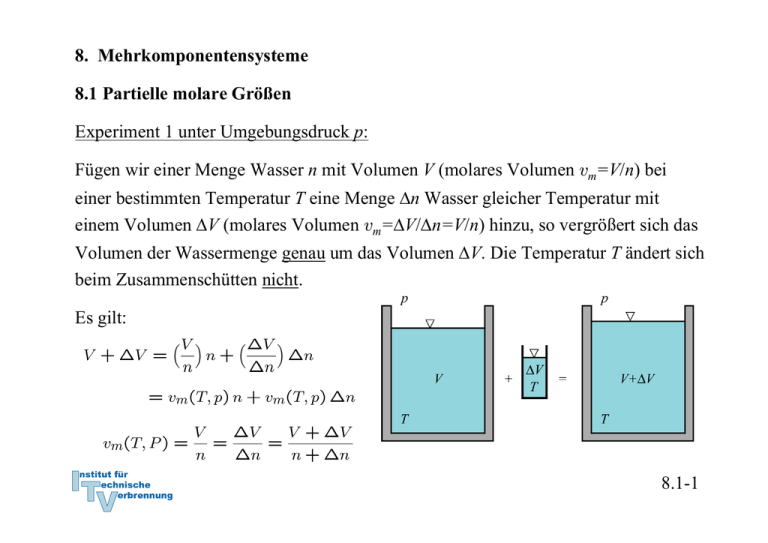
8. Mehrkomponentensysteme
8.1 Partielle molare Größen
Experiment 1 unter Umgebungsdruck p:
Fügen wir einer Menge Wasser n mit Volumen V (molares Volumen vm=V/n) bei
einer bestimmten Temperatur T eine Menge Δn Wasser gleicher Temperatur mit
einem Volumen ΔV (molares Volumen vm=ΔV/Δn=V/n) hinzu, so vergrößert sich das
Volumen der Wassermenge genau um das Volumen ΔV. Die Temperatur T ändert sich
beim Zusammenschütten nicht.
Es gilt:
8.1-1
Experiment 2 unter Umgebungsdruck p:
Fügen wir einer Menge Wasser n mit Volumen V (molares Volumen vm,w=V/n) bei
einer bestimmten Temperatur T eine Menge Δn Alkohol gleicher Temperatur mit
einem Volumen ΔV (molares Volumen vm,A=ΔV/Δn) hinzu, so ergibt sich ein
Gesamtvolumen Vges das kleiner ist als die Summe der Teilvolumina
Vges < Vw + ΔV
Außerdem ändert sich die Temperatur.
Es ergibt sich:
Pech!
Bem.: Mit Index * sollen i. F. die Stoffgrößen reiner Komponenten bezeichnet werden.
8.1-2
Anschauliche Erklärung:
Das negative Exzessvolumen Vex kann man sich dadurch erklären, dass die kleineren
Wassermoleküle Zwischenräume zwischen den größeren Alkoholmolekülen
ausnutzen können. Die Mischung wird so kompakter.
Diese rein geometrische Erklärung ist allerdings nicht vollständig, da auch Kräfte
zwischen den Molekülen Einfluss haben. Eventuelle Abstoßung zwischen den
Molekülen weist in Richtung Volumenvergrößerung.
Verallgemeinerung:
Wir folgern für das Volumen V eines beliebigen Gemisches, dass es nicht nur von der
Temperatur T und dem Druck p, sondern auch von der Zusammensetzung abhängt!
Bei k Komponenten und den Molmengen n1, n2,…nk im Gemisch ergibt sich der
funktionale Zusammenhang
8.1-3
Von der Funktion
bilden wir das vollständige Differential
Wenn wir die Mischung bei konstanter Temperatur und konstantem Druck
durchführen, ergibt sich bei Veränderung der Mischung eine Volumenänderung
Wir definieren die partiellen molaren Volumen einer Komponente i
8.1-4
Anschauliche Deutung:
Das partielle molare Volumen der Komponente i
gibt an, wie sich das Volumen V ändert (→ dV ),
wenn eine infinitesimale Menge der Komponente i
zu einem Gemisch gegebener Zusammensetzung
hinzugefügt wird, während wir dafür sorgen, dass
Temperatur und Druck konstant bleiben.
8.1-5
Bemerkung:
Eine Mischung kann statt durch Angabe der Molzahlen der Komponenten auch durch
die Angabe der Molenbrüche Xi vollständig charakterisiert werden.
Wir schreiben deshalb auch statt
üblicherweise für die partielle molaren Volumina auch die Funktion
Auf, wobei noch zusätzlich
gilt
8.1-6
Bedeutung der partiellen molaren Volumina
Das Volumen V einer Mischung bei bekannter Temperatur T und bekanntem Druck p
kann aus der Kenntnis aller partiellen molaren Volumina vi,m der Komponenten der
Mischung durch
oder kurz
berechnet werden.
8.1-7
Um die Gültigkeit von
zu zeigen, wollen wir zwei Mischungen genau gleicher Zusammensetzung
zusammenbringen.
Es gilt dabei folgender Zusammenhang (V ist homogen vom Grade 1):
Wir untersuchen die Variation von λ durch Ableitung der Identität nach λ:
Dies gilt für alle λ, also auch für λ = 1:
8.1-8
Berechnung von Exzessvolumina
Bringen wir zwei verschiedene Reinstoffe oder zwei Mischungen unterschiedlicher
Zusammensetzung bei konstanter Temperatur und konstantem Druck zusammen, so gilt
für das Gesamtvolumen, wenn keine chemischen Reaktionen stattfinden:
mit
Die Abweichung Vex wird Exzessvolumen genannt.
Sie ist mit den partiellen molaren Volumina der Mischungen a,b und c gegeben durch:
8.1-9
Ein Exzessvolumen nach Formel
tritt insbesondere dann nicht auf, wenn sich die partiellen molaren Volumina nicht von
den molaren Volumina der reinen Komponenten unterscheiden:
Reine Komponenten sollen wegen der besseren Lesbarkeit stets durch einen Index *
hervorgehoben werden.
Man kann sich denken, dass dies zum Beispiel für ideale Gase, bei denen die Moleküle
keine Ausdehnung und keine Interaktion untereinander besitzen, der Fall ist.
Die theoretische Bestimmung der partiellen molaren Größen realer Gemische ist eine
schwierige Aufgabe. In der Vergangenheit wurden diese im Allg. durch Experimente
ermittelt (siehe nachfolgendes Beispiel).
8.1-10
Beispiel Wasser-Ethanol-Gemisch
Bei Umgebungstemperatur und -druck werden 0,3 Liter Ethanol und 0,7 Liter Wasser
miteinander gemischt. Welches Gesamtvolumen hat die Mischung?
Das Diagramm experimentell ermittelter partieller molarer Volumina für das Wasser-EthanolGemisch sei gegeben.
Lösung:
Wir bestimmen die Molmengen von Wasser
und Ethanol:
8.1-11
Aus dem Diagram werden die partiellen molaren Volumina abgelesen.
Um also tatsächlich ein Liter Schnapps
mit 30 Vol % zu erhalten, müsste man eine
größere Menge Alkohol und Wasser
zusammenschütten.
8.1-12
Führt man die Auswertung für viele Mengenverhältnisse durch oder misst man das
Exzessvolumen erhält man folgendes Diagramm.
8.1-13
Es sei speziell darauf hingewiesen, dass das berechnete Exzessvolumen Vex nicht mit
dem Volumen δV der Folie 8.1-2 identisch ist.
Der Vorgang dort wurde zwar bei konstantem Druck aber nicht bei konstanter
Temperatur durchgeführt: keine Wärmebad → Wärmetönung (vergl. Folie 8.1-5)!
Wegen der Wärmetönung bei der Vermischung verschiedener Substanzen muss im
Allgemeinen gekühlt oder erwärmt werden.
Solche Exzessgrößen treten also nicht nicht nur für das Volumen, sondern auch für
energetische und entropische Größen wie innere Energie, Enthalpie und Entropie auf.
Die Wärmetönung ist wegen des konstanten Druckes eine Folge des Exzesses der
Freien Enthalpie.
Analog zum Volumen müssen wir passende partielle molare Größen definieren, um
solche Zusammenhänge rechnerisch erfassen zu können.
8.1-14
Partielle molare Zustandsgrößen
Bei einem Mehrkomponentengemisch hängen alle Zustandsgrößen Z von der
Zusammensetzung des Gemisches ab.
Es gilt also stets
Mit dem vollständiges Differential nach:
Darin ist die partielle molare Zustandsgröße definiert durch:
8.1-15
Die Interpretation der partiellen Ableitung
folgt derjenigen der partiellen molaren Volumina.
Die partielle Ableitung gibt wieder an, wie sich die
Zustandsgröße des Gemisches bei konstanter Temperatur und konstantem Druck
durch Hinzufügen einer infinitesimalen Menge einer Komponente i ändert.
Ebenso gilt wieder bei konstanter Temperatur und konstantem Druck
und beim Zusammenfügen verschiedener Mischung werden Exzessgrößen
beobachtet:
8.1-16
Beispiel: Die partielle molare Freie Enthalpie
Besonders wichtig ist die partielle molare Freie Enthalpie G, da deren natürliche
Variablen die thermischen variablen T und p sind, die in Experimenten leicht
kontrolliert werden können.
Definition der Freien Enthalpie:
Bei einem Mehrkomponentengemisch hängt die Freie Enthalpie von der
Zusammensetzung des Gemisches ab:
Ihr vollständiges Differential lautet:
8.1-17
Die partielle Ableitung
gibt wieder an, wie sich die Zustandsgröße des
Gemisches bei konstanter Temperatur und konstantem
konstantem Druck durch Hinzufügen einer infinitesimalen Menge einer Komponente i
ändert. Die partielle molare Freie Enthalpie wir Chemisches Potential μi=gi,m genannt.
Ebenso gilt wieder bei konstanter Temperatur und konstantem Druck
und beim Zusammenfügen verschiedener Mischung wird ein Freie Mischungsenthalpie
beobachtet :
8.1-18
Die Freie Mischungsentalpie ΔGM enthält zwei Anteile, nämlich die Mischungsenthalpie der idealen Mischung, Index id, und
eine Exzessenthalpie als Abweichung zur
idealen Mischung, Index ex :
Erstere ergibt sich aus der Mischungsentropie
der idealen Mischung (siehe Abb.)
Die treibende Kraft für die (ideale) Mischung ist
die Entropiezunahme bei diesem Vorgang.
Reale Mischungen besitzen eine zusätzliche Freie Mischungsenthalpie Gex, die
Exzessenthalpie.
Diese kann negativ, aber auch positiv sein (siehe 8.2, Mischungslücke).
8.1-19
Zusammenfassung
Partielle molare Größen sind stets bei konstantem Druck und konstanter Temperatur durch
die partielle Ableitung
definiert.
Der Wert der extensiven Zustandsgröße Z in einer Mischung wird aus
berechnet.
Partielle molare Zustandsgrößen unterscheiden sich im Allgemeinen von den molaren
Zustandsgrößen reiner Komponenten:
Um die funktionale Abh’ngigkeit nicht ausschreiben zu müssen sollen im Folgenden die
molaren Größen reiner Komponenten mit einem Index * gekennzeichnet werden:
8.1-19
8.2 Thermodynamische Gleichgewichte,
insbesondere Gleichgewichte in Mehrkomponentensystemen
Mechanisches und thermisches Gleichgewicht
8.2-1
Stoffliches Gleichgewicht
Beispiel Stickstoff Sauerstoff:
Desweiteren können chemische Reaktionen beim Mischen von verschiedenen
Stoffen eintreten, so dass im Gleichgewicht auch neue Komponenten auftreten
← Massenwirkungsgesetz.
8.2-2
Das Chemische Potential
Hier: Chemisches Potentials eines reinen Stoff
Ausgangspunkt: Freie Enthalpie oder Gibbssche Enthalpie G des Systems
Definition der Freien Enthalpie:
Fundamentalgleichung der molaren Freien Enthalpie eines reinen Stoffes:
8.2-3
Die Fundamentalgleichung der molaren Gibbsschen Enthalpie
legt es nahe, die intensiven Zustandsgrößen Temperatur T und Druck p als
natürliche Variablen zur Darstellung der molaren Gibbsschen Enthalpie
anzusehen:
Da wir in diesem Kapitel Mehrkomponentensysteme und Stoffmengenänderungen
betrachten werden, wollen wir die Abhängigkeit der extensiven Zustandsgrößen
von der Stoffmenge nun grundsätzlich notieren.
8.2-4
Mit
lauten die vollständigen Differentiale:
Vergleich mit der Fundamentalgleichung
liefert
und
8.2-5
Das Chemische Potential
zunächst: Chemisches Potentials eines reinen Stoff
Die molare Freie Enthalpie gm eines reinen Stoffes wird als das
Chemische Potential μ
des Stoffes bezeichnet.
Für die bessere Unterscheidung des Chemischen Potentials eines reinen Stoffes von
dem Chemischen Potential μi des in einem Mehrkomponentensystem wird das
Chemische Potential des reinen Stoffes mit einem * gekennzeichnet werden:
8.2-6
Mehrkomponentengemisch und Chemisches Potential
Bei einem Mehrkomponentengemisch hängt die Freie Enthalpie von der
Zusammensetzung des Gemisches ab:
Es gilt weiterhin die Definition:
Schreibt man wieder das vollständige Differential auf
so folgt die Fundamentalgleichung der Freien Enthalpie für ein Gemisch:
8.2-7
gi,m heißt partielle molare Freie Enthalpie der Komponente i im Gemisch. Wie alle
partiellen Größen ist gi,m bei festgehaltenem Temperatur T und festgehaltenem Druck
p und definiert.
Die partielle molare Freie Enthalpie wird als Chemisches Potential μi der Komponente
i bezeichnet.
Wegen der Definition
gilt auch die Verknüpfung mit der partiellen molaren Enthapie und der partiellen
molaren Entropie:
Die Fundamentalgleichung lässt sich schreiben:
8.2-8
Das Chemische Potential lässt sich auch durch die Innere Energie definieren.
Wegen der Definitionen G=H-TS und H=U+pV ist
und
Die Fundamentalgleichung der Inneren Energie eines Gemisches lautet also:
8.2-9
Aus dieser Darstellung des Differentials der Inneren Energie
kann abgeleitet werden, dass die natürlichen Zustandsvariablen der Inneren Energie
neben den Stoffmengen, Volumen V und Entropie S sind:
Das totale Differential lautet dann:
Bem.: In ähnlicher Weise findet man aus den Fundamentalgleichungen die natürlichen
Variablen anderer Zustandsgrößen wie der Freien Energie, der Enthalpie usw.
8.2-10
Der Vergleich zwischen Zustandsgleichung
und totalem Differential liefert
sowie offensichtlich für das Chemische Potential die alternative Darstellung:
statt
Ferner gilt:
8.2-11
Übung:
Zeigen Sie, dass das Chemischen Potential alternativ durch die Ausdrücke
oder
dargestellt werden kann, wobei H die Enthalpie und A die Freie Energie sein sollen.
8.2-12
8.2.1 Temperatur- und Druckabhängigkeit des Chemischen Potentials
Wir nutzen die Definition
Für einen reinen Stoff sind die Temperatur- und Druckabhängigkeiten identisch mit
den Abhängigkeiten der molaren Freien Enthalpie von Temperatur und Druck
Diese Abhängigkeiten sind uns aus der Definition der Freien Enthalpie aus früheren
Kapiteln vertraut.
8.2-12
Beispiel ideale Flüssigkeit
Das Chemische Potential der idealen Flüssigkeit erhalten wir aus der Definition
Bei einer idealen Flüssigkeit haben wir inkompressibles Verhalten vm = const angenommen.
Mit
folgt, dass die Innere Energie nur von der Temperatur abhängt
die Enthalpie wegen h = u + pv und Entropie durch
gegeben ist.
Das Chemische Potential der idealen Flüssigkeit ist dann:
8.2-13
Für ein Stoffgemisch gelten entsprechende Beziehungen, wenn wir alle molaren
Größen konsequent durch die partiellen molaren Größen ersetzen.
Es gilt zum Beispiel wegen der Vertauschbarkeit der Reihenfolge der Ableitungen
und wegen
Eine analoge Betrachtung liefert mit
für die Druckabhängigkeit:
8.2-13
Zusammenfassend:
Reiner Stoff
Stoffgemisch
Integrale solcher Gleichungen liefern zum Beispiel:
Das Chemische Potential einer Komponente bei konstantem Druck lässt sich also
berechnen, wenn uns das Chemische Potential bei Standardbedingungen, Index o,
bekannt (Tabellenwerke) und die Funktion si,m(T,p,n1,…,nk) gegeben ist.
8.2-14
Beispiel:
Bestimmen Sie die Druckabhängigkeit des Chemischen Potentials für ein reales Gas mit der
Zustandsgleichung
! B ist darin ein temperaturabhängiger Virialkoeffizient.
Lösung:
Das Integral lässt sich mit der angegebenen Zustandsgleichung auswerten:
Diese Formel beinhaltet für B = 0 den Druckabhängigkeit des Chemischen Potential beim
idealen Gas
8.2-15
Fugazität
Der Unterschied zwischen dem realen Gas und dem idealen Gas kann
durch Einführung eines korrigierten Druckes, die Fugazität f,
auf eine formal mit dem idealen Gas übereinstimmende Formel gebracht werden:
Der Fugazitätsfaktor ϕ errechnet sich aus:
8.2-16
8.2.2 Die Abhängigkeit des Chemischen Potentials von der Zusammensetzung
des Gemisches
Wir betrachten zunächst den einfachen Fall einer Mischung idealer Gase aus kKomponenten.
Nützlich ist ein Gedankenexperiment, bei dem wir entsprechend der k-Komponenten
das Volumen unseres Systems in k Teilvolumina mit reinen Komponenten zerfallen
lassen, in denen die Temperatur und der Druck des Gesamtsystems herrschen sollen.
Die Teilvolumina verhalten sich zum Gesamtvolumen bei idealen Gasen dann wie die
Partialdrücke der Mischung zum Gesamtdruck:
8.2-17
Die Trennwände zwischen den Volumina seien ohne Arbeitsaufwand herausnehmbar.
Wenn das Gesamtsystem adiabat ist, wird sich die Temperatur nicht ändern, da die
Innere Energie des Systems konstant bleiben muss und nicht vom Druck abhängt.
Die Gase vermischen sich in einem irreversiblen Prozess, bei dem sich der
Gesamtdruck nicht ändert, jede einzelne Komponente verhält sich so, als ob die
anderen Komponenten nicht anwesend wären, und nimmt im Gesamtvolumen ihren
Partialdruck an.
Wir erwarten einen Anstieg der Entropie im System (← irreversibler Prozess) und
wegen
eine Abnahme des Chemischen Potentials.
8.2-18
Die Änderung des Chemischen Potentials können wir aus dessen Definition
berechnen:
Für die reine Komponente i im Volumen Vi:
Für die Komponente i in der Mischung:
Änderung:
Entropieänderung bei isothermer Zustandsänderung:
Das Chemische Potential jeder Komponente verringert sich demnach in der
Mischung, da die Entropie anwächst:
8.2-19