C1/4 - Modellierung und Simulation von Neuronen
Werbung

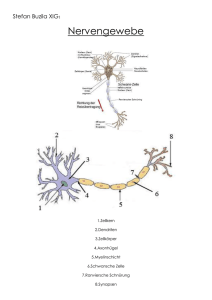
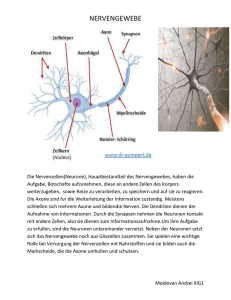
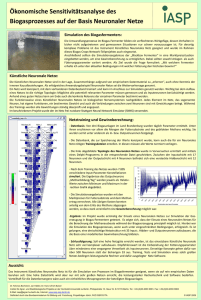
C1/4 - Modellierung und Simulation von Neuronen Merovius April 25, 2013 Merovius C1/4 - Modellierung und Simulation von Neuronen Motivation Worum geht es? Merovius C1/4 - Modellierung und Simulation von Neuronen Motivation Worum geht es? Um Neuronen. Merovius C1/4 - Modellierung und Simulation von Neuronen Motivation Worum geht es? Um Neuronen. Da ist u.a. euer Gehirn draus Merovius C1/4 - Modellierung und Simulation von Neuronen Motivation Worum geht es? Um Neuronen. Da ist u.a. euer Gehirn draus Genauer: Um mathematische Modelle Merovius C1/4 - Modellierung und Simulation von Neuronen Motivation Worum geht es? Um Neuronen. Da ist u.a. euer Gehirn draus Genauer: Um mathematische Modelle Und Warum? Merovius C1/4 - Modellierung und Simulation von Neuronen Motivation Worum geht es? Um Neuronen. Da ist u.a. euer Gehirn draus Genauer: Um mathematische Modelle Und Warum? Um herauszufinden, wie Denken/Lernen/Signalübertragung funktioniert Merovius C1/4 - Modellierung und Simulation von Neuronen Motivation Worum geht es? Um Neuronen. Da ist u.a. euer Gehirn draus Genauer: Um mathematische Modelle Und Warum? Um herauszufinden, wie Denken/Lernen/Signalübertragung funktioniert Für KI Merovius C1/4 - Modellierung und Simulation von Neuronen Motivation Worum geht es? Um Neuronen. Da ist u.a. euer Gehirn draus Genauer: Um mathematische Modelle Und Warum? Um herauszufinden, wie Denken/Lernen/Signalübertragung funktioniert Für KI Um neurologische Krankheiten (z.B. Epilepsie, Parkinson. . . ) zu verstehen Merovius C1/4 - Modellierung und Simulation von Neuronen Motivation Worum geht es? Um Neuronen. Da ist u.a. euer Gehirn draus Genauer: Um mathematische Modelle Und Warum? Um herauszufinden, wie Denken/Lernen/Signalübertragung funktioniert Für KI Um neurologische Krankheiten (z.B. Epilepsie, Parkinson. . . ) zu verstehen Für Mensch/Maschine-interfaces. . . Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons - Zellkörper Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons - Zellkörper Ionenkanäle machen die Membran halbdurchlässig für bestimmte Ionen. Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons - Zellkörper Ionenkanäle machen die Membran halbdurchlässig für bestimmte Ionen. Ionenpumpen bauen Konzentrationsgefälle auf (Ruhepotential) Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons - Zellkörper Ionenkanäle machen die Membran halbdurchlässig für bestimmte Ionen. Ionenpumpen bauen Konzentrationsgefälle auf (Ruhepotential) Zellkern macht hauptsächlich Zell-Metabolismus Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons - Dendriten Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons - Dendriten Nehmen Signale anderer Neuronen auf Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons - Dendriten Nehmen Signale anderer Neuronen auf Sind stark verzweigt und normalerweise viele Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons - Dendriten Nehmen Signale anderer Neuronen auf Sind stark verzweigt und normalerweise viele Können exitatorisch (anregend) oder inhibitorisch (hemmend) sein Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons - Axon Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons - Axon Generiert das Aktionspotential (das Neuron „feuert“) Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons - Axon Generiert das Aktionspotential (das Neuron „feuert“) Leitet das AP an andere Neuronen (z.B. auch durch den gesamten Körper) Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons - Synapsen Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons - Synapsen Hier docken Dendriten anderer Neuronen an Merovius C1/4 - Modellierung und Simulation von Neuronen Anatomie eines Neurons - Synapsen Hier docken Dendriten anderer Neuronen an Signalübertragung meistens chemisch (Neurotransmitter), manchmal elektrisch Merovius C1/4 - Modellierung und Simulation von Neuronen Künstliche Neuronale Netze Fragestellung: Wie beeinflussen sich die einzelnen Inputs der Dendriten? Merovius C1/4 - Modellierung und Simulation von Neuronen Künstliche Neuronale Netze Fragestellung: Wie beeinflussen sich die einzelnen Inputs der Dendriten? Einfachste Möglichkeit: Lineare Überlagerung: vSoma = X ai · vi i ∈Dendriten Merovius C1/4 - Modellierung und Simulation von Neuronen Künstliche Neuronale Netze Fragestellung: Wie beeinflussen sich die einzelnen Inputs der Dendriten? Einfachste Möglichkeit: Lineare Überlagerung: vSoma = X ai · vi i ∈Dendriten Man sieht, dass dies das Produkt des Zeilenvektors der Gewichte mit dem Spaltenvektor der Inputs ist. Merovius C1/4 - Modellierung und Simulation von Neuronen Künstliche Neuronale Netze Fragestellung: Wie beeinflussen sich die einzelnen Inputs der Dendriten? Einfachste Möglichkeit: Lineare Überlagerung: vSoma = X ai · vi i ∈Dendriten Man sieht, dass dies das Produkt des Zeilenvektors der Gewichte mit dem Spaltenvektor der Inputs ist. Nummerieren wir die Neuronen mit 1, . . . , n durch und nennen wir aij das Gewicht, mit dem der Output von Neuron i für das Neuron j gewichtet wird, erhalten wir: ~vSoma = A ~vOut Merovius C1/4 - Modellierung und Simulation von Neuronen Küntliche Neuronale Netze Wir erhalten die Spannung am Zellkörper durch Matrixmultiplikation ⇒ schnell. Merovius C1/4 - Modellierung und Simulation von Neuronen Küntliche Neuronale Netze Wir erhalten die Spannung am Zellkörper durch Matrixmultiplikation ⇒ schnell. Wir wollen ein binäres Outputsignal haben: ϕ : Rn → Rn 1 vi > vthresh vi 7→ 0 sonst 0 ~vOut = ϕ (A ~vOut ) Merovius C1/4 - Modellierung und Simulation von Neuronen Küntliche Neuronale Netze Wir erhalten die Spannung am Zellkörper durch Matrixmultiplikation ⇒ schnell. Wir wollen ein binäres Outputsignal haben: ϕ : Rn → Rn 1 vi > vthresh vi 7→ 0 sonst 0 ~vOut = ϕ (A ~vOut ) Wir können solche Netze verschiedener Größe kombinieren und mit verschiedenen Regeln ausstatten und erhalten so „küntliche Intelligenz“ Merovius C1/4 - Modellierung und Simulation von Neuronen Küntliche Neuronale Netze Wir erhalten die Spannung am Zellkörper durch Matrixmultiplikation ⇒ schnell. Wir wollen ein binäres Outputsignal haben: ϕ : Rn → Rn 1 vi > vthresh vi 7→ 0 sonst 0 ~vOut = ϕ (A ~vOut ) Wir können solche Netze verschiedener Größe kombinieren und mit verschiedenen Regeln ausstatten und erhalten so „küntliche Intelligenz“ Gut bei Klassifizierungsproblemen, schlecht bei ungefähr allem anderen Merovius C1/4 - Modellierung und Simulation von Neuronen Küntliche Neuronale Netze Wir erhalten die Spannung am Zellkörper durch Matrixmultiplikation ⇒ schnell. Wir wollen ein binäres Outputsignal haben: ϕ : Rn → Rn 1 vi > vthresh vi 7→ 0 sonst 0 ~vOut = ϕ (A ~vOut ) Wir können solche Netze verschiedener Größe kombinieren und mit verschiedenen Regeln ausstatten und erhalten so „küntliche Intelligenz“ Gut bei Klassifizierungsproblemen, schlecht bei ungefähr allem anderen Großes Thema ⇒ andere C1/4? Merovius C1/4 - Modellierung und Simulation von Neuronen Punktneuronen - Integrate and Fire Fragestellung: Wie wird am Axonhügel das Aktionspotential generiert? Merovius C1/4 - Modellierung und Simulation von Neuronen Punktneuronen - Integrate and Fire Fragestellung: Wie wird am Axonhügel das Aktionspotential generiert? Wir können die Zellmembran als Kondensator betrachten: Q = Cv ⇒ C v̇ = I Merovius C1/4 - Modellierung und Simulation von Neuronen Punktneuronen - Integrate and Fire Fragestellung: Wie wird am Axonhügel das Aktionspotential generiert? Wir können die Zellmembran als Kondensator betrachten: Q = Cv ⇒ C v̇ = I Dieses System konvergiert (ohne spiking) gegen einen Gleichgewichtszustand. Wir führen ein „manuelles spiken“ ein: Ist v (t ) > vthresh , rufen wir „spike“ und setzen v (t ) = vreset Merovius C1/4 - Modellierung und Simulation von Neuronen Punktneuronen - Integrate and Fire -20 3 2 -30 1 0 I v -40 -50 -1 -60 -2 -70 0 100 200 300 400 -3 500 t Merovius C1/4 - Modellierung und Simulation von Neuronen Punktneuronen - Leaky Integrate and Fire Zellmembran ist kein Isolator, sondern Halbdurchlässig für bestimmte Ionen Lösung: Leckstrom-Term: C v̇ = I − Merovius v R C1/4 - Modellierung und Simulation von Neuronen Punktneuronen - Leaky Integrate and Fire -20 3 2 -30 1 0 I v -40 -50 -1 -60 -2 -70 0 100 200 300 400 -3 500 t Merovius C1/4 - Modellierung und Simulation von Neuronen Punktneuronen - Hodgkin-Huxley In ähnlicher Weise geht es weiter: Izhikevic-Modell, IFAdEx-Modell, . . . Merovius C1/4 - Modellierung und Simulation von Neuronen Punktneuronen - Hodgkin-Huxley In ähnlicher Weise geht es weiter: Izhikevic-Modell, IFAdEx-Modell, . . . Krönung der Punktneuronen-Modelle: Hodgkin-Huxley Merovius C1/4 - Modellierung und Simulation von Neuronen Punktneuronen - Hodgkin-Huxley In ähnlicher Weise geht es weiter: Izhikevic-Modell, IFAdEx-Modell, . . . Krönung der Punktneuronen-Modelle: Hodgkin-Huxley Wir ergänzen den Leckstrom mit mehreren, spannungsabhängigen Ionenströmen: C v̇ = gL (v − vL ) + X Ii = gL (v − vL ) + i Merovius X gi (t , v )(v − vL ) i C1/4 - Modellierung und Simulation von Neuronen Punktneuronen - Hodgkin-Huxley In ähnlicher Weise geht es weiter: Izhikevic-Modell, IFAdEx-Modell, . . . Krönung der Punktneuronen-Modelle: Hodgkin-Huxley Wir ergänzen den Leckstrom mit mehreren, spannungsabhängigen Ionenströmen: C v̇ = gL (v − vL ) + X Ii = gL (v − vL ) + i X gi (t , v )(v − vL ) i gi (t , v ) = ḡi mi (t , v )pi hi (t , v )qi Modell: ḡi ist die maximale Leitfähigkeit, jedes mi ein anregendes Tor, jedes hi ein hemmendes Tor (jeweils mit Werten in [0, 1]), beschrieben durch: ṁi = αi (v )(1 − mi ) − βi (v )mi ḣi = γi (v )(1 − hi ) − δi (v )hi Merovius C1/4 - Modellierung und Simulation von Neuronen Punktneuron - Hodgkin-Huxley 120 Potential Applied current density Potential v [ms] and current density I [uA/cm2] 100 80 60 40 20 0 -20 0 50 100 150 200 250 t [ms] Merovius C1/4 - Modellierung und Simulation von Neuronen Punktneuron - Hodgkin-Huxley v I/3 m n h 100 2 1.5 v (in mV) 60 40 1 20 I and m/h/n (dimensionless) 80 0.5 0 -20 0 95 100 105 110 t (in ms) Merovius 115 120 125 C1/4 - Modellierung und Simulation von Neuronen Räumliche Modelle - Kabeltheorie Für Modellierung neuronaler Netze u.ä. sind Informationen über Signalausbreitung/Verzögerung innerhalb des Neurons nötig Merovius C1/4 - Modellierung und Simulation von Neuronen Räumliche Modelle - Kabeltheorie Für Modellierung neuronaler Netze u.ä. sind Informationen über Signalausbreitung/Verzögerung innerhalb des Neurons nötig Modellierung des Dendriten-Baumes als Folge verzweigter Zylinder Merovius C1/4 - Modellierung und Simulation von Neuronen Räumliche Modelle - Kabeltheorie Für Modellierung neuronaler Netze u.ä. sind Informationen über Signalausbreitung/Verzögerung innerhalb des Neurons nötig Modellierung des Dendriten-Baumes als Folge verzweigter Zylinder Die Membran wird modelliert als Kombination aus Kondensator und Widerstand Merovius C1/4 - Modellierung und Simulation von Neuronen Räumliche Modelle - Kabeltheorie Für Modellierung neuronaler Netze u.ä. sind Informationen über Signalausbreitung/Verzögerung innerhalb des Neurons nötig Modellierung des Dendriten-Baumes als Folge verzweigter Zylinder Die Membran wird modelliert als Kombination aus Kondensator und Widerstand Das Zellplasma (entlang der Stromrichtung) wird als Ohmscher Widerstand modelliert Merovius C1/4 - Modellierung und Simulation von Neuronen Räumliche Modelle - Kabeltheorie Für Modellierung neuronaler Netze u.ä. sind Informationen über Signalausbreitung/Verzögerung innerhalb des Neurons nötig Modellierung des Dendriten-Baumes als Folge verzweigter Zylinder Die Membran wird modelliert als Kombination aus Kondensator und Widerstand Das Zellplasma (entlang der Stromrichtung) wird als Ohmscher Widerstand modelliert Partielle Differentialgleichung zweiter Ordnung für jeden Abschnitt Merovius C1/4 - Modellierung und Simulation von Neuronen Fragen? Merovius C1/4 - Modellierung und Simulation von Neuronen