Aufgabe 1 Der Schlitten m = 400 kg hat keine Antriebskraft und

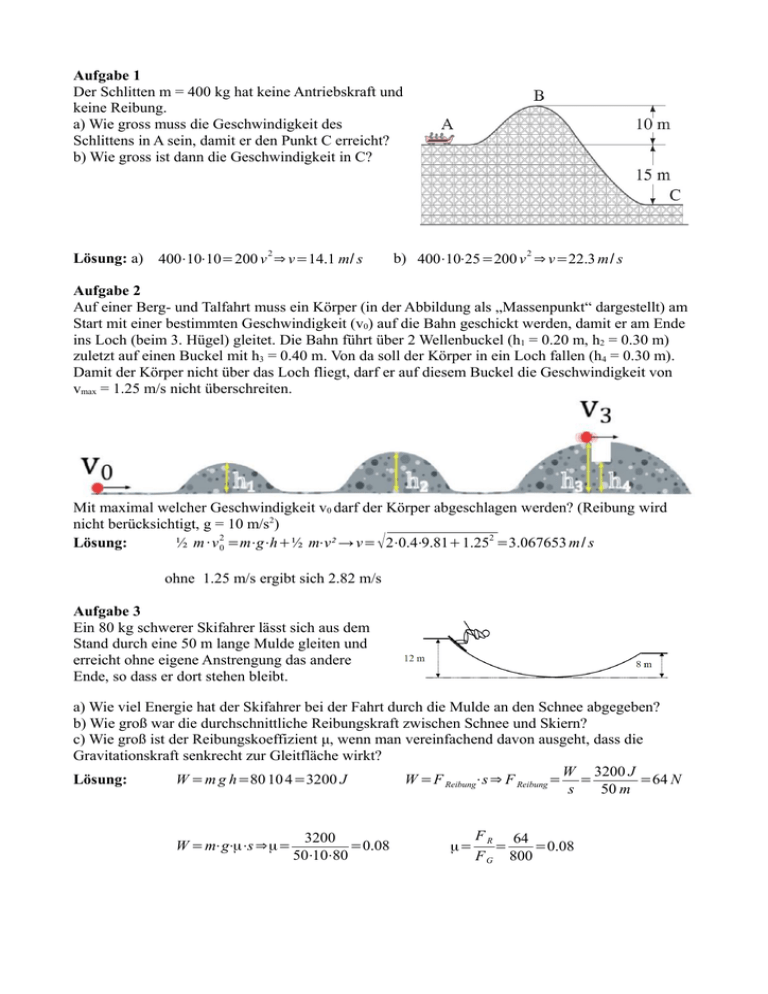
Aufgabe 1
Der Schlitten m = 400 kg hat keine Antriebskraft und
keine Reibung.
a) Wie gross muss die Geschwindigkeit des
Schlittens in A sein, damit er den Punkt C erreicht?
b) Wie gross ist dann die Geschwindigkeit in C?
Lösung: a) 400⋅10⋅10=200 v 2 ⇒ v=14.1 m/ s
b) 400⋅10⋅25=200 v 2 ⇒ v=22.3 m/ s
Aufgabe 2
Auf einer Berg- und Talfahrt muss ein Körper (in der Abbildung als „Massenpunkt“ dargestellt) am
Start mit einer bestimmten Geschwindigkeit (v0) auf die Bahn geschickt werden, damit er am Ende
ins Loch (beim 3. Hügel) gleitet. Die Bahn führt über 2 Wellenbuckel (h1 = 0.20 m, h2 = 0.30 m)
zuletzt auf einen Buckel mit h3 = 0.40 m. Von da soll der Körper in ein Loch fallen (h4 = 0.30 m).
Damit der Körper nicht über das Loch fliegt, darf er auf diesem Buckel die Geschwindigkeit von
vmax = 1.25 m/s nicht überschreiten.
Mit maximal welcher Geschwindigkeit v0 darf der Körper abgeschlagen werden? (Reibung wird
nicht berücksichtigt, g = 10 m/s2)
Lösung:
½ m· v 2 0 =m⋅g⋅h+½ m⋅v² → v= √ 2⋅0.4⋅9.81+1.252 =3.067653 m/ s
ohne 1.25 m/s ergibt sich 2.82 m/s
Aufgabe 3
Ein 80 kg schwerer Skifahrer lässt sich aus dem
Stand durch eine 50 m lange Mulde gleiten und
erreicht ohne eigene Anstrengung das andere
Ende, so dass er dort stehen bleibt.
a) Wie viel Energie hat der Skifahrer bei der Fahrt durch die Mulde an den Schnee abgegeben?
b) Wie groß war die durchschnittliche Reibungskraft zwischen Schnee und Skiern?
c) Wie groß ist der Reibungskoeffizient μ, wenn man vereinfachend davon ausgeht, dass die
Gravitationskraft senkrecht zur Gleitfläche wirkt?
W 3200 J
W =m g h=80 10 4=3200 J
W =F Reibung⋅s ⇒ F Reibung = =
=64 N
Lösung:
s
50 m
W =m⋅g⋅μ⋅s ⇒μ=
3200
=0.08
50⋅10⋅80
μ=
F R 64
=
=0.08
F G 800
Aufgabe 4
Ein Jogger mit einer Masse von 70 kg läuft eine lange Treppe in 4.0 s hoch. Die vertikale Höhe der
Treppe beträgt 4.5 m.
Schätzen Sie die Leistungsabgabe des Joggers in Watt und PS ab.
3150 J
P=
=787.5W =1.07 PS
W =m⋅g⋅h=70 4.5 10=3150 J
Lösung:
4s
Aufgabe 5
Eine Bungeespringerin mit einer Masse von 60 kg springt von einer Brücke. Sie ist an einem
Bungeeseil befestigt, das im ungedehnten Zustand 12 m lang ist, und fällt insgesamt 32 m.
Berechnen Sie die Federkonstante D des Bungeeseils und nehmen Sie dabei an, dass das
Hooke’sche Gesetz gilt.
2 W 38400
W =½ D⋅s 2 ⇒ D= 2 =
=96 N /m
W =mgh=6010 32=19200 J
Lösung:
s
202
Aufgabe 6
Ein Kind mit einer Masse von 16,0 kg rutscht eine 2,50 m hohe Rutsche hinunter und kommt mit
einer Geschwindigkeit von 2.25 m/s unten an.
Wie viel Wärme wurde in diesem Prozess auf Grund von Reibung erzeugt?
W =m⋅g⋅h=16⋅10⋅2.5=400 J
Lösung:
W = 12⋅16⋅2.252=40.5 J
W Reibung =359.5 J
Aufgabe 7
Eine Kugel der Masse 2.0 kg hängt an einer 3.5 m
langen Schnur, die bei A an der Zimmerdecke
befestigt ist.
Wir ziehen die Kugel nach rechts-oben bis zu Punkt
B, dabei bleibt die Schnur gespannt (Figur 1). Der
Punkt B liegt 0.80 m höher als der Punkt C. Nun
erteilen wir der Kugel die Geschwindigkeit 3.0 m/s
nach links-unten.
Dabei vernachlässigen wir den Luftwiderstand.
a) Bis auf welche maximale Höhe schwingt die Kugel
auf der linken Seite ?
b) Wie gross ist die maximale Geschwindigkeit, die
die Kugel erreicht?
c) Wie gross ist die Seilkraft im tiefsten Punkt?
Hinweis: Der Luftwiderstand wird vernachlässigt.
Lösung:
v2
9
= =0.45 m⇒ hmax =1.25 m
2 g 20
a)
½ mv 2=mgh⇒ h=
b)
½ m⋅v 2max=m⋅g⋅h⇒ v =√ 2 g cdozt h= √ 20⋅1.25= √25=5 m/ s
c)
F =m⋅g +
m⋅v 2
50
=20 N +
=34.28571=34.3 N
r
3.5
Aufgabe 8
Ein Student mit einer Masse von 75 kg läuft mit einer
Geschwindigkeit von 5,0 m/s, greift ein
herunterhängendes Seil und schwingt sich hinaus
über einen See . Er lässt das Seil los, wenn seine
Geschwindigkeit null beträgt.
Wie groß ist der Winkel θ , wenn er das Seil loslässt?
Lösung:
m⋅g⋅h=½ m⋅v 2 ⇒ h=
v2
=1.25 m
2g
cos α=
8.75
=0.875⇒ α=29°
10
Aufgabe 9
Die genaue Formel lautet für den Luftwiderstand lautet:
F Luft = 12 ρ⋅c w⋅A⋅v 2
Für den Rollwiderstand gilt:
F Roll =μ⋅m⋅g
a) Berechnen Sie den Luftwiderstand und die Rollreibung für v = 90 km/h.
b) Wie gross ist dann die Leistung.
c) Bei welcher Geschwindigkeit sind Luftwiderstand und Rollreibung gleich gross?
d) Berechnen Sie die Maximalgeschwindigkeit für 100 kW
Es gilt:
m = 1800 kg
ρ = 1.2 kg/m3
Lösung:
a)
μ = 0.013
F Roll =18000⋅0.013=234 N
b) P=25(234+270)=12600 W
cw = 0.3
A = 1.6 m x 1.5 m
F Luft =0.5⋅1.2⋅0.3⋅2.4⋅v 2=0.432 v 2=270 N
c) v=
√ 234
0.5 1.2 0.3 2.4
=23.27373 m/s
d) 100000=(234+0.432 v 2)v ⇒ v=58.5 m/s=210.6 km/h
Iteration
61,40052244922332476110068728445
58,327866932074325435554479022481
58,469336573886488100649404104199