Lösung Juni 2016 - Gymnasium Ohlstedt

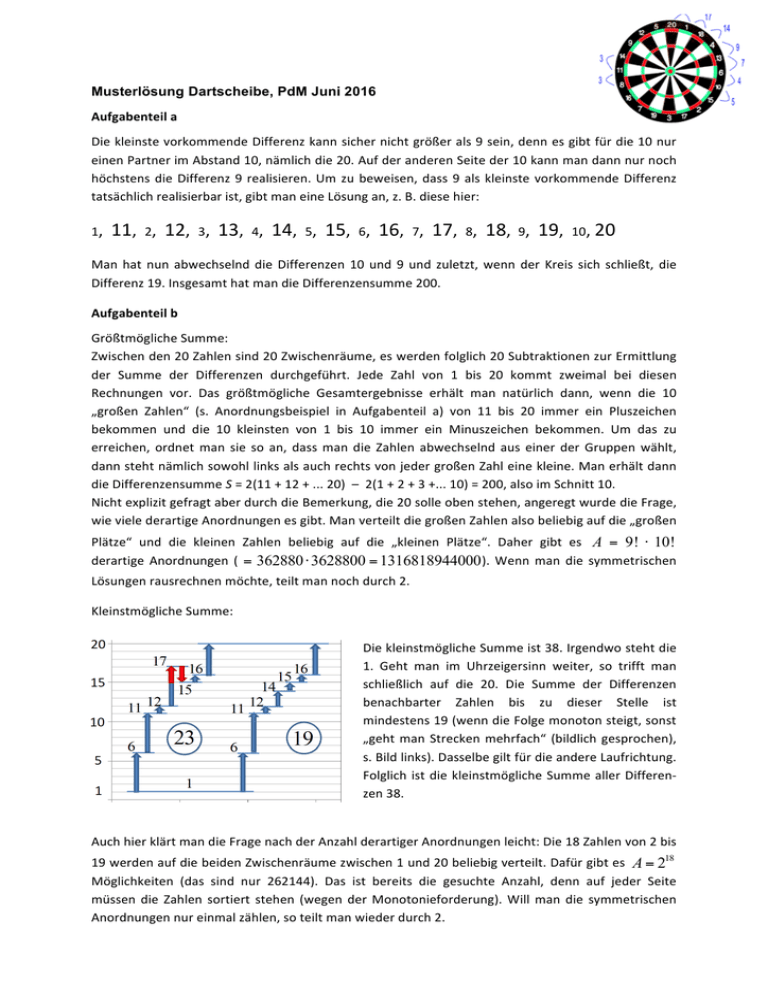
Musterlösung Dartscheibe, PdM Juni 2016
Aufgabenteila
DiekleinstevorkommendeDifferenzkannsichernichtgrößerals9sein,dennesgibtfürdie10nur
einenPartnerimAbstand10,nämlichdie20.AufderanderenSeiteder10kannmandannnurnoch
höchstens die Differenz 9 realisieren. Um zu beweisen, dass 9 als kleinste vorkommende Differenz
tatsächlichrealisierbarist,gibtmaneineLösungan,z.B.diesehier:
1,11,2,12,3,13,4,14,5,15,6,16,7,17,8,18,9,19,10,20
Man hat nun abwechselnd die Differenzen 10 und 9 und zuletzt, wenn der Kreis sich schließt, die
Differenz19.InsgesamthatmandieDifferenzensumme200.
Aufgabenteilb
GrößtmöglicheSumme:
Zwischenden20Zahlensind20Zwischenräume,eswerdenfolglich20SubtraktionenzurErmittlung
der Summe der Differenzen durchgeführt. Jede Zahl von 1 bis 20 kommt zweimal bei diesen
Rechnungen vor. Das größtmögliche Gesamtergebnisse erhält man natürlich dann, wenn die 10
„großen Zahlen“ (s. Anordnungsbeispiel in Aufgabenteil a) von 11 bis 20 immer ein Pluszeichen
bekommen und die 10 kleinsten von 1 bis 10 immer ein Minuszeichen bekommen. Um das zu
erreichen, ordnet man sie so an, dass man die Zahlen abwechselnd aus einer der Gruppen wählt,
dannstehtnämlichsowohllinksalsauchrechtsvonjedergroßenZahleinekleine.Manerhältdann
dieDifferenzensummeS=2(11+12+...20)–2(1+2+3+...10)=200,alsoimSchnitt10.
NichtexplizitgefragtaberdurchdieBemerkung,die20solleobenstehen,angeregtwurdedieFrage,
wievielederartigeAnordnungenesgibt.ManverteiltdiegroßenZahlenalsobeliebigaufdie„großen
Plätze“ und die kleinen Zahlen beliebig auf die „kleinen Plätze“. Daher gibt es A = 9! ⋅ 10!
derartige Anordnungen ( = 362880 ⋅ 3628800 = 1316818944000 ). Wenn man die symmetrischen
Lösungenrausrechnenmöchte,teiltmannochdurch2.
KleinstmöglicheSumme:
DiekleinstmöglicheSummeist38.Irgendwostehtdie
1. Geht man im Uhrzeigersinn weiter, so trifft man
schließlich auf die 20. Die Summe der Differenzen
benachbarter Zahlen bis zu dieser Stelle ist
mindestens19(wenndieFolgemonotonsteigt,sonst
„geht man Strecken mehrfach“ (bildlich gesprochen),
s.Bildlinks).DasselbegiltfürdieandereLaufrichtung.
Folglich ist die kleinstmögliche Summe aller Differenzen38.
AuchhierklärtmandieFragenachderAnzahlderartigerAnordnungenleicht:Die18Zahlenvon2bis
19werdenaufdiebeidenZwischenräumezwischen1und20beliebigverteilt.Dafürgibtes A = 218 Möglichkeiten (das sind nur 262144). Das ist bereits die gesuchte Anzahl, denn auf jeder Seite
müssen die Zahlen sortiert stehen (wegen der Monotonieforderung). Will man die symmetrischen
Anordnungennureinmalzählen,soteiltmanwiederdurch2.