log (a) - toolcase.org

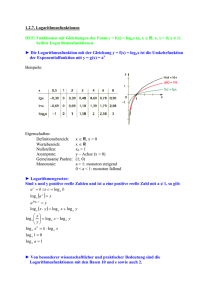
Logarithmen
Die Gleichung a=b c lässt sich relativ einfach nach b auflösen, indem man a mit
dem Kehrwert von c Potenziert: b=a 1/ c . Für das Auflösen nach c hingegen
braucht es eine neue Funktion, den Logarithmus. Der Logarithmus ist also die
Umkehrung der Potenz.
log b (a)
a=b c
b=a 1/ c
c=log b (a)
Die Logarithmus-Funktion hat wie auch die Potenz-Funktion zwei Argumente:
Die Basis wird hinter der Kurzbezeichnung log tiefergestellt notiert, der
Numerus in Klammern dahinter.
Da die meisten Problemstellungen im Alltag ohne diese Funktion auskommen, ist sie eher
unbekannt und ungewohnt.
Hinweis: Basis und Numerus eines Logarithmus müssen stets grösser Null sein,
bei der Basis ist zudem die Zahl 1 verboten1 (a>0, b>0 und b≠1). Das Ergebnis
eines Logarithmus kann aber aus dem ganzen reellen Zahlenraum (ℝ) stammen.
Termregeln
Mit einigen Überlegungen, lassen sich die Eigenschaften dieser Funktion herleiten
b log (a)=a und log b (ba )=a
Da der Logarithmus die Umkehrung der Potenz ist gilt
b
Daraus wiederum log b ( b0 )=0=log b (1) . Gilt eine Regel unabhängig von der
Basis b, kann man diese zur Verdeutlichung weglassen:
Anhand von einfachen Zahlenbeispielen und dem Potenzgesetz a b⋅a c =a b+c
entsprechende Gesetz für den Logarithmus eines Produktes herleiten
log 10 (0.1)=−1
10−1=0.1
0
log 10 (1)=0
10 =1
1
→
log 10 (10)=1
10 =10
2
log 10 (100)=2
10 =100
3
log 10 (1000)=3
10 =1000
log(1)=0
kann man das
log 10 (10)=1
log 10 (100)=2
log 10 (1000)=3=log 10 (10⋅100)
3=1+2
→ log10 (1000)=log 10 (10)+log 10 (100)
→ log 10 (b⋅c)=log 10 (b)+log 10 ( c)
Darauf basierend kann man die wichtigsten Regeln herleiten, die denen der Potenzen sehr ähneln.
Logarithmus
Potenzen
log(b⋅c )=log (b)+ log(c )
log( b/c )=log( b)−log(c)
log(1/c )=−log(c )
a b⋅a c =a b+c
a b /a c=ab −c
1/ a c=a−c
Die nächste wichtige Regel lässt sich aus log(b⋅c )=log( b)+ log(c ) herleiten. Erweitert man
diese auf 3 Elemente, dafür alle gleich gross, log(b⋅b⋅b)=log(b)+ log(b)+log( b) und fasst die
Terme zusammen zu log( b3)=3⋅log(b) erkennt man die Regeln für Logarithmen von Potenzen
c
log(b )=c⋅log(b)
1
Dies da für alle x 1x = 1 gilt.
Logarithmen
1/5
Jörg Mäder (15.4.2013)
Basiswechsel
Die bisherigen Regeln gingen immer davon aus, das man stets die selbe Basis verwendet. Die Regel
für einen Basiswechsel wird wie folgt hergeleitet. Mit a=x b gilt zum eine b=log x (a) , zum
anderen log y ( a)=log y ( x b)=b⋅log y ( x ) . Fasst man beide zusammen (b eliminieren) ergibt sich
log y (a)=log x (a)⋅log y ( x) . Üblicherweise wird diese Regel wie folgt notiert:
log x (a)=
log y (a)
log y ( x)
Dank dieser Regel reicht es aus, wenn ein Taschenrechner die Logarithmen zu einer Basis
berechnen kann. Alle anderen kann man mit dieser Regel ausrechnen2.
Übliche Werte für die Basis
Von Wachstumsprozessen abgesehen (siehe eigenes Dokument) dominieren drei Basen:
Basis
Kurzschreibweise3
Anwendung
10
Vor allem in technischen Problemstellungen
anzutreffen, da 10 die Basis unseres
Stellenwertsystem ist (siehe auch weiter unten).
lg (x )=log 10 (x )
e = 2.71828...
natürliche Zahl
Vor allem in mathematischen Problemstellungen
häufig. Am einfachsten zu berechnen und bei
Ableitungen/Integration handhabbar.
ln( x)=log e ( x )
2
In der Informatik zentral, da diese binär arbeitet.
ld (x )=lb( x)=log 2 (x )
Logarithmische Skalen
Wie oben gezeigt bleibt das Ergebnis eines Logarithmus selbst für riesige Zahlen verhältnismässig
klein. Dies wird in verschiedenen Bereichen, in denen Zahlen aus grossen Wertebereichen möglich
sind, ausgenutzt um eine zwar abstraktere aber handlichere Skala zu erhalten. Dazu werden die
originalen Werte einfach logarithmiert, meist zur Basis 10.
Die bekannteste logarithmische Skala ist die Richterskala für
Erdebenstärken. Eine Differenz von 1 auf der Richterskala
bedeutet ein Faktor 10 beim Ausschlag der Messnadel (×32
bezüglich Energie), eine Differenz von 2 entsprechend
Faktor 102=100 (1024fache Energie). Die Erdbebenskala
umfasst Werte zwischen 2 bis 10, was einem Faktor von rund
100 Millionen (108) entspricht.
Andere logarithmische Skalen sind: Schalldruck
(Lautstärke4), Helligkeit, ph-Werte (Säure/Base), Helligkeit
von Sternen, Tonleitern5.
Ob und welche logarithmische Skala verwendet wird, ist aber oft historisch bedingt.
2
3
4
5
In der Regel kennen Taschenrechner nur die Logarithmen zur Basis 10 und e
Leider ist die Verwendung nicht einheitlich. Speziell log wird uneinheitlich verwendet, hier sind
Branchenkenntnisse respektive vertiefte Abklärungen gefragt.
Der Mensch empfindet die Lautstärke näherungsweise logarithmisch.
Plus ein Halbton bedeutet ein Faktor 1.05946 bei der Frequenz, plus eine Oktave (12 Halbtöne) Faktor 2.
Logarithmen
2/5
Jörg Mäder (15.4.2013)
Grössenordnung
Der Alltagsbegriff Grössenordnung entspricht einem Faktor 10 und hat daher logarithmischen
Charakter. Eine halbe Grössenordnung entsprechend einem Faktor 3 (3² ∼ 10) und nicht etwa 5.
Münzen und Noten
Eine Art logarithmische Skala gibt es bei modernen
Bargeldmitteln (Münzen und Noten). Deren Werte
beginnen üblicherweise mit den Zahlen 1, 2 oder 5.
Das hat den Vorteil, dass der Faktor von einem Wert
zum nächsthöheren entweder 2 (1 → 2 & 5 → 10)
oder 2.5 (2 → 5) ist. Der Faktor 10 wird also in drei
ähnlich grosse Abschnitte unterteilt6, was auch die
Menge an nötigem Bargeld reduziert. Würde man mit
¼-, ½- und ¾-Münzen arbeiten, was auch
naheliegend wäre, bräuchte es Anzahl mässig mehr Münzen und Noten im Umlauf. Dies da der
Verkäufer bei Preisen um 10 Franken in 10 Rappen Schritten arbeitet, bei Preisen um 90 Franken
aber eher auf ganze Franken rundet.
Lineare versus logarithmische Skala
Die Frage stellt sich nun, wann eine lineare Skala, wann eine logarithmische angewendet werden
soll. Eine fixe Regel gibt es nicht. Wenn aber die Spannweite an möglichen Werten im Vergleich zu
den Werten selbst klein ist, ist eine lineare Skala angezeigt, ist sie gross, eine logarithmische.
Beispiel linear: Über 99% der Frauen sind zwischen 150 und 190cm gross, also eine Spannweite
von 40cm im Vergleich zum Durchschnitt von 163cm. Hier reicht eine lineare Skala völlig aus.
Beispiel logarithmisch: Kaum jemand wird die Gewichtsdifferenz zwischen einem Gummiboot
(8kg) und einem Supertanker (250'000t) berechnen, sondern den Faktor.
Spannweiten in der Natur
Die leichtesten Säugetiere (Etruskerspitzmaus) sind etwa 2
Gramm schwer, während es Blauwale auf bis zu 150 Tonnen
bringen. Das sind über 7 Grössenordnungen.
Nach aktuellen physikalischen Theorien ist die kleinste sinnvolle Länge 3.045⋅10−35 m lang
(Planck-Länge) und das Universum etwa 7.38⋅10 26 m gross (= 78 Milliarden Lichtjahre). Das
Universum umfasst also bezüglich Längen rund 60 Grössenordnungen.
6
Mathematisch ideal wäre 2.15442 = 101/3, was aber zu komischen Münzen führen würde.
Logarithmen
3/5
Jörg Mäder (15.4.2013)
Exponentialschreibweise versus logarithmische Skalen
Eine andere Variante um Zahlen mit extrem grosser Spannweite aufzuschreiben ist die
Exponentialschreibweise7. Die logarithmierte Skala hat aber ihr gegenüber den Vorteil, dass sie
gleichmässig ist. Um dies zu veranschaulichen vergleichen wir Zahlen in beiden Schreibweisen.
Exponentialschreibweise
Die Mantisse in Exponentialschreibweise mit einer Nachkommastelle liegt stets zwischen 1.0 und
9.9. Die Grössenordnung wird durch den Exponenten festgelegt. Vergleicht man zwei aufeinander
folgende Zahlen aus dieser Serie, bleibt die Differenz 90 mal konstant um anschliessend um Faktor
10 zu wachsen. Die Faktoren nehmen 90 mal leicht ab (von 1.1 auf 1.0101) um dann auf 1.1 zurück
zu springen. Differenz und Faktor sind also nicht konstant und weisen Sprünge auf.
1.1⋅103
1.2⋅103
...
9.8⋅103
9.9⋅10 3
1.0⋅10 4
1.1⋅104
1100
1200
...
9800
9900
10'000
11'000
Δ
+100
+100
...
+100
+100
+100
+1000
f
·1.1
·1.09091
...
·1.01031
·1.0102
·1.0101
·1.1
1.0⋅10
x
1000
3
Logarithmische Skala zur Basis 10
Nimmt man eine logarithmische Skala zur Basis 10 mit 2 Nachkommastellen, was in etwa die selbe
Auflösung bietet wie eine Mantisse mit einer Nachkommastelle, und vergleicht benachbarte Zahlen
erkennt man, dass die Differenzen ohne Sprünge kontinuierlich ansteigen und die Faktoren sogar
konstant bleiben. Dieses vorteilhafte Verhalten überwiegt in vielen Anwendungen den Nachteil der
schwierigeren Interpretation.
lg(x)
3.00
3.01
3.02
x
1000
1023.29
Δ
f
...
3.98
3.99
4.00
4.01
1047.13
9549.93
9772.37
10'000
10232.9
23.293
23.8356
217.383
222.446
227.628
232.93
1.02329
1.02329
1.02329
1.02329
1.02329
1.02329
Umrechnung Exponential versus 10er-Logarithmus
Zur Basis 10 logarithmierte Zahlen lassen sich relativ einfach in Exponentialschreibweise
umrechnen und umgekehrt. Dies aufgrund der folgenden Beziehung
lg (a⋅10b )=lg (a)+lg (10 b)=lg (a)+b⋅lg ( 10)=b+ lg (a)
Da für die Mantisse a 1≤a<10 gilt, gilt für deren 10er-Log per Definition 0≤lg( a)<1 .
Das heisst: die Nachkommastellen der logarithmierten Zahl werden einzig durch die Mantisse
beeinflusst, der ganzzahlige Anteil der Zahl entspricht direkt dem Exponenten
Beispiel: lg (1.2345⋅108 )=8.09149 mit 100.09149 =1.2345
7
oder das verwenden von Einheiten (m, μm, km ...), was fast auf das gleiche herauskommt.
Logarithmen
4/5
Jörg Mäder (15.4.2013)
Merkregeln für den 10er Logarithmus
Die bei der Umrechnung „Exponential-Logarithmisch“ gefundene Beziehung, kann man nutzen um
die Anfangs nicht sehr intuitiven logarithmierten Zahlen etwas zu veranschaulichen.
Aus dem ganzzahligen Anteil ergibt sich die Grössenordnung. Ein dekadisch logarithmierter Wert
von 6.49 liegt also irgendwo zwischen einer und zehn Millionen, da 1 Million = 106 gilt.
Die Nachkommastellen definieren die verschiedenen Ziffern der eigentlichen Zahl.
Merkregel: ein 5 wird logarithmiert zu 0.7, eine 3 zu 0.5.
6.49 muss also in der Gegend von 3 Millionen liegen.
Die Merkregel für die Nachkommastellen kann man auch wie folgt gebrauchen: Unterscheiden sich
zwei logarithmierte Werte um 0.7, liegt zwischen den originalen Werten etwa Faktor 5.
Berechnung von „Hand“
Die Berechnung des Logarithmus von Hand ist extrem aufwändig und auch Computer können ihn
nur näherungsweise berechnen. Der Klassische Ansatz für dieses Verfahren funktioniert zur Basis e
was auch einer der Gründe ist, warum der natürliche Logarithmus eine solch grosse Rolle spielt.
ln( x+ 1)=
x0 x2 x3 x4
− + − ...
1 2 3 4
Anmerkung: Vor dem Aufkommen von Taschenrechner hat man die Werte von Logarithmen in
grossen Logarithmentafeln notiert und bei Bedarf dort nachgeschlagen. Je nach Genauigkeit dieser
Tafeln waren es eine einzelne Seite oder ganze Bücher.
Extrem grosse Zahlen berechnen
Selbst gute Taschenrechner steigen bei extrem grossen Potenzen aus8. Mit einem kleinen Trick lässt
sich diese Grenze aber umgehen.
Problemstellung:
Wie sieht die Zahl 458961 in Exponentialschreibweise aus?
Oder anders formuliert:
Wie gross müssen a und b sein damit 458961 =a⋅10b gilt,
wobei b ganzzahlig ist und 1≤ a <10 gilt.
Lösung:
Die gesuchte Zahl wird zuerst mit lg transformiert9 und berechnet:
lg (458961 )=8961⋅lg(45)=14814.4373
Dieses Ergebnis kann man gemäss obigen Abschnitt (Umrechnung Exponential versus 10erLogarithmus) in Exponentialschreibweise umformen. Die Mantisse a lautet entsprechend
0.4373
a=10
=2.73715 der Exponent b ist 14'814, beides zusammengesetzt ergibt
8961
45
8
9
=2.73715⋅10
14814
Die meisten TR können 2332 noch berechnen (8.749·1099), bei 2333 ist aber fertig.
Diese Lösungstechnik (Aufgabe transformieren, im transformierten System lösen, Lösung rücktransformieren) ist
in der Mathematik ein häufiges Vorgehen,
Logarithmen
5/5
Jörg Mäder (15.4.2013)