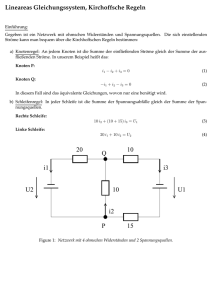
Analysis und lineare Algebra f¨ur die Informatik

Analysis und lineare Algebra für die Informatik
Amin Coja-Oghlan
[email protected]
12. Februar 2014
Zusammenfassung
Inhalt dieser Vorlesung sind die Grundlagen der Linearen Algebra und der Analysis. Die Vorlesung
ist angelehnt an Standardtexte zu diesen Themen wie insbesondere [1, 2, 3, 5]. Die Themen der Veranstaltung sind (nicht notwendigerweise in dieser Reihenfolge):
• Vektorräume, lineare Abbildungen und Matrizen.
• Skalarprodukt und Orthogonalität.
• Orthonormalbasen und Orthogonalprojektion.
• Symmetrische Matrizen, quadratische Formen, Singulärwertzerlegung.
• Eigenwerte und Eigenvektoren.
• Lokale lineare Approximation und Differentialkalkül.
• Lokale Approximation der Ordnung zwei.
• Integration.
• Die komplexe Zahlenebene und Euler-Formel.
• Exponentialfunktion, Logarithmus, trigonometrische Funktionen.
• Fourierreihen und Geometrie in Funktionenräumen.
• Jacobimatrix, Volumen und Determinante.
• Lineare dynamische Systeme.
1
Grundbegriffe
Dieser Abschnitt faßt einige Konzepte zusammen, die aus der Schulmathematik bekannt sein sollten.
In der Vorlesung werden die Begriffe der (naiven) Mengenlehre benutzt. Insbesondere bezeichnet N =
{1, 2, 3, . . .} die Menge der natürlichen Zahlen, Z = {0, −1, 1, −2, 2, . . .} die Menge der ganzen Zahlen,
Q die Menge der rationalen und R die Menge der reellen Zahlen.
Seien A, B Mengen. Die Schreibweise x ∈ A bedeutet, daß x ein Element der Menge A ist. Ferner
bedeutet A ⊂ B, daß A eine (nicht notwendigerweise echte) Teilmenge von B ist, d.h. jedes Element
von A ist auch ein Element von B. Mit A ∪ B bezeichnen wir die Vereinigung von A und B; dies ist die
Menge aller Element, die in A oder in B enthalten sind. Außerdem ist A ∩ B der Durchschnitt von zwei
Mengen, d.h. die Menge aller Elemente, die in A und B enthalten sind. Mit A \ B, gesprochen A ohne B,
bezeichnen wir die Menge aller Elemente von A, die nicht Element von B sind. Schließlich ist A × B die
Produktmenge von A und B, d.h. die Menge aller geordneten Paare (x, y) mit x ∈ A und y ∈ B.
Sind f : A → B, x 7→ f (x) und g : B → C, y 7→ g(y) Abbildungen, so bezeichnen wir mit g ◦ f die
Abbildung A → C, x 7→ g(f (x)). Eine Abbildung f : A → B heißt injektiv, falls für je zwei verschiedene
Elemente x, x0 ∈ A gilt, daß f (x) 6= f (x0 ). Ferner heißt f surjektiv, falls es zu jedem y ∈ B ein x ∈ A
mit f (x) = y gibt. Eine Abbildung, die sowohl injektiv als auch surjektiv ist, heißt bijektiv.
Für eine Abbildung f : A → B und eine Teilmenge Z ⊂ A ist f (Z) = {f (z) : z ∈ Z} das Bild von
Z unter f . Umgekehrt bezeichnen wir für C ⊂ B mit f −1 (C) die Menge aller x ∈ A mit f (x) ∈ C. Wir
nennen f −1 (C) die Urbildmenge von C. Falls f eine bijektive Abbildung ist, so hat für jedes y ∈ B die
1
1
GRUNDBEGRIFFE
2
Menge f −1 ({y}) genau ein Element x und wir schreiben einfach x = f −1 (y). Die Abbildung f −1 : B →
A, y 7→ f −1 (y) ist in diesem Fall ebenfalls bijektiv und heißt die Umkehrabbildung von f .
Für eine Menge B und eine Zahl k ∈ N bezeichnen wir mit B k die Menge aller Abbildugen f :
{1, . . . , k} → B. Anstelle der Notation f : A → B, a 7→ f (a) schreiben wir mitunter etwas lax
(f (a))a∈A . Diese Notation wird häufig verwendet, wenn A = {1, 2, 3, . . . , k} für eine Zahl k ∈ N.
Insbesondere schreiben wir die Elemente f der Menge B k als (f (1), . . . , f (k)); sie werden auch k-Tupel
(und im Fall k = 2 Paare und im Fall k = 3 Tripel) genannt. Allgemeiner bezeichnen wir mit B A die
Menge aller Abbildungen f : A → B.
Ist (Ai )i∈I eine Abbildung, die Elementen einer Menge I Teilmengen Ai einer Menge A zuordnet, so
bezeichnet
[
Ai = {x ∈ A : es gibt ein i ∈ I mit x ∈ Ai }
i∈I
die Vereinigung aller Mengen Ai . Analog ist
\
Ai = {x ∈ A : für alle i ∈ I gilt x ∈ Ai }
i∈I
der Durchschnitt aller Ai .
Mit ∅ bezeichnen wir die leere Menge. Eine endliche Menge ist eine Menge A mit einer der beiden
folgenden Eigenschaften:
• A = ∅.
• Für eine Zahl k ∈ N existiert eine bijektive Abbildung f : {1, 2, . . . , k} → A.
Mit |A| bezeichnen wir die Größe, auch genannt die Mächtigkeit oder Kardinalität, einer endlichen Menge
A, definiert als
• |A| = 0, falls A = ∅.
• |A| = k, falls zu k ∈ N eine bijektive Abbildung f : {1, 2, . . . , k} → A existiert.
Falls A nicht endlich ist, schreibt man |A| = ∞.
Sei f : A → R eine Abbildung von einer endlichen Menge A 6= ∅ in die reellen Zahlen. Dann existiert
eine Bijektion g : {1, . . . , k} → A, wobei k ∈ N. Wir definieren die Summe
X
f (a) = f (g(1)) + f (g(1)) + · · · + f (g(k)).
a∈A
und das Produkt
Y
f (a) = f (g(1)) · f (g(2)) · · · f (g(k)).
a∈A
Falls A die leere Menge ist, interpretieren wir die Summe als 0 und das Produkt als 1.
Wir benötigen die Beweismethode der Induktion. Die Grundlage des Induktionsprinzips ist folgende
Tatsache.
Jede nicht-leere Menge natürlicher Zahlen enthält eine kleinste Zahl.
Aus dieser Tatsache folgt
Lemma 1.1 (“Induktionsprinzip”) Angenommen eine Menge A ⊂ N hat die beiden folgenden Eigenschaften.
i. 1 ∈ A.
ii. Wenn 1, . . . , n ∈ A, dann gilt auch n + 1 ∈ A.
Dann gilt A = N.
1
GRUNDBEGRIFFE
3
Beweis. Angenommen A 6= N. Dann ist die Menge B = N \ A nicht leer. Folglich gibt es eine kleinste
Zahl x ∈ B. Aufgrund von i. ist x 6= 1. Ferner gilt 1, . . . , x − 1 ∈ A, weil x ja die kleinste Zahl in B ist.
Nach ii. gilt also x ∈ A, im Widerspruch zu unserer Annahme, daß x ∈ B.
2
Das Induktionsprinzip ermöglicht uns, Beweise nach folgendem Schema zu führen.
i. Zeige, daß die Behauptung für n = 1 stimmt.
ii. Weise ferner nach, daß die Behauptung für n + 1 gilt, wenn sie für 1, . . . , n gilt.
Dann folgt die Behauptung für alle n ∈ N.
Als Beispiel zeigen wir
Lemma 1.2 (“Binomischer Lehrsatz”) Für x, y ∈ R und n ∈ N gilt
n
(x + y)
=
n X
n
i=0
n
=
i
i
xi y n−i ,
n!
i!(n − i)!
wobei
mit
k! =
k
Y
für k ∈ N.
j
j=1
Beweis. Wir
führen Induktion über n. Im Fall n = 1 ist die linke Seite einfach gleich x + y. Die Rechte
Seite ist 10 x + 11 y = x + y, also stimmt die Gleichung.
Für den Induktionsschritt nehmen wir nun an, daß die Formel für (x + y)n stimmt und zeigen, daß dies
auch für (x + y)n+1 der Fall ist. Es gilt
(x + y)
n+1
=
n
(x + y) · (x + y) = (x + y) ·
n X
n
i=0
=
n X
n
i
i=0
xi+1 y n−i +
n X
n
i=0
xi y n−i
[nach Induktion]
xi y n−i+1
n X
n
n i n+1−i
xi+1 y n+1−(i+1) +
xy
(i
+
1)
−
1
i
i=0
i=0
n+1
n X n X
n i n+1−i
=
xj y n+1−j +
xy
j−1
i
j=1
i=0
n X
n
n
n+1
= x
+
+
xj y n+1−j + y n+1 .
j
−
1
j
j=1
=
n X
i
i
(1)
Ferner haben wir
n!
n!(n + 1 − j + j)
n+1
n
n
n!
+
=
=
.
+
=
j!(n − j)! (j − 1)!(n + 1 − j)!
j!(n + 1 − j)!
j
j
j−1
Setzen wir dies in (1) ein, so erhalten wir
(x + y)
n+1
=x
n+1
+
n X
n+1
j=1
wie behauptet.
j
j n+1−j
x y
+y
n+1
=
n+1
X
k=0
n + 1 k n+1−k
x y
,
k
2
2
2
VEKTORRÄUME UND LINEARE ABBILDUNGEN
4
Vektorräume und lineare Abbildungen
Das Hauptziel der ersten Hälfte dieser Vorlesung ist das Verständnis linearer Abbildungen. Dies ist ein Typ
von Abbildung (oder “Funktion”), den wir in der Tat sehr gut verstehen. Deshalb befaßt sich die zweite
Hälfte der Vorlesung in etwa damit, wie man Abbildungen, die nicht linear sind, durch lineare Abbildungen
annähern kann (“was nicht linear ist, wird linear gemacht”).
Um den Begriff der linearen Abbildung einzuführen, müssen wir beschreiben, was sie wohin abbildet.
Diese Objekte sind “Vektoren”. In diesem Abschnitt geben wir eine einfache aber zunächst ausreichende
Definition dieses Begriffs: ein Vektor x ist ein n-Tupel reeller Zahlen, das wir als Spalte schreiben:


x1
 x2 


x =  . .
 .. 
xn
Die Zahlen x1 , . . . , xn heißen die Komponenten des Vektors. Wir führen zwei Rechenregeln für Vektoren
ein: für x, y ∈ Rn definieren wir


x1 + y1
 x2 + y2 


x+y =
.
..


.
xn + yn
Mit anderen Worten:
Zwei Vektoren werden addiert, indem die einzelnen Komponenten als reelle Zahlen addiert
werden.
Außerdem definieren wir für eine reelle Zahl a und einen Vektor x ∈ Rn


a · x1
 a · x2 


a·x=
.
..


.
a · xn
Das bedeutet:
Eine Zahl wird mit einem Vektor multipliziert, indem jede einzelne Komponente mit der Zahl
multipliziert wird.
Wir definieren für x, y ∈ Rn außerdem



x − y = x + (−1) · y = 

x1 − y1
x2 − y2
..
.
xn − yn








und − y = (−1) · y = 

−y1
−y2
..
.



.

−vn
Vektoren werden also komponentenweise subtrahiert. Die Subtraktion x − y ist genaugenommen keine
neue Operation, sondern nur eine “Kurzschreibweise”, weil sie einfach auf die beiden anderen Operationen
(Multiplikation mit einer Zahl und Addition von Vektoren) zurückgeführt wird.
Ein besonders einfacher Vektor ist der Nullvektor, für den wir das Symbol 0 verwenden. Dies ist der
Vektor
 
0
 0 
 
0 =  . ,
 .. 
0
2
VEKTORRÄUME UND LINEARE ABBILDUNGEN
5
dessen Komponenten sämtlich gleich 0 sind. Der Nullvektor hat die Eigenschaft, daß x + 0 = x für jeden
Vektor x.
Natürlich kann man Mengen von Vektoren bilden (und das werden wir auch oft tun). Aber von besonderem Interesse sind Mengen, die mit den soeben definierten Operationen “verträglich sind”.
Definition 2.1 Wir nennen eine Menge E einen Vektorraum, falls die folgenden Bedingungen erfüllt sind.
V0. Es gibt eine natürliche Zahl n, so daß E ⊂ Rn . Außerdem gilt E 6= ∅.
V1. Falls x, y ∈ E, dann gilt auch x + y ∈ E.
V2. Falls x ∈ E, dann gilt für jede reelle Zahl a auch a · x ∈ E.
Mit anderen Worten: ein Vektorraum ist eine nicht-leere Menge von Vektoren in Rn , aus der man mit
den oben definierten Operationen + und · nicht “herausfallen kann”. Insbesondere enthält jeder Vektorraum E den Nullvektor. Um das einzusehen, sei x ∈ E ein Vektor. Nach V2 gilt dann auch 0 · x = 0 ∈ E.
Beispiel 2.2
1. Für jede natürliche Zahl n ist die Menge Rn ein Vektorraum.
2. Für je zwei natürliche Zahlen 1 ≤ k ≤ n ist die Menge
E = {x ∈ Rn : x1 = · · · = xk = 0}
ein Vektorraum.
3. Für jede reelle Zahl a ist die Menge
E = x ∈ R2 : x 2 = a · x 1
ein Vektorraum.
Der Vektorraumbegriff gibt Anlaß zur folgenden Kennzeichung besonderer Teilmengen eines Vektorraumes E, die ebenfalls mit den Operationen + und · verträglich sind.
Definition 2.3 Sei E ein Vektorraum. Wir nennen eine Teilmenge F Untervektorraum von E, falls folgende Bedingungen erfüllt sind.
U0. Es gilt ∅ =
6 F ⊂ E.
U1. Falls x, y ∈ F , dann gilt auch x + y ∈ F .
U2. Falls x ∈ F , dann gilt für jede reelle Zahl a auch a · x ∈ F .
Ein Untervektorraum eines Vektorraums ist also selbst wieder ein Vektorraum.
Beispiel 2.4
1. Der Vektorraum R hat nur zwei Untervektorräume: sich selbst und die Menge {0}, die
nur den Nullvektor enthält.
2. Die Untervektorräume von R2 sind genau die Mengen {0},
Fa = x ∈ R 2 : x 2 = a · x 1
mit a ∈ R,
F∞ = {(0, y) : y ∈ R} ,
(2)
und der gesamte Vektorraum R2 selbst. Geometrisch gesprochen sind die Mengen in (2) nichts anderes als die Geraden durch 0.
3. Die Untervektorräume des R3 sind entsprechend die Mengen {0} und R3 selbst sowie die Geraden
und Ebenen durch 0.
Wir kommen nun zum Hauptbegriff, um den sich der erste Teil der Vorlesung dreht.
2
VEKTORRÄUME UND LINEARE ABBILDUNGEN
6
Definition 2.5 Seien E, E 0 Vektorräume. Eine Abbildung f : E → E 0 heißt linear, falls sie die folgenden
Bedingungen erfüllt.
L1. Für je zwei Vektoren x, y ∈ E gilt f (x + y) = f (x) + f (y).
L2. Für jeden Vektor x ∈ E und jede Zahl a ∈ R gilt f (a · x) = a · f (x).
Salopp gesagt ist eine Abbildung f also linear, wenn man f mit + und · “vertauschen kann”.
Es gibt einige offensichtliche Beispiele linearer Abbildungen. Für je zwei Vektorräume E, E 0 ist die
Abbildung f : E → E 0 , x 7→ 0, die also alle Vektoren auf den Nullvektor abbildet, linear. Außerdem ist
für jeden Vektorraum E die Abbildung id : E → E, x 7→ x, die einfach x auf sich selbst abbildet, linear.
Ist allgemeiner a eine reelle Zahl, so ist die Abbildung E → E, x 7→ a · x linear. Kommen wir zu einigen
vielleicht weniger offensichtliche Beispielen.
x
Beispiel 2.6
1. Die Abbildung R2 → R2 , xy 7→ −y
ist, geometrisch gesprochen, die Spiegelung an
der x-Achse.
◦
2. Die Abbildung R2 → R2 , xy 7→ −y
x ist die Rotation um 90 .
3. Allgemeiner ist R2 → R2 , xy 7→ cos(α)x−sin(α)y
die Rotation um den Winkel α.
sin(α)x+cos(α)y
Aus gegebenen linearen Abbildungen kann man neue basteln. Für eine lineare Abbildung f : E → E 0
und b ∈ R definieren wir eine neue Abbildung b · f : E → E 0 durch x 7→ b · f (x). Außerdem definieren
wir für lineare f, g : E → E 0 die Abbildung f + g : E → E 0 durch x 7→ f (x) + g(x).
Proposition 2.7 Seien f, g : E → E 0 und h : E 0 → E 00 lineare Abbildugen.
1. Für jede Zahl b ∈ R ist b · f linear.
2. Die Abbildung f + g ist linear.
3. Die Abbildung h ◦ f : E → E 00 ist linear.
Beweis. Wir rechnen einfach die erforderlichen Eigenschaften nach. Seien x, y ∈ E und a ∈ R. Weil
f, g, h linear sind, gilt
(b · f )(x + y)
(f + g)(x + y)
h ◦ f (x + y)
= b · (f (x) + f (y)) = b · f (x) + b · f (y) = (b · f )(x) + (b · f )(y),
= f (x + y) + g(x + y) = f (x) + f (y) + g(x) + g(y) = (f + g)(x) + (f + g)(y),
= h(f (x + y)) = h(f (x) + f (y)) = h(f (x)) + h(f (y)) = h ◦ f (x) + h ◦ f (y).
Also erfüllen b · f , f + g und h ◦ f die Bedingung L1. Ferner gilt
(b · f )(a · x)
(f + g)(a · x)
h ◦ f (a · x)
= b · (a · f (x)) = a · (b · f (x)) = a · (b · f )(x),
= f (a · x) + g(a · x) = a · f (x) + a · g(x) = a · (f + g)(x),
= h(f (a · x)) = h(a · f (x)) = a · h(f (x)) = a · h ◦ f (x),
2
woraus L2 folgt.
Proposition 2.8 Sei f : E → E 0 eine bijektive lineare Abbildung. Dann ist auch ihre Umkehrabbildung
f −1 : E 0 → E linear.
Beweis. Seien x0 , y 0 ∈ E 0 Vektoren. Dann gibt es x, y ∈ E mit x0 = f (x), y 0 = f (y). Weil f linear ist, gilt
also x0 + y 0 = f (x + y). Weil f außerdem bijektiv ist, folgt
f −1 (x0 + y 0 ) = f −1 (f (x + y)) = x + y = f −1 (x0 ) + f −1 (y 0 ).
Ist ferner a ∈ R, so gilt
f −1 (a · x0 ) = f −1 (a · f (x)) = f −1 (f (a · x)) = a · x = a · f −1 (x0 ).
Also erfüllt f −1 die Bedingungen L1–L2.
2
Lineare Abbildungen werden auch oft als Homomorphismen bezeichnet. Eine bijektive lineare Abbildung heißt ein Isomorphismus.
3
3
MATRIZEN
7
Matrizen
Das Ziel in diesem Abschnitt ist, lineare Abbildungen f : Rn → Rm möglichst einfach zu beschreiben.
Dazu definieren wir ein neues Objekt: eine m × n-Matrix A ist eine Abbildung
A : {1, . . . , m} × {1, . . . , n} → R,
(i, j) 7→ Aij .
Wir schreiben eine Matrix in der Form

A11
 ..
A= .
Am1
···
..
.
···

A1n
..  .
. 
Amn
Wir nennen das n-Tupel A(i) = (Ai1 , . . . , Ain ) die i-te Zeile von A. Entsprechend heißt der Vektor


A1j


A(j) =  ... 
Amj
die j-te Spalte von A. Die einzelnen Zahlen Aij heißen die Einträge von A. Die Reihenfolge der Indices
merken wir uns mit der Eselsbrücke “Zeilen zuerst, Spalten später”. Falls m = n, nennen wir M eine
quadratische Matrix.
Was haben Matrizen mit linearen Abbildungen zu tun? Betrachten wir einmal die Vektoren
 
 
 
1
0
0
 0 
 1 
 0 
 
 
 
 
 
 
e(1) =  0  , e(2) =  0  , . . . , e(n) =  ...  ∈ Rn .
(3)
 .. 
 .. 
 
 . 
 . 
 0 
0
0
1
In Worten: e(i) ist der Vektor, dessen i-te Komponente 1 ist, während alle anderen Komponenten 0 sind.
Dann können wir jeden Vektor x ∈ Rn schreiben als


x1
n
X


xk e(k) .
x =  ...  = x1 · e(1) + · · · + xn e(n) =
k=1
xn
Ist f : Rn → Rm eine lineare Abbildung, dann ist also
!
n
n
X
X
f (x) = f
xk e(k) =
xk f (e(k) ).
k=1
(4)
k=1
Wenn wir also die n Vektoren f (e(1) ), . . . , f (e(n) ) ∈ Rm kennen, dann wissen wir f (x) für alle x ∈ Rn .
Mit anderen Worten: f is vollständig dadurch bestimmt, wohin es die Vektoren e(1) , . . . , e(n) abbildet.
Wir fassen diese n Vektoren in einer Matrix zuammen. Genauer sei M (f ) die m × n-Matrix mit Spalten
f (e(1) ), . . . , f (e(n) ). Diese Matrix heißt die darstellende Matrix von f .
Um die Gleichung (4) direkt mit der Matrix M (f ) schreiben zu können, definieren wir, wie man eine
Matrix mit einem Vektor multipliziert. Für eine mP
× n-Matrix A und einen Vektor x ∈ Rn definieren wir
n
m
A · x ∈ R als den Vektor mit i-ter Komponente j=1 Aij xj . Anders ausgedrückt,


A11 x1 + A12 x2 + · · · + A1n xn


..


.
A·x=
.
 A21 x1 + A22 x2 + · · · + A2n xn 
Am1 x1 + A12 x2 + · · · + Amn xn
3
MATRIZEN
8
Noch anders ausgedrückt, wenn wir mit A(k) die k-te Spalte


A1k
 A2k 


 .. 
 . 
Amk
von A bezeichnen, dann ist
A·x=
n
X
xj A(j) = x1 A(1) + x2 A(2) + · · · + xn A(n) .
(5)
j=1
Mit dieser Definition können wir dann (4) schreiben als
f (x) = M (f ) · x.
Die lineare Abbildung f ist also nichts anderes als Multiplikation mit der Matrix M (f ). Umgekehrt stellt
unsere Definition von “Matrix mal Vektor” sicher, daß für jede m × n Matrix A die Abbildung Rn → Rm ,
x 7→ A · x linear ist.
Beispiel 3.1 Wir hatten gesehen, daß die lineare Abbildung
x
cos(α)x − sin(α)y
2
2
f :R →R ,
7→
y
sin(α)x + cos(α)y
geometrisch gesehen die Rotation um den Winkel α ist. Die darstellende Matrix ist
cos α − sin α
M (f ) =
.
sin α cos α
Wir hatten gewissen Rechenregeln für lineare Abbildungen definiert. Beispielsweise hatten wir gesehen, daß für zwei lineare Abbildungen f, g : Rn → Rm auch f + g eine lineare Abbildung ist. Um
diese Operationen in den Matrizen M (f ), M (g), M (f + g) widerzuspiegeln, definieren wir einige weitere
Rechenarten für Matrizen. Für zwei m × n-Matrizen A, B definieren wir


A11 + B11 · · · A1n + B1n


..
..
..
A+B =
.
.
.
.
Am1 + Bm1
···
Amn + Bmn
Man addiert also Matrizen, indem man die einzelnen Einträge addiert. Für eine reelle Zahl a definieren wir
ferner


a · A11 · · · a · A1n


..
..
..
a·A=
.
.
.
.
a · Am1
···
a · Amn
Also multipliziert man eine Zahl mit einer Matrix, indem man jeden Eintrag mit der Zahl multipliziert.
Proposition 3.2 Sind f, g : Rn → Rm lineare Abbildungen, so ist M (f + g) = M (f ) + M (g). Ist ferner
a ∈ R, so ist M (a · f ) = a · M (f ).
Beweis. Per Definition der Matrizen M (f ), M (g), M (f +g), M (a·f ) genügt es, (f +g)(e(k) ), (a·f )(e(k) )
auszurechnen. Es gilt (f + g)(e(k) ) = f (e(k) ) + g(e(k) ), (a · f )(e(k) ) = a · f (e(k) ).
2
Wenn f : Rn → Rm und g : Rm → Rl lineare Abbildungen sind, können wir dann auch eine
schöne Formel für M (g ◦ f ) angeben? Dazu müßten wir verstehen, was die lineare Abbildung g ◦ f mit
3
MATRIZEN
9
den Vektoren e(j) ∈ Rn macht. Der Einfachheit halber schreiben wir A = M (f ) und B = M (g). Dann
ist


A1j


f (e(j) ) = A(j) =  ... 
Amj
die j-te Spalte von A. Wenden wir die Matrix-mal-Vektor-Formel (5) an, so erhalten wir
g ◦ f (e(j) ) = g(f (e(j) )) = g(A(j) ) =
m
X
Ahj B (h) .
h=1
Hierbei ist Ahj ∈ R die h-te Komponente des Vektors A
Der (i, j)-Eintrag der Matrix M (g ◦ f ) ist also
(M (g ◦ f ))ij =
(j)
m
X
und B (h) ∈ Rl die h-te Spalte der Matrix B.
Bih Ahj .
(6)
h=1
Wir verwandeln diese Gleichung nun in eine Definition. Ist B eine l × m-Matrix
und A eine m × nPm
Matrix, so definieren wir ihr Produkt B · A als die l × n-Matrix mit (i, j)-Eintrag h=1 Bih Ahj für alle
i ∈ {1, . . . , l} und alle j ∈ {1, . . . , n}. In Symbolen,
(B · A)ij =
m
X
Bih Ahj .
h=1
Als Eselsbrücke kann man sagen, daß man B · A erhält nach der Regel “Zeile mal Spalte”. Genauer: man
multipliziert die Einträge der i-ten Zeile von B mit den entsprechenden Einträgen der j-ten Spalte von A
und summiert die Produkte auf. Die Gleichung (6) zeigt nun, daß
M (g ◦ f ) = M (g) · M (f ).
(7)
Für quadratische Matrizen benutzen wir auch die Potenzschreibweise . Mit Ak für k ∈ N bezeichnen
wir also das Produkt
Ak = A
| · A{z· · · A} .
k mal
Einige Matrizen spielen eine besondere Rolle. Für jede Größe m × n bezeichnen wir mit 0 die Matrix,
deren Einträge alle gleich 0 sind. Diese Matrix hat die Eigenschaft, daß A + 0 = 0 + A = A für alle A.
Außerdem bezeichnet id die n × n-Matrix, deren Diagonaleinträge gleich 1 sind, während alle anderen
Einträge gleich 0 sind. Für jede n × n-Matrix A gilt id · A = A · id = A. Ferner gilt id · x = x für jeden
Vektor x ∈ Rn . Allgemeiner bezeichnen wir für einen Vektor a ∈ Rn mit diag(a) die n × n-Matrix, deren
Diagonale gerade der Vektor a ist, während alle anderen Einträge gleich 0 sind. Für jeden Vektor x ∈ Rn
gilt dann


a1 x1
 a2 x2 


diag(a) · x =  .  .
 .. 
an xn
Schließlich sagen wir, daß eine m×n-Matrix D Diagonalform hat, wenn aus Dij 6= 0 folgt, daß i = j (i =
1, . . . , m; j = 1, . . . , n). Mit anderen Worten: nur die Diagonaleinträge Dii dürfen von Null verschieden
sein.
Bemerkung 3.3 Die Multiplikation von Matrizen ist nicht kommutativ, d.h. A · B ist im allgemeinen nicht
dasselbe wie B · A. In der Tat sind beide Produkte überhaupt nur dann definiert, wenn A, B beide quadratisch und von derselben Größe sind. Aber auch in diesem Fall stimmen A · B und B · A im allgemeinen
nicht überein. Als Gegenbeispiel betrachte
0 1
1 1
A=
,
B=
.
0 0
0 0
4
BASEN UND DIE DIMENSION
Wir erhalten
10
A·B =
0
0
0
0
,
B·A=
0
0
1
0
.
Wenn man Matrizen addieren und multiplizieren kann, kann man sie dann auch durcheinander “dividieren”?
Definition 3.4 Seien A, B n × n-Matrizen. Wir sagen, daß B zu A invers ist, wenn A · B = B · A = id.
Falls es eine Matrix B gibt, die zu A invers ist, heißt A invertierbar oder regulär, andernfalls heißt A
singulär.
Obige Bemerkung zeigt, daß nicht jede Matriz invertierbar ist. Es kann sogar passieren, daß A · B = 0,
obwohl A 6= 0 und B 6= 0. Wir können invertierbare Matrizen wie folgt charakterisieren.
Proposition 3.5 Eine n × n-Matrix A ist genau dann invertierbar, wenn die lineare Abbildung x ∈ Rn 7→
A · x ein Isomorphismus ist.
Beweis. Angenommen die lineare Abbildung f : Rn → Rn , x 7→ A · x ist ein Isomorphismus. Dann
ist auch f −1 : Rn → Rn ein Isomorphismus. Sei B = M (f −1 ) die Matrix, die diesen Isomorphismus
darstellt. Dann gilt
id = M (f ◦ f −1 ) = M (f ) · M (f −1 ) = A · B und id = M (f −1 ◦ f ) = M (f −1 ) · M (f ) = B · A.
Also ist B zu A invers.
Nehmen wir nun umgekehrt an, daß A ein Inverses B hat, so definieren wir die lineare Abbildung
g : x 7→ B · x. Dann gilt für jeden Vektor x ∈ Rn
f ◦ g(x) = f (g(x)) = A · B · x = id · x = x,
g ◦ f (x) = g(f (x)) = B · A · x = id · x = x.
Folglich ist f bijektiv und g die Umkehrabbildung von f .
2
Der Beweis von Proposition 3.5 zeigt, daß eine invertierbare Matrix A eine eindeutige inverse Matrix
hat (nämlich die Matrix M (f −1 ) in obigem Beweis). Wir bezeichnen diese Matrix durch A−1 . Aus (7)
folgt, daß für zwei invertierbare n × n-Matrizen A, B gilt
(A · B)−1 = B −1 · A−1 .
Beispiel 3.6
1. Die Diagonalmatrix A = diag(a1 , . . . , an ) ist genau dann invertierbar, wenn a1 , . . . , an 6=
−1
0. Ihr Inverses ist in diesem Fall A−1 = diag(a−1
1 , . . . , an ).
2. Die darstellende Matrix
cos α
sin α
− sin α
cos α
der Rotation um den Winkel α ist invertierbar. Ihr Inverses ist die Matrix
cos α sin α
,
− sin α cos α
die die Rotation um den Winkel −α darstellt.
4
Basen und die Dimension
Wir führen ein Maß für die “Größe” eines Vektorraums ein, die Dimension. Beispielsweise wird die Dimension des Vektorraumes Rn gleich n sein. Um den Begriff der Dimension einzuführen, benötigen wir
folgende
Definition 4.1 Seien x1 , . . . , xk ∈ E Vektoren in einem Vektorraum E. Wir nennen x1 , . . . , xk linear
unabhängig, falls folgendes gilt.
4
BASEN UND DIE DIMENSION
11
Sind a1 , . . . , ak reelle Zahlen, so daß
Pk
i=1
ai xi = 0, so folgt ai = 0 für i = 1, . . . , k.
Beispiel 4.2 Die Vektoren e(1) , . . . , e(n) ∈ Rn sind linear unabhängig. Denn für reelle a1 , . . . , an gilt


a1
n
 a2 
X


ai e(i) =  .  .
 .. 
i=1
an
Dies ist nur dann der Nullvektor, wenn a1 = a2 = · · · = an = 0.
Für Vektoren x1 , . . . , xk definieren wir
[x1 , . . . , xk ] =
( k
X
)
ai · xi : a1 , . . . , ak ∈ R .
i=1
Dies ist ein Vektorraum, den wir den von x1 , . . . , xk aufgespannten Vektorraum nennen. Der Kernbegriff,
den wir benötigen, um die Dimension zu definieren, ist der der Basis.
Definition 4.3 Seien x1 , . . . , xk Vektoren in einem Vektorraum E. Wir nennen x1 , . . . , xk eine Basis von
E, falls die beiden folgenden Bedingungen erfüllt sind.
B1. x1 , . . . , xk sind linear unabhängig.
B2. Es gilt E = [x1 , . . . , xk ].
Eine Basis hat die folgende wichtige Eigenschaft.
Proposition 4.4 Ist x1 , . . . , xk eine Basis
Pk des Vektorraums E, so gibt es zu jedem Vektor y ∈ E genau ein
k-Tupel a1 , . . . , ak ∈ R, so daß y = i=1 ai xi .
Pk
Beweis. Weil E = [x1 , . . . , xk ], gibt es zu jedem y ∈ E Zahlen a1 , . . . , ak mit y = i=1 ai xi . Nehmen
Pk
wir nun an, daß b1 , . . . , bk ∈ R ein weiteres k-Tupel ist, so daß y = i=1 bi xi . Dann gilt
0=y−y =
k
X
(bi − ai )xi .
i=1
Weil die Vektoren x1 , . . . , xk linear unabhängig sind, folgt bi = ai für alle i.
2
Wir würden gern die Dimension des Raumes E definieren als die Anzahl der Vektoren in einer Basis
von E. Dazu müssen wir uns allerdings noch zwei Dinge überlegen:
• Jeder Vektorraum hat eine Basis.
• Alle Basen bestehen aus gleichvielen Vektoren.
Dazu benötigen wir
Proposition 4.5 Angenommen x1 , . . . , xn ist eine Basis von E und die Vektoren y1 , . . . , yk ∈ E sind
linear unabhängig. Dann ist k ≤ n und es gibt eine injektive Abbildung τ : {k + 1, . . . , n} → {1, . . . , n},
so daß
y1 , . . . , yk , xτ (k+1) , . . . , xτ (n)
eine Basis von E ist.
Der Beweis dieser Aussage benötigt einen Zwischenschritt.
Lemma 4.6 Sei x1 , . . . , xn eine Basis des Vektorraums E. Falls z = a1 x1 + · · · + an xn ein Vektor ist mit
a1 6= 0, so ist z, x2 , . . . , xn eine Basis von E.
4
BASEN UND DIE DIMENSION
12
Beweis. Angenommen es gibt reelle Zahlen b1 , . . . , bn , so daß
b1 z + b2 x2 + · · · + bn xn = 0.
Indem wir z = a1 x1 + · · · + an xn einsetzen, erhalten wir
b1 a1 x1 + (b1 a2 + b2 )x2 + · · · + (b1 an + bn )xn = 0.
Aus der linearen Unabhängigkeit von x1 , . . . , xn folgt b1 a1 = 0. Weil a1 6= 0 bedeutet das, daß b1 = 0.
Wiederum aus der linearen Unabhängigkeit von x1 , . . . , xn folgt also bi = b1 ai + bi = 0 für i = 2, . . . , n.
Folglich sind z, x2 , . . . , xn linear unabhängig.
Da x1 , . . . , xn eine Basis ist, läßt sich ferner jeder Vektor y ∈ E darstellen als
y=
n
X
ci x i
mit c1 , . . . , cn ∈ R.
i=1
Folglich gilt
y=
n X
a i c1
c1
z+
xi .
ci −
a1
a1
i=2
2
Dies zeigt [z, x2 , . . . , xn ] = E.
Beweis von Proposition 4.5. Wir führen Induktion über k, beginnend mit k = 1. Der Vektor y1 läßt sich
darstellen als
y1 = a1 x1 + · · · + an xn
mit a1 , . . . , an ∈ R.
Da y1 6= 0 (aufgrund der linearen Unabhängigkeit), gibt es ein ai 6= 0. Lemma 4.6 zeigt also, daß wir eine
Basis erhalten, indem wir xi durch y1 ersetzen. D.h. x1 , . . . , xi−1 , y1 , xi+1 , . . . , xn ist eine Basis.
Wir führen nun den Induktionsschritt durch. Nach geeigneter Umnumerierung der Vektoren dürfen wir
annehmen, daß y1 , . . . , yk−1 , xk , . . . , xn eine Basis ist, und daß n ≥ k − 1. Insbesondere läßt sich der
Vektor yk darstellen als
n
k−1
X
X
bi x i .
bi y i +
yk =
i=1
i=k
Weil y1 , . . . , yk linear unabhängig sind, gibt es ein i ≥ k mit bi 6= 0. Daraus folgt, daß n ≥ k. Numerieren
wir der Einfachheit halber wir die Vektoren xk , . . . , xn so um, daß bk 6= 0, so zeigt Lemma 4.6, daß
y1 , . . . , yk , xk+1 , . . . , xn eine Basis ist.
2
Korollar 4.7 Sind x1 , . . . , xn und y1 , . . . , yk Basen des Vektorraums E, so gilt k = n.
Satz 4.8 Jeder Vektorraum E 6= {0} hat eine Basis.
Beweis. Nach unserer Defintition von Vektorraum gibt eine natürliche Zahl n mit E ⊂ Rn . Der Vektorraum
Rn hat die Basis bestehend aus den in (3) eingeführten Vektoren e(1) , . . . , e(n) . Sind x1 , . . . , xk ∈ E ⊂ Rn
linear unabhängige Vektoren, zeigt Proposition 4.5 also, daß k ≤ n. Wähle in der Tat k größtmöglich, so
daß es linear unabhängige x1 , . . . , xk ∈ E gibt. Wir behaupten, daß x1 , . . . , xk eine Basis von E ist.
Denn wäre z ∈ E \ [x1 , . . . , xk ], so wären die k + 1 Vektoren z, x1 , . . . , xk linear unabhängig. Um dies
einzusehen, seien a0 , . . . , ak ∈ R Zahlen mit
a0 z + a1 x1 + · · · + ak xk = 0.
(8)
Falls a0 = 0, folgt aus der linearen Unabhängig von x1 , . . . , xk , daß a1 = · · · = ak = 0. Ist ferner a0 6= 0,
so zeigt (8), daß
k
X
ai
xi ∈ [x1 , . . . , xk ] ,
z=−
a
i=1 0
im Widerspruch zu der Annahme, daß z 6∈ [x1 , . . . , xk ].
Korollar 4.7 und Satz 4.8 ermöglichen folgende Definition.
2
4
BASEN UND DIE DIMENSION
13
Definition 4.9 Sei E ein Vektorraum und x1 , . . . , xk eine Basis von E. Dann nennen wir k die Dimension
von E und schreiben dim E = k.
Wir nennen zwei Vektorräume E, E 0 isomorph, falls es einen Isomorphismis f : E → E 0 gibt. Die
folgende Proposition zeigt, daß es zu jeder Dimension “im wesentlichen” nur einen einzigen Vektorraum
gibt; formal bedeutet das, daß je zwei Vektorräume derselben Dimension isomorph sind.
Proposition 4.10 Jeder Vektorraum E der Dimension n ≥ 1 ist isomorph zu Rn .
Beweis. Sei x1 , . . . , xn eine Basis von E. Wir definieren


a1
n
X
 .. 
f : Rn → E,
7
ai xi .
 . →
i=1
an
(9)
Diese Abbildung ist linear. Außerdem ist f injektiv, weil x1 , . . . , xn linear unabhängig sind, und surjektiv,
weil E = [x1 , . . . , xn ].
2
In Abschnitt 3 haben wir gelernt, lineare Abbildungen g : Rn → Rm durch Matrizen darzustellen. Erlauben auch lineare Abbildungen g : E → E 0 zwischen anderen Vektorräumen E, E 0 eine solche Darstellung? Das geht tatsächlich, allerdings müssen wir zuvor Basen von E, E 0 festlegen. Sei also
A = (x1 , . . . , xn ) eine Basis von E und B = (y1 , . . . , ym ) eine Basis von E 0 . Wir benutzen den Isomorphismus aus Proposition 4.10, um g als Matrix darzustellen. Bezeichne dazu f den in (9) definierten
Isomorphismus und h den analog definierten Isomorphismus


b1
m
X
 .. 
bi yi .
h : Rm → E 0 ,
 .  7→
i=1
bm
Dann ist h−1 ◦ g ◦ f : Rn → Rm eine lineare Abbildung. Ihre darstellende Matrix M (h−1 ◦ g ◦ f )
bezeichnen wir mit MA,B (g). Explizit können wir ihre Einträge wie folgt beschreiben. Das Bild f (xj ) des
jten Basisvektors von A läßt sich schreiben als
g(xj ) =
m
X
cij yi ,
i=1
weil B ja eine Basis von E 0 ist. Dann gilt

MA,B (g) = (cij )i=1,...,m;j=1,...n
c11
 ..
= .
cm1
···
..
.
···

c1n
..  .
. 
cmn
Ein wichtiger Spezialfall ergibt sich, wenn E = Rn und E 0 = Rm . In diesem Fall erhalten wir also zu
je zwei Basen A von Rn und B von Rm eine darstellende Matrix MA,B (g) der linearen Abbildung g. Wie
verhält sich diese Matrix zu der “natürlichen” Matrix M (g)? Die beiden Isomorphismen f : Rn → Rn
und h : Rm → Rm können ebefalls durch Matrizen dargesellt werden, und nach der Definition gilt
MA,B (g) = M (h−1 ◦ g ◦ f ) = M (h−1 ) · M (g) · M (f ) = M (h)−1 · M (g) · M (f ).
Anhand der Definition von f und g sieht man ferner, daß M (f ) die Matrix ist, deren Spalten die Basisvektoren A sind. Entsprechend ist M (h) die Matrix, deren Spalten die Basisvektoren B sind. Ein wesentliches
Ziel der folgenden Abschnitte wird sein, Basen A, B zu finden, so daß die Matrix MA,B (f ) eine möglichst
einfache Gestalt hat.
5
5
LINEARE GLEICHUNGSSYSTEME
14
Lineare Gleichungssysteme
Für eine gegebene lineare Abbildung f : E → E 0 und einen Vektor y ∈ E 0 möchten wir einen Vektor
x ∈ E mit f (x) = y finden, falls es ein solches x gibt. Weil f durch eine Matrix dargestellt werden kann
(durch Wahl von Basen für E, E 0 ), genügt es, das folgende, konkretere Problem zu lösen: für eine m × nMatrix A und einen Vektor b ∈ Rm ist x ∈ Rn mit Ax = b zu bestimmen, falls es ein solches x gibt.
Genauer gesagt möchten wir alle solchen Vektoren x bestimmen.
Zur Lösung des linearen Gleichungssystems Ax = b verwenden wir die Gaußsche Eliminiationsmethode. In dieser Methode wird die Matrix durch Umformungen in eine Form gebracht, in der der linke untere
Teil der Matrix aus Nullen besteht. Genauer sagen wir, daß eine m×n-Matrix B Zeilenstufenform hat, falls
es eine Folge j1 < j2 < · · · < jm natürlicher Zahlen gibt, so daß Bij = 0 falls j < ji und Biji 6= 0 falls
ji ≤ n. Wenn die Matrix in Zeilenstufenform gebracht ist, kann man eine Lösung des Gleichungssystems
Ax = b direkt ablesen. In der Tat erhält man unmittelbar alle Lösungen dieses Gleichungssystems.
Um die Matrix auf diese Form zu bringen, geht man wie folgt vor. Sei j1 der kleinste Spaltenindex,
so daß in Splate A(j1 ) eine von Null verschiedene Zahl vorkommt. Sei i1 der kleinste Zeilenindex, so daß
Ai1 j1 6= 0. Zunächst vertauschen wir die Zeile i1 mit der ersten Zeile der Matrix. Gleichzeitig wird bi1
mit b1 vertauscht. Seien A0 , b0 die Matrix und der Vektor, die dabei entstehen. Dann addieren wir passende
Vielfache der ersten Zeile von A0 zu den anderen Zeilen von A0 , so daß in der resultierenden Matrix A00
gilt A00ij1 = 0 für alle i > 1. Dieselben Operationen werden an dem Vektor b ausgeführt, und b00 bezeichne
den resultierenden Vektor. Nun wiederholen wir das Verfahren auf der kleineren Matrix A000 , die aus A00
durch Weglassen der ersten Zeile entsteht, und dem Vektor b000 , der aus b00 durch Fortlassen der ersten
Komponente entsteht.
Beispiel 5.1 Wir lösen das Gleichungssystem Ax = b mit


−1 −1 0 2
 −1 0 0 3 

A=
 −1 0 1 2  ,
2
1 0 −4

−1
 −1 

b=
 −1  .
3

Um die Umformungen zugleich an A und b durchführen zu können, schreiben wir b als Spalte neben die
Matrix A; allerdings merken wir uns, daß diese Spalte eine besondere Rolle spielt:


−1 −1 0 2 −1
 −1 0 0 3 −1 


 −1 0 1 2 −1  .
2
1 0 −4 3
Wir subtrahieren nun die erste Zeilen von der zweiten und erhalten


−1 −1 0 2 −1
 0
1 0 1
0 


 −1 0 1 2 −1  .
2
1 0 −4 3
Anschließend subtrahieren wir die erste Zeile von der dritten; das Ergebnis ist


−1 −1 0 2 −1
 0
1 0 1
0 
.

 0
1 1 0
0 
2
1 0 −4 3
Dann wird das 2-fache der ersten Zeile zur letzten Zeile addiert:


−1 −1 0 2 −1
 0
1 0 1 0 

.
 0
1 1 0 0 
0 −1 0 0 1
5
LINEARE GLEICHUNGSSYSTEME
15
Damit haben wir die erste Zeile und Spalte abgearbeitet. Wir fahren jetzt auf dem Rest fort, indem wir die
zweite Zeile zur dritten addieren und von der letzten subtrahieren:


−1 −1 0 2 −1
 0
1 0 1
0 
.

 0
0 1 −1 0 
1
0
0 0 1
Wir haben die Matrix auf Zeilenstufenform gebracht. Man liest jetzt die Lösung x4 = 1, x3 = 1, x2 = −1,
x1 = 4 ab.
Satz 5.2 Zu jeder m×n-Matrix A gibt es eine invertierbare m×m-Matrix C, so daß C·A Zeilenstufenform
hat.
Beweis. Wir haben gesehen, daß eine Matrix durch das Gaußschen Eliminationsverfahren in Zeilenstufenform gebracht werden kann. Dabei werden die folgenden Operationen durchgeführt:
• Vertauschen von zwei Zeilen.
• Addieren des Vielfachen einer Zeile zu einer anderen Zeile.
Zu Indices 1 ≤ i1 < i2 ≤ m sei nun S[i1 , i2 ] die m × m-Matrix, die aus der Einheitsmatrix id durch
Vertauschen der i1 ten und der i2 ten Zeile hervorgeht. Dann ist S[i1 , i2 ] · A die Matrix, die aus A durch
Vertauschen der Zeilen i1 und i2 entsteht. Außerdem ist S[i1 , i2 ] invertierbar, da S[i1 , i2 ] · S[i1 , i2 ] = id.
Ferner definieren wir zu i1 , i2 ∈ {1, . . . , m}, i1 6= i2 , und λ ∈ R eine Matrix T [i1 , i2 , λ], deren
Diagonaleinträge alle gleich 1 sind, deren Eintrag in Zeile i1 und Spalte i2 gleich λ ist, und deren übrige
Einträge gleich 0 sind. Dann ist T [i1 , i2 , λ] · A die Matrix, die aus A durch addieren des λ-Fachen der Zeile
i2 zur Zeile i1 entsteht. Weil T [i1 , i2 , −λ] · T [i1 , i2 , λ] = 1, ist T [i1 , i2 , λ] invertierbar. Die Operationen,
die im Gaußschen Eliminationsverfahren durchgeführt werden, entsprechen also einfach der Multiplikation
von links mit invertierbaren Matrizen S[i1 , i2 ], T [i1 , i2 , λ]. Die Matrix C ist das Produkt derselben.
2
T
Zu einer m × n-Matrix A definieren wir eine n × m-Matrix A , die transponierte Matrix, durch
ATji = Aij für i = 1, . . . , m und j = 1, . . . , n. Ist B eine l × m-Matrix, so ist (BA)T = AT B T . Ist ferner
A eine invertierbare quadratische Matrix, so trifft dies auch auf AT zu und (AT )−1 = (A−1 )T .
Korollar 5.3 Zu jeder m × n-Matrix A gibt es eine invertierbare m × m-Matrix C und eine invertierbare
n × n-Matrix D und eine Zahl r ≤ min {m, n}, so daß C · A · D = Er , wobei Er die Matrix ist, deren
erste r Diagonaleinträge gleich 1 sind und deren übrige Einträge gleich 0 sind.
Beweis. Zunächst wenden wir das Gaußsche Eliminationsverfahren an, um eine invertierbare Matrix C
zu erhalten, so daß CA Zeilenstufenform hat. Dann wenden wir das Gaußsche Eliminationsverfahren auf
die transponierte Matrix (CA)T an. Dies gibt eine invertierbare n × n-Matrix F , so daß F (CA)T eine
n × m-Matrix ist, die nur auf der Diagonalen von Null verschiedene Einträge hat. Durch Multiplikation
mit einer geeigneten invertierbaren n×n-Diagonalmatrix G kann man erreichen, daß die Matrix GF (CA)T
Diagonalform hat mit Einträgen 1 oder 0. Die transponierte Matrix CA(GF )T ist also eine m × n-Matrix
2
in Diagonalform mit Einträgen 1 oder 0, und die Matrix D = (GF )T ist invertierbar.
Korollar 5.3 liefert eine erste Lösung des Problems, eine lineare Abbildung durch eine möglichst einfache Matrix darzustellen. Sehen wir nämlich die m×n-Matrix A als eine lineare Abbildung f : Rn → Rm ,
x 7→ Ax, so gibt Korollar 5.3 Basen A, B von Rn und Rm , so daß MA,B (f ) = Er . Genauer ist A die
Basis, die aus den Spalten der Matrix D besteht, während B aus den Spalten von C −1 besteht. Zwar ist
MA,B (f ) = Er eine sehr einfache Matrix und diese Darstellung ist auch durchaus hilfreich (s. die folgenden Anwendungen). Jedoch sind leider die Basen A, B im allgemeinen nicht besonders “schön”. Wir
setzen uns daher weiterhin das (zugegebenermaßen etwas vage) Ziel, lineare Abbildungen durch möglichst
einfache Matrizen darzustellen, allerdings bezüglich möglichst “schöner” Basen.
n
(1)
(n)
Ist A eine m×n-Matrix, so sind die Zeilen A(1) , . . . , A(m) Vektoren
in R . Die Spalten
A ,...,A
m
sind Vektoren in R . Wir definieren den Zeilenrang von A als dim A(1) , . . . , A(m) . Der Spaltenrang
von A ist dim A(1) , . . . , A(n) .
5
LINEARE GLEICHUNGSSYSTEME
16
Korollar 5.4 Für jede Matrix A stimmen Zeilen- und Spaltenrang überein.
Beweis. Mit den Bezeichnungen von Korollar 5.3 sieht man, daß r sowohl der Zeilen- als auch der Spaltenrang von A ist.
2
Aufgrund von Korollar 5.4 kann man einfach vom Rang der Matrix A sprechen.
Korollar 5.5 Sei A eine m × n-Matrix und b ∈ Rm . Es gibt genau dann ein x ∈ Rn mit Ax = b, wenn
die Matrix A denselben Rang hat wie die Matrix (A b), die aus A durch Hinzufügen von b als n + 1ter
Spalte entsteht.
Für eine lineare Abbildung f : E → E 0 nennen wir f −1 (0) = {x ∈ E : f (x) = 0} den Kern von f .
Dieser ist ein Untervektorraum von E. Entsprechend definieren wir den Kern einer Matrix A als den Kern
der linearen Abbildung x 7→ Ax. Sind A eine m × n-Matrix, b ∈ Rm und x ∈ Rn so, daß Ax = b, so
gilt für jeden Vektor z im Kern von A, daß A(x + z) = b. Ist umgekehrt x0 ein Vektor mit Ax0 = b, so ist
z = x − x0 im Kern von A.
Korollar 5.6 Sei A eine m × n-Matrix vom Rang r. Sei l die Dimension des Kerns von A. Dann gilt
n = r + l. Ferner ist A genau dann invertierbar, wenn m = n = r.
Beweis. Seien C, D die Matrizen aus Korollar 5.3, so daß CAD = Er . Die Anzahl der Spalten der m × nMatrix Er , die gleich Null sind, ist dann die Dimension des Kerns von A. Also hat der Kern die Dimension
n − r. Dies zeigt die erste Behauptung.
Wenn A invertierbar ist, muß notwendigerweise m = n gelten. Außerdem ist in diesem Fall die lineare
Abbildung Rn → Rn , x 7→ Ax bijektiv, d.h. der Kern besteht nur aus dem Nullvektor. Aus der ersten
Behauptung folgt also r = n. Wenn umgekehrt r = n ist, dann ist CAD = id. Die inverse Matrix von A
ist also einfach DC.
2
Wie der letzte Beweis zeigt, erlauben uns die Umformungsregeln des Gaußverfahrens, zu einer gegebenen n × n-Matrix A festzustellen, ob sie invertierbar ist, und ggf. ihre inverse Matrix zu berechnen. Dazu
geht man wie folgt vor. Zunächst bringt man die Matrix A mit dem Gaußverfahren auf Zeilenstufenform.
An der Zeilenstufenform von A kann man den Rang ablesen, und A ist genau dann invertierbar, wenn der
Rang gleich n ist. In diesem Fall führt man weitere Zeilenumformungen durch, bis aus A eine Diagonalmatrix geworden ist. Dann multiplizieren wir jede Zeile mit einer reellen Zahl, um die Einheitsmatrix id
zu erhalten. Parallel dazu führt man dieselben Umformungen ausgehend von der Einheitsmatrix id durch.
Die Matrix B, die dabei aus der Einheitsmatrix entsteht, ist A−1 .
Beispiel 5.7 Wir invertieren die Matrix

−1
 −1
A=
 −1
2
−1
0
0
1

0 2
0 3 
.
1 2 
0 −4
Zunächst subtrahieren wir die erste Zeile von der zweiten und dritten und addieren ihr 2-faches zur vierten.
Dieselben Umformungen führen wir auch ausgehend von der Matrix id durch und erhalten




−1 −1 0 2
1 0 0 0
 0


1 0 1 

 und  −1 1 0 0  .
 0


1 1 0
−1 0 1 0 
0 −1 0 0
2 0 0 1
Als nächstes subtrahieren wir die zweite Zeile von der dritten und addieren sie zur vierten:




−1 −1 0 2
1
0 0 0
 0


1 0 1 

 und  −1 1 0 0  .
 0


0 1 −1
0 −1 1 0 
0
0 0 1
1
1 0 1
6
DIE DETERMINANTE
17
An dieser Stelle erkennen wir, daß die Matrix A Rang 4 hat, also invertierbar ist. Wir fahren fort, indem
wir die letzte Zeile zur dritten Zeile addieren, von der zweiten Zeile abziehen und zweimal von der ersten
Zeile abziehen. Dieselben Umformungen führen wir an der rechten Matrix durch und erhalten




−1 −1 0 0
−1 −2 0 −2
 0


1 0 0 

 und  −2 0 0 −1  .
 0


0 1 0
1
0 1 1 
0
0 0 1
1
1 0 1
Als nächsten Schritt addieren wir in beiden Matrizen die zweite Zeile zur ersten. Dies ergibt




−3 −2 0 −3
−1 0 0 0
 −2 0 0 −1 
 0 1 0 0 

.


 0 0 1 0  und  1
0 1 1 
1
1 0 1
0 0 0 1
Schließlich multiplizieren wir die erste Zeile beider Matrizen mit −1:




1 0 0 0
3 2 0 3
 0 1 0 0 
 −2 0 0 −1 




 0 0 1 0  und  1 0 1 1  .
0 0 0 1
1 1 0 1
Wir haben also ausgerechnet, daß

A−1
6
3
 −2
=
 1
1

2 0 3
0 0 −1 
.
0 1 1 
1 0 1
Die Determinante
In diesem Abschnitt ordnen wir einer Matrix eine reelle Zahl zu, die gewisse geometrische Eigenschaften
der Matrix widerspiegelt. Dazu müssen wir uns zunächst mit Permutationen befassen. Eine Permutation
der Länge n ist eine Bijektion σ : {1, . . . , n} → {1, . . . , n}. Wir bezeichnen die Menge aller Permutationen der Länge n mit Sn . Man überlegt sich leicht, daß |Sn | = n!. Ferner definieren wir das Vorzeichen
oder Signum von σ ∈ Sn als
Y σ(i) − σ(j)
sign(σ) =
.
i−j
1≤i<j≤n
Lemma 6.1 Es gilt sign(σ) ∈ {−1, 1} für alle σ ∈ Sn , und für alle σ, τ ∈ Sn gilt
sign(σ ◦ τ ) = sign(σ) · sign(τ ).
Beweis. Es gilt

sign(σ)2
= 
Y
1≤i<j≤n
2
Y σ(i) − σ(j)
σ(i) − σ(j) 
=
= 1;
i−j
i−j
i6=j
6
DIE DETERMINANTE
18
das letzte Gleichheitszeichen stimmt, weil σ eine Permutation ist. Daraus folgt, daß sign(σ) ∈ {−1, 1}.
Ferner gilt
sign(σ ◦ τ )
Y
=
1≤i<j≤n
=
sign(τ ) ·
σ ◦ τ (i) − σ ◦ τ (j)
=
i−j
Y
1≤i<j≤n
=
1≤i<j≤n:τ (i)<τ (j)
Y
=
sign(τ ) ·
=
sign(τ ) · sign(σ),
1≤i<j≤n
σ ◦ τ (i) − σ ◦ τ (j)
·
τ (i) − τ (j)
Y
1≤i<j≤n
τ (i) − τ (j)
i−j
σ ◦ τ (i) − σ ◦ τ (j)
τ (i) − τ (j)
Y
sign(τ ) ·
Y
1≤i<j≤n:τ (i)<τ (j)
σ ◦ τ (i) − σ ◦ τ (j)
·
τ (i) − τ (j)
Y
σ ◦ τ (i) − σ ◦ τ (j)
·
τ (i) − τ (j)
Y
1≤i<j≤n:τ (i)>τ (j)
1≤i<j≤n:τ (i)>τ (j)
σ ◦ τ (i) − σ ◦ τ (j)
τ (i) − τ (j)
σ ◦ τ (j) − σ ◦ τ (i)
τ (j) − τ (i)
2
wie behauptet.
Definition 6.2 Die Determinante einer n × n-Matrix A ist
det A =
X
sign(σ)
σ∈Sn
n
Y
Aiσ(i) .
(10)
i=1
Wir erinnern, daß die Zeilen einer n × n-Matrix A mit A(1) , . . . , A(n) bezeichnet werden.
Proposition 6.3 Seien A, B, C drei n × n-Matrizen. Die Determinante hat die folgenden Eigenschaften.
DET1. det(id) = 1.
DET2. Falls A zwei identische Zeilen hat, gilt det A = 0.
DET3. Die Determinante ist linear in jeder Zeile, d.h. die beiden folgenden Bedingungen sind erfüllt.
• Angenommen es gibt ein i ∈ {1, . . . , n}, so daß A(i) + B(i) = C(i) , während A(h) = B(h) =
C(h) für alle h 6= i. Dann gilt det(A) + det(B) = det(C).
• Angenommen es gibt ein i ∈ {1, . . . , n} und ein z ∈ R, so daß B(i) = z · A(i) , während
B(h) = A(h) für alle h 6= i. Dann gilt det(B) = z · det(A).
Insbesondere gilt det(A) = 0 wenn A eine Zeile hat, die nur aus 0en besteht.
DET4. Wenn B aus A durch Vertauschen von zwei Zeilen entsteht, gilt det(B) = − det(A).
DET5. Seien i, j ∈ {1, . . . , n} verschieden und z ∈ R. Wenn B aus A durch Addieren des z-fachen der
i-ten Zeile zur j-ten Zeile entsteht, gilt det(B) = det(A).
Qn
DET6. Wenn A in Zeilenstufenform ist, gilt det(A) = i=1 Aii .
DET7. Es gilt det(A · B) = det(A) · det(B).
DET8. Die Matrix A ist invertierbar genau dann, wenn det(A) 6= 0. In diesem Fall gilt
det(A−1 ) = 1/ det(A).
DET9. Es gilt det(AT ) = det A.
6
DIE DETERMINANTE
19
Beweis. DET1 folgt unmittelbar aus der Definition. Um DET2 zu zeigen, nehmen wir an, daß die Zeilen
i1 und i2 von A identisch sind (i1 6= i2 ). Sei τ ∈ Sn die Permutation, die die Zahlen i1 und i2 vertauscht,
während τ (h) = h für alle h ∈ {1, . . . , n} \ {j1 , j2 }. Dann gilt
"
#
n
n
n
X
Y
Y
Y
1 X
sign(σ)
sign(σ)
det(A) =
Aiσ(i) =
Aiσ(i) + sign(σ ◦ τ )
Ai τ ◦σ(i) .(11)
2
i=1
i=1
i=1
σ∈Sn
σ∈Sn
Nun zeigt Lemma 6.1, daß sign(τ ◦ σ) = sign(τ ) · sign(σ). Weil τ einfach zwei Zahlen i1 , i2 vertauscht,
zeigt die Definition von sign(τ ), daß sign(τ ) = −1. Daher können wir (11) schreiben als
" n
#
n
Y
Y
1 X
sign(σ)
Aiσ(i) −
Ai σ◦τ (i) .
(12)
det(A) =
2
i=1
i=1
σ∈Sn
Weil die i1 -te Zeile und die i2 -te Zeile von A übereinstimmen, erhalten wir
n
Y
Aiσ(i)
=
Ai1 σ(i1 ) Ai2 σ(i2 ) ·
i=1
Y
Aiσ(i)
i6∈{i1 ,i2 }
=
Ai1 σ(i2 ) Ai2 σ(i1 ) ·
Y
Aiσ(i)
i6∈{i1 ,i2 }
=
Y
Ai1 σ◦τ (i1 ) Ai2 σ◦τ (i2 ) ·
Aiσ(i) =
i6∈{i1 ,i2 }
n
Y
Ai σ◦τ (i) .
i=1
Folglich zeigt (12), daß det(A) = 0.
Um DET3 zu zeigen, betrachten wir A, B, C, so daß A(i) + B(i) = C(i) , während alle anderen Zeilen
der drei Matrizen übereinstimmen. Dann gilt
det(C)
=
X
σ∈Sn
=
X
sign(σ)
n
Y
Cjσ(j) =
j=1
X
sign(σ)Aiσ(i)
Y
Cjσ(j) +
sign(σ)Aiσ(i)
Y
j6=i
Ajσ(j) +
Y
Cjσ(j)
j6=i
X
sign(σ)Biσ(i)
σ∈Sn
j6=i
σ∈Sn
=
sign(σ)(Aiσ(i) + Biσ(i) )
σ∈Sn
σ∈Sn
=
X
X
Y
Cjσ(j)
j6=i
sign(σ)Biσ(i)
σ∈Sn
Y
Bjσ(j)
j6=i
det(A) + det(B).
Der Nachweis der zweiten Bedingung geht analog. Die Eigenschaften DET4–DET8 können aus DET1–
DET3 hergeleitet werden, während DET9 aus Lemma 6.1 und (10) folgt.
2
Bemerkung 6.4
1. Sei A eine n × n-Matrix mit Spalten A(i) . Geometrisch ist die Menge
( n
)
X
(i)
P =
ai A : a1 , . . . , an ∈ [0, 1]
i=1
ein “schiefer Quader”, ein sogenanntes Parallelepiped. Anschaulich ist | det A| das Volumen von P .
2. Im allgemeinen gilt nicht det(A + B) = det(A) + det(B).
3. Aufgrund von DET9 gelten DET2–DET 6 auch entsprechend für die Spalten der Matrix.
4. Ist A eine 2 × 2-Matrix, so folgt aus (10), daß det A = A11 A22 − A12 A21 .
6
DIE DETERMINANTE
20
Die Formel (10) ist, zumindest für größere Matrizen, nicht zur praktischen Berechnung der Determinante geeignet. Der Grund dafür ist die große Anzahl von n! Summanden. Andererseits ermöglichen die
Aussagen DET1–DET6 eine geschicktere Berechnung der Determinante: wir können die Matrix n × n mit
dem Gaußverfahren (d.h. durch geeignetes Vertauschen von Zeilen und Addieren eines Vielfachen einer
Zeile zu einer anderen) auf Zeilenstufenform bringen. Dabei verändert sich dabei der Betrag der Determinante nicht. Das Vorzeichen ändert sich jedesmal, wenn wir zwei Zeilen vertauschen. Und die Determinante
einer Matrix in Zeilenstufenform können wir mit DET6 unmittelbar ausrechnen. Wenn also B die Matrix
in Zeilenstufenform ist, die wir mit dem Gaußschen Eliminationsverfahren bekommen, und k die Anzahl
der Zeilenvertauschungen ist, die wir auf dem Weg von A zu B durchgeführt haben, gilt
det A = (−1)k det B.
Beispiel 6.5 Wir möchten die Determinante von

1
A =  −1
−1
bestimmen. Nach Gauß addieren wir die ersten Zeile
sich die Determinante dabei nicht:

1 0
 0 0
0 2

0 −3
0 4 
2 2
(13)
zur zweiten und dritten Zeile; wegen DET5 ändert

−3
1 
−1
Um die Matrix in Zeilenstufenform zu bringen, brauchen wir nur noch die zweite und dritte Zeile zu tauschen. Dies ergibt


1 0 −3
B =  0 2 −1  .
0 0 1
Nun zeigt DET6, daß det B = 1·2·1 = 2. Die Gesamtzahl der Zeilenvertauschungen, die wir durchgefürht
haben, ist k = 1. Also zeigt DET4, daß det A = (−1)k det B = − det B = −2.
Sei A eine n × n-Matrix. Die Determinante liefert eine generelle Formel für die inverse Matrix A−1
(falls sie existiert) und zur Lösung von linearen Gleichungssystemen Ax = b, die “Cramersche Regel”. Zur
Herleitung derselben bezeichnen wir mit A0(i,j) die (n − 1) × (n − 1)-Matrix, die aus A durch Entfernen
der i-ten Zeile und der j-ten Spalte entsteht. Die zu A komplementäre Matrix ist die n × n-Matrix à mit
Einträgen
Ãij = (−1)i+j det A0(j,i)
(i, j ∈ {1, . . . , n}).
Man beachte, daß sich die Indices “umdrehen”!
Beispiel 6.6 Wir bestimmen die komplementäre Matrix von A aus (13). Durch Streichen der ersten Zeile
und der ersten Spalte entsteht die 2 × 2-Matrix
0 4
0
A(1,1) =
2 2
mit Determinante det A0(1,1) = 0 · 2 − 4 · 2 = −8. Streicht man die erste Zeile und die zweite Spalte, so
erhält man
−1 4
A0(1,2) =
.
−1 2
Es gilt A0(1,2) = −1 · 2 − 4 · (−1) = 2. Wenn man die erste Zeile und die dritte Spalte aus A streicht, ergibt
sich die Matrix
−1 0
A0(1,3) =
−1 2
6
DIE DETERMINANTE
21
mit det A0(1,3) = −2. Durch Streichen der zweiten Zeile und der ersten Spalte erhält man analog
A0(2,1)
=
0
2
−3
2
mit det A0(2,1) = 6. Die übrigen Determinanten ergeben sich als
det A0(2,2) = −1, det A0(2,3) = 2,
det A0(3,1) = 0,
det A0(3,2) = 1,
det A0(3,3) = 0.
Die komplementäre Matrix ist also

−8
à =  −2
−2
−6
−1
−2

0
−1  .
0
Proposition 6.7 Sei A eine n × n-Matrix und à die zu A komplementäre Matrix. Dann gilt
A · Ã = Ã · A = det(A) · id.
Beweis. Wir bestimmen direkt die Einträge der Matrix B = A · Ã. Für i, j ∈ {1, . . . , n} erhalten wir
Bij
=
n
X
Aih Ãhj =
h=1
n
X
Aih · (−1)h+j det A0(j,h) .
(14)
h=1
Um fortzufahren, benötigen wir eine weitere Hilfsmatrix. Wir definieren A00(j,h) als die n × n-Matrix mit
den folgenden Einträgen. Für s, t ∈ {1, . . . , n} ist der Eintrag in der s-ten Zeile und t-ten Spalte von A00(j,h)
• gleich Ast , wenn s 6= j und t 6= h,
• gleich 0, wenn entweder s = j und t 6= h oder s 6= j und t = h,
• gleich 1, wenn s = j und t = h.
Man erhält A00(j,h) also aus A, indem man die Einträge in der j-ten Zeile und der h-ten Spalte durch 0en
ersetzt, außer daß der “Kreuzpunkt”, d.h. der (j, h)-te Eintrag, gleich 1 ist. Indem man j − 1 Zeilen- und
h − 1 Spaltenvertauschungen durchführt, erhält man aus A00(j,h) die Matrix





1
0
..
.
0···0

A0(j,h)


,

(15)
0
deren unterer rechter (n − 1) × (n − 1)-Block gerade die Matrix A0(j,h) ist. Ihre Determinante ist



(−1)j+h det A00(j,h) = det 

1
0
..
.
0···0

A0(j,h)


 = det A0(j,h) ,

0
denn um (15) in Zeilenstufenform bringen, bringt man einfach A0(j,h) in Zeilenstufenform. Wir können
also (14) schreiben als
Bij
=
n
X
h=1
Aih · det A00(j,h) .
(16)
7
ORTHOGONALITÄT
22
(h)
Sei nun A000
, A(j+1) , . . . , A(n) . Dann gilt
(j,h) die Matrix mit den Zeilen A(1) , . . . , A(j−1) , e
det A00(j,h) = det A000
(j,h) .
(17)
Denn indem man geeignete Vielfache der j-ten Zeile der Matrix A000
(j,h) zu den anderen Zeilen addiert, kann
man sie in die Matrix A00(j,h) umformen. Wir bezeichnen ferner mit A0000
(i,j) die n × n-Matrix, die aus A
dadruch entsteht, daß man die j-te Zeile durch die i-te Zeile ersetzt. (Ist insbesondere i = j ist, erhält man
A0000
(i,j) = A.) Mit DET3 wird aus (16) und (17) dann
Bij
=
n
X
0000
Aih · det A000
(j,h) = det A(i,j) .
(18)
h=1
Es gibt nun zwei Fälle.
Fall 1: i = j. Dann ist A0000
(i,j) = A, also zeigt (18), daß Bij = det A.
Fall 2: i 6= j. Die Matrix A0000
(i,j) hat zwei identische Zeilen (nämlich die i-te und die j-te). Aus DET2 folgt
also Bij = 0.
Insgesamt erhalten wir also B = det A · id, wie behauptet. Das Produkt à · A kann man entsprechend
berechnen.
2
Korollar 6.8 Wenn A eine n × n-Matrix mit det A 6= 0 ist, gilt A−1 =
1
det A
· Ã.
Korollar 6.9 (“Cramersche Regel”) Sei A eine n × n-Matrix mit det A 6= 0 und b ∈ Rn . Dann gibt es
genau ein x ∈ Rn mit Ax = b, und zwar ist dies der Vektor mit den Komponenten
det A(1) · · · A(i−1) b A(i+1) · · · A(n)
xi =
(i = 1, . . . , n).
det A
In Worten: xi ist die Determinante der n × n-Matrix, die aus A entsteht, wenn man die i-te Spalte von A
durch den Vektor b ersetzt, gebrochen durch die Determinante von A.
Beweis. Der gesuchte Vektor ist x = A−1 b. Mit der Notation aus dem Beweis von Proposition 6.7 erhalten
wir
xi
=
n
X
n
A−1
ij bj =
j=1
=
n
1 X
1 X
bj Ãij =
(−1)i+j bj det A0(j,i)
det A j=1
det A j=1
n
det A(1) · · · A(i−1) b A(i+1) · · · A(n)
1 X
000
,
bj det A(j,i) =
det A j=1
det A
2
wobei die letzte Gleichung aus DET3 folgt.
7
Orthogonalität
Für zwei Vektor x, y ∈ Rn definieren wir das Skalarprodukt
hx, yi =
n
X
xi yi .
i=1
Es gilt hx, yi = hy, xi. Außerdem ist für jeden Vektor y ∈ Rn die Abbildung Rn → R, z 7→ hz, yi linear.
Die euklidische Norm eines Vektors x ∈ Rn ist definiert als
v
u n
p
uX
kxk = hx, xi = t
x2i .
i=1
7
ORTHOGONALITÄT
23
Lemma 7.1 (“Cauchy-Schwarz-Ungleichung”) Für Vektoren x, y ∈ Rn gilt stets | hx, yi | ≤ kxk · kyk.
Beweis. Wir dürfen annehmen, daß x, y 6= 0. Für jede reelle Zahl a gilt
0
≤
2
kx − a · yk = hx − a · y, x − a · yi = hx, xi − 2a hx, yi + a2 hy, yi .
Insbesondere gilt diese Ungleichung für a =
hx,yi
hy,yi .
Setzt man dieses a in (19) ein, ergibt sich
2
0 ≤ hx, xi − 2
(19)
2
hx, yi
hx, yi
+
.
hy, yi
hy, yi
2
Durch Umstellen erhält man die Behauptung.
Korollar 7.2 Die folgenden drei Aussagen gelten für alle x, y ∈ Rn und a ∈ R.
1. kxk = 0 genau dann, wenn x = 0.
2. ka · xk = |a| · kxk.
3. kx + yk ≤ kxk + kyk (“Dreiecksungleichung”).
Beweis. Die ersten und die zweite Behauptung folgen unmittelbar aus der Definition der Norm. Für die
dritte Behauptung berechnen wir
2
kx + yk
= hx + y, x + yi = hx, xi + 2 hx, yi + hy, yi
≤
=
2
2
kxk + 2 kxk kyk + kyk
[nach Cauchy-Schwarz]
2
(kxk + kyk) .
Zieht man auf beiden Seiten die Quadratwurzel, erhält man 3.
Definition 7.3
0.
2
1. Wir nennen zwei Vektoren x, y ∈ Rn orthogonal, in Symbolen x ⊥ y, falls hx, yi =
2. Allgemeiner heißen Vektoren x1 , . . . , xk orthogonal, wenn für je zwei Indices 1 ≤ i < j ≤ k gilt
xi ⊥ xj .
3. Fernen heißen x1 , . . . , xk orthonormal, wenn x1 , . . . , xk orthogonal sind und kxi k = 1 für alle
i ∈ {1, . . . , k}.
4. Sei E ein Vektorraum. Wir nennen x1 , . . . , xk eine Orthonormalbasis von E, falls x1 , . . . , xk eine
Basis von E ist und die Vektoren x1 , . . . , xk orthonormal sind.
Beispielsweise bilden die Vektoren e(1) , . . . , e(n) eine Orthonormalbasis des Rn . Das Hauptergebnis
dieses Abschnittes ist der folgende Satz.
Satz 7.4 Jeder Vektorraum hat eine Orthonormalbasis.
Beweis. Wir führen Induktion über die Dimension des Vektorraums E. Nach Satz 4.8 hat E eine Basis
x1 , . . . , xn (wobei n = dim E). Ist n = 1, so ist y1 = x1 / kx1 k eine Orthonormalbasis.
Im Fall n > 1 konstruieren wir aus x1 , . . . , xn die gewünschte Orthonormalbasis mit dem sogenannten
Gram-Schmidt-Verfahren. Dazu definieren wir y1 = kxx11 k und
E 0 = {z ∈ E : hz, y1 i = 0} .
Diese Menge E 0 ist ein Untervektorraum von E. Sei m = dim E 0 seine Dimension. Weil hy1 , y1 i =
hx1 ,x1 i
= 1, gilt y1 6∈ E 0 . Also ist E 0 eine echte Teilmenge von E, und folglich m < n. Nach Induktion
kx k2
1
7
ORTHOGONALITÄT
24
hat E 0 also eine Orthonormalbasis w1 , . . . , wm . Wir behaupten, daß y1 , w1 , . . . , wm eine Orthonormalbasis
von E ist.
Daß die Vektoren y1 , w1 , . . . , wm orthonormal sind, folgt unmittelbar aus der Konstruktion. Sind ferner
a1 , b1 , . . . , bm reelle Zahlen, so daß
a1 y1 + b1 w1 + · · · + bm wm = 0,
so folgt
0 = ha1 y1 + b1 w1 + · · · + bm wm , y1 i = a1 hy1 , y1 i +
m
X
2
bk hwk , y1 i = a1 ky1 k = a1 .
k=1
Weil ferner w1 , . . . , wm eine Orthonormalbasis von E 0 ist und somit w1 , . . . , wm linear unabhängig sind,
folgt b1 = · · · = bm = 0. Also sind die Vektoren y1 , w1 , . . . , wm linear unabhängig.
Ist schließlich v ∈ E ein Vektor, so betrachte u = v − hv, y1 i y1 . Es gilt
2
hu, y1 i = hv, y1 i − hv, y1 i · hy1 , y1 i = hv, y1 i − hv, y1 i · ky1 k = 0,
Pm
also u ∈ E 0 . Folglich existieren c1 , . . . , cm mit u =
k=1 bk wk . Setzen wir ferner d1 = hv, y1 i, so
erhalten wir
m
X
v = d 1 y1 +
bk wk .
k=1
Dies zeigt E = [y1 , w1 , . . . , wm ]. Also ist y1 , w1 , . . . , wm eine Orthonormalbasis von E.
In obigem Beweis haben wir folgendes beobachtet.
2
Korollar 7.5 Wenn die Vektoren x1 , . . . , xn orthonormal sind, sind sie linear unabhängig.
Das Gram-Schmidt-Verfahren aus dem obigen Beweis hat die folgende Konsequenz. Ist x1 , . . . , xn
eine Orthonormalbasis eines Vektorraums E, so läßt sich jeder Vektor v ∈ E schreiben als
v=
n
X
hv, xi i xi .
i=1
Die Zahlen hv, xi i heißen die Fourierkoeffizienten von v bezüglich der Basis x1 , . . . , xn . Insbesondere
gilt
n
X
2
2
kvk =
hv, xi i .
i=1
Der Begriff der Orthogonalität führt auf eine natürliche Zerlegung von Vektorräumen. Sei E ein Vektorraum und F ⊂ E ein Untervektorraum. Das orthogonale Komplement von F in E ist
F ⊥ = {x ∈ E : für alle y ∈ F gilt x ⊥ y} .
Die Menge F ⊥ ist ein Untervektorraum von E.
Proposition 7.6 Sei E ein Vektorraum und F ⊂ E ein Untervektorraum. Die Abbildung f : F ×F ⊥ → E,
(x, y) 7→ x + y ist bijektiv und es gilt dim F + dim F ⊥ = dim E.
Beweis. Sei x1 , . . . , xn eine Orthonormalbasis von F und y1 , . . . , ym eine Orthonormalbasis von F ⊥ . Wir
behaupten, daß x1 , . . . , xn , y1 , . . . , ym eine Orthonormalbasis von E ist. Aus der Definition von F ⊥ folgt
unmittelbar, daß die Vektoren x1 , . . . , xn , y1 , . . . , ym orthonormal und damit linear unabhängig sind. Zu
einem Vektor z ∈ E betrachten wir nun
z0 = z −
n
X
i=1
hz, xi i xi .
(20)
7
ORTHOGONALITÄT
25
Für jeden Vektor xj , j = 1, . . . , n, gilt
hz 0 , xj i = hz, xj i −
n
X
hz, xi i hxi , xj i = hz, xj i − hz, xj i = 0.
i=1
Die zweite Gleichung folgt aus der Orthonormalität von x1 , . . . , xn . Weil x1 , . . . , xn eine Basis von F ist,
können wir schließen, daß hz 0 , xi = 0 für alle x ∈ F . Also gilt z 0 ∈ F ⊥ , und somit
z0 =
m
X
hz 0 , yi i yi .
(21)
i=1
Aus (20) und (21) folgt, daß sich jeder Vektor z ∈ E darstellen läßt als
z=
n
X
hz, xi i xi +
i=1
m
X
hz, yi i yi ,
i=1
d.h. x1 , . . . , xn , y1 , . . . , ym ist eine Basis von E.
2
n
Seien x1 , . . . , xn ∈ R orthonormal. Die n × n-Matrix A mit Spalten x1 , . . . , xn stellt die lineare
Abbildung, die den Vektor e(i) auf xi abbildet (i = 1, . . . , n), dar. Weil x1 , . . . , xn die Spalten von A sind,
sind diese Vektoren genau die Zeilen der transponierten Matrix AT . Das Produkt B = AT · A hat daher die
Einträge Bij = hxi , xj i, d.h. B = id. Das bedeutet, daß AT = A−1 . Wenn umgekehrt die n × n-Matrix A
die Eigenschaft AT = A−1 hat, dann sind die Spalten von A orthonormal. Wir geben Matrizen mit dieser
Eigenschaft einen besonderen Namen.
Definition 7.7 Eine n × n-Matrix A heißt orthogonal, wenn AT A = id.
Im Zusammenhang mit dem Skalarprodukt spielt die transponierte Matrix eine besondere Rolle: ist A
eine n × n-Matrix und sind x, y ∈ Rn , so gilt
hAx, yi = x, AT y ,
(22)
wie man leicht nachrrechnet. In der Tat ist AT die einzige Matrix mit dieser Eigenschaft: wenn B eine
Matrix ist, so daß
hAx, yi = hx, Byi
für alle x, y ∈ Rn ,
so gilt B = AT . (Der Nachweis dieser Tatsache ist eine gute Übung.)
Lemma 7.8 Wenn A eine orthogonal Matrix ist, dann gilt hAx, Ayi = hx, yi für alle x, y. Ferner ist AT
orthogonal.
Beweis. Mit (22) erhalten wir hAx, Ayi = x, AT Ay = hx, id yi = hx, yi. Außerdem ist A invertierbar.
Deshalb trifft dies auch auf AT zu, und (AT )−1 = (A−1 )T = (AT )T = A.
2
Lemma 7.9 Wenn A, B orthogonale n × n-Matrizen sind, dann ist A · B orthogonal.
Beweis. Es gilt (AB)T AB = B T AT AB = B T idB = B T B = id.
2
Beispiel 7.10 Der Vektorraum Rn hat die
e(1) , . . . , e(n) , aber es gibt viele andere. Bei Orthonormalbasis
1
−1
1
1
spielsweise bilden die Vektoren √2 −1 , √2 1 eine Orthonormalbasis des R2 , die aus der Orthonor malbasis 10 , 01 durch Rotation um 45◦ entsteht. Die Matrix
1
1 −1
√
−1 1
2
ist also orthogonal. Allgemeiner ist die Matrix,
cos α
sin α
− sin α
cos α
,
8
EIGEN- UND SINGULÄRWERTE
26
2
welche die Rotation um
den
Winkel α in R darstellt, orthogonal. Eine weitere Orthonormalbasis besteht
−1
0
aus den Vektoren 0 , 1 , die geometrisch durch Spieglung der horizontalen Achse entsteht. Die entsprechende Matrix ist
−1 0
.
0 1
8
Eigen- und Singulärwerte
Sei f : E → E 0 eine lineare Abbildung zwischen zwei n-dimensionalen Vektorräumen. Wir erinnern uns
an das Ziel, “schöne” Basen A, B von E, E 0 zu finden, so daß die Matrix MA,B (f ) möglichst einfach ist.
Genauer werden wir zeigen, daß dies für Orthonormalbasen A, B möglich ist. Die Kernbegriffe in diesem
Unterfangen sind folgende.
Definition 8.1 Sei A eine n × n-Matrix.
1. Eine reelle Zahl k heißt Eigenwert von A, wenn es einen Vektor x 6= 0 gibt, so daß Ax = k · x.
2. Entsprechend heißt ein Vektor x 6= 0 Eigenvektor von A, falls Ax ∈ [x].
3. Die Matrix A heißt symmetrisch, wenn AT = A.
Mit diesen Begriffen können wir nun folgenden Satz formulieren.
Satz 8.2 Zu jeder symmetrischen n × n-Matrix A existieren eine orthogonale n × n-Matrix U und reelle
Zahlen k1 , . . . , kn , so daß
U T AU = diag(k1 , . . . , kn ).
(23)
Die Zahlen k1 , . . . , kn sind genau die Eigenwerte von A, und die Spalten von U bilden eine Orthonormalbasis, die aus Eigenvektoren von A besteht.
Satz 8.2 besagt, daß bezüglich der Orthonormalbasis A, die aus den Spalten U (1) , . . . , U (n) besteht,
die darstellende Matrix der linearen Abbildung f : Rn → Rn , x 7→ Ax, einfach die Diagonalmatrix
diag(k1 , . . . , kn ) ist. In Symbolen,
MA,A (f ) = diag(k1 , . . . , kn ).
Das bedeutet, daß wir uns die lineare Abbildung f in der Basis A hervorragend veranschaulichen können: f
“streckt” einfach den Basisvektor U (i) um den Faktor ki , für i = 1, . . . , n. Man nennt die Darstellung (23)
Diagonalisierung der Matrix A. Eine Matrix A, die eine solche Darstellung zuläßt, heißt diagonalisierbar.
Es stellen sich nun zwei offensichtliche Fragen. Erstens (aus Sicht der Mathematik): wie beweisen
wir Satz 8.2? Zweitens (aus Sicht der Praxis): wie finden wir die Matrix U zu einem gegebenen A? Im
folgenden entwickeln wir simultan die Antwort auf diese beiden Fragen.
Wir beginnen mit einer einfachen Beobachtung. Wenn k ein Eigenwert der Matrix A ist, sind die Eigenvektoren von A zum Eigenwert k genau die Lösungen x des linearen Gleichungssystems
(A − k · id)x = 0.
(24)
Wenn wir also die Eigenwerte von A kennen, können wir die zugehörigen Eigenvektoren mit dem Gaußschen Eliminationsverfahren bestimmen.
Ferner zeigt (24), daß die Matrix A − k · id genau dann nicht invertierbar ist, wenn k ein Eigenwert
von A ist. Denn wenn k ein Eigenwert von A ist, hat die Matrix A − k · id Rang kleiner als n und ist nach
Korollar 5.6 nicht invertierbar. Die Eigenschaft DET8 der Determinante zeigt also, daß k genau dann ein
Eigenwert von A ist, wenn
det(A − k · id) = 0.
(25)
Es liegt daher nahe, die Funktion
PA : R → R,
z 7→ det(A − z · id)
8
EIGEN- UND SINGULÄRWERTE
27
zu betrachten. Nach Definition der Determinate kann man diese Funktion schreiben in der Form
PA (z) = cn z n + cn−1 z n−1 + · · · + c1 z + c0 ,
wobei c0 , . . . , cn reelle Zahlen sind (die selbstverständlich von A abhängen). Eine solche Funktion nennt
man ein Polynom, und PA heißt das charakteristische Polynom von A. Wir können nun (25) wie folgt
formulieren.
Eine reelle Zahl k ist genau dann ein Eigenwert von A, wenn PA (k) = 0.
(26)
Wenn wir die Eigenwerte und Eigenvektoren von A bestimmen wollen, gehen wir also wie folgt vor.
DIAG1. Bestimme die Menge {k ∈ R : PA (k) = 0}, die sogenannten Nullstellen von PA . Ihre Elemente
sind die Eigenwerte von A.
DIAG2. Zu jeder Nullstelle k von PA bestimme die Lösungen x des linearen Gleichungssystems (24).
Während wir für DIAG2 ein systematisches Verfahren haben (die Gaußsche Eliminationsmethode), ist
kein solches allgemeines Verfahren für DIAG1 bekannt. Dieser Schritt muß praktisch mit Hilfe von Heuristiken und/oder Approximationsverfahren durchgeführt werden. Im folgenden überlegen wir uns gleichwohl, daß das Verfahren DIAG1–DIAG2 im Prinzip die in Satz 8.2 versprochene orthogonale Matrix
produziert. Dazu benötigen wir die folgende Aussage, deren Beweis über den Rahmen dieser Vorlesung
hinausgeht.
Lemma 8.3 Wenn A eine symmetrische Matrix ist, dann existieren ein n-Tupel (k1 , . . . , kn ) reeller Zahlen
und q ∈ {−1, 1}, so daß
n
Y
PA (z) = q ·
(z − ki ).
i=1
Die (nicht notwendigerweise verschiedenen) Zahlen k1 , . . . , kn sind also genau die Nullstellen des
Polynoms PA (z). Mit Hilfe von Lemma 8.3 führen wir nun den
Beweis von Satz 8.2. Wir führen Induktion über die Größe n der Matrix. Im Fall n = 1 hat die Matrix
A selbst bereits die gewünschte Form und wir wählen einfach U = (1) und k1 = A11 . Sei nun n > 1.
Lemma 8.3 zeigt, daß es eine reelle Zahl k1 gibt mit PA (k1 ) = 0. Nach (26) hat A einen Eigenvektor
x1 6= 0 mit Eigenwert k1 . Sei F1 = [x1 ]. Der Vektorraum F1⊥ besitzt eine Orthonormalbasis x2 , . . . , xn .
Sei U1 die orthogonale Matrix mit Spalten x1 , . . . , xn . Weil x1 ein Eigenvektor und A symmetrisch ist,
gibt es eine (n − 1) × (n − 1)-Matrix A0 , so daß


k1 0 · · · 0
 0



U1T AU1 =  .
.
A0 
 ..
0
Nach Induktion gibt es eine orthonormale (n − 1) × (n − 1)-Matrix U2 und reelle Zahlen k2 , . . . , kn , so
daß
U2T A0 U2 = diag(k2 , . . . , kn ).
Sei nun U die n × n-Matrix



U = U1 

1
0
..
.
0···0

U2


.

0
Nach Lemma 7.9 ist U orthogonal. Ferner gilt

k1
0···0
 0

U T AU =  .
U2T A0 U2
 ..
0



 = diag(k1 , . . . , kn ),

8
EIGEN- UND SINGULÄRWERTE
28
2
wie behauptet.
Beispiel 8.4 Wir diagonalisieren die Matrix
A=
−1
1
1
.
1
Ihr charakteristisches Polynom lautet
PA (z)
=
−1 − z
det(A − zid) = det
1
=
(−1 − z) · (1 − z) − 1 · 1 = z 2 − 2 = (z −
1
1−z
√
2) · (z +
√
2).
√
Die Nullstellen
des charakteristischen Polynoms, und damit die Eigenwerte von A, sind also k1 = − 2
√
und k2 = 2. Um auch die Eigenvektoren zu bestimmen, lösen wir die beiden linearen Gleichungssysteme
√
−1 + 2
1√
(A − k1 id)x =
x = 0,
(27)
1
1+ 2
√
1√
−1 − 2
(A − k2 id)x =
x = 0.
(28)
1
1− 2
Das Ergebnis ist, daß die Lösungsmenge von (27) gerade [v1 ] ist, wobei
√ 1/(1 − 2)
.
v1 =
1
Die Lösungsmenge von (28) ist [v2 ], wobei
v2 =
1/(1 +
1
√ 2)
.
Also ist v1 ein Eigenvektor von A zum Eigenwert k1 und v2 ein Eigenvektor von A zum Eigenwert k2 . Die
Norm dieser Vektoren ist
s
s
1
1
√
√ .
kv1 k = 1 +
,
kv2 k = 1 +
2
(1 − 2)
(1 + 2)2
Die beiden Vektoren
−1/2 √ 1/(1 − 2)
,
1
(1 − 2)2
−1/2 √ 1
1
1/(1 + 2)
√
v2 = 1 +
u2 =
1
kv2 k
(1 + 2)2
1
u1 =
v1 =
kv1 k
1+
1
√
bilden also eine Orthonormalbasis des R2 , die aus Eigenwerten besteht. Wenn U die Matrix mit den Spalten u1 , u2 ist, dann ist U orthogonal und
k1 0
T
U AU =
.
0 k2
Leider erfaßt Satz 8.2 nur symmetrische Matrizen und in der Tat gibt es Matrizen, die nicht symmetrisch sind, für die keine Zerlegung der Form (23) existiert. Allerdings kann man die Matrix in Diagnalform
bringen, indem man links und rechts mit zwei möglicherweise verschiedenen orthogonalen Matrizen multipliziert.
9
PROJEKTIONEN UND QUADRATISCHE FORMEN
29
Satz 8.5 Sei A eine m × n-Matrix. Dann existieren eine orthogonal m × m-Matrix V , eine orthogonale
n × n-Matrix U und eine m × n-Matrix D in Diagonalform, so daß V T AU = D.
Beweis. Wir beschäftigen uns zunächst mit dem Spezialfall, daß A eine invertierbare n × n-Matrix ist. Weil
die Matrix AT A ist symmetrisch ist, kann man sie nach Satz 8.2 schreiben als
U T (AT A)U = diag(k1 , . . . , kn ).
Dabei sind k1 , . . . , kn von Null verschieden, weil A invertierbar ist. Wir behaupten nun, daß die Vektoren
AU (1) , . . . , AU (n) orthogonal sind. Denn für je zwei Indices 1 ≤ i < j ≤ n gilt
E
D
E D
E
D
=
AT AU (i) , U (j) = U diag(k1 , . . . , kn )U T U (i) , U (j)
AU (i) , AU (j)
E
E D
D
=
diag(k1 , . . . , kn )U T U (i) , U T U (j) = diag(k1 , . . . , kn )e(i) , e(j)
E
D
= ki e(i) , e(j) = 0.
Analog gilt für alle i = 1, . . . , n
2 D
E
D
E
AU (i) = AU (i) , AU (i) = ki e(i) , e(i) = ki 6= 0.
Die Vektoren
1
(i)
vi = AU (i) AU
(i = 1, . . . , n)
sind also orthonormal. Folglich ist die Matrix V mit den Spalten v1 , . . . , vn orthogonal. Wir definieren
D
E
di = AU (i) , vi
und D = diag(d1 , . . . , dn ). Sei nun B = V DU T . Für i = 1, . . . , n erhalten wir
AU (i) , AU (i)
(i)
(i)
T
(i)
(i)
· AU (i) = AU (i) = AU e(i) .
BU e = BU = (V DU )U = V De = di vi =
AU (i) 2
Folglich gilt BU = AU , weshalb V DU T = B = A.
Wir befassen uns nun mit dem Fall, daß A keine invertierbare n×n-Matrix
ist. In diesem
Fall betrachten
wir E = {x ∈ Rn : Ax = 0} ⊂ Rn , den Kern von A, und F = A(1) , . . . , A(n) ⊂ Rm , den von
den Spalten von A aufgespannten Raum. Nach Korollar 5.3 haben die beiden Vektorräume E ⊥ und F
dieselbe Dimension l und die lineare Abbildung f : E ⊥ → F , x 7→ Ax ist invertierbar. Nach dem soeben
gezeigten existieren also Orthonormalbasen A0 , B 0 von E ⊥ und F sowie eine Diagonalmatrix D0 , so daß
MA0 ,B0 (f ) = D0 . Seien A00 , B 00 nun Orthonormalbasen von E und F ⊥ . Fügen wir A0 und A00 zu A sowie
B 0 und B 00 zu B zusammen, so erhalten wir eine Orthonormalbasis A von Rn und eine Orthonormalbasis B
von Rm . Sei schließlich D die m × n-Matrix in Diagonalform deren einzige von Null verschiede Einträge
0
die Einträge Dii = Dii
für i = 1, . . . , l sind. Dann ist MA,B (A) = D. Die Spalten von A und B bilden
also orthogonale Matrizen U und V , so daß A = V T DU .
2
T
Die Darstellung A = V DU aus Satz 8.5 nennt sich die Singulärwertzerlegung von A. Die Diagonaleinträge der Matrix D heißen entsprechend die Singulärwerte von A.
9
Projektionen und quadratische Formen
Eine n × n-Matrix B induziert eine Abbildung
qB : Rn → R,
x 7→ hBx, xi ,
die quadratische Form von B. In der Tat gibt es zu jeder n × n-Matrix B eine symmetrische n × n-Matrix
A, so daß qA = qB , nämlich die Matrix A = 12 (B + B T ). Die symmetrische Matrix A hat eine Zerlegung
9
PROJEKTIONEN UND QUADRATISCHE FORMEN
30
Abbildung 1: die quadratische Form x21 + x22 .
A = U DU T , wobei D = diag(k1 , . . . , kn ) in Diagonalform und U orthogonal ist. Schreiben wir den
Vektor x in der Form
n D
E
X
x=
x, U (i) U (i) ,
i=1
erhalten wir
hAx, xi =
=
=
U DU T x, x = DU T x, U T x
n X
n D
ED
ED
E
X
x, U (i) x, U (j) DU T U (i) , U T U (j)
i=1 j=1
n D
X
x, U (i)
n
E2 D
E X
D
E2
DU T U (i) , U T U (i) =
ki x, U (i) .
i=1
i=1
Beispiel 9.1
1. Die quadratische Form, die der Matrix A =
x1
q
x2
1
0
0
entspricht, ist
1
= x21 + x22 .
Ihr Graph ist in Abbildung 1 dargestellt.
2. Die quadratische Form, die der Matrix A =
x1
q
x2
1
0
0
entspricht, ist
−1
= x21 − x22 .
Ihr Graph ist in Abbildung 2 dargestellt.
Die Matrizen A, so daß qA (x) = hAx, xi ≥ 0 für alle x ∈ Rn , spielen eine besondere Rolle.
(29)
9
PROJEKTIONEN UND QUADRATISCHE FORMEN
31
Abbildung 2: die quadratische Form x21 − x22 .
Definition 9.2 Eine n × n-Matrix A heißt positiv semidefinit, wenn A symmetrisch ist und hAx, xi ≥ 0
für alle x ∈ Rn .
Proposition 9.3 Seien A, B n × n-Matrizen und sei a ≥ 0 reell.
1. A ist genau dann positiv semidefinit, wenn A symmetrisch ist und alle Eigenwerte von A größer oder
gleich Null sind.
2. A ist genau dann positiv semidefinit, wenn es eine symmetrische Matrix C gibt, so daß A = C 2 .
3. Wenn A und B positiv semidefinit sind, dann ist auch A + B positiv semidefinit.
4. Wenn A positiv semidefinit ist, dann ist auch a · A positiv semidefinit.
5. Die Matrix AT A ist positiv semidefinit.
Beweis. ad 1.: Sei A eine symmetrische Matrix. Dann
existiert die Zerlegung (23). Angenommen A ist
positiv semidefinit. Dann gilt für die Eigenwerte ki = AU (i) , U (i) ≥ 0 für alle i = 1, . . . , n. Nehmen
wir umgekehrt an, daß ki ≥ 0 für i = 1, . . . , n, dann zeigt (29), daß hAx, xi = qA (x) ≥ 0. Somit ist A
positiv semidefinit.
ad 2.: Wenn A = C 2 für eine symmetrische Matrix C, dann gilt für alle x ∈ Rn
2
hAx, xi = C 2 x, x = hCx, Cxi = kCxk ≥ 0.
Ist umgekehrt A positiv semidefinit, so wissen wir aus 1., daß die Eigenwerte k1 , . . . , kn in der Zerlegung (23) größer oder gleich Null sind. Wir können also die Matrix C definieren als
p
p
C = U T diag( k1 , . . . , kn )U.
Quadrieren wir diese Matrix, erhalten wir
p
p
p
p
C 2 = (U T diag( k1 , . . . , kn )U ) · (U T diag( k1 , . . . , kn )U )
p
p
= U T diag( k1 , . . . , kn )2 U = U T diag(k1 , . . . , kn )U = A.
9
PROJEKTIONEN UND QUADRATISCHE FORMEN
32
ad 3.: Für x ∈ Rn gilt h(A + B)x, xi = hAx, xi + hBx, xi ≥ 0, weil A, B positiv semidefinit sind.
ad 4: Für x ∈ Rn gilt ha · Ax, xi= a · hAx, xi ≥ 0, weil A positiv semidefinit ist.
2
ad 5: Für x ∈ Rn gilt AT Ax, x = hAx, Axi = kAxk ≥ 0.
2
Wir befassen uns schließlich noch mit einer besonderen Art von semidefiniten Matrizen.
Definition 9.4 Eine n × n-Matrix A heißt Orthogonalprojektion oder einfach Projektion, falls A positiv
semidefinit ist und A2 = A.
Proposition 9.5 Eine symmetrische n × n-Matrix A ist eine Projektion genau dann, wenn alle ihre Eigenwerte gleich 0 oder 1 sind.
Beweis. Wenn A eine Projektion ist, ist A insbesondere symmetrisch. Folglich existiert die Zerlegung (23).
Es gilt
A2 = (U T diag(k1 , . . . , kn )U )2
= U T diag(k1 , . . . , kn )U · U T diag(k1 , . . . , kn )U
= U T diag(k12 , . . . , kn2 )U.
(30)
Weil A2 = A, erhalten wir
U T diag(k1 , . . . , kn )U = A = A2 = U T diag(k12 , . . . , kn2 )U
und folglich diag(k1 , . . . , kn ) = diag(k12 , . . . , kn2 ). Es gilt also ki2 = ki woraus ki ∈ {0, 1} folgt für
i = 1, . . . , n.
Wenn umgekehrt A symmetrisch ist mit Eigenwerten k1 , . . . , kn ∈ {0, 1}, zeigt (30), daß
A2 = U T diag(k12 , . . . , kn2 )U = U diag(k1 , . . . , kn )U = A,
2
also ist A eine Projektion.
Projektionen sind im Grunde nichts anderes als Untervektorräume. Genauer gilt folgendes.
Proposition 9.6
1. Zu jedem Untervektorraum E ⊂ Rn existiert eine Projektion A, so daß E ⊥ der
Kern von A ist und E = {Ax : x ∈ Rn }.
2. Ist umgekehrt A eine Projektion mit Kern F , so ist F ⊥ der von den Spalten von A aufgespannte
Vektorraum.
Beweis. ad 1.: der Vektorraum E hat eine Orthonormalbasis x1 , . . . , xk und E ⊥ besitzt eine Orthonormalbasis xk+1 , . . . , xn . Die Matrix U mit den Spalten x1 , . . . , xn ist orthogonal und wir definieren
A = U T diag(1, . . . , 1, 0, . . . , 0)U.
| {z }
k Stück
Dann ist A die gesuchte Projektion.
ad 2.: Die Matrix A hat eine Zerlegung der Form (23) mit k1 , . . . , kn ∈ {0, 1}. Sei
I = {i ∈ {1, . . . , n} : ki = 1} .
Dann ist der Kern F von A genau der von den Spalten U (i) , i 6∈ I, aufgespannte Raum. Weil U (1) , . . . , U (n)
eine Orthonormalbasis ist, ist folglich F ⊥ der von U (i) , i ∈ I, aufgespannte Raum. Dies sind genau die
Spalten von A.
2
10
10
AUSBLICK: KOMPLEXE UND ALLGEMEINE VEKTORRÄUME
33
Ausblick: komplexe und allgemeine Vektorräume
In den vergangegen Abschnitten haben wir uns mit Untervektorräumen des Rn befaßt. Allerdings können
viele der angestellten Überlegungen weitgehend verallgemeinert werden. Die naheliegendste Verallgemeinerung besteht darin, Vektorräume über den komplexen Zahlen C zu definieren. Dazu diskutieren wir
zunächst die kompexen Zahlen C.
Als Menge definieren wir C = R × R. Die Paare (x, y) ∈ C schreiben wir in der Form x + iy; das
Symbol i nennen wir die imaginäre Einheit, während x der Realteil und y der Imaginärteil von x + iy
heißt. Man kann sich die komplexe Zahl x + iy also als einen Punkt in der Ebene vorstellen (“komplexe
Zahlenebene”). Wir führen nun folgende Rechenregeln ein: wir definieren
(x + iy) + (s + it)
=
(x + s) + i(y + t),
(x + iy) · (s + it)
=
(xs − yt) + i(ys + xt).
Insbesondere gilt also
i2 = (0 + i1)2 = −1.
Mit anderen Worten: die imaginäre Einheit i ist eine Quadratwurzel von −1. Ferner definieren wir die
konjugierte komplexe Zahl von x + iy als
x + iy = x − iy.
Der Betrag von x + iy wird definiert als
|x + iy| =
q
p
x2 + y 2 = (x + iy) · (x + iy).
Mit 0 bezeichnen wir die komplexe Zahl 0 + i0 und mit 1 die komplexe Zahl 1 + i0. Man prüft nach, daß
mit diesen Definitionen die von R gewohnten Rechenregeln gelten. Insbesondere hat jede komplexe Zahl
x + iy 6= 0 ein multiplikatives Inverses, nämlich
1
x
y
= (x + iy)−1 = 2
−i 2
.
x + iy
x + y2
x + y2
(Allerdings ist es nicht möglich, die Ordnung der reellen Zahlen (“≤”) auf C zu übertragen.)
Die in den Abschnitten 2–6 angestellten Betrachtungen lassen sich problemlos von R auf C übetragen.
Das bedeutet, dass wir Vektoren in Cn und Matrizen mit komplexen Einträgen genauso behandeln können.
Auch das Material der Abschnitte 7–9 kann auf C verallgemeinert werden, allerdings mit einigen subtilen
Änderungen. Beispielsweise definieren man das Skalarprodukt für x, y ∈ Cn als
hx, yi =
n
X
xi ȳi .
i=1
Für eine eingehende Behandlung komplexer Vektorräume sei auf [3] verwiesen.
Bei genauerer Betrachtung stellt sich heraus, daß die Begriffe und Konzepte der linearen Algebra eine
noch deutlich weitergehende Verallgemeinerung zulassen. Im wesentlichen ist die Grundvoraussetzungen,
um lineare Algebra betreiben zu können, daß man eine Addition von Vektoren mit sowie eine Multiplikation von Vektoren mit “Skalaren” (z.B. reellen oder komplexen Zahlen) mit gewissen natürlichen Eigenschaften erklären kann. Dies führt auf den allgemeinen Vektorraumbegriff, für den wir wiederum auf [3]
verweisen.
Ein Beispiel eines allgemeineren Vektorraums ist die Menge E aller Funktion f : R → R. Wir können
zwei solche Funktionen addieren, indem wir zu f, g ∈ E einfach f + g : R → R als die Abbildung
x 7→ f (x) + g(x) definieren. Entsprechend definieren wir zu a ∈ R und f ∈ E das Produkt a · f als die
Abbildung R → R, x 7→ a · f (x). Allerdings gibt es einen wesentlichen Unterschied zwischen diesem
Vektorraum E und den bisher behandelten Vektorräumen: der Vektorraum E hat zwar eine Basis, aber
keine, die aus endlich vielen Vektoren besteht. Um derartige Vektorräume sinnvoll zu behandeln, müssen
wir uns mit einem weiteren Teilgebiet der Mathematik befassen, der Analysis. Diese ist Thema der zweiten
Hälfte der Vorlesung.
11
FOLGEN UND REIHEN
11
34
Folgen und Reihen
Das Thema des nun folgenden zweiten Abschnittes der Vorlesung ist die Analysis zunächst auf R, dann
auch auf Rn . Wir beginnen mit dem Begriff des Grenzwertes. Eine Folge reeller Zahlen ist eine Abbildung
N → R, n 7→ an , die man häufig in der Form (an )n∈N schreibt.
Definition 11.1 Eine Zahl x ∈ R heißt Grenzwert oder Limes der Folge (an )n∈N , wenn folgende Bedingung erfüllt ist.
Zu jeder reellen Zahl ε > 0 existiert eine Zahl N (ε) ∈ N, so daß für alle n > N (ε) gilt
|an − x| < ε.
In diesem Fall schreibt man x = limn→∞ an und sagt, daß (an )n∈N gegen x konvergiert.
Beispiel 11.2 Die Folge (an )n∈N mit an = 1/n hat den Grenzwert 0. Denn zu gegebenem ε > 0 definieren
wir N (ε) = 1/ε. Für alle n > N (ε) gilt dann |an − 0| = an = 1/n < ε.
Der Begriff des Grenzwerts ist eng verbunden mit dem folgenden Konzept. Sei A ⊂ R eine Menge
reeller Zahlen. Wir nennen eine Zahl x ∈ R eine obere Schranke für A, falls für alle a ∈ A gilt a ≤ x.
Analog heißt y ∈ R eine untere Schranke für A, falls für alle a ∈ A gilt a ≥ y. Die Menge A heißt nach
oben/unten beschränkt, falls sie eine obere/untere Schranke hat. Falls beides zutrifft, nennt man A einfach
beschränkt.
Sei A eine nach oben beschränkte Menge. Wir nennen x ∈ R das Supremum von A, falls x eine
obere Schranke von A ist und für jede obere Schranke z von A gilt z ≥ x. Entsprechend heißt y ∈ R das
Infimum einer nach unten beschränkten Menge A, falls y eine untere Schranke von A ist und für jede untere
Schranke z von A gilt z ≤ y. Die folgende Tatsache werden wir nicht beweisen, weil dies eine genauere
Beschäftigung mit den reellen Zahlen voraussezten würde, als der Rahmen dieser Vorlesung erlaubt.
Fakt 11.3 Jede nach oben beschränkte Menge A ⊂ R hat ein Supremum, und jede nach unten beschränkte
Menge hat ein Infimum.
Beispiel 11.4 Sei A die Menge aller x ∈ R mit x2 < 3. Die Menge √
A ist beschränkt, denn jedes x ∈ A
3, als auch ein Infimum, und zwar
erfüllt
−2
≤
x
≤
2.
Folglich
hat
A
sowohl
ein
Supremum,
nämlich
√
−√3. Diese Beispiel zeigt insbesondere, daß Fakt 11.3 in den rationalen Zahlen Q nicht zutrifft, denn
± 3 sind irrational.
Wir nennen eine Folge (an )n∈N nach oben/unten beschränkt, falls die Menge {an : n ∈ N} diese
Eigenschaft hat. Ferner heißt (an )n∈N monoton wachsend, falls an+1 ≥ an für alle n ∈ N, und monoton
fallend, falls an+1 ≤ an für alle n ∈ N. Falls diese Bedingungen mit > statt ≥ bzw. mit < statt ≤ erfüllt
sind, spricht man von einer streng monoton wachsenden/fallenden Folge.
Proposition 11.5 Sei (an )n∈N eine Folge.
1. Wenn (an )n∈N monoton wachsend und nach oben beschränkt ist, dann konvergiert diese Folge gegen
sup {an : n ∈ N}.
2. Wenn (an )n∈N monoton fallend und nach unten beschränkt ist, dann konvergiert diese Folge gegen
inf {an : n ∈ N}.
Beweis. Wir zeigen nur 1.; die zweite Behauptung folgt daraus, indem man zu der Folge (−an )n∈N übergeht. Sei also s = sup {an : n ∈ N} und sei ε > 0. Weil s das Supremum ist, gibt es ein N (ε), so daß
aN ≥ s − ε. Für alle n > N (ε) gilt folglich s ≥ an ≥ aN ≥ s − ε.
2
Beispiel 11.6 Sei 0 ≤ b < 1. Die Folge (an )n∈N mit an = bn hat den Grenzwert 0. Denn diese Folge ist
monoton fallend und ihr Infimum ist 0.
Sei (an )n∈N eine Folge und (mn )n∈N eine streng monoton wachsende Folge. Dann ist (amn )n∈N eine
Folge, die wir eine Teilfolge von (an )n∈N nennen.
11
FOLGEN UND REIHEN
35
Lemma 11.7 Jede Folge (an )n∈N hat eine Teilfolge, die monoton wachsend ist, oder eine Teilfolge, die
monoton fallend ist.
Beweis. Sei B die Menge aller Zahlen n ∈ N, so daß an > aj für alle j > n. Wir betrachten zwei Fälle.
Fall 1: die Menge B ist unendlich. Sei (mn )n∈N streng monoton wachsend, so daß {mn : n ∈ N} ⊂ B.
Dann ist die Folge (amn )n∈N (streng) monoton fallend.
Fall 2: die Menge B ist endlich. Dann hat B eine obere Schranke n0 ∈ N. Wir konstruieren die Folge
mn induktiv, beginnend mit m1 = n0 + 1. Wenn mn bereits definiert ist, definieren wir
Cn+1 = {k ∈ N : ak ≥ amn , k > mn } .
Diese Menge ist nicht leer, weil mn 6∈ B. Sei also mn+1 = min Cn+1 . Dann ist (amn )n∈N monoton
wachsend.
2
Können wir einer Folge irgendwie ansehen, ob sie konvergiert oder nicht, ohne notwendigerweise den
Grenzwert zu kennen? Um dies zu beantworten, benötigen wir eine weitere
Definition 11.8 Eine Folge (an )n∈N heißt eine Cauchyfolge, wenn es zu jedem ε > 0 ein N (ε) ∈ N gibt,
so daß für alle n > N (ε) und alle m > N (ε) gilt |am − an | < ε.
Proposition 11.9 Eine Folge (an )n∈N konvergiert genau dann, wenn sie eine Cauchyfolge ist.
Beweis. Angenommen (an )n∈N konvergiert gegen z ∈ R. Sei ε > 0 und sei N (ε) ∈ N so, daß |an −z| < ε
für alle n ≥ N (ε). Dann gilt für alle n, m > N (ε)
|an − am | ≤ |an − z| + |am − z| < 2ε.
Folglich ist (an )n∈N eine Cauchyfolge.
Nehmen wir also umgekehrt an, daß (an )n∈N eine Cauchyfolge ist. Dann ist (an )n∈N beschränkt. Ferner existiert eine monotone Teilfolge (amn )n∈N , die nach Proposition 11.5 gegen eine Zahl z ∈ R konvergiert. Sei nun ε > 0 und wähle N (ε) so, daß |aN (ε) − an | < ε für alle n > N (ε). Weil limn→∞ amn = z,
existiert ein k ∈ N, so daß mk > N (ε) und |amk − z| < ε. Für alle n > N (ε) gilt folglich
|an − z| ≤ |amk − z| + |amk − an | ≤ 2ε.
Daraus folgt limn→∞ an = z.
2
Reihen sind eine besonders wichtige Art von Folgen. Sei dazu (an )n∈N eine Folge. Wir definieren eine
weitere Folge
n
X
An =
ak ,
k=1
die wir die Reihe mit den Gliedern (an )n∈N nennen. Wenn die Folge (An )n∈N gegen eine Zahl z ∈ R
konvergiert, schreiben wir
∞
X
z=
an .
n=1
P∞
an auch, um einfach die Folge (An )n∈N zu bezeichnen.
P∞
Beispiel 11.10 Zu x ∈ R definieren wir die geometrische Reihe als die Reihe n=1 xn−1 mit den Gliedern xn−1 . Falls x 6= 1 gilt für N ∈ N
Man verwendet die Schreibweise
n=1
N
X
n=1
xn−1 =
1 − xN
;
1−x
das sieht man, indem man beide Seiten der Gleichung mit 1 − x multipliziert. Ist also −1 < x < 1, so gilt
∞
X
n=1
xn−1 = 1/(1 − x).
12
STETIGKEIT
36
P∞
P∞
Proposition 11.11 Die Reihe n=1 an konvergiert, wenn n=1 |an | konvergiert.
Pn
Pn
Beweis. Sei An = k=1 ak und Bk = k=1 |ak |. Für N ∈ N und n > N gilt
n
X
|An − aN | = |
ak | ≤
k=N +1
n
X
|ak | = |Bn − BN |.
k=N +1
2
Wenn (Bn )n∈N eine Cauchyfolgt ist, trifft dies also auch auf (An )n∈N zu.
Korollar 11.12 Die Reihe
xn−1 für alle n ∈ N.
P∞
n=1
an konvergiert, wenn es eine reelle Zahl 0 < x < 1 gibt, so daß |an | ≤
Beweis. In diesem Fall konvergiert
2
Beispiel 11.13 Die Reihe
P∞
P∞
1
n=1 n2n
n=1
|an |, weil
PN
n=1
|an | ≤
PN
n=1
xn−1 und
P∞
n=1
xn−1 =
1
1−x .
konvergiert.
In diesem Abschnitt haben wir der Einfachheit halber Folgen und Reihen betrachtet, deren Index n die
natürlichen Zahlen durchläuft. Alles läßt sich einfach verallgemeinern auf den Fall,
n eine nach unten
P∞daß −n
beschränkte
unendliche
Teilmenge
von
Z
durchläuft.
Beispielsweise
bedeutet
2
nichts anderes
n=0
P∞
als n=1 2−(n−1) .
12
Stetigkeit
In diesem Abschnitt behandeln wir Funktionen die man, anschaulich gesprochen, “zeichnen kann, ohne
den Stift abzusetzen”. Um diese Intuition mathematisch zu erfassen, beginnen wir mit
Definition 12.1 Sei u ∈ R, X ⊂ R und f : X → R. Wir sagen f (x) konvergiert gegen y ∈ R für
x → u, in Symbolen: limx→u f (x) = y, falls die beiden folgenden Bedingungen erfüllt sind:
• Zu jedem δ > 0 gibt es ein x ∈ X mit |x − u| < δ.
• Zu jedem ε > 0 gibt es ein δ > 0, so daß für alle x ∈ X mit |x − u| < δ gilt |f (x) − y| < ε.
Für zwei Funktionen f, g : X → R ist bekanntlich f + g : X → R die Funktion x 7→ f (x) + g(x).
Analog ist f · g : X → R die Funktion x 7→ f (x) · g(x).
Proposition 12.2 Seien f, g : X → R Funktionen und u ∈ R. Wenn limx→u f (x) = y und limx→u g(x) =
z, dann gilt
lim f (x) + g(x) = y + z
und
lim f (x) · g(x) = y · z.
x→u
x→u
Beweis. Zu ε > 0 sei δ > 0 so, daß |f (x) − y| < ε und |g(x) − z| < ε, falls |x − u| < δ. Dann gilt für
solche x
|(f + g)(x) − (y + z)| ≤ |f (x) − y| + |g(x) − z| < 2ε.
Daraus folgt die erste Behauptung.
Um die zweite Behauptung zu zeigen, bemerken wir, daß
|f · g(x) − y · z| =
≤
|(f (x) − y) · g(x) + y · (g(x) − g(u))|
|g(x)| · |f (x) − y| + |y| · |g(x) − z|.
(31)
Wir wählen also δ > 0 klein genug, so daß für alle x mit |x − u| < δ gilt
|g(x)| ≤ |z| + 1,
|f (x) − y| < ε/(|z| + 1)
Dann zeigt (31), daß |f · g(x) − y · z| < 2ε.
und
|g(x) − z| < ε/(1 + |y|).
2
13
DIE ABLEITUNG
37
Proposition 12.3 Seien f : X → Y , h : Y → R Funktionen und u ∈ X, v ∈ Y , z ∈ R so, daß
limx→u f (x) = v und limy→v h(y) = z. Dann gilt limx→u h ◦ f (x) = z.
Beweis. Zu jedem ε > 0 existiert δ > 0, so daß für alle y ∈ Y mit |v − y| < δ gilt |h(y) − z| < ε.
Ferner gibt es ein γ > 0, so daß für alle x ∈ X mit |x − u| < γ gilt |f (x) − v| < δ. Für diese x gilt also
|h(f (x)) − z| < ε.
2
Definition 12.4 Sei X ⊂ R, f : X → R und u ∈ X. Wir nennen f stetig im Punkt u, falls
lim f (x) = f (u).
x→u
Ist ferner S ⊂ X, so heißt f stetig auf S, falls f stetig in jedem Punkt u ∈ S ist.
Anschaulich bedeutet Stetigkeit, daß die Funktion f keinen “plötzlichen Sprung” im Punkt u macht.
Ein Gegenbeispiel ist die Funktion
−1 falls x < 0,
R → R,
x 7→
1
falls x ≥ 0.
Beispiele für eine stetige Funktion sind die Funktionen x 7→ x und x 7→ c für jede Zahl c ∈ R. Proposition 12.2 liefert uns viele neue Beispiele stetiger Funktionen, insbesondere die Polynome
R → R,
x 7→ an xn + an−1 xn−1 + · · · + a1 x + a0 ,
mit a0 , a1 , . . . , an ∈ R.
Seien (a, b) reelle Zahlen. Wir bezeichnen mit (a, b) = {x ∈ R : a < x < b} das offene Intervall von
a bis b. (Trotz der identischen Schreibweise ist dies natürlich nicht dasselbe wie das Paar (a, b).) Ferner
bezeichnet [a, b] = {x ∈ R : a ≤ x ≤ b} das abgeschlossene Intervall von a bis b. Stetige Funktionen
haben die folgende wichtige Eigenschaft.
Satz 12.5 (“Zwischenwertsatz”) Seien a < b reelle Zahlen und sei f : [a, b] → R stetig auf dem gesamten Intervall [a, b]. Wenn f (a) < 0 aber f (b) > 0, dann existiert eine Zahl c ∈ (a, b) mit f (c) = 0.
Beweis. Die Menge Z = {x ∈ [a, b] : f (x) < 0} ist beschränkt und nicht leer und b 6∈ Z. Sei c = sup Z.
Die Funktion f ist stetig in c.
Wir behaupten, daß f (c) ≤ 0. Denn angenommen f (c) > 0. Dann setzen wir ε = f (c)/2 und wählen
δ > 0 so klein, daß |f (x) − f (c)| < ε wenn |x − c| < δ. Nach Definition des Supremums gibt es eine Zahl
x ∈ Z mit |x − c| < δ; folglich erhalten wir den Widerspruch
0 > f (x) ≥ f (c) − ε ≥ f (c)/2 > 0.
Wir wissen also, daß f (c) ≤ 0. Andererseits behaupten wir, daß f (c) ≥ 0. Denn angenommen f (c) <
0. In diesem Fall setzen wir ε = −f (c)/2 > 0. Weil f stetig ist in c, gibt es eine Zahl δ > 0, so daß
|f (c) − f (x)| < ε/2 sofern |x − c| < δ. Ferner gibt es, da c = sup Z < b, eine Zahl c < x < b mit
|x − c| < δ. Weil x 6∈ Z, gilt f (x) ≥ 0, und folglich erhalten wir den Widerspruch
0 ≤ f (x) ≤ f (c) + ε ≤ f (c)/2 < 0.
Die einzige verbleibende Möglichkeit ist also f (c) = 0.
13
2
Die Ableitung
Stetigkeit, d.h. daß eine Funktion keine “plötzlichen Sprünge” macht, ist ein einfaches aber wichtiges Konzept. Der Stetigkeitsbegriff erlaubt, aus dem Wert einer Funktion in einem Punkt u Schlüsse zu ziehen die
Funkionswerte für x “in der Nähe” von u betreffend. Allerdings ist die Art von Schluß, die man ziehen
kann, noch recht rudimentär. Um genauere Aussagen zu treffen, führen wir nun den Begriff der Differenzierbarkeit ein. Dieser erlaubt wesentlich genauere Aussagen über das lokale Verhalten einer Funktion: die
Idee ist, eine Funktion lokal durch eine lineare Funktion zu approximieren. Der Nachteil ist, daß nicht jede
stetige Funktion differenziert werden kann.
13
DIE ABLEITUNG
38
Definition 13.1 Sei f : X → R eine Funktion und sei u ∈ X ein Punkt, so daß es zu jedem ε > 0 ein
x ∈ X \ {u} mit |x − u| < ε gibt. Wir sagen, daß die Funktion f differenzierbar ist im Punkt u, falls
folgendes gilt:
Sei g : X \ {u} → R, x 7→
f (x)−f (u)
.
x−u
Dann konvergiert g(x) für x → u.
In diesem Fall nennen wir limx→u g(x) die Ableitung von f in u.
(u)
die Steigung der Geraden durch die Punkte (x, f (x)), (u, f (u)) ∈
Anschaulich gesprochen ist f (x)−f
x−u
R . Da wir den Limes x → u betrachten, können wir uns die Ableitung also als die Steigung der Funktion
df
f im Punkt u vorstellen. Für die Ableitung von f im Punkt u schreiben wir oft f 0 (u) oder dx
(u). Wenn f
df
0
auf der gesamten Menge X differenzierbar ist, können wir also f (oder dx ) als eine Abbildung X → R
auffassen.
2
Proposition 13.2 Wenn die Funktion f : X → R im Punkt u ∈ X differenzierbar ist, dann ist sie dort
auch stetig.
Beweis. Sei 0 < ε < 1. Wähle 0 < δ < 2(1+|fε 0 (u)|) so klein, daß für alle x ∈ X mit |x − u| < δ gilt
f (x) − f (u)
0
− f (u) < ε/2.
x−u
Dann gilt
f (x) − f (u) · |x − u| ≤ f (x) − f (u) − f 0 (u) + |f 0 (u)| · |x − u|
|f (u) − f (x)| = x−u
x−u <
εδ
+ δ|f 0 (u)| ≤ ε2 /4 + ε/2 < ε.
2
Also ist f stetig in u.
2
Ähnlich wie im Fall von stetigen Funktionen kann man aus gegebenen differenzierbaren Funktionen
neue basteln.
Proposition 13.3 Angenommen die Funktionen f : X → R, g : X → R sind differenzierbar im Punkt
u ∈ X. Dann gilt folgendes.
1. Die Funktion f + g : X → R, x 7→ f (x) + g(x) ist differenzierbar in u und
(f + g)0 (u) = f 0 (u) + g 0 (u).
2. Die Funktion f · g : X → R, x 7→ f (x) · g(x) ist differenzierbar in u und
(f · g)0 (x) = f 0 (x) · g(x) + f (x) · g 0 (x).
Beweis. Es gilt
(f + g)(x) − (f + g)(u)
f (x) − f (u) g(x) − g(u)
=
+
.
x−u
x−u
x−u
Wenn also
f (x)−f (u)
x−u
lim
x→u
und
g(x)−g(u)
x−u
für x → u konvergieren, gilt nach Proposition 12.2
(f + g)(x) − (f + g)(u)
f (x) − f (u)
g(x) − g(u)
= lim
+ lim
.
x→u
x→u
x−u
x−u
x−u
Daraus folgt die erste Behauptung.
Ferner gilt
(f · g)(x) − (f · g)(u)
x−u
=
=
f (x)g(x) − f (u)g(x) − (f (u)g(u) − f (u)g(x))
x−u
f (x) − f (u)
g(x) − g(u)
g(x) ·
+ f (u) ·
.
x−u
x−u
13
DIE ABLEITUNG
39
Proposition 13.2 zeigt, daß limx→u g(x) = g(u). Aus Proposition 12.2 folgt also
lim
x→u
(f · g)(x) − (f · g)(u)
x−u
f (x) − f (u)
g(x) − g(u)
+ f (u) lim
x→u
x−u
x−u
g(u)f 0 (u) + f (u)g 0 (u),
lim g(x) · lim
=
x→u
=
x→u
2
wie behauptet.
Proposition 13.4 (“Kettenregel”) Angenommen die Funktion f : X → Y ist differenzierbar im Punkt
u ∈ X und die Funktion h : Y → R ist differenzierbar im Punkt v = f (u). Dann ist h ◦ f differenzierbar
im Punkt u und
(h ◦ f )0 (u) = h0 (f (u)) · f 0 (u).
Beweis. Wir führen die Kurzschreibweise t = f (x) − f (u) ein. Es gilt
h ◦ f (x) − h ◦ f (u)
x−u
h(v + t) − h(v)
x−u
(h(v) + th0 (v)) − h(v) h(v + t) − h(v) − th0 (v)
+
x−u
x−u
th0 (v) h(v + t) − h(v) − th0 (v)
+
.
x−u
x−u
=
=
=
Wir erhalten
(32)
h0 (v)(f (x) − f (u)))
th0 (v)
= lim
= h0 (v)f 0 (u).
x→u
x→u x − u
x−u
(33)
h(v + t) − h(v)
h(v + t) − h(v) − th0 (v)
t
0
lim
= lim
− h (v) .
x→u
x→u x − u
x−u
t
(34)
lim
Ferner gilt, sofern t 6= 0,
Nach Definition der Ableitung h0 (v) bzw. f 0 (v) gilt
lim
s→0
h(v + s) − h(v)
− h0 (v) = 0,
s
lim
x→u
t
= f 0 (u).
x−u
Also zeigt (34), daß
h(v + t) − h(v) − th0 (v)
= 0.
x→u
x−u
Schließlich folgt die Behauptung, indem man (33) und (35) in (32) einsetzt.
lim
(35)
2
Proposition 13.5 Die Funktion f : R \ {0} → R, x 7→ 1/x is differenzierbar. Es gilt f 0 (x) = −1/x2 .
Beweis. Wir zeigen zunächst, daß die Funktion f stetig in x ∈ R \ {0} ist. Denn
f (u) − f (x) =
1
1
x−u
− =
.
u x
ux
(36)
Wenn |x − u| hinreichend klein ist, gilt |u| ≥ 12 |x|. Dann zeigt (36)
|f (u) − f (x)| ≤
|x − u|
2|x − u|
≤
.
|ux|
|x|2
Folglich gilt
lim |f (u) − f (x)| = 0,
u→x
also ist f stetig im Punkt x.
(37)
13
DIE ABLEITUNG
40
Ferner folgt aus (36), daß
f (u) − f (x)
u−x
=
−
1
.
ux
(38)
Aus (37) und (38) ergibt sich schließlich
lim
u→x
f (u) − f (x)
−1
1
= lim
= − 2,
u→x ux
u−x
x
2
wie behauptet.
Korollar 13.6 Seien f : X → R, g : X → R zwei Funktionen, die im Punkt x ∈ X differenzierbar sind.
Wenn g(y) 6= 0 für alle y ∈ X, dann ist f /g im Punkt x differenzierbar und
0
f 0 (x)g(x) − f (x)g 0 (x)
f
(x) =
.
g
g(x)2
Beweis. Proposition 13.3 zeigt, daß
0
0
0
f
1
1
1
(x) =
f·
(x) = f 0 (x) ·
+ f (x)
(x).
g
g
g(x)
g
(39)
Sei h : R \ {0}, z 7→ 1/z. Aus Proposition 13.4 folgt
0
1
1
g 0 (x)
(x) = (h ◦ g)0 (x) = g 0 (x) · h0 (g(x)) = g 0 (x) · −
=−
.
2
g
g(x)
g(x)2
Aus (39) und (40) folgt schließlich die Behauptung.
(40)
2
Der Beweis des folgenden Satzes benötigt einige Überlegungen, die den Rahmen dieser Vorlesung
sprengen.
Satz 13.7 (“Satz über die Umkehrfunktion”) Sei f : (a, b) → (c, d) eine stetige bijektive Funktion, die
im Punkt x ∈ (a, b) differenzierbar ist. Dann ist die Umkehrfunktion f −1 : (c, d) → (a, b) im Punkt
y = f (x) differenzierbar mit Ableitung 1/f 0 (x).
Was sagt die Ableitung über das lokale Verhalten der Funktion aus? Wir beginnen mit der folgenden
Beobachtung.
Satz 13.8 (“Satz von Rolle”) Sei f : [a, b] → R eine differenzierbare Funktion mit f (a) = f (b) = 0.
Dann gibt es ein c ∈ (a, b) mit f 0 (c) = 0.
Beweis. Wir nehmen zunächst an, daß es ein d ∈ (a, b) gibt mit f (d) > 0. Sei Z = {f (x) : x ∈ [a, b]}. Wir
zeigen zunächst, daß die Menge Z nach oben beschränkt ist. Angenommen, sie wäre es nicht. Dann gibt
es zu jeder natürlichen Zahl n ein xn ∈ [a, b], so daß f (xn ) > n. Die Folge (xn )n∈N hat eine monotone
Teilfolge (xkn )n∈N , die nach Proposition 11.5 gegen eine Zahl x∗ ∈ [a, b] konvergiert. Weil f stetig ist,
folgt f (x∗ ) > n für alle n ∈ N, was unmöglich ist. Dieser Widerspruch zeigt, daß Z nach oben beschränkt
ist.
Folglich existiert s = sup Z. Nach Definition des Supremums gibt es zu jedem n ∈ N eine Zahl
yn ∈ [a, b], so daß |s − f (yn )| < 1/n. Die Folge (yn )n∈N hat eine monotone Teilfolge (ykn )n∈N , die
nach Proposition 11.5 gegen eine Zahl c ∈ [a, b] konvergiert. Folglich gilt f (c) = s. Weil s > 0, folgt
c 6∈ {a, b}, also c ∈ (a, b).
Wir behaupten, daß f 0 (c) = 0. Denn angenommen f 0 (c) > 0. Dann gibt es ein kleines δ > 0, so daß
mit ε = f 0 (c)/2 gilt
f (c + δ) − f (c)
≥ f 0 (c) − ε > 0.
δ
14
DAS INTEGRAL
41
Daraus folgt, daß f (c + δ) > f (c) = s. Das kann nicht angehen, weil s das Supremum der Menge
Z = {f (x) : x ∈ [a, b]} ist. Also folgt f 0 (c) ≤ 0.
Ist entsprechend f 0 (c) < 0, so gibt es ein kleines δ > 0, so daß mit ε = −f 0 (c)/2 gilt
f (c − δ) − f (c)
≥ −f 0 (c) − ε > 0.
δ
Also finden wir, daß f (c − δ) > f (c) = s, was wiederum einen Widerspruch ergibt. Dies zeigt f 0 (c) = 0.
Was, wenn f (x) ≤ 0 für alle x ∈ (a, b)? Wenn es ein x ∈ (a, b) gibt mit f (x) < 0, dann wenden wir
das obige Argument auf die Funktion −f an und erhalten ein c mit −f 0 (c) = 0, also auch f 0 (c) = 0. Und
wenn f (x) = 0 für alle x ∈ (a, b), dann folgt unmittelbar, daß f 0 (x) = 0 für alle x.
2
Korollar 13.9 (“Mittelwertsatz der Differentialrechnung”) Sei f : [a, b] → R differenzierbar. Es gibt
ein c ∈ [a, b], so daß f (b) − f (a) = f 0 (c) · (b − a).
Beweis. Die Funktion
g : [a, b] → R,
x 7→ f (x) − f (a) −
f (b) − f (a)
· (x − a)
b−a
erfüllt die Voraussetzungen des Satzes von Rolle. Folglich existiert ein c ∈ [a, b] mit
0 = g 0 (c) = f 0 (c) −
f (b) − f (a)
.
b−a
Umstellen dieser Gleichung liefert die Behauptung.
2
Wir nennen eine Funktion f : [a, b] → R monoton wachsend, falls für je zwei reelle Zahlen x, y mit
a ≤ x < y ≤ b gilt f (x) ≤ f (y). Ferner heißt f streng monoton wachsend, falls für je zwei reelle Zahlen
x, y mit a ≤ x < y ≤ b gilt f (x) < f (y). Analog heißt f monoton fallend, falls x, y mit a ≤ x < y ≤ b
stets gilt f (x) ≥ f (y), und streng monoton fallend, wenn für x, y wie zuvor gilt f (x) < f (y).
Korollar 13.10 Sei f : [a, b] → R differenzierbar.
1. Wenn f 0 (c) ≥ 0 für alle c ∈ [a, b], dann ist f monoton wachsend.
2. Wenn f 0 (c) > 0 für alle c ∈ [a, b], dann ist f streng monoton wachsend.
3. Wenn f 0 (c) ≤ 0 für alle c ∈ [a, b], dann ist f monoton fallend.
4. Wenn f 0 (c) < 0 für alle c ∈ [a, b], dann ist f streng monoton fallend.
Sei f : [a, b] → R eine Funktion. Ein Punkt c ∈ [a, b] heißt lokales Maximum von f , wenn es ein
ε > 0 gibt, so daß für alle x ∈ [a, b] mit |x − c| < ε gilt f (x) ≤ f (c). Entsprechend nennt man c ein
lokales Minimum von f , falls es ein ε > 0 gibt, so daß für alle x ∈ [a, b] mit |x − c| < ε gilt f (x) ≥ f (c).
Wenn c ein lokales Minimum oder ein lokales Maximum ist, nennt man c ein lokales Extremum.
Korollar 13.11 Sei f : [a, b] → R differenzierbar. Wenn c ∈ [a, b] ein lokales Extremum ist, gilt f 0 (c) = 0.
14
Das Integral
Für eine Funktion f : [a, b] → R möchten wir die Fläche, die f mit der x-Achse einschließt, bestimmen.
Ist beispielsweise f die Funktion f : [0, 1] → R, x 7→ 1, so ist der Flächeninhalt 1. Im Fall der Funktion
g : [0, 1] → R, x 7→ −1, ist der Flächeninhalt −1.
Für bestimmte besonders einfache Funktionen kann man den Flächeninhalt leicht bestimmen. Wir nennen eine Funktion t : [a, b] → R eine Treppenfunktion, wenn es Zahlen a = a0 < a1 < · · · < ak = b
und c1 , . . . , ck ∈ R gibt, so daß
t(x) = ci
für alle x ∈ (ai−1 , ai )
(i = 1, . . . , k).
14
DAS INTEGRAL
42
In diesem Fall definieren wir
b
Z
t(x) dx =
a
k
X
ci (ai − ai−1 ).
i=1
Sei nun allgemeiner f : S → R eine Funktion und seien a, b Zahlen, so daß [a, b] ⊂ S. Sei ferner
T ∗ (f, [a, b]) die Menge aller Treppenfunktionen t : [a, b] → R, so daß t(x) ≥ f (x) für alle x ∈ [a, b].
Analog sei T∗ (f, [a, b]) die Menge aller Treppenfunktionen t : [a, b] → R, so daß t(x) ≤ f (x) für alle
x ∈ [a, b]. Wir nennen eine Funktion f : [a, b] → R integrierbar auf [a, b], falls
(Z
)
(Z
)
b
b
∗
t(x)dx : t ∈ T (f, [a, b]) = sup
t(x)dx : t ∈ T∗ (f, [a, b]) .
inf
a
a
In diesem Fall definieren wir das Integral von f über [a, b] als
)
(Z
Z b
b
t(x)dx : t ∈ T∗ (f, [a, b]) .
f (x)dx = sup
a
a
Welche Funktionen sind integrierbar? Wir nennen eine Funktion f : [a, b] → R stückweise stetig,
wenn es Zahlen c > 0 und a = a0 < a1 < · · · < ak = b gibt, so daß f auf jedem der Intervalle (ai−1 , ai )
stetig ist für i = 1, . . . , k, und |f (x)| ≤ c für alle x ∈ [a, b].
Proposition 14.1 Wenn f : [a, b] → R stückweise stetig ist, ist f integrierbar auf [a, b].
Der Beweis von Proposition 14.1 ist relativ aufwendig und übersteigt daher den Rahmen dieser Vorlesung.
Beispiel 14.2 Wir integrieren die Funktion f : [0, 1] → R, x 7→ x. Zu diesem Zweck konstruieren wir
“untere” und “obere” Treppenfunktionen. Sei n ≥ 1 eine natürliche Zahl. Wir erhalten eine untere Treppenfunktion un , indem wir definieren
1
k
un (x) = · max k ∈ Z : ≤ x .
n
n
Entsprechend erhält man eine obere Treppenfunktion on :
1
k
on (x) = · min k ∈ Z : ≥ x .
n
n
Die Integrale dieser Treppenfunktionen können wir leicht ausrechnen:
Z 1
Z 1
n
n−1
X i
X
(n − 1)n
i
n(n + 1)
=
,
o
(x)dx
=
=
.
un (x)dx =
n
2
2
2
n
2n
n
2n2
0
0
i=0
i=1
Weil
Z
lim
n→∞
folgt
R1
0
1
Z
un (x)dx = lim
n→∞
0
1
on (x)dx =
0
1
,
2
f (x)dx = 1/2.
Die folgende Tatsache folgt relativ leicht aus der Konstruktion des Integrals.
Proposition 14.3 Seien f : [a, b] → R, g : [a, b] → R auf [a, b] integrierbare Funktionen. Sei c ∈ R.
Dann sind die Funktionen f + g, c · f integrierbar und
Z b
Z b
Z b
Z b
Z b
(f + g)(x)dx =
f (x)dx +
g(x)dx,
(c · f )(x)dx = c ·
f (x)dx.
a
a
a
a
Wenn ferner f (x) ≤ g(x) für alle x ∈ (a, b), dann gilt
Z b
Z
f (x)dx ≤
a
a
b
g(x)dx.
a
14
DAS INTEGRAL
43
Wenn f auf [a, b] integrierbar ist, definieren wir
Z a
Z
f (x)dx = −
b
b
f (x)dx.
a
Wenn a ≤ b ≤ c reelle Zahlen sind und f auf [a, c] integrierbar ist, gilt
Z c
Z b
Z c
f (x)dx =
f (x)dx +
f (x)dx.
a
a
b
Proposition 14.4 (“Mittelwertsatz der Integralrechnung”) Wenn f auf [a, b] stetig ist, gibt es ein c ∈
[a, b], so daß
Z b
f (x)dx = (b − a) · f (c).
a
Beweis. Wir betrachten die stetige Funktion g : [a, b] → R, x 7→ f (x) · (b − a). Es gilt
Z b
inf {g(x) : x ∈ [a, b]} ≤
f (x)dx ≤ sup {g(x) : x ∈ [a, b]} .
a
Nach dem Zwischenwertsatz gibt es also ein c ∈ [a, b], so daß
Z b
(b − a)f (c) = g(c) =
f (x)dx,
a
wie behauptet.
2
Sei S ⊂ R und f : S → R eine Funktion. Eine Funktion F : S → R, die auf S differenzierbar ist,
heißt Stammfunktion von f , falls
f (x) = F 0 (x)
für alle x ∈ S.
Proposition 14.5 Sei S ⊂ R und f : S → R. Angenommen F1 , F2 sind Stammfunktionen von f . Dann
gibt es eine Zahl c ∈ R, so daß
F1 (x) = F2 (x) + c
für alle x ∈ S.
Beweis. Die Funktion F1 − F2 hat Ableitung (F1 − F2 )0 (x) = F10 (x) − F20 (x) = f (x) − f (x) = 0. Nach
Korollar 13.10 ist F1 − F2 also sowohl monoton wachsend als auch monoton fallend. Das bedeutet, daß es
eine Zahl c ∈ R gibt, so daß F1 (x) − F2 (x) = c für alle x ∈ S.
2
Satz 14.6 (“Hauptsatz der Differential- und Integralrechnung”) Sei f : [a, b] → R stetig. Dann ist
Z x
F : [a, b] → R,
x 7→
f (y)dy
a
eine Stammfunktion von f .
Beweis. Sei x ∈ [a, b]. Falls x < b, gibt es nach Proposition 14.4 zu jeder hinreichend kleinen Zahl h > 0
ein s(h) ∈ [x, x + h], so daß
Z x+h
Z x
Z x+h
F (x + h) − F (x) =
f (y)dy −
f (y)dy =
f (y)dy = h · f (s(h)).
(41)
a
a
x
Weil f stetig ist, gilt limh→0 f (s(h)) = f (x). Falls x > a, gibt es entsprechend zu jedem hinreichend
kleinen h > 0 ein t ∈ [x − h, x], so daß
Z x−h
Z x
Z x−h
F (x − h) − F (x) =
f (y)dy −
f (y)dy =
f (y)dy = −h · f (t(h)).
(42)
a
a
x
15
DER LOGARITHMUS UND DIE EXPONENTIALFUNKTION
44
Wiederum aufgrund der Stetigkeit von f gilt limh→0 f (t(h)) = f (x). Aus (41) und (42) folgt also
F (x + h) − F (x)
= f (x),
h→0
h
F 0 (x) = lim
wie behauptet.
2
Proposition 14.5 und Satz 14.6 ermöglichen es uns, viele Integrale auszurechnen. Das folgende Korollar
verrät das allgemeine Rezept.
Korollar 14.7 Sei f : [a, b] → R stetig und sei F eine Stammfunktion von f . Dann gilt
b
Z
f (y)dy = F (b) − F (a).
a
Rx
Beweis. Sei G(x) = a f (y)dy. Nach Satz 14.6 ist G eine Stammfunktion von f . Nach Proposition 14.5
existiert also eine Zahl c ∈ R, so daß F (x) = G(x) + c für alle x ∈ [a, b]. Daraus folgt, daß
Z
b
F (b) − F (a) = G(b) − G(a) =
Z
f (y)dy −
a
a
b
Z
Z
f (y)dy − 0 =
f (y)dy =
a
a
b
f (y)dy,
a
2
wie behauptet.
R1
Beispiel 14.8 In Beispiel 14.2 haben wir ausgerechnet, daß 0 xdx = 1/2. Mit Korollar 14.7 können wir
dieses Integral einfacher ausrechnen. Denn die Funktion f : [0, 1] → R, x 7→ x hat die Stammfunktion
R1
F : [0, 1] → R, x 7→ x2 /2. Also erhalten wir 0 f (x)dx = F (1) − F (0) = 1/2.
Mit Hilfe von Korollar 14.7 gewinnen wir aus den Ableitungsregeln, insbesondere der Produkt- und der
Kettenregel, Rechenregeln für das Integrieren. Um diese Regeln formulieren zu können, benötigen wir noch
einen weiteren Begriff: eine Funktion f : S → R heißt stetig differenzierbar, falls f auf S differenzierbar
ist und die Ableitung f 0 : S → R eine stetige Funktion ist.
Korollar 14.9 (“Partielle Integration”) Seien f, g : [a, b] → R stetig differenzierbar. Dann gilt
Z
b
f 0 (y)g(y)dy = f (b)g(b) − f (a)g(a) −
a
Z
b
f (y)g 0 (y)dy.
a
Korollar 14.10 (“Substitutionsregel”) Sei f : [c, d] → R stetig und g : [a, b] → [c, d] stetig differenzierbar. Dann gilt
Z b
Z g(b)
f (g(y))g 0 (y)dy =
f (y)dy.
a
15
g(a)
Der Logarithmus und die Exponentialfunktion
Im folgenden benutzen wir die Differential- und Integralrechnung, um einige wichtige Funktionen einzuführen. Die erste ist der natürliche Logarithmus: wir definieren die Funktion
Z x
1
dt.
ln : R>0 = {x ∈ R : x > 0} → R,
x 7→
1 t
Nach Satz 14.6 hat diese Funktion die Ableitung
d
1
ln(x) = .
dx
x
(43)
ln(1) = 0.
(44)
Ferner gilt nach Konstruktion des Integrals
15
DER LOGARITHMUS UND DIE EXPONENTIALFUNKTION
45
Proposition 15.1 Für alle a, x > 0 gilt ln(a · x) = ln(a) + ln(x).
Beweis. Sei f : R>0 → R, x 7→ ln(a · x) und g : R>0 → R, x 7→ ln(a) + ln(x). Nach der Kettenregel
gilt
1
1
1
f 0 (x) = a ·
= , und ferner g 0 (x) = .
a·x
x
x
Also sind f, g Stammfunktionen der Funktion x 7→ 1/x. Weil außerdem f (1) = ln(a) = g(1), folgt
f (x) = g(x) für alle x > 0.
2
Durch wiederholte Anwendung der Proposition erhält man
Korollar 15.2 Sei x > 0 und n eine natürliche Zahl. Dann gilt ln(xn ) = n ln(x).
Wie (43) zeigt ist die Ableitung des Logarithmus’ stets positiv. Aus Korollar 13.10 folgt also, daß die
Funktion ln(x) streng monoton wachsend ist. Insbesondere gilt z.B. ln(2) > 0. Aus Korollar 15.2 folgt
außerdem, daß ln(2n ) = n · ln(2). Der Logarithmus ln(x) nimmt also für hinreichend große x beliebig
große Werte an. Weil entsprechend ln(1/2) < 0 und ln((1/2)n ) = n ln(1/2), nimmt ln(x) für kleine
x > 0 auch beliebig kleine (negative) Werte an. Nach dem Zwischenwertsatz ist ln : R>0 → R somit eine
bijektive Abbildung.
Folglich hat ln : R>0 → R eine Umkehrfunktion. Wir bezeichnen sie mit exp : R → R>0 und
nennen sie die Exponentialfunktion. Aus (44) folgt, daß exp(0) = 1. Ferner folgt aus (15.1), daß
exp(x + y) = exp(x) · exp(y)
für alle x, y ∈ R.
(45)
Aus (43) und dem Satz über die Umkehrfunktion folgt, daß die Funktion exp differenzierbar ist mit Ableitung
d
exp(x) = exp(x).
dx
Der Wert der Funktion x 7→ exp(x) an der Stelle x = 1 spielt eine besondere Rolle und wird die
eulersche Zahl genannt:
e = exp(1).
Man kann ausrechnen, daß
e = 2, 718 . . . .
Aus (45) folgt, daß für jede natürliche Zahl n gilt
en = exp(n).
(46)
Wir nehmen die Gleichung (46) zum Anlass, um die Potenz ex für jedes reelle x einzuführen: wir definieren
ex = exp(x)
für x ∈ R.
Noch allgemeiner definieren wir für a > 0, x ∈ R
ax = exp(x · ln(a)).
Insbesondere definieren wir
√
a = a1/2 .
Analog definieren wir für b > 1 noch den Logarithmus zur Basis b durch
logb (x) =
ln x
.
ln b
Diese Definitionen stellen sicher, daß für jedes b > 1 und jedes x ∈ R gilt
logb (bx ) = x.
Aus unsere Definition der Potenz folgt die folgende nützliche Rechenregel.
16
DIE TRIGONOMETRISCHEN FUNKTIONEN
46
Lemma 15.3 Sei q ∈ R \ {0}. Die Funktion f : R>0 → R, x 7→ xq hat die Ableitung f 0 (x) = qxq−1 .
Beweis. Mit der Kettenregel erhalten wir
f 0 (x) =
d
d
q
exp(q · ln x) = exp(q · ln x) ·
q · ln(x) = xq · = qxq−1 ,
dx
dx
x
2
wie behauptet.
16
Die trigonometrischen Funktionen
Wie im vorherigen Abschnitt tun wir so, also ob wir noch nichts über die trigonometrischen Funktionen
sin, cos, tan etc. gehört hätten. Wir wollen diese Funktionen mit Hilfe der Differential- und Integralrechnung definieren. Wir beginnen mit dem Arcustangens:
Z x
1
dy.
arctan : R → R,
x 7→
2
0 1+y
Weil seine Ableitung strikt positiv ist, ist arctan(x) streng monoton wachsend. Außerdem folgt aus der
Definition unmittelbar, daß
arctan(−x) = − arctan(x) und
arctan(0) = 0.
(47)
Mit Hilfe des Arcustangens können wir eine Zahl einführen, die eine ganz besondere Rolle spielt: wir
definieren
π = 4 · arctan(1) = 3, 1415 . . . .
Lemma 16.1 Für alle x > 0 gilt arctan(x) + arctan(1/x) = π/2.
Beweis. Mit der Kettenregel erhalten wir für x > 0
1
1
1
d
[arctan(x) + arctan(1/x)] =
− 2·
= 0.
dx
1 + x2
x 1 + (1/x)2
Also gilt für alle x > 0, daß arctan(x) + arctan(1/x) = 2 arctan(1) = π/2.
2
Korollar 16.2 Für alle x ∈ R gilt arctan(x) ∈ (−π/2, π/2). Genauer ist die Abbildung
arctan : R → (−π/2, π/2),
x 7→ arctan(x)
bijektiv.
Die Umkehrabbildung des Arcustangens nennen wir den Tangens, d.h. wir definieren
tan : (−π/2, π/2) → R,
x 7→ arctan−1 (x).
Wir setzen tan zu einer Funktion R → R fort, indem wir definieren
tan(x + k · π) = tan x
für k ∈ Z.
Aus (47) folgt
tan(−x) = − tan(x)
für alle x ∈ R.
Außerdem liefert der Satz über die Umkehrfunktion, daß
d
tan(x) = 1 + tan2 (x).
dx
(48)
17
TAYLORENTWICKLUNG
47
Mit Hilfe des Tangens’ können wir nun Sinus und Cosinus definieren: für x ∈ (−π/2, π/2) sei
1
cos(x) = p
,
1 + tan2 (x)
tan(x)
sin(x) = p
.
1 + tan2 (x)
Wir definieren ferner cos(−π/2) = cos(π/2) = 0, sin(−π/2) = −1 und sin(π/2) = 1. Ferner setzen wir
cos, sin zu Funktionen R → [0, 1] fort durch
cos(x + k · π) = (−1)k cos(x),
sin(x + k · π) = (−1)k sin(x)
(x ∈ [−π/2, π/2], k ∈ Z).
Aus (48) erhält man, daß
d
cos(x) = − sin(x),
dx
d
sin(x) = cos(x).
dx
Außerdem
überlegt man sich mit Hilfe der Definition (und des Zwischenwertsatzes) leicht, daß es zu jedem
Punkt xy ∈ R2 mit x2 + y 2 genau eine Zahl a ∈ [−π, π) gibt, so daß
x
cos(a)
=
.
y
sin(a)
Diese Beobachtung kann man benutzen, um die Umkehrabbildungen arccos : [−1, 1] → [0, π], arcsin :
[−1, 1] → [−π/2, π/2] einzuführen.
17
Taylorentwicklung
Wir haben die Ableitung eingführt: zu einer Funktion f : (a, b) → R, die auf dem gesamten Intervall (a, b)
differenzierbar ist, erhalten wir eine Funktion f 0 : (a, b) → R. Diese Funktion ist nicht notwendigerweise
differenzierbar (und in der Tat womöglich nicht einmal stetig). Aber wenn sie es ist, kann man sie wiederum
differenzieren und erhält eine weitere Funktion f 00 : (a, b) → R. Diese nennen wir die zweite Ableitung
von f . Induktiv kann man auf diese Art selbstverständlich auch die dritte, vierte, . . . Ableitung definieren.
Allgemein bezeichnen wir die k-te Ableitung von f durch f [k] . Wir nennen f k-mal stetig differenzierbar,
wenn die Ableitungen f [1] , . . . , f [k] existieren und f [k] : (a, b) → R eine stetige Funktion ist.
Wie wir gesehen haben, stellt die Ableitung f 0 eine “lokale Approximation” von f durch eine lineare
Funktion dar:
f (x + h) = f (x) + hf 0 (x) + h · r(h),
wobei lim r(h) = 0.
h→0
Können wir mit Hilfe der höheren Ableitungen von f eine noch genauere lokale Approximation erhalten?
Sei f : (a, b) → R eine k-mal differenzierbare Funktion und x ∈ (a, b). Wir definieren das k-te
Taylorpolynom von f im Punkt x als
t(y) = f (x) +
k
X
f [j] (x)
j=1
j!
· yj .
Wie man leicht nachrechnet gilt
t(0) = f (x),
t[j] (0) = f [j] (x) für 1 ≤ j ≤ k.
Mit anderen Worten: die ersten k Ableitungen von t im Punkt 0 stimmen mit den ersten k Ableitungen von
f im Punkt x überein. Die folgende Aussage quantifiziert, wie gut das Taylorpolynom t die Funktion f
approximiert.
Satz 17.1 (“Taylor-Formel”) Angenommen die Funktion f : (a, b) → R ist (k + 1)-mal stetig differenzierbar. Sei t das k-te Taylorpolynom von f im Punkt x ∈ (a, b), und sei z ∈ (a, b). Dann gibt es ein
a ∈ [0, 1], so daß
f (z)
=
t(z − x) +
f [k+1] (y)
· (z − x)k+1 ,
(k + 1)!
wobei y = (1 − a) · x + a · z.
17
TAYLORENTWICKLUNG
48
Der Beweis der Taylor-Formel geht über den Rahmen dieser Vorlesung hinaus. Wir sehen stattdessen einige wichtige Beispiele. Die Ableitung der Exponentialfunktion exp(x) ist, wie wir in Abschnitt 15
gesehen haben, einfach die Exponentialfunktion selbst, d.h. exp0 (x) = exp(x). Folglich ist die Exponentialfunktion k-mal differenzierbar für jede natürliche Zahl k; man sagt, sie ist beliebig oft differenzierbar.
Ferner ist exp(0) = 1. Das k-te Taylorpolynom im Punkt x = 0 ist also
tk (y) = exp(0) +
k
X
exp(0)
j!
j=1
· yj =
k
X
yj
j=0
j!
,
mit der Konvention, daß y 0 = 1 für alle y. Mit Satz 17.1 erhalten wir nun
Proposition 17.2 Für jede reelle Zahl y gilt
exp(y) =
∞
X
yj
j=0
.
j!
Beweis. Satz 17.1 zeigt, daß für jedes y ∈ R
exp(y)
= tk (y) + rk (y),
wobei
exp(ak · y) k+1
rk (y) =
·y
,
für ein ak ∈ [0, 1].
(k + 1)!
Unser Ziel ist, zu zeigen, daß exp(y) = limk→∞ tk (y). Das bedeutet, wir müssen zeigen, daß
lim rk (y)
k→∞
=
0.
(49)
Sei dazu l die kleinste natürliche Zahl, die größer als |y| ist. Dann können wir rk (y) für k > l großzügig
abschätzen durch
|rk (y)| ≤ exp(l)
lk−l
lk+1
exp(l)ll+1
≤ exp(l)ll+1 · Qk
= Qk
.
j
(k + 1)!
j=l+1 j
j=l+1
(50)
l
Der Zähler des letzten Ausdrucks ist unabhängig von k. Andererseits wird für große k der Nenner in (50)
auch beliebig groß. Also folgt (49) aus (50).
2
Die trigonometrischen Funktionen sin, cos lassen eine ganz ähnliche Reihenentwicklung zu. Weil
sin0 (x) = cos(x) und cos0 (x) = − sin(x),
erhalten wir
[k]
cos (0) =
(−1)k/2
0
falls k gerade ist,
falls k ungerade ist.
Das 2k-te Taylorpolynom von cos(x) im Punkt 0 lautet also
k
X
(−1)j
j=0
(2j)!
· y 2j ,
mit der Interpretation, daß y 0 = 1 für alle y. Entsprechend erhält man
(−1)(k−1)/2 falls k ungerade ist,
[k]
sin (0) =
0
falls k gerade ist.
Das (2k + 1)-te Taylorpolynom von sin(x) im Punkt 0 ist also
k
X
(−1)2j+1
j=0
(2j + 1)!
· y 2j+1 .
17
TAYLORENTWICKLUNG
49
Abbildung 3: die Taylorpolynome t2 (x), t4 (x), t6 (x), t8 (x) im Punkt 0 (rot, von links oben nach rechts
unten) der Funktion cos(x) (blau, gepunktet).
Proposition 17.3 Für jede reelle Zahl y gilt
cos(y) =
∞
X
(−1)j
j=0
(2j)!
· y 2j ,
sin(y) =
∞
X
(−1)j
· y 2j+1 .
(2j
+
1)!
j=0
Der Beweis von Proposition 17.3 beruht auf einem ähnlichem Arugment wie der von Proposition 17.2;
wir verzichten auf die Details. Abbildung 3 zeigt, wie die Taylorentwicklung uns immer bessere Approximationen an die Funktion cos(x) beschert.
Wenn wir uns an die imaginäre Einheit i erinnern, ergibt sich zwischen den Reihendarstellungen von
exp(x), cos(x), sin(x) ein interessanter Zusammenhang: weil i2 = −1, erhalten wir für y ∈ R
exp(iy)
=
cos(y) + i sin(y).
(51)
Weil
exp(i(y1 + y2 )) = exp(iy1 ) · exp(iy2 ),
(52)
18
FOURIERREIHEN
50
kann man mit Hilfe von (51) Zusammenhänge zwischen den trigonometrischen Funktionen herleiten, die
sogenannten “Additionstheoreme”.
Bemerkung 17.4 Um der Argumentation im vorherigen Absatz zu folgen, müßte man genaugenommen den
Konvergenzbegriff für komplexe Zahlen einführen. Das ist kein Problem: in allen Definitionen wird einfach
der reelle Betrag durch den komplexen ersetzt. Wir verzichten auf eine detaillierte Diskussion ebenso wie
auf den Beweis von (52).
18
Fourierreihen
Viele Funktionen lassen sich besser durch die trigonometrischen Funktionen sin(x), cos(x) approximieren als durch Polynome wie in der Taylorentwicklung. Diese Approximation durch Fourierreihen spielt
insbesondere in der Signalverarbeitung eine Rolle, in der Funktionen auftreten, die Überlagerungen von
Schwingungen sind (z.B. ein Audiosignal). Dieses Kapitel ist angelehnt an [4, Kapitel 23].
Um Fourierreihen einzuführen, ist es sinnvoll, das Integral von Funktionen f : R → C mit Werten in
den komplexen Zahlen zu definieren. Weil sich jede komplexe Zahl schreiben läßt als x + iy, kann man f
zerlegen in der Form
f (x) = g(x) + ih(x)
mit g, h : R → R.
Naheliegenderweise nennen wir f integrierbar, wenn g und h integrierbar sind. In diesem Fall definieren
wir
Z b
Z b
Z b
f (x)dx =
g(x)dx + i
h(x)dx.
a
a
a
Insbesondere ist also f integrierbar, wenn g und h stückweise stetig sind; in diesem Fall nennen wir f
selbst stückweise stetig.
Beispiel 18.1 Sei t ∈ R \ {0}. Die Funktion f : R → C, x 7→ exp(itx) = cos(tx) + i sin(tx) ist
integrierbar. Ihr Integral ist
Z b
1
i
i
exp(itx)dx = − [exp(itb) − exp(ita)] = [sin(tb) − sin(ta)] + [cos(ta) − cos(tb)] .
t
t
t
a
R 2π
Insbesondere ist 0 exp(itx)dx = 0.
Angenommen f, g : [0, 2π] → C sind Funktionen, so daß die Funktion
f¯ · g : [0, 2π] → C,
x 7→ f (x) · g(x)
integrierbar ist; dies ist insbesondere dann der Fall, wenn f, g stückweise stetig sind. Dann definieren wir
Z 2π
1
hf, gi =
f (x) · g(x)dx.
2π 0
Ferner definieren wir
kf k2 =
p
hf, f i ≥ 0,
sofern f¯ · f integrierbar ist. Der Beweis der folgenden Rechnenregeln ergibt sich unmittelbar aus den
Definitionen.
Proposition 18.2 Angenommen die Funktionen f, g, h : [0, 2π] → C sind stückweise stetig und a ∈ C.
Dann gilt folgendes.
1. hf + g, hi = hf, hi + hg, hi und hf, g + hi = hf, gi + hf, hi.
2. ha · f , hi = ā hf, hi und hf, a · hi = a hf, hi.
3. hf, hi = hh, f i.
18
FOURIERREIHEN
51
4. ka · f k2 = |a| · kf k2 .
5. kf + gk2 ≤ kf k2 + kgk2 .
Man nennt kf k2 die Norm von f . Wenn f : [0, 2π] → C eine Funktion ist und wenn zu jeder natürlichen Zahl Fn : [0, 2π] → C eine Funktion ist, so daß
lim kf − Fn k2 = 0,
n→∞
dann sagt man, die Folge von Funktionen (Fn )n∈N konvergiert gegen f im quadratischen Mittel.
Der Hauptgegenstand dieses Abschnittes sind Funktionen, die eine besondere Eigenschaft haben: eine
Funktion f : [0, 2π] → C heißt periodisch, falls f (2π) = f (0). Ein Beispiel ist die Funktion
ek : [0, 2π] → C,
x 7→ exp(ikx)
für jedes k ∈ Z.
Unser Ziel ist, eine gegebene Funktion f : [0, 2π] → C mit Hilfe der Funktionen ek darzustellen. Wir
beginnen mit der folgenden Beobachtung.
Lemma 18.3 Für k, l ∈ Z gilt
hek , el i =
1
0
falls k = l,
falls k 6= l.
Beweis. Es gilt
hek , el i =
1
2π
2π
Z
exp(−ikx) · exp(ilx)dx =
0
Falls l = k, gilt exp(i(l − k)x) = 1 für alle x, somit
Falls l 6= k folgt aus Beispiel 18.1, daß hek , el i = 0.
R 2π
0
1
2π
Z
2π
exp(i(l − k)x)dx.
0
exp(i(l − k)x)dx = 2π und daher hek , el i = 1.
2
Für eine integrierbare Funktion f : [0, 2π] → R nennen wir die Zahlen
1
hek , f i =
2π
2π
Z
exp(−ikx)f (x)dx
mit k ∈ Z
0
die Fourierkoeffizienten. (Wenn f integrierbar ist, trifft dies auch auf die Funktion ēk · f zu; also macht es
Sinn, hek , f i zu schreiben.) Ferner heißt die Funktion [0, 2π] → C,
x 7→
∞
X
n
X
hek , f i · ek (x) = lim
n→∞
k=−∞
hek , f i · ek (x)
(53)
k=−n
die Fourierreihe von f .
Satz 18.4 Angenommen f : [0, 2π] → C ist integrierbar. Sei
Fn : [0, 2π] → C,
x 7→
n
X
hek , f i · ek (x).
(54)
k=−n
Dann gilt limn→∞ kf − Fn k2 = 0. Außerdem gilt
∞
X
2
hek , f i = kf k2 .
k=−∞
Satz 18.4 zeigt, daß die Fourierreihe (53) von f im quadratischen Mittel gegen f konvergiert. Das
bedeutet, daß man jede integrierbare Funktion (also insbesondere jede stückweise stetige Funktion) in
gewisser Weise durch ihre Fourierreihe “approximieren” kann.
18
FOURIERREIHEN
52
Abbildung 4: die Funktionen aus Beispiel 18.5: f (rot), F1 (blau), F3 (grün), F5 (orange).
Beispiel 18.5 Die Funktion
f : [0, 2π] → C,
x 7→
−1
1
falls x ≤ π,
falls x > π
ist eine Treppenfunktion und folglich integrierbar. Für die Funktionen Fn aus (54) rechnet man nach, daß
F1 (x)
=
F3 (x)
=
=
F5 (x)
=
=
2i
4
[exp(ix) − exp(−ix)] = − sin(x),
π π
2i 1
1
exp(3ix) + exp(ix) − exp(−ix) − exp(−3ix)
π 3
3
4
sin(3x)
−
sin(x) +
,
π
3
1
1
1
2i 1
exp(5ix) + exp(3ix) + exp(ix) − exp(−ix) − exp(−3ix) − exp(−5ix)
π 5
3
3
5
4
sin(3x) sin(5x)
−
sin(x) +
+
.
π
3
5
Abbildung 4 zeigt die Graphen der entsprechenden Funktionen.
Beispiel 18.5 zeigt, daß die Funktionswerte Fn (x) aus (54) nicht notwendigerweise in jedem Punkt x ∈
[0, 2π] gegen die Funktion f konverigeren. Das überrascht kaum, denn die Funktionen Fn sind periodisch,
was auf f nicht zuzutreffen braucht (und in Beispiel 18.5 nicht zutrifft).
Allerdings kann man unter gewissen Annahmen an die Funktion f eine “bessere” Art von Konvergenz
erhalten. Angenommen f : [0, 2π] → C und Fn : [0, 2π] → C, n ∈ N, sind Funktionen. Wir sagen, die
Folge von Funktionen (Fn )n∈N konvergiert gleichmäßig gegen f , wenn
lim
sup |f (x) − Fn (x)| = 0.
n→∞ x∈[0,2π]
Insbesondere muß also für alle x ∈ [0, 2π] gelten, daß limn→∞ Fn (x) = f (x).
Satz 18.6 Angenommen die Funktion f : [0, 2π] → C ist stetig differenzierbar und periodisch. Dann
konvergiert die Funktionenfolge (Fn )n∈N aus (54) gleichmäßig gegen f .
19
AUSBLICK: DIFFERENTIALRECHNUNG IM RN
53
Abbildung 5: die Funktionen aus Beispiel 18.7: f (rot), F1 (blau), F2 (grün), F3 (orange).
Beispiel 18.7 Sei f : [0, 2π] → C die Funktion x 7→ (x − π)2 . Man rechnet nach, daß
F1 (x)
=
F2 (x)
=
=
F3 (x)
=
=
π2
π2
+ 2 exp(−ix) =
+ 4 cos(x),
3
3
1
π2
1
exp(2ix) + 2 exp(ix) +
+ 2 exp(−ix) + exp(−2ix)
2
3
2
π2
+ 4 cos(x) + cos(2x),
3
2
1
π2
1
2
exp(3ix) + exp(2ix) + 2 exp(ix) +
+ 2 exp(−ix) + exp(−2ix) + exp(−3ix)
9
2
3
2
9
π2
4
+ 4 cos(x) + cos(2x) + cos(3x).
3
9
2 exp(ix) +
Abbildung 5 zeigt die Graphen der entsprechenden Funktionen.
Die Beweise von Satz 18.4 und 18.6 gehen über den Rahmen der Vorlesung hinaus. Der interessierte
Leser sei auf [4, Kapitel 23] verwiesen, wo sich auch weiteres Material zu Fourierreihen findet.
19
Ausblick: Differentialrechnung im Rn
Bisher haben wir uns mit Funktionen f : X → R von einer Teilmenge X ⊂ R in die reellen Zahlen
befaßt. Häufig treten aber auch Funktionen f : X → Rm von einer Teilmenge X ⊂ Rn in den Rm auf.
Wie können wir die Ableitung für solche Funktionen einführen?
Zunächst beobachten wir, daß die Funktion f : X → Rm in einzelne Funktion fi : X → R, i =
1, . . . , m, zerlegt werden kann. Denn f bildet jeden Punkt x ∈ X auf einen m-dimensionalen Vektor


f1 (x)
 .. 
 . 
fm (x)
ab.
19
AUSBLICK: DIFFERENTIALRECHNUNG IM RN
54
Abbildung 6: die Funktion aus Beispiel 19.1.
Sei nun x ∈ X. Zu jeder Zahl j = 1, . . . , n betrachten wir die Menge Xj,x aller u ∈ R, so daß


x1
xj,u
 .. 
 . 


xj−1 


=  u  ∈ X.
x 
 j+1 
 . 
 .. 
xn
(In Worten: wir können die j-te Koordinate durch u ersetzen, ohne die Menge X zu verlassen.) Dann
erhalten wir zu jedem i ∈ {1, . . . , m}, x ∈ X und j ∈ {1, . . . , n} eine Funktion
fi,j,x : Xj,x → R,
u 7→ fi (xj,u ).
Falls diese Funktion differenzierbar ist im Punkt xj , nennen wir ihre Ableitung die partielle Ableitung von
fi nach xj im Punkt x, geschrieben als
∂fi
0
(x) = fi,j,x
(xj ).
∂xj
Die partielle Ableitung erhält man also, indem man fi nach der j-ten Variable xj differenziert und die
anderen Variablen xh , h 6= j, als Konstanten betrachtet. Sofern alle Ableitungen existieren, nennt man die
m × n-Matrix
∂fi
(x)
Df (x) =
∂xj
i=1,...,m;j=1,...,n
die Jacobimatrix von f im Punkt x.
Wir haben gelernt, uns die Ableitung einer Funktion als Approximation der Funktion durch eine lineare
Abbildung vorzustellen. Das Konzept der Jacobimatrix paßt sehr gut in diese Vorstellung, weil eine Matrix
ja nichts andere als eine lineare Abbildung ist. Die Abbildung, Df : x 7→ Df (x), die einem Punkt x die
Jacobimatrix von f im Punkt x zuordnet (sofern diese existiert), nennen wir die Ableitung von f .
Beispiel 19.1 Die Funktion f : R2 → R sei definiert durch f xx12 = sin(x1 · x22 ). Ihre partiellen Ableitungen sind
∂f
∂f
= x22 · cos(x1 · x22 ),
= 2x1 x2 · cos(x1 · x22 ).
∂x1
∂x2
19
AUSBLICK: DIFFERENTIALRECHNUNG IM RN
55
Die Jacobimatrix ist also die 1 × 2-Matrix
Df (x) = (x22 · cos(x1 · x22 )
2x1 x2 · cos(x1 · x22 )).
Der Graph der Funktion für x1 , x2 ∈ [−2, 2] ist in Abbildung 6 skizziert.
Viele der Aussagen und Zusammenhänge, die wir in der “eindimensionalen” Differentialrechnung kennengelernt haben, lassen sich auf den mehrdimensionalen Fall verallgemeinern. Auch höhere Ableitungen
lassen sich einführen und die Taylorformel hat eine mehrdimensionale Verallgemeinerung. Details dazu
finden sich etwa in [2].
Als Anwendung der mehrdimensionalen Differentialrechung betrachten wir sogenannte “lineare dynamische Systeme”; der folgende Text folgt dem (englischen) Wikipedia-Artikel zu diesem Thema1 . Sei also
f : [0, 1] → Rn eine Funktion vom Ein- ins Mehrdimensionale. Wir können uns f als eine Kurve im Raum
vorstellen. Sei ferner A eine n × n-Matrix. Angenommen es gilt
Df (t) = A · f (t)
(55)
für alle t ∈ [0, 1]. Was können wir dann über f aussagen?
Angenommen die Matrix A hat eine Orthonormalbasis v1 , . . . , vn bestehend aus Eigenvektoren mit
den Eigenwerten k1 , . . . , kn . Dann können wir jeden Funktionswert f (t) schreiben als
f (t) =
n
X
ei (t) · vi
(56)
i=1
mit ei : [0, 1] → R. Differenzieren von f ergibt
Df (t) =
n
X
e0i (t) · vi ,
(57)
i=1
weil die Vektoren vi ja nicht von t abhängen. Setzt man ferner (56) in A · f (t) ein, so erhält man
A · f (t) =
n
X
ei (t) · ki vi .
(58)
i=1
Aus (55), (57) und (58) folgt also
n
X
e0i (t)
· vi =
i=1
n
X
ei (t) · ki vi .
(59)
i=1
Weil die Vektoren v1 , . . . , vn eine Basis bilden, zeigt (59)
e0i (t) = ki ei (t)
für i = 1, . . . , n.
(60)
Aufgrund unserer Kenntnis der Exponentialfunktion sehen wir also, daß
ei (t) = ci · exp(ki t)
(61)
für gewisse c1 , . . . , cn ∈ R. Setzen wir t = 0 in (61) ein, so ergibt sich
ci = ei (0) für i = 1, . . . , n.
Die Zahlen ci sind also durch die sogenannte “Anfangsbedingung” f (0) bestimmt. Umgekehrt erlaubt die
obige Herleitung die Lösung der Gleichung (55), also das Berechnen von f , sofern die Matrix A diagonalisierbar und die Anfangsbedingung f (0) bekannt ist.
1 http://en.wikipedia.org/wiki/Linear
dynamical system
LITERATUR
Literatur
[1] T. Bröcker: Analysis 1.
[2] T. Bröcker: Analysis 2.
[3] G. Fischer: Lineare Algebra.
[4] O. Forster: Analysis 1.
[5] G. Strang: Lineare Algebra.
56